
Fuzzy Singleton Congestion Games
Litsa Alexandra and Sbabou Samir
Center of Research in Economics and Management, University of Caen, Caen, France
Keywords:
Fuzzy Singleton Congestion Games, Fuzzy Nash Equilibria, Topsis, Fuzzy Number, Weight.
Abstract:
In traditional game theory, the players attempt to maximize their utility functions. However, in real world there
are many situations where payoffs have uncertainty and are fuzzy in nature. In this paper, we analyze fuzzy
singleton congestion games with fuzzy payoff functions using tools from fuzzy set theory. We model this kind
of games and we employ the ‘technique for order performance by similarity to ideal solution’ with fuzzy data
in order to rank fuzzy payoffs, and consequently alternatives, with respect to multiple criteria. Based on this
ranking we find possible solutions of these games which correspond to fuzzy Nash equilibria. Our method is
adequate to model real-life situations, where players make more subtle decisions.
1 INTRODUCTION
Congestion games are a special class of non-
cooperative games introduced by Rosenthal in 1973.
This kind of games provides a natural frameworkfor a
wide range of economics and computer science appli-
cations such as resource allocation, routing and net-
work design problems. In Rosenthal’s model (Rosen-
thal, 1973), a set of players competes for a set of
resources and the payoff of each resource depends
only on the number of players using it. The utility
a player derives from a combination of resources is
the sum of the payoffs associated with each resource
included in his choice. A slightly different formula-
tion of congestion games was introduced by Milch-
taich in 1996 under the name of congestion games
with player-specific payoff functions. As a matter of
fact, all players are restricted to the selection of a sin-
gle resource and either they all share the same utility
function - symmetric case - or each of them has his
own payoff function - nonsymmetric case. In these
games, the specific payoff functions are decreasing to
the number of players. A key game-theoretic prop-
erty of these games is that they always admit at least
one Nash equilibrium. In this paper, we focus on con-
gestion games in the sense of Milchtaich, also called
singleton congestion games.
This kind of games can be seen as decision mak-
ing problems. In routing problems for example, each
individual has to choose a specific road to reach his
destination. Thus, he has to take a decision with re-
spect to different kinds of constraint like the time he
has to reach the destination or the cost of his trip. The
latter aspect calls for multiple criteria. A process of
decision making, consisting in deriving the best op-
tion from a feasible set, is present in just about every
conceivable human task. However, the basic model
of a decision in the classical decision theory has very
little in common with the real decision making as all
information is supposed to be precisely known - crisp
data. The only componentin which uncertainty is per-
mitted is the occurrence of the different states of na-
ture, for which probabilistic descriptions are allowed.
Nevertheless, when the uncertainty is of qualitative
nature, the use of other techniques is necessary. Fuzzy
set theory, introduced by Zadeh in 1965, provide the
flexibility needed to represent the uncertainty resulted
from the lack of knowledge.
In the context of congestion games, the outcomes
faced by the players cannot be known in a precise
manner as human judgements are often vague. In
other words, it is difficult to have strict values of pay-
offs, because players are sometimes not able to ana-
lyze certain data of a game and as a result, their infor-
mation is not complete. In this work, inspired by the
theory of ordinal singleton congestion games and the
fact that the decisions made by rational players may
be imprecise because of players’ doubts, we model
fuzzy singleton congestion games. The payoff func-
tions of players are represented as triangular fuzzy
numbers - which allow to consider the uncertainty as-
sociated with the mapping of human perception on a
number - and the importance weights of various crite-
ria are assessed by means of linguistic variables. But
377
Alexandra L. and Samir S..
Fuzzy Singleton Congestion Games.
DOI: 10.5220/0004106803770382
In Proceedings of the 4th International Joint Conference on Computational Intelligence (FCTA-2012), pages 377-382
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

the question is how we can establish a preference or-
dering of alternatives knowing that the payoff func-
tions arefuzzy. To do so, we use the ‘Technique for or-
der performance by similarity to ideal solution’ (TOP-
SIS) method with fuzzy data, introduced by Chen in
2000. In order to provide a complete analysis of such
games, we firstly rank the choice of alternatives of all
players and afterwards, we examine the existence of
equilibria.
This paper is arranged into five sections. In sec-
tion 2 we present some basic definitions and no-
tations concerning singleton congestion games and
fuzzy sets. The intent of section 3 is to introduce
fuzzy singleton congestion games and to provide the
TOPSIS procedure with fuzzy data which leads us to
the presentation of fuzzy Nash equilibria in this kind
of games. A numerical example is used to illustrate
the feasibility of our model in section 4. The last sec-
tion concludes.
2 PRELIMINARIES
2.1 Background of Singleton
Congestion Games
Monotone singleton congestion games (singleton
congestion games for short) are defined by a tuple
Γ(N, R, (d
i,r
)
i∈N,r∈R
), where N = {1, . . . , n} is a set of
n players, R = {1, . . . , m} is a set of m resources and
d
i,r
: {1, . . .,m} → R is a non-increasing payoff func-
tion associated with resource r. Let S
i
be a finite set
of strategies available to player i and σ = (σ
i
)
i∈N
its
elements, called strategy profiles. For a profile σ and
a resource r, the congestion on r, i.e. the number of
players using r, is defined by n
r
(σ) = |{ i ∈ N : r ∈
σ
i
}|. The vector (n
1
(σ), . . . , n
m
(σ)) is the congestion
vector corresponding to σ.
In this kind of games each player is allowed to
choose any resource from R but must choose only
one. Thus, a player’s strategy consists of a single re-
source in R. Since the utility an anonymous player
derives from selecting a single resource depends only
on the number of the players doing the same choice,
the utility function is a mapping u : R× N → R, with
(r, n
r
(σ)) 7→ u(r, n
r
(σ)), where u decreases with the
number of players sharing the same resource r. The
utility of player i for a profile σ is given by u
i
(σ) =
d
i,r
(n
r
(σ)), with r ∈ σ
i
.
We should not forget that in a singleton conges-
tion game all data is given in crisp values and the aim
is to obtain a decreasing order of preferences for each
player or, in other words, a ranking of payoffs, which
leads us to identify all possible solutions of the game.
The approach of Milchtaich (Milchtaich, 1996) en-
ables to do so and leads to the conclusion that such
games admit at least one Nash equilibrium.
However, crisp data are inadequate to model real-
life situations since it is impossible to have a pre-
cise estimation of the payofffunctions obtained by the
players and the human perception of criteria is often
expressed linguistically.
Thus, a fuzzy approach is provided in this article
to examine such cases. More precisely, we introduce
a new class of games namely, the fuzzy singleton con-
gestion games where the data are fuzzy when players
have to make a decision on the congestion they have
to choose. Before going over our analysis, we need
the following basic definitions.
2.2 Concepts from Fuzzy Set Theory
The earliest formulation of the concepts of fuzzy sets
is due to Zadeh (Zadeh, 1965) who generalized the
idea of a crisp set by extending the range of its char-
acteristic function. Actually, he considered that the
latter can take any value in the interval [0, 1].
Let X be a set of objects whose generic elements
are denoted by x. The membership in a crisp subset
of X is a characteristic function µ
Φ
from X to {0, 1}
such that:
µ
Φ
=
1 if and only if x ∈ Φ,
0 otherwise,
where {0, 1} is called a valuation set. If the latter
is the interval [0, 1], Φ is called a fuzzy set and is
denoted by
e
Φ. We say that µ
e
Φ
(x) is the degree of
membership of x in
e
Φ.
Definition 1. If
e
Φ is a fuzzy set, then
e
Φ
is characterized by the set of ordered pairs:
e
Φ = {(x, µ
e
Φ
(x))|x ∈ X}.
Definition 2. A fuzzy set
e
Φ of the universe of
discourse X is convex if and only if for all x
1
, x
2
in X,
µ
e
Φ
(λx
1
+ (1 − λ)x
2
) ≥ min(µ
e
Φ
(x
1
), µ
e
Φ
(x
2
)), where
λ ∈ [0, 1].
Definition 3. The height of a fuzzy set is the largest
membership grade attained by any element in that
set. A fuzzy set
e
Φ in the universe of discourse X is
called normalized when the height of
e
Φ is equal to 1,
i.e. ∃x ∈ X such that µ
e
Φ
(x) = 1.
Definition 4. A fuzzy number is a fuzzy subset in
the universe of discourse X that is both convex and
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
378
normal.
Definition 5. The α-cut of a fuzzy number ea is
defined ea
α
= {x|µ
ea
(x) ≥ α, x ∈ X}, where α ∈ [0, 1].
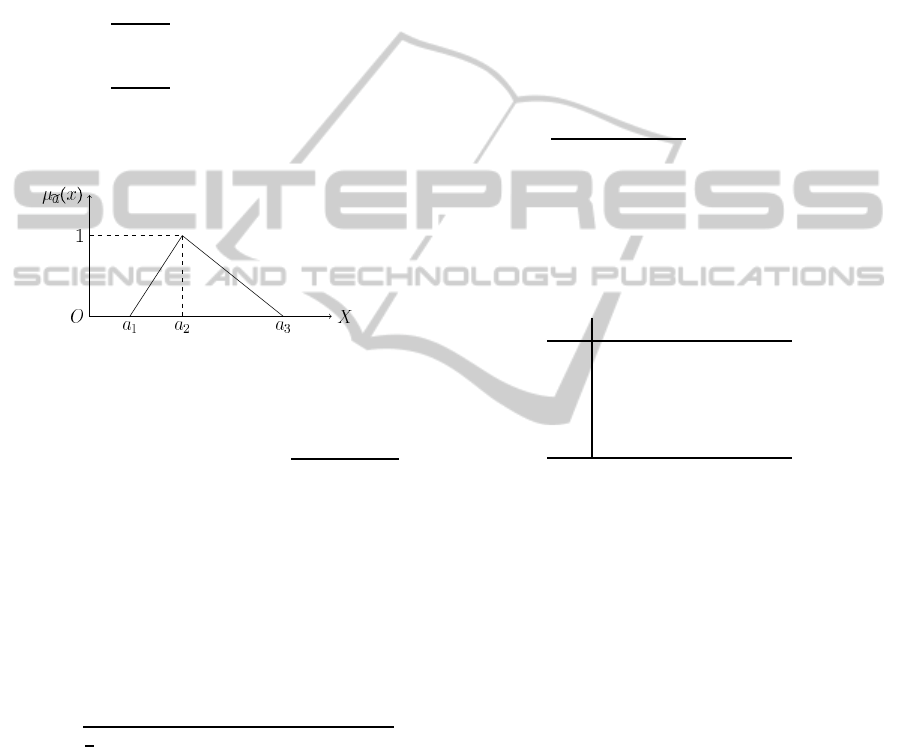
Definition 6. A triangular fuzzy number ea is defined
by a triplet (a
1
, a
2
, a
3
) shown in Figure 1. The mem-
bership function µ
ea
(x) is defined as :
µ
ea
(x) =
0, x < a
1
,
x− a
1
a
2
− a
1
, a
1
≤ x ≤ a
2
,
x− a
3
a
2
− a
3
, a
2
≤ x ≤ a
3
,
0, x > a
3
.
Figure 1: Fuzzy triangular number.
Definition 7. The graded mean integration rep-
resentation of a given a triangular fuzzy number
ea = (a
1
, a
2
, a
3
) is defined as : P(ea) =
a
1
+ 4a
2
+ a
3
6
.
In this paper, without loosing integrity and just
to simplify the calculations, we assume that the
fuzzy triangular numbers are symmetric and their
corresponding crisp value is given by the graded
mean integration representation.
Definition 8. Let ea = (a
1
, a
2
, a
3
) and
e
b = (b
1
, b
2
, b
3
) be two triangular fuzzy num-
bers. Then the distance between them can
be calculated by using the vertex method :
δ(ea,
e
b) =
q
1
3
[(a
1
− b
1
)
2
+ (a
2
− b
2
)
2
+ (a
3
− b
3
)
2
].
Definition 9. A linguistic variable is a variable whose
values are expressed in linguistic terms.
The concept of a linguistic variable is very useful
in dealing with situations, which are too complex or
not well defined to be reasonably described in conven-
tional quantitative expressions. For example, ‘weight’
is a linguistic variable whose values are : very low,
low, medium, high, very high, etc. These values can
also be represented by fuzzy numbers.
3 FUZZY SINGLETON
CONGESTION GAMES
Fuzzy noncooperative games were first developed by
Butnariu (Butnariu, 1978) and later refined by Billot
(Billot, 1992). In their formulation each player’s be-
liefs about the actions of the other players are mod-
eled as fuzzy sets. Inspired by their approach, we
define fuzzy singleton congestion games by a tuple
e
Γ(N, R, (
e
d
i,r
)
i∈N,r∈R
), where N = {1, . . . , n} is a set of
players, R = {1, . . . , m} is a set of resources and
e
d
i,r
is a fuzzy non-increasing payoff function associated
with resource r, expressed by a triangular fuzzy num-
ber (a
1
ir
, a
2
ir
, a
3
ir
) and such that its defuzzified value
is given by
a
1
ir
+ 4a
2
ir
+ a
3
ir
6
.
As for ordinal singleton congestion games, the
utility function decreases with the number of players
sharing the same resource and for a given profile σ is
given by eu
i
(σ) =
e
d
i,r
(n
r
(σ)), with r ∈ σ
i
.
A fuzzy singleton congestion game can be repre-
sented by the following fuzzy decision matrix:
1 2 ... m
C
1
e
d
11
e
d
12
...
e
d
1m
C
2
e
d
21
e
d
22
...
e
d
2m
.
.
.
C
n
e
d
n1
e
d
n2
...
e
d
nm
with
e
W = [ ew
1
, ew
2
, . . . , ew
n
].
This means that there are m resources among
which a player has to choose. Each resource is eval-
uated through n criteria C
i
(i = 1, . . . , n) which corre-
spond to the congestion vector n
r
(σ), i.e. the number
of players choosing a resource. The element
e
d
ir
repre-
sents the rating of resource r with respect to criterion
C
i
, that is to say the payoff function associated with r.
Each player in the game may judge how im-
portant a criterion is. The weighting vector
e
W =
[ ew
1
, ew
2
, . . . , ew
n
], with ew
i
= { ew
1
i
, ..., ew
m
i
}, represents
the relative importance of n criteria C
i
. In this paper,
the importance weights of various criteria are consid-
ered as linguistic variables. These variables can be
expressed in triangular fuzzy numbers as shown in Ta-
ble 1.
Given the fuzzy decision matrix and the fuzzy
weighting vector
e
W, the objective is to rank all the
resources with respect to all criteria, so as to obtain
a decreasing order of preferences for each player and
identify possible solutions of fuzzy singleton conges-
tion games. At this point, the following question is
raised. How can we rank fuzzy data? The best way to
FuzzySingletonCongestionGames
379

do so in our context is to apply the TOPSIS procedure
with fuzzy data proposed by Chen (Chen, 2000).
Table 1: Linguistic variables for the importance weight of
each criterion.
Very Low (VL) (0, 0, 0.2)
Low (L) (0.1, 0.2, 0.3)
Medium Low (ML) (0.2, 0.35, 0.5)
Medium (M) (0.4, 0.5, 0.6)
Medium High (MH) (0.5, 0.65, 0.8)
High (H) (0.7, 0.8, 0.9)
Very High (VH) (0.8, 1, 1)
3.1 Topsis Procedure with Fuzzy Data
At the beginning, resources should be generated and
criteria should be identified. Then, the following steps
are carried out.
Step 1: Construct the fuzzy decision matrix
e
D. Let
e
d
ir
= (a
1
ir
, a
2
ir
, a
3
ir
) be a triangular fuzzy number
such that its defuzzified value is given by d
ir
=
a
1
ir
+ 4a
2
ir
+ a
3
ir
6
, for all i = 1, 2, . . . , n and r =
1, 2, . . . , m.
Step 2: Choose the appropriate linguistic variables
to evaluate the importance weight of each criterion
1
.
These linguistic variables can be expressed in positive
triangular fuzzy numbers as in Table 1.
Step 3: Construct the normalized fuzzy decision ma-
trix
e
Z = [ez
ir
]
n×m
, where, for B and C being the set of
benefit and cost criteria, respectively, we have
ez
ir
= (
a
1
ir
a
3
i
,
a
2
ir
a
3
i
,
a
3
ir
a
3
i
), with a
3
i
= max
r
a
3
ir
when i ∈ B
or
ez
ir
= (
a
1
i
a
3
ir
,
a
1
i
a
2
ir
,
a
1
i
a
1
ir
), with a
1
i
= min
r
a
1
ir
when i ∈ C.
The normalization method mentioned above is de-
signed to preserve the property in which the elements
ez
ij
are normalized triangular fuzzy numbers that be-
long to [0, 1].
Step 4: Considering the different importance of each
criterion, construct the weighted normalized fuzzy de-
cision matrix
e
V = [eu
ir
]
n×m
, i = 1, 2, . . . , n and r =
1, 2, . . . , m, where eu
ir
= ez
ir
· ew
i
.
1
In our context, the utility is decreasing with the number
of players sharing a resource, i.e. the criteria, and so the
respective importance weights.
Step 5: All elements eu
ir
, for all 1 ≤ i ≤ n and
1 ≤ r ≤ m, are normalized positive triangular fuzzy
numbers and their ranges belong to [0, 1]. So, we can
determine the fuzzy positive and fuzzy negative ideal
solutions as:
e
V
+
= (eu
+
1
, . . . , eu
+
n
) and
e
V
−
= (eu
−
1
, . . . , eu
−
n
),
where eu
+
i
= (1, 1, 1) and eu
−
i
= (0, 0, 0), i = 1, 2, . . . , n.
Step 6: Calculate the distance of each resource from
the fuzzy positive and fuzzy negative ideal solution,
respectively, as :
e
δ
+
ir
=
e
δ(eu
ir
, eu
+
r
) and
e
δ
−
ir
=
e
δ(eu
ir
, eu
−
r
),
using the vertex method to compute the distance
between two fuzzy numbers (Definition 8).
Step 7: Calculate the relative closeness coefficient
of each resource to the ideal solution defined as :
CC
ir
=
e
δ
−
ir
e
δ
+
ir
+
e
δ
−
ir
. Since
e
δ
ir
≥ 0, clearly CC
ir
∈ [0, 1].
Step 8: According to the closeness coefficient, the
resources are ranked in descending order. The best
resource is the one with the shortest distance to the
fuzzy positive ideal solution and with the longest
distance to the fuzzy negative ideal solution.
Therefore, in a fuzzy singleton congestion game,
each player is capable to determine which resource
maximizes his satisfaction with respect to multi-
ple criteria (number of players sharing the same re-
source).
3.2 Equilibrium Analysis
It is the nature of multi-criteria decision making prob-
lems (MCDM) to have conflicting attributes (Hwang
and Yoon, 1981). We should not forget that each
alternative can be characterized by a large number of
attributes, chosen by the decision maker’s conception
of criteria. That is why, usually, there is no optimal
solution to a MCDM problem. However, there may
exist many possible efficient solutions as, in real-life
situations, players make a choice with a random
behavior and the attributes are not deterministic but
rather fuzzy/impricise. Such solutions correspond to
fuzzy Nash equilibria.
Definition 10. A strategy profile σ
∗
=
(σ
∗
1
, . . . , σ
∗
i
, . . . , σ
∗
n
) is a fuzzy Nash equilib-
rium of a fuzzy singleton congestion game
e
Γ(N, R, (
e
d
i,r
)
i∈N,r∈R
) if and only if
∀i ∈ N, ∀σ
i
, σ
∗
i
∈ S
i
, eu
i
(σ
∗
i
, σ
∗
−i
) ≥ eu
i
(σ
i
, σ
∗
−i
)
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
380

where σ
∗
−i
refers to all strategies except those chosen
by the player i.
In our setting, fuzzy Nash equilibria can be ob-
tained (Sbabou et al., 2012) by the ranking of re-
sources at the end of the TOPSIS procedure
2
.
In the coming section, an example is introduced
to illustrate the TOPSIS procedure and to show the
computation process of fuzzy Nash equilibria.
4 ILLUSTRATIVE EXAMPLE
Consider the following symmetric
3
singleton conges-
tion game, applied in a routing problem: there are
three drivers (players) who want to reach a destina-
tion and three roads (resources). Each driver chooses
the path between his origin and destination in such a
way that his utility is maximized. He must choose
only one resource and all drivers have the same utility
function which is non-increasing and depends on the
number of drivers making the same choice. The pay-
off matrix is common for all drivers and the payoff of
each of them is determined through the principle: ‘I
earn much more when I am the only person to take
this road’.
In reality, however, it is very difficult to have
the traffic situation at one’s finger tips. Human
perception and intuitive judgement play an important
role in route choices. Therefore, it is impossible to
have a precise estimation of the payoff of each driver.
Example 1. Let
e
Γ(N, R, (eu
i
)
i∈N
) be a symmetric
fuzzy singleton congestion game with N = {1, 2, 3},
R = {a, b, c} and such that 3a ≺ 2a ≺ a, 3b ≺ 2b ≺ b,
3c ≺ 2c ≺ c.
The drivers’ payoff functions can be estimated,
but not very precisely. Suppose that they have the fol-
lowing conception of the game : ‘If I choose road a
my payoff is as much as 10, if I choose b my utility
and approximately 8 and if I opt for c my utility is no
less than 9. Once I am alone on the road, it is great
for me (VH). However, sharing the road with some-
one else is less nice (H). If I share road a with one
more person my payoff is approximately 7, if both of
us choose b my payoff is at least 6, otherwise my util-
ity is no less than 7. Finally, if we are three to go from
road a my payoff is as much as 1, if we choose b my
payoff is at most 2 and if we select resource c my util-
2
For detailed information about fuzzy Nash equilibria in
noncooperative games, please refer to (Billot, 1992).
3
In a nonsymmetric singleton congestion game the pro-
cedure works in the same way.
ity is as much as 5. In this case my trip is of medium
quality (M).’
It can be easily understood that in this context
the payoff values cannot be denoted by real numbers.
However, fuzzy numbers can describe this kind of
fuzzy information as well as the importance weights
of various criteria. In Section 3 we raised the question
of how we can rank such fuzzy data and the answer
was by applying the TOPSIS procedure with fuzzy
data. The proposed method is currently applied to
the game
e
Γ and the computational procedure is dia-
grammed below.
Step 1: Construct the fuzzy decision matrix.
Driver 1/2/3
a b c
C
1
(5, 10, 15) (6, 8, 10) (7, 9, 11)
C
2
(5, 7, 9) (2, 6, 10) (5, 7, 9)
C
3
(0.5, 1, 1.5) (1, 2, 3) (3, 5, 7)
Step 2: The drivers evaluate the importance weight
of each criterion in linguistic terms and present it be-
low. Then, the linguistic evaluation is converted into
triangular fuzzy numbers according to Table 1
4
.
Driver 1/2/3
C
1
VH
C
2
H
C
3
M
Step 3: Construct the normalized fuzzy decision ma-
trix, common for all drivers
5
.
a b c
C
1
(0.33, 0.67, 1) (0.4, 0.53, 0.67) (0.47, 0.6,0.73)
C
2
(0.5, 0.7, 0.9) (0.2, 0.6, 1) (0.5, 0.7, 0.9)
C
3
(0.07, 0.14, 0.21) (0.14, 0.29, 0.43) (0.43, 0.71, 1)
Step 4: Construct the weighted normalized fuzzy de-
cision matrix.
a b c
C
1
(0.26, 0.67, 1) (0.32,0.53, 0.67) (0.38, 0.6, 0.73)
C
2
(0.35, 0.56, 0.81) (0.14, 0.48, 0.9) (0.35, 0.56, 0.81)
C
3
(0.03, 0.07, 0.13) (0.06, 0.15, 0.26) (0.17, 0.36, 0.6)
Step 5: Determine the fuzzy positive
and fuzzy negative ideal solutions as :
e
V
+
= [(1, 1, 1), (1, 1, 1), (1, 1, 1)] and
e
V
−
=
[(0, 0, 0), (0, 0, 0), (0, 0, 0)].
Step 6 & 7: Calculate the distance of each resource
from the fuzzy positive (DFP) and fuzzy negative
4
If the game was nonsymmetric each player would have
his own decision matrix and importance weight of each cri-
terion.
5
In this example we deal with benefit criteria as we make
use of utilities.
FuzzySingletonCongestionGames
381

(DFN) ideal solution, respectively, as well as the rela-
tive closeness coefficient (CC) of each resource to the
ideal solution:
(DFP) (DFN) (CC)
e
δ
+
1a
= 0.467
e
δ
−
1a
= 0.71
CC
1a
= 0.6
e
δ
+
2a
= 0.466
e
δ
−
2a
= 0.6
CC
2a
= 0.56
e
δ
+
3a
= 0.94
e
δ
−
3a
= 0.087
CC
3a
= 0.08
e
δ
+
1b
= 0.51
e
δ
−
1b
= 0.527
CC
1b
= 0.5
e
δ
+
2b
= 0.58
e
δ
−
2b
= 0.594
CC
2b
= 0.5
e
δ
+
3b
= 0.85
e
δ
−
3b
= 0.18
CC
3b
= 0.17
e
δ
+
1c
= 0.45
e
δ
−
1c
= 0.588
CC
1c
= 0.56
e
δ
+
2c
= 0.466
e
δ
−
2c
= 0.6
CC
2c
= 0.56
e
δ
+
3c
= 0.65
e
δ
−
3c
= 0.41
CC
3c
= 0.39
Step 8: Rank the resources in descending order ac-
cording to the closeness coefficient.
3a ≺ 3b ≺ 3c ≺ 2b ∼ b ≺ 2c ∼ c ∼ 2a ≺ a
The fuzzy Nash equilibria of the game, provided by
the ranking, are (2a, c) and (2c, a).
Remark: If the game were crisp, that is if we had
a common order of preferences for all players repre-
sented by 3a ≺ 3b ≺ 3c ≺ 2b ≺ 2c ∼ 2a ≺ b ≺ c ≺
a, then the Nash equilibrium of the game would be
(a, b, c). As in the proposed method payoffs are fuzzy
and we also include the players’ viewpoint of a given
situation, through the notion of the weight, Nash equi-
libria are fuzzy and we deal with them randomness,
fuzziness and uncertainties.
5 CONCLUSIONS
In this work, we have studied fuzzy singleton conges-
tion games with fuzzy payoff values. Our research
was inspired by the fact that until today, the theory of
congestion games, as most of the economic theories,
has been based on classical set theory, two-valued
logic and classical theory of additive measures, which
is not realistic in economics. Human reasoning and
decision making in natural language, which play a
crucial role in economic situations, involve a kind of
uncertainty that cannot be modeled with the use of
classical mathematics. Fuzzy set theory facilitate the
modeling of such situations but it seems that after al-
most fifty years is still at its beginning, perhaps be-
cause of the difficult incentive issues raised!
Our approach seems to have an important theoret-
ical and applicable value in many other domains such
as soft computing and resource allocations. As Klir
and Yuan mention (Klir and Yuan, 1995), for exam-
ple, in soft computing the aim is to develop computa-
tional methods that produce acceptable approximate
solutions at low cost - fuzzy hardware and computer
architectures for approximate reasoning. And the ca-
pability of communicating with robots, so as to allo-
cate them miscellaneous tasks that have to be done
as fast as possible, involves natural language, that is
fuzzy logic.
Obviously, there are still many open questions and
problems left for further research, especially as it is
the first time that a study on fuzzy congestion games is
provided. Firstly, the case where the utility decreases
with the number of players sharing the same resource
but the importance weight of each criterion goes to the
opposite direction needs to be examined. Secondly,
an experimental survey of our result would be impor-
tant in order to determine the choice of an itinerary.
Finally, we hope to extend our result to standard con-
gestion games, network design problems and resource
allocations.
REFERENCES
Billot, A. (1992). Economic Theory of Fuzzy Equilibria ;
An Axiomatic Analysis. Springer-Verlag, New York.
Butnariu, D. (1978). Fuzzy games: A description of the
concept. Fuzzy Sets and Systems, 1:181–92.
Chen, C. T. (2000). Extensions of the topsis for group
decision-making under fuzzy environment. Fuzzy Sets
and Systems, 114:1–9.
Hwang, C. L. and Yoon, K. (1981). Multiple Attribute De-
cision Making Methods and Applications. Springer,
Berlin Heidelberg.
Klir, G. J. and Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic:
Theory and Applications. Prentice-Hall Inc., USA.
Milchtaich, I. (1996). Congestion games with player-
specific payoff functions. Games and Economic Be-
havior, 13:111–124.
Rosenthal, R. (1973). A class of games possessing pure-
strategy Nash equilibrium. International Journal of
Game Theory, 2:65–67.
Sbabou, S., Smaoui, H., and Ziad, A. (2012). Nash equi-
libria in singleton congestion games: Symmetric case.
Working paper. La Reunion University.
Zadeh, L. A. (1965). Information and control. Fuzzy sets,
8:338–353.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
382
