STATISTICAL MECHANICS OF PROTEINS IN THE RANDOM

COIL STATE

Cigdem Sevim Bayrak and Burak Erman

Computational Science and Engineering Program, Koc University, 34450, Sariyer, Istanbul, Turkey

Keywords: Rotational isomeric state, Random coil, Denatured state.

Abstract: Denatured proteins are mostly partially folded and compact proteins. A statistical analysis on

thermodynamic properties is presented to describe and characterize denatured proteins. Conformational free

energy, energy, entropy and heat capacity expressions are derived using the Rotational Isomeric States

model of polymer theory. The state space and the probabilities of each state are comprised from a coil

database. Properties for the denatured state are obtained for a sample set of proteins taken from the Protein

Data Bank. Thermodynamic expressions of denatured state are derived.

1 INTRODUCTION

Random configurations of protein chains are

obtained under the constraints imposed by chain

connectivity and the torsion states of the backbone

torsion angles

and





in the absence of sequence-

distant long-range interactions. The term ‘randomly

coiled proteins’ describing this state have been

studied in detail by Flory and collaborators, based on

the Rotational Isomeric States (RIS) Model of

polymer theory (Flory, 1969); (Brant and Flory,

1965); (Brant et al., 1969); (Conrad and Flory,

1976); (Flory and Jernigan, 1965); (Rehahn et al.,

1997); (Engin et al., 2009).The RIS model for a

protein chain consists of two major components: (1)

The statistical weights of the torsion states of the

and





angles, and (2) The proper matrix

multiplication operations leading to the partition

function of the chain. Thermodynamics of the single

chain then follows upon proper matrix operations

based on the partition function and its derivatives

(Callen, 1985); (Flory, 1974). Understanding the

random configurations of proteins is important due

to several reasons: Firstly, the set of random

configurations covers all possible initial

conformations of proteins. Depending on the

primary sequence, some conformations emerge as

highly probable due to the amino acid specific

regions of the

(, )





angles. Secondly, under

strongly denaturing conditions, a wide range of

values become available to

and





, and

conformations are close to those of the random coil

(Dill and Shortle, 1991); (Tanford, 1968). These

conformations are many in number, and therefore a

statistical characterization is required to understand

the thermodynamics of the denatured state. Thirdly,

the functionally important ‘intrinsically disordered

protein’ concept where the primary sequence

prohibits the folded state, may suitably be analyzed

by the tools used to understand the random

conformations (Tompa, 2011); (Orosz and Ovádi,

2011).

Thus, a better statistical understanding of

denatured proteins is required for answering

questions referring to functional properties of

proteins. The number of states available to the

denatured chain may vary from an enormous set to

only a few in numbers as observed in switches. The

general statistical mechanical model that we adopt is

not restricted with this variation. The size of

available states is determined by the probabilities of

the latter, and several sources for such probabilities

are either available and may be extracted from

various databases, or may be generated by suitable

training techniques of bioinformatics, depending on

the constraints and requirements of the problem at

hand. In the present study, we extract the

probabilities from the Ramachandran plots obtained

from the coil library (Fitzkee et al., 2005) which is

accepted to be representative of the random coiled

state of proteins (Ormeci et al., 2007); (Engin et al.,

2009); (Unal et al., 2010). Having characterized the

probabilities from the knowledge data base, we

220

Sevim Bayrak C. and Erman B..

STATISTICAL MECHANICS OF PROTEINS IN THE RANDOM COIL STATE.

DOI: 10.5220/0003785202200225

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 220-225

ISBN: 978-989-8425-90-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

apply the matrix multiplication technique to obtain

the partition function, and the thermodynamic

functions such as energy, entropy and heat capacity

for the denatured state. Finally we present random

coil results for thermodynamic functions for several

proteins whose primary sequences are chosen from

the Protein Data Bank.

2 STATISTICAL EVALUATION

A denatured protein assumes a multitude of

conformations, each subject to a certain probability

determined by the configurational features of the

residues which are either of local or nonlocal nature.

Local effects result from interactions among

neighboring amino acids along the chain. We refer

to this state the random coiled state of the protein.

Determination of the conformation of a chain using

near neighbor interactions only reduces the problem

to a Markov process. Nonlocal effects are those

among residues separated by more than two residues

along the chain. Having adopted the probabilities

from the coil library, where the sequence-distant

long-range interaction are absent because secondary

or tertiary structures are lacking, is a good

approximation to the Markov nature of the coiled

state.

Markov statistics of denatured proteins have an

important place in protein statistics in general,

because: (i) This is the first approximation to the

difficult problem of non-Markov behavior, (ii)

Markov behavior is responsible for a large body of

observed phenomena, (iii) There is already a

powerful and successful Markov model of

characterizing the conformations of polymers, i.e.,

the Rotational Isomeric States (RIS) model that has

been studied in some detail. The specific aim of the

present paper is to extend the RIS model to calculate

the thermodynamic properties of denatured chains

using data generated from the denatured components

of chains from the PDB.

Rotational Isomeric State (RIS) formalism

(Flory, 1969) replaces the continuous distribution of

backbone torsion angles by a distribution over

several discrete states, and integrals over the energy

surface are approximated by summations over these

states. The native state of a protein is obtained when

each torsion angle selects a single unique value. Two

torsion angles around the alpha carbon,



describe the local conformation of a residue. The

Flory isolated pair hypothesis suggests that each pair

of torsion angles is independent of the angles

occupied by neighboring pairs (Brant and Flory,

1965); (Flory, 1969). Rose and coworkers. Zaman et

al., (2003), Jha et al., (2005) and Keskin et al.,

(2004), Esposito et al., (2005) and Colubri et al.,

(2006) showed the existence of significant

correlations between neighboring torsion angle

pairs. In a recent work it has been shown that the

usage of









provides more information on

backbone behavior as opposed to independent usage

of residues (Lennox et al., 2009).

Some values of torsion angles are more favorable

than others, and different amino acid types have

different propensities to occur in different angles

(Karplus, 1996). The dependence between the

torsion states of two neighboring residues is a

function of the type of the residues (Keskin et al.,

2004). We elaborate further on this point in

discussing the construction of energy maps below.

Figure 1: Torsion angles of the i

amino acid.

The frequency of occurrence of a given amino

acid at a given torsion state leads to the probabilities.

For calculations of the random denatured

conformations of proteins, a coil library serves as the

source of information where torsion angle data is

taken from the set of amino acids those are not in

helical or beta structures. In this paper, we use the

Rose Protein Coil Library (Fitzkee et al., 2005).

2.1 States

The backbone torsion angles for the ith amino acid

are shown in Figure 1. Each bond can assume

different angles, with different preferences. Each

residue has three torsion angles,

, , and





. The

occurrence of a residue in a given

and





state,

irrespective of its type is presented in Figure 1. An

examination of this figure shows that the choice of

isomeric states for the

and





angles is more

complicated than the choice in synthetic polymer

applications. In the latter, usually there are a few

states like trans, gauche+ and gauche-, and their

combinations for two successive bonds along the

chain. In the protein case, there are several discrete

states centered on different regions for the

successive

and





angles, and for different amino

acids.

STATISTICAL MECHANICS OF PROTEINS IN THE RANDOM COIL STATE

221

We construct state probabilities over the

Ramachandran map for each residue. 13 states are

identified for the following



axis intervals: (-180,-

150), (-150,-120), (-120,-105), (-105,-75), (-75,-40),

(-40,-20), (-20,-10), (-10,30), (30,70), (70,105),

(105,130), (130,155), (155,180). The corresponding

intervals over



axis are: (-180,-160), (-160,-135),

(-135,-105), (-105,-75), (-75,-40), (-40,-15), (-15,

20), (20, 60), (60, 90), (90,110), (110,130),

(130,160). For the



angle, there are two states,

one is either (-180,-160) or (160,180), and the other

is (-20, 20). The states chosen in this manner are

representative of the regions given by Karplus

(1996) and also in (Unal et al., 2009). Thus, we

identified 13 states for the angle



, 13 states for



and 2 states for



as rotational isomeric states.

2.2 State Probabilities

The pair wise dependent probabilities of observed

states of angles are defined as

 



Xii Xii X

Yii XYii XY

PN N

 

 

 







(1)

where



Xii





is the number of residue type X

observed in the indicated states, and



is the

total number of conformations (Keskin et al., 2004);

(Unal et al., 2009). Similarly,



XY i i





is the

number of dipeptides of XY in the given

conformations. Here,





Xii





and





Xii





are the probabilities of observing residue X to be in

state







, and in state







respectively.



XY i i





is the joint probability of observing

residue X in state







and Y in state









. The

neighbor-dependence introduced in the third of (1

) is

a dependence that originates from the residue type

differences. Otherwise, (1

) acknowledge the Flory

isolated pair hypothesis. The conformational

energies are defined as



  



 



  

,ln

Xii

XiX i

Xii

XiXi

XY i i

XY i XY i

ERT







































(2)

where the superscript 0 indicates the uniform

distribution probabilities. Hence, they are directly

proportional to the size of the angular intervals;









113

Xi X i





and







 .

Statistical weights







, and

1ii







corresponding to the energies may be defined by











;

exp , /

XXii

XY XY i i

uERT

















(3)

where R is the gas constant, T is the temperature.

The statistical weight matrix for a configuration

can be written as a product of statistical weights of

each bond pair,









,, ,, and ,



 

. For this

purpose, the statistical weight matrix for a given

residue X is defined as





















, and

1ii











. Depending

on the number of states of each angle, dimensions of

the statistical weight matrices







, and





, are 13×13, 13×2, and 2×13, respectively. The

superscripts

















, and









identify the

bond pairs over which statistical weights are

calculated.

2.3 Calculation of the Thermodynamic

Quantities

The partition sum of statistical weights for all

configurations of the chain is given by (Flory, 1974)

1112

JUUUUU UU J



 

 

(4)

where





10 0J  





11 1J column 

The thermodynamic properties, and the

coefficients derived from them depend not only on a

single conformation of the peptide, but on all

possible configurations. In the remaining equations,

we give the relevant expressions for calculating

these averages.

2.3.1 Helmholtz Free Energy

Since the Helmholtz free energy in canonical

formalism is additive over the energies, it can be

calculated using the partition function of the chain

(Callen, 1985).





(5)

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

222

where, 1/kT



 .

2.3.2 Mean Energy

The average energy is given by



ddZ

dZd



 

(6)

The matrix multiplication formalism of the partition

function leads to matrix multiplication scheme of its

derivatives in the following way









(7)

where

00LJ













00L column J 

and Û is the super matrix whose elements are

matrices













(8)







(9)

Therefore, the mean energy can be obtained using

the following multiplication scheme



LGL





(10)

where













(11)

2.3.3 Entropy

The entropy of the chain can be expressed in terms

of Z and its derivatives with respect to β. Following

the equality

Sk dFd



 , is obtained.

11ln

ln ln



















(12)

Using the matrix multiplication formalism of Z and

its first derivative with respect to



, the entropy can

be calculated as









JUJ











(13)

2.3.4 Heat Capacity

The heat capacity is one of the most important

properties of the proteins, both native and denatured.

When force acting on the chain is taken as zero,

denoted below by the subscript

0f  , the heat

capacity can be calculated as

















(14)

Similar to (7), second derivative can be obtained as

















(15)

where

000000MJ













and





000000

column J 

, and

00 0

UUUU







































(16)

'''

dU U











(17)

The second derivative of

on the right hand side

of the equation is written in terms of the first and

second derivatives of the partition function:

22 2

ln 1 1









 









(18)

Hence the heat capacity to be calculated by the

matrix notation



 

MUM

LUL

JUJ JUJ



























 



























(19)

3 RESULTS

In this section, the free energy, energy, entropy, and

heat capacity of peptides of different sizes ranging

from 10 to 800 amino acids are calculated using the

RIS model, over a temperature range of 200-700 K.

Table 1 lists the protein set taken from the PDB.

The variation of the free energy, energy, entropy

and heat capacity is evaluated by repeating the

calculations. Results are presented in Figure 2.

The curves shown in the four panels of Figure 2

are not independent from each other, and are related

by the thermodynamic relations given by (5), (6),

(12), and (14). It is seen that the curves in the figures

all scale with the number of residues N.

STATISTICAL MECHANICS OF PROTEINS IN THE RANDOM COIL STATE

223

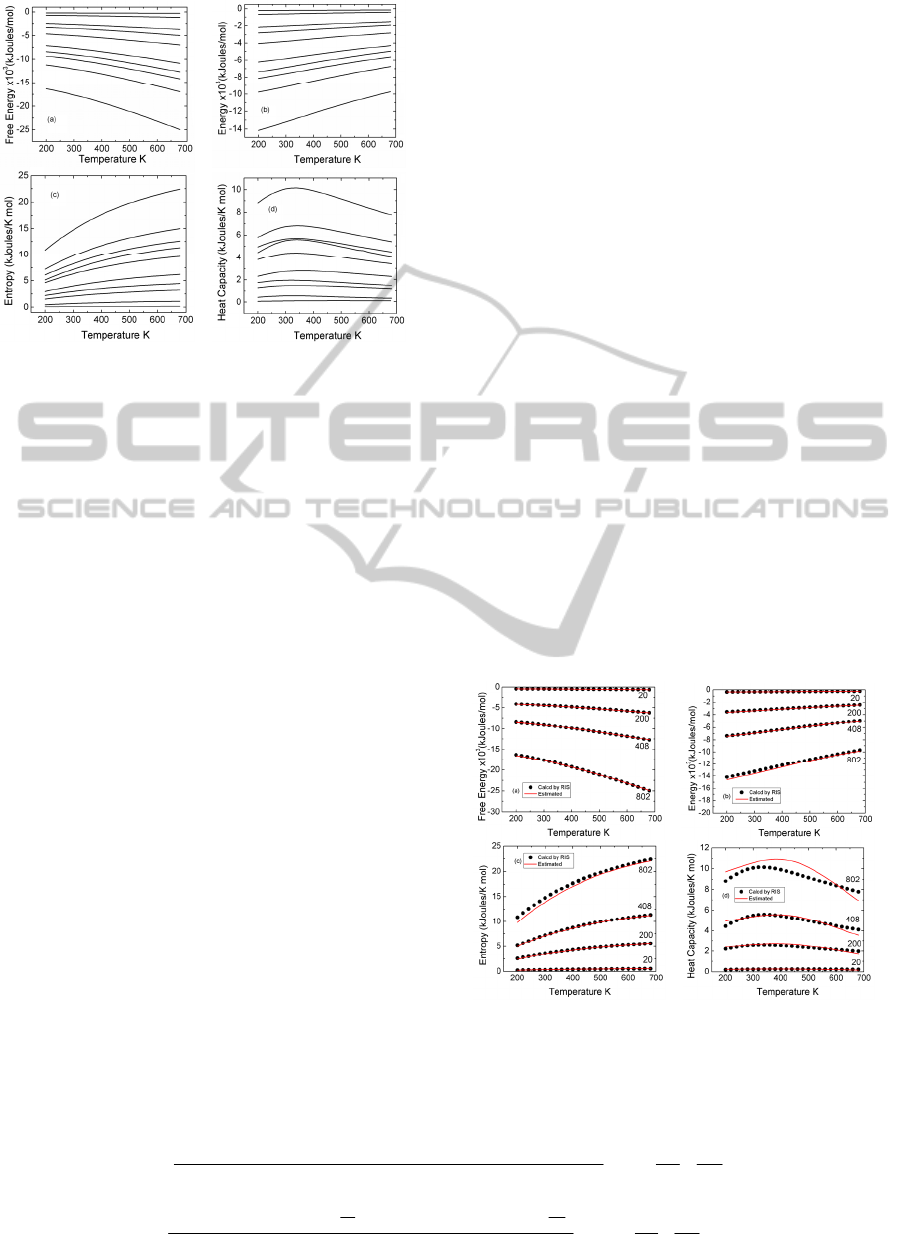
Figure 2: (a) The free energy as a function of temperature,

T, for different length proteins. (b) energy as a function of

T. (c) entropy as a function of T. (d) heat capacity as a

function of T. The curves in parts (a),(b), and (c) are

ordered from top to bottom represent proteins with the

following numbers of residues: 10, 40, 120, 160, 226, 349,

408, 456, 545, and 802, respectively. In part (d) they are in

reverse order.

In order to find analytical functions that will give

the curves shown in Figure 2, we first chose an

analytical form for the heat capacity as





(, )

BT DT

CTNNTAe Ce





(20)

keeping in mind the thermodynamic postulates. We

inspired the Debye model of heat capacity in a solid

that shows the dependence of T

. Then, by

integration subject to the conditions imposed by (5),

(6), (12), and (14), we obtain the remaining

thermodynamic functions as given in Eqs. (21)-(23).

We obtain the coefficients of (20)-(23) by curve

fitting as

1.5 10A



 kJoules/K

mol,

7.2 10B



  1/K,

2.6 10C



 kJoules/K

mol,

2.3 10D



  1/K, and 4083E  kJoules/mol.

4 CONCLUSIONS

The use of the RIS model depends critically on two

items: (i) the choice of the states, and (ii) the choice

of the database with which the probabilities of these

states are evaluated. The states are described in

terms of the populated regions on the Ramachandran

map, and the possible states for the

and





angles

of different amino acids are determined following

the work of Karplus (Karplus, 1996). In order to

apply the RIS model, however, the states available

to the torsion angles

, , and





are required

separately. The state space is obtained in our

formulation as 13 states for



and 13 states for



and two states for



. Evaluation of the probabilities

follows the choice of the state space. For proof of

principle, we used a coil library for the

determination of the probabilities. One could

alternatively construct a databank of known

denatured proteins, or a subset of them depending on

the nature of the investigation. Once the states are

determined, the RIS model is independent of the

databases used. We observed that the per residue

thermodynamic properties of proteins in the random

coil state scales only with the temperature. While

entropy and energy increases with the temperature,

free energy decreases. Heat capacity represents a

decrease around 340 Kelvin that implies an energy

barrier for a possible transition state. The explicit

expressions that we determined for the

thermodynamic functions form a thermodynamically

consistent set which may be used to obtain other

thermodynamic potentials by applying the known

Legendre transformation techniques (Callen, 1985).

Figure 3: Comparison of (a) free energy, (b) mean energy,

are calculated by matrix multiplication scheme, estimated

values are calculated by fundamental relation. The lengths

of chains are shown on each curve.

322 3 22

33 3 3

( 2 2) ( 2 2)

(, ) 2

BT DT

DNeBTBT CBNeDTDT AC

ST N N

BD B D

 









(21)

322 3 22

33 3 3

(4) ( 4)

(, ) 2

BT DT

AD Ne B T T CB Ne D T T

FT N NT EN

BD B D

 



   





(22)

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

224

3232 3 232

(36) ( 36)

BT DT

AD Ne B T BT T CB Ne D T DT T

UFTS EN

 

  

(23)

REFERENCES

Brant, D. A. and Flory, P. J. 1965. The Configuration Of

Random Polypeptide Chains. Ii. Theory. Journal Of

The American Chemical Society, 87, 2791-2800.

Brant, D. A., Tonelli, A. E. & Flory, P. J. 1969. The

Configurational Statistics Of Random Poly(Lactic

Acid) Chains. Ii. Theory. Macromolecules, 2, 228-

235.

Callen, H. B. 1985. Thermodynamics And An Introduction

To Thermostatistics, New York, Wiley.

Colubri, A., Jha, A. K., Shen, M. Y., Sali, A., Berry, R. S.,

Sosnick, T. R. & Freed, K. F. 2006. Minimalist

Representations And The Importance Of Nearest

Neighbor Effects In Protein Folding Simulations. J

Mol Biol, 363, 835-57.

Conrad, J. C. & Flory, P. J. 1976. Moments And

Distribution Functions For Polypeptide Chains. Poly-

L-Alanine. Macromolecules, 9, 41-47.

Dill, K. A. & Shortle, D. 1991. Denatured States Of

Proteins. Annu Rev Biochem, 60, 795-825.

Engin, O., Sayar, M. & Erman, B. 2009. The Introduction

Of Hydrogen Bond And Hydrophobicity Effects Into

The Rotational Isomeric States Model For

Conformational Analysis Of Unfolded Peptides. Phys

Biol, 6, 016001.

Esposito, L., De Simone, A., Zagari, A. & Vitagliano, L.

2005. Correlation Between [Omega] And [Psi]

Dihedral Angles In Protein Structures. Journal Of

Molecular Biology, 347, 483-487.

Fitzkee, N. C., Fleming, P. J. & Rose, G. D. 2005. The

Protein Coil Library: A Structural Database Of

Nonhelix, Nonstrand Fragments Derived From The

Pdb. Proteins, 58, 852-4.

Flory, P. J. 1969. Statistical Mechanics Of Chain

Molecules, New York,, Interscience Publishers.

Flory, P. J. 1974. Foundations Of Rotational Isomeric

State Theory And General Methods For Generating

Configurational Averages. Macromolecules, 7, 381-

392.

Flory, P. J. & Jernigan, R. L. 1965. Second And Fourth

Moments Of Chain Molecules, Aip.

Jha, A. K., Colubri, A., Freed, K. F. & Sosnick, T. R.

2005. Statistical Coil Model Of The Unfolded State:

Resolving The Reconciliation Problem. Proc Natl

Acad Sci U S A, 102, 13099-104.

Karplus, P. A. 1996. Experimentally Observed

Conformation-Dependent Geometry And Hidden

Strain In Proteins. Protein Sci,

5, 1406-20.

Keskin, O., Yuret, D., Gursoy, A., Turkay, M. & Erman,

B. 2004. Relationships Between Amino Acid

Sequence And Backbone Torsion Angle Preferences.

Proteins: Structure, Function, And Bioinformatics, 55,

992-998.

Lennox, K. P., Dahl, D. B., Vannucci, M. & Tsai, J. W.

2009. Density Estimation For Protein Conformation

Angles Using A Bivariate Von Mises Distribution And

Bayesian Nonparametrics. J Am Stat Assoc, 104, 586-

596.

Ormeci, L., Gursoy, A., Tunca, G. & Erman, B. 2007.

Computational Basis Of Knowledge-Based

Conformational Probabilities Derived From Local-

And Long-Range Interactions In Proteins. Proteins:

Structure, Function, And Bioinformatics, 66, 29-40.

Orosz, F. & Ovádi, J. 2011. Proteins Without 3d Structure:

Definition, Detection And Beyond. Bioinformatics, 27,

1449-1454.

Pappu, R. V., Srinivasan, R. & Rose, G. D. 2000. The

Flory Isolated-Pair Hypothesis Is Not Valid For

Polypeptide Chains: Implications For Protein Folding.

Proc Natl Acad Sci U S A, 97, 12565-70.

Rehahn, M., Mattice, W. L. & Suter, U. 1997. Rotational

Isomeric State Models In Macromolecular Systems,

Springer.

Tanford, C. 1968. Adv. Protein Chem., 23, 121-282.

Tompa, P. 2011. Unstructural Biology Coming Of Age.

Curr Opin Struct Biol, 21, 419-25.

Unal, E. B., Gursoy, A. & Erman, B. 2009.

Conformational Energies And Entropies Of Peptides,

And The Peptide-Protein Binding Problem. Physical

Biology, 6.

Unal, E. B., Gursoy, A. & Erman, B. 2010. Vital: Viterbi

Algorithm For De Novo Peptide Design. Plos One, 5,

E10926.

Zaman, M. H., Shen, M.-Y., Berry, R. S., Freed, K. F. &

Sosnick, T. R. 2003. Investigations Into Sequence And

Conformational Dependence Of Backbone Entropy,

Inter-Basin Dynamics And The Flory Isolated-Pair

Hypothesis For Peptides. Journal Of Molecular

Biology, 331, 693-711.

STATISTICAL MECHANICS OF PROTEINS IN THE RANDOM COIL STATE

225