A PERFECTLY INVERTIBLE RANK ORDER CODER

Khaled Masmoudi

, Marc Antonini

and Pierre Kornprobst

I3S laboratory, UNS–CNRS, Sophia-Antipolis, France

NeuroMathComp Team Project, INRIA, Sophia-Antipolis, France

Keywords:

Rank Order Code, Bio-inspired Image Coding, Frame Theory, Scalability.

Abstract:

Our goal is to revisit rank order coding by proposing an original exact decoding procedure for it. Rank order

coding was proposed by Simon Thorpe et al. to explain the impressive performance of the human visual

system in recognizing objects. It is based on the hypothesis that the retina represents the visual stimulus by

the order in which its cells are activated. A classical rank order coder/decoder was then designed (Van Rullen

and Thorpe, 2001) involving three stages: (i) A model of the stimulus transform in the retina consisting in

a redundant ﬁlter bank analysis; (ii) A sorting stage of the ﬁlters according to their activation degree; (iii) A

straightforward decoding procedure that consists in a weighted sum of the most activated ﬁlters. Focusing

on this last stage, it appears that the decoding procedure employed yields reconstruction errors that limit the

model Rate/Quality performances when used as an image codec. Attempts made in the literature to overcome

this issue are time consuming and alter the coding procedure or are infeasible for standard size images and

lacking mathematical support. Here we solve this problem in an original fashion by using the frames theory,

where a frame of a vector space designates an extension for the notion of basis. Our contribution is threefold.

First we add an adequate scaling function to the ﬁlter bank under study that has both a mathematical and a

biological justiﬁcation. Second, we prove that the analyzing ﬁlter bank considered is a frame, and then we

deﬁne the corresponding dual frame that is necessary for the exact image reconstruction. Finally, to deal with

the problem of memory overhead, we design an original recursive out-of-core blockwise algorithm for the

computation of this dual frame. Our work provides a mathematical formalism for the retinal model under

study and speciﬁes a simple and exact reverse transform for it. Furthermore, the framework presented here

can be extended to several models of the visual cortical areas using redundant representations.

1 INTRODUCTION

Neurophysiologists made substantial progress in bet-

ter understanding the early processing of visual sti-

muli. Especially, several efforts proved the ability of

the retina to code and transmit a huge amount of data

under strong time and bandwidth constraints (Thorpe,

1990; Meister and Berry, 1999; Gollisch and Meis-

ter, 2008). The retina does this by means of a neu-

ral code consisting in a set of electrical impulses: the

spikes (Rieke et al., 1997). Based on these results, our

aim is to use the computational neuroscience models

that mimic the retina behavior to design novel lossy

coders for static images.

In the literature, numerous retina models are pro-

posed. Although there is no clear evidence on how

the spikes encode a given visual stimulus, we assume

in this paper that the relevant encoding feature is the

order in which the retina neurons emit their ﬁrst spike.

This assumption was motivated by Thorpe et al. neu-

rophysiologic results on ultra-rapid stimulus catego-

rization (Thorpe, 1990; Thorpe et al., 1996). Authors

showed that still image classiﬁcation can be achieved

by the visual cortex within very short latencies of

about 150 ms or even faster. As an explanation, it was

stated that: There is information in the order in which

the cells ﬁre, and thus the temporal ordering can be

used as a code. This code termed as rank order coding

(ROC) was further studied in (Van Rullen and Thorpe,

2001; Thorpe, 2010) and yielded the conception of a

classical retina model (Van Rullen and Thorpe, 2001).

However, one major limit of the ROC coder de-

ﬁned in (Van Rullen and Thorpe, 2001) prevents us

from its use for the design of image codecs. The

proposed decoding procedure is inaccurate. Indeed,

the bio-inspired retina model that generates the spikes

is based on a redundant ﬁlter bank image analysis,

where the considered ﬁlters are not strictly orthogo-

nal. Thus, the ﬁlter overlap yields reconstruction er-

rors that limit the Rate/Quality performance (Perrinet

153

Masmoudi K., Antonini M. and Kornprobst P..

A PERFECTLY INVERTIBLE RANK ORDER CODER.

DOI: 10.5220/0003696701530162

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 153-162

ISBN: 978-989-8425-89-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

et al., 2004; Bhattacharya and Furber, 2010; Mas-

moudi et al., 2010). In this work we tackle expli-

citly this issue. Attempts made in the literature to

correct this overlap are time consuming and alter the

coding procedure (Perrinet et al., 2004; Bhattacharya

and Furber, 2010) or are infeasible for standard

size images and lacking mathematical support (Bhat-

tacharya and Furber, 2007; Bhattacharya and Furber,

2010). In this paper, we give an original solution rely-

ing on the so-called frames theory (Dufﬁn and Schaef-

fer, 1952; Kovacevic and Chebira, 2008). The mathe-

matical concept of frames extends the notion of basis

to sets of ﬁlters which are linearly dependent. Their

use for redundant signal analysis and reconstruction

has already been experienced with success (Burt and

Adelson, 1983; Rakshit and Anderson, 1995; Do and

Vetterli, 2003). Our method requires the computa-

tion of a reverse operator once for all and keeps the

bio-inspired coding scheme unchanged. We more-

over verify that the reconstructed image that we get

is equal to the original stimulus.

The present work brings three main contributions:

(i) We add to the original retinal ﬁlter bank an ade-

quate scaling function, and (ii) we provide an original

mathematical demonstration that the ﬁlter bank thus

deﬁned is a frame. Then we propose an algorithm for

errorless reconstruction through the construction of a

so-called “dual frame”; (iii) We solve the technical

issue of memory overhead that prevented the use of

frames for high dimension spaces, with a novel out-

of-core algorithm that computes the dual frame.

This paper is organized as follows: In Section 2,

we present the bio-inspired retina model under study.

Then in Section 3 we introduce a matrix-based for-

malism for the retinal transform and use it to deﬁne

an exact decoding scheme through the construction of

a dual frame. Finally in Section 4 and Section 5, we

summarize and discuss the results and show the gain

that we obtain in terms of Rate/Quality tradeoff.

2 THE RANK ORDER CODER

This Section summarizes the three stages of the ROC

coder/decoder deﬁned in (Van Rullen and Thorpe,

2001). First we present in Section 2.1 the image trans-

form as performed by a bio-inspired retina model.

Then we give the speciﬁcation of the subsequent neu-

rons rank ordering in section 2.2. Finally we describe

the decoding procedure and show its inaccuracy in

Section 2.3.

2.1 The Image Transform in the

Bio-inspired Retina Model

Neurophysiologic experiments have shown that, as

for classical image coders, the retina encodes the

stimulus representation in a transform domain. The

retinal stimulus transform is performed in the cells of

the outer layers. Quantitative studies such as (Field,

1994; Rodieck, 1965) have proven that the outer cells

processing can be approximated by a linear ﬁlter-

ing. In particular, neurophysiologic experiments con-

ducted in (Field, 1994) yielded the largely adopted

DoG ﬁlter which is a weighted difference of spatial

Gaussians that is deﬁned as follows:

DoG(x, y) = w

(x, y) − w

(x, y), (1)

where w

and w

are the respective positive weights

of the center and surround components of the recep-

tive ﬁelds, σ

and σ

are the standard deviations of

the Gaussian kernels G

and G

, such that σ

< σ

The DoG cells can be arranged in a dyadic grid Γ of

K layers to sweep all the stimulus spectrum as shown

in Figure 1(b) (Van Rullen and Thorpe, 2001; Per-

rinet et al., 2004; Masmoudi et al., 2010). As in

the retina topology, the cells density and scale are in-

versely proportional. This keeps the model strongly

inspired from the mammalians retina, though the au-

thors in (Van Rullen and Thorpe, 2001) do not claim

biological plausibility. Each layer 0 6 k < K in the

grid Γ, is tiled with ﬁltering cells, denoted by DoG

having a scale k and generating a transform subband

such that:

DoG

(x, y) = w

(x, y) − w

(x, y), (2)

where σ

k+1

and σ

k+1

. Each DoG

ﬁl-

ter has a size of (2M

+ 1)

, with M

= 3σ

. Authors

in (Van Rullen and Thorpe, 2001) chose the biologi-

cally plausible parameters established in (Field, 1994)

= w

= 1, σ

∀k, and σ

K−1

= 0.5 pixel.

In order to measure the degree of activation c

kij

a given retina cell, such that (k, i, j) ∈ Γ, we compute

the convolution of the original image f by the DoG

ﬁlter. Yet each layer k in the dyadic grid Γ is under-

sampled with a pace of 2

K−k−1

pixels with an orig-

inal offset of ⌊2

K−k−2

⌋ pixels, where ⌊.⌋ is the ﬂoor

operator. Having this, we deﬁne the function u

, such

that the c

kij

coefﬁcients are computed at the locations



(i), u

( j)



as follows:

(i) = ⌊2

K−k−2

⌋ + 2

K−k−1

i, ∀k ∈ J0, K − 1K. (3)

can be seen as an undersampling function. We

notice that u

K−1

(i) = i, and that the other functions

)

k∈J0,K−2K

are undersampled versions of u

K−1

. We

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

154

also deﬁne N

N−⌊N−2

K−k−2

⌋

K−k−1

, such that N

is the

number of cells in B

, the k

layer of Γ. We also no-

tice here that N

K−1

= N. Having these deﬁnitions, c

kij

is then computed as follows:

kij

x=u

(i)+M

,y=u

( j)+M

∑

x=u

(i)−M

,y=u

( j)−M

DoG

(i) − x, u

( j) − y) f(x, y). (4)

(a) (b)

(c)

Figure 1: 1(a):cameraman. The image f size is 257x257

pixels. 1(b): Example of a dyadic grid of DoG’s used for

the image analysis (from (Van Rullen and Thorpe, 2001)).

1(c): The transform result c with the different generated

subbands B

(here shown in a logarithmic scale).

This transform generates a vector c of (

− 1)

coefﬁcients c

kij

for an N

-sized image (if N is a power

of 2). This architecture is similar to a Laplacian pyra-

mid (Burt and Adelson, 1983). An example of such a

transform performed on the cameraman test image is

shown in Figure 1.

2.2 The Generation of the ROC

Thorpe et al (Thorpe, 1990; Thorpe et al., 1996) pro-

posed that the order in which spikes are emitted en-

codes the stimulus. This yielded the ROC which re-

lies on the following simplifying assumptions:

i) From stimulus onset, only the ﬁrst spike emitted

is considered.

ii) The time to ﬁre of each cell is proportional to its

degree of excitation.

iii) Only the order of ﬁring of the neurons encodes the

stimulus.

The neurons responses (c

kij

)

kij∈ Γ

(cf. Equation (4))

are then sorted in the decreasing order of their ampli-

tude |c

kij

The ﬁnal output of this stage, the ROC, is the

sorted list of N

couples (p, c

) such that |c

| > |c

p+1

with p being the index p(k, i, j) = k.N

+ i.N

+ j and

the number of cells in the subband B

. Such a

code gives a biologically plausible interpretation to

the rapidity of the visual stimuli processing in the hu-

man visual system. Indeed, it seems that most of the

processing is based on feed-forward mechanism be-

fore any feedback occurs (Thorpe et al., 1996). The

generated series (p, c

)

06p<N

is the only data trans-

mitted to the decoder. Note that in some implementa-

tions as (Van Rullen and Thorpe, 2001; Perrinet et al.,

2004), the exact values of the coefﬁcients c

are omit-

ted and recovered through a look-up-table (but this is

out of the scope of this paper).

2.3 Decoding Procedure of the ROC

We consider the set of the ﬁrst N

generated spikes

forming the ROC of a given image f. The estimation

of the original input f is deﬁned (Van Rullen and

Thorpe, 2001) by:

(x, y) =

−1

∑

p(k,i, j)=0

DoG

(i) − x, u

( j) − y).

(5)

Equation (5) gives a progressive reconstruction de-

pending on N

. Indeed, one can restrict the code to

the most valuable coefﬁcients c

, i.e the most acti-

vated neurons of the retina. This feature makes the

coder be scalable (Masmoudi et al., 2010).

An example of such a reconstruction is given in

Figure 2, with all the retina cells taken into account.

Figure 2 also shows that the retina model decoding

procedure, though giving a good approximationof the

stimulus, is still inaccurate. In this example, recon-

struction quality is evaluated to 27 dB of PSNR.

3 INVERTING THE RETINA

MODEL

In this section, we deﬁne an original and exact image

reconstruction algorithm starting from the ROC. First,

we introduce in Section 3.1 a low-pass scaling func-

tion in the analyzing ﬁlter bank. This modiﬁcation

will be shown to be necessary for the transform in-

vertibility. Then, in Section 3.2, we give a matrix-

based formalism for the transform and we use it to

prove that our ﬁlter bank is a frame in Section 3.3. Fi-

nally, in Section 3.4, we show the exact reconstruction

A PERFECTLY INVERTIBLE RANK ORDER CODER

155

(a) (b)

Figure 2: Result of the decoding procedure with the origi-

nal approach using the totality of the retina cells. 2(a): The

reconstructed image

. The PSNR quality measure of

yields 27 dB. 2(b): The error image shown in a logarith-

mic scale: high frequencies are the ones that are the most

affected by this approach.

results using the dual frame and introduce an out-of-

core algorithm to construct it.

3.1 Introduction of a Low-pass Scaling

Function

We introduce a low-pass scaling function in the ﬁlter

bank used for image analysis. This modiﬁcation does

not alter the ROC coder architecture and has both a

mathematical and a biological justiﬁcation.

Indeed, the Fourier transform of a Gaussian is an-

other Gaussian, so that F (DoG

) is a difference of

Gaussians. Therefore, with w

= w

= 1 (cf. Equa-

tion (2)), we have:

F (DoG

) = 2π(σ

)

(

)

−1

−2π(σ

)

(

)

−1

. (6)

We can easily verify that for the central Fourier coef-

ﬁcient of each DoG

ﬁlter we have:

F (DoG

)



(0), u

(0)



= 0, ∀k, (7)

and that for the other coefﬁcients we have:

F (DoG

)(i, j) > 0, ∀(i, j) 6=



(0), u

(0)



. (8)

This assertion is also veriﬁed on Figure 3(b). In order

to cover up the centre of the spectrum, we propose to

replace the DoG

ﬁlter, with no change in the nota-

tion, by a Gaussian low-pass scaling function consist-

ing in its central component, such that:

DoG

(x, y) = w

(x, y). (9)

Figures 3(a) and 3(b) show the spectrum partition-

ing with the different DoG

ﬁlters (k > 1, in blue) and

the spectrum of the new scaling function DoG

(in

red dashed line) which covers low frequencies. With

no scaling function, all constant images would be

mapped into the null image 0 and this would make the

transform be non-invertible. Here we overcome this

(a) (b)

Figure 3: 3(a): Spectrum of the DoG ﬁlters. The abscissa

represents the frequencies.The ordinate axis represents the

different DoG

ﬁlters gain in dB. 3(b): Half of the spectrum

in 3(a) with the abscissa having a logarithmic step. The

scaling function DoG

is plotted in red dashed line.

problem as the central Fourier coefﬁcient of DoG

veriﬁes:

F (DoG

)



(0), u

(0)



> 0. (10)

The scaling function introduction is further justi-

ﬁed by the actual retina behavior. Indeed, the sur-

round component G

in Equation (2) appears pro-

gressively across time driving the ﬁlter passband from

low frequencies to higher ones. So that, the Gaussian

scaling function DoG

represents the very early state

of the retina cells.

In order to deﬁne an inverse for the new transform,

we demonstrate in the following that the set of DoG

ﬁlters augmented with the DoG

scaling function is

a “frame”. So that, we will deﬁne the adequate nota-

tions in Section 3.2 and give the proofs in Section 3.3.

3.2 Matrix Notations for ROC

Unlike the implementations in (Van Rullen and

Thorpe, 2001; Perrinet et al., 2004; Masmoudi et al.,

2010), we use a matrix Φ to compute the image

transform through the modelled retina. The lines

of Φ are the different analyzing DoG

ﬁlters. This

yields an “undersampled Toeplitz-bloc” sparse mat-

rix (see Figure 4(a)). Such an implementation allows

fast computation of the multi-scale retinal transform

through sparse matrix speciﬁc algorithms (Golub and

Van Loan, 1996). This will in addition help us cons-

truct the dual frame of Φ. The DoG transform is out-

lined in the following equation:

c = Φ f. (11)

Interestingly, the straightforward synthesis as deﬁned

in (5) amounts to the multiplication of the vector out-

put by Φ

∗

the Hermitian transpose of Φ (see Fig-

ure 4(b)). The reconstruction procedure is then out-

lined in the following equation:

= Φ

∗

c. (12)

Though small, the synthesis yields an error that limits

the ability of the model to be used as a codec.

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

156

(a) (b)

Figure 4: Template of the DoG analysis and synthesis matri-

ces (Φ and Φ

∗

). In this paper, Φ and Φ

∗

are represented as

matrices where blue dots correspond to non-zero elements.

Note here that Φ and Φ

∗

are highly sparse matrices.

3.3 The DoG Transform is a Frame

Operator

Our aim is to prove that the bio-inspired retina image

transform presented amounts to a projection of the

input image f onto a frame of a vector space. The

frame is a generalization of the idea of a basis to sets

which may be linearly dependent (Dufﬁn and Scha-

effer, 1952; Kovacevic and Chebira, 2008). These

frames allow a redundant signal representation which,

for instance, can be employed for coding with er-

ror resilience. By proving the frame nature of this

transform, we will be able to achieve an exact reverse

transform through the construction of a dual frame.

A set of vectors is a frame if it veriﬁes the so-

called “frame condition” (Dufﬁn and Schaeffer, 1952;

Kovacevic and Chebira, 2008) which states that ∃ β >

α > 0 such that :

αk f k

∑

kij∈ Γ



kij



6 βk fk

, ∀ f. (13)

Positioning with Respect to the State of the Art.

Pyramid architectures are very common in signal pro-

cessing and involvea wide range of ﬁlters (Van Rullen

and Thorpe, 2001; Do and Vetterli, 2003; Rakshit

and Anderson, 1995). Some works in the literature

made the connection between the pyramidal architec-

ture and frames. For example, in (Rakshit and An-

derson, 1995) the authors proved experimentally that

the classical Laplacian pyramid is a frame. How-

ever, in our case, we prove that the pyramid intro-

duced in (Van Rullen and Thorpe, 2001) -which is

not Laplacian- is a frame. We showed this mathemati-

cally through an original demonstration. Also, in (Do

and Vetterli, 2003) the authors proposed the design of

a set of orthogonal vectors inspired from the Lapla-

cian pyramid to conceive a new orthogonal and tight

(α = β cf. Eq. (13)) frame. The ﬁlter bank deﬁned

from (Van Rullen and Thorpe, 2001) form a frame

that is neither orthogonal nor tight.

Upper Bounding. Let us prove the upper bounding

in Equation (13). We have:

∑

kij∈ Γ



kij



∑

K−1

k=0

, (14)

where B

is the subband of scale k generated by the

image transform with:

(i, j) =

x=u

(i)+M

,y=u

( j)+M

∑

x=u

(i)−M

,y=u

( j)−M

DoG

(i) − x, u

( j) − y) f(x, y).

If we denote by U

the undersampling operator corre-

sponding to the function u

(cf. Equation (3)), we can

write the following:

= U

(DoG

∗ f). (15)

Then, we have the following obvious inequalities:

k = kU

(DoG

∗ f)k 6 kU

(|DoG

| ∗ | f |)k

6 k|DoG

| ∗ | f |k

6 kDoG

kk fk.

Then, we get back to (14) and infer the following

bounding:

∑

kij∈ Γ



kij



K−1

∑

k=0

K−1

∑

k=0

kDoG

k fk

= βk fk

. (16)

Lower Bounding. Now, let us demonstrate the

lower bounding in Equation (13). We start from the

fact that:

K−1

∑

k=0

> kB

K−1

+ kB

, (17)

which amounts to write the following inequalities:

∑

kij∈ Γ



kij



K−1

∑

k=0

>kDoG

K−1

∗ fk



DoG

∗ f



(0), u

(0)



=kF (DoG

K−1

)F ( f)k



F (DoG

)F ( f)



(0), u

(0)



N−1

∑

i, j=0



F (DoG

K−1

)(i, j)F ( f)(i, j)



+kF (DoG

)



(0), u

(0)



F ( f)



(0), u

(0)



A PERFECTLY INVERTIBLE RANK ORDER CODER

157

where F designates the discrete Fourier trans-

form. We know that F (DoG

K−1

)(i, j) > 0, ∀(i, j) 6=



(0), u

(0)



and that F (DoG

K−1

)



(0), u

(0)



0. We also have F (DoG

)



(0), u

(0)



> 0 (cf.

Section 2.1). So, if we deﬁne a set S

K−1

by S

K−1

J0, N − 1K



(0), u

(0)



and α by:

α =min

F (DoG

)



(0), u

(0)





F (DoG

K−1

)

(i, j), (i, j) ∈ S

K−1



> 0,

then we get the following:

N−1

∑

i, j=0



F (DoG

K−1

)(i, j)F ( f)(i, j)



+ kF (DoG

)



(0), u

(0)



F ( f)



(0), u

(0)



∑

i, j∈S

K−1



F (DoG

K−1

)(i, j)F ( f)(i, j)



+ kF (DoG

)



(0), u

(0)



F ( f)



(0), u

(0)



> α

∑

i, j∈J0,N−1K



F ( f)(i, j)



=αk fk

and Finally,

∑

kij∈ Γ



kij



> αk f k

. Thus, the set of

DoG ﬁlters satisﬁes the frame condition (13).

3.4 Synthesis using the Dual DoG

Frame

We introduce in this section a correction means for

the reconstruction error in the retina model presented

through the frame theory.

The straightforward analysis/synthesis procedure

can be outlined in the relation between the input i-

mage and the reconstruction estimate:

= Φ

∗

Φf. (18)

As we already demonstrated that the DoG transform

is a frame, Φ

∗

Φ is said to be the frame operator.

To have an exact reconstruction of f, one must con-

struct the dual DoG vectors. A preliminary step is

to compute (Φ

∗

Φ)

−1

, the inverse frame operator. We

then get a corrected reconstruction f

∗

, deﬁned by:

∗

= (Φ

∗

Φ)

−1

. If N

is the total number of the

retina model cells, we have:

∗

= (Φ

∗

Φ)

−1

= (Φ

∗

Φ)

−1

∗

= (Φ

∗

Φ)

−1

∗

Φ f

∗

= f. (19)

As made clear through Equation (19), the dual vec-

tors are the lines of (Φ

∗

Φ)

−1

∗

. Besides, (Φ

∗

Φ) is

a square, deﬁnite positive invertible matrix (Kovace-

vic and Chebira, 2008). This is a crucial issue as it

ensures the exactness of the reverse frame operator.

We compute the reverse frame operator (Φ

∗

Φ)

−1

and get the results shown in Figure 5. The reconstruc-

tion obtained by the means of the dual frame operator

is accurate and requires only a simple matrix multi-

plication. In this example, reconstruction quality is

evaluated to 295 dB of PSNR.

(a) (b)

Figure 5: Result of the decoding procedure with the dual

DoG frame using the totality of the retina cells. 5(a): The

reconstructed image f

∗

. The PSNR quality measure of f

∗

yields 295 dB. 5(b): The error image in logarithmic scale.

This shows that the reconstruction using the dual frame is

very precise.

Dual vectors resemble the DoG analyzing ﬁlters.

This is obvious as the straightforward image recon-

struction

is already close to f , which means that

∗

Φ is close to identity. However, the dual ﬁlters

lose the symmetry property of the primal ones. An

example of dual vectors constructed as the rows of

(Φ

∗

Φ)

−1

∗

is shown in Figure 3.4. Figure 3.4 shows

also that the exact reconstruction of f is obtained by

a slight relaxation in the symmetry constraint of the

DoG ﬁlters.

3.4.1 The Recursive Out-of-core Blockwise

Inversion Algorithm

Though the mathematical fundamentals underlying

this work are simple, the implementation of such a

process is a hard problem. In spite of the sparsity

of Φ and Φ

∗

, the frame operator Φ

∗

Φ is an N

-sized

dense matrix for an N

-sized image f. For instance,

if N = 257, Φ

∗

Φ holds in 16 Gbytes, and 258 Gbytes

if N = 513. As noticed in (Do & Vetterli 2003): A

key observation is that one should use the dual frame

operator for the reconstruction. While this seems a

somewhat trivial observation, it has not been used in

practice, probably because the usual reconstruction,

while suboptimal, is very simple. Indeed due to its

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

158

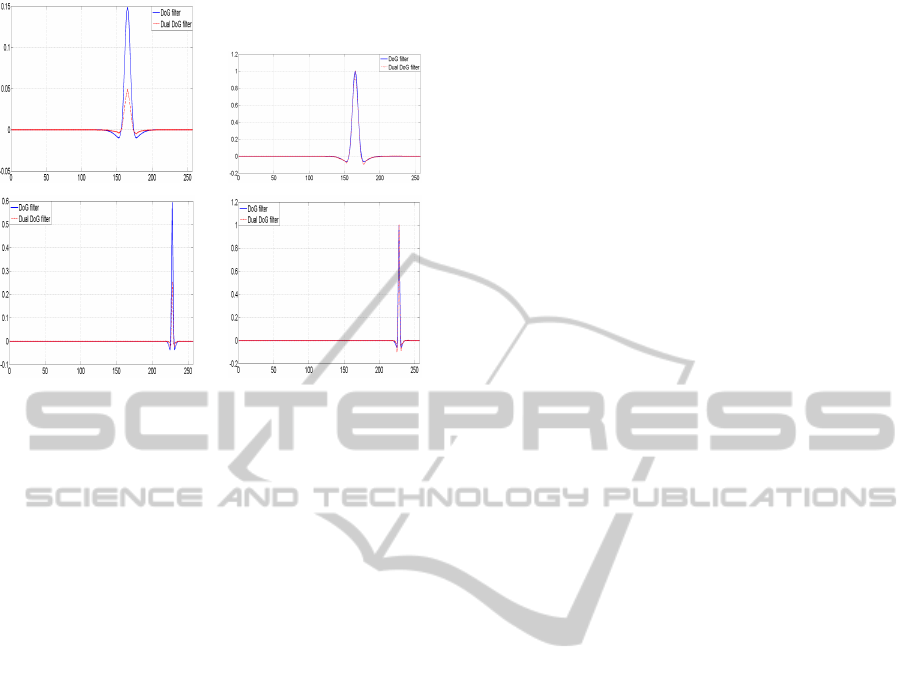
(a) (b)

Figure 6: 6(a)- 6(c): Comparison between the DoG ﬁlters

(in blue line) and their duals (in red dashed line). 6(b)-

6(d): Same as previous with the highest value of each ﬁlter

normalized to 1. Though close in shape to the DoG ﬁlters,

the dual DoG ﬁlters are asymmetric.

technical difﬁculty, there is no solution in the litera-

ture that computes explicitly the dual of a frame in

a general case like ours. In our work, we tackled this

technical issue and resolved it with success by design-

ing an original “out-of-core” inversion algorithm.

The frame operator Φ

∗

Φ is constructed bloc by

bloc, and each bloc is stored separately on disk. The

inversion is then performed using a recursive algo-

rithm that relies on the blockwise matrix inversion

formula that follows:



A B

C D



−1



−1

+ A

−1

−A

−1

−Q

−1



(20)

where Q is the Schur complement of A, such that:

Q = D −CA

−1

Thus, inverting a matrix amounts to the inversion of

two matrices, A and D (cf. Equation (20)), that are

4 times smaller. The inversion consists then in sub-

dividing the problem by a factor 4 at each recursion

level until we reach a single bloc problem. Thereby,

we invert the single bloc remaining matrix using a

classical Gauss-Jordan elimination procedure. Obvi-

ously, this algorithm requires out-of-core blockwise

matrix routines for multiplication, subtraction and ad-

dition, that we implemented in a “multi-threaded”

fashion to accelerate the computation.

Advantages of our Approach. (Φ

∗

Φ) is a square,

deﬁnite positive, and invertiblematrix (Kovacevicand

Chebira, 2008). Thus (Φ

∗

Φ)

−1

exists and obviously

the exact reverse transform of Φ too. Another advan-

tage of our method is that (Φ

∗

Φ) is well conditioned,

with a conditioning number estimated to around 16,

so that its inversion is stable. This is a crucial issue as

previous work aimed at conceiving the DoG reverse

transform tried to invert the original ﬁlter bank with

no scaling function DoG

(Bhattacharya and Furber,

2007; Bhattacharya and Furber, 2010). This is obvi-

ously mathematically incorrect as the ﬁlter bank thus

deﬁned is not a frame and thus its pseudo inverse

(Φ

∗

Φ)

−1

∗

does not exist. The solution proposed by

the authors of (Bhattacharya and Furber, 2007; Bhat-

tacharya and Furber, 2010) gives only a least squares

solution to an ill-conditioned problem. Our method

instead is stable. Besides through the out-of-core al-

gorithm that we designed we can invert (Φ

∗

Φ) even

for large images whereas authors in (Bhattacharya

and Furber, 2007; Bhattacharya and Furber, 2010) are

restricted to a maximum size of 32× 32. Indeed, we

were able to reconstruct 257 × 257 and 513 × 513 i-

mages through our new approach.

The exactness of our decoding schema is con-

ﬁrmed when applied on several classical test images.

For example cameraman reconstruction quality in-

creases from 27 dB with the classical decoder to 296

dB with ours (see Figure 7). The same test on Lena

leads to an increase from 31 to 300 dB of PSNR (see

Figure 8). Numerically, the only limitation comes

from the machine precision which is ﬁnite. Given this

fact, and with a 64-bit machine precision, a value of

PSNR that is greater than 290 dB means that the re-

construction is numerically exact. We also conﬁrm

these results by using quality metrics that are more

consistent than PSNR with the human eye perception.

Here we show the mean structural similarity measure

(SSIM) (Wang et al., 2004) (an index between 0 and

1) which also conﬁrms the precision of our new de-

coder with an increase in quality from 0.9 to 1 when

all the retina cells have ﬁred (Figures 7 and 8 cap-

tions).

Furthermore, correcting the reconstruction errors

using the adequate dual frame does not alter the cod-

ing procedure. Indeed, methods introduced in (Per-

rinet et al., 2004; Bhattacharya and Furber, 2010) are

based on the matching pursuit (MP) algorithm. MP

is time consuming and depends on the order in which

the “match and update” mechanism is performed. Our

method keeps the coding procedure straightforward,

multi-threadable and order-independent.

Besides, the results presented here are also bene-

ﬁcial to the image coders that we previously designed

A PERFECTLY INVERTIBLE RANK ORDER CODER

159

∗

0.5%

10%

100%

Figure 7: Reconstruction of the cameraman image f us-

ing different percentages of signiﬁcant coefﬁcients. To get

this reconstruction coefﬁcients are set to 0 if under a de-

scending threshold. The left column shows the progressive

synthesis. The right column shows f

∗

. PSNR for the

left/right image is from top to bottom: (19.2 dB/19.5 dB),

(20.4 dB/20.8 dB), (24.08 dB/25 dB), (25.8 dB /27.5 dB),

and (27.9 dB/296 dB). The mean SSIM for the upper/lower

image is from top to bottom: (0.49 /0.57), (0.56 /0.61), (0.72

/0.76), (0.77 /0.81), and (0.91 /1).

and that are based on this same retina model (Mas-

moudi et al., 2010; Masmoudi et al., 2011).

∗

0.5%

10%

100%

Figure 8: Reconstruction of the Lena image f using differ-

ent percentages of signiﬁcant coefﬁcients. To get this re-

construction coefﬁcients are set to 0 if under a descending

threshold. The left column shows the progressive

syn-

thesis. The right column shows f

∗

. PSNR for the left/right

image is from top to bottom: (20.06 dB/20.17 dB), (21.73

dB/21.83 dB), (25.93 dB/26.65 dB), (27.97 dB /28.84 dB),

and (31.23 dB/299.60 dB). The mean SSIM for the up-

per/lower image is from top to bottom: (0.38 /0.38), (0.46

/0.46), (0.69 /0.72), (0.77 /0.81), and (0.90 /1).

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

160

4 RESULTS

We experiment our new decoder in the context of scal-

able image decoding. We reconstruct the test image

using an increasing number N

of signiﬁcant coefﬁ-

cients (cf. Equation (5)). We then compare the re-

sults when using the original DoG ﬁlters in Φ and

their dual DoG ﬁlters in (Φ

∗

Φ)

−1

∗

for the decod-

ing procedure.

Figures 7 and 8 show two example results ob-

tained for cameraman and Lena. In both ﬁgures the

left column shows the progressive straightforward re-

construction

and the right column shows the cor-

rected progressive reconstruction f

∗

using the dual

frame.

Qualitatively speaking, the high frequencies

which were the most altered by the straightforward

synthesis are now well rendered. This is obvious

even for low rates and we can verify it in the cam-

era contours (Figure 7) or in Lena hair details (Fig-

ure 8). This is an important issue as contours and

salient points are the most important features used for

categorization tasks. Bearing in mind that the retina

model under study was ﬁrst designed for fast catego-

rization, our results become crucial.

Quantitatively speaking, the gain in PSNR is sig-

niﬁcant for low rates (around 0.2 dB for both cases)

and very high when we consider the totality of the

retina cells in the reconstruction (over 260 dB for both

cases). Figure 9 compares the Rate/quality curves of

the two methods and shows the high improvement we

obtain. Here the rate is implicitly related to the num-

ber of neurons taken into account for the image recon-

struction. In all the curves shown the abscissa rep-

resents the percentage of the highest responses used

for the reconstruction and he ordinate represents the

reconstruction quality in terms of PSNR. This ﬁgure

shows that the PSNR gain grows exponentially with

the number of neurons taken into account for the re-

construction. This means that the dual frame correc-

tion, though already signiﬁcant for low rates, becomes

extremely important for high rates.

5 DISCUSSION

We proposed in this work an original exact decoding

procedure for the classical rank order coder deﬁned

in (Van Rullen and Thorpe, 2001). The authors has

then designed a bio-inspired retina model for the im-

age transform and reconstruction. Our contribution

encompasses a theoretical and a technical aspect.

Regarding the theoretical aspect, (i) we proved

that the bio-inspired transform used to model the

(a) (b)

Figure 9: PSNR quality of the reconstruction using the DoG

ﬁlters (Van Rullen and Thorpe, 2001) (in blue solid line)

and the dual DoG ﬁlters (in red dashed line). Results for

cameraman are shown in the ﬁrst line and results for Lena

are shown in the second line. The abscissa represents the

percentage of the highest responses used for the reconstruc-

tion. The ordinate represents the reconstruction quality in

terms of PSNR. 9(a)- 9(c): Results shown for percentages

between 0% and 100%. 9(b)- 9(d): Results shown for per-

centages between 0% and 10%.

retina in (Van Rullen & Thorpe 2001) is non-

invertible as it is, and (ii) we gave an original mathe-

matical proof that this transform if augmented with an

adequate scaling function is a frame. We also showed

that the scaling function besides its mathematical jus-

tiﬁcation has a biological one. We then deﬁned the

corresponding dual frame that is necessary for the ex-

act image reconstruction.

Regarding the technical aspect, we overcame

the problem of memory overhead encountered while

computing this dual frame. Up to our knowledge,

no work in the literature concerned with high dimen-

sionality frame inversion tackled explicitly this prob-

lem (Rakshit and Anderson, 1995; Do and Vetterli,

2003). Indeed usual reconstruction algorithms avoid

such a calculation by using inaccurate, though very

simple, methods. Thus we designed an original recur-

sive out-of-core blockwise algorithm. Our algorithm

is general and could be used in a variety of applica-

tions requiring a high dimension matrix inversion.

Furthermore, the method presented in this pa-

per does not alter the coding procedure and keeps

it straightforward unlike the stimulus-dependent MP

methods in (Perrinet et al., 2004; Bhattacharya and

Furber, 2010). In fact, MP-like algorithms require the

computation of a speciﬁc reconstruction ﬁlter bank

for each speciﬁc image. On the contrary, in our case

the dual vectors used for the reconstruction (i) are

computed once for all and (ii) are the same for all im-

ages. This keeps the decoding procedure committed

to the rank order coding philosophy. Yet, the rank or-

A PERFECTLY INVERTIBLE RANK ORDER CODER

161

dering supposes that the retina cells are independent

and ﬁre asynchronously.

One last major advantage is that our algorithm is

multi-threadable. Indeed, there is no possible data

hazard in the decoding procedure. Each value of f

∗

independent from the others and the concurrent read-

ing in Φ

∗

Φ does not alter the data.

Though it is to be noted that, in some implementa-

tions, the rank order decoder inaccuracy is enhanced

for a supplemental reason: the inexactness of the

look-up-table that might be used used to re-generate

the transform coefﬁcients c

. In this work and for a

sake of clarity, we considered only the ﬁlters over-

lap as a source of error. Otherwise the reader could

not distinguish the part of error due to the ﬁlters over-

lap and the other part that is due to the look-up-table.

In our case, the decoder is supposed to be provided

with an optimal look-up table. Still the approach pre-

sented remains (i) relevant because the inaccuracy of

any look-up-table that might be used will affect both

the ”classical” reconstruction and the ”dual frame”,

(ii) novel through the introduction of the frames the-

ory and (iii) general and thus could be extended to

several models of cortical areas using redundant rep-

resentations.

REFERENCES

Bhattacharya, B. S. and Furber, S. (2007). Maximising in-

formation recovery from rank-order codes. In Pro-

ceedings of SPIE, volume 6570, Orlando, FL, U.S.A.

Bhattacharya, B. S. and Furber, S. (2010). Biologically

inspired means for rank-order encoding images: A

quantitative analysis. IEEE Trans. Neural Netw.,

21(7):1087 –1099.

Burt, P. and Adelson, E. (1983). The Laplacian pyramid

as a compact image code. IEEE Trans. Commun.,

31(4):532–540.

Do, M. and Vetterli, M. (2003). Framing pyramids. IEEE

Trans. Signal Process., 51(9):2329–2342.

Dufﬁn, R. J. and Schaeffer, A. C. (1952). A class of non-

harmonic fourier series. Transactions of the American

Mathematical Society, 72(2):pp. 341–366.

Field, D. (1994). What is the goal of sensory coding? Neu-

ral Comput., 6(4):559–601.

Gollisch, T. and Meister, M. (2008). Rapid neural coding

in the retina with relative spike latencies. Science,

319(5866):1108–1111.

Golub, G. and Van Loan, C. (1996). Matrix computations.

Johns Hopkins Univ Pr.

Kovacevic, J. and Chebira, A. (2008). An introduction to

frames. Foundations and Trends in Signal Processing,

Now Pub.

Masmoudi, K., Antonini, M., Kornprobst, P., and Perrinet,

L. (2010). A novel bio-inspired static image com-

pression scheme for noisy data transmission over low-

bandwidth channels. In Proceedings of ICASSP, pages

3506–3509. IEEE.

Masmoudi, K., Antonini, M., Kornprobst, P., and Perrinet,

L. (2011). A bio-inspired image coder with temporal

scalability. In Proceedings of ACIVS, pages 447–458.

Springer.

Meister, M. and Berry, M. (1999). The neural code of the

retina. Neuron, pages 435–450.

Perrinet, L., Samuelides, M., and Thorpe, S. (2004). Cod-

ing static natural images using spiking event times:

do neurons cooperate? IEEE Trans. Neural Netw.,

15(5):1164–1175.

Rakshit, S. and Anderson, C. (1995). Error correction with

frames: the Burt-Laplacian pyramid. IEEE Trans. Inf.

Theory, 41(6):2091–2093.

Rieke, F., Warland, D., de Ruyter van Steveninck, R., and

Bialek, W. (1997). Spikes: Exploring the Neural

Code. The MIT Press, Cambridge, MA, USA.

Rodieck, R. (1965). Quantitative analysis of the cat reti-

nal ganglion cells response to visual stimuli. Vision

Research, 5(11):583–601.

Thorpe, S. (1990). Spike arrival times: A highly efﬁcient

coding scheme for neural networks. In Eckmiller, R.,

Hartmann, G., and Hauske, G., editors, Parallel Pro-

cessing in Neural Systems and Computers, pages 91–

94. Elsevier.

Thorpe, S. (2010). Ultra-rapid scene categorization with a

wave of spikes. In Biologically Motivated Computer

Vision, pages 335–351. Springer.

Thorpe, S., Fize, D., and Marlot, C. (1996). Speed of pro-

cessing in the human visual system. Nature, 381:520–

522.

Van Rullen, R. and Thorpe, S. (2001). Rate coding versus

temporal order coding: What the retinal ganglion cells

tell the visual cortex. Neural Comput., 13:1255–1283.

Wang, Z., Bovik, A., Sheikh, H., and Simoncelli, E. (2004).

Image quality assessment: from error visibility to

structural similarity. IEEE Transactions on Image

Processing, 13(4):600–612.

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

162