
A MARKOV-CHAIN-BASED MODEL FOR SUCCESS PREDICTION
OF EVOLUTION IN COMPLEX ENVIRONMENTS
Lukas K
¨
onig, Sanaz Mostaghim and Hartmut Schmeck
Institute AIFB, Karlsruhe Institute of Technology, Kaiserstr. 89, 76128 Karlsruhe, Germany
Keywords:
Evolutionary robotics, Swarm robotics, Success prediction, Mathematical model, Markov chain, Selection.
Abstract:
In this paper, a theoretical and experimental study of the influence of environments on the selection process
in evolutionary swarm robotics is conducted. The theoretical selection model is based on Markov chains. It is
proposed to predict the success rate of evolutionary runs which are based on a selection mechanism depending
on implicit environmental properties as well as an explicit fitness function. In the experiments, the interaction
of explicit and implicit selection is studied and a comparison with the model prediction is performed. The
results indicate that the model prediction is accurate for the studied cases.
1 INTRODUCTION
Evolutionary Robotics (ER) is a methodology for the
automatic creation of robotic controllers. Similarly to
classic Evolutionary Computation (EC) methods, in
ER individuals from a population of robot controllers
are selected for mating (optionally using recombina-
tion) and are randomly mutated to achieve some de-
sired behavioral property of a single robot or a collec-
tion of robots (swarm). For instance, a single robot
can be trained to avoid obstacles or a swarm of robots
can be trained to collectively transport a heavy ob-
ject (Gross and Dorigo, 2009). While the field of ER
goes beyond the evolution of robot controllers and
captures, e. g., approaches to evolve real robot hard-
ware, in this paper, we focus on the evolution of con-
trollers for a swarm of mobile robots, i. e., the field of
Evolutionary Swarm Robotics (ESR) or, more gener-
ally, on the evolution of agent behaviors in complex
environments.
A key problem in ESR is to accurately select
evolved controllers for producing offspring with re-
spect to performing a desired behavior (Nolfi and Flo-
reano, 2001). This means that “better” controllers in
terms of the desired behavioral qualities should have
a higher chance of being selected than “worse” ones.
However, it is usually not possible to grade arbitrary
evolved controllers detached from the environment in
which the desired task has to be accomplished. There-
fore, ESR scenarios typically require the existence of
an environment (real or abstracted) where the con-
trollers can be tested in. Using an environment to
establish the quality of controllers makes ESR more
closely related to natural evolution than most classic
EC approaches. Here, the selection process can be
seen from the classic EC or the biological point of
view.
The Classic EC Point of View. In classic EC, selec-
tion is usually performed by considering the fitness
(i. e., a numeric value that reflects the relative qual-
ity of an individual) of all individuals of a population
and favoring the better ones. In ESR, fitness is com-
puted by observing an individual’s performance in an
environment. This environmental fitness calculation
can be noisy, fuzzy or time-delayed. Additionally, the
environment is often responsible for an implicit pre-
selection of individuals. In such cases the individuals
have to match some environmental requirement (e. g.,
spatial proximity) to be even considered for fitness-
based selection. For instance, in a decentralized sce-
nario where robots perform reproduction when they
meet, evolution selects implicitly for the ability to
find other robots – in addition to the explicit selection
based on a given fitness function (Bredeche and Mon-
tanier, 2010). Nolfi and Floreano refer to these two
different factors influencing selection as explicit vs.
implicit fitness (Nolfi and Floreano, 2001). We will
stick to this denomination in the following; for abbre-
viation we will also write “fitness” when meaning ex-
plicit fitness. Thus, the environment adds fuzziness,
noise and time-dependencies to the calculation of fit-
90
König L., Mostaghim S. and Schmeck H..
A MARKOV-CHAIN-BASED MODEL FOR SUCCESS PREDICTION OF EVOLUTION IN COMPLEX ENVIRONMENTS.
DOI: 10.5220/0003677700900102
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 90-102
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

ness and it introduces a complex implicit fitness to the
selection process. Furthermore, by performing adap-
tive parameter control (Eiben et al., 2000), which is a
promising approach for reducing parameter complex-
ity in ESR, even more complicated fitness functions
can arise. Finally, an erroneous design of the fitness
function can also corrupt the fitness measure.
The Biological Point of View. In evolutionary biol-
ogy, the reproductive fitness of an individual is cal-
culated from the ability of the individual to both sur-
vive and reproduce with the consequence of contribut-
ing to the gene pool of future generations. There are
several competing definitions on how to exactly cal-
culate reproductive fitness in nature (e. g., short-term
vs. long-term calculations), cf. (Sober, 2001), which,
however, are beyond the scope of this paper. Repro-
ductive fitness in nature as well as explicit and im-
plicit fitness in ESR reflect the ability of an individual
to be selected to produce offspring. However, while
reproductive fitness in natural evolution is an observ-
able but (mostly) unchangeable property, implicit and
explicit fitness in ESR can be designed to guide the
evolution in a certain direction. There, explicit fit-
ness is rather straight-forward to design as it captures
properties that can be encoded and calculated as num-
bers. For example, when evolving collision avoid-
ance, driving can give positive fitness points while
being close to a wall or producing a collision can be
graded negatively. Implicit fitness, on the other hand,
is more complex and difficult to influence as the entire
environment has to be designed accordingly. Implicit
fitness can also include complex long-term proper-
ties. E. g., A robot can promote its own offspring by
helping its descendants to produce new offspring. As
the offspring contains partially the same genes as the
robot itself, the robot’s implicit fitness increases due
to the higher chance of contributing to the gene pool
although its own reproduction rate is not improved.
As opposed to nature, in ESR we want to direct
evolution in a certain direction. Therefore, we can de-
sign the explicit fitness function and, to some extent,
implicit environmental selection properties according
to desired behavioral criteria. For instance, we can
look at a swarm that is explicitly selected for the abil-
ity to find a shortest path from a nest to some forage
place. If the shortest path is too narrow to fit all the
individuals passing it at a time, evolution might im-
plicitly select for individuals that use a longer path or
those who can decide to take a path based on conges-
tion rates. Depending on the exact properties of the
different paths, implicit selection might completely
overrule explicit selection in this example. Overall, it
turns out that in complex environments explicit fitness
can play a subordinated role while implicit fitness has
the major impact on selection. On the other hand, ex-
plicit fitness is easier to define in a proper way to drive
evolution in a desired direction. Therefore, both im-
plicit and explicit selection have to be used to induce
a successful ESR run. In (Bredeche and Montanier,
2010), the impact of the environment has been ex-
perimentally investigated on a similar scenario using
only implicit selection. There, robots evolved to ex-
plore the environment as they were selected for mat-
ing when they came spatially close to each other. In
a second experiment, robots learned foraging being
implicitly forced to collect energy or to die otherwise.
There are many approaches from the field of clas-
sic EC (namely EA, ES, GA, GP, EP, spatially dis-
tributed EA, etc.) to model the selection processes
in a population of an evolutionary run, e. g., (Pr
¨
ugel-
Bennett and Rogers, 2001), (Arnold, 2001), (Pietro
et al., 2004), etc.; furthermore, there are models of
natural processes from the field of evolutionary biol-
ogy, e. g., (Kessler et al., 1997), and general concepts
like genetic drift (Kimura, 1985) and schema theory
(Holland, 1975). However, these models do not ap-
ply well to ESR scenarios due to the above mentioned
differences concerning explicit and implicit selection.
The goal in this paper is to theoretically and ex-
perimentally study the influence of environment on
the evolution. We present a model based on Markov
chains that can be used to predict the success of an
ESR run depending on implicit selection properties
and the selection confidence of a system, i. e., a mea-
sure for the probability of selecting the “better” out of
two different robots in terms of the desired behavioral
properties. We use a mating procedure that is based
on the idea of tournament selection meaning that k
robots are selected (implicitly) by the environment,
one of which is selected (explicitly) to overwrite the
controllers of the k − 1 other ones by its own. In bi-
ological terms, this can be described as sexual repro-
duction without recombination with k parents and no
genders, i. e., every individual can mate with all oth-
ers. Both selection confidence and implicit selection
probabilities of the environment are parameters to the
model. We focus on the selection process without di-
rectly modeling a controller mutation, i. e., we look at
the process “between mutations”. The model can be
used to estimate the success probabilities of superior
mutations over inferior ones in an evolutionary run
before it is actually performed in a real environment.
2 PRELIMINARIES
In this section we first describe the algorithm for the
evolutionary model that is the basis for the presented
A MARKOV-CHAIN-BASED MODEL FOR SUCCESS PREDICTION OF EVOLUTION IN COMPLEX
ENVIRONMENTS
91

theoretical framework. Then we make some prelim-
inary assumptions and define Markov chains as used
throughout this paper.
The Evolutionary Model. We assume an environ-
ment E including a population of n robots. We leave
the terms “environment” and “robot” (or, more gen-
erally, “agent”) loosely defined as we want to cap-
ture as many as possible of the numerous and partially
conflicting definitions in the literature. For a discus-
sion of the definitions of environments in multi-agent
systems, cf. (Weyns et al., 2005). In this paper, an
environment is thought of as a system that is at ev-
ery point in time in some state out of a specific state
space. Robots (or agents) are entities that can get in-
formation about the current environment state over a
defined set of sensors and influence the succeeding
state by a defined set of actions. Being in some sense
part of the environment themselves, robots can also
get information about their own internal state through
sensors and change it through actuators. The process
of deciding from sensory data which actions to per-
form is described by the controller of a robot.
Alg. 1 describes the evolutionary process as pre-
sumed for applying the proposed prediction model.
The algorithm is stated from a population point of
view, but it can also be applied in a decentralized way
as in (Watson et al., 2002) (cf. Sec. 5). The func-
tion Initialize places n robots at random positions in
the environment E and assigns them some arbitrary
(empty or pre-defined) controllers from the vector
~
Γ.
We assume that the population of robots is identi-
fied by the population of controllers
~
Γ = (γ
1
, . . . γ
n
).
The controllers may be of any common type like ar-
tificial neural networks or finite state machines; the
latter ones are used in this paper. Execute(
~
Γ) runs
the controllers for one step; this can occur sequen-
tially or concurrently (as required for decentralized
scenarios). The fitnesses of the controllers are stored
in
~
F and computed by an explicit fitness function
f . Function Mutate indicates the mutation operator
which is performed repeatedly at time intervals of
mutInterval. Since mutation is not part of the pre-
diction model, it is assumed that the model is applied
between mutation operations (or at least between such
mutations that actually change the behavioral quality
of a robot). The mating process is a variant of the
well-known tournament selection from classic evolu-
tionary computation: Function Match selects a set
of controllers T with size k. This selection can de-
pend on environmental properties (e. g., spatial prox-
imity). Among the selected controllers T , the con-
troller index is fitness-proportionally chosen by the
function S elect to overwrite the controllers in T.
Assumptions. In the following, we declare three as-
Algorithm 1: Basic ESR run as required for the
application of the prediction model.
input : Population of n initial controllers
~
Γ = (γ
1
, . . . γ
n
); environment E;
tournament size k; maximal runtime
maxT ime; explicit fitness function f .
output: Evolved population.
Initialize(
~
Γ, E)
for t ← 1 to maxT ime do
Execute(
~
Γ) // Run controllers
~
F B f (
~
Γ) // Compute explicit fitnesses
if t mod mutInterval == 0 then
Mutate(
~
Γ) // Mutation
end
//Mating
T B Match(k,
~
Γ, E)
if T , ∅ then
index B S elect(T, F)
forall the Γ(i) ∈ T do
Γ(i) = Γ(index)
end
end
end
return
~
Γ
sumptions that are valid throughout this paper. These
assumptions should provide a simplified view on an
ESR run, and still capture its essential properties.
1. Mating is based on a variant of tournament selec-
tion in which the building of tournaments is not
necessarily uniformly randomized (see Alg. 1).
Tournament selection is a natural choice in ESR
scenarios due to the existence of communica-
tion constraints (e. g., a limited communication
distance or a limited number of communication
channels). An obvious way to deal with this is to
select small groups of robots that match the con-
straints and to let them reproduce.
2. At any time step, the population
~
Γ can be divided
into two subpopulations each of which contains
only individuals of (nearly) equal quality in terms
of the desired behavior. Without loss of general-
ity, we say that S is a subpopulation with superior
behavior in terms of the desired behavior than the
inferior subpopulation I =
~
Γ\S. We denote this
relation of behavioral quality of
~
Γ as R(
~
Γ) =
s
/
i
with s = |S| and i = |Γ| − s = |I| being the num-
ber of individuals in population S and I, respec-
tively. Shorter, we write just R(
~
Γ) = s = |S| if
|
~
Γ| is known denoting only the superior individu-
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
92

als. I. e., , only one or maximally two basically
different behaviors are existing at the same time;
they can obviously be split into a better (or equal)
subpopulation S and a worse (or equal) subpopu-
lation I. This assumption is less restrictive than it
looks like, as it describes the most commonly ob-
served situation during typical ESR runs. Further-
more, it reflects the biological situation where a
major factor of evolution, especially in small pop-
ulations, is thought to be genetic drift. This leads
to large neutral plateaus of nearly equal fitness
that are rather rarely affected by superior or infe-
rior mutations (Kimura, 1985). From this point of
view the capability of selecting superior individu-
als over inferior ones reflects the expected success
of evolution.
3. On average, the reproduction capability of a robot
depends only on its own controller and the con-
trollers of the other agents and not on other fac-
tors from the environment. Particularly, a robot’s
long-term chance of being selected has to be in-
dependent of its current state in the environment.
For instance, if robots reproduce when meeting
each other, we assume that there is no obstacle
in the environment which prohibits reproduction
for parts of the population by separating them in
a closed area. This assumption should hold in all
“reasonable” scenarios where the robots are capa-
ble of improving their chance for reproduction by
altering their controller. Of course, in a real-world
scenario it can happen, e. g., that a robot falls into
a hole which it cannot leave whatever controller it-
self or the other robots have. However, this seems
to be a situation which cannot be resolved by an
improvement of the evolution process, but rather
is a problem of appropriate hardware design for a
given scenario. Therefore, we assume that such
situations do not occur during an ESR run.
Markov Chains. Given a finite state space M a (first
order) Markov chain is given by the probabilities to
get from one state to another. There, the Markov
property has to be fulfilled, which requires that future
states depend only on the current state, but not on the
past states. We define a Markov chain in a common
way according to (Grinstead and Snell, 1997).
Definition 1. Markov Chain.
A Markov chain is given by a finite state space
M = {m
1
, . . . , m
|M|
} and a matrix of probabilities
p
i j
, 1 ≤ i, j ≤ |M| determining the probability to get
in one step from m
i
to m
j
.
3 COMPLETELY IMPLICIT
SELECTION (CIS)
In this section, we investigate a Completely Implicit
Selection process using a homogeneous Markov chain
model. It works without any explicit fitness function,
i. e., the function f returns the constant 1.
3.1 Mating Size 2
First we start with the mating size set to k = 2 (CIS-
2). This is the most simple version of the model and
a natural starting point.
An example for a scenario that is captured by the
CIS-2 model is an environment where a robot has to
come close to another robot for mating. Mating is per-
formed by randomly selecting one robot that copies
its controller to the other one. Here, the environ-
ment implicitly selects for the ability of finding an-
other robot – maybe in a labyrinth; however, selection
pressure is quite low as a robot that waits for another
one to come has during mating the same chances of
passing on its controller as the other one that actively
explored the environment. Therefore, superior indi-
viduals are necessary for making mating possible but
they are not explicitly selected for.
In the general CIS-2 scenario, two robots mate
when they match some arbitrary mating criterion. The
winner is then chosen by uniform distribution (as the
fitness function returns always 1) which means that it
is uniformly random which robot gives its controller
to the other one. As each of the robots in a mating
tournament may be from one of the sets S or I, one
of the four situations II, IS, SI, SS can occur in a
mating tournament. For the cases II and SS, there
is no change made to the population; for the cases
IS and SI chances are 0.5 for both overwriting the
controller from S with the controller from I and vice
versa. Therefore, the population will either gain a new
S robot and lose an I one or the other way around, cf.
Fig. 1).
The mating process of a population with n individ-
uals can be written as an n+1×n+1 transition matrix.
The rows and columns correspond to the different
possible states of a population and the entries denote
the probabilities for a state transition. The n + 1 dif-
ferent possible states are denoted by
0
/
n
,
1
/
n-1
, . . . ,
n
/
0
where
i
/
s
means i superior and s = n −i inferior robots
in the population (we will also write simply i for this
situation if n is known). An entry p
i j
is the probability
that a population that is currently in state i changes to
state j after one mating event. This implies that every
row of the matrix sums up to 1.
A MARKOV-CHAIN-BASED MODEL FOR SUCCESS PREDICTION OF EVOLUTION IN COMPLEX
ENVIRONMENTS
93

I
I
S
S
I
S
S
I
No change to population
50 % +1 superior / -1 inferior
50 % -1 superior / +1 inferior
Figure 1: Without any explicit fitness, the winner of a tour-
nament is drawn in a uniformly random way. For k = 2,
there are equal chances for the population to gain or to lose
a superior individual.
For the mating procedure described above, the ma-
trix P
CIS −2
is given by
P
CIS −2
=
0
/
n
· · ·
i-1
/
n-i+1
i
/
n-i
i+1
/
n-i-1
· · ·
n
/
0
0
/
n
1
.
.
.
.
.
.
0
i
/
n-i
c
i
2
s
i
c
i
2
.
.
. 0
.
.
.
n
/
0
1
with
∀i ∈ {1, . . . , n − 1} : c
i
, s
i
∈ [0, 1], c
i
+ s
i
= 1.
There, the c
i
, s
i
are the probabilities that in population
state
i
/
n-i
a mating induces a state change (c
i
, i. e., two
different robots mate) or the population stays in the
same state (s
i
, i. e., two uniform robots mate). In the
states
0
/
n
and
n
/
0
there are no different individuals in
the population, therefore, no state change can be in-
duced by mating. These states cannot be left once one
of them is entered and the population remains stable
henceforth. In a transition matrix such a state is al-
ways indicated by a 1 at a diagonal entry.
3.2 Eventual Stable States (k = 2)
We are now interested in the long-term development
of a population, namely in the question if the popula-
tion will eventually enter the stable state
n
/
0
. This is
the desired case where all individuals received a su-
perior controller. On the other hand, if the population
enters the state
0
/
n
this means that there are only infe-
rior individuals in the population left and the selection
mechanism was not capable of preserving the supe-
rior controller. Therefore, the probability for eventu-
ally entering the stable state
n
/
0
is an indicator for the
quality of the chosen selection mechanism.
The transition matrix P
CIS −2
from above defines
a homogeneous Markov chain with the states S =
{
0
/
n
,
1
/
n-1
, . . . ,
n
/
0
}
. Note that two states of the chain
are absorbing in the sense that there is no way to leave
them. The set of absorbing states is A = {
n
/
0
,
0
/
n
} ⊂ S .
As an absorbing state can be reached from every state
s ∈ S \A, the matrix P is called absorbing and the
non-absorbing states T = S \A are called transient.
If the matrix is raised to the power of n, an entry
p
i j
of the resulting matrix displays the probability that
state j is reached after n steps if the population started
in state i. As we are interested in the eventual stable
state of the system we want to calculate the limit
P
∞
CIS −2
= lim
n→∞
P
n
CIS −2
.
As shown in (Grinstead and Snell, 1997) the matrix
P
∞
CIS −2
exists meaning every entry p
(∞)
i j
converges.
The limit can generally be calculated for every ab-
sorbing Markov chain (thus, particularly for all chains
in this paper). The limit matrix has non-zero entries
in the columns which denote the absorbing states and
zero entries at all other positions (as there is a non-
zero chance for every transient state to reach an ab-
sorbing state). Therefore, it is only necessary to cal-
culate the absorbing columns of the limit matrix.
For any absorbing Markov matrix P the non-zero
columns of P
∞
can be calculated by the following
procedure. First, the canonical form CF
P
of the ma-
trix P is generated by shifting all absorbing states to
the end in rows and columns such that an identity sub-
matrix is built at the right bottom corner of P. For the
matrix P
CIS −2
the
0
/
n
-state is already at the correct po-
sition; the
n
/
0
-state has to be shifted to the next to last
position (in rows and columns):
CF
P
CIS −2
B
s
1
c
1
· · · c
1
0
.
.
.
0 0
· · · c
j
s
j
c
j
· · ·
.
.
.
.
.
.
.
.
.
0 0
· · · c
n−1
s
n−1
0 c
n−1
0 · · · 0 1 0
0 · · · 0 0 1
The new matrix has now generally the form
CF
P
=
Q R
0 I
!
where Q consists of transitions between transient
states, R consists of transitions from transient states
to absorbing states, I is an identity matrix reflecting
transitions within absorbing states and 0 is a zero ma-
trix. The matrix N
P
with
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
94

N
P
= (I − Q)
−1
(where I is an identity matrix with the same size as Q)
is called the fundamental matrix. Now, in the matrix
L
P
= N
P
· R
an entry l
i j
is the probability that the absorbing chain
will be absorbed in the absorbing state j if the process
starts in state i. Therefore, L contains exactly the non-
zero columns of the desired limit matrix P
∞
.
For the matrix P
CIS −2
the limit calculates to
L
P
CIS −2
=
0
/
n
n
/
0
0
/
n
1 0
1
/
n-1
1 −
1
n
1
n
2
/
n-2
1 −
2
n
2
n
.
.
.
.
.
.
.
.
.
n-2
/
2
2
n
1 −
2
n
n-1
/
1
1
n
1 −
1
n
n
/
0
0 1
independently of the c
i
and s
i
probabilities. Note that
the probability for ending in the superior state in-
creases linearly with the number of superior robots
at the beginning. Simultaneously, the probability for
ending in the inferior state decreases at the same
range. This result is quite intuitive as in the CIS-2
scenario the winner within a tournament is drawn by
uniform probabilities. The order in which they are put
together to tournaments does not have an influence on
the overall probabilities of reaching one of the stable
states.
The fact that the probabilities for entering the su-
perior state are symmetrical to entering the inferior
state has as a consequence that the long-term success
of CIS scenarios is compromised. During evolution,
a population does not persist in a stable state, but is
attacked by mutations that can cause a transition from
one stable state (neutral plateau) to another. If the
chances for an inferior mutation to overrule the popu-
lation are the same as for a superior mutation, the pop-
ulation cannot constantly remain in an improvement
process. Usually the initial population has a low be-
havioral quality, therefore, a CIS-2 scenario can lead
to improvements in the beginning, but they cannot re-
main stable in the long-term.
3.3 Mating Size k
The above CIS-2 scenario can be stated in a more gen-
eral form for a mating neighborhood of size k (CIS-k).
At first, an explicit fitness function is still omitted.
The CIS-k scenario considers an k-sized tourna-
ment for mating. One of the k controllers is selected
by a uniform probability to be copied to all other
robots in the tournament during mating. Using the
same notation as in Sec. 3.1, the CIS-k transition ma-
trix P
CIS −k
is given in Fig. 2.
As in the CIS-2 case an entry p
i j
of the matrix
P
CIS −k
is the probability that a population in state i
switches to state j by a mating event. By c
i j
we de-
note the probability that in a population that is cur-
rently in state
i
/
n-i
the next mating event is based on a
j
/
k-j
tournament, i. e., a tournament with j superior and
k − j inferior individuals. The diagonal elements of
the matrix (marked by a box in the figure) denote the
probability that the population state does not change
by a mating. Therefore, they are given by the sum of
the probabilities for a tournament with only superior
and a tournament with only inferior individuals, i. e.,
p
ii
= c
i0
+ c
ik
.
For calculating the left/bottom non-diagonal en-
tries p
i j
(i > j) we have to consider the probability
c
i,i− j
that a
i-j
/
k-i+j
tournament occurs in an
i
/
n-i
popu-
lation; such a tournament can turn a population from
state
i
/
n-i
to
j
/
n-j
. This probability has to be multiplied
by the probability that an inferior individual will win
the tournament (since j < i means that the number
of superior individuals decreases). As the individuals
are drawn by uniform distribution from the tourna-
ment, this probability is depending only on the num-
ber of superior and inferior individuals. It is given by
k−(i− j)
k
. The overall probability that defines an entry
p
i j
, i > j is given by
p
i j
=
k − (i − j)
k
· c
i,i− j
Analogously the right/top non-diagonal entries
p
i j
, i > j can be computed by
p
i j
=
k − ( j − i)
k
· c
i,k− j+i
It has to hold for all c
i j
in the matrix P
CIS −k
:
∀i ∈ {1, . . . , n − 1} :
min(k,i)
X
j=max(0,i+k−n)
c
i j
= 1
c
i j
∈ [0, 1]
.
This implies that the sum of every row i of the matrix
P
CIS −k
is 1.
During one mating, at most k − 1 individuals can
be turned from S to I or vice versa. That is reflected
by the fact that all probabilities c
i j
with j < 0 or j > k
are zero. Therefore, at most the k − 1 elements left
and right of the diagonal elements in matrix P
CIS −k
are non-zero. Furthermore, in populations with i < k
superior (n − i < k inferior) individuals all probabil-
ities c
i j
with j > i ( j > n − i) have to be zero as at
most i superior (n − i inferior) individuals can be in a
tournament. Therefore, the matrix C which is given
A MARKOV-CHAIN-BASED MODEL FOR SUCCESS PREDICTION OF EVOLUTION IN COMPLEX
ENVIRONMENTS
95

P
CIS −k
=
0
/
n
1
/
n-1
2
/
n-2
· · ·
k
/
n-k
k+1
/
n-k-1
· · ·
i-2
/
n-i+2
i-1
/
n-i+1
i
/
n-i
i+1
/
n-i-1
i+2
/
n-i-2
. . .
0
/
n
1 0 0 0 0 0 0 0 0 0
1
/
n-1
k−1
k
c
1,1
c
1,0
+ c
1,k
0
.
.
.
1
k
c
1,1
0
.
.
. 0 0 0 0 0 . . .
2
/
n-2
k−2
k
c
2,2
k−1
k
c
2,1
c
2,0
+ c
2,k
2
k
c
2,2
1
k
c
2,1
0 0 0 0 0
.
.
.
.
.
.
i
/
n-i
0 0 0 0 0 · · ·
k−2
k
c
i,2
k−1
k
c
i,1
c
i,0
+ c
i,k
k−1
k
c
i,k−1
k−2
k
c
i,k−2
. . .
.
.
.
.
.
.
.
.
.
Figure 2: General transition matrix for selection without an explicit fitness function in a population of size n, using mating
tournaments of size k. Diagonal elements are marked by a surrounding box; they represent transitions where no state change
occurs as only one agent type (“superior” or “inferior”) is selected in a tournament. The matrix has at most k − 1 non-zero
elements at the left and the right side of the diagonal elements of every row. All rows sum up to 1.
by the probabilities c
i j
for 0 ≤ i ≤ n, 0 ≤ j ≤ k has
the form
C =
0
/
k
1
/
k-1
2
/
k-2
· · ·
k-1
/
1
k
/
0
0
/
n
1 0 0 · · · 0 0
1
/
n-1
c
1,0
c
1,1
0 · · · 0 0
.
.
.
.
.
.
.
.
.
i
/
n-i
c
i,0
c
i,1
c
i,2
· · · c
i,k−1
c
i,k
.
.
.
.
.
.
.
.
.
n-1
/
1
0 0 0 · · · c
n−1,k−1
c
n−1,k
n
/
0
0 0 0 · · · 0 1
There are k · (n − k) + n + 1 non-zero entries in C.
Every row has to sum up to 1 in this matrix as well.
3.4 Eventual Stable States (Arbitrary k)
By the same procedure as in Sec. 3.2 the probability
for a population eventually reaching the stable states
0
/
n
and
n
/
0
when starting in some state
i
/
n-i
can be com-
puted. As the choice of an individual in a tournament
is still uniform, it is not surprising that for all mat-
ing sizes k and all probability matrices C the prob-
ability distribution is the same as in the CIS-2 case:
L
P
CIS −k
= L
P
CIS −2
.
However, the expected time to absorption, i. e.,
the number of mating events until a stable state is
reached, decreases if k is increased. The expected
time to absorption of a Markov chain given by matrix
P is given by a vector t; a position t
i
of the vector is
the expected number of mating events until the chain
is in an absorbing state if it starts in state i. The vector
t can be computed by
t = N
P
· v
where N
P
is the fundamental matrix of P (cf. Sec. 3.2)
and v is a column vector all of whose entries are 1.
For example, the expected time to absorption is
depicted in Fig. 3 for population size n = 10 and tour-
nament sizes k = 2, . . . , 9. Obviously, the time to
absorption decreases drastically from mating size 2 to
mating sizes 3 and 4. However, it is important to note
that “time” is measured here in terms of the number
of mating events. Depending on the environment it
may take longer in terms of evolution time to select
tournaments of bigger size than those of smaller size.
30
40
50
60
70
80
k=2
k=3
k=4
k=5
k=6
k=7
a
tingeventstoconvergence
0
10
20
0/10 1/9 2/8 3/7 4/6 5/5 6/4 7/3 8/2 9/1 10/0
k=8
k=9
Expected m
a
Initialpopulationstate
Figure 3: Expected time to absorption as a function of the
initial population state (
0
/
10
, . . . ,
10
/
0
) for tournament sizes
k = 2, . . . , 9 in a population with n = 10 individuals.
4 COMBINATION OF EXPLICIT
AND IMPLICIT SELECTION
(EIS)
In the CIS scenarios above, explicit fitness has not
been considered in the model. In this section an ex-
tension is introduced to model explicit fitness. We in-
troduce an explicit fitness to the model by making the
probability for superior individuals to be winners in
a tournament higher than that of inferior individuals.
In the evolution process described by Alg. 1 explicit
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
96

T. M.
i-k+1
/
n-i+k-1
.
i-2
/
n-i+2
i-1
/
n-i+1
i
/
n-i
i+1
/
n-i-1
i+2
/
n-i-2
.
i+k-1
/
n-i-k+1
Tourn.
k-1
/
1
.
2
/
k-2
1
/
k-1
k
/
0
or
0
/
k
k-1
/
1
k-2
/
2
.
1
/
k-1
i
/
n-i
1−c
k
c
i,k−1
.
(k−2)(1−c)
k
c
i,2
(k−1)(1−c)
k
c
i,1
c
i,k
+ c
i,0
k−(1−c)
k
c
i,k−1
k−2(1−c)
k
c
i,k−2
.
k−(k−1)(1−c)
k
c
i,1
Figure 4: Non-zero entries of an inner row
i
/
n-i
of a general EIS transition matrix. The first heading denotes the column of the
transition matrix, the second one the corresponding mating tournament, i. e., the column of the probability matrix C the c
i, j
values are taken from.
fitness is given by the function f . It is calculated from
environmental variables and is intended to measure
the desired behavioral qualities. Factors like noise in
the environment, delayed fitness calculation and erro-
neous design of the fitness function can corrupt the
fitness measure. Therefore, the probability that a su-
perior individual is selected explicitly over an inferior
individual is usually below 1.
To reflect the influence of f to selection, a con-
fidence factor c ∈
[
0, 1
]
is introduced which states
how accurately f differentiates between superior and
inferior individuals. A low value for c means that the
explicit fitness cannot increase the chance that a supe-
rior individual is chosen in a tournament. For a value
c = 0 the EIS model is equivalent to the CIS model.
A high value means that it is likely for a superior in-
dividual to be chosen; c = 1 means that in every tour-
nament that contains at least one superior individual
such an individual will win.
The confidence factor is included to the model as
follows: at the left/bottom side of the diagonal of the
transition matrix the entries are multiplied by (1 − c).
At the right/top side of the diagonal the enumerator
k−( j−i) is replaced by k−( j−i)(1−c). By this means
the chance for switching to a state right of the diago-
nal gets higher when c is increased (to maximally the
c
i,i− j
value) while the chance for switching to a state
left of the diagonal decreases (to minimally 0). The
diagonal entries do not have to be changed as the cor-
responding tournaments consist of uniform individu-
als. It is obvious that each row of the matrix still sums
up to 1.
Generally, for population size n, tournament size
k and fitness confidence factor c the n + 1 × n + 1
transition matrix P
EIS −k
is given by
p
i j
=
c
i0
+ c
ik
if i = j,
(k−(i− j))(1−c)
k
c
i,i− j
if i − k < j < i,
k−( j−i)(1−c)
k
c
i,k− j+i
if i < j < i + k,
0 otherwise
A complete inner row of the most general form of
the transition matrix is given in Fig. 4. Note that the
restrictions to the tournament probability values given
in matrix C in Sec. 3.3 are valid as well here.
Influence of the Probability Matrix C. The proba-
bility matrix C (cf. Sec. 3.3) defines the probabilities
for different mating tournaments to occur. It is influ-
enced by the environment and the concrete selection
strategy. For a real ESR scenario it has to be identi-
fied experimentally in preliminary tests or estimated.
A first guess can be a uniform distribution within ev-
ery row.
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Purely_I
Cubic_I
Quadratic_I
Linear I
0.0
0.1
0.2
0.3
0.4
0123456789101112131415161718192021222324252627282930
Linear
_
I
Uniform
Linear_S
Quadratic_S
Cubic_S
Purely_S
Figure 5: Probabilities for converging eventually to the su-
perior state
n
/
0
as a function of the initial population state
(the numbers i labeling the X-axis denote the initial popu-
lation state
i
/
n-i
); plotted for population size n = 30, tourna-
ment size k = 4, confidence factor c = 0.2, and 9 different
tournament probability distributions C. The plot “Uniform”
refers to a uniform distribution in C. The plots “Cubic I”,
“Quadratic I” and “Linear I” refer to the distributions of
C where the chances for inferior tournaments are higher,
the plots “Cubic S”, “Quadratic S” and “Linear S” to those
where the chances for superior tournaments are higher; the
plots “Purely I” and “Purely S” refer to the extreme cases
where only
1
/
3
and
3
/
1
tournaments are selected, respectively
(cf. description in text).
In an EIS scenario, the probabilities in C can have
an impact on the convergence probabilities of an evo-
lutionary run. Fig. 5 shows the probabilities of a pop-
ulation for converging to the superior state (i. e., all
individuals are superior) as a function of the initial
population state (i. e., the number of superior individ-
uals in the initial population) for different probability
distributions C. The thick black plot in the middle
corresponds to a uniform distribution in every row of
C. For the 3 gray plots right of the middle, the prob-
ability for a tournament
i
/
k-i
to occur is increased in
a linear, quadratic or cubic manner with the number
of superior individuals (i. e., the probability is set to
(i + 1)
e
for e ∈ {1, 2, 3} and then normalized such that
every row of C sums up to 1; the population state
A MARKOV-CHAIN-BASED MODEL FOR SUCCESS PREDICTION OF EVOLUTION IN COMPLEX
ENVIRONMENTS
97

is not taken into account). Symmetrically, For the
3 gray plots left of the middle, the probability is in-
creased with the number of inferior individuals (i. e.,
for a tournament
i
/
k-i
it is set to (k − i + 1)
e
and then
normalized). The leftmost and rightmost plots labeled
“Purely I” and “Purely S”, respectively, belong to the
extreme settings where selection is performed with a
probability of 1.0 in
1
/
3
and
3
/
1
tournaments, all other
entries of C being set to 0 (except for the impossible
cases in the three upper or lower rows; here the col-
umn which is as near as possible to the
1
/
3
or
3
/
1
tour-
nament, respectively, is set to 1.0). These two plots
can be seen as the limits of the polynomial plots de-
scribed above for e → ∞, i. e., within this range all
the polynomial plots lie, when e is allowed to be an
arbitrary number.
Note that the plots that gain the highest chances
for eventually converging to the superior state (left
of the middle) are those that have the highest chance
of selecting inferior tournaments. Accordingly, the
plots with the lowest success rate are those that select
mainly for superior tournaments. This observation is
against the intuition that selection should always favor
superior individuals over inferior ones. In the given
scenario selecting tournaments with few superior in-
dividuals that, in consequence, have a relatively high
chance of converting a lot of inferior individuals pays
off more than selecting superior tournaments which
can convert few inferior individuals at a time and in-
clude a risk that an inferior individual converts a lot
of superior ones.
5 EXPERIMENTS
The presented model is firstly applied to two rather ar-
tificial ESR scenarios with a centralized selection op-
erator. Secondly, a more realistic decentralized ESR
scenario is studied. In the first part of this section the
evolutionary setup is described. Afterwards, the ex-
perimental results are presented and discussed.
5.1 Evolutionary Setup
In the experiments, we utilize the evolutionary setup
described in (K
¨
onig et al., 2009) based on finite state
machines (FSM).
Robot Platform. The experiments have been per-
formed on a simulated Jasmine-IIIp robot platform.
The Jasmine IIIp series is a swarm of micro-robots
sized 29 × 29 × 26 mm
3
(cf. Fig. 6(a)). Every robot
can process simple motoric commands like driving
forward or backward or turning left or right. Every
robot has seven infra-red sensors (as depicted in Fig. 6
(b)) returning values from 0 to 255 in order to mea-
sure distances to obstacles. The Jasmine-IIIp robot
has more sensory capabilities which are described at
www.swarmrobot.org. In this paper only the above
described capabilities are used. In simulation a robot
drives 4 mm per simulation step or turns 10 degrees to
the left or right. When a robot collides with another
robot or with a wall, a crash simulation is performed
that positions the robot at a new random free place at a
distance of at most 4 mm from the crash position and
turns it by a random angle (if no such position exists,
the robot remains at its last position before the crash).
(a) (b)
3
4
5
6
7
1
Forward movement
2
Figure 6: Jasmine-IIIp robot. (a) Photography of a Jas-
mine IIIp next to a 1-Euro coin. (b) Placement of infra-
red sensors for distance measurement around a Jasmine IIIp
robot; sensors 2 to 7 are using an infra-red light source with
an opening angle of 60 degrees to detect obstacles in every
direction of vision. Sensor 1 has an angle of 20 degrees to
allow detection of more distant obstacles in the front.
Controller Model. Robot controllers are encoded as
FSMs which implement a model called Moore Au-
tomaton for Robot Behavior (MARB) as presented
in (K
¨
onig and Schmeck, 2008) and (K
¨
onig et al.,
2009). Each state of a MARB defines one elementary
action for the robot to execute. The transitions be-
tween the states are attached to conditions that can be
evaluated using the sensory input of the robot. Condi-
tions can be atomic (i. e., true, f alse or a comparison
of two sensor outputs or constants using one of the
relations “<, >, ≤, ≥, =, ,, ≈, 0”) or conjunctions and
disjunctions of other conditions.
Example conditions are: true; h
1
< h
2
; 20 > h
7
;
(h
1
≈ h
2
OR h
2
0 120). A condition is evalu-
ated to true or f alse by replacing the sensor variables
h
1
, . . . , h
7
by the current sensor data of the infra-red
sensors 1, . . . , 7. There, the relation ≈ is true if and
only if the two operands differ by at most 5. For a
current state of the automaton the next state is calcu-
lated by evaluating the outgoing conditions and taking
the first transition whose condition evaluated to true.
Fig. 7 shows an example MARB. The dotted tran-
sitions do not have to be defined explicitly: to avoid
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
98
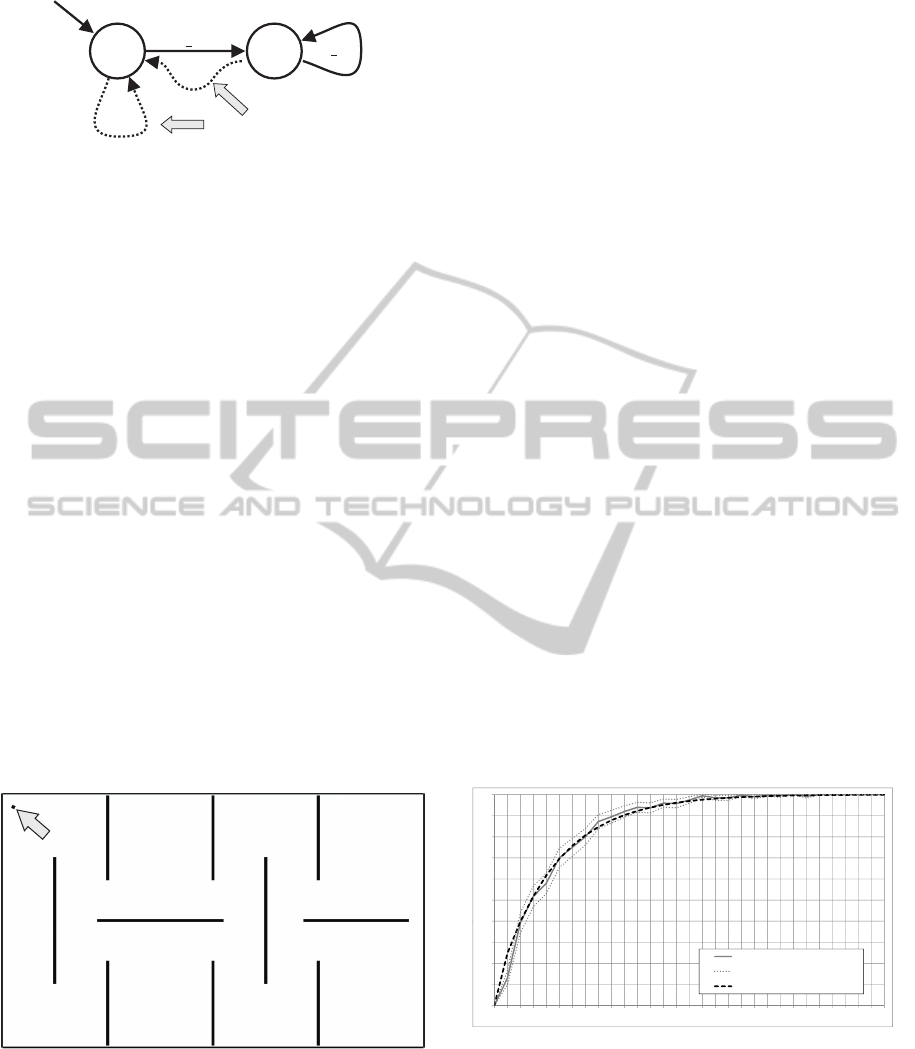
h < 30
2
h < 30
2
Move
Turn
Right
h > 30
2
h > 30
2
implicit transitions
Figure 7: An example MARB with two states. The dot-
ted transitions are inserted implicitly by the model. The
states perform the operations Move and Turn Right, respec-
tively. The automaton represents a simple collision avoid-
ing behavior moving forward as long as no obstacle is ahead
(h
2
< 30) and turning right if an obstacle is ahead (h
2
≥ 30).
deadlocks the initial state is always the successor of
a state that has no outgoing conditions that evaluate
to true. For more information on MARBs we refer
to (K
¨
onig et al., 2009).
Note that it is not important for the applicability of
the prediction model that FSM controllers are used;
e. g., artificial neural networks or any other controller
model could as well be used.
Scenario. The experimentation environment is given
in Fig. 8. In all experiments the populations consist of
n = 30 robots which are placed at random positions
in the environment facing in random directions. The
desired behavior (in terms of “superiority”) is the ca-
pability of driving as far distances as possible. The
explicit fitness function f is calculated by summing
up every 10 simulation steps the distance driven dur-
ing the last 10 steps. Additionally, the whole sum is
divided by 1.3 afterwards (cf. evaporation in (K
¨
onig
et al., 2009)). The evolutionary runs are performed
until convergence to a stable state.
Robot
Figure 8: The experimentation environment with a robot
drawn to scale. Black rectangles denote walls.
5.2 Experimental Results
We investigate the capability of the EIS model for pre-
dicting correctly the probabilities of converging to the
superior (
n
/
0
) or inferior (
0
/
n
) stable state. As a con-
vergence to the superior state means that the selec-
tion mechanisms worked as desired, the percentage
of convergence to the superior state can be used as
a measure of success. The initial populations are di-
vided in two sets S and I of individuals which per-
form the desired behavior in a superior and inferior
way, respectively.
The initial population state is varied within the
state space S
0
= {
1
/
29
,
2
/
28
, . . . ,
29
/
1
} (the states
0
/
30
and
30
/
0
are already converged, therefore, they are not
tested). The superior individuals are equipped with
a wall following behavior that makes the robots ex-
plore parts of the arena. The inferior individuals are
constantly driving small circles by switching in every
other step between a driving and a turning state and,
therefore, they are expected to have a lower fitness
than the superior ones (although, as in every complex
environment, this is not necessarily the case).
In the first tests, a global selection operator is as-
sumed that is based on a fixed probability matrix C to
select the mating tournaments (cf. Sec. 3.3), i. e., if a
population is in state
i
/
n-i
, row i of matrix C is used to
determine the probabilities for the tournament types
(
0
/
k
, . . . ,
k
/
0
) to select. According to these probabili-
ties, a tournament type
j
/
k-j
is selected and such a tour-
nament is chosen randomly from the current popula-
tion for mating. Afterwards, the tournament winner is
chosen according to the explicit fitness as described
in Alg. 1. As the quality of the fitness function is
not known in advance, the confidence factor c is un-
known. The aim of these tests is to show that there
exists a confidence factor c such that the experimental
data matches the model prediction.
04
0.5
0.6
0.7
0.8
0.9
1.0
0.0
0.1
0.2
0.3
0
.
4
0 1 2 3 4 5 6 7 8 9 101112131415161718192021222324252627282930
Experimentdata
95%confidenceinterval(ttest)
Modelprediction(c=0.2)
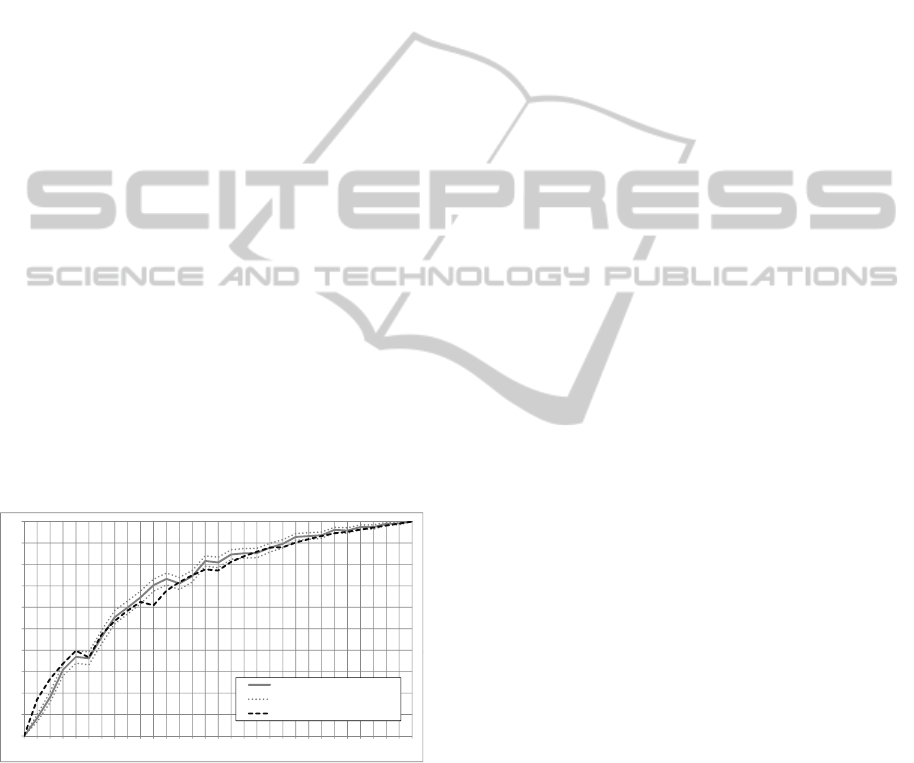
Figure 9: Probabilities of converging to the superior stable
state
30
/
0
as a function of the initial population state i ˆ=
i
/
n-i
.
Matrix C is set to a uniform distribution in every row. Tour-
nament size is set to k = 4. The gray solid line shows the
average values from the experimental data, the gray dotted
lines denote the according 95% confidence interval. The
black dashed line is the model prediction with c = 0.2.
Furthermore, this experimental setup could be
used as a preliminary experiment for a real evolution-
A MARKOV-CHAIN-BASED MODEL FOR SUCCESS PREDICTION OF EVOLUTION IN COMPLEX
ENVIRONMENTS
99
ary scenario to find a c that matches the experimental
data best. However, that is only possible if c is inde-
pendent of the matrix C. This is not the case for the
setup described here, see below.
Fig. 9 shows the results of an experiment where
the probabilities of matrix C are uniformly distributed
within every row, i. e., every tournament formation
has an equal selection probability within the same
row of C (except for impossible formations which are
set to 0, cf. Sec. 3.3). The tournament size was set
to k = 4. The experiment has been run 400 times
for each of the non-stable initial population states
1
/
29
, . . . ,
29
/
1
.
The chart shows the probabilities of converging to
the superior state
30
/
0
as a function of the initial popu-
lation state. The percentage of experimental runs that
converged to the superior state are shown by the gray
solid line. Two gray dotted lines denote the accord-
ing 95% confidence interval given by a statistical Stu-
dent’s ttest calculation. The black dashed line denotes
a prediction by the EIS model using a confidence fac-
tor c = 0.2. This confidence factor is determined by
a minimal error calculation in steps of 0.1. I. e., all
model data points are subtracted from the according
experiment data points, adding the absolut values to
an error sum; then the value of c ∈ {0.0, 0.1, . . . , 1.0}
is determined for which the error sum is minimal.
As the experimental data follows the model pre-
diction, mostly within the 95% confidence interval,
we conclude that the model prediction is accurate in
this case.
04
0.5
0.6
0.7
0.8
0.9
1.0
0.0
0.1
0.2
0.3
0
.
4
0123456789101112131415161718192021222324252627282930
Experimentdata
95%confidenceinterval(ttest)
Modelprediction(c=0.2)
Figure 10: Probabilities of converging to the superior stable
state (cf. above chart). Tournament size is set to k = 8,
matrix C is set to favor
4
/
4
tournaments. As above, the gray
lines denote experiment data and the black dashed line is
the model prediction with c = 0.2.
The next experiment is performed with a tourna-
ment size of k = 8 by using a matrix C that has
a high probability of selecting a tournament
4
/
4
and
a low probability for selecting all the other tourna-
ments. Namely, the probability for selecting a
4
/
4
tour-
nament is set to 1 − 10
−4
while all the other possi-
bilities uniformly divide the remaining value of 10
−4
among them. (In rows where the
4
/
4
tournament is
not applicable, the other tournaments are uniformly
distributed.) Due to the symmetry of the preferred
tournament
4
/
4
this matrix has a counterintuitive prop-
erty: using it, the model predicts that there should be
“jumps” in the probability plot, i. e., an increase in
the number of superior individuals in the initial pop-
ulation can cause the probability of converging to a
superior state to decrease. This is, e. g., the case at
population state
5
/
25
.
This experiment has been repeated 1000 times for
each of the 29 non-stable initial population states. The
chart in Fig. 10 shows the according experimental re-
sults. Again, the best-fitting confidence factor has
been calculated to c = 0.2. For most of the data
points the model lies within the 95% confidence in-
terval which, however, is tighter than in the above ex-
periment. Furthermore, the jumps occur in the exper-
imental data as well, which has been interpreted as a
strong indicator that the model works. However, the
second jump does not occur at state
10
/
20
as predicted,
but later at state
12
/
18
(the other jumps seem to be at
their correct positions). While it is possible that this
is due to statistical errors, this seems rather unlikely
as the two sequent values for states
11
/
19
and
12
/
18
are
considerably outside the 95% confidence interval. We
were not able to establish the reason for this inconsis-
tency, therefore, it has to be left for future work.
The last experiment without mutation is per-
formed in a more realistic scenario using a decen-
tralized selection method. Here, robots are selected
for a mating tournament if they came spatially close
to each other. After being selected for a tournament,
the robots are excluded from selection for 50 steps
to allow for a new fitness calculation. The radius for
mating is set to 210 mm which is big enough to as-
sure that nearly all runs converged eventually. For the
small percentage of runs that did not converge in the
first 200, 000 simulation steps the run was terminated
and counted as superior if the number of superior in-
dividuals in the last population was at least 15 and
inferior in all other cases. The tournament size was
set to 4. This experiment was repeated 400 times for
each non-stable initial population state.
In this case the tournaments are selected in a
decentralized way, therefore, there is no predefined
probability matrix C. Instead, C is given by the envi-
ronment and the given selection parameters, and can
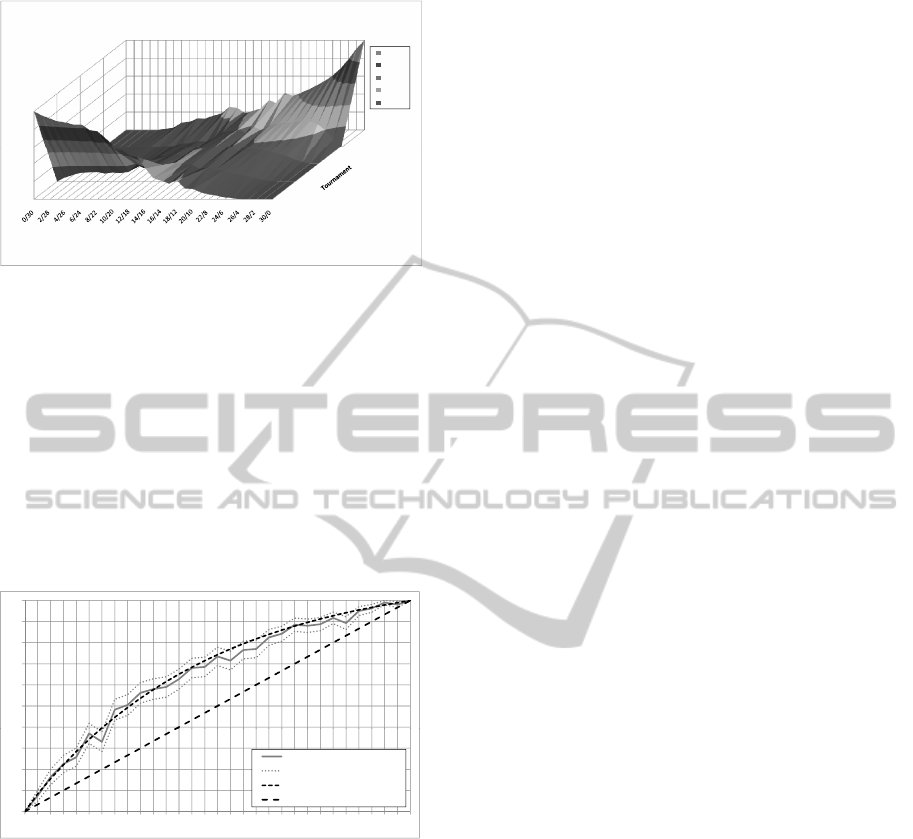
be measured during a run. The chart in Fig. 11 vi-
sualizes the probabilities of the matrix found by av-
eraging over all occurred tournaments during all the
400 · 29 = 11, 600 runs of this experimental setup. It
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
100
3/1
4/0
06
0.8
1
r
obability
0.8‐1
0.6‐0.8
0.4‐0.6
0.2‐0.4
0‐0.2
0/4
1/3
2/2
3/1
0
0.2
0.4
0
.
6
TournamentP
r
Populationstate
Figure 11: Probability matrix C that originates from the de-
centralized mating strategy in the third experiment.
can be observed that for a rather heterogeneous pop-
ulation with an approximately equal number of supe-
rior and inferior individuals the tournament probabil-
ities are roughly uniform. With more superior indi-
viduals in the population, the probability for superior
tournaments grows, and the other way around. This
seems to be quite intuitive and it can be suspected that
similar decentralized selection methods always yield
similar probability distributions.
04
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0
.
4
0123456789101112131415161718192021222324252627282930
Experimentdata
95%confidenceinterval(ttest)
Modelprediction(c=0.06)
CISmodel(c=0)
Figure 12: Probabilities of converging to the superior stable
state (cf. above charts). Tournament size was set to k = 4,
matrix C was given implicitly by the decentralized selec-
tion method; the according probability values are depicted
in Fig. 11. As above, the gray lines denote experimental
data and the black short-dashed line is the EIS model pre-
diction with c = 0.06. The long-dashed line reflects the CIS
model without an explicit fitness function.
Fig. 12 shows the convergence probabilities re-
sulting from this experiment. The EIS model predic-
tion has this time been calculated using the measured
values for matrix C as depicted in Fig. 11. The confi-
dence factor c is set to 0.06 which is the best approx-
imation by a precision of 0.01. Additionally, a plot
of the CIS model is depicted in the chart as a com-
parison. Obviously, the chance of converging to the
superior state is raised by the explicit fitness function.
However, the confidence factor c is decreased con-
siderably compared to the above experiments with a
global selection operator. This is a clear sign that the
confidence factor is not independent of the matrix C
in this scenario. As a consequence, the chance for
reaching the superior state is lower in this experiment
than in the above experiments. The model prediction
is, again, for nearly all data points within the 95%
confidence interval.
6 CONCLUSIONS AND FUTURE
WORK
In this paper, a mathematical model based on Markov
chains has been introduced that can be utilized to es-
timate the probability that an ESR run will be suc-
cessful in terms of being capable of improving a pop-
ulation until a desired behavior is found. The first
version of the model presented here focuses solely on
the selection process. It is assumed that selection is
performed by tournament selection which is based on
two types of fitness: first an implicit fitness which de-
pends on potentially hidden environmental properties,
and second an explicit fitness that is calculated from
environmental variables and that can be fuzzy, noisy
or delayed. In complex environments both fitnesses
may not reflect the desired behavior perfectly (fur-
thermore, especially the implicit fitness is hard to in-
fluence and mostly given by the scenario). Our model
takes into account the chances for both the implicit
and explicit part of the selection process to select the
superior of two types of individuals, and calculates
the probabilities that a certain population state will
eventually converge to a superior state, i. e., a state
with only superior individuals. Furthermore, the ex-
pected time to convergence in terms of the number of
mating events necessary to reach a superior state can
be calculated. The model is applicable to nearly all
types of ESR scenarios including offline and central-
ized as well as online and decentralized approaches.
It can help predicting the performance of an ESR run
in cases where success is of critical importance or
where failures are expensive (this is often, but not ex-
clusively, the case in decentralized online scenarios).
There are no restrictions to controller types or evolu-
tionary operators except for selection. Experiments
in simulation show that the predictions of the model
coincide with actual experimental data.
The model depends on a quite large number of pa-
rameters arising from probability values that depend
on the environment and the fitness calculation proce-
dure. These parameters have a major influence on
the results. As the model is only useful if these pa-
A MARKOV-CHAIN-BASED MODEL FOR SUCCESS PREDICTION OF EVOLUTION IN COMPLEX
ENVIRONMENTS
101

rameters can be estimated properly before an actual
run is performed (e. g., in simulation before starting
a real-world run), future work will cover studies of
how these parameters can be discovered. One simu-
lation approach to this end has been presented in this
paper, but it still has to be studied how well the re-
sults match a real-world scenario. The model so far
does not cover mutation directly, but assumes rather
long selection phases without behavior-changing mu-
tations. Furthermore, while tournament selection is a
natural selection method in evolutionary robotics, it is
still a constraint of the model that is not categorically
necessary. It is planned to extend the model to cover
mutations and to be applicable on selection methods
different than tournament selection.
ACKNOWLEDGEMENTS
The authors thank Lisa Hofmann for preparatory
work on the topic of implicit environmental selection
in ESR.
REFERENCES
Arnold, D. V. (2001). Evolution strategies in noisy
environments- a survey of existing work, pages 239–
250. Springer-Verlag, London, UK.
Bredeche, N. and Montanier, J.-M. (2010). Environment-
driven embodied evolution in a population of au-
tonomous agents. In Parallel Problem Solving from
Nature, pages 290–299, Berlin Heidelberg. Springer.
Eiben, A. E., Hinterding, R., and Michalewicz, Z. (2000).
Parameter control in evolutionary algorithms. IEEE
Transactions on Evolutionary Computation, 3:124–
141.
Grinstead, C. and Snell, L. (1997). Introduction to Proba-
bility. American Mathematical Society.
Gross, R. and Dorigo, M. (2009). Towards group transport
by swarms of robots. Int. J. Bio-Inspired Comput.,
1:1–13.
Holland, J. (1975). Adaptation in Natural and Artificial Sys-
tems. University of Michigan Press.
Kessler, D., Levine, H., Ridgway, D., and Tsimring, L.
(1997). Evolution on a smooth landscape. Journal
of Statistical Physics, 87:519–543.
Kimura, M. (1985). The Neutral Theory of Molecular Evo-
lution. Cambridge University Press.
K
¨
onig, L., Mostaghim, S., and Schmeck, H. (2009). Decen-
tralized evolution of robotic behavior using finite state
machines. Int. Journal of Intelligent Computing and
Cybernetics, 2(4):695–723.
K
¨
onig, L. and Schmeck, H. (2008). Evolving collision
avoidance on autonomous robots. In Biologically
Inspired Collaborative Computing (Proceedings of
BICC 2008), pages 85–94.
Nolfi, S. and Floreano, D. (2001). Evolutionary Robotics.
The Biology, Intelligence, and Technology of Self-
Organizing Machines. MIT Press.
Pietro, A. D., While, L., and Barone, L. (2004). Applying
evolutionary algorithms to problems with noisy, time-
consuming fitness functions.
Pr
¨
ugel-Bennett, A. and Rogers, A. (2001). Modelling ge-
netic algorithm dynamics, pages 59–85. Springer-
Verlag, London, UK.
Sober, E. (2001). The two faces of fitness. In Singh, R.,
Paul, D., Krimbas, C., and Beatty, J., editors, Think-
ing about Evolution: Historical, Philosophical, and
Political Perspectives.
Watson, R., Ficici, S., and Pollack, J. (2002). Embodied
evolution: Distributing an evolutionary algorithm in
a population of robots. In Robotics and Autonomous
Systems, pages 1–18.
Weyns, D., Schumacher, M., Ricci, A., Viroli, M.,
and Holvoet, T. (2005). Environments in multia-
gent systems. The Knowledge Engineering Review,
20(02):127–141.
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
102
