DISTRIBUTED OPTIMIZATION BY WEIGHTED ONTOLOGIES

IN MOBILE ROBOT SYSTEMS

Lucia Vacariu

, George Fodor

Department of Computer Science, Technical University of Cluj Napoca, 26 Baritiu str, Cluj Napoca, Romania

ABB AB Process Automation, Vasteras, Sweden

Gheorghe Lazea, Octavian Cret

Department of Automation, Technical University of Cluj Napoca, Cluj Napoca, Romania

Department of Computer Science, Technical University of Cluj Napoca, Cluj Napoca, Romania

Keywords: Mobile cooperating robots, Heterogeneous agents, Subgradient optimization, Distributed ontology.

Abstract: Heterogeneous mobile robots are often required to cooperate in some optimal fashion following specific

cost functions. A global cost function is the sum of all agents’ cost functions. Under some assumptions it is

expected that a provable convergent computation process gives the optimal global cost for the system. For

agents that can exchange ontological information via a network, different variables in the global vector are

relevant when ontology instances have been recognized and communicated among agents. It means the

optimization depends on what is known to each agent at the current time. There are two ways to solve an

optimization of this kind: (a) to weight agents according to the ontology instances or (b) to add ontology-

defined optimization constraints. This paper illustrates the benefits of the weighted optimization method.

1 INTRODUCTION

Intended applications for the optimization method

proposed in this paper are systems of cooperating

robots, where each robot is designed using an agent

architecture. Each robot has specific sensors and

actuators, thus robots and agents are in general

heterogeneous.

In order to fulfil goals at an abstract level, agents

can exchange ontological information (Văcariu,

Chintoanu, Lazea and Creţ, 2007). As shown in

Section 2, ontological concepts are mapping the

sensed world with non-trivial modes of actuation

and goal seeking. Using a symbolic layer with

ontologies means that agents can undergo rather

discontinuous changes when recognizing different

types of environment that are associated to complex

actions and goals.

It is typical for applications with many sensors,

actuators and high-level of intelligence that the same

goal could be achieved in many ways and at

different costs. Thus optimization of cost functions

of agents is an important requirement for a practical

solution. We consider a total number of M agents

acting in all the robots; each agent has an index i

(i=1,…,M) and a related convex cost function f

(x).

The argument x is a vector in R

of resources.

Initially, agents know their own resources but they

have a degree of uncertainty about the resources

available to other agents. In time, each agent tries to

compute the best estimate of the resource vector x

that optimizes the agent’s own cost function. By

exchanging resource vectors and ontologies among

agents, the optimization can make a better resource

allocation using common resources. Thus, the cost

function for each agent converges to an (almost)

optimal value and the overall cost function

∑

xfK

)(

will be also minimized.

In our model, the non-smooth cost functions

obtained by discrete changes in resource vectors by

ontology update are not differentiable over the

whole domain, thus these functions are optimized by

a subgradient method (Shor, Kiwiel, and

Ruszcaynski, 1985).

180

Vacariu L., Fodor G., Lazea G. and Cret O. (2010).

DISTRIBUTED OPTIMIZATION BY WEIGHTED ONTOLOGIES IN MOBILE ROBOT SYSTEMS.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 180-185

DOI: 10.5220/0002914701800185

 SciTePress

2 AGENT MODEL

In traditional applications, the components of a

resource vector used for optimization are physical

measured values. In more advanced applications,

resource vectors change, an interesting case being

when agents exchange ontologies.

Here we describe the relationship between the

resource vector x and the symbolic part of the agents

ontological representation.

We consider that each robot is built on an agent

architecture that can host a number of specialized

agents. These can use local robot resources. We

have a set of cooperating robots Ro, indexed from 1

to M. The set of sensors of a system of robots is:

Se: Ro x Ns (1)

where Ns = number of sensors.

The decisions made by agents are not based

directly on raw sensor data. Normally, a so called

perception relation is the result of processing the

data from several sensors. For a robot with Kr

sensors, a perception relation is defined as a

mapping of sensors to indices Np:

Re: Se

x Np (2)

Perception relations are associated symbolic

names by a mapping from the set of perception

relations Re to a vocabulary (set of words) Tv called

symbolic perceptions:

RelS:

x N → Tv

(3)

where |Re| is the index of a relation in (2) and N is

the index of the robot.

Ontology is a formal representation of a set of

concepts within a domain and the relationship

between these concepts (Noy and McGuinness,

2001). These concepts being specific to a domain, it

generally means that there is no obvious one-to-one

mapping between ontological concepts and the

perception relations. If the set of ontological

concepts is Z, a robot-specific ontology is defined as

the relation between the perception relations and a

relationship between a set of L ontological concepts:

Ont: Tv → Z

(4)

Depending on the inclusion relation between the

specific ontology and the perception relations, there

are three cases. A specific ontology is (1)

fundamental when

LKr

ZSe ≡

; (2) is minor relative

to the perception relations if

LKr

ZSe ⊂

; (3) is

major relative to perception relations if

LKr

ZSe ⊃

We consider here major specific ontologies.

Agents are using the actuator gear of robots to

achieve goals. Actuators are denoted:

Ac: Ro x Na (5)

with Na being the actuator index and Ro the set of

robots. A relation of actuation is a mapping from the

symbolic perceptions Tv to actuators:

RelA: Tv → Ac

(6)

which shows the intended action for each symbolic

perception in Tv. Finally, it is assumed that since

each action is executed under known conditions, the

intended effect of the action is known as a specified

next symbolic perception. This is called the

actuation effect relation (or actuation relation) EfA:

EfA: Ac x Tv → Tv

(7)

The dynamics of the data evaluation is shown in

the Figure 1 below:

RelS

EfA

Figure 1: Data evaluation.

3 MULTI-AGENT MODEL

In the multi-agent system each robot has a number

of agents, each agent having a specific set of

relations of the type (1) – (5). All agents are

assumed to use the same domain ontology since this

ensures that common goals can be achieved and that

communication is not robot manufacture-dependent.

Each agent has only a subset of the common domain

ontology, subset that was considered appropriate for

its sensors, actuators and goals at the design time.

During the cooperation phase, agents are exchanging

information such as sensor data, ontology concepts

or resource vectors. It is also assumed that all agents

have a bounded communication time interval T.

There are several mechanisms for ontological

communication but we describe only the method

called Simple Ontological Substitution (SOS).

Let t

and t

be two symbolic perceptions in the

Tv set of a local agent such that according to relation

(7), we have t

= EfA(a

) (Figure 2).

DISTRIBUTED OPTIMIZATION BY WEIGHTED ONTOLOGIES IN MOBILE ROBOT SYSTEMS

181

Local agent executing SOS

Remote agent

Figure 2: Simple Ontological Substitution.

Formally, the intended sequence towards a goal

is as follows: sensors of the local agent expect

reading data which is used to interpret the symbolic

perception t

as true. The associated actuation a

expected to materialize the symbolic perception t

However, the environment of the robot changes such

that no symbolic perception among those of the T

set of the local agent will become true. The agent

cannot recognize the environment state in which it

acts. The local agent has information according to its

EfA relation about the wanted perception to realize

. Another agent in some remote robot has a

corresponding relation EfA of the type t

= EfA(_,_).

The local agent is sending a request for all agents in

the system, with the following content: (a) a remote

agent should have the EfA resulting in t

and (b) the

remote agent should send this EfA together with the

corresponding Z

(see Figure 1) to the local agent.

If such a remote agent exists, and answers with

the t

= EfA(a

), then the local agent will ask for

the execution of a

that will result in t

. Next time,

when a similar situation happens, the local agent has

the ontology knowledge to cope with this situation.

4 OPTIMIZATION

4.1 Optimizing Individual Agents

Each agent i, i = 1,…,n has an individual cost

function f

: R

→ R expressing e.g. energy, material

or wear and tear costs. A minimum value of the cost

function means finding a so called optimal resource

vector x* such that:

(x*) ≤ f

(x)

∀

x ∈ R

(8)

All cost functions are assumed convex:

f(ta + (1 – b)t) ≤ tf(a) – (1 – t)f(b)

(9)

For each convex function a local optimum is also

a global optimum. This makes the computation of an

optimum easy when the function is smooth (it has

derivatives of high order). For example, from the

truncated Taylor expansion:

)("

)(')()( h

hxfxfhxf ++≈+

by differentiation on h we obtain

0)('

)("

2 =⋅+⋅⋅ dhxf

dhh

, and after reductions,

)("

)('

h −=

. This gives the iteration which is

Newton’s method for solving

0)(' =xf

(k is the

iteration index).

k+1

= x

+ h (10)

The example above shows the two important

parts of a program solving an optimization

application (Bonnans, Gilbert, Lemaréchal, and

Sagastizábal, 2002):

(a) The Algorithm for Searching the x Space.

This

manages the update of the argument x to the fastest

convergence rate of the sequence x

, x

,…, x

,…, x*.

There are two types of search methods: one is a

direct search, i.e. the traditional Nelder-Mead

method (Fletcher, 2003); the other is to use

information about the functions to be optimized,

such as its higher derivatives. For example, the

corresponding of the Newton method (relation (10))

for the multi-dimensional case is:

)()(

1 kkfkk

xfsHxx ∇−=

−

(11)

To determine the iteration step, must be solve the

linear system: H

= – ∇f(x) such that relation

(11) becomes x

k+1

= x

+ s

(b) The Simulator. For each new iteration

determined by the search algorithm, a computation

is done using the new x in the problem P to be

optimized to find a gradient descent or an equivalent

“good” direction. Often the initial problem P is

replaced by a simpler problem P

which computes a

direction along a line of the solution.

The method can be illustrated with subgradients

on non-smooth functions. Let f(x) to be a non-

smooth, convex function, defined on R, with values

in R (Figure 3). Let x

be a point of discontinuity of

the function. A subgradient is any line of direction c

containing the point (x

, f(x

)), such that: f(x) – f(x

)

≥ c(x – x

), a line “below” a convex function and

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

182

f(x)

f(x0)

f(x)-f(x0)

x-x0

subgradient

f(x)

tg(a)*(x-x0) = c(x-x0)

f(x)-f(x0)>c(x-x0)

Figure 3: Subgradient in R

which intersects the function in only one point.

For vectors in R

a subgradient is a vector s

)

such that:

f(x) – f(x

) ≥ s

(x)

(x – x

)

(12)

The set of all subgradients of f at x

is called the

subdifferential of f at x

and it is denoted as

∂

f(x

). In

Figure 3 the subdifferential is the set of lines through

the point (x

, f(x

)) placed between the lines S1 and

S2 defined by the directions of the non-smooth

function. Using the results obtained until now, the

iterative algorithm for an agent i at iteration k+1 is:

(k+1) = x

(k) –

(k)d

(k)

(13)

where

(k) is the size of the step used by agent i and

(k) is a subgradient of agent’s i objective function

at x

(k).

4.2 Optimization of the Multi-agent

System

A global optimization means that a vector x*

representing common resources to all agents,

minimizes the sum of cost functions f

(x*) of each

agent i. Initially, before a new optimization cycle

begins, each agent may have different values for its

vector x. However, the size of the vector and the

resource or physical meaning of each element in the

vector is common to all agents.

An algorithm shown to converge for optimizing

multi-agent systems (Nedic, Ozdaglar, 2009), uses

the subgradient method shown in formula (13), but

with the difference that at each step k, an agent

combines its resource vector with a weighted value

of the resource vectors of all other agents. For an

agent i, its weight relative to an agent j at iteration k

Rkw

∈)(

. Weights are normalized

1)(

∑

for each agent i and each iteration k. With this

change, formula (13) becomes:

)()()()()1(

kdkkxkwkx

⋅−⋅=+

∑

(14)

The index j ranges over all M agents. As in

relation (13),

(k) is a scalar being the step size

used by agent i and d

(k) is a vector in R

, the

subgradient of agent’s i objective function at x

(k).

While the weights in the work of Nedic and

Ozdaglar (2009, p. 49) uses a concept of agents

close to each other, in this work we use information

about shared ontologies and EfA relations described

in (7) and Figure 1.

4.3 Optimization in the Presence of

Ontological Communication

The relative weight of agent i to agent j,

)(kw

shows how “close” resources of the two agents are.

Resources can be “close” even when their physical

nature is very different.

Using ontologies, as shown in relations (3)-(7)

and Figure 1, an agent can determine which

resources are used as these are mapped to

ontologies. As agents act continuously, the weights

)(kw

change to reflect that some other set of

resources are currently used.

The resource vector is a vector x ∈ R

, so it

contains as components only numerical, real values.

In the chain of relations RelS

→

information from sensors are interpreting perception

relations RelS, which are determining which

symbols in Tv have the value True, which are

determining which ontological concepts are

identified. When an ontological concept is

identified, it means all its properties are considered

to hold.

It is important that at each new symbolic

perception, the corresponding ontology is shared

with other agents. Some of the previous resources

will still be used while some new are going to be

used. The choice of the weights

)(kw

must reflect

these transitions.

Thus, to find the weight factor among agents

means determining a concept of distance among

ontologies. One definition for distance uses a tree-

ontology metrics: a distance using a formal

representation of the ontology, by a measure of the

path length between concepts. According to this

measure, if c

and c

are two nodes in a formal

representation of the ontology, l is the shortest path

between the concepts and h is the depth of the

DISTRIBUTED OPTIMIZATION BY WEIGHTED ONTOLOGIES IN MOBILE ROBOT SYSTEMS

183

deepest concept subsuming both concepts, then the

distance between c

and c

hkhk

eccsim

)2,1(

−

⋅=

(15)

and k

are scaling parameters for the shortest path

vs. the depth) (Debenham, and Sierra, 2008). This

type of measure can be done for asserted ontologies.

Another style of metrics is based on set-theoretic

principles, by counting intersections and unions of

ontological concepts. Best known is Tversky’s

similarity measure between two objects a and b and

with properties (feature sets) A and B:

||)),(1(||),(||

),(

ABbaBAbaBA

bas

−−+−+∩

∩

αα

(16)

where |.| is the cardinality of the set, minus is the set

difference and

(a,b) in the interval [0,..,1] is a

tuning factor that weights the contribution of the

first reference model (Tversky’s similarity measure

is not symmetrical).

Besides Tversky’s measure, similarity measure

functions available in most scientific mathematical

libraries are, for example Cosine, Dice, Euclidian,

Manhattan or Tanimoto.

The algorithm for using any of the similarity

measures above to determine the weight between

two agents is the following:

1. Generate the set of all ontological properties (both

numerical and non-numerical) of agent i as a union

of all ontological properties valid at iteration k. Let

this set be A and the cardinality of the set be |A|;

2. Generate in the same manner the set of all

ontological properties for agent j; let this set be B

with cardinality |B|;

3. Compute the cardinality of the intersection, union,

differences, symmetric difference, as needed by the

selected similarity formula;

4. Compute the similarity index. The resulting value

is the weight

)(kw

5 EXAMPLE

To demonstrate the weighted method we present an

example with a cooperation multi-robot system used

in supermarket supervision. Two of the robots in the

system have both common and distinct sensors.

Robot 1, Ro1, has sensors (see relation (1)):

Distance = Se(1,1); Shape (cube, cylinder, sphere) =

Se(1,2); Dimensions (length, width, height,

diameter) = Se(1,3); Temperature = Se(1,4); Colour

= Se(1,5).

The second robot, Ro2, has sensors to obtain

information for: Distance = Se(2,1); Shape =

Se(2,2); Dimensions Se(2,3); Weight = Se(2,4).

Combining Ro1 sensors information, we obtain

possible perception relations (see relation (2)), e.g.:

Re([Se(1,1), Se(1,2), Se(1,3)], 1) – for a

combination of Distance, Shape and Dimension and

Re([Se(1,1), Se(1,4), Se(1,5)], 5) – for a

combination of Distance, Temperature and Colour.

These perception relations have associated

symbolic perceptions (see relation (3)), as shown in

Table 1.

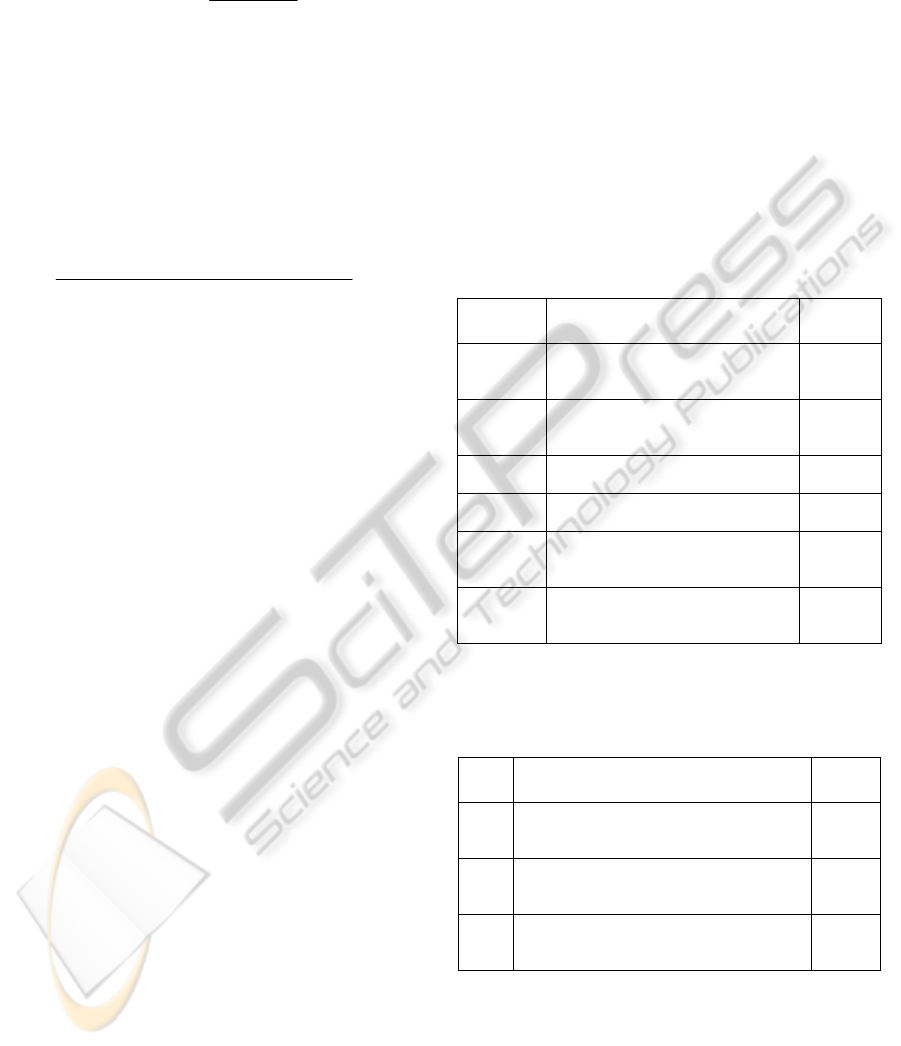
Table 1: Symbolic perceptions Ro1.

Index Re Perception Relation Re

(symbol)

1 Distance < 10m AND Shape =

Parallelepiped AND Dimension >

10m x 2m x 2m

shelf

2 Distance < 5m AND Shape =

Parallelepiped OR Cube AND

Dimension < 1m x 1m x 0.5m

box

3 Distance < 5m AND Shape =

Sphere AND Dimension < 1m

ball

4 Distance < 5 m AND Shape =

Sphere AND Dimension < 0.5m

balloon

5 Distance < 50m AND

Temperature > 200

C AND Colour =

Red OR Orange

fire

6 Distance < 10m AND

Temperature > 50

C AND Colour =

White OR Yellow

lamp

A similar computation for robot 2 gives the

results in Table 2.

Table 2: Symbolic perceptions Ro2.

Index

Perception Relation Re

(symbol)

1 Distance < 10m AND Shape =

Parallelepiped AND Dimension > 10m x 2m

x 2m

shelf

2 Distance < 5m AND Shape =

Parallelepiped OR Cube AND Dimension <

1m x 1m x 0.5m AND Weight > 3 kg

box

3 Distance < 5m AND Shape =

Parallelepiped AND Dimension < 1.5m x

0.5m x 1m AND Weight < 3 kg

cart

We have now two sets of symbols for the two

robots (agents): P={shelf, box, ball, balloon, fire,

lamp} and Q={shelf, box, cart}. We compute the set

operations required e.g. using the “dice” similarity

measure:

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

184

bothABonlyBonlyA

bothAB

BAsim

dice

⋅++

⋅

),(

∪ Q| = |{shelf, box, ball, balloon, fire, lamp,

cart}| = 7; |P-Q| = |{ball, balloon, fire, lamp}| = 4

and |Q-P| = |{cart}| = 1. So the weight

w between

agent 1 and 2 is:

73,0

7214

⋅++

⋅

The full matrix of weight is computed in this

fashion for all agents.

The example is using three agents with three

different cost functions of type

)( BxAxxf +=

with parameters from Table 3.

Table 3: Agents cost functions.

Agent A B Init vector

Agent 1 0.5 2.5 [1 3]

Agent 2 1.0 4.0 [3 6]

Agent 3 3.0 1.0 [4 5]

Figure 4 shows that indeed vectors converge

towards the intended minimum value [0 0].

−2 −1 0 1 2 3 4

−2

−1

Figure 4: Convergence results.

The relation between the convergence precision

and step size is shown in Figure 5.

Figure 5: Convergence precision vs. step size.

An optimum step size is in the range 0.6 – 1;

outside this range, the convergence precision

decreases.

6 CONCLUSIONS

This paper capitalizes on recent results showing

convergence of optimization in distributed agent

applications. The optimization is based on

establishing weights between agents, such that a

weighted recursive computation shown in formula

(14) gives a shared optimal resource allocation. This

approach is appropriate for cooperative multi-robot

system.

The paper’s contribution is to demonstrate that a

natural approach to compute a “distance” (the

weight) among agents that exchange ontologies

among them is the degree of shared ontologies the

agents are using at the current computation step.

This allows both numerical and symbolical

ontological concepts to be used by set-theoretic

similarity measures.

REFERENCES

Debenham, J, Sierra, C., 2008. Unifying trust, honour and

reliability. In 2

IEEE Int’l Conf.on Digital

Ecosystems and Technologies, 2008, pp. 470-475.

Fletcher, R., 2003. Practical Methods of Optimization.

Wiley. UK. 2

edition.

Min, X., Luo, Z., Qianxing, X., 2009.

Semantic Similarity

between Concepts Based on OWL Ontologies. In 2

Int’l Workshop on Knowledge Discovery and Data

Mining, 2009, Moscow, pp. 749-752.

Nedic, A., Ozdaglar, A., 2009. Distributed Subgradient

Methods for Multi-Agent Optimization. In IEEE

Transactions On Automatic Control, Vol. 54, No. 1,

pp. 48-61.

Noy, N.F., McGuinness, D.L., 2001. Ontology

Development 101: A Guide to Creating Your First

Ontology. Stanford Knowledge Systems Laboratory

Technical Report KSL-01-05 and Stanford Medical

Informatics Technical Report SMI-2001-0880.

Shor, N.Z., Kiwiel, K.C., Ruszcaynski, A., 1985.

Minimization Methods for Non-differentiable

Functions. Springer-Verlag. New York, USA.

Văcariu, L., Chintoanu, M., Lazea, G., Creţ, O., 2007.

Communication at Ontological Level in Cooperative

Mobile Robots System. In Proceedings of the 4th

International Conference on Informatics in Control,

Automation and Robotics, ICINCO 2007, May 9-12,

2007, Angers, France, pp. 455-460.

DISTRIBUTED OPTIMIZATION BY WEIGHTED ONTOLOGIES IN MOBILE ROBOT SYSTEMS

185