
OPTIMAL CONTROL OF HAZARDOUS MATERIALS
TRAFFIC FLOW
The Case of Transport through a Critical Infrastructure
Chiara Bersani, Riccardo Minciardi, Michela Robba, Roberto Sacile and Angela Maria Tomasoni
DIST, Department of Communication, Computer and System Sciences, Italy
Keywords: Optimal control, Hazardous materials, Transport, Traffic.
Abstract: In this work, a preliminary study as regards the possibility to define optimal control strategies for the
hazmat (hazardous material) traffic flowing towards one critical road infrastructure (e.g. as in the case study
a tunnel) at the macroscopic level is introduced. Specifically, the simplified model that is studied is related
to part of a highway, on which the hazmat traffic can flow from one entrance. The control variables are
represented by the number of vehicles that are allowed to enter the highway during a specific time interval,
while the state variables are the queue of vehicles before the entrance, the number of vehicles in the various
tracts of the highway, and the number of vehicles that enter the tunnel. The objective function to be
minimized is characterized by three main terms: the queue, the hazard over the road, and the hazard related
to the tunnel.
1 INTRODUCTION
Hazardous materials cover a wide range of products
(explosives, gases, flammable liquids and solids,
radioactive materials, hazardous wastes, etc. (Verter
and Kara, 2008)). Transportation of these materials
(that is, in general, multi-modal: road, pipelines,
railway, ship) is a relevant problem to be considered
because of the significant amount of material that
flows among roads, territory and infrastructures
(Bersani et al., 2008). Defining strategies for
hazardous materials (hazmat) transportation
management is a complex task because it is
necessary to take into account different objectives
(minimize risks, satisfy goods demand
transportation), different decision makers (fleet
managers, local authorities, infrastructures
managers), and different approaches (mainly based
on the different spatial-temporal scales to be
considered: strategic planning, tactical planning,
operational management).
In the literature of hazardous materials
transportation on road, there are few, thought
important and relevant, works on this subject (for
example: Berman et al., 2007; Verter and Kara,
2007; Kara and Verter, 2004; Sadjadi, 2007; Bell,
2009; Bell and Cassir, 2002, Bersani et al., 2008a;
Serafini, 2006; Beroggi and Wallace, 1994). The
majority of these works is based on optimization
models for planning and design purposes. The
preliminary approach presented in this work is
instead based on real time operational management
(like the work presented by Bersani et al., 2008b)
with specific reference to the case of critical
infrastructures.
The transportation of hazardous materials
(hazmat) on road has important consequences in the
overall traffic management (Minciardi et al., 2008).
This fact is more evident when a vehicle requires to
move towards a critical road infrastructure, such as a
tunnel or a bridge. The control of traffic networks
has been the subject of a great amount of literature
from different viewpoints. The main articles related
to the case of a tunnel are reported in (Minciardi et
al., 2008). The aim of this preliminary study regards
the possibility to define optimal control strategies for
the hazmat traffic flowing towards one critical road
infrastructure (e.g. as in the case study a tunnel).
A given number of vehicles transporting
hazardous material has to use a highway and to
reach one critical infrastructure (e.g. a tunnel). They
can stop in a park before the highway entrance and
start their travel according to the exigencies of a
decision maker that can be identified as the tunnel
manager. The park may be taken into account as an
311
Bersani C., Minciardi R., Robba M., Sacile R. and Tomasoni A.
OPTIMAL CONTROL OF HAZARDOUS MATERIALS TRAFFIC FLOW - The Case of Transport through a Critical Infrastructure.
DOI: 10.5220/0002249003110316
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2009), page
ISBN: 978-989-8111-99-9
Copyright
c
2009 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

inventory in which the state of the system is
represented by the vehicles that are present at a
specific time instant. The flow dynamics of
hazardous material vehicles on the highway has also
to be modelled. In particular, the problem is defined
at a macroscopic level, in which the state and the
control variables correspond to the number of
vehicles, for which the integrity condition may be
relaxed, in order to obtain a continuous-variable
decision problem. The control variables are
represented by the number of vehicles that are
allowed to enter the highway during a specific time
interval, while the state variables are the queue of
vehicles before the entrance, the number of vehicles
in the various tracts of the highway, and the number
of vehicles that enters the tunnel. The objective
function to be minimized is characterized by three
main terms: the queue, the hazard over the road, and
the hazard related to the tunnel.
The resulting optimal control problem is linear
quadratic with non-negativity constraints over the
state and control variables. A receding horizon
control scheme is used to derive the solution and to
allow the model to be suitable in real time decision
frameworks. An optimization package (Lingo 9.0,
www.lindosystems.com) is used to solve the
problem at each step.
In fact, the explicit form of the optimal control
law of a given linear, discrete-time, time-invariant
process subject to a quadratic cost criterion is well
known in the unconstrained case, while, even for
simple constraints, solution is hard to achieve. In
(Castelein and Johnson, 1989), the authors use the
controllable block companion transformation and
derive sufficient conditions on the weighting
matrices of the cost criterion to ensure that the
closed-loop response of the original process with the
standard, unconstrained optimal feedback law will
be nonnegative. Bertsimas and Brown (2007) assess
that the celebrated success of dynamic programming
for optimizing quadratic cost functions over
linear systems is limited by its inability to tractably
deal with even simple constraints, and present an
alternative approach based on results from robust
optimization to solve the stochastic linear-quadratic
control (SLQC) problem.
For this reason, interesting developments of this
work will be devoted to the definition of
methodologies to find efficient solutions for the
optimal control strategies.
In the next subsections, the system model is
described in detail. Then, the decision problem is
formalized. Finally, results and conclusion are
drawn.
2 THE SYSTEM MODEL
Figure 1 shows the schematic representation of the
decision framework: the highway directed towards
one critical infrastructure is modelled as a line
divided in highway tracts. As a simplification, two
highway tracts have been considered.
t
V
t
I
t
X
Y
t
Z
t
Figure 1: The considered system.
The physical inputs of the whole system are the
quantities
t
V , i.e., the (known) number of vehicles
entering the park near the highway entrance in time
interval (t, t +1), t = 0,…,T-1. The control variables
correspond to the number of vehicles that enter the
highway
t
X in a specific time interval (t, t+1),
while the state variables correspond to the number of
vehicles in the inventory/queue,
t
I
, the number of
vehicles per tract of the highway (
t
N
1
,
t
N
2
), and the
number of vehicles going out from tract 1 and
entering the tunnel (
tt
ZY , ).
Two different kinds of state equations have to be
introduced, regarding, respectively, the queue in the
park at the highway entrance, and the highway
tracts. Moreover, the hazard has been formalized as
a function of the state and control variables.
2.1 The Queue State Equation
The state equation is:
)(
1 tttt
XVII −+=
+
t=0,…, T-1 (1)
where:
t
I
is the number of vehicles stored, at time
instant
t, in the park near the entrance, i.e., the
inventory of the entrance park area, in time
interval (
t, t+1);
t
X is the number of vehicles that enter the
highway in time interval (
t, t+1), from the
entrance park area;
t
V is the (known) number of vehicles that enters
the entrance park in time interval (
t, t+1).
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
312

2.2 The Highway Tract State
Equations
These state equations describe the evolution over
time of a state variable that represents the number of
hazmat vehicles (per unit length) present in a
specific tract of the highway. The speed of these
vehicles is related to the overall vehicle density over
the considered tract. It is assumed that the vehicle
flow can be represented through an average speed,
which is common to hazmat and non-hazmat
vehicles. In agreement with the literature dealing
with traffic models, it is assumed that the (average)
vehicle speed is never so high to allow the complete
covering of a highway tract within a single time
interval (of course, this may be also seen as a
constraint over the space discretization of the
highway). The equations are given by
11
1
1
1
L
Y
L
X
NN
tt
tt
−+=
+
t=0,…,T-1 (2)
22
2
1
2
L
Y
L
Z
NN
tt
tt
+−=
+
t=0,…,T-1 (3)
with
tvelNY
ttt
Δ=
11
t=0,…, T-1 (4)
tvelNZ
ttt
Δ=
22
t=0,…, T-1 (5)
where:
t
N
1
,
t
N
2
are the number of (hazmat) vehicles per
unit length that is present in the highway road in
tracts 1 and 2, in time instant
t;
21
, LL
are the tracts lengths;
tΔ is the time interval length;
tt
velvel
21
, are the (average) velocities in the tracts
in time interval (
t, t+1), which is assumed to be
imposed by the ordinary traffic (i.e., non
hazmat), assuming that the hazmat vehicle flow
is only a negligible part of the overall traffic
flow;
t
Y is the number of vehicles that passes from
tract 1 to tract 2 in time interval (
t, t+1);
t
Z is the number of vehicles that reaches the
tunnel in time interval (
t, t+1).
2.3 Hazard Assessment
The hazard of accidents depends on different
structural and environmental parameters that may
vary for each time interval and for each highway
tract, and on the number of vehicles (Fabiano et al.,
2002; Fabiano et al., 2005). In this work, the hazard
t
HAZ is simply represented as a time-varying a-
dimensional parameter
t
HAZ
η
multiplied by the
number of vehicles in the specific tract. That is,
t
t
HAZ
t
t
HAZ
t
t
HAZ
t
ZLNLNHAZ
3
12
2
11
1
ηηη
++=
t=0,…, T-1 (6)
3 THE DECISION PROBLEM
The objective function has to take into account the
number of vehicles in the park entrance, the number
of vehicles per unit length in each tract of the
highway, and the number of vehicles that enter the
tunnel. In particular the following terms have to be
minimized:
the number of vehicles waiting in the park
entrance;
the number of vehicles per unit length for tract
1,
t
N
1
;
the number of vehicles per unit length for tract
2,
t
N
2
;
the difference between the number of vehicles
per unit length in tract 1 and tract 2,
tt
NN
21
− ;
the number of vehicles that enter the tunnel.
Thus, the objective function can be expressed as
() ( ) ( )
()()
22
21
2
2
1
0
2
1
2
min
ttt
t
T
t
tt
ZNN
NNI
δγ
βα
+−+
+++
∑
−
=
(7)
where:
t
N
1
,
t
N
2
are the number of (hazmat) vehicles per
unit length that is present in the highway road in
tracts 1 and 2, in time instant
t;
t
I is the number of vehicles stored, at time
instant
t, in the park near the entrance, i.e., the
inventory of the entrance park area, in time
interval (
t, t+1);
t
Z
is the number of vehicles that reaches the
tunnel in time interval (
t, t+1);
α
,
β
,
γ
,
δ
are specific weighting factors.
OPTIMAL CONTROL OF HAZARDOUS MATERIALS TRAFFIC FLOW - The Case of Transport through a Critical
Infrastructure
313

4 THE STATEMENT OF THE
OPTIMAL CONTROL
PROBLEM
The optimal control problem reported in equations
(1)-(7) can be expressed in the following form
∑
−
=
1
0
min
T
t
t
t
T
t
u
xQx
t
(8)
where
t
x is the space vector and
t
Q a matrix of time
dependent parameters. Specifically,
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
t
t
t
t
N
N
I
x
2
1
t=0,…,T-1 (9)
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
Δ++−
−+=
22
0
0
001
tvel
Q
t
t
δγβγ
γγα
t=0,…,T-1 (10)
s.t.
t
t
t
t
t
dubxAx
+
+=
+1
t=0,…,T-1 (11)
0≥
t
u t=0,…,T-1 (12)
0≥
t
x
t=0,…,T-1 (13)
where
tt
Xu = are the control variables,
t
A is a
matrix of time dependent parameters,
b a vector of
parameters, and
t
d
a vector of time dependent
parameters.
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
Δ
−
Δ
Δ
−=
2
2
2
1
1
1
10
010
001
L
tvel
L
tvel
L
tvel
A
tt
t
t
t=0,…,T-1 (14)
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
=
0
1
1
1
L
b
t
t=0,…,T-1 (15)
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
0
0
t
t
V
d
t=0,…,T-1 (16)
The optimal control problem expressed by equations
(8)-(16) is a linear-quadratic one, with non
negativity constraints over the state and control
variables.
5 RESULTS
The space-time discretization of equations (2)-(3)
has been chosen in order to avoid instability of the
traffic flow (i.e., in the time interval, the vehicles are
not allowed to pass the tract length), and in order to
have a meaningful time interval for traffic flow
simulation (Kotsialos and Papageorgiou, 2004). That
is,
]/[6.16
]/[6.16
][800
][800
][10
15
2
1
2
1
smvel
smvel
mL
mL
st
T
t
t
=
=
=
=
=Δ
=
Firstly, the optimization problem (1)-(7) has been
solved, with the following inputs:
0] 0, 0, 0, 3, 2, 0, 0, 0, 0, 0, 0, 2, 3, 10,[
=
V , and the
following weights in the objective function:
5444
102,102,102,102 ⋅=⋅=⋅=⋅=
δγβα
.
A receding-horizon control scheme has been applied
and, in Table 1 and Table 2, the optimization results
are reported.
Table 1: Results of the optimization problem:
t
X
,
t
Z
,
t
I
.
Time
t
X
t
Z
t
I
0 8.38 0 0
1 0.56 0 1.62
2 0.6
4
1026.0
−
⋅
4.06
3 0.66
4
1026.0
−
⋅
5.46
4 0.74
4
1025.0
−
⋅
4.8
5 0.86
4
1024.0
−
⋅
4.06
6 1
4
1023.0
−
⋅
3.2
7 1.19
4
1021.0
−
⋅
2.2
8 1
4
1019.0
−
⋅
1
9 2
4
1017.0
−
⋅
0
10 2.23
4
1014.0
−
⋅
0
11 0.77
4
1012.0
−
⋅
0.76
12 0
5
1083.0
−
⋅
0
13 0
5
1044.0
−
⋅
0
14 0 0 0
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
314
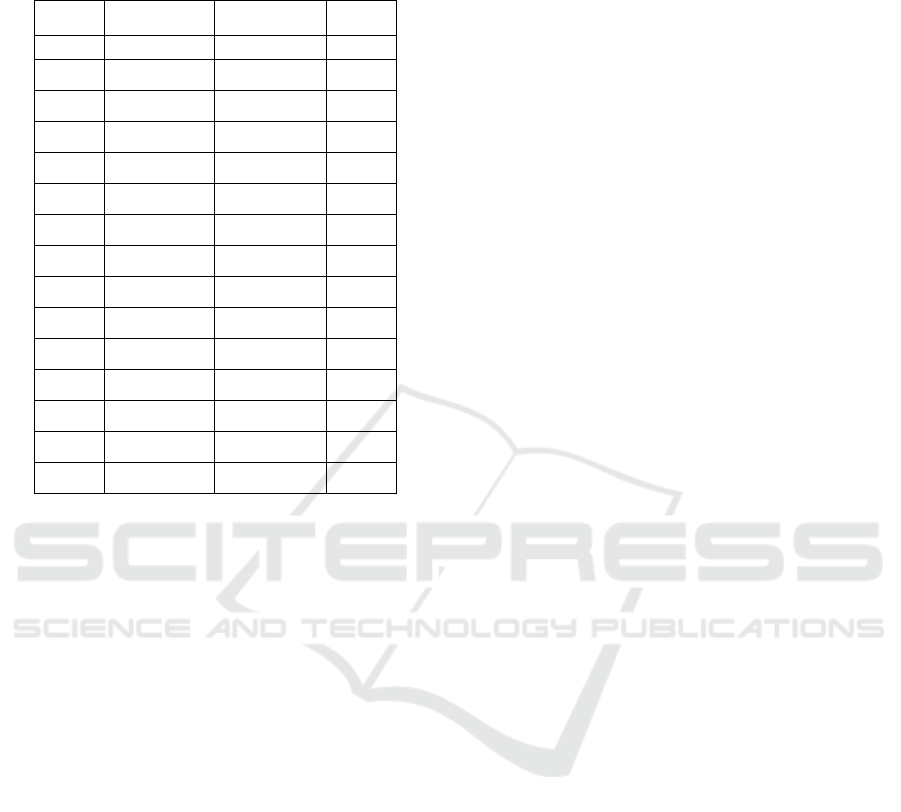
Table 2: Results of the optimization problem:
t
N
1
,
t
N
2
,
t
Y
.
Time
t
N
1
t
N
2
t
Y
0 0 0 0
1
1
101.0
−
⋅
0 1.74
2
2
109.0
−
⋅
2
1022.0
−
⋅
1.49
3
2
1079.0
−
⋅
2
104.0
−
⋅
1.3
4
2
1071.0
−
⋅
2
1057.0
−
⋅
1.17
5
2
1065.0
−
⋅
2
1071.0
−
⋅
1.08
6
2
1063.0
−
⋅
2
1085.0
−
⋅
0.04
7
2
1062.0
−
⋅
2
1098.0
−
⋅
1.03
8
2
1064.0
−
⋅
1
1011.0
−
⋅
1.06
9
2
1063.0
−
⋅
1
1012.0
−
⋅
1.05
10
2
1075.0
−
⋅
1
1014.0
−
⋅
1.25
11
2
1087.0
−
⋅
1
1015.0
−
⋅
1.45
12
2
1079.0
−
⋅
1
1017.0
−
⋅
1.31
13
2
1063.0
−
⋅
1
1019.0
−
⋅
1.04
14
2
1049.0
−
⋅
1
102.0
−
⋅
0.82
The overall hazard is (summation over time of
equation (6)) equal to 1978, with
10
321
===
t
HAZ
t
HAZ
t
HAZ
ηηη
.
Then, the non-negativity constraints have been
removed. The optimal values are the same like in the
constrained case.
Similar results, in the unconstrained case, can be
found through the use of the Riccati equation.
Instead, for the constrained case an efficient method
of solution has to be found. A possible approach can
be the one reported in (Bertsimas and Brown, 2007).
Otherwise, one can try to use dynamic programming
and reduce the explosion of computation that arises.
6 CONCLUSIONS
A preliminary approach for the optimal control of
hazardous materials traffic flow has been presented.
The novelties of the presented approach in the
literature of hazmat transportation have been
highlighted, as well as the methodological
approaches that might characterize the solution of
the optimal control problem.
Future research related to the present work will
regard the development of methods to derive the
optimal control law to the considered problem in a
closed form. After that, the decision problem could
be extended to the optimal control of two fleets of
hazardous material that have to flow through a
tunnel in both competitive and collaborative cases.
Moreover, a hierarchical control can be formalized
in which a decision maker related to the tunnel has
to decide the price to assign to the two fleets on the
basis of the costs, the goods demand, and the risk to
be minimized in the overall system, while the fleets
aim at minimizing their own benefits and hazards.
REFERENCES
Bell, M., 2009. A multi-path Astar algorithm for risk
averse vehicle navigation, Transportation Research
Part B: Methodological, 43 (1), 97-107.
Bell, M., Cassir, C., 2002. Risk-averse user equilibrium
traffic assignment: An application of game theory,
Transportation Research Part B: Methodological, 36
(8), 671-681.
Berman, O., Verter, V., Kara, B.Y., 2007. Designing
emergency response networks for hazardous materials
transportation, Computers and Operations Research,
34(5), 1374-1388.
Beroggi, G., Wallace, W., 1994. Operational Risk
Management: A New Paradigm for Decision Making,
IEEE Transactions on Systems, Man and Cybernetics,
24 (10), 1450-1457
Eds Bersani, C., Boulmakoul, A., Garbolino, E., Sacile,
R., 2008a, Advanced Technologies and Methodologies
for Risk Management in the Global Transport of
Dangerous Goods, NATO Science for Peace and
Security Series - E: Human and Societal Dynamics
(ISSN 1874-6276) Volume 45 ISBN 978-1-58603-
899-1. Amsterdam: IOS Press.
Bersani, C., Minciardi, R., Sacile, R., Tomasoni, A.,
Trasforini, E., 2008b. An Integrated System for the
Hazardous Materials Transport in a Sub-Regional
Scale Area, in Advanced Technologies and
Methodologies for Risk Management in the Global
Transport of Dangerous Goods, Eds C.Bersani, A.
Boulmakoul, E. Garbolino, R. Sacile, NATO Science
for Peace and Security Series - E: Human and Societal
Dynamics (ISSN 1874-6276) Volume 45 ISBN 978-1-
58603-899-1. Amsterdam: IOS Press.
Bertsimas, D., Brown, D., 2007. Constrained Stochastic
LQC: A Tractable Approach, IEEE Transactions on
Automatic Control, 52 (10), 1826-1841.
Bonvicini, S., Spadoni, G., 2008. A hazmat multi-
commodity routing model satisfying risk criteria: A
case study, Journal of Loss Prevention in the Process
Industries 21, 345–358
Castelein, R., Johnson, A., 1989. Constrained Optimal
Control, IEEE Transactions on Automatic Control, 34
(I), 122-126
Fabiano, B., Currò, F., Palazzi, E., Pastorino, R., 2002. A
framework for risk assessment and decision-making
OPTIMAL CONTROL OF HAZARDOUS MATERIALS TRAFFIC FLOW - The Case of Transport through a Critical
Infrastructure
315

strategies in dangerous good transportation, Journal of
Hazardous Materials 93, 1–15.
Fabiano, B., Currò, F., Reverberi, A.P., Pastorino R.,
2005. Dangerous good transportation by road: from
risk analysis to emergency planning, Journal of Loss
Prevention in the Process Industries 18, 403–413.
Kara, B., Verter, V., 2008. A Path-Based Approach for
Hazmat Transport Network Design, Management
Science 54 (1), 29-40.
Kara, B.Y., Verter, V., 2004. Designing a road network
for hazardous materials transportation, Transportation
Science, 38 (2), 188-196.
Kotsialos, A., Papageorgiou, M., 2004. Nonlinear optimal
control applied to coordinated ramp metering, IEEE
Transactions on Control Systems Technology 12 (6),
920-933.
Minciardi, R., Robba, M., Sacile, R., 2008. Traffic
optimization in hazardous materials transport on roads
flowing towards one critical road infrastructure, in
Advanced Technologies and Methodologies for Risk
Management in the Global Transport of Dangerous
Goods, Eds C.Bersani, A. Boulmakoul, E. Garbolino,
R. Sacile, NATO Science for Peace and Security
Series - E: Human and Societal Dynamics (ISSN
1874-6276) Volume 45 ISBN 978-1-58603-899-1.
Amsterdam: IOS Press.
Sadjadi, S.J., 2007. An application of efficient frontier in
transportation of hazardous materials, Computers &
Industrial Engineering 53, 357–360.
Serafini, P., 2006. Dynamic programming and minimum
risk paths, European Journal of Operational Research
175, 224–237.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
316
