
DOUBLE
WELL POTENTIAL AS DIFFUSIVE FUNCTION
FOR PDE-BASED SCALAR IMAGE RESTORATION METHOD
A. Histace
ETIS UMR CNRS 8051, ENSEA-UCP, 6 avenue du Ponceau, 95014 Cergy, France
M. M
´
enard
L3i, University of La Rochelle, Pole Sciences et Technologie, 17000 La Rochelle, France
Keywords:
Image Diffusion, Double well potential, Directional diffusion, Selectivity.
Abstract:
Anisotropic regularization PDE’s (Partial Differential Equation) raised a strong interest in the field of image
processing. The benefit of PDE-based regularization methods lies in the ability to smooth data in a nonlinear
way, allowing the preservation of important image features (contours, corners or other discontinuities). In this
article, we propose a PDE-based method restoration approach integrating a double-well potential as diffusive
function. It is shown that this particular potential leads to a particular regularization PDE which makes it
possible integration of prior knowledge about the gradients intensity level to restore. As a proof a feasibility,
results of restoration are presented both on ad hoc and natural images to show potentialities of the proposed
method.
1 INTRODUCTION
Since the pioneering work of Perona-Malik (Perona
and Malik, 1990), anisotropic regularization PDE’s
raised a strong interest in the field of image process-
ing. Many regularization schemes have been pre-
sented so far in the literature, particularly for the
problem of scalar image restoration (see (Histace and
M
´
enard, 2008) for a complete review). In (Deriche
and Faugeras, 1996) authors propose a synthetic for-
mulation to express the global scheme of PDE-based
restoration approaches. More precisely, if we denote
ψ(r,t) : R
2
×R
+
→ R the time intensity function of a
corrupted image ψ
0
= ψ(r,0), the corresponding reg-
ularization problem of ψ
0
is equivalent to the mini-
mization problem described by the following PDE:
∂ψ
∂t
= c
ξ
(k∇ψk)
∂
2
ψ
∂ξ
2
+ c
η
(k∇ψk)
∂
2
ψ
∂η
2
, (1)
where η = ∇ψ/k∇ψk, ξ⊥η and c
ξ
and c
η
are
tw
o weighting functions (also called diffusive func-
tions). This PDE can be interpreted as the super-
position of two monodimensional heat equations, re-
spectively oriented in the orthogonal direction of the
gradient and in the tangential direction: It is charac-
terized by an anisotropic diffusive effect in the priv-
ileged directions ξ and η allowing a non-linear de-
noising of scalar image. Eq. (1) is of primary im-
portance, for all classical methods can be expressed
in that global scheme: For instance, if we consider
the former anisotropic diffusive equation of Perona-
Malik’s (Perona and Malik, 1990) given by
∂ψ
∂t
= d
iv(c(k∇ψk)∇ψ) , (2)
with ψ(r,0) = ψ
0
and c(.) a monotonic decreasing
function, it is possible to express it in the global
scheme of Eq. (1) with
(
c
ξ
= c(k∇ψk)
c
η
= c
0
(k∇ψk).|∇ψ| + c(k∇ψk)
(3)
Formulation of Eq. (1) is also interested, for it makes
stability study of classical proposed methods possi-
ble. What we proposed in this article is a prospective
study for the integration of a double well potential
as a diffusive function c(.) in Eq. (2). Our aim and
motivation for such a study are mainly to show that,
firstly, such a choice can lead to a stable PDE-based
approach for scalar image denoising that can over-
pass classical approach of Perona-Malik’s from which
it is derived and which presents instability problems
as formerly shown in (Catt
´
e et al., 1992), and, sec-
ondly, that this approach overcomes some drawbacks
of the classical methods like corner smoothing or pin-
hole effect. Layout of this article is the following one:
401
Histace A. and Ménard M. (2009).
DOUBLE WELL POTENTIAL AS DIFFUSIVE FUNCTION FOR PDE-BASED SCALAR IMAGE RESTORATION METHOD.
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 401-404
DOI: 10.5220/0002191304010404
Copyright
c
SciTePress
In section two, we introduce the double well func-
tion and derive the corresponding PDE in the global
scheme of Eq. (1). We also proposed in that section a
study of the stability of the derived PDE compared to
the stability of Perona-Malik’s approach. Third sec-
tion is dedicated to experimental and quantitative re-
sults. Fourth and last section contains conclusion and
discussion.
2 DOUBLE WELL POTENTIAL
AND CORRESPONDING PDE
2.1 Diffusive Function
The double well potential considered in this article is
defined by the following function:
c
DW
(u) = 1 −φ(u) = 1 −
Z
u
0
v(α− v)(v − 1)dv . (4)
Some graphical representations of Eq. (4) for differ-
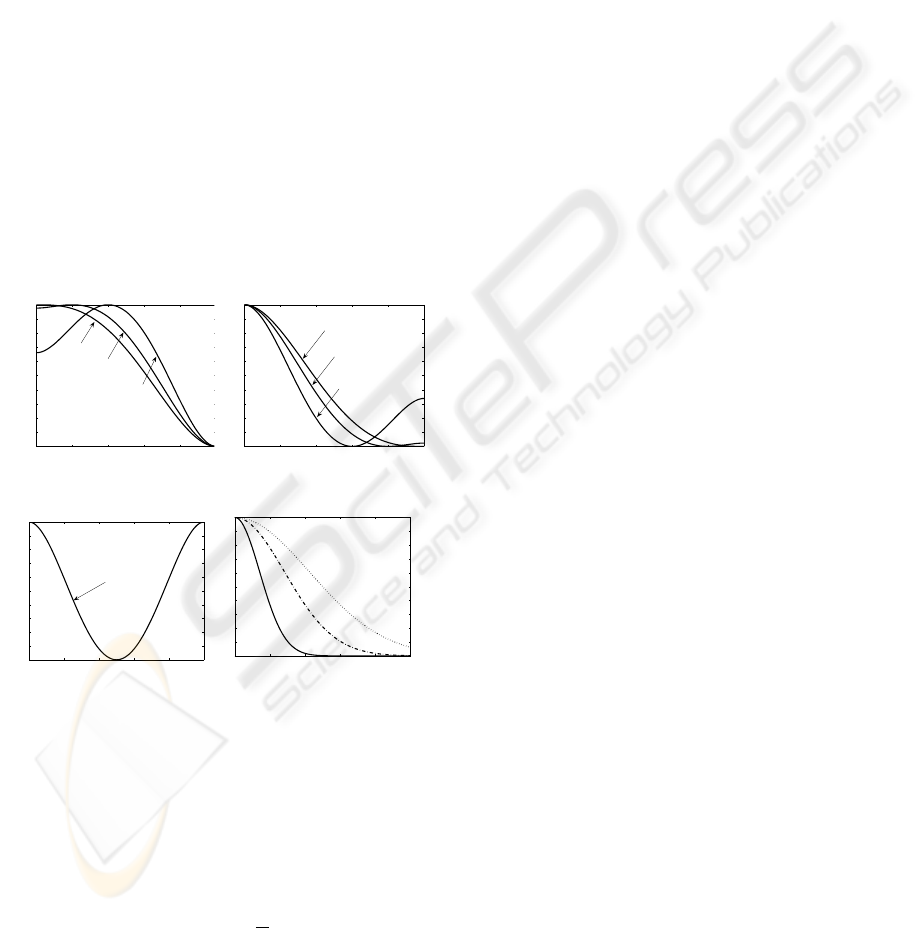
ent values of α are proposed Fig. 1.
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
u
c
DW
(u)
α=0
α=0.2
α=0.4
(a)
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
u
c
DW
(u)
α=1
α=0.8
α=0.6
(b)
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
u
c
DW
(u)
α=0.5
(c)
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
u
c
PM
(u)
(d)
Figure 1: (a), (b), (c) Plots of function c
DW
(.) of Eq. (4)
for different values of α: (a) 0 < α < 0.5, (b) 0.5 < α < 1,
and (c) α = 0.5. (d) Plots of function c
PM
(.) of Eq. (5) for
different values of k and α. Solid lines stand for k = 0.2,
dash-dotted lines for k = 0.4, and dotted lines for k = 0.6.
This function has to be compared with the classical
Perona-Malik’s function c
PM
(.) given by:
c
PM
(u) = e
−
u
2
k
2
, (5)
with k a soft threshold defining selectivity of
c
PM
(.) regarding values of image gradients. Fig. 1.(d)
shows graphical representations of c
PM
(.) defined by
Eq. (5) for different values of k. As one can notice on
Fig. 1.(d), for k∇ψk → 0, c
PM
(k∇ψk) → 1, whereas
for k∇ψk → 1, c
PM
(k∇ψk) → 0. As a consequence,
boundaries within images which are on a threshold,
function of k, are preserved from the smoothing ef-
fect of Eq. (2). One can notice on Fig. 1 that φ(.)
has been normalized. As a consequence, we are able
to ensure that 0 ≤ c
DW
(u) ≤ 1 for all values of u like
classical PM’s function of Eq. (2). Global variations
of c
DW
can be compared to those of c
PM
for α = 0
and α = 1. For 0 ≤ α < 1, since c
DW
is issued from
a double well potential, selectivity of Eq. (2) is more
important and centered on a particular gradient value
function of α. For instance, for α = 0.5, only gradi-
ents of value 0.5 are totally preserved from the diffu-
sive effect that can be interpreted as an integration of
directional constrains within the restoration process.
Moreover, we are now going to show, that integration
of c
DW
as diffusive function leads to interesting sta-
bility property of corresponding PDE.
2.2 Study of Stability
As mentioned in first section, classical Perona-
Malik’s PDE presents instability problems. More pre-
cisely, as shown in (Catt
´
e et al., 1992), sometimes
noise can be enhanced instead of being removed. This
can be explained considering Eq. (3). If we con-
sider c
PM
(.) function, it appears that corresponding c
η
function of Eq. (3), in the global scheme of Eq. (1),
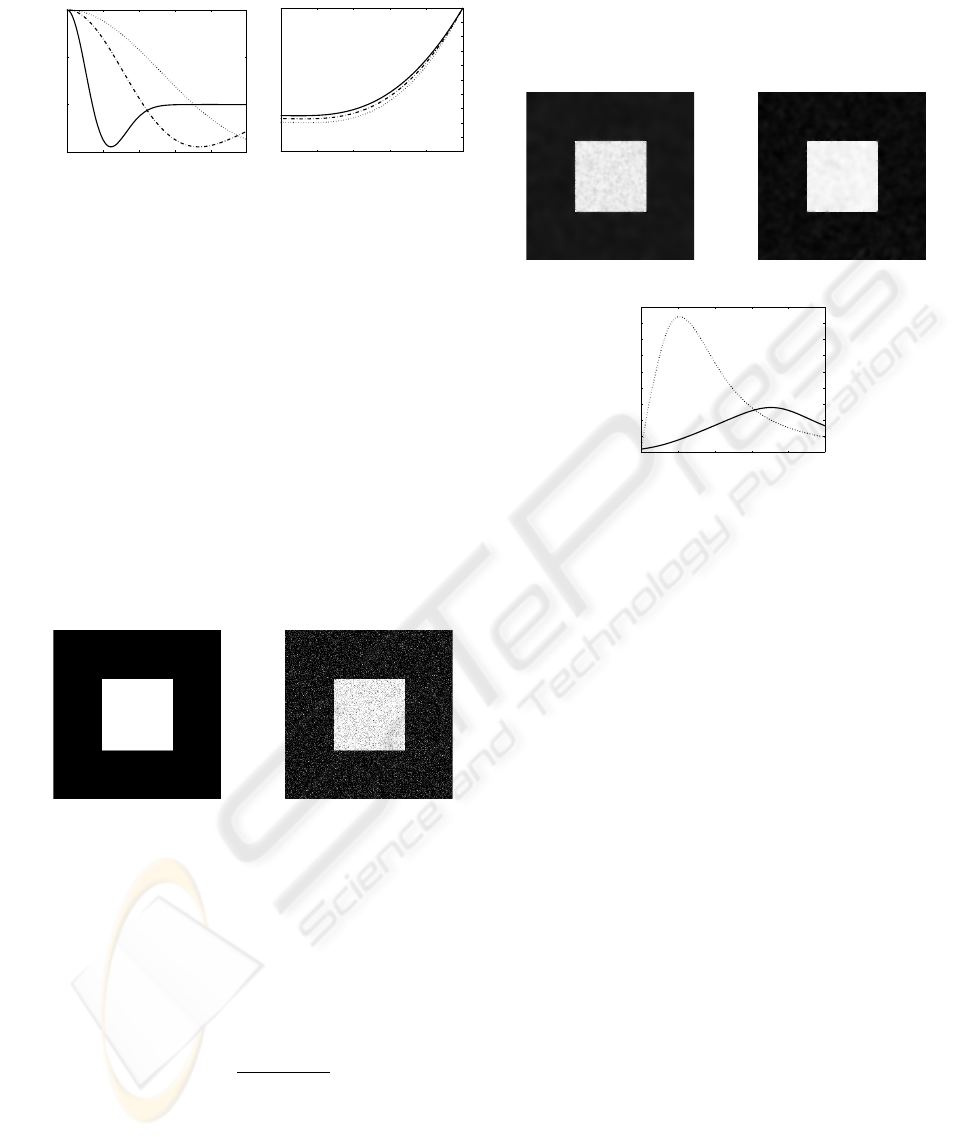
can sometimes takes negative values (see Fig. 2.(a)
for illustrations). This leads to local instabilities of the
Perona-Malik’s PDE which degrades the processed
image instead of denoising it. Now, if we calculate
mathematical expression of c
η
with c(.) = c
DW
(.) of
Eq. (4), one can obtain that:
c
η
(k∇ψk) = c
0
DW
(k∇ψk).|∇ψ| + c
DW
(k∇ψk) , (6)
Considering Eq.(6), if we plot this function, one can
notice that corresponding c
η
function never takes neg-
ative values (see Fig. 2.(b) for illustrations): Diffusive
process remains stable for all gradient values of pro-
cessed image which is of primary importance.
3 EXPERIMENTAL RESULTS
We propose in this section to make a visual and quan-
titative comparison between classical Perona-Malik’s
PDE of Eq. (2) with diffusive function c(.) = c
PM
(.)
of Eq. (5), and proposed derived PDE with c(.) =
c
DW
(.) of Eq. (4) as diffusive function. For quantita-
tive comparisons, we will consider adapted measure
of similarity between non corrupted initial image and
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
402
0 0.2 0.4 0.6 0.8 1
−0.5
0
0.5
1
u
c
η
PM
(a)
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
u
c
η
DW
(b)
Figure 2: Plots of function c
η
PM
and c
η
DW
for different val-
ues of k and α. Solid lines stand for k = 0.2 and α = 0.5,
dash-dotted lines for k = 0.4 and α = 0.7 and dotted lines
for k = 0.6 and α = 1.
restored one. This measure will depend on the nature
of original image. For practical numerical implemen-
tations, the process of Eq. (2) is sampled with a time
step τ. The restored images ψ(t
n
) are calculated at
discrete instant t
n
= nτ with n the number of itera-
tions.
3.1 Synthetic Image
The first proposed image is the binary image of Fig.
3.(a) corrupted by a white gaussian noise of mean zero
and standard deviation σ.
(b)
(w)
(a) (b)
Figure 3: (a) Original synthetic image and (b) its corrupted
version ψ
0
. Corrupting noise is a white Gaussian one of
mean zero and standard deviation σ = 0.05.
Considering binary nature of non corrupted image
(Fig. 3.(a)), quantification of the denoising effect of
Eq. (2) with c(.) = c
PM
(.) and c(.) = c
DW
(.), will be
estimated with Fisher’s index given by
I
Fisher
=
(m
w
− m
b
)
2
σ
2
w
+ σ
2
b
, (7)
with m
w,b
the average value of the pixels of the re-
stored image ψ(t
n
) being originally in the white (w)
or black (b) part of original image (Fig. 3.(a)) and
σ
w,b
the corresponding standard deviation. Because
aim of this article is to show potentiality of the de-
scribed restoration method, only optimal results for
both compared approaches are presented Fig. 4: Val-
ues of k and α parameters are empirically chosen and
strategy for optimal choice is not describe here.
(a) (b)
0 100 200 300 400 500
0
100
200
300
400
500
600
700
800
900
n
I
Fisher
(c)
Figure 4: (a) Restored image with c(.) = c
PM
(.) (classical
Perona-Malik’s approach), (b) Restored image with c(.) =
c
DW
(.) (proposed approach), (c) Fisher index function of
iteration number n, solid lines stands for classical Perona-
Malik’s approach, dotted line stands for proposed method.
k is equal to 0.4, α is equal to 0.5 (these values have been
empirically tuned).
As one can notice on Fig. 4, both visually and
quantitatively, restoration of binary image of Fig.
3.(a) is better with the diffusive function of Eq. (4).
More precisely, stability property of the double well
function prevents restoration process from possible
enhancement of corrupting Gaussian noise. Homoge-
nous areas of Fig. 4.(b) does not visually shows os-
cillations, nor corners of the white square as in Fig.
4.(a). This visual impression is confirmed by vari-
ations of Fisher’s index in Fig. 4.(c) that reaches a
level third times more important than with classical
approach of Perona-Malik’s. The value of α parame-
ter corresponding to best result is 0.5: this is not sur-
prising, for it is also the value of the gradient intensity
characterizing the boundaries of the with square. As a
consequence, this experiment also confirmed the pos-
sible gradient intensity selectivity of the proposed ap-
proach interpreted as a directional diffusion process.
We shall now experiment the proposed approach in
the context of restoration of real scalar images.
3.2 Real Images
In this section, we propose to compare both our pro-
posed method with PM’s approach on the classical
DOUBLE WELL POTENTIAL AS DIFFUSIVE FUNCTION FOR PDE-BASED SCALAR IMAGE RESTORATION
METHOD
403

“cameraman” image. For our purpose, this latter has
been corrupted by a white gaussian noise of mean
zero and standard deviation σ (see Fig. 5).
(a) (b)
Figure 5: (a) Original image “cameraman” and (b) its cor-
rupted version ψ
0
. Corrupting noise is a white Gaussian one
of mean zero and standard deviation σ = 0.05.
Considering nature of non corrupted image (Fig.
5.(a)), quantification of the denoising effect of Eq.
(2) with c(.) = c
PM
(.) and c(.) = c
DW
(.), will be es-
timated with a classical PSNR measurement. Once
again, because aim of this article is to show potential-
ity of the described restoration method, only optimal
results for both compared approaches are presented
Figs. 6 and 7.
(a) (b)
Figure 6: (a) Restored image with c(.) = c
PM
(.) (clas-
sical Perona-Malik’s approach), (b) Restored image with
c(.) = c
DW
(.) (proposed approach). k is equal to 1 for
PM’s restoration approach, α is equal to 0.2 for proposed
approach (these values have been empirically tuned).
One can notice on Figs. 6 and 7 that both visu-
ally and quantitatively, it is possible to find a value
of α that can outperform results of classical PM’s ap-
proach. Quantitatively speaking PSNR is around 2dB
higher and visually speaking, boundaries on Fig. 6 are
preserved in a better way from the diffusion effect.
4 CONCLUSIONS
In this article, we have proposed an alternative diffu-
sive function for restoration of scalar images within
the framework of PDE-based restoration approaches.
The proposed diffusive function allows integrating
0 20 40 60 80 100 120
132
134
136
138
140
142
144
146
148
iteration number (n)
PSNR (dB)
Figure 7: PSNR function of iteration number n, solid lines
stands for classical Perona-Malik’s approach, dotted line
stands for proposed method. k is equal to 1, α is equal to
0.2 (these values have been empirically tuned). These two
curves have been computed by calculation of the mean re-
sults obtained for one hundred different realizations of the
gaussian corrupting noise.
prior knowledge on the gradient level to restore thanks
parameter α of Eq. (4) and remains always stable
on the contrary of classical PM’s approach. Pro-
posed method also remains fast and easy to com-
pute. Quantitatively speaking, better restoration re-
sults have been obtained. Concerning possible out-
looks, this proposed method could be associated to
the orientation selectivity of a PDE-based method al-
ready presented in the framework of that conference
in (Histace et al., 2007). Association of both proper-
ties should lead to a restoration method with interest-
ing directional properties for “vision in robotics” area
for example.
REFERENCES
Catt
´
e, F., Coll, T., Lions, P., and Morel, J. (1992). Im-
age selective smoothing and edge detection by nonlin-
ear diffusion. SIAM Journal of Applied Mathematics,
29(1):182–193.
Deriche, R. and Faugeras, O. (1996). Les edp en traitements
des images et visions par ordinateur. Traitement du
Signal, 13(6):551–578.
Histace, A., Courboulay, V., and M
´
enard, M. (2007). Selec-
tive image diffusion for oriented pattern extraction. In
4th International Conference on Informatics in Con-
trol, Automation and Robotics (ICINCO), pages 270–
274.
Histace, A. and M
´
enard, M. (2008). Robotics, Automation
and Contol Book: PDE based approach for oriented
pattern segmentation, chapter 22, pages 207–218. In-
tech Education and Publishing.
Perona, P. and Malik, J. (1990). Scale-space and edge
detection using anistropic diffusion. IEEE Transca-
tions on Pattern Analysis and Machine Intelligence,
12(7):629–639.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
404
