EFFICIENT CLASSIFICATION FOR LARGE-SCALE PROBLEMS

BY MULTIPLE LDA SUBSPACES

Martina Uray

Institute of Digital Image Processing

Joanneum Research, Austria

Peter M. Roth, Horst Bischof

Institute for Computer Graphics and Vision

Graz University of Technology, Austria

Keywords:

LDA, Image classiﬁcation, Large databases.

Abstract:

In this paper we consider the limitations of Linear Discriminative Analysis (LDA) when applying it for large-

scale problems. Since LDA was originally developed for two-class problems the obtained transformation

is sub-optimal if multiple classes are considered. In fact, the separability between the classes is reduced,

which decreases the classiﬁcation power. To overcome this problem several approaches including weighting

strategies and mixture models were proposed. But these approaches are complex and computational expensive.

Moreover, they were only tested for a small number of classes. In contrast, our approach allows to handle a

huge number of classes showing excellent classiﬁcation performance at low computational costs. The main

idea is to split the original data into multiple sub-sets and to compute a single LDA space for each sub-set.

Thus, the separability in the obtained subspaces is increased and the overall classiﬁcation power is improved.

Moreover, since smaller matrices have to be handled the computational complexity is reduced for both, training

and classiﬁcation. These beneﬁts are demonstrated on different publicly available datasets. In particular, we

consider the task of object recognition, where we can handle up to 1000 classes.

1 INTRODUCTION

Linear Discriminative Analysis (LDA) is a popular

and widely used statistical technique for dimension

reduction and linear classiﬁcation. Important appli-

cations include face recognition (Belhumeur et al.,

1997), speech recognition (Hunt, 1979), or image re-

trieval (Swets and Weng, 1996). The main idea is to

search for a linear projection, that preserves a maxi-

mum amount of discriminative information when pro-

jecting the original data onto a lower dimensional

space. In fact, Fisher (Fisher, 1936) introduced a pro-

jection that minimizes the Bayes error for two classes.

Hence, by maximizing the Fisher criterion (see Sec-

tion 2), that analyzes the between scatter versus the

within scatter for two classes, an optimal solution

with respect to the Bayes error is obtained. For more

details see, e.g., (Fukunaga, 1990).

Later this approach was extended for multiple

classes by Rao (Rao, 1948). But Loog et al. (Loog

et al., 2001) showed that for more than two classes

maximizing the Fisher criterion provides only a sub-

optimal solution. In general, the Fisher criterion

maximizes the mean squared distances between the

classes, which, however, is different from minimizing

the Bayes error. In particular, thus obtained projec-

tions tend to overemphasize distances of already well

separable classes (in the original space). Neighboring

classes may overlap in the projected subspace, which

reduces the separability and the classiﬁcation perfor-

mance. But for many practical applications (e.g., face

recognition) only a small number of well separable

classes are considered. Under this condition even the

sub-optimal solution mostly provides an approxima-

tion of sufﬁcient accuracy to solve the speciﬁc task.

In contrast, in this paper, we apply LDA for multi-

class classiﬁcation for large-scale problems (i.e., up to

1000 classes). Hence, we expect that due to the sub-

optimal projection an increasing number of classes

would decrease the classiﬁcation performance. This

299

Uray M., M. Roth P. and Bischof H. (2009).

EFFICIENT CLASSIFICATION FOR LARGE-SCALE PROBLEMS BY MULTIPLE LDA SUBSPACES.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 299-306

DOI: 10.5220/0001754802990306

 SciTePress

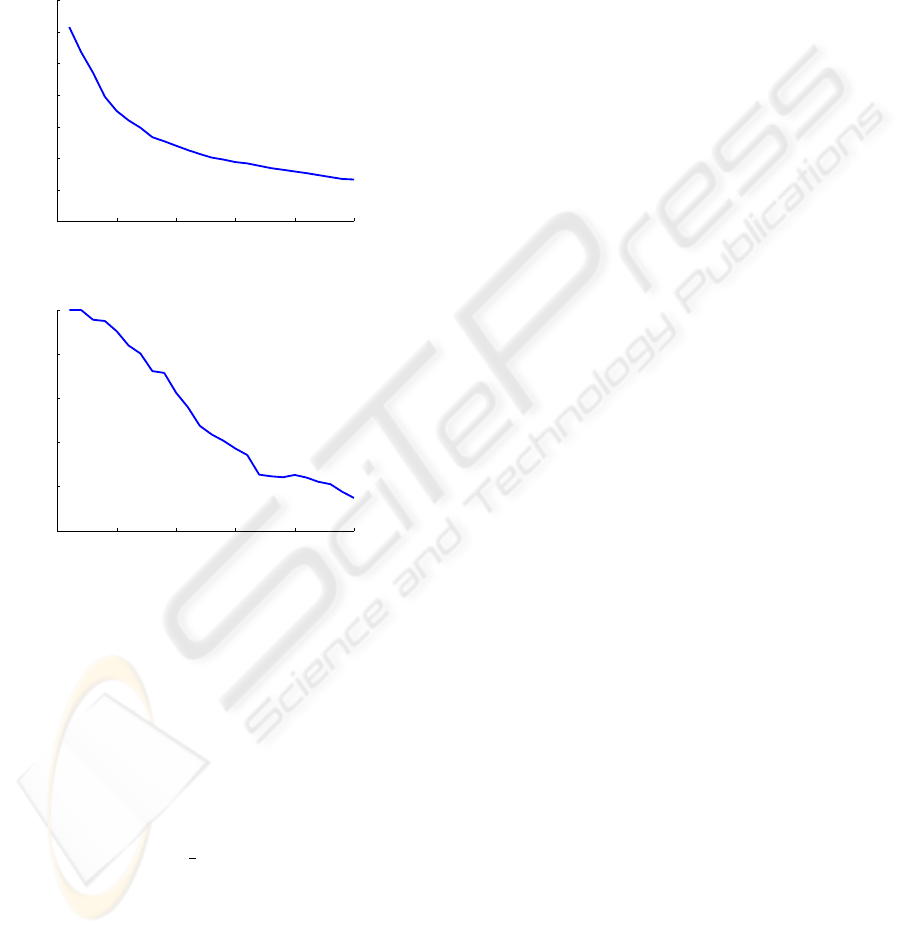
is illustrated for an image classiﬁcation task (i.e., on

the ALOI database (Geusebroek et al., 2005)). From

Figure 1(a) it can be seen that for an increasing num-

ber of classes (i.e, starting from 10 up to 250) the dis-

tances between the class centers and thus the separa-

bility are decreased. As a consequence, the classiﬁca-

tion rate is successively decreased, which is shown in

Figure 1(b).

0 50 100 150 200 250

500

1000

1500

2000

2500

3000

3500

number of classes

mean distances between cc

(a)

0 50 100 150 200 250

100

number of classes

recognition rate in %

(b)

Figure 1: Decreasing classiﬁcation performance for in-

creasing number of classes: (a) mean distances between

class centers and (b) related corresponding classiﬁcation

rates.

To overcome these drawbacks several approaches

were proposed that are based on implicit weighting

schemes (Zhou and Yang, 2004; Loog et al., 2001) or

the estimation of mixture models (Kim et al., 2003).

Loog et al. (Loog et al., 2001) introduced a modi-

ﬁed Fisher criterion that is more closely related to the

classiﬁcation error. For that purpose, they decompose

the c-class criterion into

c(c − 1) two-class criteria.

This allows to deﬁne weighting functions penalizing

classes that are close together, such that the contri-

bution of each pair of classes for the overall criterion

directly depends on the Bayes error between the two

classes (weighted pairwise Fisher criteria). But due

to its computational complexity and the occurrence of

the small sample size problem this approach can not

directly be applied for high-dimensional data such as

images. Thus, Zhou and Yang (Zhou and Yang, 2004)

reduce the dimension of the input data by discarding

the null-space of the between-class scatter matrix and

apply the weighted LDA approach on the thus dimen-

sion reduced data. In contrast, Kim et al. (Kim et al.,

2002; Kim et al., 2003) propose to estimate LDA mix-

ture models (especially, to cope with multi-modal dis-

tributions). The main idea is to apply PCA mixture

models (Tipping and Bishop, 1999) to cluster indi-

vidual classes ﬁrst. Then, individual LDA projection

matrices are estimated and classiﬁcation is done by

the standard nearest neighbor search over all projec-

tions.

The methods described above reduce the problems

resulting from the sub-optimal projection, but they

have two disadvantages. First, they are computational

very expensive. For the weighted LDA approaches

the pairwise Fisher criteria have to be estimated for

all pairs. Similarly, for the LDA mixture approach the

PCA mixture models have to be estimated in an iter-

ative way using the EM-algorithm (Dempster et al.,

1977). In both cases these computations might be

quite expensive, especially, if the number of classes

is very large. Second, these methods were only evalu-

ated for small datasets (i.e., up to 128 classes). Hence,

in this paper we propose a method that is computa-

tionally much cheaper; even for very large-scale prob-

lems!

The main idea is to reduce the complexity of the

problem by splitting the data into a pre-deﬁned num-

ber of equal sized sub-clusters that can still be han-

dled by a single LDA model. Since, in this work we

are mainly focused on reducing the problem’s com-

plexity these clusters are selected randomly. Once the

LDA subspaces were estimated an unknown sample

can be classiﬁed by projecting it onto all subspaces.

The classiﬁcation is ﬁnally done by a nearest neigh-

bor search. Since the subspaces are isometric the

Euclidean norm is equivalent over all subspaces and

the closest class center can be chosen. As shown in

the experiments, in this way the classiﬁcation per-

formance can signiﬁcantly be improved; especially

if the number of classes is very large. Moreover,

since smaller matrices have to be handled the com-

putational costs as well as the memory requirements

can be dramatically reduced; especially in the training

stage!

The outline of the remaining paper is as follows:

First, in Section 2 we review the standard LDA ap-

proach and introduce the multiple LDA subspace rep-

resentation. Next, experimental results are given in

Section 3. Finally, we conclude the paper in Section 4.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

300

2 MULTIPLE LDA SUBSPACES

2.1 Standard LDA

Given a dataset X = [x

,. .. ,x

] ∈ IR

m×n

of n sam-

ples, where each sample belongs to one of c classes

,. .. ,C

. Then, LDA computes a classiﬁcation

function

g(x) = W

x , (1)

where W is selected as the linear projection, that min-

imizes the within-class scatter

∈ IR

m×m

∑

i=1

(µ

− µ)(µ

− µ)

(2)

whereas it maximizes the between-class scatter

∈ IR

m×m

∑

i=1

∑

x∈C

(x − µ

)(x − µ

)

, (3)

where µ is the mean over all samples, µ

is the mean

over class C

, and n

is the number of samples in class

. In fact, this projection is obtained by maximizing

the Fisher-criterion

opt

= argmax



. (4)

The optimal solution for this optimization problem is

given by the solution of the generalized eigenproblem

W = ΛS

W , (5)

or directly by computing the eigenvectors for S

−1

Since the rank of S

−1

is bounded by the rank of

there are c − 1 non-zero eigenvalues resulting in a

(c − 1)-dimensional subspace L = W

X ∈ IR

(c−1)×n

which preserves the most discriminant information.

For classiﬁcation of a new sample x ∈ IR

the class

label ω ∈ {1, ...,c} is assigned according to the re-

sult of a nearest neighbor classiﬁcation. For that pur-

pose, the Euclidean distances d of the projected sam-

ple g(x) and the class centers ν

= W

in the LDA

space are compared:

ω = argmin

1≤i≤c

d (g(x), ν

) . (6)

2.2 Multiple Class LDA

To overcome the limitations of the standard LDA

approach when applying it for large-scale problems

we propose to reduce the complexity by splitting the

problem into sub-problems. This can be motivated

on basis of a theoretic criterion proposed by Mart

ınez

and Zhu (Mart

ınez and Zhu, 2005), that describes the

linear separability of classes:

K =

c − 1

c−1

∑

i=1

max

∀r≤s





. (7)

The parameter

K is estimated by analyzing the angle

between the eigenvectors u

and v

, obtained by solv-

ing the eigenproblem for the scatter matrices S

and

U = Λ

U (8)

V = Λ

V . (9)

In fact, it was shown that a large value

K, which is

equivalent to a small angle, corresponds to a high

probability of incorrect classiﬁcation. To investigate

the separability for an increasing number of classes

we analyzed the parameter

K for varying datasets of

different complexity. In particular, we considered

growing sub-sets of ALOI (in steps of ten classes)

for different levels of variability in the training data

(i.e., small versus large changes between the training

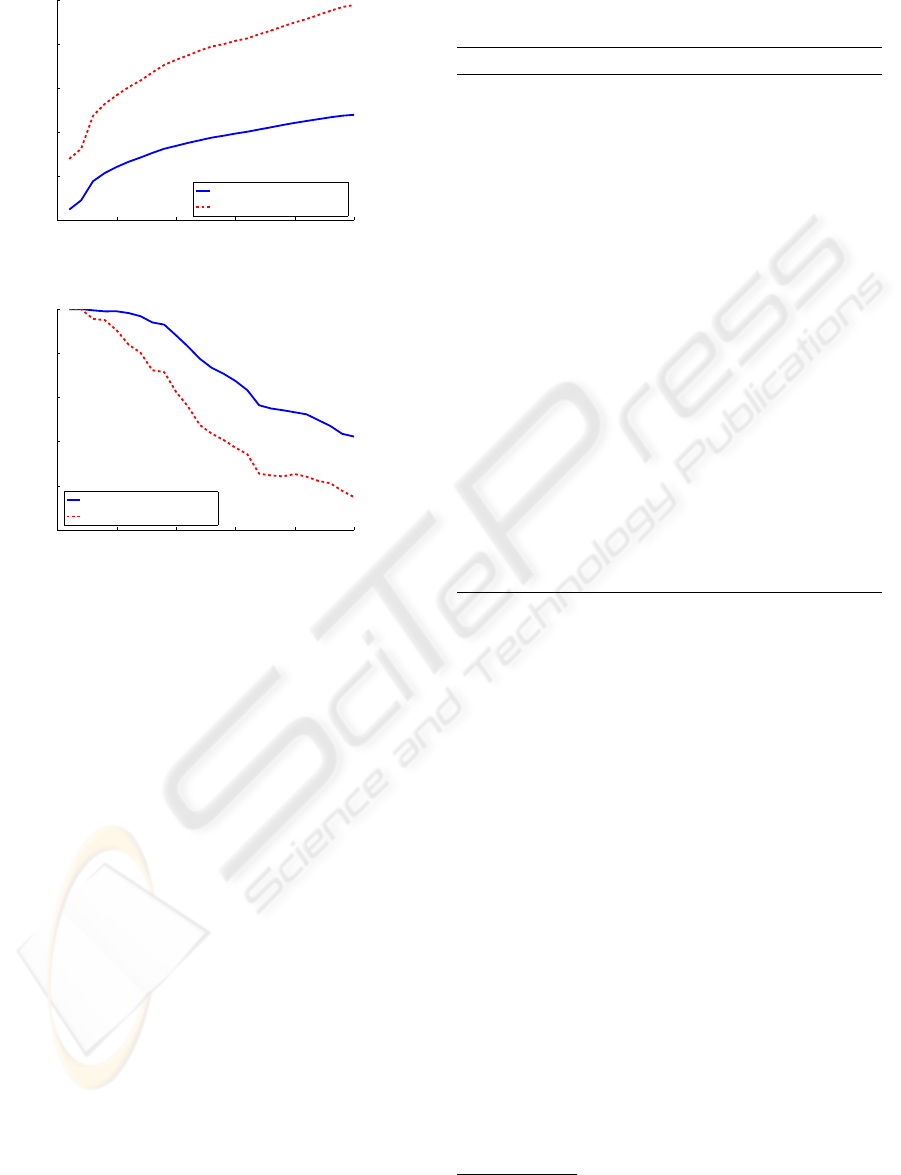
views). From Figure 2(a) it can be seen that increas-

ing the complexity of the problem (i.e., increasing the

number of classes) also increases

K. That is, the sepa-

rability and thus, as illustrated in Figure 2(b), the clas-

siﬁcation performance is decreased. Moreover, it can

be seen that in addition to the number of classes the

similarity between training and testing data has also a

large inﬂuence on the separability. 5

From this observation we can deduce that simpli-

fying the complexity of the problem by reducing the

number of classes increases the classiﬁcation power.

Consequently, instead of building a single large sub-

space we propose to split the data into several sub-

clusters and to build multiple small (well separable)

subspaces.

More formally, given a dataset X = [x

,. . . ,x

] ∈

m×n

of n samples, where each sample belongs

to one of c classes C

,. . . ,C

. First, X is ran-

domly split into k non-overlapping clusters X

∈

m×n

, each consisting of l classes C

,. . . ,C

, such

that X = {X

∪ . . . ∪ X

}. In addition, the class

means {µ

,. . . ,µ

} ⊂ {µ

,. . . ,µ

} and the over-

all cluster mean µ

are estimated. Next, for each

cluster X

an (l − 1)-dimensional LDA subspace

= W

∈ IR

(l−1)×n

is estimated by solving the

individual eigenvalue problems

−1

w j

b j

= Λ

, (10)

EFFICIENT CLASSIFICATION FOR LARGE-SCALE PROBLEMS BY MULTIPLE LDA SUBSPACES

301

0 50 100 150 200 250

0.03

0.05

0.07

0.09

0.11

0.13

number of classes

K value

small training variation

large training variation

(a)

0 50 100 150 200 250

100

number of classes

recognition rate in %

small training variation

large training variation

(b)

Figure 2: Decreasing linear separability for increasing num-

ber of classes for varying complexity of the training data:

(a) Quality criterion

K and (b) corresponding recognition

rates.

where

w j

∑

i=1

∑

x∈C

− µ

)(x

− µ

)

(11)

b j

∑

i=1

(µ

− µ

)(µ

− µ

)

. (12)

Finally, for each LDA subspace l class centers

∈ IR

l−1

are determined by projecting class means

onto the corresponding subspaces:

= W

, i = 1,... , l . (13)

Each of the k subspaces internally describes l

classes C

. Thus, the class centers ν

have to be

reassigned to their original labels. Since there is no

intersection of clusters (i.e., each class is assigned to

exactly one cluster) the relabeling is unique, giving

the original number of c class centers:

[

j=1

{ν

,. . . ,ν

} 7→ {ν

,. . . ,ν

} . (14)

The whole training procedure is summarized in Algo-

rithm 1.

Algorithm 1 : Multiple LDA learning.

Input: Dataset X ∈ IR

m×n

, number of sub-clusters k

and data labels ω ∈ {1,. ..,c}

Output: LDA matrices W

∈ IR

m×(l−1)

and class

centers {ν

,. . . ,ν

} with ν

∈ IR

(l−1)

1: Sample l = c/k random objects for each cluster:

} ⊂ {1,. ..,c}, |L

| = l

and {L

} ∩ {L

} = {}, ∀r 6= s

2: Split the dataset:

⊂ X according to {L

}, X

∈ IR

m×n

3: for j = 1 to k do

4: Calculate PCA+LDA on each dataset X

∈ IR

m×(l−1)

5: Project class means onto LDA space:

= W

, i = 1,... , l

6: end for

7: Reassign sub-cluster class centers the overall

class label:

j=1

{ν

,. . . ,ν

} 7→ {ν

,. . . ,ν

}

Once the k LDA subspaces were estimated the

crucial step is the classiﬁcation. For that purpose a

test sample x ∈ IR

is projected onto all k subspaces.

Since all clusters are of the same size the resulting

(Euclidean) LDA subspaces are of the same dimen-

sion. From Linear Algebra it is known that vector

spaces of the same dimension are isomorphic

and

that isomorphic structures are structurally identical

(see, e.g., (Strang, 2006)). Hence, the Euclidean dis-

tances in these subspaces accord and can directly be

compared. Thus, the class label ω ∈ {1,. . .,c} for an

unknown test sample x can be estimated by searching

for the closest class center over all projected spaces:

(x) = W

x (15)

ω = arg min

1≤i≤c,1≤ j≤k

d (g

(x),ν

) . (16)

3 EXPERIMENTAL RESULTS

In this section, we show the beneﬁts of the proposed

approach. First, we discuss the typical problems that

occur when the number of classes is increasing. For

An isomorphism is a one-to-one map from a vector

space onto itself.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

302

that purpose, we analyze the distances between the

class centers in relation to the number of classes and

discuss the inﬂuence of how the sub-clusters are se-

lected. Next, we compare the proposed approach with

a standard LDA approach, which encompasses only

a single subspace

. In fact, we will show that our

method can handle large databases (even with large

variability in the appearance) considerably better than

the standard approach. Finally, we show that there is

also a beneﬁt in terms of memory requirements and

computational costs.

The experiments were carried out on two large

publicly available databases, that were slightly

adapted:

1. The Columbia Image Database Library (COIL-

100) (Nene et al., 1996) consists of 100 objects

with 72 colored images of views from 0 to 360

degrees taken in 5 degree steps.

2. The Amsterdam Library Of Images ALOI-

1000 (Geusebroek et al., 2005) consists of 1000

objects with 72 colored images of views from 0 to

360 degrees taken in 5 degree steps. The images

contain the objects in their original size as well

as some background. To deﬁne tasks of different

complexity, we created two additional datasets:

ALOI-100, which consists of the ﬁrst 100 objects,

and ALOI-250, which consists of 250 randomly

chosen objects.

In order to emphasize the inﬂuence of data com-

plexity we used training images describing viewpoint

changes of 15

◦

and 30

◦

having two levels of difﬁculty

(see Figure 3). All other images were used for testing,

respectively.

(a)

(b)

Figure 3: Training images for one object of ALOI: (a) 15

◦

dataset and (b) 30

◦

dataset.

3.1 Cluster Analysis

As discussed in Section 2 an increasing number of

classes encompassed by a single subspace results in

decreasing distances of the class centers. Moreover,

the distances between the class centers and the (test)

We are using the PCA+LDA approach (Belhumeur

et al., 1997) for subspace construction.

samples are increasing. Both, in fact, reduce the sep-

arability between the classes. This behavior is illus-

trated in Table 1, where the mean distances between

the class centers and the mean distances between the

test data and the class centers are listed for the 15

◦

and the 30

◦

datasets.

Table 1: Mean distances between class centers and between

test data and correctly assigned class centers (single sub-

space LDA): (a) 15

◦

datasets and (b) 30

◦

datasets.

dataset center to center test to center

COIL-100 267.78 116.38

ALOI-100 479.71 88.90

ALOI-250 294.21 240.76

ALOI-1000 167.02 89.48

(a)

dataset center to center test to center

COIL-100 509.74 251.14

ALOI-100 718.27 188.71

ALOI-250 661.92 477.46

ALOI-1000 375.75 326.67

(b)

It can be seen that the mean distances between the

class centers are reduced to half when the number of

classes is decoupled. Similarly, the mean distance be-

tween the test data and the class centers is doubled.

This shows clearly that the ﬁnal classiﬁcations get in-

creasingly unreliable. Thus, it is clear that smaller

clusters would give better results!

In order to build appropriate clusters we analyzed

which cluster size would give the best recognition

results. For that purpose, we divided each of the

datasets randomly into all valid sub-clusters (i.e, all

subspaces have to have the same size). For instance,

for ALOI-100 we got l ∈ {2,4, 5, 10,20,25,50}. The

obtained recognition rates for all datasets are depicted

in Figure 4. It can be seen that the maxima lie between

10 and 25 objects per cluster. Since there are no sig-

niﬁcant differences between the classiﬁcation errors

in this range the selection of l = 10 is reasonable (also

other datasets showed good performance using this

sub-cluster size). The drop of the recognition rates for

growing subspaces emphasizes the observation that a

small subspace better spans the cluster centers of the

objects, reducing the probability of a fail in classiﬁca-

tion. On the contrary, if the number of sub-clusters is

too small the recognition is not reliable either. This re-

sults from the fact that the classes mutually inﬂuence

each other when building the subspace such that an

unknown sample has no clear class correspondence.

But if there are only two classes one class center is al-

ways favored, being affected by only one other class.

EFFICIENT CLASSIFICATION FOR LARGE-SCALE PROBLEMS BY MULTIPLE LDA SUBSPACES

303

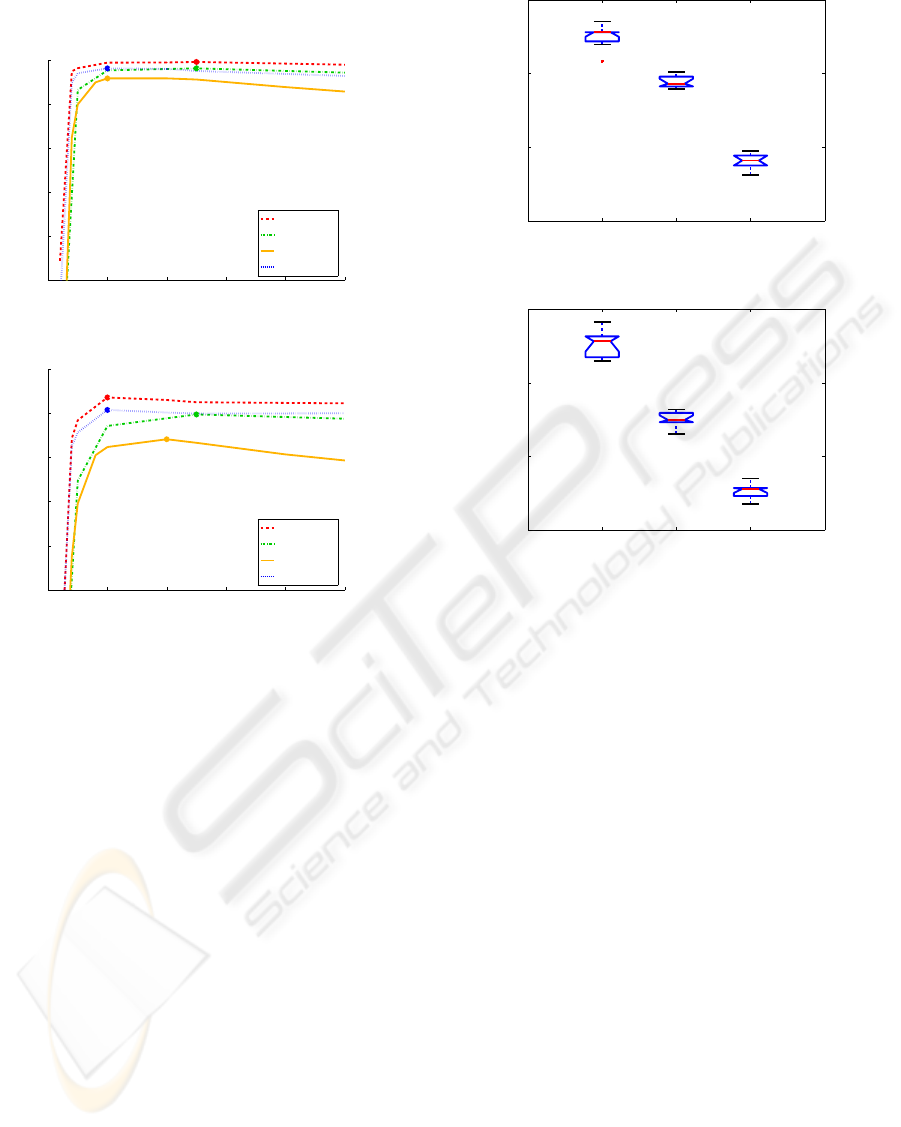
As a result the closest distances in all clusters are sim-

ilar and a correct assignment is not possible.

0 10 20 30 40 50

100

number of classes per cluster

recognition rate in %

ALOI100

ALOI250

ALOI1000

COIL100

(a)

0 10 20 30 40 50

100

number of classes per cluster

recognition rate in %

ALOI100

ALOI250

ALOI1000

COIL100

(b)

Figure 4: Recognition rates for different cluster sizes, where

the marker indicates the highest recognition rate: (a) 15

◦

datasets and (b) 30

◦

datasets.

In this work we are mainly concerned with re-

ducing the complexity of the classiﬁcation problem.

Thus, the sub-clusters were selected randomly. But in

the following we show that the selection of the clus-

ters has only little inﬂuence on the performance of

our approach. For that purpose, we randomly split the

three different datasets of ALOI into sub-clusters of

size 10 and applied the proposed multiple subspace

method. This procedure was repeated ten times; hav-

ing different clusters each time! The results are sum-

marized in Figure 5.

From the box-plots it can be seen that the vari-

ance in the recognition rates for varying selections is

quite small (i.e., approx. ±0.5% for the 15

◦

datasets

and approx. ±1.0% for the 30

◦

datasets). Thus, the

composition of the clusters has only little inﬂuence on

the recognition rate and the discrimination between

arbitrary classes is mainly sensitive to the number of

classes.

100 250 1000

100

recognition rate in %

number of classes

(a)

100 250 1000

recognition rate in %

number of classes

(b)

Figure 5: Box plots of the recognition rates of the ALOI

datasets by repeated random sampling of sub-clusters con-

taining 10 objects each: (a) 15

◦

datasets and (b) 30

◦

datasets.

3.2 Classiﬁcation Results

The crucial step in the multiple subspace recognition

is that the assignment of clusters implicitly also re-

turns the “hidden” nearest class center. Thus, each

sub-cluster label has to be mapped to the overall class

label, which, in fact, is a simple lookup. As can

be seen from Table 2 the cluster assignment works

very well for both training scenarios (i.e., 15

◦

and 30

◦

datasets), resulting in a much higher recognition rate

than for the single LDA subspace. More precisely, the

cases, where the correct clusters are found but the ob-

jects are miss-classiﬁed, are quite rare. In addition,

in Table 2 we give a comparison of results obtained

using the proposed approach employing sub-clusters

of size 10 compared to a standard LDA approach for

four datasets of different complexity.

It can be seen that the proposed method out-

performs the single subspace LDA for all datasets

and that the recognition rate can be drastically in-

creased. Especially, for the different subsets of the

ALOI database the relative improvement of the ﬁnal

recognition rate is increasing with increasing com-

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

304

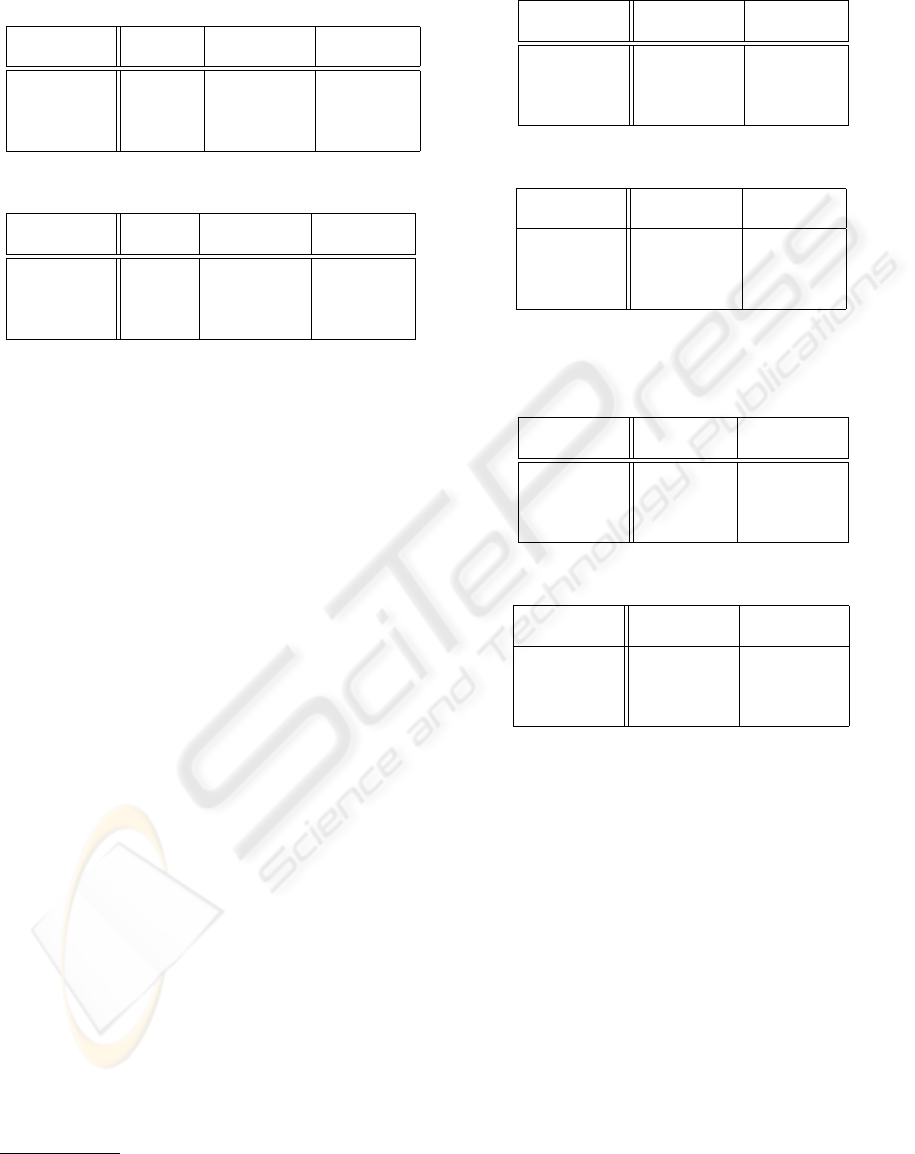
Table 2: Classiﬁcation performance: correct sub-cluster and

ﬁnal recognition rate (10 objects per cluster) vs. recognition

rate in full LDA space: (a) 15

◦

datasets and (b) 30

◦

datasets.

dataset

correct multiple single

cluster LDA spaces LDA space

COIL-100 98.04 % 98.04% 85.79%

ALOI-100 99.75 % 99.75% 96.25%

ALOI-250 97.58 % 97.52% 71.12%

ALOI-1000 95.77 % 95.76% 62.24%

(a)

dataset

correct multiple single

cluster LDA spaces LDA space

COIL-100 90.75% 89.75% 69.67%

ALOI-100 93.58% 93.08% 87.42%

ALOI-250 89.73% 88.77% 57.40%

ALOI-1000 84.12% 83.97% 37.31%

(b)

plexity of the task. In fact, for the ALOI-1000 we

ﬁnally achieve an improvement of 34% for the 15

◦

dataset and even 47% for the 30

◦

dataset. Similar re-

sults (i.e., a recognition rate of 94% − 98%) for such

large image datasets (i.e., ALOI-1000 ) were only re-

ported by Kim et al. (Kim et al., 2007). But the results

can not be directly compared, since the database was

adapted slightly different (i.e., only 500 classes were

considered and the training and test sets were deﬁned

differently).

3.3 Memory Requirements and

Computation Time

An additional advantage of smaller subspaces is that

smaller matrices have to be handled, resulting in

lower memory requirements and reduced computa-

tional costs. This especially credits for the training,

which heavily depends on the eigenvalue decompo-

sition of the training data in the PCA step and of the

scatter matrices in the LDA step. This is demonstrated

in Table 3 and in Table 4, where we summarized the

computation times

and memory requirements for the

◦

datasets, respectively.

It can be seen that for increasing complexity the

relative computation time for training compared to

the standard approach is reduced. Starting from a

reduction factor 4 for COIL-100 to a factor 165(!)

for ALOI-1000 ! During evaluation the effect is less

signiﬁcant since the total representation size is only

slightly reduced (i.e., from c − 1 to c − k). But still

the evaluation effort is approximately halved.

The experiments were carried out in MATLAB on an

Intel Xeon 3.00GHz machine with 8GB RAM.

Table 3: Computational costs for the 30

◦

datasets: (a) train-

ing and (b) testing.

dataset

multiple single

LDA spaces LDA space

COIL-100 27.66s 103.57s

ALOI-100 16.41s 105.51s

ALOI-250 41.22s 1414.24s

ALOI-1000 166.00s 27395.22s

(a)

dataset

multiple single

LDA spaces LDA space

COIL-100 3.85s 7.14s

ALOI-100 6.41s 11.64s

ALOI-250 39.13s 72.88s

ALOI-1000 426.78s 733.80s

(b)

Table 4: Memory requirements for the 30

◦

datasets:

(a) training and (b) testing.

dataset

multiple single

LDA space LDA spaces

COIL-100 138.54MB 221.68MB

ALOI-100 161.07MB 296.56MB

ALOI-250 254.38MB 655.78MB

ALOI-1000 540.52MB 3331.25MB

(a)

dataset

multiple single

LDA spaces LDA space

COIL-100 227.15MB 257.47MB

ALOI-100 215.35MB 217.90MB

ALOI-250 489.22MB 556.30MB

ALOI-1000 2089.10MB 2175.41MB

(b)

The same applies for the memory requirements

– increasing the complexity relatively decreases the

costs. In particular, for ALOI-1000 the required

memory for training was reduced from more than

3GB to 540MB by a factor 6. But there are no sig-

niﬁcant differences for the evaluation stage since due

to the implementation all test data is kept in memory.

4 CONCLUSIONS

In this paper we presented an approach that over-

comes the main limitations when applying LDA for

a large number of classes. The main idea is to (ran-

domly) split the original data into several subsets and

to compute a separate LDA representation for each of

them. To classify a new unknown test sample it is

projected onto all subspaces, where a nearest neigh-

EFFICIENT CLASSIFICATION FOR LARGE-SCALE PROBLEMS BY MULTIPLE LDA SUBSPACES

305

bor search is applied to assign it to the correct clus-

ter and hidden class, respectively. To demonstrate

the beneﬁts of our approach we applied it for two

large publicly available datasets (i.e., COIL-100 and

ALOI). In fact, compared to a single model LDA we

get a much better classiﬁcation results, which are even

competitive for large datasets containing up to 1000(!)

classes. Moreover, since the resulting data matrices

are much smaller the memory requirements and the

computational costs are dramatically reduced. Fu-

ture work will include to apply a more sophisticated

clustering, which, in fact, would further increase the

separability and thus the classiﬁcation power of the

method.

ACKNOWLEDGEMENTS

This work was supported by the FFG project AUTO-

VISTA (813395) under the FIT-IT programme, and

the Austrian Joint Research Project Cognitive Vision

under projects S9103-N04 and S9104-N04.

REFERENCES

Belhumeur, P. N., Hespanha, J. P., and Kriegman, D. J.

(1997). Eigenfaces vs. Fisherfaces: Recognition Us-

ing Class Speciﬁc Linear Projection. IEEE Trans. on

Pattern Analysis and Machine Intelligence, 19(7):711

– 720.

Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).

Maximum Likelihood from Incomplete Data via the

EM Algorithm. Royal Statistical Society, 39(1):1 –

38.

Fisher, R. A. (1936). The Use of Multiple Measurements

in Taxonomic Problems. Annals of Eugenics, 7:179–

188.

Fukunaga, K. (1990). Introduction to Statistical Pattern

Recognition. Academic Press.

Geusebroek, J. M., Burghouts, G. J., and Smeulders, A.

W. M. (2005). The Amsterdam Library of Object Im-

ages. Computer Vision, 61(1):103 – 112.

Hunt, M. (1979). A statistical approach to metrics for word

and syllable recognition. In Meeting of the Acoustical

Society of American, volume 66, pages 535 – 536.

Kim, H., Kim, D., and Bang, S. Y. (2002). Face Recognition

Using LDA Mixture Model. In Proc. Intern. Conf. on

Pattern Recognition, volume 2, pages 486 – 489.

Kim, H., Kim, D., and Bang, S. Y. (2003). Extensions

of LDA by PCA Mixture Model and Class-Wise Fea-

tures. Pattern Recognition, 36(5):1095 – 1105.

Kim, T.-K., Kittler, J., and Cipolla, R. (2007). Discrimina-

tive Learning and Recognition of Image Set Classes

Using Canonical Correlations. IEEE Trans. on Pat-

tern Analysis and Machine Intelligence, 29(6):1005 –

1018.

Loog, M., Duin, R. P. W., and Haeb-Umbach, R. (2001).

Multiclass Linear Dimension Reduction by Weighted

Pairwise Fisher Criteria. IEEE Trans. on Pattern Anal-

ysis and Machine Intelligence, 23(7):762 – 766.

Mart

ınez, A. M. and Zhu, M. (2005). Where are Lin-

ear Feature Extraction Methods Applicable? IEEE

Trans. on Pattern Analysis and Machine Intelligence,

27(12):1934 – 1944.

Nene, S. A., Nayar, S. K., and Murase, H. (1996). Columbia

Object Image Library (COIL-100). Technical Report

CUCS-006-96, Columbia University.

Rao, C. R. (1948). The Utilization of Multiple Measure-

ments in Problems of Biological Classiﬁcation. Royal

Statistical Society – Series B, 10(2):159 – 203.

Strang, G. (2006). Linear Algebra and Its Applications.

Brooks/Cole.

Swets, D. L. and Weng, J. (1996). Using Discriminant

Eigenfeatures for Image Retrieval. IEEE Trans. on

Pattern Analysis and Machine Intelligence, 18(8):831

– 837.

Tipping, M. E. and Bishop, C. M. (1999). Mixtures of

Probabilistic Principal Component Analyzers. Neural

Computation, 11(2):443 – 482.

Zhou, D. and Yang, X. (2004). Face Recognition Using

Direct-Weighted LDA. In Proc. of the Paciﬁc Rim

Int. Conference on Artiﬁcial Intelligence, pages 760 –

768.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

306