GENERATING QUALITY TETRAHEDRAL MESHES FROM
BINARY VOLUMES
Mads Fogtmann Hansen, Jakob Andreas Bærentzen and Rasmus Larsen
Department of Informatics and Mathematical Modeling, Technical University of Denmark
Richard Petersens Plads, Blg. 321, Kgs. Lyngby, Denmark
Keywords:
Tessellation, Mesh generation, Tetrahedron quality, Signed distance map.
Abstract:
This paper presents two new quality measures for tetrahedra which are smooth and well-suited for gradient
based optimization. Both measures are formulated as a distance from the regular tetrahedron and utilize the fact
that the covariance of the vertices of a regular tetrahedron is isotropic. We use these measures to generate high
quality meshes from signed distance maps. This paper also describes an approach for computing (smooth)
signed distance maps from binary volumes as volumetric data in many cases originate from segmentation
of objects from imaging techniques such as CT, MRI, etc. The mesh generation is split into two stages; a
candidate mesh generation stage and a compression stage, where the surface of the candidate mesh is moved
to the zero iso-surface of the signed distance maps, while one of the quality measures ensures that the quality
remains high.
We apply the mesh generation algorithm on four examples (torus, Stanford dragon, brain mask, and pig back)
and report the dihedral angle, aspect ratio and radius-edge ratio. Even though, the algorithm incorporates none
of the mentioned quality measures in the compression stage it receives a good score for all these measures.
The minimum dihedral angle is in none of the examples smaller than 15
o
.
1 INTRODUCTION
High quality tetrahedral mesh generation is an im-
portant element in many medical imaging applica-
tion such as virtual surgery (Suzuki et al., 1998;
K¨uhnapfel et al., 2000; De et al., 2006), image regis-
tration (Brock et al., 2005; Montagnat and Delingette,
2005) and biological modeling (McInerney and Ter-
zopoulos, 1996; Cootes et al., 1995). Creation of
meshes, which can sustain large soft tissue deforma-
tions, is challenging due to high demands in accu-
racy, efficiency and structural integrity. Efficiency is
achieved by having only the minimum required res-
olution in all areas of the mesh. High resolution is
required in high curvature areas near the interface of
the object, while lower resolution is sufficient in ar-
eas far from the interface and in areas with low curva-
ture. Accuracy and structural integrity are primarily a
matter of ensuring that the number of very anisotopic
tetrahedra are kept at an absolute minimum. Such
tetrahedra will often be biased
1
or/and invert under
deformation. Unfortunately, efficiency does not go
1
They exhibit a preferred direction of deformation
hand-in-hand with accuracy and structural integrity
as anisotopic tetrahedra will emerge when large and
small tetrahedra are in close proximity of each other.
In this paper, we propose to generate quality
meshes from signed distance maps (SDMs) by gen-
erating a candidate mesh as proposed by Molino et al.
(Molino et al., 2003) and subsequently compressing
the candidate mesh to the surface of the object. The
compression is formulated as a gradient based opti-
mization problem where the surface points of the can-
didate mesh iteratively are moved to zero iso-surface
of SDM. A selected quality measure is applied during
the compression to regularize the evolution in order to
ensure that the quality of the final mesh is high.
An extensive number of quality measures for tri-
angles and tetrahedra can be found in the literature,
c.f. (Shewchuk, 2002a; Parthasarathy et al., 1994)
for surveys. Most of these measures are non-smooth,
only piecewise smooth or difficult to differentiate,
and thus not suited for gradient based optimization.
Therefore, we propose two new quality measures for
tetrahedra which essentially measure the distance or
deviation from a given tetrahedron to the regular tetra-
hedron. They are both differentiable (smooth) and
5
Fogtmann Hansen M., Andreas Bærentzen J. and Larsen R. (2009).
GENERATING QUALITY TETRAHEDRAL MESHES FROM BINARY VOLUMES.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 5-12
DOI: 10.5220/0001654700050012
Copyright
c
 SciTePress

rotation- and scale-invariant.
In many of the above mentioned applications the
objects to be tesselated are segmented from medical
images and therefore represented as binary volumes.
We convert a binary volume to a SDM by comput-
ing all distances in the volume to the nearest zero-
crossing voxel, fitting an implicit function to a suit-
able narrow band of the zero-crossing distance map
and finally computing the distances to the zero iso-
surface of the implicit function.
2 RELATED WORK
Early mesh generation in 2D was pioneered with the
Delaunay triangulation (Shewchuk, 1996), and it is
probably the most widely used technique for 2D mesh
generation today. The extension of the Delaunay
triangulation to 3D (Weatherhill and Hassan, 1994;
Shewchuk, 1998) has unfortunately proven to be un-
suitable for many practical application as it admits
so-called slivers which are collapsed tetrahedra with
a neglilable volume. Several methods for sliver re-
moval (Cheng et al., 2000; Edelsbrunner and Guoy,
2002) have been proposed yet none of these meth-
ods have proven to work convincingly (Shewchuk,
1996). Another problem with Delaunay triangula-
tion is that it tessellates the entire convex region of
the set of input points, and thus it does not conform
to the boundary of the object. Constrained Delau-
nay methods (Chew, 1989; De Floriani and Puppo,
1992; Shewchuk, 2002b) have been proposed but they
are complex and maybe too complex for unstructured
mesh generation.
A number of unstructured mesh generation tech-
niques implement a two stage strategy which is simi-
lar to our approach . Neugebauer and Klein (Neuge-
bauer and Klein, 1997) use a marching cube mesh as
a candidate mesh, Radovitzky and Ortiz (Radovitzky
and Ortiz, 2000) use a face-centered cubic lattice,
Molino et al. (Molino et al., 2003) use a body-
centered cubic (BCC) lattice followed by a subdivi-
sion strategy and finally Fuchs (Fuchs, 1997) uses a
Delaunay triangulation of vertices placed on a BCC
lattice.
In general, two types of strategies have been sug-
gested for the compression: projection and evolu-
tion. Neugebauer and Klein (Neugebauer and Klein,
1997) and Grosskopf and Neugebauer (Grosskopf and
Neugebauer, 1998) implement projection strategies
while Kobbelt et al. (Kobbelt et al., 1999), Wood et
al. (Wood et al., 2000) and Molino et al. (Molino
et al., 2003) apply evolution strategies using connec-
tivity, spring forces or Laplacian smoothing to reg-
ularize the evolution. Molino et al. (Molino et al.,
2003) also suggest using aspect ratio (defined as the
shortest altitude divided by the longest edge) as a reg-
ularizer in a discrete optimization scheme.
3 METHODS
We wish to construct a tetrahedral mesh representa-
tion of an object Ω given a signed distance map or
binary volume representation of the object. For now
we will assume a SDM representation is available and
later in this section present an approach for convert-
ing a binary volume to a SDM. Formally, we define
the Euclidian SDM of an object Ω as a function
Φ(x) = sgn(x)min
y∈Γ
kx−yk,
where
sgn(x) =

−1 x ∈Ω
1 x /∈Ω
and Γ is the interface/boundary of the object.
A candidate mesh is generated as described in
Molino et al. (Molino et al., 2003). A BCC lattice
covering the boundary box of the object is chosen as
an initial mesh. Tetrahedra, which are certain to be
outside the object, are removed and the resolution of
the mesh is increased in the high curvature areas of
the SDM of the object using a Red-Green subdivision
approach. More tetrahedra are removed in a final
step, such that (i) the boundary is a manifold, (ii) no
tetrahedra have all four nodes on the boundary, and
(iii) no interior edge connects to boundary nodes, c.f.
(Molino et al., 2003) for a detailed description. The
process is illustrated in Figure 4.
In the compression phase the surface points of
the candidate mesh are moved towards the zero iso-
surface of the signed distance map (SDM) while a
regularizer is applied to ensure a high mesh quality.
This is done by minimizing the functional
F(∆V) =
N
s
∑
1
Φ(V
s
i
+ ∆V
s
i
)
2
+ γ
N
t
∑
i=1
r(V
T
i
+ ∆V
T
i
), (1)
where V are the vertices of the candidate mesh, ∆V
are the displacements of the vertices, s is the set of
boundary vertices, T
i
contains the id’s of the vertices
of the ith tetrahedron and r is a regularizer, which
measures the quality of a single tetrahedron.
3.1 The Quality of a Tetrahedron
As mentioned, we are interested in generating meshes
which are suitable for large deformations, and as such
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
6

we wish to define the quality of a tetrahedron in terms
of its ability to handle large deformations. In general,
if a mesh is biased, such that the tetrahedra are primar-
ily elongated in one direction, the mesh will tend to be
either more soft or stiff in the thin direction (Molino
et al., 2003). Essentially, the optimal tetrahedron is
a regular (equitaterel) tetrahedron. It is however not
possible to tessellate a 3D Euclidian space with regu-
lar tetrahedra.
Therefore, we wish to describe the quality of a tetra-
hedron in terms of its distance from a regular tetra-
hedron. A unique property of a regular tetrahedron is
that the covariance matrix of the vertices is isotropic.
Theorem 3.1. The covariance matrix Σ
T
of the ver-
tices of a tetrahedron T is isotropic Σ
T
= sI iff T is a
regular tetrahedron, where s is a scaling factor.
Proof. Let T be an arbitrary tetrahedron represented
by a 3x4 matrix Q containing the four vertices of T.
Without loss of generality we will assume that the
barycenter of T lie in the origin. Thus, we must prove
that
Σ
T
= QQ
T
= I, (2)
iff T is a regular tetrahedron. s is neglected as it is
just a scaling factor.
The regular tetrahedron
˜
Q represented by the ver-
tices (−
1
√
2
,−
1
√
12
,
1
√
6
), (
1
√
2
,−
1
√
12
,
1
√
6
), (0,
√
3
2
,0)
and (0,−
1
√
12
,−
√
2
√
3
) is a solution to Eq. 2.
For any Q there exists a transformation matrix A
such that Q = A
˜
Q. If Q fulfills Eq. 2 we get
QQ
T
= A
˜
Q
˜
Q
T
A = AA
T
= I.
Thus, A is a rotation matrix, which implies that all
solutions are geometrically equivalent. It follows that
all solutions are regular tetrahedra.
In contrast to the regular tetrahedron, an elongated
tetrahedron has a high variance in the stretched di-
rection and smaller variation perpendicular to that di-
rection. As such an eigenvalue decomposition of the
covariance matrix of an elongated tetrahedron will
give one eigenvalue (corresponding to the stretched
direction) which is relative large compared to the
two remaining eigenvalues. The normalized covari-
ance matrix of a regular tetrahedron has eigenvalue
1 with multiplicity 3 (isotropic). This implies that
the disparity of the eigenvalues is related to the de-
gree of anisotropicness of a tetrahedron. Inspired by
the Riemannian elastic (Pennec et al., 2005) and the
St Venant-Kirchoff elastic (Ciarlet, 1988) energies we
propose to use the measures
r
log
(V) =
3
4
tr log
2
Σ(V)
det(Σ(V))
1
3
!!
=
1
4


3
3
∑
i=1
log(λ
i
)
2
−
3
∑
i=1
log(λ
i
)
!
2


,(3)
and
r
eig
(V) =
1
4
tr


Σ(V)
det(Σ(V))
1
3
−I
!
2


=
1
4
3+
∑
3
i=1
λ
2
i
(
∏
3
i=1
λ
i
)
2
3
−2
∑
3
i=1
λ
i
(
∏
3
i=1
λ
i
)
1
3
!
,(4)
where Σ(V) is the covariance of the vertices V (rep-
resented by a 3x4 matrix), λ
i
is the ith eigenvalue of
covariance matrix Σ and log is the natural logarithm
(matrix logarithm when applied to a matrix). The
term
Σ
det(Σ)
1
3
will be denoted the normalized covari-
ance matrix. The two measures r
log
and r
eig
are sim-
ilar to the above mentioned elastic energies with the
exception that the Cauchy-green deformation tensor
has been replaced by the normalized covariance ma-
trix. Note, that both measures are rotation-invariantas
they are based purely on the eigenvalues of the covari-
ance matrix, and scale-invariant as we normalize the
covariance matrix. Figure 1 illustrates how the two
quality measures behave when a tetrahedron deviates
from the regular tetrahedron. A nice property of both
measures is that they will evaluate to infinity when V
describes a collapsed tetrahedron. Furthermore, both
quality measures will return zero when applied to a
regular tetrahedron.
Given the eigenvalue decomposition Σ = RLR
T
,
we can compute the derivative of the measures with
respect to Σ by
∂
Σ
r
log
=
1
2
RL
−1
3log(L) −I
3
∑
i=1
log(λ
i
)
!
R
T
.
and
∂
Σ
r
eig
=
1
2
∑
3
i=1
λ
i
(
∏
3
i=1
λ
i
)
1
3
−
∑
3
i=1
λ
2
i
(
∏
3
i=1
λ
i
)
2
3
!
Σ
−1
−
1
(
∏
3
i=1
λ
i
)
1
3
I +
1
(
∏
3
i=1
λ
i
)
2
3
Σ
!
Let P
o
denote the projection matrix which centers
a tetrahedron such that its barycenter lie in the origin.
Hence, E(V) = VP
o
P
T
o
V
T
. Thus, the derivatives of
the measures with respect to V are
∂
V
r
log
= 2P
o
P
T
o
V
T
∂
Σ
r
log
and
∂
V
r
eig
= 2P
o
P
T
o
V
T
∂
Σ
r
eig
.
GENERATING QUALITY TETRAHEDRAL MESHES FROM BINARY VOLUMES
7

(a) Deformation illustration.
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
0
5
10
15
20
25
30
Deformation
Quality
r
eig
r
log
(b) Quality as a function of deformation.
Figure 1: Comparison plot of quality measures. Tetrahedra were generated by moving a vertex along the line defined by the
normal and the barycenter of the opposite face (regular triangle). The deformation has been scaled such that -1 corresponds
to the collapsed tetrahedron and 0 corresponds to the regular tetrahedron.
3.2 Converting a Binary Volume to a
Signed Distance Map
A binary volume can be converted to a discretized
SDM by computing the Euclidian signed distance
Φ
zc
(x) from all voxels in the binary volume to the
nearest zero-crossing voxel, fitting an implicit surface
I
srf
(x,w) to a suitable narrow band of Φ
zc
(x), and
finally computing the distances
˜
Φ(x) from all voxels
to the zero iso-surface of I
srf
(x,w).
In this paper, we model the implicit surface
I
srf
(x,w) with a set of cubic B-spline basis functions
placed on a regular lattice. The weight parameters w
are estimated by minimizing
F(w) =
N
∑
i=1
C(x
i
,w) + α(k∇I
srf
(x
i
,w)k−1)
2
, (5)
where
C(x, w) =



(∆d(x,w) −
1
2
s)
2
if ∆d(x,w) >
1
2
s
(∆d(x,w) +
1
2
s)
2
if ∆d(x,w) < −
1
2
s
0 otherwise
,
∆d(x,w) = Φ
zc
(x) −I
srf
(x,w) and s is the width of
the voxels. The reason to use C(x,w) as measure of
the ‘fit’ and not the usual least-squares fit is that the
error of d
zc
(x) is uniformly distributed. The term
(k∇I
srf
(x
i
,w)k−1) provides a natural regularization,
especially in the zero-crossing areas, as kΦ(x)k = 1
is a fundamental property of the Euclidian distance
field. The property is not applied as a hard constraint
as the B-spline will not be able to fulfill the constraint
in the entire narrow band, and the narrow band might
contain areas where the true Euclidian distance field
is discontinuous.
Given the implicit surface we can find the short-
est distance from any voxel x to the zero level set of
I
srf
using the nearest zero-crossing voxel as an initial
guess of y. Thus, the task is to find the point y which
minimizes
˜
Φ
2
(x,y) = kx − yk
2
s.t. I
srf
(y,w) = 0.
This problem can be solved with the Augmented La-
grangian method (Madsen et al., 2004). Alternatively,
y can be updated iteratively with −τdy, where dy is
given by
dy = ∇I
srf
(y,w)I
srf
(y,w) + β(I −nn
T
)(x−y), (6)
and n =
∇I
srf
(y,w)
kI
srf
(y,w)k
is normal of the iso-surface at the
point y. The first term of dy pushes the point y towards
the zero iso-surface, while the second term tries to
minimize the distance between x and y by moving y
in the tangential plane of the surface. A suitable τ can
be found with line-search. Selecting β = 0.1 seems to
work in most cases.
4 IMPLEMENTATION ISSUES
If Eq. 1 is differentiable it can be minimized by a
gradient based optimization scheme. As the discrete
representation of the SDM is obviously not differen-
tiable we wrap the SDM with a cubic B-spline inter-
polator such that the signed distances and derivatives
can be evaluated in the entire Euclidean space. Fur-
thermore, as the regularization term in Eq. 1 works
independently on each tetrahedron it does not directly
discourage overlap between the tetrahedra in a mesh.
We handle this issue by having the regularizer return
infinity if an invertion/overlap occurs. This is theoret-
ically correct as our measures evaluate to infinity in
the case of a collapsed tetrahedron - in an evolution
based approach a tetrahedron must collapse before it
can invert. We minimize Eg. 1 using a limited mem-
ory BFGS optimizer.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
8

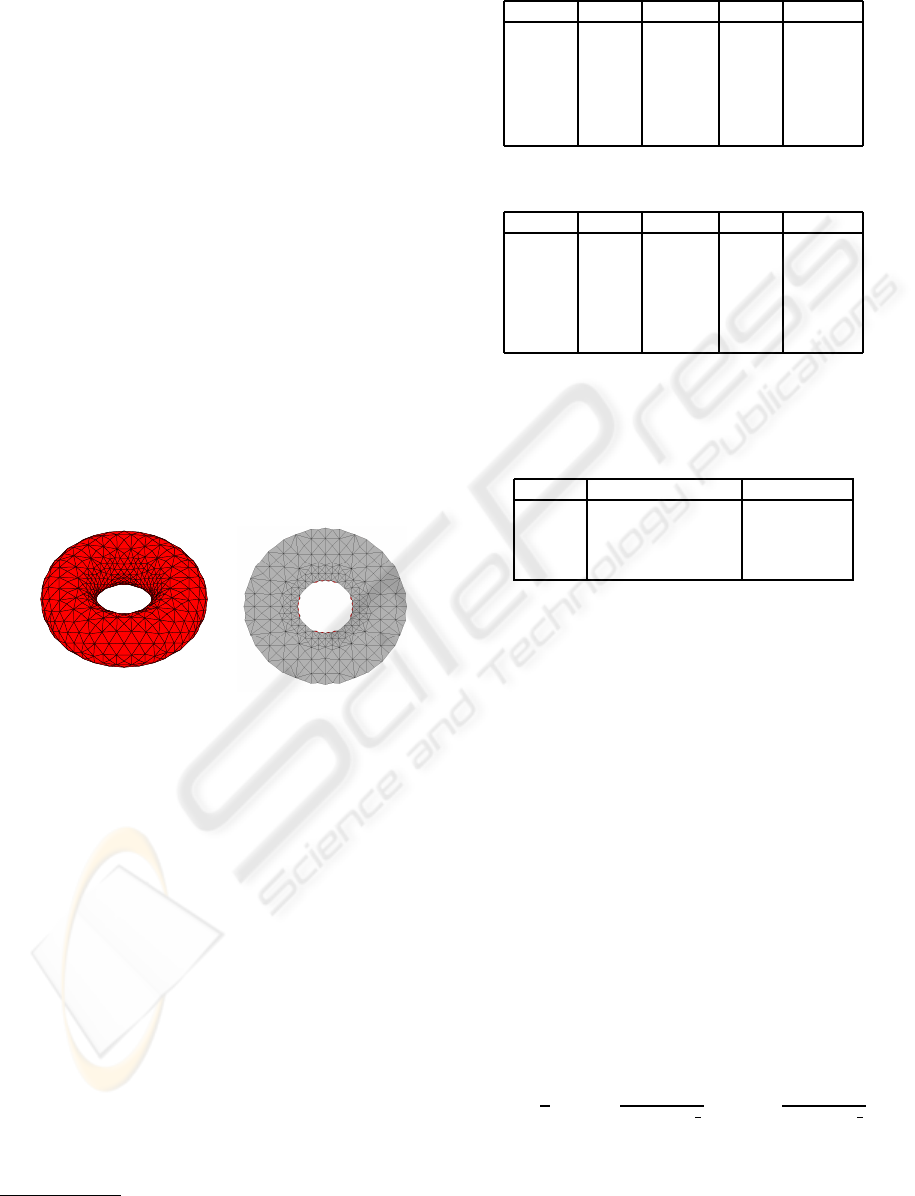
5 RESULTS
To test the quality measures, we have selected four ex-
amples. The first example is the torus where the SDM
was computed directly from the parametrization of
the torus. The second example is the Stanford dragon
where the SDM was computed from the polygonal
mesh. The third example is a brain mask which was
extracted from a MRI of a human brain. The final ex-
ample is a half pig back which was extracted from a
CT scan by thresholding the background. The SDMs
of the two last examples were computed as described
in Section 3.2.
The resulting tetrahedral meshes are displayed in
Figures 2, 3, 4 and 5. The meshes shown in the fig-
ures were generated with r
eig
. Tables 1 and 2 list
the minimum and maximum dihedral angles (MiDA
and MaDA), the maximum and average aspect ratio
(MaAR and AvAR) as well as the maximum and av-
erage radius-edge
2
ratio (MaRE and AvRe) for r
log
and r
eig
, respectively. From Tables 1 and 2 we note
that r
eig
in general obtain slightly better results than
r
log
.
(a) Full (b) Sliced
Figure 2: Tetrahedral mesh of torus.
Molino et al. (Molino et al., 2003) report the
MiDA, MaDA MaAR and AvAR for a tetrahedral
mesh of the Stanford dragon consisting of approx-
imately 500k elements (comparable to our dragon
mesh) as shown in Table 3. In the case of the Stanford
dragon our measures r
log
and r
eig
obtain better scores
for MiDA and AvAR and a worse score for MaDa
than the two approaches in Molino et al. Futhermore,
Molino et al. are only able to obtain a lower MaAR
when minimizing the aspect ratio. It should be noted
that our approach regardless of the quality measure
is able to obtain a lower AvAR than Molino et al.,
even though they use the aspect ratio as an regular-
izer. The elastic regularizer reported in Molino et al.
is likewise able to obtain a better AvAR which indi-
cates that the applied optimization procedure fails to
produce the optimal result.
2
Radius of circum-cycle over the minimum edge length
Table 1: Quality of generated meshes using r
log
.
Torus Dragon Brain Carcass
MiDA 36
o
19
0
26
o
15
o
MaDA 144
o
157
0
146
o
165
o
MaRE 1.1 2.3 1.5 2.2
AvRE 0.7 0.8 0.8 0.8
MaAR 3.3 6.7 4.4 7.9
AvAR 1.8 1.9 1.8 2.1
Table 2: Quality of generated meshes using r
eig
.
Torus Dragon Brain Carcass
MiDA 36
o
19
o
27
o
16
o
MaDA 144
o
159
o
144
o
163
o
MaRE 1.1 2.4 1.3 2.3
AvRE 0.8 0.8 0.8 0.8
MaAR 3.1 6.4 3.9 7.9
AvAR 1.8 1.9 1.8 2.0
Table 3: Quality of dragon mesh (500K elements) reported
in (Molino et al., 2003). Two different regularizers were
applied in the compression phase; one which uses elastic
springs and one which tries to minimize the aspect ratio.
Elastic regularizer Aspect ratio
MiDA 13
o
16
o
MaDA 154
o
150
o
MaAR 7.6 5.3
AvAR 2.2 2.3
6 DISCUSSION
We have proposed two new quality measures and
tested them on four examples. In section 5 Results we
compared our results for the Stanford dragon with the
results presented in (Molino et al., 2003). It should
be stated that comparison may not be fair, as we have
not used the same SDM or candidate mesh as Molino
et al (Molino et al., 2003). Our final dragon mesh
is visually close to identical with the dragon mesh in
(Molino et al., 2003), and the numbers of the tetra-
hedra in the two meshes are comparable. Thus, we
believe that the comparison is quite fair. In the future,
we will test the proposed measures in different appli-
cations and develop them further. E.g. it is possible
to incorporate a weighting matrix into the quadratic
form of the measures allowing for preferred directions
of deviation from the regular tetrahedron
r
W
(V) =
3
4
tr log
Σ(V)
det(Σ(V))
1
3
!
W log
Σ(V)
det(Σ(V))
1
3
!!
and to normalize the covariance matrix with its trace
(sum of eigenvalues) instead of its determinant (prod-
uct of eigenvalues)
GENERATING QUALITY TETRAHEDRAL MESHES FROM BINARY VOLUMES
9

r
tr
(V) =
3
4
tr

log
2

3
Σ(V)
tr(Σ(V))

.
REFERENCES
Brock, K., Sharpe, M., Dawson, L., Kim, S., and Jaffray,
D. (2005). Accuracy of finite element model-based
multi-organ deformable image registration. Medical
Physics, 32:1647.
Cheng, S., Dey, T., Edelsbrunner, H., Facello, M., and Teng,
S. (2000). Silver exudation. Journal of the ACM
(JACM), 47(5):883–904.
Chew, L. (1989). Constrained Delaunay Triangulations. Al-
gorithmica, 4(1):97–108.
Ciarlet, P. (1988). Mathematical Elasticity, Vol. I. Studies
in Mathematics and its Applications, 20.
Cootes, T., Taylor, C., Cooper, D., Graham, J., et al.
(1995). Active Shape Models-Their Training and Ap-
plication. Computer Vision and Image Understanding,
61(1):38–59.
De, S., Lim, Y., Manivannan, M., and Srinivasan, M.
(2006). Physically Realistic Virtual Surgery Using
the Point-Associated Finite Field (PAFF) Approach.
PRESENCE: Teleoperators and Virtual Environments,
15(3):294–308.
De Floriani, L. and Puppo, E. (1992). An on-line algo-
rithm for constrained Delaunay triangulation. CVGIP:
Graphical Models and Image Processing, 54(4):290–
300.
Edelsbrunner, H. and Guoy, D. (2002). An Experimental
Study of Sliver Exudation. Engineering with Comput-
ers, 18:229–240.
Fuchs, A. (1997). Automatic Grid Generation with
Almost Regular Delaunay Tetrahedra. SFB 404,
Gesch¨aftsstelle.
Grosskopf, S. and Neugebauer, P. (1998). Fitting geomet-
rical deformable models to registered range images.
Lecture notes in computer science, pages 266–274.
Kobbelt, L., Vorsatz, J., Labsik, U., and Seidel, H. (1999). A
Shrink Wrapping Approach to Remeshing Polygonal
Surfaces. Computer Graphics Forum, 18(3):119–130.
K¨uhnapfel, U., C¸ akmak, H., and Maaß, H. (2000). Endo-
scopic surgery training using virtual reality and de-
formable tissue simulation. Computers & Graphics,
24(5):671–682.
Madsen, K., Nielsen, H., and Tingleff, O. (2004). A com-
parison of tetrahedron quality measures. Technical re-
port, Technical university of Denmark.
McInerney, T. and Terzopoulos, D. (1996). Deformable
models in medical image analysis: a survey. Medical
Image Analysis, 1(2):91–108.
Molino, N., Bridson, R., Teran, J., and Fedkiw, R.(2003). A
crystalline, red green strategy for meshing highly de-
formable objects with tetrahedra. In In 12th Int. Mesh-
ing Roundtable, pages 103–114.
Montagnat, J. and Delingette, H. (2005). 4D deformable
models with temporal constraints: application to 4D
cardiac image segmentation. Medical Image Analysis,
9(1):87–100.
Neugebauer, P. and Klein, K. (1997). Adaptive triangulation
of objects reconstructed from multiple range images.
IEEE Visualization97, Late Breaking Hot Topics.
Parthasarathy, V., Graichen, C., and Hathaway, A. (1994).
A comparison of tetrahedron quality measures. Finite
Elements in Analysis and Design, 15(3):255–261.
Pennec, X., Stefanescu, R., Arsigny, V., Fillard, P., and Ay-
ache, N. (2005). Riemannian Elasticity: A Statis-
tical Regularization Framework for Non-linear Reg-
istration. LECTURE NOTES IN COMPUTER SCI-
ENCE, 3750:943.
Radovitzky, R. and Ortiz, M. (2000). Tetrahedral mesh gen-
eration based on node insertion in crystal lattice ar-
rangements and advancing-front-Delaunay triangula-
tion. Computer Methods in Applied Mechanics and
Engineering, 187(3-4):543–569.
Shewchuk, J. (1996). Triangle: Engineering a 2D Quality
Mesh Generator and Delaunay Triangulator. Lecture
Notes In Computer Science; Vol. 1148, pages 203–
222.
Shewchuk, J. (1998). Tetrahedral mesh generation by De-
launay refinement. Proceedings of the fourteenth an-
nual symposium on Computational geometry, pages
86–95.
Shewchuk, J. (2002a). A comparison of tetrahedron quality
measures. Technical report, University of California
at Berkeley.
Shewchuk, J. (2002b). Constrained Delaunay Tetrahe-
dralizations and Provably Good Boundary Recov-
ery. Proceedings of the 11th International Meshing
Roundtable, pages 193–204.
Suzuki, N., Hattori, A., Ezumi, T., Uchiyama, A., Kumano,
T., Ikemoto, A., Adachi, Y., and Takatsu, A. (1998).
Simulator for virtual surgery using deformable organ
models and force feedback system. Stud Health Tech-
nol Inform, 50:227–33.
Weatherhill, N. and Hassan, O. (1994). Efficient three-
dimensional Delaunay triangulation with automatic
point creation and imposd boundary constraints. Inter-
national journal for numerical methods in engineer-
ing, 37(12):2005–2039.
Wood, Z., Schroder, P., Breen, D., and Desbrun, M. (2000).
Semi-regular mesh extraction from volumes. IEEE Vi-
sualization: Proceedings of the conference on Visual-
ization’00, 2000:275–282.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
10

Figure 3: Tetrahedral mesh of dragon (540K elements).
(a) Initial (b) Candidate (c) Final
Figure 4: Tetrahedral mesh from mask of human brain (80K elements).
GENERATING QUALITY TETRAHEDRAL MESHES FROM BINARY VOLUMES
11

Figure 5: Tetrahedral mesh of half pig back (280k elements).
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
12