
DUAL CONTROLLERS FOR DISCRETE-TIME STOCHASTIC
AMPLITUDE-CONSTRAINED SYSTEMS
A. Kr
´
olikowski and D. Horla
Pozna
´
n University of Technology
Institute of Control and Information Engineering
ul.Piotrowo 3A, 60-965 Pozna
´
n, Poland
Keywords:
Input constraint. Suboptimal dual control.
Abstract:
The paper considers a suboptimal solution to the dual control problem for discrete-time stochastic systems in
the case of amplitude constraint imposed on the control signal. The objective of the control is to minimize the
variance of the output around the given reference sequence. The presented approaches are based on: an MIDC
(Modified Innovation Dual Controller) derived from an IDC (Innovation Dual Controller), a TSDSC (Two-
stage Dual Suboptimal Control, and a PP (Pole Placement) controller. Finally, the certainty equivalence (CE)
control method is included for comparative analysis. In all algorithms, the standard Kalman filter equations
are applied for estimation of the unknown system parameters. Example of second order system is simulated in
order to compare the performance of control methods. Conclusions yielded from simulation study are given.
1 INTRODUCTION
Much work has been done on the optimal control of
stochastic systems which contain parametric uncer-
tainty. The problem is inherently related with the dual
control problem originally presented by Fel’dbaum
who suggested that in the dual control, the problems
of learning and control should be considered simul-
taneously in order to minimize the cost function. In
general, learning and controlling have contradictory
goals, particularly for the finite horizon control prob-
lems. The concept of duality has inspired the devel-
opment of many control techniques which involve the
dual effect of the control signal. They can be sepa-
rated in two classes: explicit dual and implicit dual
(Bayard and Eslami, 1985). Unfortunately, the dual
approach does not result in computationally feasible
optimal algorithms. A variety of suboptimal solutions
has been proposed and many of them were heuris-
tic identifier-controller structures. Other controllers
like minimax controllers (Sebald, 1979), Bayes con-
trollers (Sworder, 1966) or MRAC (Model Reference
Adaptive Controller) (
˚
Astr
¨
om and Wittenmark, 1989)
are available.
The objective of this paper is to present and com-
pare different approaches to suboptimal solution of
the minimum variance control problem of discrete-
time stochastic systems with unknown parameters. In
this paper, an amplitude-constrained control input is
considered which is an important practical case. A
majority of proposed solutions in the literature does
not include the input constraint into the design of con-
trol system. The saturation imposed on control sig-
nal deteriorates the probability density function (pdf)
of the state from the Gaussian which makes finding
an optimal control difficult even when system param-
eters are known. The dual methods described here
are: the MIDC method which is the modification of
the IDC (R. Milito and Cadorin, 1982) approach, the
method based on the two-stage dual suboptimal con-
trol (TSDSC) approach (Maitelliand and Yoneyama,
1994) and the method based on the pole placement
approach (Filatov and Unbehauen, 2004).
The Iteration in Policy Space (IPS) algorithm and
its reduced complexity version were proposed by Ba-
yard (Bayard, 1991) for a general nonlinear system.
In this algorithm the stochastic dynamic program-
ming equations are solved forward in time ,using
a nested stochastic approximation technique. The
method is based on a specific computational architec-
ture denoted as a H block. The method needs a filter
propagating the state and parameter estimates with as-
130
Królikowski A. and Horla D. (2007).
DUAL CONTROLLERS FOR DISCRETE-TIME STOCHASTIC AMPLITUDE-CONSTRAINED SYSTEMS.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 130-134
DOI: 10.5220/0001620401300134
Copyright
c
SciTePress

sociated covariance matrices.
In (Kr
´
olikowski, 2000), some modifications in-
cluding input constraint have been introduced into the
original version of the IPS algorithm and its perfor-
mance has been compared with MIDC algorithm.
This paper has a tutorial nature, and the possibility
of incorporating the input constraint into the control
algorithms was the motivation for a selection of the
overviewed approaches.
Performance of the considered algorithms is il-
lustrated by simulation study of second-order system
with control signal constrained in amplitude.
2 CONTROL PROBLEM
FORMULATION
Consider a discrete-time linear single-input single-
output system described by ARX model
A(q
−1
)y
k
= B(q
−1
)u
k
+ w
k
, (1)
where A(q
−1
) = 1 + a
1,k
q
−1
+ ··· + a
na,k
q
−na
,
B(q
−1
) = b
1,k
q
−1
+ ··· + b
nb,k
q
−nb
, y
k
is the output
available for measurement, u
k
is the control sig-
nal, {w
k
} is a sequence of independent identically
distributed gaussian variables with zero mean and
variance σ
2
w
. Process noise w
k
is statistically inde-
pendent of the initial condition y
0
. The system (1)
is parametrized by a vector θ
k
containing na + nb
unknown parameters {a
i,k
} and {b
i,k
} which in
general can be assumed to vary according to the
equation
θ
k+1
= Φθ
k
+ e
k
(2)
where Φ is a known matrix and {e
k
} is a sequence of
independent identically distributed gaussian variables
with zero mean and variance matrix R
e
. Particularly,
for the constant parameters we have
θ
k+1
= θ
k
= θ
= (b
1
, ··· , b
nb
, a
1
, ···a
na
)
T
, (3)
and then Φ = I, e
k
= 0 in (2).
The control signal is subjected to an amplitude
constraint
| u
k
|≤ α (4)
and the information state I
k
at time k is defined by
I
k
= [y
k
, ..., y
1
, u
k−1
, ..., u
0
, I
0
] (5)
where I
0
denotes the initial conditions.
An admissible control policy Π is defined by a se-
quence of controls Π = [u
0
, ..., u
N−1
] where each con-
trol u
k
is a function of I
k
and satisfies the constraint
(4). The control objective is to find a control policy
Π which minimizes the following expected cost func-
tion
J = E[
N−1
∑
k=0
(y
k+1
− r
k+1
)
2
] (6)
where {r
k
} is a given reference sequence. An admis-
sible control policy minimizing (6) can be labelled by
CCLO (Constrained Closed-Loop Optimal) in keep-
ing with the standard nomenclature, i.e. Π
CCLO
=
[u
CCLO
0
, ..., u
CCLO
N−1
]. This control policy has no closed
form, and control policies presented in the following
section can be viewed as a suboptimal approach to the
Π
CCLO
.
3 SUBOPTIMAL DUAL
CONTROL METHODS
In this section, we shall briefly describe three meth-
ods giving an approximate solution to the problem
formulated in Section 2. The first one is the MIDC
algorithm based on the IDC approach (R. Milito and
Cadorin, 1982) which is an explicit dual control ap-
proach.
3.1 Method based on the Innovation
Dual Control (IDC) Approach:
Derivation of Π
MIDC
The IDC has been derived for system (1) with uncon-
strained control and constant parameters (3). The fol-
lowing cost function was considered
J =
1
2
E[(y
k+1
− r
k+1
)
2
− λ
k+1
ε
2
k+1
|I
k
] (7)
where λ
k+1
≥ 0 is the learning weight, and ε
k+1
is the
innovation, see (16).
The modified IDC, u
MIDC
k
, takes the constraint
into account which results in the following closed-
form expression
u
MIDC
k
=
=−sat
[(1−λ
k+1
)p
T
b
1
θ
∗
,k
+
ˆ
θ
∗
T
k
ˆ
b
1,k
]s
∗
k
−
ˆ
b
1,k
r
k+1
(1− λ
k+1
)p
b
1
,k
+
ˆ
b
2
1,k
;α
(8)
where
s
k
= (u
k
, u
k−1
, . . . , u
k−nb+1
, −y
k
, . . . , −y
k−na+1
)
T
=
= (u
k
, s
∗
T
k
)
T
, (9)
and following partitioning is introduced for parame-
ter covariance matrix P
k
P
k
=
"
p
b
1
,k
p
T
b
1
θ
∗
,k
p
b
1
θ
∗
,k
P
θ
∗
,k
#
(10)
DUAL CONTROLLERS FOR DISCRETE-TIME STOCHASTIC AMPLITUDE-CONSTRAINED SYSTEMS
131

corresponding to the partition of θ
θ = (b
1
, θ
∗T
)
T
(11)
with
θ
∗
= (b
2
, . . . , b
nb
, a
1
, . . . , a
na
)
T
. (12)
The estimates
ˆ
θ
k
needed to calculate u
MIDC
k
can be
obtained in many ways. A common way is to use the
standard Kalman filter in a form of suitable recursive
procedure for parameter estimation, i.e.
ˆ
θ
k+1
= Φ
ˆ
θ
k
+ k
k+1
ε
k+1
(13)
k
k+1
= ΦP
k
s
k
[s
T
k
P
k
s
k
+ σ
2
w
]
−1
(14)
P
k+1
= [Φ− k
k+1
s
T
k
]P
k
Φ
T
+ R
e
, (15)
ε
k+1
= y
k+1
− s
T
k
ˆ
θ
k
. (16)
3.2 Method based on the Two-stage
Dual Suboptimal Control (TSDSC)
Approach: Derivation of Π
TSDSC
The TSDSC proposed in (Maitelliand and Yoneyama,
1994) has been derived for system (1) with stochastic
parameters (2). Below this method is extended for the
input-constrained case. The cost function considered
for TSDSC is given by
J =
1
2
E[(y
k+1
− r)
2
+ (y
k+2
− r)
2
|I
k
] (17)
and according to (Maitelliand and Yoneyama, 1994)
can be obtained as a quadratic form in u
k
and u
k+1
,
i.e.
J =
1
2
[au
k
+ bu
k+1
+ cu
k
u
k+1
+ du
2
k
+ eu
2
k+1
] (18)
where a, b, c, d, e are expressions depending on cur-
rent data s
∗
k
, reference signal r and parameter esti-
mates
ˆ
θ
k
(Maitelliand and Yoneyama, 1994). Solving
a necessary optimality condition the unconstrained
control signal is
u
TSDSC,un
k
=
bc− 2ae
4de− c
2
. (19)
This control law has been taken for simulation anal-
ysis in (Maitelliand and Yoneyama, 1994). Imposing
the cutoff the constrained control signal is
u
TSDSC,co
k
= sat(u
TSDSC,un
k
;α). (20)
The cost function (18) can be represented as a
quadratic form
J =
1
2
[u
T
k
Au
k
+ b
T
u
k
] (21)
where u
k
= (u
k
, u
k+1
)
T
, and
A =
d
1
2
c
1
2
c e
, b
=
a
b
. (22)
The condition 4de− c
2
> 0 together with d > 0 im-
plies positive definitness and guarantees convexity.
Minimization of (21) under constraint (4) is a stan-
dard QP problem resulting in u
TSDSC,qp
k
. The con-
strained control u
TSDSC,qp
k
is then applied to the sys-
tem in receding horizon framework.
3.3 Method based on the Pole
Placement (PP) Approach:
Derivation of Π
PP
Let the desired stable closed-loop polynomial be de-
scribed by A
∗
(q
−1
) = 1 + a
∗
1
q
−1
+ ··· + a
n
∗
q
−n
∗
. A
dual version of a direct adaptive PP controller pro-
posed in (N.M. Filatov and Keuchel, 1993; Filatov
and Unbehauen, 2004) has been derived for system
(1) where integral actions can be included. To this
end, a bicriterial approach has been used to solve the
synthesis problem. The two criteria correspond to the
two goals of the dual adaptive control, namely to con-
trol the system output close to the reference signal,
and to accelerate the parameter estimation process for
future control improvment. Incorporating the ampli-
tude constraint of the control input yields
u
PP
k
= sat
u
CAUT
k
+
+ η trP
k
sign(p
d
0
,k
¯u
CAUT
k
+ p
T
d
0
p
1
,k
m
1,k
) ; α
(23)
where u
CAUT
k
is the cautious action given by
u
CAUT
k
= −
(p
T
r
0
p
0
,k
+ ˆp
T
0,k
ˆr
0,k
)m
0,k
− ˆr
0,k
r
k
p
r
0
,k
+ ˆr
2
0,k
, (24)
¯u
CAUT
k
= u
CAUT
k
+
∑
n
∗
i=1
a
∗
i
u
k−i
, p
0
=
(s
0
, . . . , s
ns
, r
1
, . . . , r
nr
)
T
, m
0,k
= (y
k
, . . . , y
k−ns
,
u
k−1
, . . . , u
k−nr
)
T
, and η ≥ 0 is the parameter re-
sponsible for probing. In this case the following
partitioning is introduced for parameter covariance
matrix P
k
P
k
=
"
p
d
0
,k
p
T
d
0
p
1
,k
p
d
0
p
1
,k
P
p
1
,k
#
(25)
corresponding to the partition of parameter vector p
p = (−d
0
, p
T
1
)
T
(26)
where
p
1
= (−d
1
, . . . , d
nd
, − f
1
, . . . , − f
nf
, r
0
, . . . , r
nr
, s
0
, . . . , s
ns
)
T
(27)
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
132

and
m
k
= ( ¯u
k
, m
T
1,k
)
T
(28)
with m
1,k
= ( ¯u
k−1
, . . . , ¯u
k−nd
, ¯y
k
, . . . , ¯y
k−n f+1
, u
k−l+1
,
. . . , u
k−l−nr+2
, y
k−l+2
, . . . , y
k−l+ns+2
)
T
. The filtered
output and input signals are obtained as ¯y
k
=
A
∗
(q
−1
)y
k
, ¯u
k
= A
∗
(q
−1
)u
k
.
The corresponding diophantine equation and Be-
zout identity are
A(q
−1
)[r
0
+q
−1
R(q
−1
)]+q
−1
B(q
−1
)S(q
−1
)=r
0
A
∗
(q
−1
),
(29)
A(q
−1
)D(q
−1
) + B(q
−1
)F(q
−1
) = r
0
q
−l+2
, (30)
where the polynomial degrees are: nr = na − 1, ns =
na−κ−1, l = na+nb, nd = nb− 2, nf = na−1, and
κ is the number of possible integrators in the system.
It can be shown that the filtered output ¯y
k
can be
represented in the following regressor form
¯y
k
= p
T
m
k−1
+ v
k
(31)
For estimation of parameters p
(note that parameters
p
0
are included into p
) the Kalman filter algorithm
(13)-(16) can again be used where
ˆ
θ
k
should be re-
placed by ˆp
k
, s
k
should be replaced by m
k
, ε
k+1
should
be calculated as ε
k+1
= ¯y
k+1
−m
T
k
ˆp
k
, and the variance
σ
2
w
should be replaced by the variance σ
2
v
which can
be evaluated from (29), (30), (1).
4 SIMULATION TESTS
Performance of the described control methods is illus-
trated through the example of a second-order system
with the following true values: a
1
= −1.8, a
2
= 0.9,
b
1
= 1.0, b
2
= 0.5, where the Kalman filter algorithm
(13)-(16) was applied for estimation. The initial pa-
rameter estimates were taken half their true values
with P
0
= 10I. The reference signal was a square
wave ±3, and then the minimal value of constraint
α ensuring the tracking is α
min
= 3
|A(1)|
|B(1)|
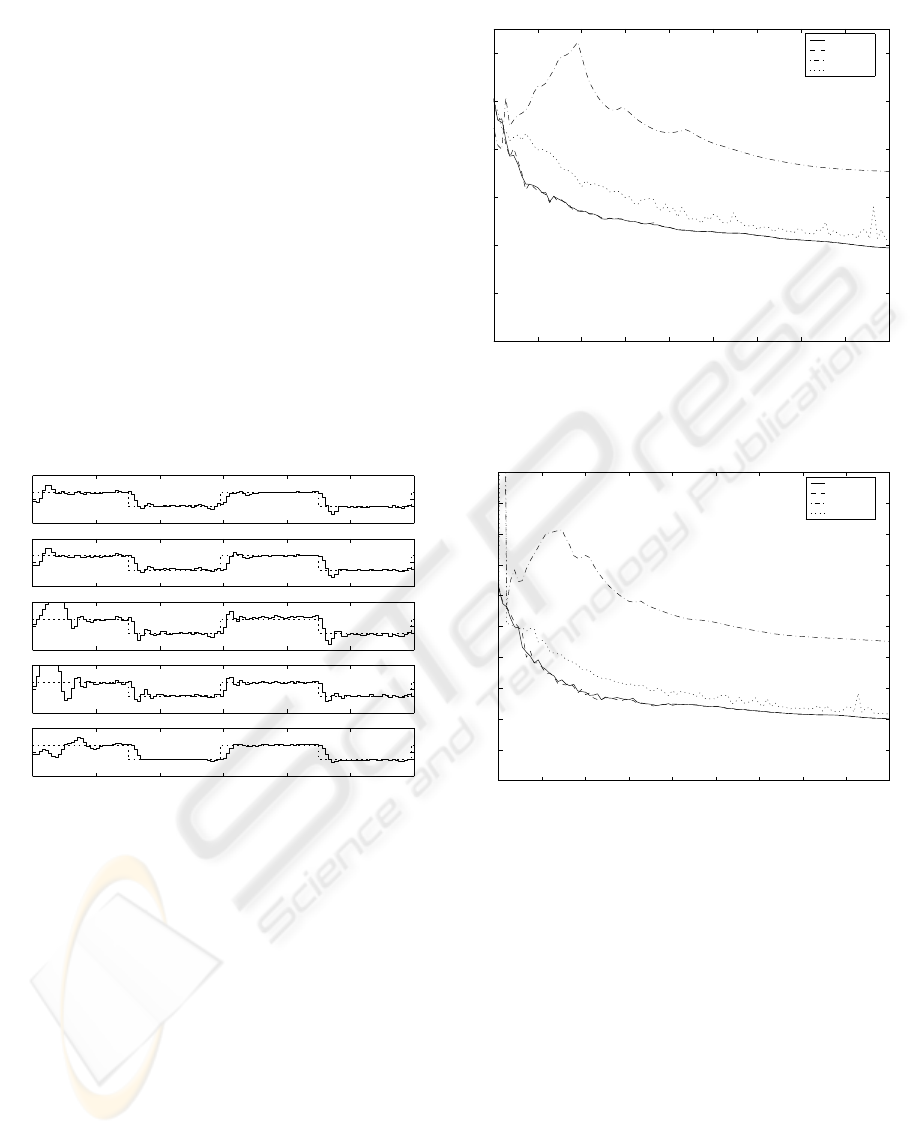
= 0.2. Fig.
1 shows the reference, output and input signals dur-
ing tracking process under the constraint α = 1 for all
control policies.
For the control policy Π
MIDC
the constant learn-
ing weight was λ
k
= λ = 0.98. The policy Π
PP
was
simulated for third order polynomial A
∗
(q
−1
) having
poles at 0.2± i0.1, −0.1, and for the probing weight
η = 0.2. The control policy Π
CE
can easily be ob-
tained from MIDC by taking p
b
1
,k
= 0, p
T
b
1
θ
∗
,k
= 0.
Next, the simulated performance index
¯
J =
N−1
∑
k=0
(y
k+1
− r
k+1
)
2
was considered. The plots of
¯
J versus the constraint
α are shown in Figs. 2, 3 for σ
2
w
= 0.05, 0.1, re-
spectively, and N = 1000. The control u
TSDSC,qp
k
was
obtained solving the minimization of quadratic form
(20) using MATLAB function quadprog. The perfor-
mance of this control is not included in plots of Figs.
5, 6, because it performs surprisingly essentially in-
ferior with respect to u
TSDSC,co
k
. In the latter case,
a short-term behaviour phenomenon (G.P. Chen and
Hope, 1993) can be observed in Figs. 2, 3. This
means that when the cutoff method is used then the
range of constraint α can be found where for increas-
ing α the performance index is also increasing.
5 CONCLUSIONS
This paper presents various approaches toward a sub-
optimal solution to the discrete-time dual control
problem under the amplitude-constrained control sig-
nal. A simulation example of second-order system is
given and the performance of the presented control
policies is compared by means of the simulated per-
formance index.
The MIDC method seems to be a good suboptimal
dual control approach, however it has been found that
the MIDC control is quite sensitive to the value of the
learning weight λ. In (Kr
´
olikowski, 2000) it has been
found that this method often performs very close to
the IPS algorithm (Bayard, 1991).
Performance of all control policies except
Π
TSDSC,co
is comparable, however the differences be-
tween all methods are less noticeable when the con-
straint α gets tight, i.e. when α → α
min
. In all con-
sidered control policies except u
TSDSC,co
k
, the perfor-
mance index increases when the input amplitude con-
straint gets more tight. This means that for u
TSDSC,co
k
the effect of the short term behaviour phenomenon
discussed in (G.P. Chen and Hope, 1993) could ap-
pear.
REFERENCES
˚
Astr
¨
om, H. and Wittenmark, B. (1989). Adaptive Control.
Addison-Wesley.
Bayard, D. (1991). A forward method for optimal stochastic
nonlinear and adaptive control. IEEE Trans. Automat.
Contr., 9:1046–1053.
Bayard, D. and Eslami, M. (1985). Implicit dual control for
general stochastic systems. Opt. Contr. Appl.& Meth-
ods, 6:265–279.
Filatov, N. and Unbehauen, H. (2004). Dual Control.
Springer.
DUAL CONTROLLERS FOR DISCRETE-TIME STOCHASTIC AMPLITUDE-CONSTRAINED SYSTEMS
133
G.P. Chen, O. M. and Hope, G. (1993). Control limits
consideration in discrete control system design. IEE
Proc.-D, 140(6):413–422.
Kr
´
olikowski, A. (2000). Suboptimal lqg discrete-time con-
trol with amplitude-constrained input: dual versus
non-dual approach. European J. Control, 6:68–76.
Maitelliand, A. and Yoneyama, T. (1994). A two-stage dual
suboptimal controller for stochastic systems using ap-
proximate moments. Automatica, 30:1949–1954.
N.M. Filatov, H. U. and Keuchel, U. (1993). Dual pole-
placement controller with direct adaptation. Automat-
ica, 33(1):113–117.
R. Milito, C.S. Padilla, R. P. and Cadorin, D. (1982). An
innovations approach to dual control. IEEE Trans. Au-
tomat. Contr., 1:132–137.
Sebald, A. (1979). Toward a computationally efficient opti-
mal solution to the lqg discrete-time dual control prob-
lem. IEEE Trans. Automat. Contr., 4:535–540.
Sworder, D. (1966). Optimal Adaptive Control Systems.
Academic Press, New York.
0 20 40 60 80 100 120
−10
0
10
t
MIDC
0 20 40 60 80 100 120
−10
0
10
CE
0 20 40 60 80 100 120
−10
0
10
TSDSC, co
0 20 40 60 80 100 120
−10
0
10
TSDSC − opt.
0 20 40 60 80 100 120
−10
0
10
t
PP
Figure 1: Reference, output and control signals for Π
MIDC
,
Π
CE
, Π
TSDSC
, Π
PP
and α = 1.
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
1
2
3
4
5
6
α
J
Performance indices, α
MIDC
= 0.98, σ
ξ
2
= 0.05, N = 1000
MIDC
CE
TSDSC,co
PP
Figure 2: Plots of performance indices for σ
2
w
= 0.05.
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
1
2
3
4
5
6
7
8
9
10
α
J
Performance indices, α
MIDC
= 0.98, σ
ξ
2
= 0.1, N = 1000
MIDC
CE
TSDSC,co
PP
Figure 3: Plots of performance indices for σ
2
w
= 0.1.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
134
