
Novel Clustering based on Discrete Morse Technique
Jian Ping Zhang
1
, Xi Yu Liu
1
and Yong Li
2
1
School of Management Science and Engineering, Shandong Normal University, No.88 Culture East Road, Ji’nan, China
2
Institute of Information Engineering, BinZhou University, No.391 Huanghe Road, BinZhou, China
Keywords: Density Clustering, Simplicial Complexes, Discrete Morse Function, Discrete Gradient Vector Field.
Abstract: A new clustering algorithm based on discrete Morse theory is proposed for cluster analysis in this paper.
Firstly, an energy surface is defined on data set by Gaussian kernel functions. Secondly, a simplicial
complex can be obtained by hull Triangulation on the energy surface. Finally, the optimization model based
on discrete Morse theory is adopted to find cluster centers and clusters on a simplicial complex. It is a novel
approach. The experimental results on some synthetic and UCI data sets have demonstrated that the new
algorithm can discover clusters with arbitrary shapes and densities at different levels, moreover it can
successfully divide data points overlapping into many meaningful clusters. The results show the feasibility
and effectiveness of the new clustering algorithm.
1 INTRODUCTION
Clustering analysis (Han and Kamber,2006) is used
to handle classification problem by mathematical
methods, and is an important part of non-supervised
pattern classification in pattern recognition. In recent
30 years, it has been developed drastically. The aim
of Clustering (Chan et al., 2003) (Kaufman and
Rousseeuw, 2009) (Hubert et al., 1999) (Chen et al.,
1996)is that the intracluster similarity is maximized
and the intercluster similarity is minimized.
Clustering in the sample space is an optimization
problem of objective function. There have been
many kinds of clustering algorithms based on
computational intelligence(CI) techniques, such as
fuzzy control, neural networks, evolutionary
computation, swarm intelligence, artificial life and
DNA computation (Graves and Pedrycz, 2007) (Pal
et al., 1993) ( Babu and Murty,1994) (Bader et al.,
2004). The CI-based clustering analysis models have
a good ability to adapt to characteristics of objects
and it can make up for the disadvantages of classical
clustering algorithms. However, the data mining
system should process more complex data sets with
arbitrary shapes , arbitrary distribution and densities
at different levels with the application fields of data
mining technology expanding continuously.
Therefore, new techniques are still a good choice to
get more insight into cluster analysis.
Morse theory appears in topology of smooth
manifolds (Milnor,1963). Discrete Morse theory is a
combinatorial analogue of Morse theory developed
by Forman (Forman,1995) (Forman,1998). Making
the points more dense does not allow one to use
smooth methods to analyze the qualitative behavior
of f. This problem was addressed by Edelsbrunner in
(Edelsbrunner et al., 2003). Researchers find that
discrete Morse theory is a discrete analogue of a
technology called steepest descent method, which
has extreme importance in optimization. In (Zhang
and Liu, 2014), we propose a method to construct
discrete Morse function that mirrors the large-scale
behavior of f and has the minimum possible number
of critical cells by optimization analysis on given f in
3-D or higher dimension space and present an
optimization model based on discrete Morse theory
that can obtain an optimal value or approximate
optimal one
In this paper, we have proposed a new
clustering algorithm based on discrete Morse
optimization model. The algorithm is mainly to
adopt to the thought of hierarchical clustering based
on kernel density estimation. In our approach, local
minima (the density attractors) are chosen to
generate the center-defined data partition, and finally
the center-defined clusters are iteratively merged
into one cluster by cancelling critical cells. The
experimental results on two synthetic data sets and
UCI data sets have demonstrated that the new
algorithm can discover clusters with arbitrary
shapes, arbitrary distribution and densities at
Zhang, J., Liu, X. and Li, Y.
Novel Clustering based on Discrete Morse Technique.
DOI: 10.5220/0006681805550562
In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 555-562
ISBN: 978-989-758-276-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
555

different levels. The comparisons with DBSCAN
method further show that the proposed algorithm can
successfully divide data points overlapping in the
feature space into many meaningful clusters.
2 OPTIMIZATION MODEL
BASED ON DISCRETE MORSE
THEORY
In this section we present a general discrete structure
which will be useful for clustering and propose an
optimization model based on discrete Morse theory.
Now we will present some notation. A finite
data set is denoted by
12
{ , ..., }
n
n
X x x x R
,
12
[ , ,..., ]
i i i id
x x x x
,
1,2,...,in
.
:h X R
is a map
function defined on a data set X. A function
1
{( , ( )) | 1,2,... }
n
ii
S x h x i n R
is called a discrete
surface. A q-simplex σ (denoted by
()q
) is the
convex hull of q+1 affinely independent points
01
( , ,... )
q
A a a a
. The cone from a vertex x(
()q
i
x
)
to a q-simplex
()q
is the convex hull of x and
()q
which yields a (q+1)-simplex
( 1)q
. A simplicial
complex
K
is a set of simplices that satisfies the
following conditions: 1.
K
if
K
and
2.
12
or
1 2 1 2
,,
if
12
, K
.
2.1 The Discrete Structure:
A Simplicial Complex
In order to get discrete surfaces, we define a hull
triangulation. Let the convex hull of
12
{ , ..., }
n
n
X x x x R
be
()hull X
. If
i
xX
is an
interior point of
()hull X
, then there exists a
neighbor in
S
of
( , ( ))
ii
x h x
homeomorphic to
n
R
.
Otherwise if
i
xX
is an boundary point of
()hull X
,
then there exists a neighbor in
S
of
( , ( ))
ii
x h x
homeomorphic to the halfspace of
n
R
. Clearly the
hull triangulation is a n-dimensional manifold with
boundary.
We take Delaunay Triangulation as a tool of
hull triangulation. Firstly we generate a Delaunay
triangulation of
12
{ , ..., }
n
n
X x x x R
. A
1q
-
simplex is generated by
q
-simplex connecting one
point
i
xX
. For each simplex, the unique ball
circumscribed about the simplex contains no data
points other than the vertices. Secondly generate
simplicial complex K by replacing the vertices with
its corresponding vertices on the surface. a
simplicial complex K is composed by the following
way (Figure 1).
(a) DataSet1 in 2D. (b) D-Triangulation.
(c) a simplicial complex (d) a surface
Figure 1: The generating process of a simplicial complex.
Figure1(b) denotes that D-Triangulation on
DataSet1 in 2D and Figure1(d) means surface based
on the probability density function(σ=1) on based on
DataSet1 in 2D.
Table 1 shows the running time of generating a
simplicial complex K based on the probability
density function (the window width
=1) on a data
set
12
{ , ..., }
n
n
X x x x R
Table 1: The running time of generating a simplicial
complex.
data sets
CPU (s)
DataSet1 (300 2-D points)
0.002
DataSet2 (500 2-D points)
0.003
'Haberman s
Survival
(306 3-D points)
0.018
Iris
(150 4-D points)
0.055
2.2 Discrete Morse Theory
Definition 1[12] (discrete Morse function). A
function
:f K R
is a discrete Morse function, if
for every
()p
K
, the following two conditions
hold:
( 1) ( )
#{ : ( ) ( )} 1
pp
ff
and
( 1) ( )
#{ : ( ) ( )} 1
pp
ff
(1)
Definition 2[12] (critical simplex). Let
:f K R
be
a discrete Morse function. A simplex
()p
is critical
if the following two conditions hold:
( 1) ( )
#{ : ( ) ( )} 0
pp
ff
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
556

and
( 1) ( )
#{ : ( ) ( )} 0
pp
ff
(2)
A simplex that is not critical is called regular.
Definition 3(discrete gradient vector field). A
discrete gradient vector field
V
is a collection of
pairs
( ) ( 1)
,
pp
of simplices of
K
. for
,
, the
following two conditions hold:
and
( ) ( )ff
.
Property 1.
A discrete Morse function
f
is
generated on the discrete gradient vector field
V
,
then the function
f
is descending along
V path
.
Definition 4 (level cut). Level cut on the simplicial
complex
K
is a collection of simplices, where a
simplex
is included if values of all its
vertices
x
are below the threshold
t
.
i.e,
( ) { | ( ) , }K t K h x t x
.
Definition 5 (Simple homotopy). (Lewiner and
Lopes,2003)A simple homotopy(i.e, a continuous
deformation) is a succession of collapses and
extensions. If two complexes are related by a simple
homotopy, we say they have the same simple
homotopy type.
In this paper, discrete gradient vector field is
generated based on discrete Morse theory by using
simple homotopy expansions to grow from one
subcomplex to the next.
2.3 Optimization Algorithm:
DVF-Algorithm
The goal of our algorithm is to construct a discrete
Morse function on the simplicial complex which can
obtain the extreme value of given function. The
algorithm is based on simple homotopy expansions
which grow from
( 1)Kt
to
()Kt
iteratively. Now
we will present two definitions.
Definition 6 (lower star). (Lewiner and
Lopes,2003) The lower star
()Sx
of a
vertex
x
contains of all simplices that contain
x
as a
face, including
x
itself, and hold
( ) max ( )g x g
.i,e.
( ) { | , ( ) max ( )}
y
S x K x g x g y
.
Definition 7 (lower link). The lower
link
()Lx
of a vertex
x
consists of all faces of
simplices in the lower star that are disjoint from
x
.
i,e.
( ) { | ( ), }L x K S x x
According Definition6 and Definition7, we
present a definition of the closed lower star of a
vertex
x
:
( ) ( ) ( )S x S x L x
.
DVF-Algorithm contains two steps:
( , )ConstructDVF K g
and
( , , , )CancelCriticalCell K g j p
.
( , )ConstructDVF K g
generates critical cells
C
and
constructs discrete gradient vector field
V
;
( , , , )CancelCriticalCell K g j p
modifies
C
and
V
so that
it can produce the minimum possible number of
critical cells. Algorithm1.
( , )ConstructDVF K g
1Step
input a complex
K
, a mapping
function
0
:h K R
;
2Step
0
xK
, if
()Lx
, add
x
to
C
;
otherwise let
''
0
:h K R
be the restriction of
h
;
3Step
find the
()y L x
so that
'
()hy
is the
smallest; denote
xy
and define
[]Vx
; add all
other 1-cells from
()Sx
to
QueueZero
, add all cells
()Sx
to
QueueOne
such that
and
_ _ ( ) 1num unpaired faces
;
4Step
assign the front cell
from
QueueOne
to
, if
_ _ ( ) 0num unpaired faces
,
then
[ ( )]V pair
, delete
()pair
from
QueueZero
;
add the cells
()Sx
to
QueueOne
such
that
or
()pair
and
_ _ ( ) 1num unpaired faces
,
until
QueueOne
; if
QueueZero
, then assign the
front cell
from
QueueOne
to
C
; add
()Sx
to
QueueOne
such that
and
_ _ ( ) 1num unpaired faces
; repeat
4Step
,
until
QueueOne
and
QueueZero
5Step
Return to
2Step
, until
0
K
The algorithm1 works on the links of vertices.
There is an alternative definition of
'
h
in the lower
link of
x
with the property that the vertex with the
minimum value of
'
h
more closely approximates the
direction of steepest decrease of
h
. In the alternative
definition, we set
'
( ) ( ( ) ( ))/ ([ , ])h y h y h x l x y
(3)
where
([ , ])l x y
is the length of the edge
[ , ]xy
.
The function
_ _ ( )num unpaired faces
which returns
the number of faces of
are in
()Sx
have not yet
been inserted in either
C
or
V
. If
_ _ ( ) 0num unpaired faces
in
QueueZero
, it is
denoted that there is no
()pair
for the cell
;
otherwise if
_ _ ( ) 1num unpaired faces
in
QueueOne
, then there is exactly one
()pair
for
the cell
,which is a candidate for homotopic
expansion. In
2Step
, If
()Lx
,
x
is critical and is
a local minimum . Otherwise,
x
is paired with its
lowest incident edge
xy
, denoted
[]Vx
. this
Novel Clustering based on Discrete Morse Technique
557

is a simple homotopy expansion. In
4Step
, there is
a pair
[ ( )]V pair
, if two conditions hold:
()Lx
and
_ _ ( ) 1num unpaired faces
. The
expansion proceeds until
QueueOne
and
QueueZero
, then a critical cell is created and the
expansions then proceed from the new cell. The
algorithm terminates because there are a finite
number of 0-cells selected. Each cell in
()Sx
will be
paired and included in
V
or inserted into
C
by the
algorithm1.
In order to construct optimal discrete Morse
function which has the minimum possible number of
critical cells, we present
Algorithm2
( , , , )CancelCriticalCell K g j p
. In the
discrete gradient vector field
V
, it is necessary to
wait to cancel until we found the pair
1j
C
,
j
C
connected by exactly one gradient path so that
max ( ) max ( )hh
is minimized. In optimization
model based on discrete Morse theory, the value of
the parameter
p
that controls cancellation is as large
as possible. In our new clustering framework, we
obtain a different number of critical 0-cells by
adjusting the parameter
p
, and the critical 0-cells
can be taken as clustering centers.
Algorithm2.
( , , , )CancelCriticalCell K g j p
1Step
j
C
;
2Step
find all gradient paths
1 2 1
...
i
i i il j
C
with
max ( ) max ( )
i
il
h h p
; if
the pair
1
i
il j
C
,
j
C
connected by exactly one
gradient path, let
max{ ( )}
i
i il
mh
;
3Step
if at least one
i
m
is defined, pick
max{ }
ji
mm
. if each cell
in the gradient path
holds
()h
, execute
4Step
; otherwise return to
1Step
;
4Step
find the unique gradient path
1 1 2 2 1
...
jj
C
,thus
1
()
ii
V
,
i
is a face of
i
and
1ii
;
5Step
delete
and
from
C
; reverse
direction from
to
,
()
ii
V
;
6Step
repeat
1Step
, until no
j
C
to be
selected.
Then we propose a method to construct discrete
Morse function. The method for constructing
discrete Morse function on a simplicial complex
K
is motivated by the techniques of an extension of
h
to a discrete Morse function
f
with the same
modified Hasse diagram in (King et al., 2005). Let
x
be a vertex and let
()Sx
be its lower star. We
record the order that cells from
()Sx
inserted into
V
or
C
by Definition1 that if
()Vx
, then
will
precede
x
. This algorithm ordering is
1 2 2
,, , ,...,
k
i i i i
x
for
1,..., 2
j
i k
(
()
i
Sx
has
2k
cells). Now we can define a discrete Morse
function on
()
i
Sx
as follows: given
0
( ) ( )
i
f h x
;
( ) ( )
ii
f x h x
;
( ) ( )
j
ii
f h x j
; (4)
The definition for
f
extends to all vertices
xX
, and all cells
K
. then
f
is a discrete
Morse function on the simplicial complex
K
.
According to Algorithm1, All other faces of
must have been inserted into
V
or
C
at an earlier
point, so
is the single face of
with greater
f
-
value. If
C
, it shows that all faces of
inserted
earlier and all of its cofaces are added later, so the
conditions for a critical cell of a discrete Morse
function are also satisfied by
f
.
3 NEW CLUSTER FRAMEWORK
BASED ON DISCRETE MORSE
OPTIMIZATION MODEL
In our density-based clustering framework, we
choose discrete Morse theory as a clustering tool,
which can efficiently partition each data point into
the corresponding cluster. It's a novel method. The
new cluster framework based on discrete Morse
optimization model (CADMOM) is a graph-based
theoretic (King et al., 2005) clustering method. Each
tree represents a cluster, many trees can form a
forest. The root node of each tree represents one
vertex in bottom regions whereas most leaf nodes
are regarded as vertices situated in the valley
regions.
Definition 8 (Kernel Density Estimation).
(Fukunag, 1990) The discrete Morse optimization
model is based on the steepest descent characteristic
on discrete gradient vector field, which follows
negative gradient flow. Let
n
data points in the d-
dimensional space,
12
{ , ..., }
n
X x x x
, where the data
vector is
12
[ , ,..., ]
i i i id
x x x x
,
1,2,...,in
. The
probability density of the data is given by the
following kernel density estimation:
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
558

1
1
( ) ( )
()
N
i
i
xx
h x K
N
(5)
then we choose the Gaussian function as the
kernel, which can be described as follows:
2
2
|| ||
( ) exp( )
2
ii
x x x x
K
(6)
We can obtain the local minima of the overall
density function
()hx
in their local regions, which
are root nodes of trees and can determine
mathematically clusters.
3.1 The Formation of Initial Clusters
Each cell in
()Sx
will be paired and included in
V
or
inserted into
C
by Algorithm1, so we can obtain the
Hasse diagram of vector field. On 0-1 level,one
vertex
0
v
following steepest descent path (
V Path
)
reaches the next vertex
1
v
that can be called the
predecessor of
0
v
.
2
v
continues to look for its
predecessor
3
v
. If a node does not have a
predecessor, we call it the root node of a tree.
Correspondingly, the nodes cannot be the
predecessor of other nodes, we call them leaf nodes.
In this way, a series of branches is called a directed
path, which is discrete gradient path. Clustering on
discrete gradient vector field forms a directed tree.
When all the data points are visited, a forest will be
generated and each tree in this forest represents a
cluster. Several
V paths
:
( ) ( 1) ( ) ( 1) ( 1) ( )
0 0 1 1 1
, , , ,..., ,
p p p p p p
rr
can be obtained by Algorithm1. Data points can be
quickly divided into the corresponding clusters by
searching predecessors of nodes.
In the new clustering framework, we can take
0
C
as a cluster center, whose cluster contains
0 cells
in
V Path
taking a critical cell
0
C
as
the end points. thus the initial clusters can be
formed.
3.2 The Mergence of Clusters
Consider 0-1 level. A critical 1-simplex
1
C
is the
start of exactly two gradient paths, if τ is connected
to
0
vC
by a single gradient path, it must be
connected to some other vertex
0
wC
by a single
gradient path. If any 0-cell
y V paths
that are
from
1
C
to
0
vC
and from
1
C
to
0
wC
holds
()fy
, then we can choose
min{max ( ) max ( ),max ( ) max ( )}h h v h h w
to
merge clusters. These steps can be repeated until the
desired number of clusters is obtained by
Algorithm2.
3.3 The New Clustering Framework
based on Discrete Morse
Optimization Model
Through the above analyses, the total algorithm can
be divided into two parts: constructing the simplicial
complex on an energy surface and clustering on the
simplicial complex. Now, we can describe the whole
algorithm steps for our discrete Morse optimization
model-based clustering framework as follows:
1Step
Input the data set
12
{ , ..., }
n
X x x x
;
2Step
Compute the probability density
h(x
i
)(i=1;2;...;n) for each data according to (5) with
Gaussian kernel in (6) ;
3Step
construct the simplicial complex on a
discrete surface according to 2.1;
4Step
compute each initial clusters according
Algorithm1;
5Step
merge clusters that meet conditions
based on hierarchical clustering (Wang et al., 2009)
by Algrithm2;
In this paper, the computation is based on a
discrete surface generated by the density function, so
we should restore clustering results to clusters about
the data set
12
{ , ..., }
n
n
X x x x R
. the distribution of
data points is determined by level sets. Now we
present the new clustering framework, See Figure 2.
Figure 2: Procedure of the new clustering framework.
construct discrete Morse function f
construct the discrete gradient vector field V
N
Y
output the distribution of data points
determined by level sets
Input the data set X
construct the simplicial complex
K on a discrete surface
output
V Path
taking
0
C
as the end point
meet the conditions?
execute Algorithm2
Novel Clustering based on Discrete Morse Technique
559
4 EXPERIMENTAL RESULTS
AND ANALYSIS
In this section, we present the experimental results
and analysis of our discrete Morse optimization
model-based clustering framework on some
synthetic and UCI data sets. The implementation of
these algorithms is in Visual C++ 2010 . Matlab7.0
and Geomview are adopted to display graphics.
4.1 Parameter Setting
As shown in the algorithm in Section 3.3, the new
algorithm requires three input parameters, i.e., the
window width
, the cancelling critical simplex
parameter
p
, the threshold of the density
. the
window width
can be set to a value in the scope
of 0.1-2. the cancelling critical simplex parameter
p
can be set to a value in the scope of 0.01-0.5. the
threshold of the density
is fixed
0
for all
experiments.
4.2 Experimental Results of Synthetic
Data Sets
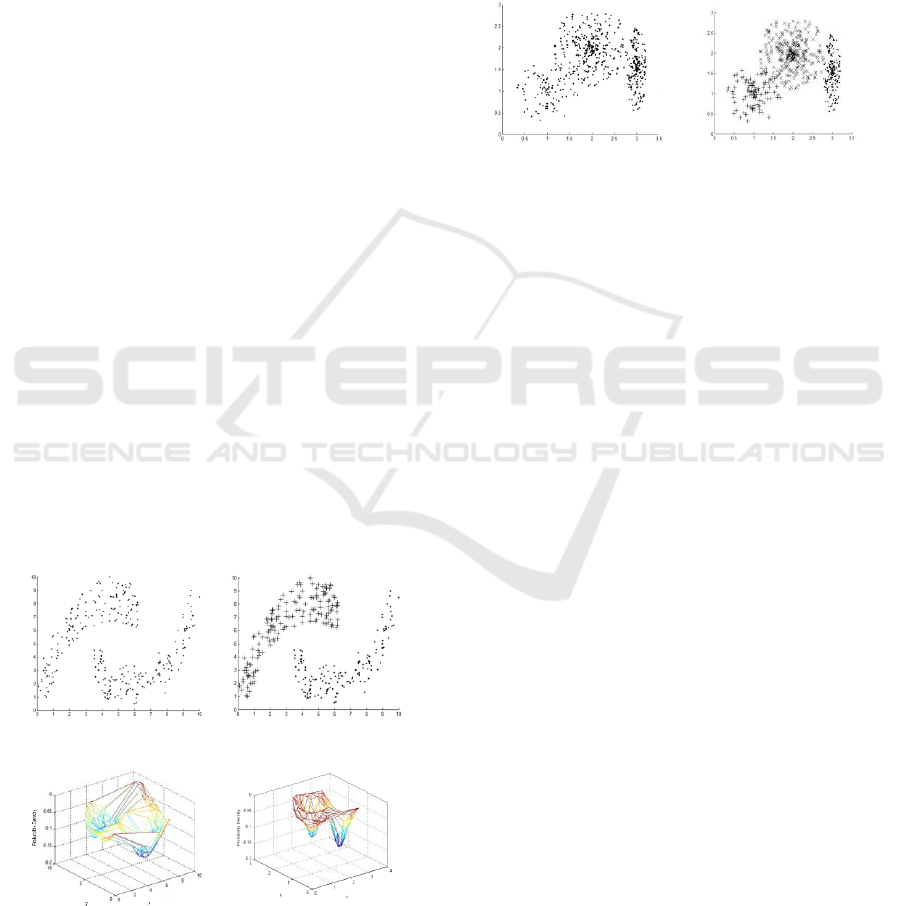
The first data set, Dataset1, contains 300 points and
has two clusters that are of irregular shapes. The
new clustering algorithm is used for clustering in
Figure 3(c) for ten times. Expected result can be
achieved every time, see Figure 3(b). One cluster
contains data points represented by '+', the other
contains data points represented by '•'. The total
processing time of our clustering framework is 1.3s.
(a) Dataset1. (b) Final clustering result.
(c) D- triangulation (d) D-triangulation
Figure 3: Clustering 2D- Dataset1 using the new clustering
algorithm.
The second data set, Dataset2, contains 600
points and has three clusters that are of different
shape, size, density. The clusters partially overlap.
The new clustering algorithm is used for Clustering
in Figure 4(a) for ten times. Expected result can be
achieved every time, see Figure 4(b). One cluster
contains data points represented by '+', one contains
data points represented by '•'. another contains data
points represented by '×'. The total processing time
of our clustering framework is 1.8s.
(a) Dataset2. (b) Final clustering result.
Figure 4: Clustering 2D- Dataset2 using the new clustering
algorithm.
4.3 Experimental Results of UCI
'Haberman s
Survival
data set and
Iris
data set are
used to test our clustering algorithms in this section
that are taken from UCI Machine Learning
repository.
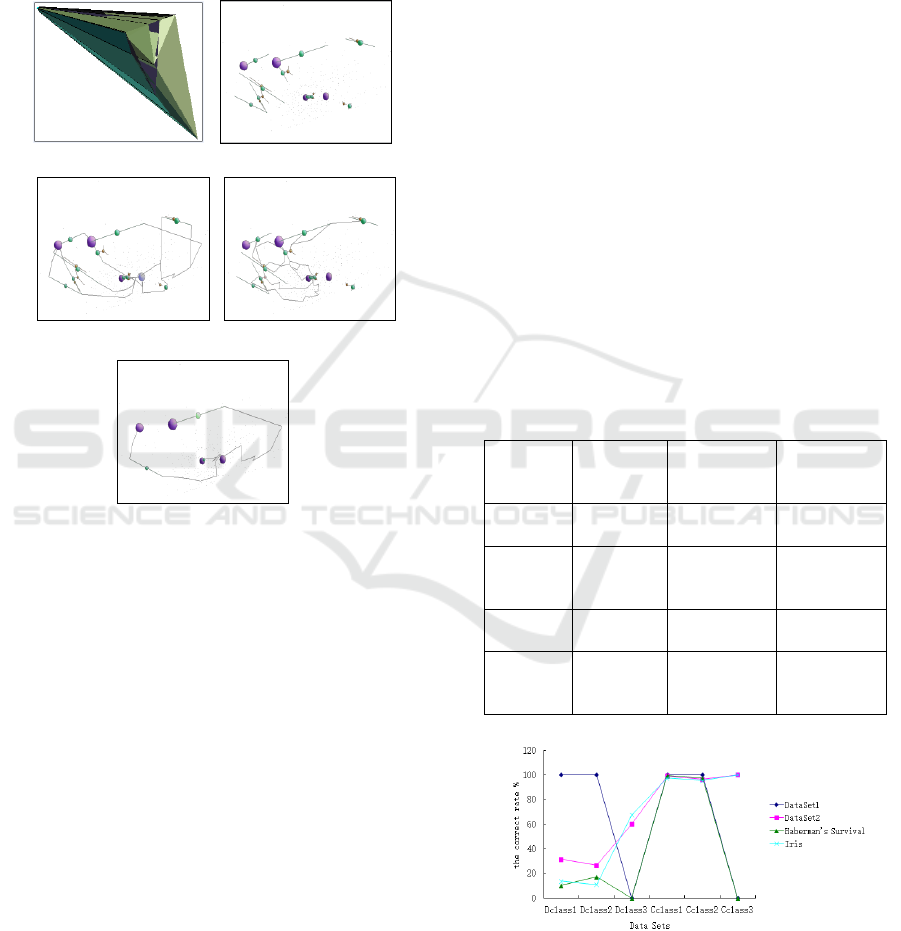
Gemview
is adopted to display graphics.
In the window, there are some black dots (which are
the vertices) and some colored balls, some with lines
coming from them (these are the critical simplices,
The balls are around the barycenter of the simplex
and the lines go to the barycenters of its
codimension one faces. a purple ball represents a
critical vertex.)
The third data set,
'Haberman s
Survival
,
contains 306 points represented by three features and
consists of two classes that partially overlap in the
feature space. The proposed clustering framework is
used to address the
'Haberman s
Survival
data set
in 4D space. The proposed clustering framework is
used for Clustering in Figure5(a). After
implementation of Algorithm1
( , )ConstructDVF K g
,
the number of critical simplices is (4,11,8,0): 4 0-
critical simplices, 11 1-critical simplices, 8 2-critical
simplices, 0 3-critical simplices. a purple ball
represents a critical vertex, a green ball represents a
1-critical simplex, An orange ball represents a 2-
critical simplex, see Figure 5(b). Figure 5(c) and
Figure 5(d) show the discrete gradient vector fields of
0-1 level and 1-2 level. Figure 5(e) gives the result
cancelling 1-2 level discrete gradient paths by
performing Algorithm2
( , , , )CancelCriticalCell K g j p
,
the number of critical simplices is (4,3,0,0). 8 2-
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
560
critical simplices and 8 1-critical simplices are
cancelled. 0-critical cells can be cancelled in
ascending order by cancelling 0-1 level discrete
gradient paths, the remaining ones are taken as the
cluster centers separately. A cluster that the cluster
center is
0
C
contains 0-cells in discrete gradient
paths taking
0
C
as the end point.
(a) D-triangulation . (b) clustering result.
(c) 0-1 level DGP. (d) 1-2 level DGP.
(e) Result cancelling 1-2 level DGP.
Figure 5: Clustering 3D-
'Haberman s
Survival
using the new
clustering algorithm.
From Figure 5,We can see that: (a) Delaunay
triangulation on the surface.(b) clustering result
executing Algorithm1.(c) 0-1 level discrete gradient
paths(denoted by gray lines). (d) 1-2 level discrete
gradient paths(denoted by gray lines).(e) Result
cancelling 1-2 level discrete gradient paths.
The new clustering algorithm is used for
clustering in Figure 5(a) for ten times. The value of
is in the scope of 0.5~2. The correct clustering
rate is 98 percent due to the overlapping between the
classes. The overall processing time is 4.3s.
The fourth data set,
Iris
, contains 150 points
and consists of three classes(Setosa , ersicolor, and
Virginica) , with 50 points per classes, represented
by four features . Setosa class is linearly separable
from the remaining two classes, while the other two
classes partially overlap in the feature space. The
proposed clustering framework is used to address the
Iris
data set in 5D space and used for Clustering for
ten times.
is in the scope of 0.1~1. The correct
clustering rate based on
Iris
data set is 96 percent
due to the overlapping between the Versicolor and
Virginica classes and the overall processing time
was 5.1s.
4.4 Comparisons with DBSCAN
Methods
The four data sets shown in 4.2 and 4.3 have been
considered to illustrate the advantages of our new
framework over other density-based clustering
methods. The DBSCAN method (Ester et al., 1996)
was used to cluster the four data sets separately. We
have set the values of
[1,10]MinPts
and that of
[0.1,1]Eps
. The DBSCAN method could produce
a correct clustering of DataSet1, otherwise the
DBSCAN method failed to find meaningful clusters
in DataSet2,
'Haberman s
Survival
and
Iris
due to
the overlapping in the clusters. However, the
proposed density clustering framework based on the
discrete Morse theory method succeeded in
detecting the correct clusters, as shown in Figure
4(b), Figure 5(e). Now we present comparisons with
DBSCAN methods. See Table 2 and Figure 6.
Table 2: Comparisons with DBSCAN methods.
datasets
Execution
times
DBSCAN
(correct rate
%)
CADMOM
(correct rate
%)
DataSet1
10
class1:100;
calss2:100
class1:100;
class2:100
DataSet2
10
class1:31.3;
calss2:26.4
calss3:60
calss1:99.1;
calss2:96.3
calss3:100
DataSet3
10
class1:10.2;
calss2:17.3
class1:99.1;
calss2:97.5
Iris
10
class1:13.5;
calss2:10.7
calss3:67.3
class1:97.2;
calss2:95.3
calss3:100
Figure 6: Comparisons with DBSCAN methods.
Viewing the experimental results, the new
clustering algorithm based on discrete Morse theory
can produce satisfactory clusters and generate more
Novel Clustering based on Discrete Morse Technique
561

accurate clusters even in the case of the failure of
classical clustering algorithms.
5 CONCLUSIONS
Inspired by an optimization model based on discrete
Morse theory, we propose the new clustering
framework that is mainly to adopt to the thought of
hierarchical clustering based on kernel density
estimation. The experimental results on some
synthetic and UCI data sets have demonstrated that
the new algorithm can discover clusters with
arbitrary shapes and densities at different levels,
moreover it can successfully divide data points
overlapping to the feature space into many correct
clusters. The results show the feasibility and
effectiveness of the new clustering algorithm.
ACKNOWLEDGEMENTS
This work is carried out under the “Taishan Scholar”
project of Shandong China. It is also supported in
part by the Natural Science Foundation of China
(61472231 , 61640201) and the Scientific and
Technology Project of Shandong Education Bureau.
REFERENCES
Han, J., Kamber, M., 2006. Data Mining Concepts and
Techniques, Morgan Kaufmann Publishers, San
Francisco, 2
nd
edition.
Chan, E., Ching, W., Ng, M., and Huang J. 2004. An
optimization algorithm for clustering using weighted
dissimilarity measures. Pattern Recognition.
Kaufman, L., Rousseeuw, P.J., 2009. Finding Groups in
Data: an Introduction to Cluster Analysis. John Wiley
& Sons, New Jersey, 3
nd
edition.
Hubert, L.J., Arabie, P., and Soete G., 1999 Clustering and
Classification. World Scientific, London, 2
nd
edition.
Chen, M.S., Han, J., and Yu, P.S., 1996. Data mining: An
overview from database perspective. IEEE
Transactions on Knowledge and Data Engineering.
Graves, D., Pedrycz, w., 2007. Performance of Kernel-
Based Fuzzy Clustering. Electronics Letters.
Pal, N. R., Bezdek, J.C. and Tsao, E.C.-K., 1993.
Generalized clustering networks and Kohonen's self-
organization. IEEE Trans. Neural Network.
Babu, G.P., Murty, M. N., 1994. Clustering with evolution
strategies. Pattern Recognition.
Bader, J.S., A. Chaudhuri, et al. 2004. Gaining confidence
in high-throughput protein interaction networks. Nat
Biotechnol.
Milnor, J.W., 1963. Morse theory. Princeton University
Press, Princeton, NJ,
Forman, R., 1995. A discrete Morse theory for cell
complexes. Geometry, Topology and Physics for
Raoul Bott. International Press, Boston.
Forman, R., 1998. Morse Theory for Cell Complexes,
Advances in Mathematics.
Edelsbrunner, H., Harer, J., and Zomorodian, A., 2003.
Hierarchical Morse-Smale Complexes for Piecewise
Linear 2-Manifolds. Discrete Comput. Geom.
Zhang, J.P., Liu, X.Y., 2014. An Optimization Model
Based on Discrete Morse theory. Systems
Engineering - Theory & Practice. In press.
Lewiner, T., Lopes, H., 2003. Gavares. Toward Optimality
in Discrete Morse Theory. J. Experimental Math.
Edelsbrunner, H., Harer, J., Natarajan, V., and Pascucci,
V., 2003. Morse-Smale Complexes for Piecewise
Linear 3-Manifolds. In Proc. 19th Ann. Sympos.
Comput. Geom. ACM Press, New York.
King, H., Knudson, K., and Mramor, N., 2005. Generating
Discrete Morse Functions from Point Data,
Experimental Mathematics.
Fukunaga, K., 1990. Introduction to Statistical Pattern
Recognition, second ed. Academic Press, Boston.
Wang, X.C., Wang, X.L., and Wilkes, D.M., 2009. A
Divide-and-Conquer Approach for Minimum
Spanning Tree-Based Clustering. IEEE Transactions
on Knowledge and Data Engineering.
Ester, M., Kriege l, H., Sander, J., and Xu, X., 1996. A
Density-Based Algorithm for Discovering Clusters in
Large Spatial Databases with Noise. Proc. Int’l Conf.
Knowledge Discovery and Data Mining.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
562
