
A Stochastic Model of Diffusion in Opinion Dynamics
Stefania Monica and Federico Bergenti
Dipartimento di Scienze Matematiche, Fisiche e Informatiche, Universit
`
a degli Studi di Parma, 43124 Parma, Italy
Keywords:
Opinion Dynamics, Multi-Agent Systems, Complex Systems.
Abstract:
This paper studies analytically the dynamics of the opinion in multi-agent systems when only the sociological
phenomenon known as diffusion is considered. First, the paper recalls a framework for the analytic study of
opinion dynamics which has been already applied to describe the effects of a number of sociological phe-
nomena. Then, the framework is specialized to the study of diffusion, according to which the opinion of an
agent can be influenced by the social context. Diffusion is introduced in the framework by stating stochastic
rules meant to describe at the microscopic level how diffusion contributes to change the opinion of an agent.
The obtained model is used to derive collective and asymptotic properties of multi-agent systems when only
diffusion is considered, which are verified against specific simulations shown in the last part of the paper. The
paper is concluded with a recapitulation of presented results and an outline of future work.
1 INTRODUCTION
This paper describes a stochastic model that is used
to derive analytic results on collective and long-time
asymptotic properties of the opinion in multi-agent
systems. Considered multi-agent systems are com-
pletely decentralized and without supervised coordi-
nation, and they are studied using a generic frame-
work that depends only on the description of the ef-
fects of microscopic interactions among agents. Mi-
croscopic rules that govern how the opinion of two in-
teracting agents change are used to derive analytically
observable macroscopic properties of the opinion in
the multi-agent system, under proper assumptions.
In this context, the term interaction is used to
denote a symmetric message exchange among two
agents, and it is assumed that message exchanges are
asynchronous. Time is modeled as a sequence of
discrete steps, which may not have the same dura-
tion, and each step corresponds to a single interaction
among two agents. Each agent is free to interact with
any other agent, and no restriction is imposed on the
topological properties of the multi-agent system. The
adopted framework assumes that each agent is asso-
ciated with a scalar attribute, and since the target ap-
plication of the framework in this paper regards the
study of the dynamics of the opinion, we assume that
such an attribute represents the opinion of an agent on
a fact, which may vary within a finite interval.
Most of existing agent-based models used to study
opinion dynamics are based on simulations (Deffuant
et al., 2000; Hegselmann and Krause, 2002; Monica
and Bergenti, 2014). Hence, their validity depends on
the specific type of multi-agent system that is simula-
ted, and on the actual values assigned to the parame-
ters of simulations. Actually, their validity depends
on how representative are simulated scenarios with re-
spect to studied phenomena (Flache et al., 2017). At
the opposite, the framework discussed in this paper is
analytic, and it provides parametric results which are
valid as long as its hypotheses remain valid.
Even if analytic models are typically simpler than
models based on simulations, they are preferred when
the interest is on how collective and long-time asymp-
totic behaviours are affected by the parameters of the
models, or when no representative cases to be simu-
lated can be found. Simulations are still very impor-
tant even if analytic models are available because they
become a means to independently verify analytic mo-
dels in interesting cases. Simulations reported in the
last part of the paper are performed independently of
discussed analytic results, and they are uniquely in-
tended to verify analytic results.
Note that the proposed framework is not limited
to the study of opinion dynamics and its approach
can be adopted to describe other collective behaviours
of multi-agent systems, provided that studied pheno-
mena emerge from decentralized interactions.
Monica, S. and Bergenti, F.
A Stochastic Model of Diffusion in Opinion Dynamics.
DOI: 10.5220/0006659601150124
In Proceedings of the 10th International Conference on Agents and Artificial Intelligence (ICAART 2018) - Volume 1, pages 115-124
ISBN: 978-989-758-275-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
115

The analytic framework adopted in this paper and
described in next section is inspired by a branch of
physics known as kinetic theory of gases and its ge-
neralizations, as described, e.g., in (Bellouquid and
Delitala, 2006). According to this approach, analy-
tic models of microscopic interactions among mole-
cules can be considered to derive macroscopic cha-
racteristics of gases concerning, for instance, tempe-
rature and pressure. Analytic frameworks that follow
the approach of the kinetic theory of gases has been
applied successfully in different fields. For instance,
the kinetic approach has been successfully applied in
economics to describe the evolution of market eco-
nomy (Cordier et al., 2005) and the distribution of
wealth (Slanina, 2004), giving birth to a discipline
known as econophysics (Chakrabarti et al., 2006). In
this paper, we focus on an application of the kinetic
approach to describe sociological processes and the
dynamics of the opinion in multi-agent systems. The
idea is not new, and it is part of an emerging discipline
known as sociophysics (Galam et al., 1982). Many
analogies between the kinetic theory of gases and the
study of opinion dynamics in multi-agent systems can
be found. First, it is evident that a parallelism bet-
ween molecules in gases and agents in multi-agent sy-
stems can be drawn. Similarly, collisions among mo-
lecules in gases can be re-interpreted as interactions
among agents in multi-agent systems. Obviously, the
detailed mathematical modeling of collisions among
molecules is based on the laws of physics and it is dif-
ferent from that of interactions among agents, which
is typically suggested by sociological studies. Due to
such differences, only few results of kinetic theory of
gases hold in the study of the dynamics of the opinion.
Many sociological phenomena can be studied ana-
lytically using the kinetic approach (Monica and Ber-
genti, 2017a), like:
• Compromise, which is the tendency of agents to
move their opinions towards those of agents they
interact with (De Groot, 1974);
• Diffusion, according to which the opinion of each
agent can be influenced by the social context (Bo-
nabeau, 2002);
• Homophily, according to which agents interact
only with those with similar opinions (Nowak
et al., 1990; Mark, 2003);
• Negative Influence, according to which agents
evaluate their peers, and they only interact with
some peers (M
¨
as and Flache, 2013);
• Opinion Noise, according to which a random ad-
ditive process may lead to arbitrary opinion chan-
ges with small probability (Pineda et al., 1982);
and
• Striving for Uniqueness, which is based on the
idea that agents want to distinguish from others
and, hence, they decide to change their opinions
if too many agents share the same opinion (M
¨
as
et al., 2010).
Kinetic models that study compromise alone have
been already proposed in (Monica and Bergenti,
2016a; Monica and Bergenti, 2016b; Monica and Ber-
genti, 2017b; Monica and Bergenti, 2017c). In ad-
dition, in (Monica and Bergenti, 2015a; Monica and
Bergenti, 2015b; Monica and Bergenti, 2015c), both
compromise and diffusion were analytically modeled
and investigated under proper assumptions. In this
paper, instead, we focus uniquely on diffusion and
we analytically derive results concerning the dyna-
mics of the opinion when only this phenomenon is
considered. The major contribution of this paper is
to study analytically collective and asymptotic pro-
perties of the opinion when only diffusion is relevant,
so that the properties of diffusion can be isolated and
studied independently of other phenomena. Note that
other models of opinion formation based on the ki-
netic theory of gases were also proposed to account
for the possibility of having different types of agents
in a multi-agent system (Bergenti and Monica, 2016;
Bergenti and Monica, 2017).
This paper is organized as follows. Section 2 sum-
marizes the main ideas of the kinetic approach and
it outlines the adopted kinetic framework. Section 3
presents a stochastic model to describe the sociologi-
cal phenomenon of diffusion. Section 4 shows ma-
jor analytic results concerning collective and asymp-
totic properties of a multi-agent system when only
diffusion is considered. Section 5 describes simu-
lations that were ran to verify analytic results. Fi-
nally, Section 6 concludes the paper and outlines fu-
ture work.
2 A KINETIC FRAMEWORK TO
STUDY OPINION DYNAMICS
In this section, we present the main ideas of classic
kinetic theory of gases and we focus on the reinter-
pretation of such ideas to study the dynamics of the
opinion in multi-agent systems. Classic kinetic the-
ory of gases assumes that, at each time t, each mole-
cule of the considered gas can be associated with re-
levant parameters, such as its position x and velocity
v, which are both modeled as three-dimensional vec-
tors. The characteristics of the considered gas are des-
cribed in terms of a density function f (x,v,t), which
represents the number of molecules whose position is
in (x,x + dx) and whose velocity is in (v, v + dv) at
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
116

time t. The density function f (x,v,t) evolves follo-
wing a proper balance equation, namely the famous
Boltzmann equation. The Boltzmann equation is an
integro-differential equation whose explicit formula-
tion is based on the analytic description of the ef-
fects of collisions among molecules. The study of
the Boltzmann equation allows deriving macrosco-
pic properties of a gas, concerning, for instance, the
average velocity of its molecules, its temperature, and
its pressure. In summary, kinetic theory of gases stu-
dies the effects of collisions among molecules from
a microscopic point of view and uses such results to
derive macroscopic properties of gases.
The same approach can be used to model opi-
nion dynamics in multi-agent systems by means of
a proper parallelism between molecules and collisi-
ons among them, and agents and interactions among
them, as proposed, for example, in (Schweitzer and
Holyst, 2000) or in (D
¨
uring et al., 2009). It is worth
noting that, since the effects of collisions among mo-
lecules differ from the effects of interactions among
agents, analytic results derived to study the dynamics
of the opinion differ significantly from well-known
results of the kinetic theory of gases. However, the
approach of kinetic theory of gases can be effectively
generalized to obtain analytic results in the field of
opinion dynamics, as follows.
Each agent is associated with a single parameter
v, which represents its opinion. Note that, in our con-
text, the term opinion is used to denote the level of
agreement on a single topic or the level of apprecia-
tion of a single item. Therefore, we assume that opi-
nion v is valid only in a closed interval
I = [−1, 1] (1)
where −1 stands for strong disagree or strong dislike,
1 stands for strong agree or strong like, and values
close to 0 are considered moderate opinions. We re-
mark that the choice of the interval I in (1) is discreti-
onal and any other closed interval can be used, provi-
ded that the following analytic developments are co-
herently changed. In agreement with the general ideas
of kinetic theory of gases, we also postulate the exis-
tence of a density function f (v,t), which represents
the number of agents with opinion in (v, v + dv) at
time t. The definition of the density function f (v,t) al-
lows computing proper macroscopic properties of the
system from an analytic point of view. For instance,
the number of agents at time t, denoted as n(t), can be
computed as
n(t) =
Z
I
f (v,t)dv. (2)
From (2), it is evident that the number of agents at
time t is obtained by integrating the density function
with respect to all values of v ∈I. In kinetic theory of
gases, a similar integral is used to compute the mass
of the considered gas. Similarly, the average opinion
of the system at time t, denoted as u(t), is obtained
by multiplying f (v,t) by v, dividing by the number of
agents, and integrating with respect to v,
u(t) =
1
n(t)
Z
I
f (v,t)vdv. (3)
Observe that the average opinion u(t) is related to the
first momentum of the density function f (v,t). In
kinetic theory of gases, a similar integral is used to
compute the average velocity of molecules in the con-
sidered gas. Finally, the variance of the opinion at
time t, denoted as σ
2
(t), can be obtained by multi-
plying f (v,t) by (v −u(t))
2
, dividing by the number
of agents, and integrating with respect to v, as follows
σ
2
(t) =
1
n(t)
Z
I
(v −u(t))
2
f (v,t)dv. (4)
Note that the variance of the opinion σ
2
(t) is related to
the second-order momentum of the density function
f (v,t). In kinetic theory of gases, similar integrals are
used to compute the pressure and the temperature of
the considered gas.
The temporal evolution of the density function
f (v,t) is governed by a balance equation, whose
explicit expression is inspired from that of the
Boltzmann equation. For this reason, we adopt the
same nomenclature of kinetic theory of gases and we
still use the term Boltzmann equation for such a ba-
lance equation. The homogeneus formulation of the
Boltzmann equation that can be used to study the dy-
namics of the opinion is
∂ f
∂t
(v,t) = Q ( f )(v,t) (5)
where the left-hand side is related to the temporal evo-
lution of the density function and in the right-hand
side Q is an operator meant to account for the effects
of interactions among agents. Keeping the same no-
menclature of the kinetic theory of gases, Q is called
collisional operator and it computes a function of va-
riables v and t by using function f .
In order to analytically study the temporal evolu-
tion of the number of agents n(t), the average opi-
nion u(t), and the variance of the opinion σ
2
(t), the
weak form of the Boltzmann equation can be used.
In functional analysis, the weak form of a differential
equation is obtained by multiplying both sides of the
equation by a suitable test function and by integrating
with respect to one of the variables. Therefore, the
weak form of the Boltzmann equation with respect to
the generic test function φ(v) can be written as
d
dt
Z
I
f (v,t)φ(v)dv =
Z
I
Q ( f )(v,t)φ(v)dv (6)
A Stochastic Model of Diffusion in Opinion Dynamics
117

where the right-hand side is called weak form of the
collisional operator Q with respect to test function
φ(v). Recalling (2), (3), and (4), it is evident that the
left-hand side of (6) can be used to compute the time
derivative of macroscopic characteristics of the multi-
agent system, provided that specific test functions are
chosen, as follows:
1. If φ(v) = 1, the left-hand side of (6) represents the
time derivative of the number of agents n(t);
2. If φ(v) = v, the left-hand side of (6) is related to
the time derivative of the average opinion; and
3. If φ(v) = (v −u(t))
2
, the left-hand side of (6) is
related to the time derivative of the variance of the
opinion.
In next section, the details of the microscopic effects
of the interactions among agents on the opinion are
outlined and, consequently, the explicit expression of
the collisional operator and of its weak form are de-
rived. Such derivations are sufficient to express ordi-
nary differential equations whose unknowns are n(t),
u(t), and σ
2
(t). The solutions of such equations ex-
press the dynamics of such quantities and they allow
studying analytically their asymptotic behaviours.
3 A STOCHASTIC MODEL OF
DIFFUSION
In order to derive explicit results using the framework
outlined in previous section, the explicit formulation
of the interaction among agents is needed. Note that
in the proposed framework interactions among agents
are not coordinated by any supervising entity, and, in
our assumptions, any agent can freely interact with
any other agent in the system. Moreover, we assume
that interactions among agents are binary, which me-
ans that they involve only two agents. This assump-
tion is not restrictive, since interactions involving a
larger number of agents can be regarded as sequences
of binary interactions. Concerning the sociological
phenomenon considered in this paper, as shortly ex-
plained in the introduction, we focus on diffusion, ac-
cording to which agents can change their opinions due
to external influence. However, we remark that the
proposed approach can be extended to take into ac-
count more complex interaction rules, including, e.g.,
homophily (Tsang and Larson, 2014), which accounts
for the fact that agents tend to communicate only with
those having similar opinions.
Diffusion can be modeled using the following in-
teraction rules, as proposed, e.g., in (Pareschi and
Toscani, 2013; Toscani, 2006). Such interaction ru-
les model how the opinions of two interacting agents
change after an interaction if only diffusion is consi-
dered relevant to opinion formation and other socio-
logical phenomena are neglected
(
v
0
= v + η
1
D(v)
w
0
= w + η
2
D(w)
(7)
where
1. v and w represent the opinions of the two agents
before the interaction, often called pre-interaction
opinions;
2. v
0
and w
0
represent the opinions of the two agents
after the interaction, often called post-interaction
opinions;
3. η
1
and η
2
are two independent random variables
that we call diffusion parameters; and
4. D(·) models the effects of diffusion on the opi-
nion of the two interacting agents, and it is called
diffusion function.
In the rest of this paper we assume that diffusion pa-
rameters have the same distribution function, which
is denoted as ϑ(·). We denote the support of ϑ(·) as
S, and we assume that the average values of the two
random variables equal 0
Z
S
ϑ(η
1
)η
1
dη
1
=
Z
S
ϑ(η
2
)η
2
dη
2
= 0. (8)
Note that according to the proposed model of diffu-
sion the post-interaction opinion of an agent depends
only on its pre-interaction opinion, and it does not de-
pend on the pre-interaction opinion of the other agent.
This models the idea that the opinion of an agent can
change simply because an interaction occurred, and
the change of the opinion does not necessarily depend
on the opinion of the other agent, which is how dif-
fusion is studied in opinion dynamics (Pareschi and
Toscani, 2013; Toscani, 2006).
Observe that from (7) it is evident that the post-
interaction opinions are obtained by adding to the
pre-interaction opinions an addend which is propor-
tional to the diffusion function evaluated in the pre-
interaction opinions according to the values of the
parameters η
1
and η
2
. Some considerations on the
choice of the diffusion function and on the choice of
the distribution functions of η
1
and η
2
are needed.
First, let us observe that different choices of the diffu-
sion function may lead to very different models. Fol-
lowing the literature (Toscani, 2006), we assume that
diffusion functions are nonzero and symmetric with
respect to the central value of the interval where opi-
nions are defined. In our assumptions, since interval
I is symmetric with respect to 0, this corresponds to
state that the diffusion function is even and, for this re-
ason, from now on we assume that D(·) is a function
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
118

of the absolute value of the opinion v. Moreover, we
assume that D(·) is not increasing with respect to |v|,
in agreement with the idea that agents with opinions
close to the bounds of I are conservative. Finally, we
also assume that the following inequalities hold to en-
sure that the magnitude of the effects of diffusion are
controlled only by diffusion parameters η
1
and η
2
0 ≤ D(|v|) ≤ 1. (9)
We call admissible any diffusion function that re-
spects mentioned assumptions, and we consider only
admissible diffusion functions in the rest of this paper.
Some considerations need to be made to guaran-
tee that post-interaction opinions v
0
and w
0
belong to
the interval of interest I. To this aim, it is necessary
to impose proper conditions on the support of the two
random variables η
1
and η
2
. Observe that the follo-
wing inequalities hold
|v + η
1
D(|v|)| ≤ |v|+ |η
1
|D(|v|)
|w + η
2
D(|w|)| ≤ |w|+ |η
2
|D(|w|).
(10)
Hence, possible sufficient conditions to guarantee that
v
0
∈ I and w
0
∈ I are
|η
1
| ≤
1 −|v|
D(|v|)
|η
2
| ≤
1 −|w|
D(|w|)
.
(11)
If (11) holds, diffusion parameters are said to be ad-
missible for the chosen D(·), and note that we con-
sider only admissible diffusion parameters in the rest
of this paper. In next section, such conditions will
be further discussed in correspondence of a specific
choice of an admissible diffusion function.
The microscopic interaction rules (7) can be fi-
nally used to derive the explicit expression of the
collisional operator, which is the integral operator
that can be evaluated as the difference between the
gain and the loss of agents whose opinions fall in
(v, v + dv). In order to do so, let us introduce the
transition rate W (v,w,v
0
,w
0
)dv
0
dw
0
which represents
the probability per unit time that after the interaction
among two agents with opinions v and w, the opinion
of the first agent is in (v
0
,v
0
+ dv
0
) and the opinion of
the second agent is in (w
0
,w
0
+ dw
0
). Following the
derivation in (Toscani, 2000), in which a different mi-
croscopic model is considered, the transition rate can
be written as
W (v,w,v
0
,w
0
)dv
0
dw
0
= ϑ(η
1
)ϑ(η
2
)dη
1
dη
2
(12)
where, as previously said, ϑ(·) denotes the distri-
bution function of the random variables η
1
and η
2
,
whose support is S. Under all mentioned assumptions,
the difference between the gain and the loss terms in
the explicit formulation of the weak form of the col-
lisional operator can be written as a unique integral,
thus obtaining the following formulation of the right-
hand side of the weak form of the Boltzmann equation
Z
S
2
Z
I
2
ϑ(η
1
)ϑ(η
2
) f (v,t) f (w,t)·
(φ(v + η
1
D(|v|)) −φ(v))dvdw dη
1
dη
2
(13)
Given the explicit formulation of the weak form of the
Boltzmann equation (13), it is finally possible to ana-
lytically study relevant macroscopic properties of the
system, as explained at the end of previous section. In
the following section we show how the choice of pro-
per test functions in (13) allow the derivation of three
first order differential equations whose unknowns are
the number of agents, the average opinion, and the
variance of the opinion, respectively.
4 COLLECTIVE AND
ASYMPTOTIC PROPERTIES
In this section we show relevant analytic results con-
cerning collective and asymptotic properties of multi-
agents systems in which agents interact following the
rules outlined in previous section. In particular, star-
ting from the weak form of the Boltzmann equation
(13), we derive proper differential equations whose
unknowns are:
1. The number of agents n(t);
2. The average opinion of the system u(t); and
3. The variance of the opinion σ
2
(t).
In the last part of this section, analytic results in
closed form are also derived for a specific diffusion
function, which is then used to run independent simu-
lations.
Proposition 1. Given a multi-agent system where
agents interact according to (7), the chosen diffusion
function D(·) is admissible, and diffusion parameters
are admissible for D(·), the number of agents n(t) in
the multi-agent system does not depend on time.
Proof. Let us consider the test function
φ(v) = 1 (14)
in (13). Since the test function (14) is a constant, the
difference
φ(v + η
1
D(|v|)) −φ(v) (15)
inside the integral in (13) equals 0. Hence, the weak
form of the Boltzmann equation relative to the chosen
A Stochastic Model of Diffusion in Opinion Dynamics
119

test function φ(v) = 1 reduces to the following rele-
vant equality
d
dt
Z
I
f (v,t)dv = 0. (16)
The left-hand side of (16) represents the time deriva-
tive of the number of agents n(t) and, hence, (16) can
be reformulated as
d
dt
n(t) = 0, (17)
and it can be finally concluded that the number of
agents is constant
n(t) = n(0), (18)
which proves the proposition.
Proposition 1 allows dropping the dependance on
time for n(t). In the rest of this paper, we denote the
number of agents as n, thus omitting the dependance
on time. We remark that analogous considerations
can be derived also when considering the Boltzmann
equation in the context of kinetic theory of gases. This
property corresponds to mass conservation in gases.
Another, much more interesting, collective and
asymptotic property of diffusion is captured by the
following proposition.
Proposition 2. Given a multi-agent system where
agents interact according to (7), the chosen diffusion
function D(·) is admissible, and diffusion parameters
are admissible for D(·), the average opinion of the
multi-agent system u(t) does not depend on time.
Proof. Let us consider the test function
φ(v) = v (19)
in (13), so that the right-hand side of the weak form
of the Boltzmann equation can be written as
Z
S
2
Z
I
2
ϑ(η
1
)ϑ(η
2
) f (v,t) f (w,t)·
η
1
D(|v|)dvdw dη
1
dη
2
.
(20)
From (3) and recalling that, according to (18), the
number of agents is constant, the left-hand side of the
weak form of the Boltzmann equation equals
n
d
dt
u(t) (21)
and it is therefore proportional to the derivative of the
average opinion with respect to time. Moreover, the
integral in (20) can be written as the product of four
terms, as follows
Z
S
η
1
ϑ(η
1
)dη
1
Z
S
ϑ(η
2
)dη
2
·
Z
I
f (v,t)D(|v|)dv
Z
I
f (w,t)dw,
(22)
and, since ϑ(·) is a distribution function, the integral
on its support S equals 1. Finally, using (2), (22) can
be simplified to
¯
η
1
n
Z
I
f (v,t)D(|v|)dv (23)
where
¯
η
1
is the average value of random variable η
1
.
Recalling that the average value of random variable
η
1
is assumed to be equal to 0, from (8), it can be
concluded that (20) equals 0, regardless of the choice
of the diffusion function D(·). Therefore, the weak
form of the Boltzmann equation corresponding to the
test function φ(v) = v can finally be written as
d
dt
u(t) = 0. (24)
Equation (24) implies that the average opinion of the
system is constant
u(t) = u(0), (25)
which proves the proposition.
As already done for the number of agents, from
now on we omit the dependance of the average opi-
nion on time and we simply denote it as u. An analo-
gous property is found in the kinetic theory of gases
and it corresponds to the conservation of momentum.
Note that if the average value of η
1
is not 0, which
equals to dropping the assumption that diffusion pa-
rameters are admissible for the chosen D(·), then the
following differential equation for the average opi-
nion can be derived
d
dt
u(t) =
¯
η
1
Z
I
f (v,t)D(|v|)dv (26)
and the validity of Proposition 2 would depend on the
actual choice of the diffusion function D(·).
Regarding the asymptotic properties of the vari-
ance of the opinion, the following proposition holds.
Proposition 3. Given a multi-agent system where
agents interact according to (7), the chosen diffusion
function D(·) is admissible, and diffusion parameters
are admissible for D(·), the variance of the opinion of
the multi-agent system σ
2
(t) is not constant.
Proof. Let us consider the test function
φ(v) = (v −u)
2
(27)
in (13), so that the right-hand side of the weak form
of the Boltzmann equation can be written as
Z
S
2
Z
I
2
ϑ(η
1
)ϑ(η
2
) f (v,t) f (w,t)·
η
2
1
D
2
(|v|) + 2η
1
D(|v|)(v −u)
dvdw dη
1
dη
2
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
120

where we used the following identity that can be ea-
sily verified by simple algebraic manipulations
(v + η
1
D(|v|) −u)
2
−(v −u)
2
=
η
2
1
D
2
(|v|) + 2η
1
D(|v|)(v −u).
Further algebraic manipulations, and the assumption
that the average value of η
1
equals 0, show that the
right-hand side of the weak form of the Boltzmann
equation can be written as
nσ
2
η
1
Z
I
f (v,t)D
2
(|v|)dv (28)
where σ
2
η
1
denotes the variance of the random varia-
ble η
1
. From the definition of σ
2
(t), and using previ-
ously obtained results on the conservation of the num-
ber of agents and of the average opinion, the left-hand
side of the weak form of the Boltzmann equation can
be shown to be proportional to the derivative of the
average opinion with respect to time. Actually, it can
be written as
n
d
dt
σ
2
(t). (29)
Therefore, the weak form of the Boltzmann equation
relative to the test function φ(v) = (v −u)
2
can be fi-
nally written as
d
dt
σ
2
(t) = σ
2
η
1
Z
I
f (v,t)D
2
(|v|)dv. (30)
Observe that f (v,t) is a density function, and the-
refore, by definition, it is non-negative. Moreover,
f (v,t) cannot be identically 0, since its integral on
I equals the number of agent n. Similarly, function
D
2
(·) is also nonnegative and it is supposed not to be
identically 0. According to these considerations, the
integral in (30) is necessarily strictly positive and it
depends on the choice of the diffusion function D(·).
Hence, it can be concluded that the variance of opi-
nion σ
2
(t) is not constant.
Note that no equivalent form of Proposition 3 is
found in the kinetic theory of gases because it follows
from the specific assumptions that we took to model
the sociological phenomenon of diffusion.
In order to explicitly solve the differential equa-
tion (30), and possibly validate obtained results on the
asymptotic behaviour of the opinion, a given admissi-
ble diffusion function needs to be fixed. We consider
the following diffusion function, which is also used in
next section
D(|v|) =
p
1 −v
2
. (31)
Observe that the chosen D(·) is admissible because it
satisfies the requirements outlined in Section 3. As
a matter of fact, it is an even function and it is a de-
creasing function of |v|. Moreover, it also satisfies
condition (9). Using this diffusion function, diffusion
parameters η
1
and η
2
are admissible if the following
conditions, derived from (11), are satisfied
|η
1
| ≤
1 −|v|
√
1 −v
2
|η
2
| ≤
1 −|w|
√
1 −w
2
.
(32)
The rest of this section is dedicated to the proof of the
following proposition.
Proposition 4. Given a multi-agent system where
agents interact according to (7) with diffusion
function (31), and assuming that diffusion parameters
are admissible for D(·), the variance of the opinion
σ
2
(t) of the multi-agent system exponentially tends to
1 −u
2
as t tends to +∞.
Proof. Let us start from the differential equation (30)
relative to the variance of opinion σ
2
(t). Considering
diffusion function (31), equation (30) becomes
d
dt
σ
2
(t) = σ
2
η
1
Z
I
f (v,t)(1 −v
2
)dv. (33)
The integral at the right-hand side of (33) can be writ-
ten as the difference
Z
I
f (v,t)dv −
Z
I
f (v,t)v
2
dv. (34)
The first integral in (34) equals the number of agents
n, while the second integral in (34) can be associated
to the definition of the variance of the opinion. As a
matter of fact, from the definition of σ
2
(t), the follo-
wing equalities can be easily derived
nσ
2
(t) =
Z
I
f (v,t)(v −u)
2
dv =
Z
I
f (v,t)v
2
dv −2nu
2
+ nu
2
where we used the definitions of the number of agents
n and of the average opinion u. Using these equations
in (30), the following differential equation for the va-
riance of the opinion σ
2
(t) can be derived from the
weak form of the Boltzmann equation
d
dt
σ
2
(t) = nσ
2
η
1
(1 −u
2
−σ
2
(t)). (35)
Observe that (35) is a non-homogeneous first-order
differential equation whose solution can be found
analytically. The solution of (34) is
σ
2
(t) = Ce
−nσ
2
η
1
t
+ (1 −u
2
) (36)
where C is a constant which has to be set in order to
satisfy the initial condition. Denoting as σ
2
(0) the
A Stochastic Model of Diffusion in Opinion Dynamics
121
initial value of the variance of the opinion, constant C
has to satisfy the following condition
σ
2
(0) = C + (1 −u
2
) (37)
and, hence, from (36) it can be concluded that the so-
lution of (34) is
σ
2
(t) = [σ
2
(0) −(1 −u
2
)]e
−nσ
2
η
1
t
+ (1 −u
2
). (38)
Let us now observe that the coefficient of t in the ex-
ponential function is negative, since both the number
of agents n and the variance of η
1
are positive. It
can then be concluded that the exponential function
in (38) tends to 0 as t tends to +∞. As a consequence,
it can be finally concluded that
lim
t→+∞
σ
2
(t) = (1 −u
2
), (39)
which proves the proposition.
5 VERIFICATION BY
SIMULATION
In this section, we show results of independent simu-
lations meant to validate analytic results derived in
previous sections. We consider a system composed
of n = 10
3
agents and, as stated in the introduction,
we assume that each agent can interact with any other
agent in the system. At each step of the simulation,
two agents are randomly chosen and an interaction
among them is simulated. This means that both of
them change their opinions according to (7) with the
chosen diffusion function D(·) in (31). We consider
three different scenarios, corresponding to different
initial distributions of the opinion and, hence, to dif-
ferent values of the average opinion u. In all consi-
dered scenarios, 1.5 ·10
5
binary interactions among
randomly chosen agents are simulated, which equals
to 300 interactions per agent on average.
We start by considering a multi-agent system
where the initial distribution of the opinion is uniform
on the entire interval I where the opinion is defined
f (v,0) = U
(−1,1)
(v). (40)
According to this assumption, the average opinion of
the system at time t = 0 is u = 0 and, as shown in the
proof of Proposition 2, it remains constant as agents
interact. Under these assumption, from Proposition 4
it is expected that the variance of the opinion tends
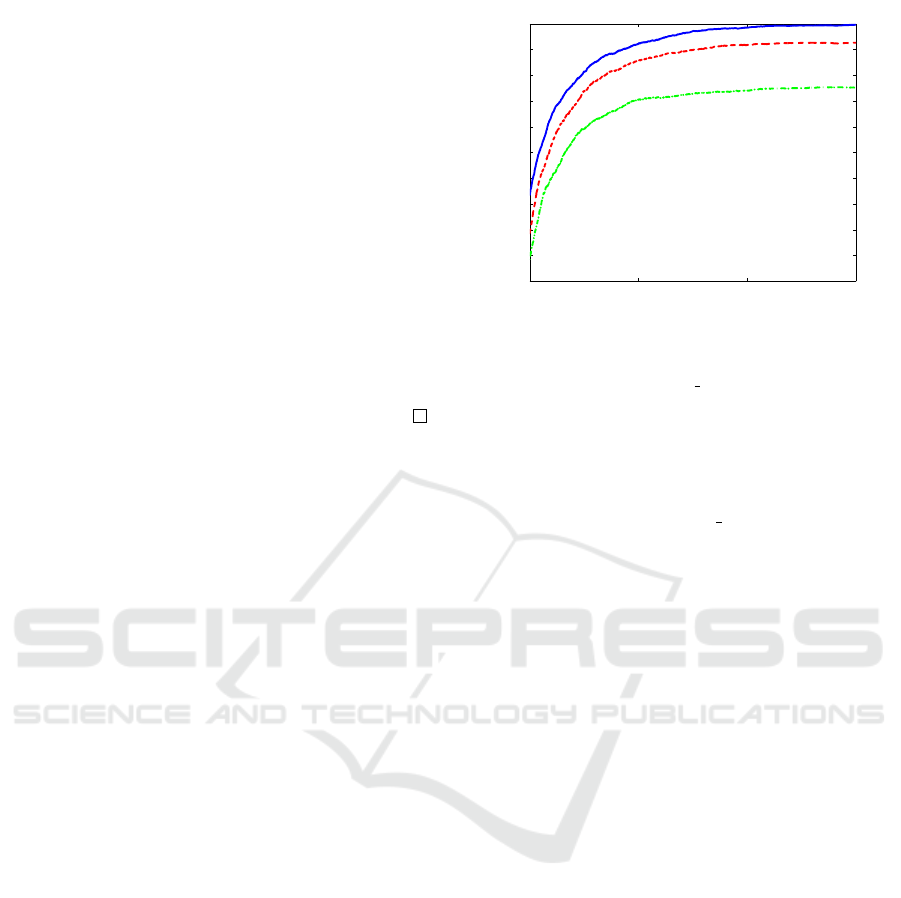
to 1 as t tends to +∞. Figure 1 shows the values of
σ
2
(t) (solid blue line) for values of t between 0 and
1.5 ·10
5
and, as expected, the variance tends to 1 as t
increases. Note that plotted line follows very closely
the expected exponential increase. Let us now consi-
0 5 10 15
x 10
4
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
t
Figure 1: The variance σ
2
(t) of the opinion as a function
of the number of interactions t when f (v, 0) = U
(−1,1)
(v)
(solid blue line), f (v,0) = U
(−
1
2
,1)
(v) (dashed red line), and
f (v, 0) = U
(−1,0)
(v) (dash-dotted green line).
der a multi-agent system where the initial distribution
of the opinion is
f (v,0) = U
(−
1
2
,1)
(v) (41)
so that the value of the average opinion is equal to
u = 1/4. In this case, from Proposition 4, it is ex-
pected that the variance of the opinion tends to 15/16
as t tends to +∞. This result is confirmed in Figure 1,
where the values of σ
2
(t) are shown as a function of
t (dashed red line). As the number of interactions in-
creases, the variance tends to 15/16 = 0.9375, as ex-
pected. Also in this case, the plot approximates well
the expected exponential increase.
Finally, we now assume that the initial distribution
of the opinion in the considered multi-agent system is
f (v,0) = U
(−1,0)
(v). (42)
In this case, the value of the average opinion equals
u = −1/2 and, hence, it is expected that the variance
of the opinion tends to 3/4 as t tends to +∞. Fi-
gure 1 shows that, as expected, the value of the vari-
ance tends to 3/4 = 0.75 (dash-dotted green line), and
the plot follows the expected exponential function.
6 CONCLUSIONS
This paper presented an analytic model of the social
phenomenon of diffusion, which is normally used as
one of the ingredients to study the dynamics of the
opinion in multi-agent systems. First, the adopted ki-
netic framework for the study of opinion dynamics
was recalled. Then, the framework was completed
with the details needed to study diffusion by intro-
ducing specific interaction rules. Adopted rules mo-
del diffusion in terms of a diffusion function and of
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
122

two stochastic diffusion parameters. Under the as-
sumption that the diffusion function is admissible and
that diffusion parameters are admissible for the dif-
fusion function, interesting asymptotic properties of
the multi-agent system were proved. In detail, the pa-
per showed proofs of the fact that diffusion does not
change the average opinion of the multi-agent system,
but that it influences its variance. In the last part of
the paper, a specific diffusion function is considered,
and expected properties of the average opinion and
of the variance of the opinion for the chosen diffu-
sion function were verified by independent simulati-
ons. Note that presented simulations do not depend
on the adopted kinetic approach. They are simple im-
plementations of the studied interaction rules.
The work reported in this paper can be extended
by considering multi-agent systems made of agents
with different propensity to change opinion because
of interactions. In (Bergenti and Monica, 2017), we
have already investigated the possibility of having dif-
ferent classes of agents in the same multi-agent sy-
stem, where different classes are associated with dif-
ferent parameters, such as different number of agents
and different values of the parameters of compromise.
Similar considerations are planned as future work for
the study of collective and asymptotic properties of
diffusion in multi-agent systems with multiple clas-
ses of agents. Finally, the model of diffusion stu-
died in this paper could be coupled with similar mo-
dels of other sociological phenomena, such as com-
promise and homophily, to study analytically the col-
lective and asymptotic properties of more complex sy-
stems. We have already studied the combined effects
of compromise and diffusion under specific assumpti-
ons in (Monica and Bergenti, 2015b), and we plan to
extend such results by modelling other phenomena.
REFERENCES
Bellouquid, A. and Delitala, M. (2006). Mathematical Mo-
deling of Complex Biological Systems. Modeling and
Simulation in Science, Engineering and Technology.
Birkh
¨
auser, Basel.
Bergenti, F. and Monica, S. (2016). Analytic study of opi-
nion dynamics in multi-agent systems with two clas-
ses of agents. In Santoro, C., Messina, F., and Be-
nedetti, M. D., editors, Proc. 17
th
Workshop “Dagli
Oggetti agli Agenti” (WOA 2016), volume 1664 of
CEUR Workshop Proceedings, pages 17–22, Catania,
Italy. RWTH Aachen University.
Bergenti, F. and Monica, S. (2017). An analytic study of
opinion dynamics in multi-agent systems. Compu-
ter and Mathematics with Applications, 73(10):2272–
2284.
Bonabeau, E. (2002). Agent-based modeling: Methods and
techniques for simulating human systems. Procee-
dings of the National Academy of Sciences, 99:7280–
7287.
Chakrabarti, B. K., Chakraborti, A., and Chatterjee, A.
(2006). Econophysics and sociophysics: Trends and
perspectives. Wiley, Berlin.
Cordier, S., Pareschi, L., and Toscani, G. (2005). On a ki-
netic model for simple market economy. Journal of
Statistical Physics, 120:253–277.
De Groot, M. H. (1974). Reaching a consensus. Journal
of the American Statistical Association, 69(345):118–
121.
Deffuant, G., Neau, D., Amblard, F., and Weisbuch, G.
(2000). Mixing beliefs among interacting agents. Ad-
vances in Complex Systems, 3:87–98.
D
¨
uring, B., Markowich, P., Pietschmann, J.-F., and Wolf-
ram, M.-T. (2009). Boltzmann and Fokker–Planck
equations modelling opinion formation in the pre-
sence of strong leaders. Proceedings of the Royal So-
ciety of London A: Mathematical, Physical and Engi-
neering Sciences, 465(2112):3687–3708.
Flache, A., M
¨
as, M., Feliciani, T., Chattoe-Brown, E., Def-
fuant, G., Huet, S., and Lorenz, J. (2017). Models of
social influence: Towards the next frontiers. Journal
of Artificial Societies and Social Simulation, 20(4).
Galam, S., Gefen, Y., and Shapir, Y. (1982). Sociophysics:
A new approach of sociological collective behaviour.
Journal of Mathematical Sociology, 9(1):1–13.
Hegselmann, R. and Krause, U. (2002). Opinion dynamics
and bounded confidence models, analysis, and simu-
lation. Journal of Artificial Societies and Social Simu-
lations, 5(3).
Mark, N. P. (2003). Culture and competition: Homophily
and distancing explainations for cultural niches. Ame-
rican Sociological Review, 68:319–345.
M
¨
as, M. and Flache, A. (2013). Differentiation without dis-
tancing: Explaining bi-polarization of opinions wit-
hout negative influence. PLOS One, 8(11).
M
¨
as, M., Flache, A., and Helbing, D. (2010). Individua-
lisazion as driving force of clustering phenomena in
humans. PLOS One, 6(10).
Monica, S. and Bergenti, F. (2014). A stochastic model
of self-stabilizing cellular automata for consensus for-
mation. In Santoro, C. and Bergenti, F., editors, Proc.
15
th
Workshop “Dagli Oggetti agli Agenti” (WOA
2014), volume 1260 of CEUR Workshop Proceedings,
Catania, Italy. RWTH Aachen University.
Monica, S. and Bergenti, F. (2015a). A kinetic study of opi-
nion dynamics in multi-agent systems. In Gavanelli,
M., Lamma, E., and Riguzzi, F., editors, AI*IA 2015
Advances in Artificial Intelligence, volume 9336 of
Lecture Notes in Computer Science, pages 116–127.
Springer.
Monica, S. and Bergenti, F. (2015b). Kinetic description
of opinion evolution in multi-agent systems: Analy-
tic model and simulations. In Chen, Q., Torroni, P.,
Villata, S., Hsu, J., and Omicini, A., editors, PRIMA
2015: Principles and Practice of Multi-Agent Sys-
tems, volume 9387 of Lecture Notes in Computer
Science, pages 483–491. Springer.
A Stochastic Model of Diffusion in Opinion Dynamics
123

Monica, S. and Bergenti, F. (2015c). Simulations of opi-
nion formation in multi-agent systems using kinetic
theory. In Di Napoli, C., Rossi, S., and Staffa, M., edi-
tors, Proc. 16
th
Workshop “Dagli Oggetti agli Agenti”
(WOA 2015), volume 1382 of CEUR Workshop Pro-
ceedings, pages 97–102. RWTH Aachen University.
Monica, S. and Bergenti, F. (2016a). An analytic study of
opinion dynamics in multi-agent systems with addi-
tive random noise. In Adorni, G., Cagnoni, S., M., G.,
and Maratea, M., editors, AI*IA 2016 Advances in Ar-
tificial Intelligence, volume 10037 of Lecture Notes in
Artificial Intelligence, pages 105–117. Springer.
Monica, S. and Bergenti, F. (2016b). A study of consensus
formation using kinetic theory. In Distributed Com-
puting and Artificial Intelligence, 13
th
International
Conference, volume 474 of Advances in Intelligent Sy-
stems and Computing, pages 213–221. Springer.
Monica, S. and Bergenti, F. (2017a). Opinion dynamics
in multi-agent systems: Selected analytic models and
validating simulations. Computational and Mathema-
tical Organization Theory, 23(3):423–450.
Monica, S. and Bergenti, F. (2017b). Outline of a genera-
lization of kinetic theory to study opinion dynamics.
In Distributed Computing and Artificial Intelligence,
14
th
International Conference, volume 620 of Advan-
ces in Intelligent Systems and Computing, pages 301–
308. Springer.
Monica, S. and Bergenti, F. (2017c). Two analytic models
of compromise in multi-agent systems. In Berndt, J.,
Petta, P., and Unland, R., editors, Proc. 15
th
German
Conference on Multiagent System Technologies (MA-
TES 2017), volume 10413 of Lecture Notes in Artifi-
cial Intelligence, pages 38–53. Springer.
Nowak, A., Szamrej, J., and Latan, B. (1990). From private
attitude to public opinion: A dynamic theory of social
impact. Psychological Review, 97:362–376.
Pareschi, L. and Toscani, G. (2013). Interacting Multiagent
Systems: Kinetic Equations and Montecarlo Methods.
Oxford University Press.
Pineda, M., Toral, R., and Hernandez-Garcia, E. (1982).
Noisy continuous-opinion dynamics. Journal of Sta-
tistical Mechanics, 9:1–13.
Schweitzer, F. and Holyst, J. (2000). Modelling collective
opinion formation by means of active brownian parti-
cles. European Physical Journal B, 15:723–732.
Slanina, F. (2004). Inelastically scattering particles and we-
alth distribution in an open economy. Physical Review
E, 69:46–102.
Toscani, G. (2000). One-dimensional kinetic models of
granular flows. ESAIM: Mathematical Modelling and
Numerical Analysis, 34:1277–1291.
Toscani, G. (2006). Kinetic models of opinion formation.
Communications in Mathematical Sciences, 4:481–
496.
Tsang, A. and Larson, K. (2014). Opinion dynamics of
skeptical agents. In Proc. 13
th
Int. Conf. Autonomous
Agents and Multiagent Systems (AAMAS 2014), pages
277–284, Paris. International Foundation for Autono-
mous Agents and Multiagent Systems.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
124
