Impact of Service Interruptions and the Variability of Service Time in

Queueing Systems: Numerical Investigations

Yang Woo Shin

and Dug Hee Moon

Department of Statistics, Changwon National University, Changwon, Gyeongnam 51140, Korea

School of Industrial Engineering and Naval Architecture,

Changwon National University, Changwon, Gyeongnam 51140, Korea

Keywords:

Service Interruptions, Variance Rate, Departure Process, Finite Buffers.

Abstract:

In this paper, we consider the queueing systems with ﬁnite buffer and service interruptions. The effects of

service interruptions and the variability of service time to measure of departure process such as the asymptotic

mean and variance of the number of departures are investigated numerically. We ﬁnd numerically so called

interruption paradox or failure paradox that the departure rate of the system with service interruptions under

preemptive-repeat-different policy can be greater than that of the system with reliable server and it increases

as the interruption rate increases for the case of large variability of service time. The results give an insight for

the effects of the system and may be helpful to design and control the more complex systems.

1 INTRODUCTION

Queueing networks that consist of nodes with ﬁnite

buffer and service interrup tions have been widely

used for modeling and analysis of the system ari-

sing from many practical situations such as computer

systems, telecommu nications and manufacturing sy-

stems. The network topology and th e characteristics

of each node such as buffer size, service time a nd the

interactions b etween interruptions and service affect

not only the performances of each node but also the

the performance of whole network.

The m ean number of customers, blocking proba-

bility of arriving customers and the idle pr obability

of the server are important performance me asures of

each node. Besides on the intern al measures of each

node, the measures related with departure process of

each node are also important to understand and ana-

lyze the whole network performance . In particula r,

the amount of pr oduction in the manufacturing sy-

stem is presented by the num ber of depar tures from

a terminal node of a network. T he long run average

of departure s, called departure rate or throu ghput is

an important measure of performa nce in manu factu-

ring system. The ﬁrst order measures can be used to

get information about the ca pabilities of a system in

the long run. However, there may be treme ndous va-

riability of the departures from a time period to pe-

riod even in a simple queueing network (Gershwin,

Section 3.2, 1994). Thus the second order measures

such as the variance of the number of depa rtures in a

given time per iod, called variance rate are also very

useful to design and control the systems in a more

effective way. For a review of recent studies on the

variance of the departures for production systems, re-

fer to the paper Tan (2013) and Lagershausen and Tan

(2015). Recently, Shin and Moon (2016,2 017) pre-

sent an algorithmic method for asymptotic variance

rate of departure process of the system with two-node-

one buffer system using the Markovian a rrival pro-

cess.

Interru ptions in queueing systems are the ele-

ments that prevent th e c ontinuous service of custo-

mers. Queueing models with service interruptions

have been used to model the situation s where a ser-

vice facility is shared by multiple queues, or where

the facility is subject to failure. Such in te rruption s

may be caused by breakdowns of the servers, arrival

of customers of a higher-priority class or scheduled

off-periods by extra jobs. Queueing models with ser-

vice interruptions and their connection with priority

models or machine brea kdowns have been studied ex-

tensively in the literature, e.g. see White and Chris-

tie (1958), Gaver (1962), Nicola (1986), Fiems etc.

(2008), Sahba et al. (2015) and refer to the survey

paper Krishnamoorthy et al. (2014) fo r mo re details.

The M/G/1 queue with a single type of Poisson inter-

ruption s was dealt with extensively by Gaver (1962)

Shin, Y. and Moon, D.

Impact of Service Interruptions and the Variability of Service Time in Queueing Systems: Numerical Investigations.

DOI: 10.5220/0006633202790286

In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 279-286

ISBN: 978-989-758-285-1

279

for a variety of serv ice-interruption interactions. The

analysis was based on the deﬁnition of the comple-

tion time. He derived the Laplace Stieltjes transfo rm

(LST) of the completion time that is the time interval

between the instant at which the customer’s service

begins and the instants at which the service of the next

customer (if any exists) may begin and used the met-

hod of imbedded Markov chain to obtain the genera-

ting function of the distribution of the number of cus-

tomers in the system. Nicola (1986) derives the LST

of completion time for the case with the simultaneous

presence of d ifferent type s of interruptions. The lite-

rature cited above deal with the inﬁnite buffer queue

and focus on analyzing the stationary distribution of

the number of customers in the system, waiting time

distribution and related performance measures such

as the mean number of customers in the system and

blocking probability.

However, the articles reviewed above do not inves-

tigate the effects of intera c tions betwe en interruptions

and variability of service time to the system perfor-

mances. In this paper, we consider the queueing sy-

stems with ﬁnite buffer and serv ic e interr uptions and

investigate numerically the effects of service interrup-

tions and the variability of service time to measure of

departure process such as the asymptotic mean and

variance of the number o f departures. Numerical re-

sults give an insight for the effects of the system and

play an important role to pre pare the analysis of the

extended system of that considered in this present.

This paper is organized as follows. In Section 2,

types of interruptions and preliminary results for com-

pletion time given by Gaver (1962) are presented. Th e

effects of interruptions and variability of service time

to the departure rate and variance rate in the saturated

system and M/PH/1/K queue are investigated nume-

rically in In Sections 3 and 4 . Concluding remarks are

given in Section 5.

2 ASSUMPTIONS AND

PRELIMINARY RESULTS

Consider the single server system with service inter-

ruption s. In this section, some assumptions and preli-

minary results to be used later are described.

Service time. Service times of successive cu-

stomers are indepen dently and identically distribu-

ted with arbitrary distribution. Denote the generic

random variable of service time by B and B(x) =

P(B ≤ x) a nd B

∗

(s) = E[e

−sB

], s ≥ 0. Let E[B

] = b

k = 1,2 and denote the squared coefﬁcient of variation

(SCV) of B by c

= Var[B]/b

Interruption. Interruptions appear ac cording to a

Poisson process with rate ν a nd e a ch interruption re-

quires ran dom time to clear the effects of this particu-

lar interru ption to th e server. Successive durations are

indepen dent r andom variables, identically distributed

with arbitrar y d istribution function and denote the ge-

neric random variable of the duration of interruptio n

by R. Let R(x) = P(R ≤ x) a nd R

∗

(s) = E[e

−sR

], s ≥ 0

and E[R

] = r

, r = 1, 2. We assume that the in ter-

ruption process is independent of the arrival process

of customers and the number of customers waiting in

line, and the elapsed time since the initial instant.

The interruption occurs only when the server is

actually working and it does not occurs during the pe-

riod while the server is id le or it is in state of inter-

rupted (durations of interruption). This type of inter-

ruption is called active interruptio n (AI) or opera tion

dependent interruption (ODI). The AI can b e classi-

ﬁed into two categories, say postponable interrupti-

ons ( PI) and preemptive interruption (PR). When a PI

appears during a service time, it does not take effect

until the end of the service time. All of the interrup-

tions ac cumulated during that service time must then

be cleared before service of next customer maybegin.

Under the PR policy, customer’s service is preempted

immediately upon the arrival of interruption. In this

presentation, we consider only the PR.

Completion Time. A completion time is the time

period between the instant at which the customer ’s

service begins a nd th e instants at which the service of

the next customer (if any exists) may begin. This pe-

riod is the sum of the customer’s service time and th e

durations of the interruptions occurring in that time.

Let C be the completio n time, and denote by C(x) and

∗

(s) the distribution function of C and its LST, re-

spectively.

The completion time may depend on the ways

of occurrence and clearance of interruptio ns. Gaver

(1962) proposed various types o f interruptions and

derive the LST’s, the ﬁrst and second mom e nts of

completion time in each case. Here, some of the re-

sults are summarized in the following for later use.

Let

E =

1/ν

1/ν + E[R]

1 + νr

The quantity E is sometimes called an efﬁciency of

the server in a m anufacturing system, e.g. see Gers-

hawin (1994).

(i) Preemptive-resume (PRS) Interruptions. In a

PRS policy, when an interruption is cleared, service is

continued from the poin t at which it was interrupted.

The LST and the mean and variance of completion

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

280

time are given by

∗

(s) = B

∗

(s + ν− νR

∗

(s)),

E[C] =

Va r[C] =

Va r[B]

+ νb

(ii) Preemptive-repeat-different (PRT-D) Interrup-

tions. In this case, when an interru ption is cleared,

service begins again from scratch , but each time anot-

her inter ruption is cleared a new independent (poten-

tial) service time whose distribution function is B(x)

begins. Service is completed when, for the ﬁrst time,

such a service time elapses without interruption.

∗

(s) =

∗

(s + ν)

1 − R

∗

(s)

s+ν

(1 − B

∗

(s + ν))

E[C] =

νE

1 − B

∗

(ν)

∗

(ν)

Va r[C] = (E[C])



νEr



E[C]

−

νE

E[Be

−νB

]

∗

(ν))

(iii) Preemptive-repeat-identical (PRT-I) Inter-

ruptions. In this case, when the interruption is cle-

ared, a service period of the same duration as the one

interrup te d begins again from scratch. Service is com-

pleted (completion time terminates) when, for the ﬁrst

time, a (repeated) serv ic e period elapses without in-

terruption. The L ST and the mean and variance of

completion time are given by

∗

(s) =

∞

−(s+ν)x

1 − R

∗

(s)

s+ν

(1 − e

−(s+ν)x

)

dB(x),

E[C] =

νE

(E[e

νB

] − 1),

Va r[C] =



Va r



νB

− 1



+ E



νB

− 1)





νEr



E[C] −

νE

E[Be

νB

where the expectations may not exist.

3 ASYMPTOTIC RATE FOR THE

NUMBER OF DEPARTURES IN

A SATURATED SYSTEM

Consider a single server system that is saturated a nd

never blocked. Th at is, the server always work s unless

it is down state and the customer leaves the sy stem

immediately after the service without blocking.

Let N(t) be the number of service completions du-

ring an interval (0 , t]. Th en N

N = {N(t), t ≥ 0} is a re-

newal pr ocess whose inter-renewal distribution is the

same as the comp letion time C. It follows from the

well known results of the re newal theory ( e.g. see

Cox (page 58, 1962)) that the lo ng run average num-

ber of departures and the variance rate of N

N are given

µ = lim

t→∞

E[N(t)]

E[C]

V = lim

t→∞

Va r[N(t)]

Va r[C]

(E[C])

Indeed , the distribution of N(t) is asymptotically nor-

mal with mean µt and variance Vt, i = 1,2.

Now, we investigate the effects of the interactions

between interruptions and service time, interruption

rate ν and the variability of service time to the depar-

ture rate µ and variance rate V . The PH-distributiion

(PH) and lognormal distribution (LN) of service ti-

mes and exponential distribution of duration R of an

interrup tion with rate η are considered. The mea n ser-

vice time and the efﬁciency of the server is ﬁxed by

= 1.0 and E = 0.85 and the repair rate is deter-

mined by η =

νE

1−E

ν for interruption rate ν > 0.

For PH-distribution, we use the Erlang distribution of

order k (E

) for C

< 1, exponential distribution

(Exp) for C

= 1 and hyperexponential distribution

of order 2 with b a la nced mean for C

> 1 denoted by

,λ

) whose probab ility density fun c tion is

f (t) = p

−λ

+ p

−λ

, t ≥ 0,

with λ

= 2p

µ, λ

= 2p

µ and

1 +

− 1

+ 1

, p

= 1 − p

Preemptive-resume versus preemptive-repeat-

different. The departu re rate µ as a f unction of c

for

the various interruption ra te ν ar e depicted in Figure

1. The ﬁgures show that the departure rates of the

systems with reliable server (ν = 0.0) and the server

with PRS policy ( denoted by Type 1) do not depend

on the SCV of service time. However, the departure

rate µ

of the system with PRT-D policy increases

as c

increases for each ν and it can be greater than

the service rate µ = 1 .0 of reliable server (ν = 0.0).

Furthermore, the departure rate increases as th e

interrup tion r ate increases for large c

. These seems

surprising and we shall phrase it the interruption

paradox or failure paradox. We have found that these

results holds for Weibul distribution and gamma

distribution of service time although the results are

not presented in this paper.

Impact of Service Interruptions and the Variability of Service Time in Queueing Systems: Numerical Investigations

281

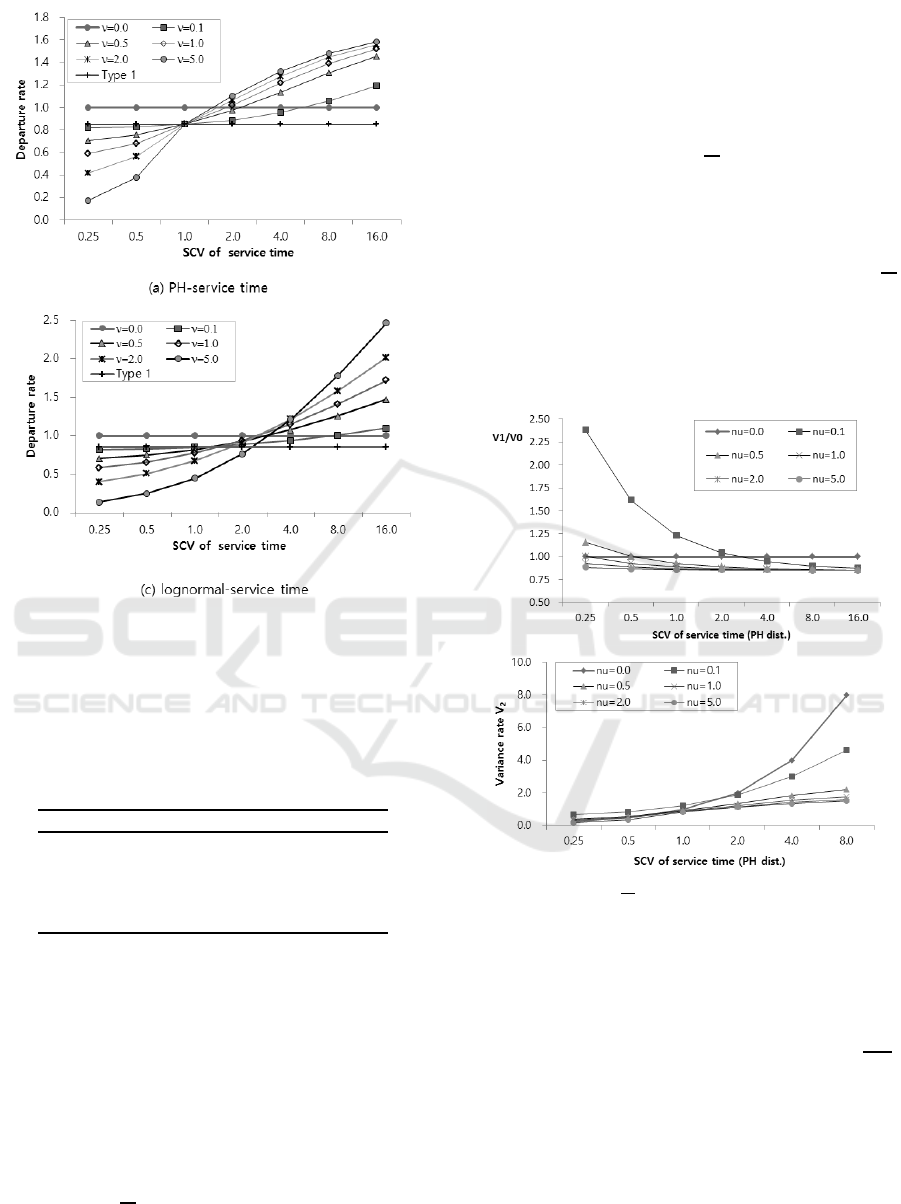
Figure 1: Departure rate as a function of SCV C

The reason of failure par adox can b e exp lained

as follows. The parameters of hyperexponential dis-

tribution H

,λ

) with mean 1.0 are listed in

Table 1.

Table 1: Parameters for H

,λ

)

1.0 0.5000 0.5000 1.0000 1.0000

2.0 0.7887 0.2113 1.5774 0.4227

4.0 0.8873 0.1127 1.7746 0.2254

8.0 0.9410 0.0590 1.8819 0.1181

16.0 0.9697 0.0303 1.9393 0.0607

It can be seen from Table 1 that p

approa c h to

1.0, and λ

increases and is greater than the service

rate 1.0 and λ

decreases as SCV increases. When a

service time of a customer is assigne d to long service

time corresponding to the rate λ

, the service time can

be interr upted by a failure and the server starts a new

service with short service time corresp onding to λ

with high probability p

. Thus a failure can make the

service time be shorter than that of the system with

reliable server.

The ratios

between the variance rate V

of the

noninterrupted system and V

of the system with PRS

policy and the variance rate V

of the system with

PRT-D policy for the system with PH-service time

are depicted in Figure 2. The ratios V

tends to

E = 0.85 as C

increases which can be expected from

the formula V

. The variance rate V

of the sy -

stem with PRT-D policy increases as SCV c

of ser-

vice time increases, but V

is less than V of the reliable

system for C

> 1. The ratio

are depicted in Figure

3. It can be seen from the ﬁgures 3 that the variance

rate V

depends severely on the distribution of service

time. We have seen from extensive numerical expe-

riments that the variance rate V

depends severely on

the distribution of service time. The variance ratio

decreases and becomes less than 1.0 for the system

with H

and Weibul distribution of service time, ho-

wever, it increases and becomes greater than 1.0 for

the system with g amma distribution of service time

as CSV of the service time increases.

Figure 2: The ratios

for the system with PH service time.

Preemptive-repeat-identical versus preemptive-

repeat-different. In case of preemp tive-repeat-

identical policy, the expectation E[e

νB

] for E[C] exists

if 1 − B(x) = o(e

−cx

) with t → ∞ for 0 < ν < c. For

example, if the distribution o f service time is gamma

distribution, then the expectations exist for ν <

If the distribution of B is Weibul, the the expec ta tion

exists only for c

< 1. If B has lognormal distribution,

then the expectation does not exist. Let E[C

] and

E[C

] denote the expectations of C f or the ca ses of

PRT-I and PRT-D, respectively. It can be easily seen

from the formulae E[C

] and E[C

] that E[C

] > E[C

]

is equivalent to

∗

(ν)B

∗

(−ν) > 1. (1)

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

282

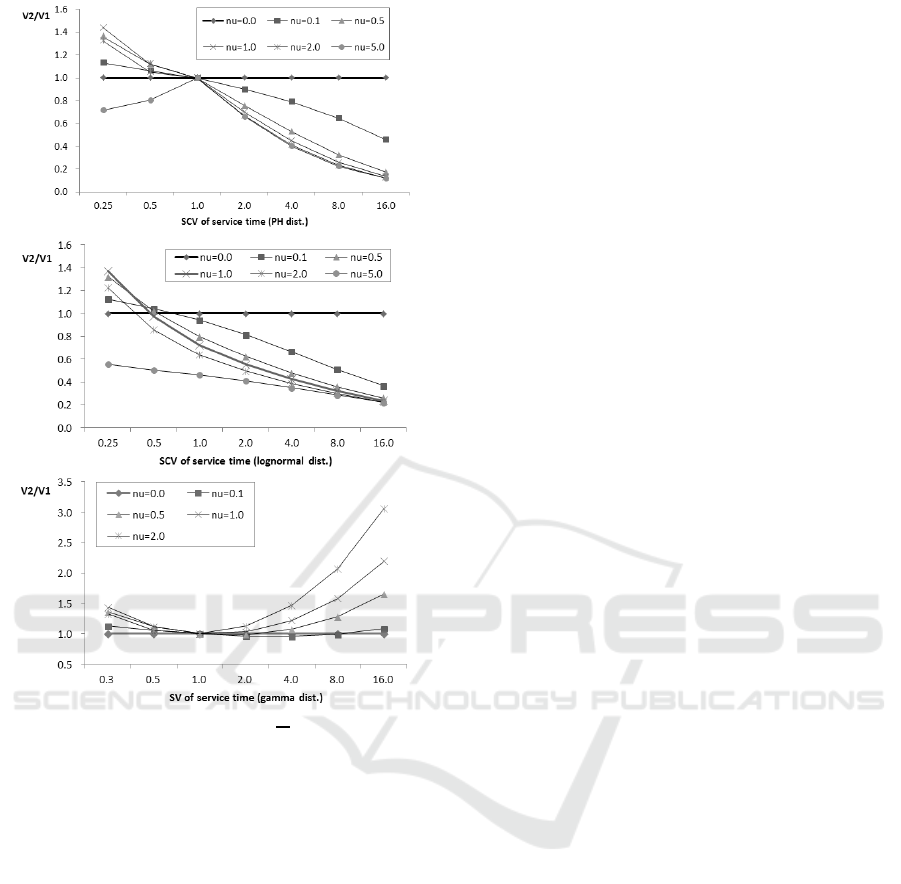
Figure 3: The ratio

It can be seen from th e formula B

∗

(s) = (1 −

−1/c

of L ST that gamma distribution and the

condition of existence of E[C

] < ∞ that gamma dis-

tribution satisﬁes (1). We showed numerically that

the Weibul distribution with c

< 1 satisﬁes (1) for

any ν > 0, but we omit the details here.

4 M/PH/1/K QUEUE WITH

SERVICE INTERRUPTIONS

4.1 Model

We conside r a M/ PH/1/K queue with service inter-

ruption an d a buffer of ﬁnite capacity K in which cu-

stomers arrive according to a Poisson process with

rate λ. Interru ptions occurs only while the server is

working. The inter occurr e nce time of interruption

is a ssumed to be exponential distribution with rate ν.

The service time and duratio n of interruption are as-

sumed to be of phase type distributions PH(α

α,S) and

PH(γ

γ,G), respectively. Let s

= −Se and g

= −Ge.

Let w and r be the number of phases of the distri-

butions of servic e time and duration of interruption,

respectively.

Let X (t) be the number of customers in the system

at time t. The state space of X(t) is {0, 1,·· · ,K}. By

(t) and J

(t)) deno te the phases of PH(α

α,S) and

PH(γ

γ,G), respectively at time t. The state M(t) of the

server M at time t is

M(t) =



(t), the server is up at time t

(t),J

(t)), the server is down at time t

Let [D

]

i j

([D

∗

]

i j

) be the rate that a transition of M(t)

occurs from i to j and no service is completed given

X(t) ≥ 1 (X(t) = 0,respectively) and [D

]

i j

([D

∗

]

i j

)

be the rate that a transition of M(t) occurs from i to

j and a service is completed given X (t) ≥ 2 (X(t) =

1,respec tively). Let M (M

∗

) be the state space of

M(t) for X(t) ≥ 1 (X(t) = 0, respectively) a nd m and

∗

be the number of elements of M and M

∗

, re-

spectively. Let P

be the m

∗

× m matrix whose (i, j)-

component [P

]

i j

is the probability that the p hase of

M is j immediately after an arrival occur s given that

X(t) = 0 and M(t) = i. The matrices D

and D

de-

pends on the service initiation policies after clearance

of interruption .

We consider the following three policies of initia-

tion of service when an interruption is cleared.

policy. Whe n an in te rruption is cleared, service

resume at the last phase in which a failure occurs. In

this case, m = w(r + 1) and m

∗

= 1 and



−νI

+ S νI

⊗γ

⊗ g

⊗ G





α O

O O

wr×wr



, D

∗



wr×1



and D

∗

= 0, P

= (α

α O

1×wr

), where O

k×n

is the ze ro

matrix of size k × n an d I

is the identity matrix of

size n.

policy. When an interruption is cleared, new

service starts anew according to a PH-distribution

PH(α

α,S). In this case, m = w + r and m

∗

= 1 and



−νI

+ S νe

α G





α O

O O

r×r



, D

∗



r×1



and D

∗

= 0, P

= (α

α O

1×r

policy. When an interruption occ urs, the cu-

stomer being served is scrapped, and the server be-

gins new service of length whose distribution is of

Impact of Service Interruptions and the Variability of Service Time in Queueing Systems: Numerical Investigations

283

PH(α

α,S) after clearance of interruption. In this case,

m = w + r and m

∗

= r + 1 and



−νI

+ S O

w×r

α G



, D

∗



0 O





α νe

O O

r×r



, D

∗



νe

O O

r×r





α O

O I



Let Z(t) = (X(t),M(t)). The stochastic process

Z = {Z(t), t ≥ 0} forms a Markov chain with genera-

tor of the form

Q =







K−1







Then the block matrix components are as follows:

= −λI

∗

+ D

∗

, B

= D

, A

= λP

, C

= D

∗

= −λI

+ D

, A

= λI

, 1 ≤ n ≤ K − 1,

= D

, 2 ≤ n ≤ K.

4.2 Departure Process

Let N(t) be the number of service completions in

the system. Then N

N = {N(t), t ≥ 0} is a Mar-

kovian arrival process (MAP) with representation

MAP(D

), where the matrices D

and D

are as

follows:

(1) S

and S

policies.







K−1



















and O is the zero matrix of appropriate size.

(2) S

policy. For the system with scrapping ,







1,0

K−1,0

K−1

K,0













1,1

2,1

K,1







where

1, j

= D

∗

1, j

, C

n, j

= D

1, j

, 2 ≤ n ≤ K, j = 0,1,

and

1,0



w×w

νe

O O

r×r



1,1



α O

O O

r×r



∗

1,0



w×1

νe

O O

r×r



∗

1,1



O O

r×r



A Markovian arrival process (MAP) with repre -

sentation MAP(D

) is a countin g process whose

inter even t time distribution is of the form

F(t) =

exp(D

u)duD

, t ≥ 0.

For details of MAP, see Lucantoni (1991) or Artalejo

et al. (2010).

Let π

π = (π(x),x ∈ S ) be the stationary distribution

of D = D

+ D

and

c = π

πD

(eπ

π− D)

−1

, d = (eπ

π− D)

−1

It is known that (e.g. Neuts,Theorem 5.4.1, 5.4.2,

1989; Artalejo et al., 20 10) in stationary state, the

mean and th e variance of N(t) are given as follows:

E[N(t)] = µt,

Va r[N(t)] = Vt + 2 (µ

− cd) + o(1).

where µ = π

πD

e and

V = µ − 2µ

+ 2cD

One can refer to Shin and Moon (2016, 2017) for an

algorithm for computing µ and V , the mean and vari-

ance of inter departure time, and the covariance bet-

ween inter departure times.

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

284

4.3 Numerical Results

In this subsection , we investigate the effects of the in-

teractions between the interruptio ns and service time

and the variability of ser vice time to the departure rate

and variance rate of departure process in M/PH/1/5

queue with arrival rate λ = 1.0, mean service time

= 1.0 and E

= 0.85. We use the Erlan g distri-

bution of order k (E

) for c

< 1, exponential

distribution (Exp) for c

= 1 and hype rexponential

distribution of order 2 with balanced mean for c

> 1.

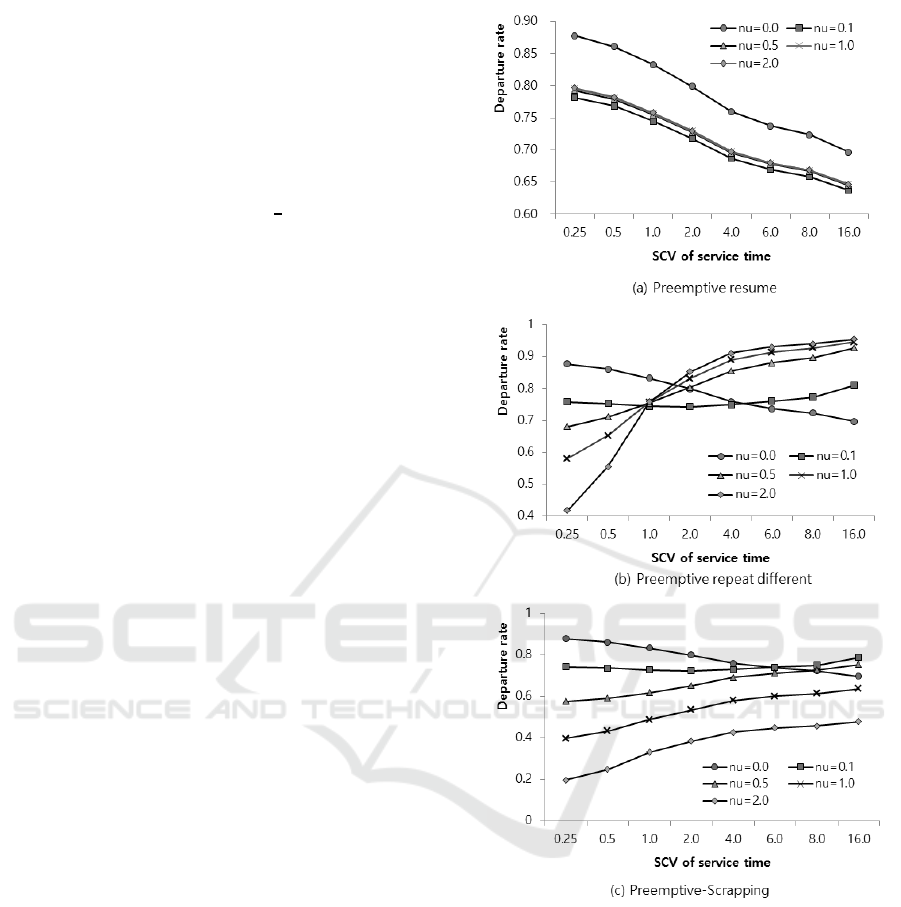
The comparisons of departure rates for the ser-

vice policies S

, S

and interruption free system

(ν = 0.0 ) are presented in Figure 4. It can be seen

from the ﬁgure that the departu re rate f or the system

with S

policy increases and can be greater than the

isolated efﬁciency while the departure ra te decreases

in the system with S

policy and reliable system as

SCV c

of service time increases. It can be a lso seen

from the ﬁgure that the departure rate of the system

with scrap can be greater than tha t of reliable system

as SCV of service time increases.

Denote the variance rates for S

by V

, i = 1,2,3

and let V

be the variance rate for interruption free

system (ν = 0). Here, the variance rates V

and V

are depicted in Figure 5. We can see from the ﬁgure

that the variance rates increase in both types of service

initiation policies as c

increases. It also can be seen

that V

> V

for c

sufﬁciently greater than 1.

Furthermore, V

decreases as ν increases for c

> 1.

We also can see from the ﬁgure that the behaviors V

are similar to those of V

5 CONCLUSIONS

In this study, the effects of struc tural parameters such

as the variabilities of service and the interactions bet-

ween interruptions and service time to th e departure

rates and variance rates have been investigated nu-

merically. We have observed from numerical experi-

ments th at the variance rate of departures increases as

the SCV of the service time increases. However, the

departure rate in the system with interruptions can be

greater than that of the interruption free system and it

can increase as the interruption rate increase for large

SCV of service time. This result is different fr om the

case of the system with reliable servers in which the

departure rate decreases as SCV’s of ser vice times in-

crease. We have coined this surprising results the in-

terruption paradox or failure paradox. The effects of

interrup tion rate to the departure rate and variance rate

are dependent of the SCV’s of service time.

Figure 4: Departure rate as a function of SCV c

It rema ins to analyze the more complicated sy-

stem su ch as the queueing system with more g e ne-

ral arrival and/or service time a nd queueing networks

with interruptions as furth er research area. Nume ri-

cal results give some insights for the more co mplica-

ted systems. So, our experiments may be helpful to

design and c ontrol the system with interrup tions an d

may play a usef ul role to prepar e the analysis of the

extended systems.

Impact of Service Interruptions and the Variability of Service Time in Queueing Systems: Numerical Investigations

285

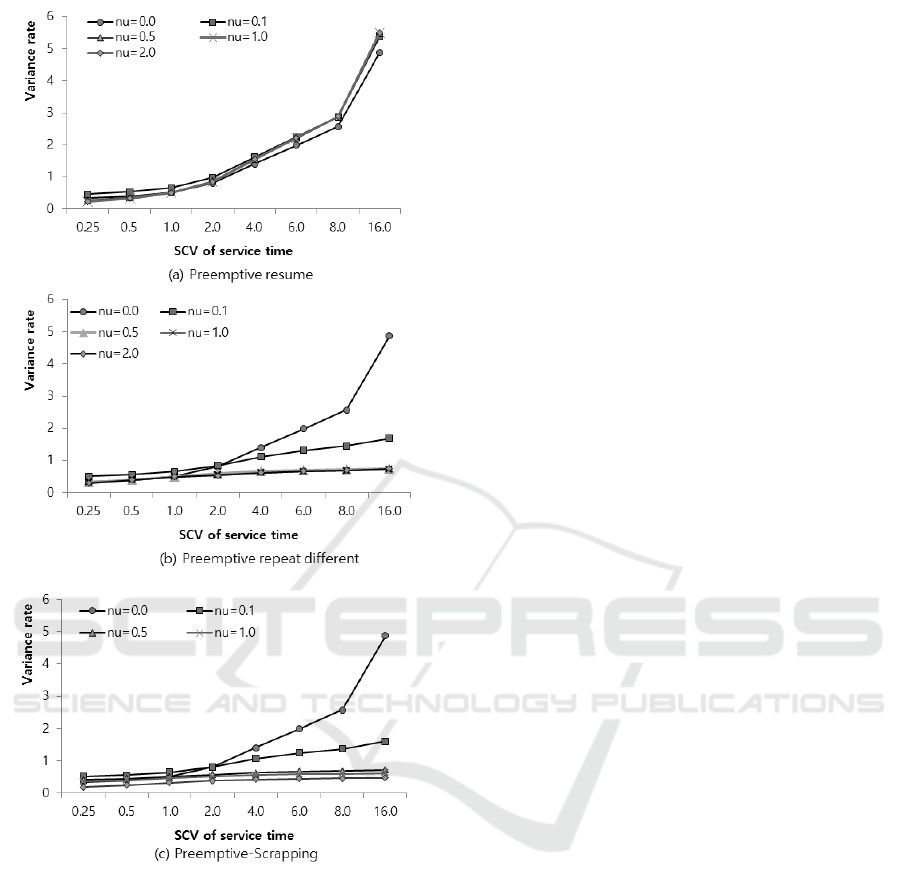
Figure 5: Variance rate as a function of c

REFERENCES

Artalejo, J. R., G´omez-Corral, A., He, Q. M. (2010). Mar-

kovian arrivals in stochastic modelling: a survey and

some new results, SORT 34 (2), 101-144.

Gaver, D. Jr. (1962). A waiting line with interrupted ser-

vice, including priorities, Journal of the Royal Statis-

tical Society, Series B24, 73-90.

Gershwin, S. B. (1994). Manufacturing systems engineer-

ing. Prentice-Hall, Englewood C liffs.

Krishnamoorthy, A., Pramod, P. K., Chakravarthy, S. R.

(2014) Queues with interruptions: a survey, TOP

22(1), 290-320.

Lagershausena, S., Tan, B. (2015). On the exact inter-

departure and inter-start time distribution of closed

queueing networks subject to blocking, IIE Transacti-

ons 47, 673-692

Lucantoni, D. M., Meier-Hellstern, K. S., Neuts, M. F.

(1990). A single server queue with server vacations

and a cl ass of non-renewal arrival processes, Advan-

ces in Applied Probability 22, 676-705.

Narayana, S., Neuts, M. F. (1992). The ﬁrst two moment

matrices of the counts for the Markovian arrival pro-

cess, Stochastic Models 8(3), 459-477.

Neuts, M. F. (1989). Structured Stochastic Matrices of

M/G/1 Type and Their Applications. Marcel Dekker,

New York.

Nicola, V. F. (1986). A single server queue with mixed types

of interruptions, Acta Informatica 23, 465-486.

Sahba, P., Balco˜glu, B. Banjevic, D. (2015). The im-

pact of disruption characteristics on the perfor-

mance of a server, Annals of Operations Research,

https://doi.org/10.1007/s10479-015-2075-2, pp1-14.

Shin, Y. W., Moon, D. H. (2016). Variability of output

in two-node t andem production line. Proceedings of

QTNA 2016, December 2016, Wellington, New Zea-

land, pp. 13-15.

Shin, Y. W., Moon, D. H. (2017). Variance of departure pro-

cess in two-node tandem queue with unreliable server

and blcking. Proceedings of ICORES 2017, February

2017, Porto, Portugal, pp. 258-264.

Tan, B. (2013). Modeling and analysis of output variabi-

lity in discrete material ﬂow production systems. In

Handbook of Stochastic Models and Analysis of Ma-

nufacturing System Operations. Tan,B. and Smith, J.

M. (eds), Springer, New York, pp. 287-311.

White, H., Christie, L. (1958). Queuing with preemp-

tive priorities or with breakdown, Operation Research

6(1), 79-95.

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

286