
Optimizing Storage Capacity of Retailers in Stochastic Periodic
Inventory Routing Problem
Ehsan Yadollahi
1,2
, El-Houssaine Aghezzaf
1
, Joris Walraevens
2
and Birger Raa
1
1
Department of Industrial Systems Engineering and Product Design,
Faculty of Engineering and Architecture, Ghent University, Gent, Belgium
2
Department of Telecommunications and Information Processing (TELIN),
Faculty of Engineering and Architecture, Ghent University, Gent, Belgium
Keywords: Safety Stock, Storage Capacity Limitation, Stochastic Demands, Inventory Routing Problem.
Abstract: A challenging question in Stochastic Periodic Inventory Routing Problem (SPIRP) is how to deal with
stochastic demand rates, while minimizing the costs (transportation, inventory, and storage) and finding the
best routing system. In this paper, we reformulate the SPIRP model to a safety stock-based SPIRP where the
inventory storage capacity at the retailers are considered as variables and retailer’s demand rate is stochastic.
The supply chain planner needs to find the best routing system to replenish the retailers with the most optimum
level of inventory, while the service level is satisfied in a long term planning horizon. Four different policies
for storage capacity optimization are presented, evaluated, and compared in an illustrative example. The
impact of storage capacity limitation is considered based on the defined policies to measure their compatibility
for different situations.
1 INTRODUCTION
Inventory-Routing Problem (IRP) integrates
inventory management and vehicle routing decisions
over several periods and has received increased
attention in recent years (Aghezzaf, 2007, Bertazzi et
al., 2013, Yadollahi et al., 2017, Federgruen and
Zipkin, 1984, Bell et al., 1983). Bell et al., (1983) are
one of the first researchers who used VRP and
inventory management together to deal with the case
where only transportation costs are included, demand
is stochastic, and customer inventory levels must be
met. Demand stochasticity means that shortages may
occur since the supplier only knows a probabilistic
distribution of demand for the retailer. To avoid
having stock-outs, a penalty is imposed whenever a
retailer runs out of stock, and this penalty is usually
paid with the unsatisfied demand (negative
inventory). Unsatisfied demand is either considered
as lost-sale or backlogged. More explanation about
IRP and SPIRP can be found in (Coelho et al., 2014a,
Coelho et al., 2014b).
Variability of service, uncertainty in demand, and
delay are the well-known characteristics of SPIRP.
The trade-off between costs (transportation and
inventory) and products’ availability makes SPIRP a
hard problem to solve. Even though there is a
noticeable body of literature about IRP and SPIRP,
only few studies have involved capacity limitation as
constraints. Stacey et al., (2007) are one of the
pioneers in specifying the significance of storage
capacity on both the routing and inventory decisions
in the context of inbound transportation. They have
evaluated the benefits of applying storage constraints
at different levels by developing two new heuristics
that sequentially take into account the inventory level
and routing decisions.
Pujawan et al., (2015) have proposed a new
method to integrate operational and strategic decision
parameters, namely shipment planning and storage
capacity decision under uncertainty. Their objective
is to provide a close to optimal solution to find the
best balance for logistics cost and product
availability. The authors develop a simulation model
to investigate the effects of various indicators on costs
and service levels in a distribution system. The model
mimics the transportation and distribution problems
of bulk cement, consisting of a silo at the port of
origin, two silos at two ports of destination, and a
number of ships that transport the bulk cement. The
outcome of their model clarifies the significant effect
of the number of ships deployed, silo capacity,
Yadollahi, E., Aghezzaf, E-H., Walraevens, J. and Raa, B.
Optimizing Storage Capacity of Retailers in Stochastic Periodic Inventory Routing Problem.
DOI: 10.5220/0006620302170223
In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 217-223
ISBN: 978-989-758-285-1
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
217

working hours of ports, and the dispatching rules of
ships on both total logistics costs and service level.
Finding the appropriate storage capacity is one of
the main objectives of SPIRP that desires more
investigation. The comparison between small and big
storage capacity can be assessed from several
different aspects such as costs, service level, silo
availability, product’s perishability, etc. In addition,
different options for storage capacity at the retailers
with different costs makes it more challenging for the
supply chain decision maker to find the most
optimum solution.
The idea of having the capacity optimized is a new
concept in SPIRP and has not been treated completely
in the literature. In this paper by involving storage
capacity constraints into SPIRP, we develop the
solutions to deal with stochasticity in demand rates
and costs minimizations while service level is
satisfied. Four different policies for storage capacity
allocation are considered in this paper. The strategies
are evaluated and compared by implementing them
on an illustrative example based on two indicators
namely costs and computation time. The outcome of
these solutions are discussed in details for the short
and long term planning horizon in order to have a
better insight of their influence on the whole system.
The rest of the paper is organized as follows;
section 2 presents the Safety Stock-based SPIRP
together with the different approaches for the capacity
optimization. In section 3, we explain all the
approaches and discuss the advantages and dis-
advantages.
2 SAFETY STOCK-BASED SPIRP
MODEL WITH STORAGE
CAPACITY LIMITATION
POLICIES
The inventory routing system studied in this paper
consists of a single depot and a set of geographically
scattered retailers. The retailers are indexed by ,
(where is the total number of retailers)
and the depot is indexed by . Each retailer has a
stochastic independent demand rate of
per unit of
time, that is assumed to be approximately based on
Gamma distribution . Let be the set of
retailers indexed by and ; and
.
Let be the planning horizon
indexed by and
be the planning
horizon that includes period . Let
be the size
in time units of each period , for example eight
working hours per day. For the deliveries, a fleet of
vehicles
each with a capacity of
is available. The supplier and each retailer agree to
a service level (
) based on a predetermined
inventory violation rate of
during each period and
retailer, and
. Let be
the number of available silos for each retailer .
Additional parameters of the model are as follows:
: the fixed handling cost (in euros) per delivery at
location
(retailers and depot) in period .
: the per unit holding cost of the product at
location (in euros per ton) in period ;
: the fixed operating cost of vehicle (in
euros per vehicle per use);
: travel cost of vehicle (in euros per km);
: average speed of vehicle (in km per hour);
: duration of a direct trip from retailer
to
retailer
(in hours);
: the initial inventory levels at each retailer in
period zero;
The cost of using a silo for each retailer , in
period
: maximum capacity of each silo , for
retailer
The variables of the model are defined as follows:
: the quantity of product remaining in vehicle
when it travels directly to location
from
location
in period . This quantity equals
zero when the trip () is not on any tour of the route
travelled by vehicle in period t;
: the quantity delivered to location in period
;
: the inventory level at location by the end of
period ;
: a binary variable set to 1 if location
is
visited immediately after location
by vehicle
in period , and 0 otherwise;
: a binary variable set to 1 if vehicle is being
used in period , and 0 otherwise;
: a binary variable set to 1 if silo is being
used for retailer in period , and 0 otherwise;
The minimization objective function is:
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
218

(1)
Subject to:
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
The objective function (1) shows the variables to
minimize the level of costs in this replenishment
system. It includes five cost components, namely,
total fixed operating cost of using the vehicle(s), total
transportation cost, total delivery handling cost, total
inventory holding cost at the end of each period, and
total cost of renting silos at the retailers.
Constraints (2) assure that each retailer is visited
at most once during each period. Constraints (3)
guarantee that a vehicle moves to the next
retailer/depot after serving the current one.
Constraints (4) prevent that the time required to
complete each tour does not exceed the duration of
the period. The quantities to be delivered to each
retailer are determined by constraints (5). These
constraints also avoid sub-tour from occurring.
Constraints (6) are capacity constraints induced by
the vehicles capacities. Constraints (7) determine the
delivered number of products from period 1 to
together with the initial inventory to be equal to the
expected demand’s values from period 1 to , safety
stock, and remaining inventory at the end of period
for each retailer . Constraints (8) insure that the level
of inventory at the end of last period is equal or larger
than initial inventory. Constraints (9) determine the
optimum number of required silos for each retailer
during each period. Finally, constraints (11) specify a
vehicle cannot be assigned to serve retailers unless
the related fixed cost is payed.
Eq. (11) presents the safety stock calculation
model to be used in constraints (7).
As is specified by equation (11), safety stock is a
function of service level parameter (
), number of
time periods (), and standard deviation of demand
(
for each retailer ). The parameter
is the
service factor determined by retailer’s requested
service level (
%) gained by the level of
. It is
used as a multiplier with the standard deviation and
number of time periods to calculate a specific
quantity (as safety stock) to meet the pre-set service
level.
(11)
Optimizing Storage Capacity of Retailers in Stochastic Periodic Inventory Routing Problem
219

3 DIFFERENT APPROACHES
FOR STORAGE CAPACITY
ALLOCATION
We propose 4 different policies in this study. These
policies are suggested based on the requirements in
short/long term planning horizons and high
variability in demand rates to evaluate their
applicability in distribution systems. Different
industries have different preferences in renting a silo.
Therefore, presenting various strategies for silo
allocation could help the decision maker to decide
wisely. In the reminder four proposed policies for silo
allocation are modelled and described.
3.1 Fixed Number of Silos
This is the basic policy that allocates a certain number
of silos to the retailers during the whole planning
horizon. Equations (1)-(10) formulate the Safety
Stock-based SPIRP for this policy. Number of silos
are fixed from period 1 to the last period. It means the
maximum required silos need to be rented in the
beginning of the planning horizon based on the
expected level of inventory from the optimization
model.
In some distribution centres where the variability
of demand rates is high, and high level of service is
promised to the customers, it is better to rent a certain
number of silos for the whole planning horizon.
Therefore, there is less risk of having limited space
for the inventory during the planning horizon. The
calculated number of silos is based on the maximum
expected level of inventory, meaning there are some
periods that some silos are not full, but the rent must
be paid. The allocation of the silos to the retailers are
based on the rental fee, and the trade-off between
inventory/silo costs and transportation costs.
3.2 Fixed Cumulative
Fixed-cumulative approach optimizes the silo
allocation mechanism, in order to use the maximum
capacity of rented silos during the periods with low
inventory level at the retailers. In other words, the
cumulative level of inventory from the beginning to
period is taken into account instead of the level of
inventory for period . To have this strategy applied
in the Safety Stock-based SPIRP, constraints (9)
needs to be replaced by constraints (13). In
constraints (13) the inventory level for all the periods
from 1 to need to be smaller or equal to storage
capacity in one period multiplied by . Retailers with
higher variability in demand rates and/or long term
planning horizon are more convenient to have this
strategy for renting the silos, since for those retailer
the risk of having excess inventory/demand in long
term is compensated by other periods with lower
demand rate.
3.3 Flexible Number of Silos
In this policy the retailers are allowed to have
different number of silos for each period. It means the
number of silos are different during the planning
horizon, but 1the decision for each period is made
only based on the inventory for that period. It makes
the inventory costs as low as possible since there is
no need to pay the rent when the silo is not used.
Equation (12) involves this flexibility in the objective
function by summing up the silo fee costs for each
period. Therefore, the model selects the number of
silos for each period differently based on the
maximum inventory level on that period. Equations
(2-10) and (12), present the Safety Stock-based
SPIRP model with flexible storage capacity.
All these decisions are made before the planning
horizon, therefore this mechanism may cause risks for
the retailers in terms of stock-out occurrence.
Generally, the retailers with lower coefficient of
variation with short term planning horizon are more
preferred to apply this policy.
3.4 Flexible Cumulative
This mechanism is similar to Fixed-cumulative, with
this difference that in this policy the retailer does not
(12)
(13)
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
220
need to keep a certain number of silos for the whole
planning horizon. The idea is to be flexible in renting
the silos as well as involving the variability in
inventory level among the periods to minimize the
costs. Equations (2-8), (10), (12), and (13) present the
Safety Stock-based SPIRP model with flexible-
cumulative approach for silo allocation.
4 ILLUSTRATIVE EXAMPLE
We consider a distribution centre with 8 retailers.
There is a fleet of vehicles with 2 available vehicles,
each one with the capacity of 40 tons. The vehicles
work 8 hours per day with an average speed of 50
km/h. Fix and variable costs of the vehicles are
presented in table 1. The retailers are scattered
randomly around the warehouse. Distances between
retailers themselves and warehouse are shown in table
3.
Table 1: Some elements.
Notation
Parameter
Cost
Delivery costs
25
Inventory holding
costs per unit per period
0.5
Travel costs for
vehicle in Euro per KM
1
Fix operating cost
of vehicle
30
Average speed of
vehicle
50
The demand rate for each retailer is considered
stochastic and follows Gamma distribution and all the
stock-outs are fully backlogged. Table 2 presents the
demand rates for 8 hours (1 period) and standard
deviations as well as their coefficient of variations.
The rest of the parameters of this example are
provided in table 1. We use CPLEX 12.5.1 for solving
all models. All the computations are performed on a
3.60 GHz Intel® Xeon® CPU.
Table 2: Demand rate parameters per period.
Retailers
Average
demand
(ton/day)
Standard
deviation
(ton/day)
CV
()
()
1
1.507
1.228
0.81
1.507
1
2
0.979
0.989
1.01
0.979
1
3
0.498
0.706
1.41
0.498
1
4
3.455
1.859
0.53
3.455
1
5
11.596
3.405
0.29
11.59
1
6
0.497
0.705
1.41
0.497
1
7
3.278
1.811
0.55
3.278
1
8
5.747
2.397
0.41
5.747
1
5 RESULTS AND DISCUSSION
The two indicators considered in this study are cost
level and computation time. Both indicators have
been measured and evaluated for the defined policies
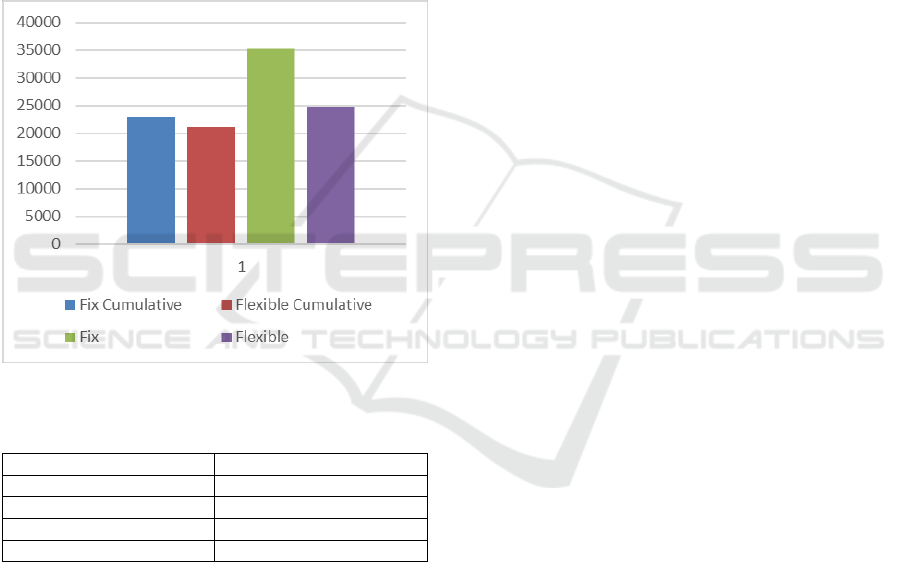
in this example to clarify the differences. Figure 1
shows the expected costs for each policy during the
whole planning horizon. As mentioned in equations
(1) and (2), these costs are fixed and variable costs of
transportations, silos, and inventory. Figure 11 clearly
indicates the low level of cost for flexible cumulative
strategy while fixed strategy is the highest. Flexible
cumulative strategy has saved 40% of the expected
costs in this model, while flexible strategy reduces the
costs by almost 30%. The cumulative approach shows
a big improvement compared to periodic approach,
by allocating the silos and trucks properly as well as
minimizing the inventory level at the retailers among
the periods.
Table 3: Duration of a trip from retailer
to retailer
(in hour).
warehouse
c1
c2
c3
c4
c5
c6
c7
c8
warehouse
0
0.5001
0.9621
0.5155
0.3106
0.4601
0.5536
0.986
0.8472
c1
0.5001
0
1.3152
0.676
0.7533
0.2581
0.9052
1.4541
1.3465
c2
0.9621
1.3152
0
1.436
0.6586
1.0973
1.3068
1.4446
0.7826
c3
0.5155
0.676
1.436
0
0.7823
0.82
0.3225
0.9552
1.0698
c4
0.3106
0.7533
0.6586
0.7823
0
0.6161
0.7071
0.9266
0.644
c5
0.4601
0.2581
1.0973
0.82
0.6161
0
0.9775
1.4446
1.2525
c6
0.5536
0.9052
1.3068
0.3225
0.7071
0.9775
0
0.6329
0.7992
c7
0.986
1.4541
1.4446
0.9552
0.9266
1.4446
0.6329
0
0.4826
c8
0.8472
1.3465
0.7826
1.0698
0.644
1.2525
0.7992
0.4826
0
Optimizing Storage Capacity of Retailers in Stochastic Periodic Inventory Routing Problem
221
We also consider computation time for each
policy in order to verify the applicability of the
strategy, particularly for larger models. Table 4
presents the computation time per policy for the
whole distribution system. Fixed and flexible silo
allocation models need the minimum time among the
other strategies, while when the model is cumulative
in storage capacity allocation, the required time
becomes larger. Fixed cumulative approach needs 87
seconds to achieve the optimized solution, while it is
even more with Flexible Cumulative approach with
106 seconds. Higher computational time specifies the
model complexity level and computation difficulty
that results in lower interest to apply the complex
solutions for large systems.
Figure 1: Overall costs for each policy.
Table 4: Computation time per policy.
Policies
Time (seconds)
Fixed
20
Fixed cumulative
87
Flexible
23
Flexible Cumulative
106
According to the results of the illustrative
example, flexible approach has got the most
reasonable results for both computation time and cost
reduction. But if the model is small in size, the fix
cumulative approach seems more reasonable, since it
is more logical to rent a silo for the whole planning
horizon.
6 CONCLUSIONS
In this paper we considered Stochastic Periodic
Inventory Routing Problem with storage capacity
limitation. The proposed safety stock-based SPIRP
model involved storage capacity as a constraint in the
model to optimize it with regard to cost minimization.
Four different policies are proposed to deal with
storage capacity limitation at retailers. The
advantages and disadvantages of these approaches
have been discussed in this paper. Finding the balance
between transportation and inventory costs together
with the storage costs (silo rent) is the most important
factor in SPIRP model. Definitely it depends on the
value of product itself, silo fee, promised service
level, demand variability rate at the retailers, length
of the planning horizon, etc., to allocate silos to the
retailers. The illustrative example presented in this
paper has revealed the advantages of flexible model
among other policies. In addition for smaller
distribution centres, fixed cumulative approach seems
to be an appropriate strategy to optimize the storage
capacity. As for future research, the applicability of
these approaches will be evaluated in some
experimental cases with design of various
experiments based on the variables. In addition, their
impact on service level, inventory and transportation
costs, and computational time will be measured and
discussed.
REFERENCES
Aghezzaf, E. H. 2007. Robust distribution planning for
supplier-managed inventory agreements when demand
rates and travel times are stationary. J Oper Res Soc, 59,
1055-1065.
Bell, W. J., Dalberto, L. M., Fisher, M. L., Greenfield, A.
J., Jaikumar, R., Kedia, P., Mack, R. G. & Prutzman, P.
J. 1983. Improving the Distribution of Industrial Gases
with an On-Line Computerized Routing and
Scheduling Optimizer. Interfaces, 13, 4-23.
Bertazzi, L., Bosco, A., Guerriero, F. & Laganà, D. 2013.
A stochastic inventory routing problem with stock-out.
Transportation Research Part C: Emerging
Technologies, 27, 89-107.
Coelho, L. C., Cordeau, J.-F. & Laporte, G. 2014a.
Heuristics for dynamic and stochastic inventory-
routing. Computers & Operations Research, 52, Part A,
55-67.
Coelho, L. C., Cordeau, J.-F. & Laporte, G. 2014b. Thirty
Years of Inventory Routing. Transportation Science,
48, 1-19.
Federgruen, A. & Zipkin, P. 1984. A Combined Vehicle
Routing and Inventory Allocation Problem. Operations
Research, 32, 1019-1037.
Pujawan, N., Arief, M. M., Tjahjono, B. & Kritchanchai, D.
2015. An integrated shipment planning and storage
capacity decision under uncertainty A simulation study.
International Journal of Physical Distribution &
Logistics Management, 45, 913-937.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
222

Stacey, J., Malini, N. & Charles, S. 2007. The storage
constrained, inbound inventory routing problem.
International Journal of Physical Distribution &
Logistics Management, 37, 484-500.
Yadollahi, E., Aghezzaf, E. H. & Raa, B. 2017. Managing
inventory and service levels in a safety stock‐based
inventory routing system with stochastic retailer
demands. Applied Stochastic Models in Business and
Industry.
Optimizing Storage Capacity of Retailers in Stochastic Periodic Inventory Routing Problem
223
