
Optics-inspired Computing
Bahram Jalali
1,2,3
, Madhuri Suthar
1
, Mohamad Asghari
1
and Ata Mahjoubfar
1,2
1
Department of Electrical Engineering, University of California Los Angeles, Los Angeles, California, U.S.A.
2
California NanoSystems Institute, Los Angeles, California, U.S.A.
3
Department of Bioengineering, University of California Los Angeles, Los Angeles, California, U.S.A.
Keywords:
Optics-inspired Computing, Photonic Time Stretch, Information Gearbox, Phase Stretch Transform, Physics-
inspired Algorithms, Edge Detection, Image Processing.
Abstract:
We show that dispersive propagation of light has properties that can be exploited for extracting features from
the waveforms. This discovery is spearheading development of a new class of digital algorithms for feature
extraction from digital images with unique and superior properties compared to conventional algorithms. In
certain cases, these algorithms have the potential to be an energy efficient and scalable substitute to syntheti-
cally fashioned computational techniques in practice today.
1 INTRODUCTION
“Human subtlety will never devise an invention more
beautiful, more simple or more direct than does na-
ture”. The elegant quote by Leonardo Da Vinci un-
derscores the important role of nature as a source of
inspiration for human ingenuity. Inspirations from
nature need not be limited to design of physical ma-
chines but should be extended to creation of new com-
putational algorithms. We expect this new paradigm
to lead to a new class of algorithms that are direct and
energy efficient while providing unprecedented func-
tionality.
Every day, the world creates nearly 2.5 exabyte
(10
18
bytes) of data. Surprisingly, 90% of the data
present in the world today has been created in the last
two years alone highlighting the exponential increase
in the amount of digital data (IBM (2016)). Process-
ing this massive data in datacentres accounts for 50-
60% of their electricity budget and a rapidly growing
fraction of total electricity consumption. This calls
for development of new computing technologies that
offer speed, energy efficiency and ease of implemen-
tation. Fortunately nature, and in particular optics-
inspired algorithms can provide a solution to certain
class of problems.
Recently, optical hardware accelerators have been
proposed as a mean to boost the speed and reduce
the power consumption of electronics (Jalali and
Mahjoubfar (2015)). In particular, it was shown that
one can create an analog optical gearbox for matching
the time-bandwidth of fast real-time optical data to
that of the much slower electronics. This information
gearbox can enable real-time processing of ultrafast
optical data while reducing the power consumption
and improving the sensitivity.
At the same time, Phase Stretch Transform (PST)
was recently introduced as a new computational ap-
proach to signal and image processing (Asghari and
Jalali (2014, 2015)). PST emerged out of research
on the Photonic Time Stretch (Bhushan et al. (1998);
Ng et al. (2014); Mahjoubfar et al. (2015); Han and
Jalali (2003)), a real-time measurement technique that
has led to the discovery of optical rogue waves (Solli
et al. (2007)), observation of relativistic electron mi-
crostructure (Roussel et al. (2014)), observation of
the birth of modelocking (Herink et al. (2016)) and
record accuracy for label-free cancer cell detection
(Chen et al. (2016)). PST is a physics-based image
processing approach that mimics the propagation of
electromagnetic waves through a diffractive medium
with engineered dispersive property (refractive index)
(Asghari and Jalali (2014, 2015)). The algorithm per-
forms edge detection and feature extraction on both
digital images as well as time domain waveforms.
It has been used for feature extraction in biomedi-
cal images (Asghari and Jalali (2015); Suthar et al.
(2016); Suthar (2016)) and Synthetic Aperture Radar
(SAR) (Ilioudis et al. (2015)). It has also been ap-
plied to resolution enhancement in super-resolution
localization microscopy where it drastically improved
the point spread function, reduced the computational
340
Jalali B., Suthar M., Asghari M. and Mahjoubfar A.
Optics-inspired Computing.
DOI: 10.5220/0006271703400345
In Proceedings of the 5th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2017), pages 340-345
ISBN: 978-989-758-223-3
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Original image
Feature detection using
conventional detectors
Feature detection using Phase
Stretch Transform (PST)
(a)
(b)
(c)
Figure 1: Comparison of feature detection using conventional derivative operator to the case of feature detection using Phase
Stretch Operator (PST). The derivative is the fundamental operation used in the popular Canny, Sobel and Prewitt edge
detection methods.
time by 400% and increased the required emitter den-
sity by the same amount (Ilovitsh et al. (2016)). The
Phase Stretch Transform algorithm was recently open
sourced on GitHub and Matlab Central File Exchange
(Asghari, M. H. and Jalali, B. (2016)), and has re-
ceived extraordinary endorsements by the software
and image processing community.
PST is a qualitatively new method of image pro-
cessing that was introduced last year. In this paper, we
show for the first time that PST has unique intrinsic
properties not offered by the current state-of-the-art
algorithms. We show that the new algorithm reveals
features invisible to human eye and to conventional
algorithms being used today. Below we prove and
explain this property using the mathematical formu-
lation of the PST response function.
To demonstrate this point, Figure 1 shows an im-
age of the planet Uranus processed by the conven-
tional edge detection algorithm (derivative based) and
by the PST. The derivative method is the underlying
function utilized by the popular Canny, Sobel and Pre-
witt algorithms. The result clearly shows the dramatic
advantage offered by the optics-inspired PST.
2 RESPONSE FUNCTION
Here we provide the underlying principle behind the
superior and unique properties of the Phase Stretch
Transform. The analysis will show that these prop-
erties stem from the wide dynamic range and built-
in equalization inherent in the algorithm. The equa-
tions are written in two dimensions however it should
be clear that they apply to one dimensional temporal
waveforms or to three and higher dimensions.
The Phase Stretch Transform (Asghari and Jalali
(2015)), represented by S{}, is defined by the follow-
ing equation that governs the operation of PST in fre-
quency domain to an image E
i
[x,y], where, x and y
are two-dimensional spatial variables.
E
o
[x,y] = S{E
i
[x,y]} (1)
where the S{} operator is defined as,
S
E
i
[x,y]
, IFFT 2
e
K[u, v] ·
e
L[u,v] ·{FFT 2{E
i
[x,y]}
(2)
and the complex output E
o
[x,y] can be defined as,
E
o
[x,y] = |E
o
[x,y]|e
jθ[x,y]
(3)
In the above equations, FFT2 is the two dimen-
sional Fast Fourier Transform, IFFT2 is the two di-
mensional Inverse Fast Fourier Transform and u and v
are frequency variables. The function
e
K[u,v] is called
the warped phase kernel and the function
e
L[u,v] is a
localization kernel implemented in frequency domain.
For simplicity, we assume here that
e
L[u,v] = 1.
The connection with physical optics and the origin
of this algorithm are as follows. Equation 3 is a two
dimensional spatial extension of a one dimensional
temporal optical electric field. Equation 2 describes
group velocity dispersion of this light field through a
medium with a dispersion induced phase
e
K[u,v]. PST
operator is defined as the phase of the transform’s out-
put,
PST
E
i
[x,y]
, ]
S{E
i
[x,y]}
(4)
where ]h·i is the angle operator. Without the loss
of generality and for simplicity, we consider operation
of PST to 1D data, i.e.,
PST
E
i
[x]
= ]
IFFT
e
K[u,v] ·FFT {E
i
[x]}
(5)
Optics-inspired Computing
341

The warped phase kernel
e
K[u] is described by a
nonlinear frequency dependent phase which can be
represented using taylor expansion as following
e
K[u] = e
jϕ[u]
= e
j
∑
M
m=2
ϕ
(m)
m!
u
m
(6)
where ϕ
(m)
is the m
th
-order discrete derivative of the
phase ϕ[u] evaluated for u = 0 and values of m are
even numbers. PST phase term ϕ[u] only contains
even-order terms in its Taylor expansion due to even
symmetry requirement for the phase term ϕ[u] for
proper operation of PST as presented in (Asghari and
Jalali (2015)). In case of 2D data, we have previously
used (Asghari and Jalali (2015)) inverse tangent func-
tion for the phase derivative profile which leads to the
following equation for PST Kernel Phase
ϕ[u,v] = ϕ
polar
[r,θ] = ϕ
polar
[r]
= S ·
W ·r ·tan
−1
(W.r) −(
1
2
) ·ln(1 + (W ·r)
2
)
W ·r
max
·tan
−1
(W.r
max
) −(
1
2
) ·ln(1 + (W ·r
max
)
2
)
(7)
where r =
√
u
2
+ v
2
and θ = tan
−1
v
u
. By con-
trolling the PST parameters, namely, strength S, and
warp W, of the phase, edges in the image can be de-
tected. Using the expression of warped phase kernel
described in Eq. (6), output complex-field data, E
o
[x],
can be evaluated as follows,
E
o
[x] = IFFT {
e
E
i
[u] ×
e
K[u]}
= IFFT
n
e
E
i
[u] ×e
j
∑
M
m=2
ϕ
(m)
m!
u
m
o
(8)
where
e
E
i
[u] is the discrete Fourier transform of the in-
put data. Simulations on images have shown that PST
works best when the applied phase is small. There-
fore, by restricting an applied phase that satisfies these
conditions, we can use small value approximation to
simplify the exponential term in Eq. (8) as
E
o
[x] = IFFT
n
e
E
i
[u] ×
1 + j
M
∑
m=2
ϕ
(m)
m!
u
m
o
(9)
→ E
o
[x] ≈
h
E
i
[x] + j
M
∑
m=2
(−1)
(m/2)
ϕ
(m)
m!(2π)
m
E
i
[x]
(m)
i
(10)
where E
i
[x]
(m)
is the m
th
-order discrete derivative of
the input data E
i
[x]. As the output data is a complex
quantity, the phase of the output data can be calcu-
lated as,
PST {E
i
[x]} = ]{E
0
[x]}
≈ tan
−1
n
∑
M
m=2
(−1)
(m/2)
ϕ
(m)
m!(2π)
m
E
i
[x]
(m)
E
i
[x]
o
(11)
Finally, since the phase is restricted to small values,
Eq.(11) can be simplified to,
PST {E
i
[x]} ≈
∑
M
m=2
(−1)
(m/2)
ϕ
(m)
m!(2π)
m
E
i
[x]
(m)
E
i
[x]
(12)
The closed-form expression presented in Eq.(12)
relates the PST output to the input. To give an ex-
ample, the core functionality of the PST as a feature
detector can be understood by closed-form expression
shown in Eq.(12). The output of the PST operator
is related directly to the derivatives of the input data
with weighting factors of
(−1)
(m/2)
ϕ
(m)
m!(2π)
m
. Derivatives
of the input data have the property to detect different
features in the input data. Thus, the weighting fac-
tors can be designed to emphasize different kind of
features in the input image data. In another words,
PST is a reconfigurable operator that can be tuned to
emphasize different features in an input image data.
One of the crucial observations from Eq. (12) is
that, output of the PST is inversely proportional to the
input brightness level. Therefore, for the same con-
trast level change, the output is large in the dark low-
light-level areas of an image. This important prop-
erty, inherent in PST, equalizes the input brightness
level and allows for a more sensitive feature detec-
tion and enhancement. In the past, a lot of study has
been done to improve feature detection algorithms by
brightness level equalization in wide dynamic range
images (Hameed and Wang (2011)). In particular, use
of a Log function as a pre-processing step is one of the
many commonly used techniques for brightness level
equalization prior to feature detection. The log func-
tion characteristics present a higher gain for lower
brightness input and vice versa. This equalizes the
brightness in images and improves feature detection.
Fortunately, PST operator has a built-in logarithmic
behaviour in it’s response function due to which it nat-
urally works over a wide dynamic range.
3 SIMULATION RESULTS
In this section, we present simulation results that con-
firm the closed-form expression for PST derived in
the previous section. We also show examples of op-
eration of PST on digital images, supporting the new
theory explained above. In the first example, we eval-
uate the effect of PST on features with different con-
trast level change at fixed brightness level and com-
pare it to the mathematical expression derived in Eq.
(12) for the PST output. The input data designed to
PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology
342
0 100 200 300 400 500
0
20
40
60
Intensity
0 100 200 300 400 500
Pixel Number
0
0.2
0.4
0.6
0.8
1
Edge Intensity (a.u.)
Phase Stretch Transform
0 100 200 300 400 500
0
20
40
60
Intensity
0 100 200 300 400 500
Pixel Number
0
0.2
0.4
0.6
0.8
1
Edge Intensity (a.u.)
Phase Stretch Transform
(a) (b)
(c)
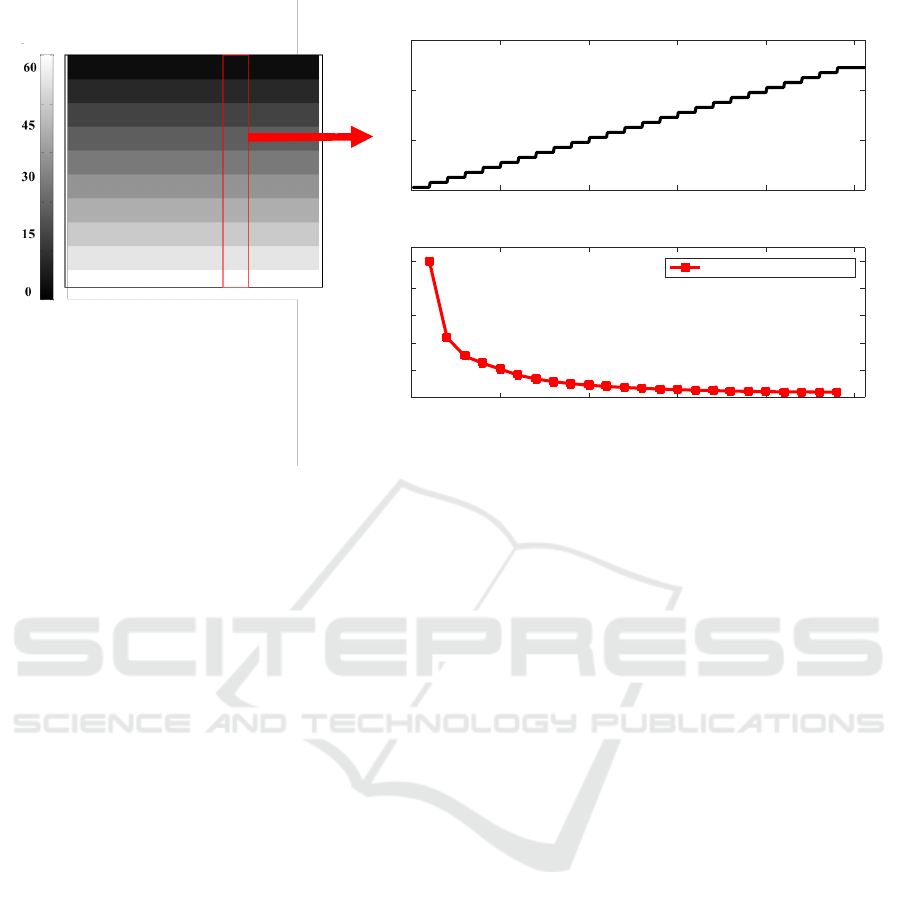
Figure 2: Effect of Phase Stretch Transform (PST) on features with fixed contrast level change at different brightness levels.
The input data was designed to have a fixed contrast level change at different brightness levels, shown in (b). Numerically
calculated output data using PST for fixed contrast level changes is different for different levels of brightness. This is due to
the inverse dependence of PST output to the input brightness level described in Eq. (12).
have different contrast level change at fixed bright-
ness level is shown in Figure 2(b). The warp, W,
and strength, S, factors used for the PST operator are
12.15 and 0.48, respectively. The red-solid line rep-
resenting the output data confirms that the relation
of PST to contrast level change at fixed brightness
level is nonlinear. This effect is due to the brightness
level equalization mechanism of PST estimated by
Eq. (12). Therefore, this simulation result presented
in Figure 2 confirms the accuracy of the closed-form
equation to estimate the output of the PST algorithm.
Figure 3 shows another example of using PST
for feature enhancement in a painting of “Minerva
of Peace”. Similar to Figure 1, the image has inter-
esting sharp features in the scroll (see red solid box
in Figure 3(a)). Results of feature detection using
conventional edge derivative operator and PST oper-
ator are shown in Figure 3(b) and 3(c) respectively.
Clearly, conventional edge derivative operator fails to
efficiently visualize the sharp features of the alphabets
in the scroll compared to the feature detection using
PST as depicted in the enlarged part of the painting.
However, PST traces the edges of alphabets and thus,
provide more information on the contrast changes in
dark areas due to its natural equalization mechanism,
see Figure3(c). Conventional edge derivative operator
was implemented from find edge function in ImageJ
software. The warp, W, and strength, S, factors used
for the PST operator are 13 and 0.4, respectively.
Figure 4 compare the effect of feature detection
using conventional edge derivative operator with fea-
ture detection using PST on another image of planet
uranus capture from a different view.The warp, W,
and strength, S, factors used for the PST operator
are 12.15 and 28, respectively. Conventional edge
derivative operator fails to visualize the sharp contrast
changes in bright areas of the image over the surface
of the planet Uranus. However, PST can clearly show
these surface contrast changes even in the bright ar-
eas due to its natural equalization mechanism. These
surface variations over the planet are consistent with
the edges detected in the Figure 1 highlighting the ef-
ficiency of PST.
4 CONCLUSIONS
New ideas are needed to deal with the exponentially
increasing amount of digital data being generated.
Fortunately, optics can provide a solution in certain
cases. The physics of light propagation in dispersive
or diffractive media has natural properties that allow
it to be used for feature extraction from data. When
implemented as a numerical algorithm, this concept is
leading to an entirely new class of image processing
techniques with high performance.
Optics-inspired Computing
343

Original image
Feature detection using
conventional detectors
Feature detection using Phase
Stretch Transform (PST)
(a)
(b)
(c)
Figure 3: Comparison of feature detection using conventional derivative operator to the case of feature detection using Phase
Stretch Operator (PST). The derivative is the fundamental operation used in the popular Canny, Sobel and Prewitt edge
detection methods. Original image is shown in (a). Results of feature detection using conventional edge derivative operator
and PST operator are shown in (b) and (c), respectively. Enlarged view of the scroll in the painting shown in the red boxes
depicts the efficiency of PST to trace the edges of alphabets in the scroll more accurately.
Original image
Feature detection using
conventional detectors
Feature detection using Phase
Stretch Transform (PST)
(a)
(b)
(c)
Figure 4: Comparison of feature detection using conventional derivative operator to the case of feature detection using Phase
Stretch Operator (PST) on an image of the planet Uranus captured from a different view as compared to the one shown in
Figure 1. The derivative is the fundamental operation used in the popular Canny, Sobel and Prewitt edge detection methods.
Original image is shown in (a). Results of feature detection using conventional edge derivative operator and PST operator are
shown in (b) and (c), respectively. PST is able to locate the sharp contrast variation over the surface of the planet which are
consistent with the edges located in Figure 1.
ACKNOWLEDGEMENTS
This work was partially supported by the National In-
stitutes of Health (NIH) grant no. 5R21 GM107924-
03 and the Office of Naval Research (ONR) Multi-
disciplinary University Research Initiatives (MURI)
program on Optical Computing.
PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology
344

REFERENCES
Asghari, M. H. and Jalali, B. (2014). Physics-inspired
image edge detection. In Signal and Information Pro-
cessing (GlobalSIP), 2014 IEEE Global Conference on,
pages 293–296. IEEE.
Asghari, M. H. and Jalali, B. (2015). Edge detection in
digital images using dispersive phase stretch transform.
Journal of Biomedical Imaging, 2015:6.
Asghari, M. H. and Jalali, B. (2016). Image-
feature-detection-using-Phase-Stretch-Transform.
https://github.com/JalaliLabUCLA/Image-feature-
detection-using-Phase-Stretch-Transform.
Bhushan, A., Coppinger, F., and Jalali, B. (1998). Time-
stretched analogue-to-digital conversion. Electronics
Letters, 34(11):1081–1082.
Chen, C. L., Mahjoubfar, A., Tai, L.-C., Blaby, I. K., Huang,
A., Niazi, K. R., and Jalali, B. (2016). Deep learning in
label-free cell classification. Scientific reports, 6.
Hameed, Z. and Wang, C. (2011). Edge detection using his-
togram equalization and multi-filtering process. In 2011
IEEE International Symposium of Circuits and Systems
(ISCAS), pages 1077–1080. IEEE.
Han, Y. and Jalali, B. (2003). Photonic time-stretched
analog-to-digital converter: fundamental concepts and
practical considerations. Journal of Lightwave Technol-
ogy, 21(12):3085.
Herink, G., Jalali, B., Ropers, C., and Solli, D. (2016). Re-
solving the build-up of femtosecond mode-locking with
single-shot spectroscopy at 90 mhz frame rate. Nature
Photonics.
IBM (2016). Bringing big data to the enterprise.
https://www-01.ibm.com/software/data/bigdata/what-
is-big-data.html.
Ilioudis, C. V., Clemente, C., Asghari, M. H., Jalali, B.,
and Soraghan, J. J. (2015). Edge detection in sar images
using phase stretch transform.
Ilovitsh, T., Jalali, B., Asghari, M. H., and Zalevsky, Z.
(2016). Phase stretch transform for super-resolution
localization microscopy. Biomedical Optics Express,
7(10):4198–4209.
Jalali, B. and Mahjoubfar, A. (2015). Tailoring wideband
signals with a photonic hardware accelerator. Proceed-
ings of the IEEE, 103(7):1071–1086.
Mahjoubfar, A., Chen, C. L., and Jalali, B. (2015). Design
of warped stretch transform. Scientific reports, 5.
Ng, W., Rockwood, T., and Reamon, A. (2014). Demonstra-
tion of channel-stitched photonic time-stretch analog-to-
digital converter with enob 8 for a 10 ghz signal band-
width. In Proceedings of the Government Microcircuit
Applications & Critical Technology Conference (GO-
MACTech’14).
Roussel, E., Evain, C., Szwaj, C., Bielawski, S., Raasch, J.,
Thoma, P., Scheuring, A., Hofherr, M., Ilin, K., W
¨
unsch,
S., et al. (2014). Microbunching instability in relativistic
electron bunches: Direct observations of the microstruc-
tures using ultrafast ybco detectors. Physical review let-
ters, 113(9):094801.
Solli, D., Ropers, C., Koonath, P., and Jalali, B. (2007).
Optical rogue waves. Nature, 450(7172):1054–1057.
Suthar, M. (2016). Decision support systems for radiolo-
gists based on phase stretch transform.
Suthar, M., Mahjoubfar, A., Seals, K., Lee, E. W., and Jalaii,
B. (2016). Diagnostic tool for pneumothorax. In Photon-
ics Society Summer Topical Meeting Series (SUM), 2016
IEEE, pages 218–219. IEEE.
Optics-inspired Computing
345
