
A Branch and Bound for the Large Live Parsimony Problem
Rog
´
erio G
¨
uths
1
, Guilherme P. Telles
2
, Maria Emilia M. T. Walter
3
and Nalvo F. Almeida
1
1
School of Computing, Federal University of Mato Grosso do Sul, Campo Grande, MS, Brazil
2
Institute of Computing, University of Campinas, Campinas, SP, Brazil
3
Department of Computer Science, University of Brasilia, Brasilia, DF, Brazil
Keywords:
Phylogeny, Character State Phylogeny, Live Phylogeny, Parsimony, Algorithms.
Abstract:
In the character-based phylogeny reconstruction for n objects and m characters, the input is an n × m-matrix
such that position i, j keeps the state of character j for the object i and the output is a binary rooted tree, where
the input objects are represented as leaves and each node v is labeled with a string of m symbols v
1
...v
m
,
v
j
representing the state of character j, with minimal number of state changes along the edges of the tree,
considering all characters. This is called the Large Parsimony Problem. Live Phylogeny theory generalizes
the phylogeny theory by admitting living ancestors among the taxonomic objects. This theory suits cases
of fast-evolving species like virus, and phylogenies of non-biological objects like documents, images and
database records. In this paper we analyze problems related to most parsimonious tree using Live Phylogeny.
We introduce the Large Live Parsimony Problem (LLPP), prove that it is NP-complete and provide a branch
and bound solution. We also introduce and solve a simpler version, Small Live Parsimony Problem (SLPP),
which is used in the branch and bound.
1 INTRODUCTION
Character state phylogeny reconstruction aims to ex-
plain the evolutionary history of taxonomic objects
and their relations by common ancestors, based on
states of the characters that each object possesses.
This is done by building a binary rooted tree, where
leaves represent the objects of interest and the internal
nodes represent hypothetical ancestors.
An approach for character state phylogeny recon-
struction is parsimony, where one tries to minimize
the total number of character state changes along the
edges of the tree (Felsenstein, 2004; Setubal and Mei-
danis, 1997).
The Large Parsimony Problem (LPP) takes as in-
put n objects, each one labeled by a string of m sym-
bols s
1
... s
m
where s
j
represents the state of char-
acter j, and a symmetric score function δ(a,b) that
expresses the cost of changing any character from
state a to state b. The output is a binary rooted tree
T where the leaves are the input objects, and each
internal node v is labeled with a string of m sym-
bols v
1
... v
m
, with symbol v
j
representing the state
of character j, such that d(v,w) =
∑
m
j=1
δ(v
j
,w
j
) and
S(T ) =
∑
(v,w)∈T
d(v,w) is minimum. The distance
d(v,w) between adjacent nodes v,w expresses the cost
of changes that occurred between them. This mini-
mum value is called minimum parsimony score. This
problem is NP-hard (Go
¨
effon et al., 2011).
An easier version of LPP is the Small Parsimony
Problem (SPP), where the tree is also given, and it
remains only to label the internal nodes minimizing
the total score (Jones and Pevzner, 2004).
An extended theory called Live Phylogeny was de-
fined in (Telles et al., 2013). Live phylogeny gen-
eralizes traditional phylogeny reconstruction by ad-
mitting the presence of living ancestors, called live
internal nodes, among the input objects. Live phy-
logeny suits well for sets of fast-evolving objects, like
viruses (Castro-Nallar et al., 2012; Gojobori et al.,
1990), or for non-biological ones, such as documents
or relational database entries (Cuadros et al., 2007;
Paiva et al., 2011).
Here we introduce new versions of LPP and SPP
using live internal nodes, called Large Live Parsimony
Problem (LLPP) and Small Live Parsimony Problem
(SLPP), respectively. These new problems general-
ize LPP and SPP allowing live internal nodes in trees.
LLPP can produce a tree with live internal nodes. In
SLPP, the input is a tree where not only the leaves, but
also some internal nodes may be previously labeled.
Before dealing with LLPP we will focus on SLPP
184
GÃijths R., Telles G., Walter M. and Almeida N.
A Branch and Bound for the Large Live Parsimony Problem.
DOI: 10.5220/0006219001840189
In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 184-189
ISBN: 978-989-758-214-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

because, although SLPP is easier than LLPP, we need
a solver for SLPP to construct a branch and bound al-
gorithm for LLPP. Furthermore, SLPP may be useful
to solve the LLPP in the same fashion that SPP is used
by many heuristics to solve the LPP (Yan and Bader,
2003).
The text is organized as follows. In Section 2 we
describe solutions for two variants of SPP. Section 3 is
devoted to solve SLPP for both variants. In Section 4
we prove that LLPP is NP-complete and in following
section we provide a branch and bound solution. In
Section 6 we conclude this work.
2 THE SMALL PARSIMONY
PROBLEM (SPP)
We assume that characters evolve independently, so
SPP can be solved separately for each character. We
will consider two types of score function: general and
binary. Each state of a character is a symbol from a
set S , |S | = k.
2.1 SPP with General Score Function
Sankoff (Sankoff, 1975) solved SPP using dynamic
programming. Let s
t
(v) be the minimum parsimony
score of subtree rooted at node v labeled with state t.
Recall that the problem is being solved for a single
character. Thus, s
t
(v) can be easily calculated:
s
t
(v) = min
i∈S
{s
i
(u) + δ(i,t)} + min
j∈S
{s
j
(w) + δ( j,t)},
(1)
where u and w are the children of v. The initializa-
tion for this bottom-up algorithm consists in setting,
for each leaf v and each state t, s
t
(v) = 0 if v is la-
beled with t, or s
t
(v) = ∞ otherwise. At each step,
after computing s
t
(u) and s
t
(w) for all t, s
t
(v) may
be calculated also for all t. At the end, the minimum
parsimony score is given by min
t∈S
s
t
(root).
As usual in dynamic programming, by backtrack-
ing the choices made at the nodes, it is possible to
reconstruct an optimal assignment of labels. The al-
gorithm takes time O(nk
2
).
2.2 SPP with Binary Score Function
Fitch (Fitch, 1971), even before Sankoff and using a
similar approach, solved this problem in time O(nk)
for the particular scoring function δ(a,b) = 1 if a 6= b,
and δ(a,b) = 0 if a = b.
The algorithm uses an auxiliary structure S
v
, the
set of possible values for label v. The algorithm per-
forms two steps. First it does a post-order tree tra-
versal. If v is a leaf labeled with t, S
v
= {t}. Other-
wise
S
v
=
S
u
∪ S
w
if S
u
∩ S
w
=
/
0,
S
u
∩ S
w
if S
u
∩ S
w
6=
/
0.
(2)
where u and w are the children of v. Secondly it does
a preorder tree traversal. The root is labeled with any
element in S
root
. Then, every node w with parent v is
labeled as follows:
label(w)=
label(v) if label(v) ∈ S
w
,
any element of S
w
if label(v) /∈ S
w
.
(3)
It is important to notice that Equation 3 works even if
w is a leaf, since S
w
contains only one element.
3 THE SMALL LIVE
PARSIMONY PROBLEM (SLPP)
In this section we provide solutions for SLPP, as de-
fined in Section 1, for both kinds of score function,
modifying Sankoff’s and Fitch’s algorithms.
In both cases we need to change the way we deal
with internal nodes representing objects, named live
internal nodes. Like a leaf, a live internal node has
its label already defined by the input and we cannot
change it.
3.1 SLPP with General Score Function
The modified version of Sankoff’s algorithm pre-
serves the original initialization, but this time includ-
ing all live internal nodes. So, the algorithm starts by
assigning, for each leaf v, zero to s
t
(v) if v is labeled
with t, or ∞ otherwise. The same assignment is made
for each live internal node.
Considering the δ function as defined in Table 1.
Figure 1 shows an example of this initialization step,
where gray rectangles show the values of s
A
(v), s
C
(v),
s
G
(v), s
T
(v) for each leaf or live internal node v.
Table 1: Function δ used in the examples, with characters
from S ={A, C, G, T}.
δ A C G T
A 0 2 1 2
C 2 0 2 1
G 1 2 0 2
T 2 1 2 0
At each step, let v be an internal node with chil-
dren u and w. If v is not live, then Equation 1 is used
as before. Otherwise, let
¯
t be the state already defined
for v. Since label
¯
t of v cannot be changed, the al-
gorithm does not change any s
t
(v),t 6=
¯
t, previously
defined as ∞, but instead calculates only s
¯
t
(v) using
A Branch and Bound for the Large Live Parsimony Problem
185

Figure 1: First step of the algorithm for SLPP with one live
internal node: evaluation of s
t
(v) for leaves and live internal
nodes.
Equation 1. Although the label of v does not change,
s
¯
t
(v) needs to be calculated in order to make sure that
the minimum parsimony score for the subtree rooted
by v is correctly computed, provided that
¯
t is the label
of v. Figure 2 shows this calculation and the arrow
shows its direction (from leaves to root). The last part
Figure 2: Second step of the algorithm for SLPP with one
live internal node: evaluation of s
t
(v) for internal nodes.
of the algorithm (recovering the best choices and la-
beling the nodes) works exactly as before, since that
if the root is a live internal node with label
¯
t then
s
t
(root) = ∞ for each t 6=
¯
t, and s
¯
t
(root) 6= ∞. Thus,
as in Sankoff’s Algorithm, the minimum parsimony
score is given by min
t∈S
s
t
(root). We can see this part
in Figure 3. The big arrow shows the direction of la-
beling (from root to leaves) and small arrows shows,
at each internal node, the characters of children that
minimizes the (minimum) operators of equation 1.
The algorithm correctness is as follows. Let T be
a binary rooted tree with a labeling of all live inter-
nal nodes, and δ(a,b) the symmetric function defin-
ing the cost of changing any character from state a
to state b. By induction in the height h of T , if h = 0
then T has only one labeled live internal node r. After
initialization, s
¯
t
(r) = 0, and s
t
(r) = ∞ for each t 6=
¯
t,
where
¯
t is the label of r. The minimum possible value
that can be reached by s
¯
t
(r) is zero. Assume that for
each tree rooted by node r with height less than h,
each state t is such that s
t
(r) = ∞ or is the minimum
parsimony, and there exists at least one t such that
Figure 3: Third step of the algorithm for SLPP with one live
internal node: final labeling of nodes.
s
t
(r) is not infinite. Now, let T be a tree rooted by r
and height h > 0. Let u,w be the children of r. For
each t, s
t
(r) is calculated using Equation 1. By induc-
tion hypothesis, there exists at least one state t
1
such
that s
t
1
(u) 6= ∞ and minimum, and at least one state
t
2
such that s
t
2
(w) 6= ∞ and minimum. The algorithm
chooses, among all states t, one that minimizes s
t
(r).
Then the modified Sankoff’s Algorithm calculates the
minimum parsimony score of T .
The running time is the same, O(nk
2
), and the fi-
nal labeling is optimal under the assumption that each
live internal node label was previously chose.
3.2 SLPP with Binary Score Function
To efficiently solve SLPP with binary score function,
we introduced two modifications in the Fitch’s Algo-
rithm. In the initialization step the algorithm sets, for
each leaf and also for each live internal node v labeled
with t, S
v
= {t}. Figure 4 shows the tree after this first
step of the algorithm. During the post-order traversal
we cannot apply Equation 2 for live internal nodes,
because in SLPP they already have their correspond-
ing sets with a single letter representing their respec-
tive labels. Figure 5 shows this calculation step.
Figure 4: First step of the algorithm for SLPP with binary
score function and one live internal node: evaluating sets
for leaves and live internal nodes.
In the final step, the preorder traversal is the same
as in Fitch’s Algorithm, since Equation 3 works well
for live internal nodes, as it works for leaves.
The correctness of this algorithm follows easily
from the traversals in the tree. In the top-down phase,
BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms
186

Figure 5: Second step of algorithm for SLPP with binary
score function and one live internal node: final evaluation
of sets.
if the label of a node was computed from the intersec-
tion of its children sets, then both children are labeled
with the same state assigned to their father, resulting
in cost zero for both edges. Otherwise, the label was
computed from their union, and since the intersection
of the children sets was empty, there is an edge of
cost zero and the other edge of cost one, which is the
minimum number of changes.
4 THE LARGE LIVE
PARSIMONY PROBLEM (LLPP)
The definition of LLPP is the same as LPP (Sec-
tion 1), except for the output. Here the binary rooted
tree T may have input objects representing internal
nodes (the live internal nodes). In this section we
prove that LLPP is NP-complete and provide a branch
and bound solution for it.
To prove that LLPP is NP-complete, we state
the decision version of the problem by adapting the
original optimization problem defined in Jones (Jones
and Pevzner, 2004). Let S(T ) be the score of a tree T .
Large Live Parsimony Problem (LLPP)
Instance: A matrix M
n×m
and a constant B ∈ R
+
Question: Is there a tree T , fully labeled, with l ≥ 0
live internal nodes and n − l leaves labeled by n rows
of M, such that S(T ) ≤ B ?
Theorem 1 LLPP is NP-complete.
Proof. First we observe that LLPP is in NP. Given
a fully labeled tree T , for every adjacent nodes v,w
we obtain distance d(v,w) in polynomial time and we
calculate S(T ) by traversing T . Then we check if
S(T ) ≤ B in polynomial time.
To complete the proof we will reduce LPP, which
is NP-complete, to LLPP.
Given an instance (M,B) of LPP, we generate an
instance (M
0
,B
0
) for LLPP by making M
0
= M and
B
0
= B.
We prove the reduction showing that an answer
yes for (M,B) implies to an answer yes for (M
0
,B
0
)
and vice-and-versa.
If (M,B) has an answer yes for LPP, then exists a
fully labeled tree T , with exactly n leaves and l = 0
live internal nodes labeled by n rows of M such that
S(T ) ≤ B. Thus, the same T answers yes to (M
0
,B
0
).
Conversely, if the instance (M
0
,B
0
) = (M,B) has
an answer yes for LLPP, then exists a fully labeled
tree T
0
, with l ≥ 0 live nodes and n − l leaves labeled
by n rows of M, such that S(T
0
) ≤ B
0
= B.
We construct T , a solution for LPP, according to
one of the following cases:
• If T
0
does not have live nodes (l = 0), just take
T = T
0
. T is a fully labeled tree with exactly n
leaves labeled by n rows of M, with S(T ) ≤ B,
which corresponds to an answer yes to LPP.
• If T
0
has live internal nodes (l > 0), then construct
T from T
0
creating, for each live internal node v,
two internal nodes v
1
and v
2
with the same la-
beling of v. Each child of v becomes child of
v
2
; and v
1
is father of v
2
and v. Figure 6 shows
this transformation. As the two nodes inserted
into T has the same labeling of v, T will have
exactly the same parsimony score of T
0
, that is,
S(T ) = S(T
0
). This transformation is applied re-
peatedly in all live internal nodes until no live in-
ternal nodes remain. As the transformation pre-
serves the parsimony score, the tree T obtained at
the end of this sequence of transformations is such
that S(T ) = S(T
0
) ≤ B and has exactly n leaves la-
beled by n rows of the matrix M. Thus T gives
answer yes to LPP.
Although the tree T built from T
0
in this reduction
may contain internal nodes with labels from the input
set, it still is an answer for LPP, since it is a binary
rooted tree where the leaves are the input objects.
In both cases the construction of T can be made in
polynomial time. This reduction from LPP to LLPP
completes the proof of the theorem.
Figure 6: Transformation of a live node v of T
0
into a leaf
of T .
A Branch and Bound for the Large Live Parsimony Problem
187
5 BRANCH AND BOUND FOR
LLPP
The basic idea for the branch and bound is to apply
the same strategy used for LPP, proposed in (Hendy
and Penny, 1982). It is based on an incremental con-
struction of the tree, inserting one species at a time
and analyzing all possible edges where the new node
can be included. Before completing the construction
of the tree, the parsimony score is calculated, solv-
ing the SPP, and then compared to the best score ob-
tained so far. If the current score is greater than or
equal to the current best, the tree under construction
is discarded and the algorithm continues from the next
possible alternative.
We will extend the traditional strategy allowing
species to be inserted into hypothetical internal nodes,
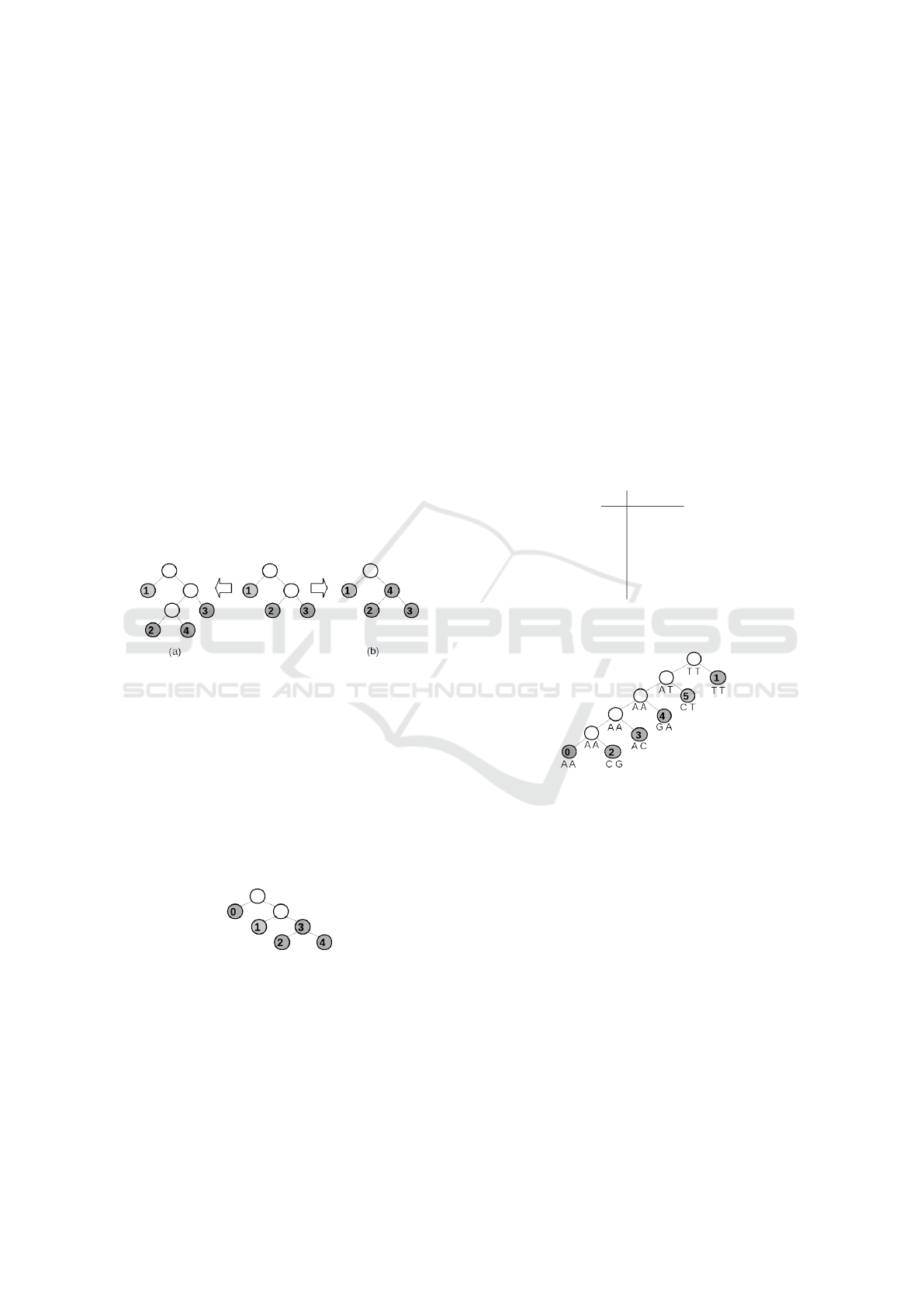
turning them to live internal nodes. Figure 7 il-
lustrates two possibilities for the inclusion of node
4 (among others not shown). Figure 7(a) and Fig-
ure 7(b) show the inclusion of node 4 as a leaf and
as a live internal node, respectively.
Figure 7: Two possible inclusion scenarios for node 4.
One of the premises of branch and bound is that all
possible trees can be obtained and some of them are
discarded by a good pruning. In the traditional case,
as noted by (Hendy and Penny, 1982), the order of
inclusion of the species does not matter. However, in
live phylogeny, depending on the previously defined
order of inclusion of the nodes, some trees will not be
generated, as we can see on Figure 8 if the order of
the species is 0, 1,2,3, 4. We avoid this problem with
extra computational effort.
Figure 8: A tree that cannot be reached if the order of
species inclusion is 0,1,2,3,4.
The algorithm works with three nested loops. The
outer loop generates all possible orders of inclusion
the species stored in a n-position array OS. The next
loop generates all possible orders of construction of
trees, controlling at which edge or node each species
will be included. This order will be stored in an n-
position array OC. Finally, the inner loop repeats the
following sequence of steps, controlled by i, to com-
plete the tree or give up the current construction: (1)
traverse the partial tree setting numbers for the edges
and internal nodes; (2) insert species OS[i] breaking
the edge OC[i] or at the internal node indicated by
OC[i] (making it live); (3) test whether the partial tree
can generate an optimal solution, and if it don’t, in-
terrupt the loop, indicating i as the position where
the current search for the optimal tree failed and re-
questing the next OC position. At this step, we use
the polynomial-time solution of SLPP to calculate the
parsimony score of the partial tree and test against the
best score so far.
To illustrate the branch, we will use the input ma-
trix M shown in Figure 9, with six species and two
characters. By using the inclusion order of species
0,1,. .. 5 and construction order 0,0,0,0, 0,0, we get
the tree shown in Figure 10.
1 2
0 A A
1 T T
2 C G
3 A C
4 G A
5 C T
Figure 9: Input matrix M with species 0, 1, . . . , 5 and two
characters 1 and 2 with states A, C, G and T.
Figure 10: Initial tree with score 7, obtained by using inclu-
sion order 0,1,...,5 and construction order 0,0,0,0,0,0.
As another example, the central tree shown in Fig-
ure 11 is obtained using the inclusion order of species
0,1,2, 3 and construction order 0,0,1. Figures 11(a)
and 11(b) show, respectively, possible inclusions of
species 3 as a leaf and as a live internal node.
Figure 12 shows a most parsimonious tree with
minimal score for M obtained by the proposed branch
and bound strategy. Note that a most parsimonious
tree obtained by branch and bound may be equal to
the tree obtained by traditional branch and bound, or
at least have the same score. If we want a most parsi-
monious tree with l > 0 live internal nodes, we only
need to change the second loop to generate construc-
tion orders that have l live internal nodes.
As pointed by (Hendy and Penny, 1982), the
running time of traditional branch and bound for n
BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms
188

Figure 11: Partial trees to be built and tested by the inclu-
sion of species 3 as a leaf (a) or as a live internal node (b).
Figure 12: Most parsimonious tree for M with score 6, ob-
tained by branch and bound.
species and m characters is O(mn
n
), although this
time is not reached in most cases with biological se-
quence data. Because we included another external
loop that generates all permutations of species, our
branch and bound running time is O(n!mn
n
). This
branch and bound will be useful to construct bench-
marks for future heuristics on LLPP.
Two samples, one with 8 species and 10 charac-
ters and other with 9 species and 10 characters were
solved by branch and bound in approximately 54 min-
utes and 20 hours, respectively, in an Intel Core i5-
4590 CPU 3.30GHz with 4GB of memory.
6 CONCLUSION
In this paper we analyzed problems related to how to
find the most parsimonious tree in the Live Phylogeny
problem.
We introduced the Large Live Parsimony Problem
(LLPP), and a simpler version, called Small Live Par-
simony Problem (SLPP). SLPP is a version of Small
Parsimony Problem (SPP), but this time admitting live
ancestors in the phylogenetic tree. Polynomial-time
solutions for two variants of SLPP have been provided
(both general and binary score functions) based on
previously well-known solutions for SPP. We proved
the NP-completeness of LLPP and also presented a
branch and bound algorithm for it using as a subrou-
tine the polynomial-time solution of SLPP.
This is an ongoing work and deeper validations
are necessary. We believe that SLPP may be used as
subroutine in heuristics to solve LLPP.
ACKNOWLEDGEMENTS
RG and NFA thank Fundect grants TO141/2016
and TO007/2015. NFA also thanks CNPq grants
305857/2013-4, 473221/2013-6 and CAPES grant
3377/2013. GPT thanks CNPq grant 310685/2015-0.
MEMT thanks CNPq grant 308524/2015-2.
REFERENCES
Castro-Nallar, E., Perez-Losada, M., Burton, G., and Cran-
dall, K. (2012). The evolution of HIV: Inferences us-
ing phylogenetics. Mol. Phylog. Evol., 62:777–792.
Cuadros, A., Paulovich, F., Minghim, R., and Telles, G.
(2007). Point placement by phylogenetic trees and its
application to visual analysis of document collections.
In Proc. of the 2007 IEEE Symposium on Visual Ana-
lytics Science and Technology, pages 99–106.
Felsenstein, J. (2004). Inferring Phylogenies. Sinauer As.
Fitch, W. (1971). Toward defining the course of evolution:
Minimum change for a specific tree topology. System-
atic Zoology, 20:406–416.
Go
¨
effon, A., Richer, J., and Hao, J. (2011). Heuristic Meth-
ods for Phylogenetic Reconstruction with Maximum
Parsimony, pages 579–597. John Wiley & Sons, Inc.
Gojobori, T., Moriyama, E., and Kimura, M. (1990).
Molecular clock of viral evolution, and the neutral the-
ory. P. Natl. Acad. Sci., 87(24):10015–10018.
Hendy, M. and Penny, D. (1982). Branch and bound algo-
rithms to determine minimal evolutionary trees. Math-
ematical Biosciences, 59(2):277 – 290.
Jones, N. C. and Pevzner, P. A. (2004). An Introduction to
Bioinformatics Algorithms, volume 2004. MIT Press.
Paiva, J., Florian, L., Pedrini, H., Telles, G., and Minghim,
R. (2011). Improved similarity trees and their appli-
cation to visual data classification. IEEE Trans. Vis.
Comp. Graphics, 17(12):2459–2468.
Sankoff, D. (1975). Minimal mutation trees of sequences.
SIAM Journal of Applied Mathematics, 28(1):35–42.
Setubal, J. and Meidanis, J. (1997). Introduction to Molec-
ular Computational Biology, volume 1997. PWS.
Telles, G., Almeida, N., Minghim, R., and Walter, M.
(2013). Live phylogeny. Journal of Computational
Biology, 20(1):30–37.
Yan, M. and Bader, D. A. (2003). Fast character optimiza-
tion in parsimony phylogeny reconstruction. Tec. Re-
port TR-CS-2003-53, Univ. of New Mexico.
A Branch and Bound for the Large Live Parsimony Problem
189
