
Supporting Efficient Global Moves on Sequences in Constraint-based
Local Search Engines
Renaud De Landtsheer, Gustavo Ospina, Yoann Guyot, Fabian Germeau and Christophe Ponsard
CETIC Research Centre, Charleroi, Belgium
Keywords:
Sequence, Local Search, CBLS, Global Constraints, Global Moves, OscaR.cbls.
Abstract:
Constraint-Based Local Search (CBLS) is an approach for quickly building local search solvers based on
a declarative modelling framework for specifying input variables, constraints and objective function. An
underlying engine can efficiently update the optimization model to reflect any change to the input variables,
enabling fast exploration of neighbourhoods as performed by local search procedures. This approach suffers
from a weakness when moves involve modifying the value of a large set of input variables in a structured
fashion. In routing optimization, if one implements the optimization model by means of integer variables, a
two-opt move that flip a portion of route requires modifying the value of many variables. The constraint on
this problems are then notified about many updates, but they need to infer that these updates constitute a flip,
and waste a lot of time. This paper presents this multi-variable limitation, discusses approaches to mitigate it,
and proposes an efficient implementation of a variable type that represents sequences of integers to avoid it.
The proposed implementation offers good complexities for updating and querying the value of sequences of
integers and some mechanisms to enable the use of state-of-the art incremental global constraints.
1 INTRODUCTION
Constraint-Based Local Search (CBLS) is an ap-
proach for representing declarative optimization mod-
els for local search optimization where the optimiza-
tion problem is represented by means of variables and
invariants (Van Hentenryck and Michel, 2009). In-
variants are directed constraints that have designated
input and output variables and that maintain the value
of these output variables according to their specifica-
tion and to the value of the input variables. Decision
variables are not the output of any such directed con-
straints. A local search procedure can explore neigh-
bourhoods by modifying these decision variables and
query the value of a variable that is maintained by the
model and represents the objective function.
This is the approach implemented by the frame-
works Comet, Kangaroo, OscaR.cbls, LocalSolver,
and InCELL (Van Hentenryck and Michel, 2009;
Newton et al., 2011; De Landtsheer and Ponsard,
2013; Benoist et al., 2011; Pralet and Verfaillie,
2013). In such frameworks, several variable types
might be available, such as Boolean, Integer, Float,
Set of Integer, and List of Integer. A key aspect that
updating invariant should be as efficient as possible in
order to provide fast neighbourhood exploration.
An important drawback of the CBLS approach is
the potential loss of efficiency of the model compared
to a dedicated model to evaluate structured moves
involving several variables. We call it the multi-
variable limitation. The multi-variable limitation oc-
curs when a move requires modifying a large number
of input variables altogether, and this move actually
implements some structurally consistent modification
of the model that could be captured in a more sym-
bolic and global way with a O(1) sized representa-
tion. Such more symbolic representation of the move
would typically enable efficient global reasoning of
the impact of that move onto the constraint of the
problem.
For instance, a routing problem, such as a Travel-
ling Salesman Problem (TSP) (Schrijver, 2005), can
be represented by a series of integer variables, called
“next”, each of them being associated with a node
of the routing problem, and specifying the node that
must be reached when leaving the associated node.
Evaluating a 2-opt move, that flips a section of a
route, requires modifying each “next” variable asso-
ciated with nodes included in the flipped section, thus
requiring O(n) updates (Croes, 1958). An invariant
maintaining the routed distance from a distance ma-
trix is then notified about the change of each modified
De Landtsheer R., Ospina G., Guyot Y., Germeau F. and Ponsard C.
Supporting Efficient Global Moves on Sequences in Constraint-based Local Search Engines.
DOI: 10.5220/0006201901710180
In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 171-180
ISBN: 978-989-758-218-9
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
171

variable and is therefore updated in O(n) time, sim-
ply because it is notified about O(n) updates. The
cost of evaluating such move is therefore O(n) time,
because of the O(n) updated variables, and the O(n)
notifications sent to the listening invariant. A routing
optimization engine implemented with a dedicated al-
gorithm could easily reason on the logical meaning of
a 2-opt and evaluate the same neighbour in O(1) time,
especially if the distance matrix is symmetric (Glover
and Kochenberger, 2003).
There are several ways to mitigate the multi-
variable limitation, namely, change the order of ex-
ploration, transmit more symbolic information beside
variables, use symbolic differentiation, or add more
structured variable types. Let us review them in order
to motivate our approach.
Choosing the Order of Exploration of the
Neighbourhood (Glover and Kochenberger, 2003).
In the case of the aforementioned 2-opt move, one
can gradually widen the flipped route segment, so that
each neighbour can be explored in turn, and going
from one neighbour to another one requires moving
two points. We call this exploration mode the circle
mode, as opposed to the star mode. In star mode, the
state of the model is rolled back to the initial state
between each explored neighbour. Circle mode ex-
ploration is however hard to combine with heuristics
such as selecting nodes among the k-nearest ones in
vehicle routing, that allows one to suggest a few rele-
vant neighbours among e.g. a 2-opt and explore these
moves exclusively.
Transmitting additional symbolic information
through the model, e.g. by proposing the notion of
“aggregate of variables” such as “array of integer vari-
ables” and transmit the symbolic nature of the move to
the invariants listening to the aggregate, so that they
can update their output value efficiently using global
algorithms. This approach would not fully solve the
issue because the O(n) variables involved in the move
would be updated anyway since they exist, and their
value might be queried by the invariants listening to
the aggregate.
Performing symbolic differentiation of the
model to automatically use the best algorithm for
evaluating neighbours. This option is complex be-
cause it requires reasoning on the structure and global
semantic of the model. It also requires to deploy
additional reasoning tool, e.g. SMT-solvers like Z3
(De Moura and Bjørner, 2008).
Introducing structured variable types, so that
complex moves are performed on the value of the
variable and can be described in a more symbolic way
as a delta on this value. Those moves can be imple-
mented efficiently and then used as powerful primi-
tives for writing efficient global algorithms.
This paper focuses on this last approach and pro-
poses an implementation of a variable type represent-
ing sequences of integers, suitable for a CBLS solver.
The goal is to achieve similar algorithmic complexity
to the one achievable by a dedicated implementation,
while still providing a high degree of declarativity as
proposed by the CBLS approach.
We focus on this type of variable for two reasons.
First, sequence of integers could be deployed to rep-
resent various optimization problems that have a no-
tion of sequencing including car sequencing, routing,
flow-shop scheduling, etc. Routing optimization is an
area where local search is widely used; it can benefit
from our sequence variable. Second, string solving is
an active topic of research (Abdulla et al., 2015; Fu
et al., 2013; Ganesh et al., 2011; Scott et al., 2015).
Providing a variable of type ”sequence of integers”
supporting efficient global updates within a generic
local search engine can constitute an opportunity to
make the development inherent to such research eas-
ier (Bj
¨
ordal, 2016).
This paper is focusing a lot on the efficiency of the
underlying data-structures for representing sequences
of integers. It often uses the complexity notation
O(...). It implicitly refers to the time complexity, un-
less otherwise specified.
The paper is structured as follows: Section 2
presents various frameworks for implementing local
search and the way they support global constraints
on sequences, it also introduces the OscaR.cbls en-
gine with more details; Section 3 presents the require-
ments over an implementation of such sequence vari-
able in a CBLS framework; Section 4 discusses the
data-structure and the API of our implementation and
concludes with complexity; Section 5 validates our
approach by presenting how global constraints can
easily be implemented based on our API (Applica-
tion Programming Interface); Section 6 presents some
benchmarks of our implementation; Finally, Section 7
concludes.
2 BACKGROUND
This section first presents several CBLS frameworks,
and then introduces the necessary vocabulary of
CBLS for the remaining of the paper, based on the
OscaR.cbls engine.
2.1 Local Search Frameworks
Local search frameworks aim at making the devel-
opment of local search solutions much simpler. To
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
172

this end, they provide different degrees of support for
the modelling of the problem or the elaboration of the
search procedure.
EasyLocal++ is a framework that requires a ded-
icated model to be developed from scratch using ad-
hoc algorithms. It mainly provides support for declar-
ing the search procedure (Di Gaspero and Schaerf,
2003). As such, it does not suffer from the multi-
variable limitation, but it does not provide as much
assistance in the development of a model as a CBLS
framework would. Notably it does not allow the de-
veloper to package efficient global constraints that can
be instantiated on demand.
There are a few tools supporting constraint-based
local search, namely: Comet (Van Hentenryck and
Michel, 2009), Kangaroo (Newton et al., 2011), Os-
caR.cbls (OscaR Team, 2012), LocalSolver (Benoist
et al., 2011), and InCELL (Pralet and Verfaillie,
2013).
Comet, Kangaroo, and OscaR.cbls support Inte-
gers and Sets of Integers. InCELL supports a notion
of variable that is a sequence of other variables. How-
ever, it does not offer a unified data structure for rea-
soning on the sequence itself, and no information is
available about the added value of such sequence of
variables (Pralet and Verfaillie, 2013). LocalSolver
supports a variable of type list of integers, where each
value can occur at most once (Benoist et al., 2011).
No detail is given about how these lists of integers are
actually implemented and it supports very few invari-
ants and constraints related to this list variable.
Beside CBLS tools, there are many global con-
straint algorithms that have been developed, notably
for routing optimization. The most classical exam-
ple is the route distance invariants that computes the
distance driven by a vehicle, given its route, and that
quickly updates this distance when a routing move
is performed such as a 2-opt or a 3-opt (Glover and
Kochenberger, 2003). Another example is the travel-
ling delivery man problem described in (Mladenovi
´
c
et al., 2013) that relies on pre-computation to update
a complex metrics in O(1) for a large proportion of
classical routing moves. Such global constraints only
require a high-level description of the move to per-
form their update efficiently. Implementing such al-
gorithm therefore requires something in the vein of
our proposed sequence variable. Our contribution
is to propose such implementation within a generic
framework, under the form of a dedicated variable
with the appropriate underlying data structure, so that
these global constraints can be implemented easily,
and instantiated in a flexible way as done with other
constraints in a CBLS engine.
2.2 CBLS, the OscaR Way
Since this contribution has been done in the context
of the OscaR.cbls tool, we further introduce the ba-
sic concepts of CBLS using the vocabulary of Os-
caR.cbls. As usual in local search, solving a problem
involves specifying a model and a search procedure.
The model is composed of incremental variables
(integers and set of integers at this point), and invari-
ants which are incremental directed constraints main-
taining one or more output variables according to the
atomic expressions they implement (e.g. Sum: the
sum of inputs). Constraints are special invariants that
maintain their violation as an output variable. They
are Lagrangian relaxations of their specification. Be-
side they also maintain some information about which
variable cause the violation.
The search procedure is expressed using neigh-
bourhoods, which can be queried for a move, given
the current state of the model, an acceptance crite-
rion, and an objective function. Combinators are a set
of operators on neighbourhoods that combine them
and incorporate various metaheuristics, so that a com-
plex search strategy is represented by a composite
neighbourhood totally expressed in a declarative way
(De Landtsheer et al., 2015). A library of combina-
tors is available for specifying standard metaheuris-
tics (e.g. simulated annealing, restart, hill climbing),
for managing solution (e.g. when to save the current
state, or restore a saved state), and for expressing stop
criteria.
In order to set up the floor for the introduction of
the new sequence variable, we give details on how
the model is represented and it is updated during the
search.
The data structure behind a model is a graph,
called the propagation graph, which we can approxi-
mate to a directed acyclic graph, where the nodes are
variables and invariants. Variables have an associ-
ated type and implement specific algorithms related
to their type. Invariants have specific definitions, and
implement this definition mostly through incremental
algorithms. Edges in the graph represent data flows
from variables to listening invariants and from in-
variants to controlled variables. The directed acyclic
graph starts with input (a.k.a. decision) variables, and
typically ends at a variable whose value is maintained
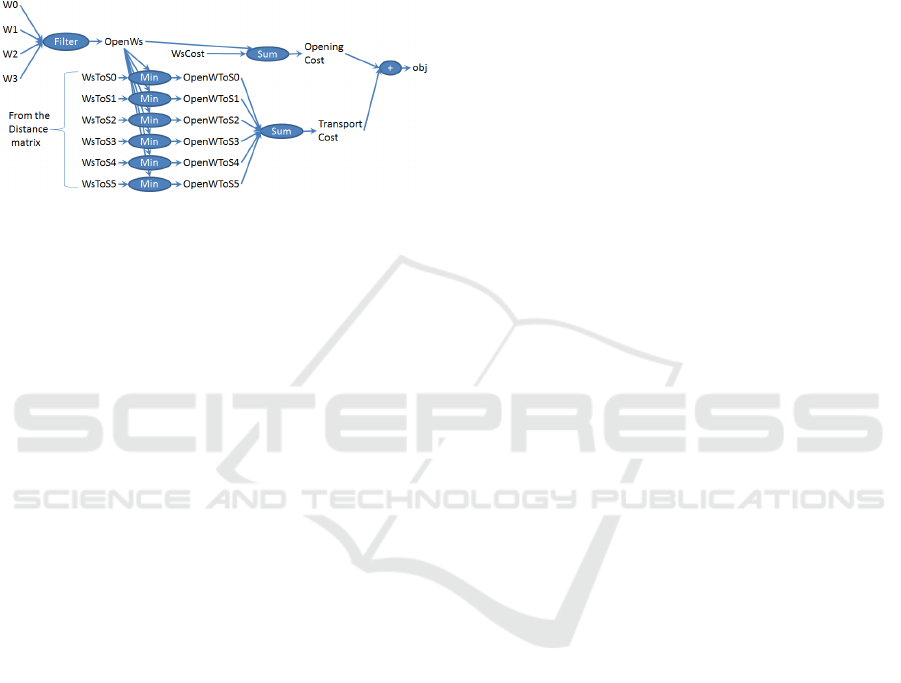
to be the one of the objective function. Figure 1 il-
lustrates a propagation graph for a simple warehouse
location problem.
In such engine, propagation is about propagating
updates along the propagation graph in such a way
that a node is reached at most once by the update
wave, and only if one of its inputs has changed and
Supporting Efficient Global Moves on Sequences in Constraint-based Local Search Engines
173
if needed by the model update. OscaR.cbls manages
this wave by sorting the nodes based on the distance
from the decision variables. The propagation is co-
ordinated through a dedicated heap that aggregates
nodes at the same distance in a list. This offers a
slightly better time complexity than the classical ap-
proach based on topological sort initially presented in
(Van Hentenryck and Michel, 2009).
Figure 1: Propagation graph on a warehouse location prob-
lem.
The search for a solution starts from an initial
solution and explores the specified neighbourhood.
Each neighbour solution is examined by modifying
the input variables, and querying the objective func-
tion of the model which is updated through propaga-
tion.
During propagation, variables notify each invari-
ant listening to them about their value change. Such
notifications carry the necessary information about
the value change of the variable. For integer variables,
it carries a reference to the variable, and the old and
new value of the variable. For set variables, it carries
a reference to the variable, the old value of the vari-
able, the new value of the variable, and both the set
of values that have been added and removed from the
variable. All values transmitted by variables, through
notification or through queries to the variables are im-
mutable, to make the implement of algorithms in in-
variants easier.
3 REQUIREMENTS OVER A
SEQUENCE VARIABLE
Our contributed sequence variable implements the
following set of requirements, which have been iden-
tified from the way such variables are to be used in a
CBLS engine, and from opportunities that they could
open up, notably for supporting efficient global con-
straints:
• speed-exploration Sequence variables value
should be updated very quickly in the context of
neighbourhood exploration to reflect moves that
are typically explored in routing, such as insert
value, remove value, 1-opt, 2-opt, 3-opt.
• symbolic-large-delta Sequence variables should
transmit the symbolic structure of such move that
involve large modification of their value, so that
invariants that derive values out of sequences of
integer receive the high-level information of the
delta that the variable has encountered.
• pre-computation There should be some kind of
mechanism for invariants to know when they can
perform pre-computation on the current value of
a sequence variable, so that they can exploit such
pre-computation in order to quickly update the
neighbour values during neighbourhood explo-
ration.
• speed-move-taken Sequence variables should be
updated quickly to reflect move that are being
taken, considering the same moves as the require-
ment speed-exploration. This requirement has a
lower priority than speed-exploration since there
are more neighbours explored than moves taken.
• immutable-value The value representing a se-
quence of integers should be non-mutable, that
is: once transmitted to an invariant or saved, it
should not be modified. A variable can of course
change its value. This requirement is relevant be-
cause sequences are represented by complex and
non-atomic data structures.
From the set of neighbourhoods mentioned in
the speed-exploration and speed-move-taken require-
ments, we identify the following basic updates that
our implementation must support:
• insert an integer value at a given position, and
shift the tail of the sequence by one position up-
wards. The parameters of this update are: the po-
sition of the insert, and the inserted value.
• delete the integer value at a given position, and
shift the tail of the sequence by one position
downwards. This update has one parameter that
is the position of the deleted integer.
• seq-move that moves a sub-sequence to another
position, and optionally, flip it during the move.
This update has four parameters: the start posi-
tion of the moved segment, the end position of the
moved segment, the position after which the seg-
ment must be moved to, and a Boolean specifying
if the subsequence is flipped during the move.
These updates can be composed together to consti-
tute a composite update, such as a two point move in
Pick-up and Delivery Problems (PDP) (Savelsbergh
and Sol, 1995), or a value assign in string optimiza-
tion that is a composition of delete and insert.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
174

4 IMPLEMENTATION
This section presents our implementation of a se-
quence of integers. It starts by a description of our
dedicated data structures for representing immutable
sequence values. Then, we introduce how sequence
variables interact with sequence values, as well as our
check-pointing mechanisms. We wrap up with a ta-
ble presenting the complexity of all the queries and
update operations of our sequence variable.
4.1 Sequences as Mappings
Sequences can be represented using several data
structures. Typically, they can be represented using
lists, arrays or mappings from positions to values. All
these data-structures can be mutable or non-mutable.
Mutable data structures are forbidden altogether in
our approach because of the immutable-value require-
ment. Non-mutable lists and array have O(n) com-
plexity for insert, delete and seq-move operations.
Besides, lists do not enable accessing their elements
by positions efficiently.
Our approach is to represent sequences of inte-
gers as a continuous mapping from positions to val-
ues, where positions are integer values ranging from
zero to the length of the sequence minus one.
Exploring such relations for consecutive values
is therefore costly because they are typically imple-
mented through O(log(n)) balanced trees data struc-
tures. Our implementation provides a standard mech-
anism for speeding up sequence explorations. An ex-
plorer is a temporary non-mutable object represent-
ing a certain position in a given sequence. It can be
queried for the position in the sequence and the value
at its position. Besides, an explorer can be queried for
the explorer at the next or at the previous position in
the sequence. For instance, an explorer on a red-black
tree supports the value and position queries in O(1)
and the next and prev operation in O(1), amortized.
4.2 Stacked and Concrete Updates
Thanks to the representation as a map, we can im-
plement the speed-exploration requirement through
stacked updates: when a move is explored, a dedi-
cated non-mutable class is created that offers the same
API as a sequence, and behaves according to the value
it represents by translating and forwarding queries it
receives to the original non-modified sequence. Such
dedicated non-mutable class representing modified
sequences can be instantiated in O(1) and are called
stacked updates because they constitute a stack of up-
dates, starting at the concrete sequence. For each of
the three update classes (insert, remove, seq-move),
a dedicated class implementing a sequence modified
according to this move class can be implemented.
For instance, considering the remove operation,
the query that gets the value at a given position is im-
plemented as follows:
c l a s s R emov ed Po in tS eq ue nc e (
o r i g i n a l S e q u e n c e : I n t S e q u e n c e ,
p os i t io n O fR e m ov e : I n t )
e x t en d s I n t S e q u e n c e {
d ef g e t V a l u e A t P o s i t i o n ( po s : I n t ) =
o r i g i n a l S e q u e n c e . g e t V a l u e A t P o s i t i o n (
i f ( p os < p o s it i o nO f R em o v e ) pos
e l s e p os +1)
}
Each forwarding performed by the stacked up-
dates adds up to the complexity of such queries, gen-
erally a O(1) term, which can have a more-less im-
portant constant weight. Stacked updates are de-
signed for neighbourhood exploration, provided the
exploration is performed in a star mode, and provided
each move is performed on the initial value of the se-
quence. They are however not adapted to exploration
performed in circle mode, nor to committing moves
when they are actually taken, because they would ac-
cumulate and the overhead would make them imprac-
tical. Such updates are therefore performed on the
concrete representation of sequences.
The concrete representation of a sequence repre-
sents the map from positions to values through a dou-
ble mapping that maps positions to an internal posi-
tion and then maps the internal position to the actual
value.
The first mapping is a piecewise affine bijection,
where each affine piece has a slope +1 or −1 and
an offset. Each of these affine transformations apply
within a given interval of value taken from the range
of positions in the sequence. A red-black tree maps
the starting value of the interval of each affine trans-
formation to the actual transformation. Given a po-
sition in the sequence, the corresponding internal po-
sition can thus be identified in O(log(k)) where k is
the number of affine transformations in this mapping.
The reverse transformation is also available with the
same representation. This mapping is illustrated in
Figure 2.
The second mapping is made of two red black
trees, one maps the internal position to the actual
value, and the other is the reverse; it maps a value
to the set of internal positions where it occurs.
The purpose of the double mapping is that the first
mapping can be efficiently updated in O(k ∗ log(k))
to reflect the three update operations considered here.
Applying such update can increase or decrease the
Supporting Efficient Global Moves on Sequences in Constraint-based Local Search Engines
175
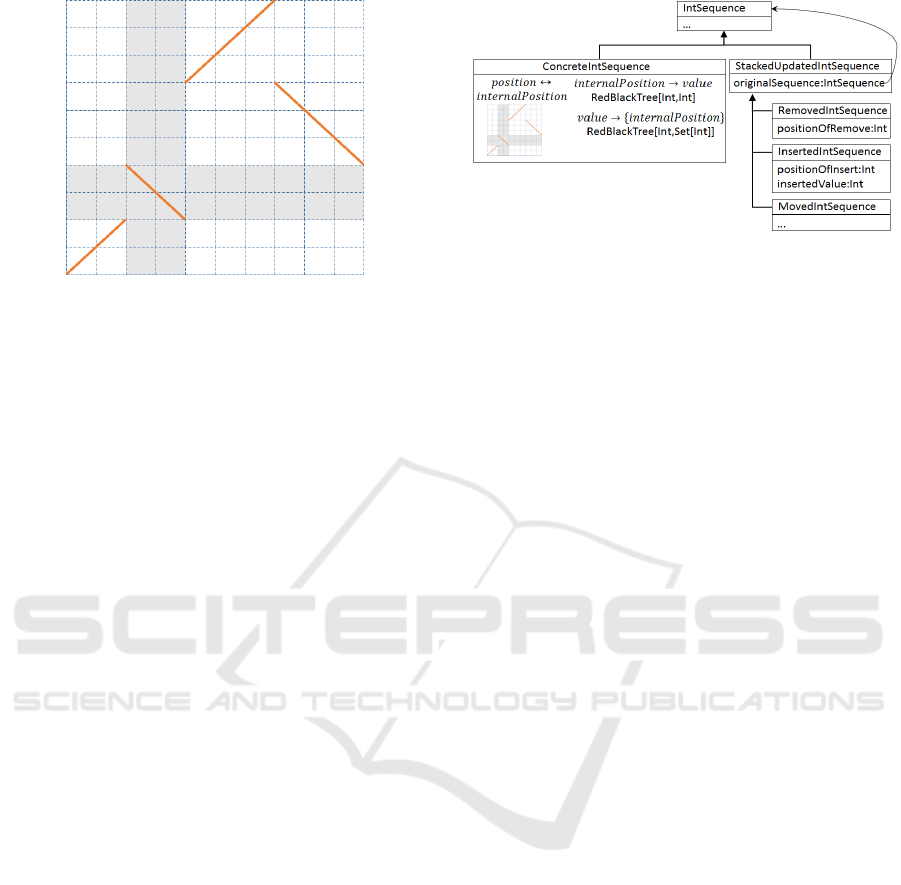
Figure 2: Illustrating the piecewise affine bijection that
maps positions to internal positions.
number of affine functions in the first mapping. The
update procedure of this mapping ensures that the
number of affine functions is minimal, in most cases.
This is how the requirement speed-move-taken is im-
plemented in our system.
To avoid a significant increase of the number of
affine segments in the first mapping, it is bounded at
start-up to a maximal value. Whenever this value is
reached, a regularization operation is performed to
simplify the first mapping to the identify function, and
correct the two potentially large red black trees of the
second mapping accordingly. The choice of this max-
imal k value is a key choice and will be investigated in
more detail later in this paper, both from the theoreti-
cal point of view of the resulting complexity and from
the practical point of view through some benchmarks.
The concrete representation and the stacked up-
dates are all implemented through non-mutable data
structures exclusively to comply with the requirement
immutable-value.
An illustration of the object actually created in
shown in Figure 3 in the case of a sequence with a
stacked delete update. It shows the internal structure
of the concrete sequence, with its bijection and the
two red black trees, and the stacked update represent-
ing the sequence where the value at a given position
has been deleted. They both implement the API of
IntSequence.
4.3 Checkpointing
Sequence variables support a notion of checkpoint
that serves the following purposes:
• notify invariants about the possibility to perform
pre-computation that they can exploit in order
to evaluate neighbour solutions in the context of
neighbourhood exploration. Neighbourhoods op-
erating on a sequence variable are therefore re-
quired to notify to the variable when they start
Figure 3: Architecture behind our sequence data structure.
a star-mode exploration and register the current
value as a checkpoint, and must release the check-
point after the exploration is completed.
• provide an operation “roll back to checkpoint”
to neighbourhoods, so that a neighbourhood can
simply invoke this update operation, and the vari-
able can reload the previous value in O(1) by re-
verting to the previous value (which is still stored
in the internal structure of the variable)
• provide a notification message that the sequence
variable can send to the invariant to notify that
the value has been reverted to the latest declared
checkpoint. Invariants might be able to update
their output and/or internal state efficiently, know-
ing this high-level information.
The OscaR.cbls framework supports the cross-
product of neighbourhoods (De Landtsheer et al.,
2015). It is implemented by nesting one neighbour-
hood into another, with optional, user-specified prun-
ing. The check-pointing mechanism proposed here
must therefore support stacked checkpoints, so that
the outer and the inner neighbourhoods can both de-
clare their checkpoint and interact with the variable as
if they were operating alone.
We can distinguish three strategies for communi-
cating checkpoints between neighbourhoods and in-
variants. First, a transparent-checkpoint approach can
be used, where all checkpoint definition and release
are communicated to the listening invariant. Sec-
ond, only the topmost checkpoint is communicated,
third, only the latest checkpoint is communicated; ad-
ditional release instructions are inserted in this last
communication by the sequence variable to ensure a
coherent presentation of the checkpoint definition and
release. So far, Our system so far incorporates the
latest-checkpoint strategy.
To use this mechanism, neighbourhoods must first
notify that they will explore around the current value
of the variable, setting it as a checkpoint, so that in-
variants are notified that they should perform their
pre-computations on this value. Then, the neighbour-
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
176

hood can perform its exploration by repeatedly mov-
ing to a neighbour solution, evaluating the objective
function, and performing a roll-back to the declared
checkpoint. When the exploration is completed, the
neighbourhood must release its checkpoint through a
dedicated method call.
This mechanism of checkpoint is not to be mixed
up with the one presented in (Van Hentenryck and
Michel, 2005). The checkpoints presented here aim
at performing pre-computation, making it possible to
reach the efficiency of what Comet calls differentia-
tion (Van Hentenryck and Michel, 2009).
4.4 The Sequence Variable and its Delta
To modify a sequence variable, neighbourhoods use
the update operations supported by the sequence
value. They can also specify a checkpoint to the vari-
able, and call a rollBackToCheckpoint to this defined
checkpoint. These operations are available through
the API of sequence variables.
Upon propagation, a sequence variable notifies its
update to all its listening invariants through dedicated
data structures representing the succession of updates
that have been performed on it since its previous prop-
agation, namely: a succession of insert, delete, seq-
move, and checkpoint definitions, starting up with a
roll-back to a defined checkpoint, an assignment, or a
marker denoting the previously last notified value.
4.5 Complexity of Operations on
Sequence Values
The complexity of the main queries implemented on
sequence values are summarized in Table 1, where k
is the maximal number of affine functions in the first
mapping of the concrete sequence, and n is the length
of the sequence. It shows the cost on the concrete se-
quence as well as the additional cost for each stacked
update. Computing value at position if logarithmic
both in n and k while computing position at value is
less efficient. Moving to the next value using an ex-
plorer is O(1) in amortized cost.
The complexity of the main update operations are
summarized in Table 2. The first column shows the
complexity of quick updates. The second column
represent the complexities of the concrete updates
assuming that no regularization occurs. The third
column is the complexity of the concrete updates,
considering the amortized complexity of regulariza-
tion. The regularization operation has a complexity
of O(n ∗ log(k)), takes place at most every Ω(k) up-
dates, so it adds O(n ∗ log(k)/k) amortized complex-
ity. The regularization is not O(n ∗ log(n)) although
it requires rebuilding red black trees of size O(n) be-
cause the trees are built in a batch mode on already
sorted keys, thus in O(n). To compare with, the com-
plexities of these updates on a concrete representation
made of a single mapping through red black trees is
O(n) for each of these updates.
Concretely, in our implementation, the user can
control the value of k through a percentage of the ratio
k/n with a default value of 4%
The overall run time of a full-fledged local search
solver is dominated by the cost of exploring neigh-
bours, and in a much smaller way, by the cost of
performing the moves and performing some pre-
computations. Pre-computations being performed by
the invariants, they are not considered here. If we
exclusively focus on the cost incurred by the data
structures, these amount to O(1) per neighbour, and
O(log(x) + log(k) ∗ (k + n/k)) (with x being n or k,
depending on the move), respectively.
Table 1: Time complexity of queries on a sequence value.
value at position positions of value explorer explorer.next
concrete O(log(n) O(#positions ∗ log(k) O(log(n) O(1) amortized
sequence +log(k)) +log(n)) +log(k))
added cost for O(1) O(#positions) O(1) O(1) amortized
each stacked update
Table 2: Time complexity of updates on a sequence value.
quick update concrete update concrete update
without regularization with amortized regularization
insert O(1) O(log(n) + k ∗ log(k)) O(log(n) + log(k ) ∗ (k + n/k))
delete O(1) O(log(n) + k ∗ log(k)) O(log(n) + log(k ) ∗ (k + n/k))
seq-move O(1) O(k ∗ log(k)) O(log(k) ∗ (k + n/k))
Supporting Efficient Global Moves on Sequences in Constraint-based Local Search Engines
177

5 VALIDATING THE CONCEPT
OF SEQUENCE VARIABLE
This section validates our concept of sequence vari-
able by explaining how a few representative global
constraints or objective functions can be modelled
and benefit from our state-of-the-art algorithms. We
focus on three examples, two of them are taken from
the context of vehicle routing problem: symmetric
constant routing distance, and node-vehicle restric-
tions. The last example is more generic: sequence
flipping.
The routes of v vehicles are represented as a single
sequence of integers where each integer is present at
most once, and represent a node of the routing prob-
lem. Their start nodes are 0 to v−1 and should always
be in the sequence, and in this order. A vehicle implic-
itly comes back to its start node at the end of its route.
Figure 4 shows this encoding for a problem with 3 ve-
hicles and 9 nodes. Also, there is a convention that a
subsequence that is moved by a seq-move cannot in-
cludes a start node. All our routing neighbourhoods
have such behaviour.
Figure 4: Encoding of a routing problem with three vehicles
using a single sequence.
The rationale for this representation is that moves
involving two vehicles can be performed efficiently
using our efficient data structures since there is no
need to transfer data between two sequences.
5.1 Symmetric Constant Routing
Distance
Symmetric constant routing distance is an invariant
that maintains the total distance driven by all vehicles,
based on a distance matrix specifying the distance be-
tween each pair of node, knowing that this matrix is
symmetric. This metric is very frequent at least in
academic literature. It is also a classic example where
a global constraint can update its value in O(1) run
time against the classical routing neighbourhoods (1-
opt, 2-opt, 3-opt) (Glover and Kochenberger, 2003).
We illustrate it on the 2-opt only for conciseness and
consider a single vehicle.
Upon a two-opt move, the global constraint is no-
tified about a mode update, which is a simple flip.
This update specifies a start position and an end po-
sition in the sequence that are the start and end of
the flipped segment. From these value, it is able to
compute the delta on the global distance driven by the
considered vehicle since it only is impacted by the
changes at the extremities of the flipped segment.
5.2 Node-vehicle Restriction
Given a number of atomic constraints specifying for-
bidden couples (node; vehicle), a global constraint for
node-vehicle restrictions maintains a degree of viola-
tion, i.e. the number of such couples that occur in
the current routes. A fundamental observation is that
the violation degree only changes when nodes are in-
serted, deleted or when a segment of route is moved
from one vehicle to another one. We focus on the last
move exclusively as the two others are trivial.
This invariant relies on pre-computation to evalu-
ate such moves efficiently. The pre-computation pro-
cess examines the routes at the checkpoint, and dec-
orates each step of each route with a map relying
each vehicle to number of nodes since the start of the
route that cannot be reached by this vehicle, accord-
ing to given individual constraints. Evaluating a move
that moves a segment from one vehicle to another
one requires counting the number of nodes within the
moved segment that cannot be reached by the vehicle
from which the segment is removed, and the number
of such nodes that cannot be reached by the vehicle to
which the segment is moved. These two values can be
obtained in O(log(v)) from the pre-computed values,
since we need to identify the vehicles involved by the
moves.
5.3 Sequence Flipping
This invariant maintains an output sequence variable
to be the flipped value of an input sequence variable.
It is not specifically related to routing and clearly
demonstrates the flexibility of our framework. This
invariant is implemented by translating the moves on
the input sequence variable into moves operated on
the output sequence variable. It mainly requires trans-
lating all indices i appearing in notification messages
received from the input sequence variable by trans-
forming them into length − i when the message are
forwarded to the output sequence variable.
6 BENCHMARKING
This section presents a benchmark to illustrate the ef-
ficiency of sequence variables and the impact of the k
factor of our sequence of integers.
The benchmark exclusively focuses on this vari-
able; run times are to be considered with the greatest
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
178
care since they are heavily dependent on the search
procedure in use. The latter is under the responsibil-
ity of the OR practitioner.
The benchmark is a VRP with 100 vehicles and
various numbers of nodes on a symmetric distance
matrix and no other constraint. The total distance
driven by all vehicles must be minimized. The prob-
lem roughly declares as follows, using various bricks
of our framework:
v a l r o u t e s =
CBLSSeqVar (m, 0 t o v−1, n −1 ,
KNFacto r )
v a l t o t a l D i s t a n c e =
C o n s t a n t R o u t i n g D i s t a n c e ( r o u t e s , v ,
s y m m e t r i c D i s t a n c e M a t r i x )
v a l o b j = t o t a l D i s t a n c e
+ 1 00 00 ∗( n − S i z e ( r o u t e s ) )
It starts with no node routed, and uses a mix of in-
sert point, one point move, two opt and three opt with
various parameters. An important parameter of these
neighbourhood is a w factor; when considering neigh-
bour nodes, only the w nearest one are considered by
the neighbourhood. For the sake of completeness, the
search procedure is given here below. It is instan-
tiated using neighbourhood combinators (De Landt-
sheer et al., 2015). It combines different classical
VRP neighbourhoods using a variant of hill climbing,
and ends up with tree opt neighbourhood with a larger
w factor.
v a l s e a r c h =
B e s t S l o p e F i r s t (
I n s e r t P o i n t U n r o u t e d F i r s t (w= 1 0 ) ,
I n s e r t P o i n t R o u t e d F i r s t (w=1 0 ) ,
on ePo int Mo ve (w= 1 0) ,
twoOpt (w= 2 0 ) ,
t h r e e O p t (w= 1 0 ) )
e xh a us t t h r e e O p t (w=20 )
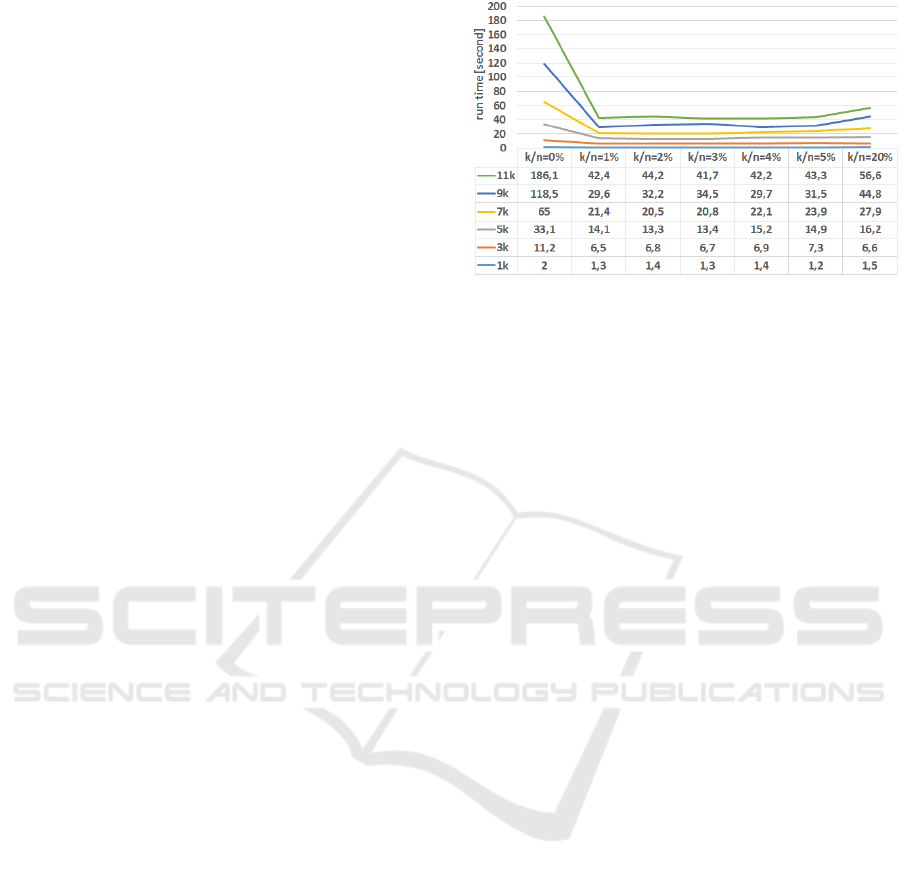
Figure 5 shows the run time of the optimization
engine for various values of the k/n percentage. Each
curve reports on a set of benchmark performed with
a given value for n, ranging from 1k to 11k by step
of 2k. The runs have been performed three times, and
the median value is reported. The benchmarks have
been executed on a laptop with Intel Core i7 2.3GHz
with 16Go of RAM, and 4 Gb allocated to the Java
Runtime Environment.
On this diagram, we clearly see the impact of the
k/n percentage on the run time. A value of zero
is clearly suboptimal; it actually disables the system
of piecewise affine bijection presented in Section 4.
Above 1, the impact of this factor on the run time
reaches a plateau. Efficiency decreases again if the
k/n ratio gets too large; a sample value of 20 is il-
Figure 5: Run time (in seconds) vs. various values of k/n
for various values of n.
lustrated. Another phenomenon to be noted is that
the impact of this mechanism grows with the size of
the considered problem; this is probably due to the
non-linear nature of the complexities, as presented in
Section 4.5. A last phenomenon that is clearly visi-
ble on the figure is that all curves seem to experience
the same behaviour at the same value, although this
is possibly due to the coarse steps used in the bench-
mark. This is an indication that controlling the k via a
ratio k/n is an adequate approach.
7 CONCLUSION
This paper presented an implementation of variables
of type “sequence of integers” that is suited for declar-
ative local search frameworks that manipulate con-
cepts such as variable and invariants, also known as
Constraint-Based Local Search. The goal is to effi-
ciently represent and apply global moves such as the
ones applied in vehicle routing, and to communicate
such moves in a concise way to invariants, so that they
can apply efficient global algorithms.
A very important open issue to validate our work
is to perform comparative benchmark between our ap-
proach and other implementations. Such benchmark
is however not easy to set up since similar tools men-
tioned in the background use different models and dif-
ferent search procedure with different trade-offs be-
tween seed and optimality. The efficiency of such tool
is somehow the product of the efficiency of the model
and the efficiency of the search procedure.
Having defined the possible updates to sequence
values, and a few global invariants, our next step will
be to extend our library of invariants with additional
global invariants operating on sequences. The trav-
elling delivery man metrics defined in (Mladenovi
´
c
et al., 2013) is an example of relevant global con-
straints that can be added to our framework. Such
Supporting Efficient Global Moves on Sequences in Constraint-based Local Search Engines
179

extension will be of course tailored to our API, which
will force us to have quite generic implementations
that can operate on any neighbourhoods, since they
express their moves through the sequence API. Sim-
ilarly, an appropriate set of generic neighbourhoods
operating on sequences must also be proposed to
make this sequence variable fully usable. So far, only
routing neighbourhoods have been implemented.
Our sequence variable features a checkpoint
mechanism that is useful for global constraints to per-
form pre-computations. As discussed above, there are
several policies on how to manage such checkpoints.
Our framework only implements one of these poli-
cies, but other policies can be added to the engine. Be-
sides, this mechanism is restricted to sequence vari-
ables. It should be made pervasive in the model, so
that invariants with other type of variables could also
perform such pre-computations.
This new variable type will be included in the
CBLS engine of OscaR 4.0 to be released in Spring
2017 (OscaR Team, 2012). With this additional
type of variable, we hope that OscaR.cbls will be
even more appealing both to users that benefit from
highly efficient global constraints in a declarative lo-
cal search engine, and to researchers who aim at de-
veloping new global constraints and will benefit from
the whole environment of OscaR.cbls, so they can fo-
cus on their own contribution. This implementation
will also offer a common benchmarking environment
to compare the efficiency of e.g. global constraints
within a standard setting.
ACKNOWLEDGEMENTS
This research was conducted under the SAMOBI
CWALITY research project from the Walloon Region
of Belgium (grant number 1610019).
REFERENCES
Abdulla, P. A., Atig, M. F., Chen, Y.-F., Hol
´
ık, L., Rezine,
A., R
¨
ummer, P., and Stenman, J. (2015). Norn: An
SMT Solver for String Constraints, pages 462–469.
Springer International Publishing, Cham.
Benoist, T., Estellon, B., Gardi, F., Megel, R., and Nouioua,
K. (2011). Localsolver 1.x: a black-box local-search
solver for 0-1 programming. 4OR, 9(3):299 – 316.
Bj
¨
ordal, G. (2016). String variables for constraint-based
local search. Master’s thesis, UPPSALA university.
Croes, G. A. (1958). A method for solving traveling sales-
man problems. Operations Research, 6:791–812.
De Landtsheer, R., Guyot, Y., Ospina, G., and Ponsard, C.
(2015). Combining neighborhoods into local search
strategies. In Proceedings of MIC’2015.
De Landtsheer, R. and Ponsard, C. (2013). Oscar.cbls :
an open source framework for constraint-based local
search. In Proceedings of ORBEL’27.
De Moura, L. and Bjørner, N. (2008). Z3: An effi-
cient SMT solver. In Proc. of the Theory and Prac-
tice of Software, 14th Int. Conf.on Tools and Algo-
rithms for the Construction and Analysis of Systems,
TACAS’08/ETAPS’08.
Di Gaspero, L. and Schaerf, A. (2003). EASYLOCAL++:
an object-oriented framework for the flexible design
of local-search algorithms. Software: Practice and
Experience, 33(8):733–765.
Fu, X., Powell, M. C., Bantegui, M., and Li, C.-C. (2013).
Simple linear string constraints. Formal Aspects of
Computing, 25(6):847–891.
Ganesh, V., Kie
˙
zun, A., Artzi, S., Guo, P. J., Hooimeijer,
P., and Ernst, M. (2011). HAMPI: A String Solver for
Testing, Analysis and Vulnerability Detection, pages
1–19. Springer Berlin Heidelberg, Berlin, Heidelberg.
Glover, F. and Kochenberger, G. (2003). Handbook of
Metaheuristics. International Series in Operations Re-
search & Management Science. Springer US.
Mladenovi
´
c, N., Uro
ˇ
sevi
´
c, D., and Hanafi, S. (2013). Vari-
able neighborhood search for the travelling delivery-
man problem. 4OR, 11(1):57–73.
Newton, M. A. H., Pham, D. N., Sattar, A., and Maher, M.
(2011). Kangaroo: an efficient constraint-based local
search system using lazy propagation. In Proceedings
of CP’11, pages 645–659.
OscaR Team (2012). OscaR: Operational research in
Scala. Available under the LGPL licence from
https://bitbucket.org/oscarlib/oscar.
Pralet, C. and Verfaillie, G. (2013). Dynamic online plan-
ning and scheduling using a static invariant-based
evaluation model. In ICAPS.
Savelsbergh, M. W. P. and Sol, M. (1995). The general
pickup and delivery problem. Transportation Science,
29:17–29.
Schrijver, A. (2005). On the history of combinatorial opti-
mization (till 1960). In K. Aardal, G. N. and Weisman-
tel, R., editors, Discrete Optimization, volume 12 of
Handbooks in Operations Research and Management
Science, pages 1 – 68. Elsevier.
Scott, J., Flener, P., and Pearson, J. (2015). Constraint solv-
ing with bounded string variables. In Michel, L., ed-
itor, CP-AI-OR 2015, volume 9075 of LNCS, pages
373–390. Springer.
Van Hentenryck, P. and Michel, L. (2005). Control abstrac-
tions for local search. Constraints, 10(2):137–157.
Van Hentenryck, P. and Michel, L. (2009). Constraint-based
Local Search. MIT Press.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
180
