Optimized Limited Memory and Warping LCSS for Online Gesture

Recognition or Overlearning?

Baptiste Lemarcis

, Valère Plantevin

, Bruno Bouchard

and Bob-Antoine-Jerry Ménélas

Department of Mathematics and Computer Science, Université du Québec à Chicoutimi (UQAC), Chicoutimi,

QC, G7H 2B1, Canada

IEEE Senior, Chicoutimi, QC, Canada

Keywords: Online Gesture Recognition, Streaming, Template Matching Method, LCSS, LM-WLCSS.

Abstract: In this paper, we present and evaluate a new algorithm for online gesture recognition in noisy streams. This

technique relies upon the proposed LM-WLCSS (Limited Memory and Warping LCSS) algorithm that has

demonstrated its efficiency on gesture recognition. This new method involves a quantization step (via the K-

Means clustering algorithm). This transforms new data to a finite set. In this way, each new sample can be

compared to several templates (one per class) and gestures are rejected based on a previously trained rejection

threshold. Then, an algorithm, called SearchMax, find a local maximum within a sliding window and output

whether or not the gesture has been recognized. In order to resolve conflicts that may occur, another classifier

could be completed. As the K-Means clustering algorithm, needs to be initialized with the number of clusters

to create, we also introduce a straightforward optimization process. Such an operation also optimizes the

window size for the SearchMax algorithm. In order to demonstrate the robustness of our algorithm, an exper-

iment has been performed over two different data sets. However, results on tested data sets are only accurate

when training data are used as test data. This may be due to the fact that the method is in an overlearning state.

1 INTRODUCTION

In everyday communications, a large part of infor-

mation is conveyed thought gestures. As a result, it

appears that some benefits would certainly come in

exploiting gesture recognition technics in Human-

Computer Interactions. Gesture recognition has be-

come important in a wide variety of applications such

as gesture-to-speech in sign languages (Kılıboz and

Güdükbay, 2015, Rung-Huei and Ming, 1998). In the

past years, smartphones and smartwatches have be-

come omnipresent in everyday life (Guiry et al.,

2014), being equipped with multiple motion-related

sensors such as accelerometers, gyroscopes and mag-

netometers, they allow sensing raw data related to

movements of users. With the treatment of these data

streams, multiple techniques allow to detect per-

formed gestures. The literature regarding online ges-

ture recognition counts many methods such as Hidden

Markov Model (Hyeon-Kyu and Kim, 1999), Support

Vector Machine (Dardas and Georganas, 2011) and

Template Matching Methods (TMMs). TMMs ex-

press gestures as templates that are compared with the

data-stream afterward. The objective of such a com-

putation is to find similarities, where the highest af-

finity involves the recognition of the fittest gesture.

To do so, TMMs may employ Dynamic Time Warp-

ing (DTW) as similarity measure (Reyes et al., 2011).

Although DTW-based TMMs achieve accurate

results, the work described in (Vlachos et al., 2003)

shows that this method is not well suited to handle

time series and noise produced by inertial sensors. In

that sense, the LM-WLCSS (Limited Memory and

Warping Longest Common Sub-Sequence) aims at

overcoming issues brought by DTW. This method re-

lies upon the WLCSS method, an extension of the

LCSS problem. However, Roggen et al. (2015) did

not focus on class optimization and set arbitrary pa-

rameters for the clustering algorithm and the size of

the window. In this paper, we want to improve the

LM-WLCSS algorithm, hence we present a new

method based on that algorithm by focusing on the

class optimization process to spot gestures of a

stream. To achieve it, we train and optimize the LM-

WLCSS for each class. More precisely, the process

that convert the uncountable set of accelerometer data

to a countable one, called the quantization process, is

108

Lemarcis B., Plantevin V., Bouchard B. and MÃl’nÃl’las B.

Optimized Limited Memory and Warping LCSS for Online Gesture Recognition or Overlearning?.

DOI: 10.5220/0006151001080115

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 108-115

ISBN: 978-989-758-229-5

performed for each gesture independently as the en-

tire recognition flow. The final decision is achieved

through a decision fusion.

The remainder of this paper is organized as fol-

lows. Section 2 reviews template matching methods

based on the longest common subsequence (LCSS).

Section 3 describes the proposed method. Next, sec-

tion 4 exposes data sets used for our experiments.

Section 5 reviews and discusses the results obtained.

Finally, Section 6 draws a conclusion.

2 RELATED WORK

In this paper we present a new approach, based on the

LM-WLCSS. Our state of the art briefly summarizes

related methods. We first introduce the training phase

of the Segmented and Warping LCSS. Then, the

recognition phase of these methods are described re-

spectively. We also present the LM-WLCSS as our

technique is derived from it. Finally, we present our

contributions to the LM-WLCSS.

Templates matching methods (TMMs) (Hart-

mann and Link, 2010) based on Dynamic Time Warp-

ing (Hartmann and Link, 2010), were demonstrated

as non-efficient in presence of noisy raw signals (Vla-

chos et al., 2003). To handle such data, Long-Van et

al. (2012) have introduced two new methods, based

on Longest Common Subsequence (LCSS), Segment-

edLCSS and WarpingLCSS. Both methods share the

same training phase. This training allows converting

accelerometer data into strings. This is due to the fact

that LCSS is based on a problem that relies upon

strings. For this, raw signals must be quantized. The

quantization step, proposed in (Long-Van et al.,

2012), involves computing clusters upon the training

data with the K-Means algorithm. Those centroids are

associated with pre-defined symbols to form strings.

Therefore, each gesture instance is represented as a

sequence of symbols. A LCSS score is associated

with each sequence. The higher the LCSS score is be-

tween two elements, the greater the similarity is. A

gesture instance is thus defined as a temporary tem-

plate. The final motif is chosen based on the one with

the highest average LCSS score. However, in order to

be able to compute whether a signal belongs to a ges-

ture class or not, a rejection threshold is associated

with the template. This threshold is defined as the

minimum LCSS between the previously elected tem-

plate and all other gesture instances of the same class.

Yet, Nguyen-Dinh et al. (2014b) have suggested a

new rejection threshold calculation, based on the

mean μ

and standard deviation σ

of LCSS scores for

the given class c. The resulting threshold ε is defined

as ε= μ

-h·σ

, where h is an integer that allows ad-

justing the sensitivity of the algorithm for this class.

In the Segmented LCSS recognition process, the

stream is stored in a sliding window OW. Each sam-

ple of this window is associated with previously gen-

erated centroids and its related symbol, based on the

minimum Euclidean distance. Then, this new string is

entirely compared to the template computed during

the training. If the resulting score exceeds the rejec-

tion threshold, of the associated class, then the gesture

is associated to c. However, a gesture may be spotted

as belonging to more than one class. To resolve such

conflicts, a resolver may be added, as proposed in

(Long-Van et al., 2012). It is based on the normalized

similarity

NormSim(A, B) = LCSS(A,B)/max(

‖

), where

‖



‖

and

‖



‖

are respectively the length of A and B

strings. The class with the highest NormSim is then

marked as recognized. However, the Segmented

LCSS method implies to recompute the score each

time the sliding window is shifted. As a result, the

computation time is O(T

) (with T the size of the

longest template) in the worst case. However, without

OW the LCSS algorithm cannot find boundaries of in-

coming gestures. In this way, Long-Van et al. (2012)

have introduced a new variant of the LCSS called

WLCSS (WLCSS).

The WLCSS method removes need of a sliding

window and improves the computational cost as it au-

tomatically determines gesture boundaries. In this

new variant, quantized signals are still compared to

the template of a given class. Nevertheless, this ver-

sion only update the score for each new element,

starting from zero. This score grows when a match

occurs and decreases thanks to penalties otherwise.

The penalty consists of a weighted Euclidean distance

between symbols, whether it is a mismatch, a repeti-

tion in the stream or even in the template. In a newer

version presented in (Nguyen-Dinh et al., 2014b), the

distance is normalized. Once the matching score is

updated, the final result is output by the same decision

maker used in the SegmentedLCSS method. The re-

sulting time complexity for this new method is O(T).

Although the computational cost WLCSS is one order

of magnitude lower than the SegmentedLCSS, the

memory usage remains O(T

) in the worst case.

Recently, Roggen et al. (2015) have proposed a

new, microcontroller optimized, version of the

WLCSS algorithm called Limited Memory and

WLCSS (LM-WLCSS). Identically to previous meth-

ods, this one is designed to spot motif in noisy raw

signals and focuses on a single sensor channel. In this

way, a quantization step may not be required. More-

over, the training phase of this new variant has also

Optimized Limited Memory and Warping LCSS for Online Gesture Recognition or Overlearning?

109

been modified to be embedded. This new step con-

sists in recording all gestures, and defining the first

instance as the template. The rejection threshold for

this template is then computed thanks to the LM-

WLCSS instead of the LCSS. As the WLCSS has

edged issues, authors have modified the formula, and

the resulting matching score is computed as follows:

j,i













0 ,ifi0orj0

j‐1,i‐1

R ,ifS

‐T

ε

max

j‐1,i‐1

‐P∙S

‐T



j‐1,i

‐P∙S

‐T



j,i‐1

‐P∙S

‐T



,ifS

‐T

ε



1

Where S

and T

are respectively defined as the first

i sample of the stream and the first j sample of the

template. The resulting score,

j,i

, starts from zero

and increases of reward R, instead of just one, when

the distance between the sample and the template

does not exceed a tolerance threshold

ε. Otherwise,

the warping occurs and the matching score

j,i

de-

creases of a penalty different from the WLCSS. This

last one is always equal to the weighted distance be-

tween

and T

, instead of relying on a mismatch, that

is to say, a repetition in the stream or even in the tem-

plate. Then, the resulting updated score is given to a

local maximum searching algorithm called Search-

Max, which filters scores exceeding the threshold

within a sliding window of size W

. Then, a one-bit

event is sent whether a gesture is spot or not. When a

match occurs, the start point of the gesture may be

retrieved by backtracking signals. This is performed

via a window of size W

to reduce unnecessary stored

elements. Thus, the overall memory usage, for a word

of size ws, is defined by NT∗wsNT∗WB with

NT representing the size of the template.

Moreover, in order to be able to manage multiple

acquisition channels with the LM-WLCSS technique,

two fusion methods were proposed. They are: the sig-

nal fusion (Nguyen-Dinh et al., 2014b, Long-Van et

al., 2012) and the decision fusion (Bahrepour et al.,

2009, Zappi et al., 2012). Observed performance

evaluations with these usages were obtained from the

Opportunity “Drill run”, representing 17 distinct ac-

tivities, and from 1 to 13 nodes. The resulting FScore

is 85% for the decision fusion and 80% for the signal

one. It demonstrates that higher is the number of

nodes, better is the recognition performance. Even

though other decision fusion methods have been pro-

posed in (Nguyen-Dinh et al., 2014a, Chen and Shen,

2014), there is no previous work, to the best of our

knowledge, that focus on optimizing the LM-WLCSS

for one class and perform a final decision fusion.

Hence, we introduce in this work a new variant of the

LM-WLCSS capable to handle multi-class, as well as,

a straightforward optimization for the quantization

and the windows size W

3 A NEW OPTIMIZED LIMITED

MEMORY AND WARPING

LCSS APPROACH FOR

ONLINE GESTURE

RECOGNITION

In this section, we introduce the Optimized LM-

WLCSS (OLM-WLCSS), our proposed approach for

online gesture recognition. This technique is robust

against noisy signals and strong variability in gesture

execution as well as methods we previously de-

scribed. This section first describes the quantization

step, following by the training phase. Then, the recog-

nition block for one class and the optimization pro-

cess are presented. Finally, we describe the decision-

making module.

3.1 Quantization

Similarly to the WLCSS, we use K-Means algorithm

to cluster the 



data of the sensor in the quantization

step. Each sample from the sensor is represented as a

vector (e.g. an accelerometer is represented as a 3D

vector). Thus, each sensor vectors are associated with

their closest cluster centroid by comparing their Eu-

clidean distances. Since the WLCSS do store symbols

we suggest preserving centroids instead.

3.2 Training

This subsection presents the overall vision of our of-

fline training method on one class . In the case of

two or more classes, the process is repeated. Tem-

plates matching methods find similarities in the signal

and detect gesture via a motif. The template can be

elected as the best representation over the whole pos-

sible alternatives of the gesture in a training phase.

Such patterns maximize the recognition performance.

The overall process of our training is illustrated in

Figure 1. Raw signals are first quantized to create a

transformed training set. Next, this new data set is

used for electing a template. Finally, resulting motif

is given, as a parameter, to the rejection threshold cal-

culation method that output the tuple (template,

threshold).

HUCAPP 2017 - International Conference on Human Computer Interaction Theory and Applications

110

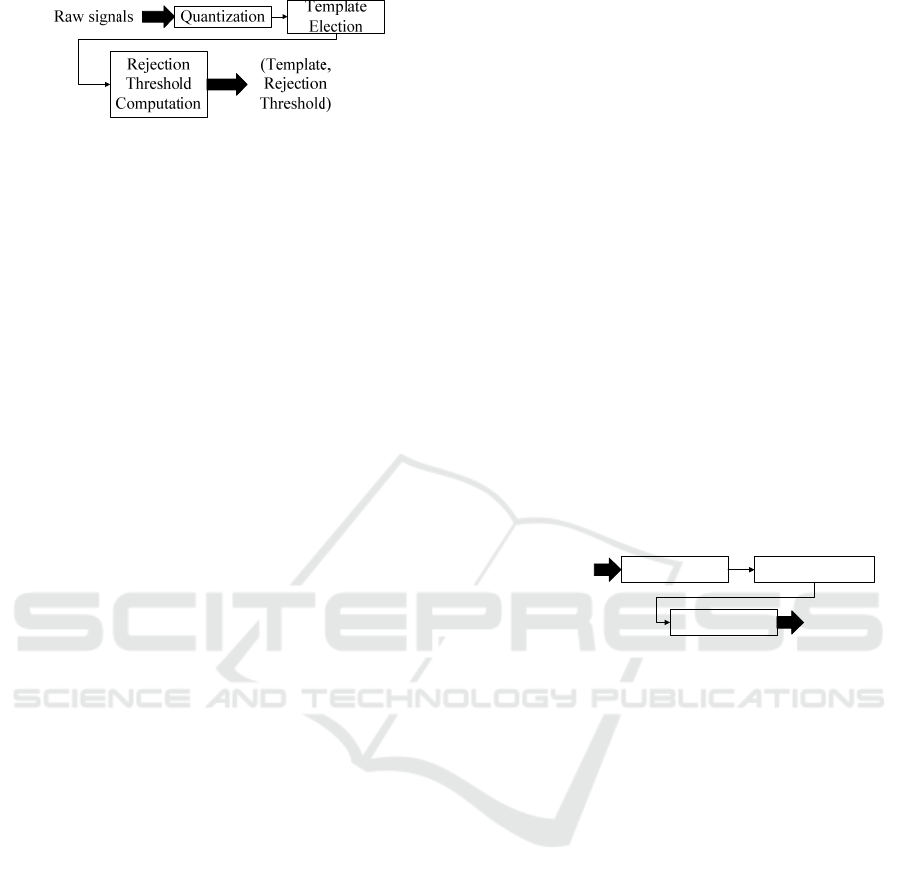
Figure 1: Overall training flow.

3.2.1 Template Election

Once the quantization phase is achieved, the next step

is to elect the best template. As described in (Long-

Van et al., 2012), such process is performed via the

LCSS method that has been modified to handle vector

instead of symbols. Each instance was defined as a

temporary template and then compared to the other

ones. The reference template is defined thanks to the

mean resulting score.

3.2.2 OLM-WLCSS

The core component of the presented method is the

computation of the matching score. This is achieved

thanks to the following formula:

j,i













0 ifi0orj0

j‐1,i‐1

R ifdS



0

max

j‐1,i‐1

‐P

j‐1,i

‐P

j,i‐1

‐P

ifdS





0



2



β∙d











(3)

Let d be the Euclidean distance between two cen-

troids,





the -th value of the quantized stream, and





the -th value of the template. Identically to its pre-

decessors, the initial value of the matching score



,

is zero. Then, this score is increased with the value of

R for every match when S

equal to T

. Otherwise, a

penalty P weighted by  is applied. The resulting pen-

alty is expressed according to three distinct cases.

Firstly, when a mismatch between the stream and the

template occurs. Secondly, when there is repetition in

the stream and finally, when there is repetition in the

template. Similarly to the LM-WLCSS, only the last

column of the matching score is required to compute

the new one. It should be noted that a backtracking

method can be implemented to retrieve the starting

point of the gesture.

3.2.3 Rejection Threshold Calculation

The rejection threshold calculation is like the one pre-

sented in the LM-WLCSS algorithm. The score be-

tween the template and all the gesture instances of

class  is computed with the core component of our

algorithm. Then, the matching score mean µ

and the

standard deviation σ

are calculated. The following

formula determines the resulting threshold:

Thd = µ - h · σ,h ∈

(3)

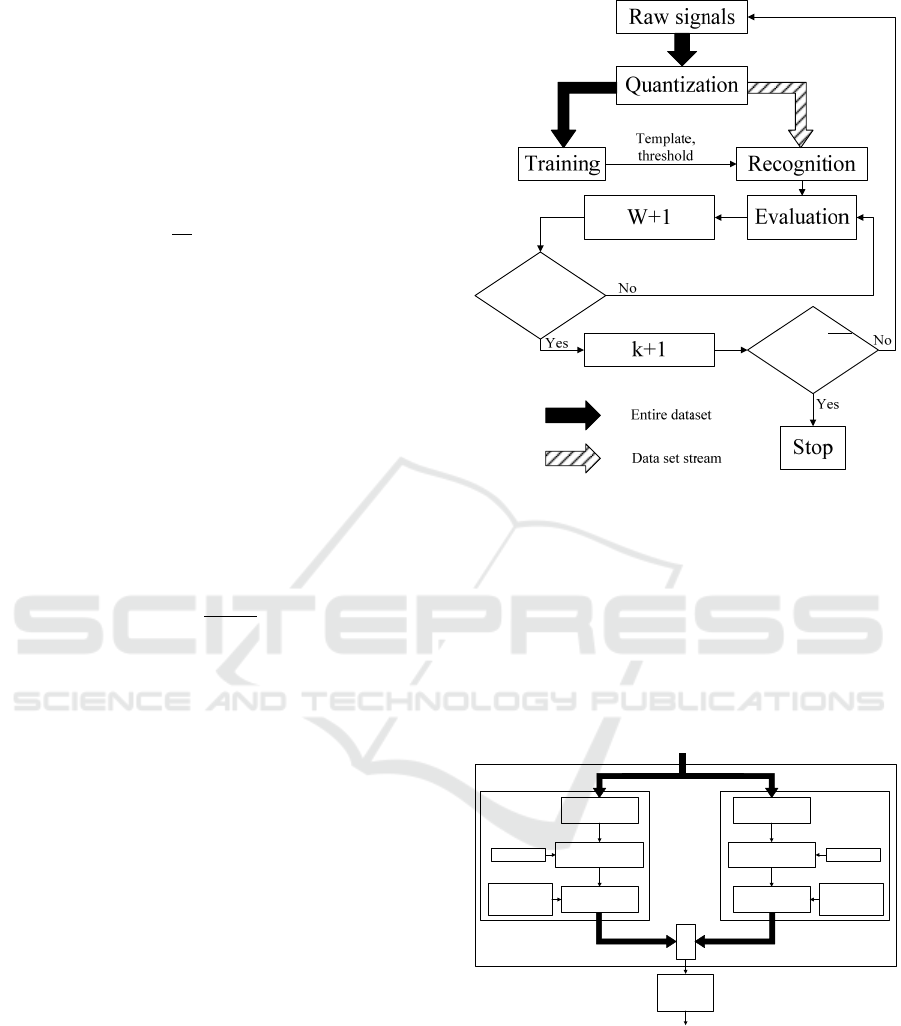
3.3 Recognition Blocks for One Class

The outcome of the previous phase is the best tuple

(template, rejection threshold) for each class. These

two elements define parameters that allow matching

a gesture to the incoming stream. Figure 2 illustrates

the recognition flow. As for the training, raw signals

are first quantized. The resulting sample and the pre-

viously elected template are given to the OLM-

WLCSS method presented in the training phase.

Next, the matching score is given to the SearchMax

algorithm that sends a binary event.

Quantization OLM-WLCSS

SearchMax

Raw Signals

Output

Figure 2: Overall single class recognition flow.

3.3.1 SearchMax

The matching score computed in previous steps

should increase and exceed the threshold if a gesture

is performed. However, noisy signals imply fluctua-

tions and undesired detections. To overcome such is-

sues, we used the SearchMax algorithm which was

introduced in (Roggen et al., 2015). Its goal is to find

local maxima among matching scores in sliding win-

dow W

. SearchMax loops over the scores and com-

pares the last and the current score to set a flag; 1 for

a new local maximum (Max

) and 0 for a lower

value. A counter (K

) is increased at each loop.

When K

exceeds the size of W

the value of Max

is compared to the threshold Thd. Eventually, the al-

gorithm returns a binary result; 1 if the local maxi-

mum is above Thd to indicate that a gesture has been

recognized, 0 otherwise.

3.4 Quantization and SearchMax

Optimization

The previously described quantization phase associ-

ates each new sample to the nearest centroid of the

Optimized Limited Memory and Warping LCSS for Online Gesture Recognition or Overlearning?

111

class c. Thus, each class has a parameter 



that de-

fined the number of clusters generated in the training

phase. In prior work, Long-Van et al. (2012) have de-

fined it with a value of 20 after they ran some tests. In

this way, we have also performed some tests with var-

ious cluster numbers. It appears that this parameter

highly impacts the performance of the algorithm.

Thus, we propose a straightforward optimization as

illustrated in Figure 3.This step consists of iteratively

running the training process with different 



. There-

fore, we define 2,



 as boundaries for 



, where

is the number of samples used for the training of

the class c. For the same reason, we tried to vary the

sliding windows W

we previously introduced, and

noticed better performances from one to another.

Consequently, we choose to adopt the same way as

for 



, and increment W

from zero to twice the tem-

plate size. The resulting best pair is elected based on

its performance. To perform the evaluation, we de-

cide to base the vote on the Cohen Kappa, as advice

in (Ben-David, 2007), instead of accuracy that could

be high due to a mere chance. The Kappa is computed

from observed probabilities (P



) and expected ones



) as follows:

Kappa =

- P

1 - P

(4)

3.5 Final Decision

Previous steps were independently performed for

each gesture class. However, noise in raw signals and

high variations in gesture execution can lead to mul-

tiple detections. Several methods are available to re-

solve conflicts, such as the weighted decision de-

scribed in (Banos et al., 2012). In our system, we

choose to employ the lightweight classifier C4.5

(Quinlan, 2014), that requires a supervised training.

The overall representation of the recognition flow is

illustrated in Figure 4.

k>



W > W

Figure 3: Overall optimization process.

The training of C4.5 comes directly after the op-

timization step. It is performed using a 10-Fold cross-

validation on a data set previously created. This file

may be considered as a ∗ matrix, with  is the

number of samples from the template training data

set, and M is the amount of recognition blocks. Each

element r

i,j

of this matrix represents the result of the

j-th recognition block for the i-th sample.

Raw signals

Quantization

OLM-WLCSS

SearchMax

⋮

Quantization

OLM-WLCSS

SearchMax

Template

Rejection

Threshold

Template

Rejection

Threshold

Decision

Making

FinalDecision

Decisionvector

Figure 4: Overall recognition flow for m class.

4 DATA USED FOR OUR

EXPERIMENTS

In order to evaluate the reliability of our algorithm,

we have exploited two different data sets. None of

HUCAPP 2017 - International Conference on Human Computer Interaction Theory and Applications

112

these sets are the ones used in (Roggen et al., 2015).

Indeed, in (Roggen et al., 2015) results were obtained

on a private data set with arbitrary parameter. In this

way a proper comparison with this algorithm is not

possible.

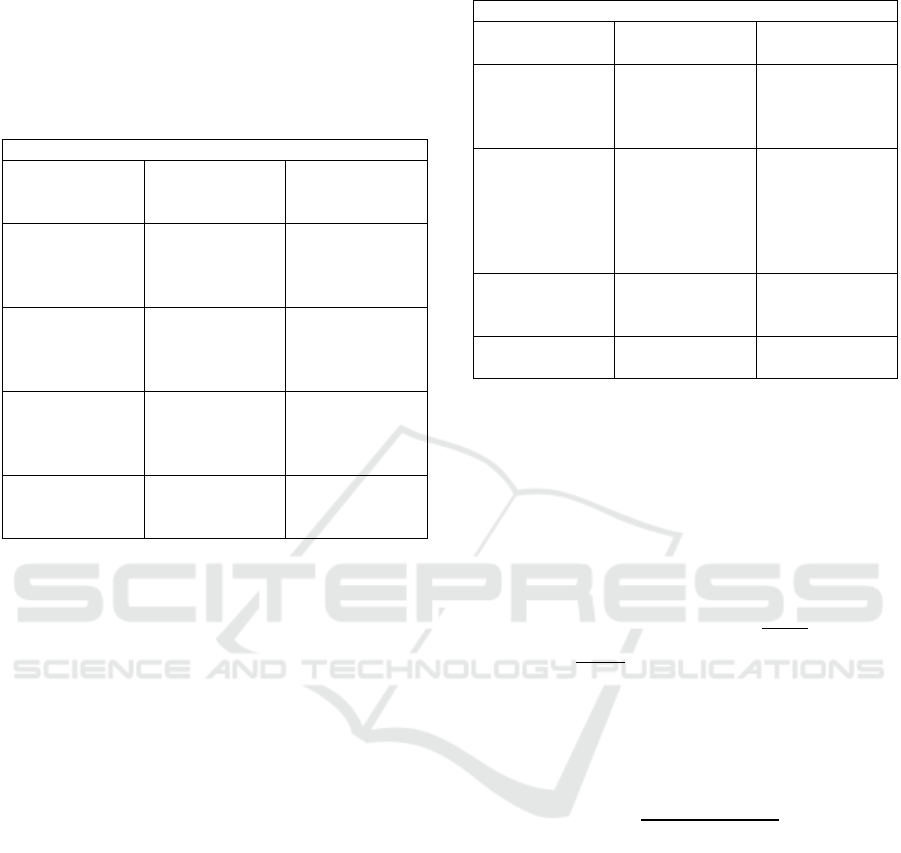
Table 1: All gestures of Make Coffee data set.

Make Coffee Gestures

opening the

brew basket lid

(G1)

getting the

measuring

spoon (G6)

getting the de-

canter (G11)

pushing the

shower head

(G2)

adding six

spoons of coffee

in the filter (G7)

pouring the wa-

ter into the wa-

ter reservoir for

5 seconds (G12)

putting filter

into the filter

basket (G3)

putting away

the measuring

spoon (G8)

putting the de-

canter onto the

warmer plate

(G13)

putting the cof-

fee box in front

of the coffee-

maker (G4)

closing the cof-

fee box (G9)

and closing the

water lid (G14)

opening the cof-

fee box (G5)

putting away

the coffee box

(G10)

The first focuses on a unique activity, to make cof-

fee. This activity is repeated 30 times. Since such an

activity admit 14 distinct gestures, we have split them

into 14 classes as enumerated in Table 1:.The data set

was created from data that came from two 9-DoF in-

ertial measurement units (LSM9DS0). Each sensor

was associated to an Intel Edison platform which was

powered with a Lithium battery. The sampling rate of

IMU was fixed at 20 Hz as advice in (Karantonis et

al., 2006), indeed, most of body movements are

largely under such a frequency. Once the configura-

tion of IMUs was completed, the two nodes were

placed on the subject’s wrists. Data were sent to the

computer via Wi-Fi. To record the activity, two mem-

bers of our team have been selected. The first one was

making coffee inside our laboratory, while the other

one was labeling each incoming sample. To ensure a

good execution, the activity was achieved several

times by the subject, as a training, without any record-

ing.

The second data set we use was suggested by the

Bilkent University (Altun et al., 2010). It includes

data from eight subjects, where each of them wore

five 9-DoF inertial measurement units (IMU). The

data set represents 19 daily or sports activities enu-

merated in Table 2:.The realized experiment only ex-

ploits records from the first subject.

Table 2: All gestures of Bilkent University data set.

Bilkent University Gestures

Sitting (A1)

moving around in

an elevator (A8)

exercising on a

cross-trainer (A14)

Standing (A2)

walking in a park-

ing lot (A9)

cycling on an exer-

cise bike in hori-

zontal and vertical

positions (A15-16)

lying on back and

on right side (A3-

walking on a tread-

mill with a speed

of 4 km/h (in flat

and 15 deg in-

clined positions)

(A10-11)

rowing (A17)

ascending and de-

scending stairs

(A5-6)

running on a tread-

mill with a speed

of 8 km/h (A12)

umping (A18)

standing in an ele-

vator still (A7)

exercising on a

stepper (A13)

playing basketball

(A19)

4.1 Evaluation Metrics

The performance of the presented method was evalu-

ated on three well-known metrics: Accuracy (Acc),

FScore and Kappa measures. However, the last one

was prioritized and provides the recognition perfor-

mance of our algorithm. The first two were included

as comparison purpose since they are widely used in

classification problems. The FScore is based on the

precision expressed by, precision=

TP+FP

and the re-

call recall =

TP + FN

. Where TP is true positive values,

FP false positives, TN true negatives and FN false

negatives. These values were obtained after compu-

ting a confusion matrix. The final overall formula for

the FScore computation is given as follows:

FScore= 2 ∙

precision∙recall

recision+recall

(5)

5 RESULTS AND DISCUSSION

This section presents and discusses results we obtain

with the two previously described data sets. Figure 5

and Figure 6 summarize metric values for the data set

Make Coffee on the training and testing sets respec-

tively. Abscess values are the axis taken into account

for each iteration of the given method. We have taken

different sensors into account for each run. 3 axes rep-

resent the accelerometer, 6 refer to the accelerometer

and the gyroscope, 9 all the IMU and 18 the two

IMUs. The ordinate represents the Kappa, FScore and

Accuracy, expressed in percentages, for each combi-

nation.

Optimized Limited Memory and Warping LCSS for Online Gesture Recognition or Overlearning?

113

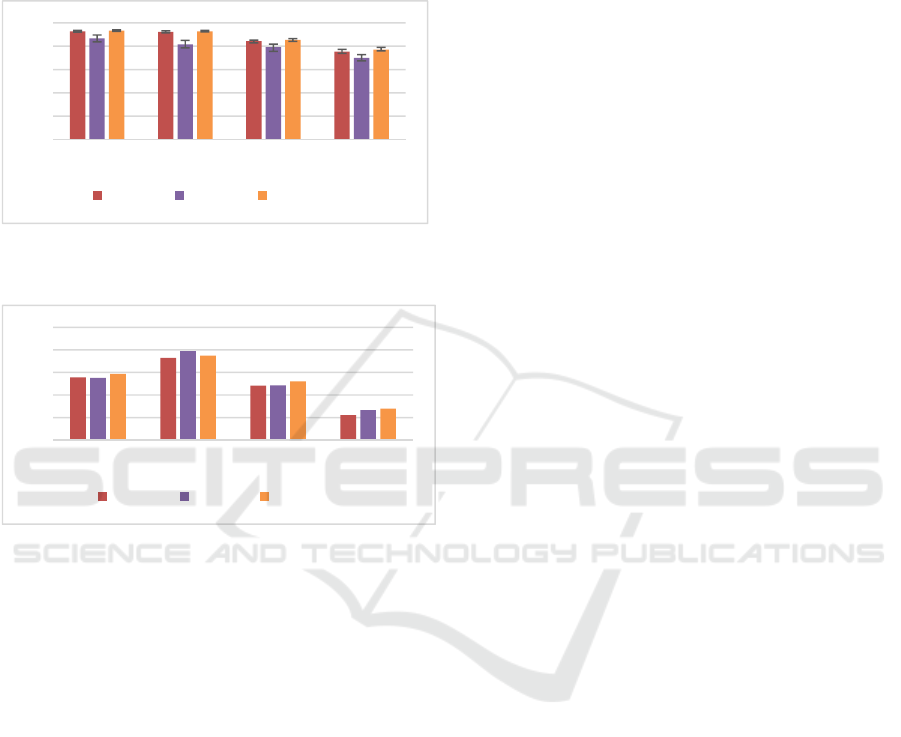
Performance results on the Make Coffee data set

show a considerable drop in the Kappa measure be-

tween the training set and the testing set for every

axis. The second data set present similar result with a

Kappa of 81% for the training set and 37% with the

testing set.

Figure 5: Results observed for the 10-Fold on the training

set, for the make coffee data set.

Figure 6: Results observed for supplied test set on the make

coffee data set.

The observed difference between obtained re-

sults, illustrates a significant limitation regarding the

performance. This contrast may be due to both the op-

timization of parameters (such as clusters from K-

Means and the size of the window for the SearchMax

algorithm) and of each classifier over training data.

We review some methods that falls in the same situa-

tion, meaning good results on training sets but low

ones on testing sets, that were identified as over-

learned (Gamage et al., 2011). Indeed, as described

by Witten and Frank (2005), a classifier trained and

optimized on the same set will achieve accurate re-

sults on this one, but should fall down with independ-

ent test data. Consequently, our proposed method

may be in an overlearning situation, explaining such

results. This is probably due to the fact that the pa-

rameters, of the proposed method, have been opti-

mized for the training data set.

6 CONCLUSIONS

In this paper, we have proposed a new TMM derived

from the LM-WLCSS technique which aims at recog-

nizing motifs in noisy streams. Several parameters

were evaluated such as a suitable number of clusters

for the quantization step, as well as, an adequate size

of the window. The evaluation we have performed

suggests promising results over the training set

(92.7% of Kappa for 3-axis), but we have observed a

serious drop with testing data (55.7% of Kappa for 3-

axis). Such a contrast may be due to the fact that our

method is overly dependent on the training data,

which refers to the proper definition of an overlearn-

ing situation. In a future work we plan to remove pa-

rameters from our method and don’t fall again into an

overlearning situation.

REFERENCES

Altun, K., Barshan, B. & Tunçel, O. 2010. CoAltun, K.,

Barshan, B. & Tunçel, O. 2010. Comparative study on

classifying human activities with miniature inertial and

magnetic sensors. Pattern Recognition, 43, 3605-3620.

Bahrepour, M., Meratnia, N. & Havinga, P. J. M. Sensor

fusion-based event detection in Wireless Sensor

Networks. Mobile and Ubiquitous Systems:

Networking & Services, MobiQuitous, 2009.

MobiQuitous '09. 6th Annual International, 13-16 July

2009 2009. 1-8.

Banos, O., Damas, M., Pomares, H. & Rojas, I. 2012. On

the use of sensor fusion to reduce the impact of

rotational and additive noise in human activity

recognition. Sensors, 12, 8039-8054.

Ben-David, A. 2007. A lot of randomness is hiding in

accuracy. Engineering Applications of Artificial

Intelligence, 20, 875-885.

Chen, C. & Shen, H. 2014. Improving Online Gesture

Recognition with Warping LCSS by Multi-Sensor

Fusion. In: Wong, W. E. & Zhu, T. (eds.) Computer

Engineering and Networking. Springer International

Publishing.

Dardas, N. H. & Georganas, N. D. 2011. Real-Time Hand

Gesture Detection and Recognition Using Bag-of-

Features and Support Vector Machine Techniques.

Instrumentation and Measurement, IEEE Transactions

on, 60, 3592-3607.

Gamage, N., Kuang, Y. C., Akmeliawati, R. & Demidenko,

S. 2011. Gaussian Process Dynamical Models for hand

gesture interpretation in Sign Language. Pattern

Recognition Letters, 32, 2009-2014.

Guiry, J. J., Van De Ven, P. & Nelson, J. 2014. Multi-sensor

fusion for enhanced contextual awareness of everyday

activities with ubiquitous devices. Sensors, 14, 5687-

5701.

100

3 axis 6 axis 9 axis 18 axis

Kappa FScore Accuracy

100

3 axis 6 axis 9 axis 18 axis

Kappa Fscore Accuracy

HUCAPP 2017 - International Conference on Human Computer Interaction Theory and Applications

114

Hartmann, B. & Link, N. Gesture recognition with inertial

sensors and optimized DTW prototypes. Systems Man

and Cybernetics (SMC), 2010 IEEE International

Conference on, 10-13 Oct. 2010 2010. 2102-2109.

Hyeon-Kyu, L. & Kim, J. H. 1999. An HMM-based

threshold model approach for gesture recognition.

Pattern Analysis and Machine Intelligence, IEEE

Transactions on, 21, 961-973.

Karantonis, D. M., Narayanan, M. R., Mathie, M., Lovell,

N. H. & Celler, B. G. 2006. Implementation of a real-

time human movement classifier using a triaxial

accelerometer for ambulatory monitoring. IEEE

Transactions on Information Technology in

Biomedicine, 10, 156-167.

Kılıboz, N. Ç. & Güdükbay, U. 2015. A hand gesture

recognition technique for human–computer interaction.

Journal of Visual Communication and Image

Representation, 28, 97-104.

Long-Van, N.-D., Roggen, D., Calatroni, A. & Troster, G.

Improving online gesture recognition with template

matching methods in accelerometer data. Intelligent

Systems Design and Applications (ISDA), 2012 12th

International Conference on, 27-29 Nov. 2012 2012.

831-836.

Nguyen-Dinh, L.-V., Calatroni, A., Tr, G., #246 & Ster

2014a. Towards a unified system for multimodal

activity spotting: challenges and a proposal.

Proceedings of the 2014 ACM International Joint

Conference on Pervasive and Ubiquitous Computing:

Adjunct Publication. Seattle, Washington: ACM.

Nguyen-Dinh, L. V., Calatroni, A. & Tröster, G. 2014b.

Robust online gesture recognition with crowdsourced

annotations. Journal of Machine Learning Research,

15, 3187-3220.

Quinlan, J. R. 2014. C4. 5: programs for machine learning,

Elsevier.

Reyes, M., Dominguez, G. & Escalera, S. Featureweighting

in dynamic timewarping for gesture recognition in

depth data. Computer Vision Workshops (ICCV

Workshops), 2011 IEEE International Conference on,

6-13 Nov. 2011 2011. 1182-1188.

Roggen, D., Cuspinera, L., Pombo, G., Ali, F. & Nguyen-

Dinh, L.-V. 2015. Limited-Memory Warping LCSS for

Real-Time Low-Power Pattern Recognition in Wireless

Nodes. In: Abdelzaher, T., Pereira, N. & Tovar, E.

(eds.) Wireless Sensor Networks. Springer International

Publishing.

Rung-Huei, L. & Ming, O. A real-time continuous gesture

recognition system for sign language. Automatic Face

and Gesture Recognition, 1998. Proceedings. Third

IEEE International Conference on, 14-16 Apr 1998

1998. 558-567.

Vlachos, M., Hadjieleftheriou, M., Gunopulos, D. &

Keogh, E. 2003. Indexing multi-dimensional time-

series with support for multiple distance measures.

Proceedings of the ninth ACM SIGKDD international

conference on Knowledge discovery and data mining.

Washington, D.C.: ACM.

Witten, I. H. & Frank, E. 2005. Data Mining: Practical

Machine Learning Tools and Techniques, Second

Edition (Morgan Kaufmann Series in Data

Management Systems), Morgan Kaufmann Publishers

Inc.

Zappi, P., Roggen, D., Farella, E., Tr, G., #246, Ster &

Benini, L. 2012. Network-Level Power-Performance

Trade-Off in Wearable Activity Recognition: A

Dynamic Sensor Selection Approach. ACM Trans.

Embed. Comput. Syst., 11, 1-30.

Optimized Limited Memory and Warping LCSS for Online Gesture Recognition or Overlearning?

115