
Extended Shortest Path Problem
Generalized Dijkstra-Moore and Bellman-Ford Algorithms
Maher Helaoui
Higher Institute of Business Administration, University of Gafsa, Rades, Tunisia
Keywords:
Combinatorial Optimization, Valuation Structure, Extended Shortest Path Problem, Longest Path Problem,
Generalized Dijkstra-Moore Algorithm, Generalized Bellman-Ford Algorithm.
Abstract:
The shortest path problem is one of the classic problems in graph theory. The problem is to provide a solution
algorithm returning the optimum route, taking into account a valuation function, between two nodes of a graph
G. It is known that the classic shortest path solution is proved if the set of valuation is R or a subset of R and
the combining operator is the classic sum (+). However, many combinatorial problems can be solved by using
shortest path solution but use a set of valuation not a subset of R and/or a combining operator not equal to
the classic sum (+). For this reason, relations between particular valuation structure as the semiring and diod
structures with graphs and their combinatorial properties have been presented. On the other hand, if the set of
valuation is R or a subset of R and the combining operator is the classic sum (+), a longest path between two
given nodes s and t in a weighted graph G is the same thing as a shortest path in a graph −G derived from G
by changing every weight to its negation.
In this paper, in order to give a general model that can be used for any valuation structure we propose to
model both the valuations of a graph G and the combining operator by a valuation structure S. We discuss
the equivalence between longest path and shortest path problem given a valuation structure S. And we present
a generalization of the shortest path algorithms according to the properties of the graph G and the valuation
structure S.
1 INTRODUCTION
The shortest path problem is one of the classic prob-
lems in graph theory. The problem is to provide a so-
lution algorithm returning the optimum route, taking
into account a valuation function, between two nodes
of a graph G.
In (Shimbel, 1955; Ford and Lester, 1956; Bellman,
1958; Sedgewick and Wayne, 2011) the classic short-
est path solution is proved if
• the set of valuation is R or a subset of R.
• the combining operator is the classic sum (+)
Many combinatorial problems like Fuzzy, Weighted,
Probabilistic and Valued Constraint Satisfaction Prob-
lem (Schiex et al., 1995; Cooper, 2003; Cooper,
2004; Allouche et al., 2009) use a set of valuation
E not subset of R and a combining operator ⊕ 6= +
for weighted, fuzzy, probabilistic . . . valuations. In
(Cooper, 2003), the shortest path algorithm has been
used to solve Fuzzy and Valued Constraint Satisfac-
tion Problem.
In (Erickson, 2010), author observes that the classical
maximum flow problem (Ford and Fulkerson, 1955;
Ford and Fulkerson, 1962) in any directed planar
graph G can be reformulated as a parametric short-
est path problem in the oriented dual graph G
∗
. In
(Cohen et al., 2004; Helaoui et al., 2013), a submod-
ular decompositions approach has been presented to
solve Valued Constraint Satisfaction Problem. This
solution use the maximum flow algorithm.
Dijkstra-Moore and Bellman-Ford Algorithms are the
most known algorithmic solutions for the shortest
path problem.
• Since 1971, the Dijkstra-Moore Algorithm has
been used if the set of valuation is R
+
or a subset
of R
+
and the combining operator is the classic
sum (+).
• The Bellman-Ford Algorithm is the result of
(Shimbel, 1955; Ford and Lester, 1956; Bellman,
1958) works. It is used if the set of valuation is R
or a subset of R and the combining operator is the
classic sum (+).
As many combinatorial problems can be solved by us-
ing shortest path solution but use a set of valuation
306
Helaoui M.
Extended Shortest Path Problem - Generalized Dijkstra-Moore and Bellman-Ford Algorithms.
DOI: 10.5220/0006145303060313
In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 306-313
ISBN: 978-989-758-218-9
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

not a subset of R and/or a combining operator not
equal to the classic sum (+), then in (Gondran and
Minoux, 2008), authors present new models and al-
gorithms discussing relations between particular val-
uation structure: the semiring and diod structures with
graphs and their combinatorial properties.
In (Sedgewick and Wayne, 2011), a longest path be-
tween two given nodes s and t in a weighted graph
G is the same thing as a shortest path in a graph −G
derived from G by changing every weight to its nega-
tion. Therefore, if shortest paths can be found in −G,
then longest paths can also be found in G. This result
remains true if we have a valued graph G by a valua-
tion structure S?
In this paper, we provide an answer to this question
by discussing equivalence between longest path and
shortest path problem given a valuation structure S.
We present a generalization of Dijkstra-Moore Algo-
rithm for a graph G with a S
⊕
valuation structure. And
we present a generalization of Bellman-Ford Algo-
rithm with a more general valuation structure S.
We propose to model both the valuations of a graph G
and the combining operator by a valuation structure
S, in order to discuss the generalization of the short-
est path algorithms according to the properties of the
graph G and the valuation structure S:
• The valuation structure of G is S
⊕
.
• The graph G and the valuation structure S are ar-
bitrary.
The paper is organized as follows: the next Section
introduces definitions and notations needed in pre-
senting the generalization of the shortest path algo-
rithms. In Section 3 we study the extended Shortest
Path Notion and the equivalence between longest path
and shortest path problem. We propose a generalized
shortest path algorithms in Section 4. The paper is
concluded in Section 5.
2 DEFINITIONS AND
NOTATIONS
2.1 A Directed Digraph G
The peculiarity of the shortest path problem requires
to distinguish two directions between any two nodes.
In this case, the connection between two nodes x and
y can be defined by the directed connection between
an original node for example x and a destination node
y.
Definition 1. A directed digraph G = (E
S
,E
~
A
) is de-
fined by a set of nodes E
S
and a set of directed edges
E
~
A
, each edge (arc) is the connection between an
original node and a destination node.
If x and y are two nodes:
• the directed connection from x to y (denoted ~xy), if
it exists, is a directed connection (arc) of a graph
G.
• An arc ~xx: the directed connection from x to x is
known as a loop.
• A p-graph is a graph wherein there is never more
than p arcs ~xy between any two nodes.
• A Monograph is a graph wherein there is never
more than 1 arc ~xy between any two nodes and
there is never a loop.
2.2 A Valuation Structure
We assume that E the set of all possible valuations, is
a totally ordered set where ⊥ denotes its minimal ele-
ment and > its maximal element. In addition, we will
use a monotone binary operator ⊕. These elements
form a valuation structure defined as follows
Definition 2. A valuation structure S of a graph G is
the triplet S = (E,⊕,) such as
• E is the set of possible valuations;
• is a total order on E;
• ⊕ is commutative, associative and monotone.
We define below a fire and strictly monotone valua-
tion structure.
Definition 3. A valuation structure S is fire if for each
pair of valuations α,β ∈ E, such as α β, there is a
maximum difference between β and α denoted β α.
An aggregation operator ⊕ is strictly monotonic if for
any α,β,γ in E such as α ≺ β and γ 6= >, we have
α ⊕ γ ≺ β ⊕ γ.
A valuation structure S is strictly monotonic if it has
an aggregation operator strictly monotonic.
In the remainder of this paper, we use only fire and
strictly monotone valuation structures.
The fire and strictly monotone valuation structures
satisfy the following two Lemmas, that has been
proved in (Cooper, 2004), (Lemma 7 and Theorem
38).
Lemma 1. Let S = (E,⊕,) a valuation structure
fire and strictly monotone. Then for all α,β,γ ∈ E
such as γ β, we have (β γ) β and (α ⊕ γ) ⊕
(β γ) = α ⊕ β.
Lemma 2. Let S = (E,⊕,) a valuation structure
fire and strictly monotone. Then for all α,β,γ ∈ E
such as γ β, we have (α ⊕ β) γ = α ⊕ (β γ).
Extended Shortest Path Problem - Generalized Dijkstra-Moore and Bellman-Ford Algorithms
307

Using both Lemmas (Lemma 1 and Lemma 2) pre-
sented above we can get Lemma 3:
Lemma 3. Let β ≺ α and γ ≺ α
α β ≺ α γ if and only if γ α ≺ β α.
Proof. (⇒ ) If we have α β ≺ α γ
then α β ⊕ (β α ⊕ γ α) ≺ α γ ⊕ (β
α ⊕ γ α)
then γ α ≺ β α
(⇐ ) If we have γ α ≺ β α
then γ α ⊕ (α β ⊕ α γ) ≺ β α ⊕ (α
β ⊕ α γ)
then α β ≺ α γ.
We define below a particular valuation structure,
widely used in practice, that we will note S
⊕
Definition 4. A valuation structure S
⊕
of a graph G
is the triplet S
⊕
= (E
⊕
,⊕,) such as:
• E
⊕
is the set of possible valuations such as for all
α,β,λ ∈ E
⊕
if α β then α β ⊕ λ;
• is a total order on E;
• ⊕ is commutative, associative and monotone.
3 SHORTEST PATH NOTION
3.1 Extended Shortest Path Problem
In the beginning of this paragraph we formally define
the shortest path between two nodes x and y of a graph
G.
For this way, we start by defining the arc and path
valuations.
Definition 5. Let G = (E
S
,E
~
A
) a valued directed
graph. In each arc ~xy we associate a valuation func-
tion ϕ : E
S
×E
S
→ E such as ϕ(x,y) is the valuation of
~xy arc. A path between two nodes x and y is denoted
CH(x, y) from the node x to a node y.
For each path CH(x, y) we associate a valuation
Φ(CH(x, y)).
Φ(CH(x, y)) = [
M
~x
i
x
j
∈CH(x,y)
ϕ(x
i
,x
j
)]
Now we can define the shortest path:
Definition 6. Let G = (E
S
,E
~
A
) a valued directed
graph. The shortest path between x and y is the path
µ(x,y) started from a node x and finished at y such as:
Φ(µ(x,y)) = Min
CH(x,y)
[Φ(CH(x, y))]
3.2 Equivalent Problems of Shortest
Path Problem (SPP)
If we have to find the Longest Path, is it possible to
use the Shortest Path solution?
Finding the Longest Path is it equivalent to finding the
Shortest Path?
Theorem 1. Given a fire and strictly monotone valu-
ation structure S, finding the Longest Path Problem is
equivalent to finding the Shortest Path Problem.
Proof Theorem 1. (⇒) We start from a shortest path
problem. We replace each valuation (α β) by the
valuation (β α) and we prove that a shortest path
problem can be transformed in a longest path prob-
lem.
Let
Φ(µ(s,t)) = min Φ(CH(s,t))
Φ(µ(s,t)) = (α β
0
) Φ(CH
1
(s,t)) = (α β
1
)
. ..
Φ(CH
n
(s,t)) = (α β
n
)
If we replace each valuation (α β) by the valuation
(β α)
We get
Φ(µ(s,t)) = (β
0
α) Φ(CH
1
(s,t)) = (β
1
α)
. ..
Φ(CH
n
(s,t)) = (β
n
α)
then we get
Φ(µ(s,t)) = max Φ(CH(s,t)) = Φ(L (s,t))
(⇐) Now we start from a longest path problem. We
replace each valuation (α β) by the valuation (β
α) and we prove that a longest path problem can be
transformed in a shortest path problem.
Let
Φ(L (s,t)) = max Φ(CH(s,t))
Φ(L (s,t)) = (α β
0
) Φ(CH
1
(s,t)) = (α β
1
)
. ..
Φ(CH
n
(s,t)) = (α β
n
)
If we replace each valuation (α β) by the valuation
(β α)
We get by Lemma 3
Φ(L (s,t)) = (β
0
α) Φ(CH
1
(s,t)) = (β
1
α)
. ..
Φ(CH
n
(s,t)) = (β
n
α)
Then we get
Φ(L (s,t)) = min Φ(CH(s,t)) = Φ(µ(s,t))
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
308
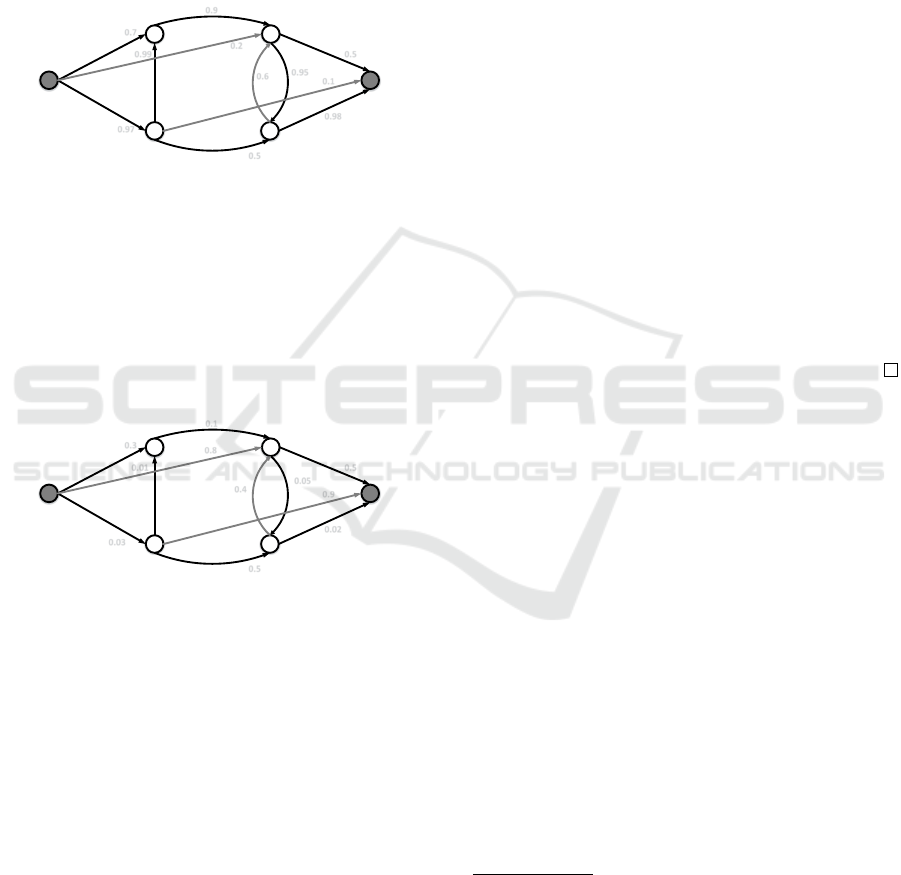
Example 1. In February 2017, a large multinational
X in Porto wishes to invest the sum of 3.000.000 e
in a new project Π. To do this, each year X has d in-
vestment choices. One study allowed him to estimate
the certainty of acceptable profitability (probabilities)
according to the various decisions taken. In order to
maximize the certainty of an acceptable overall yield
of Π, X wishes to find the longest path in the mono-
graph G
1
, such that, S
1
= (]0,1[, ×,≤).
b d
c e
0.9
a f
0.7
0.5
0.1
0.98
0.2
0.97
0.99
0.5
0.6
0.95
Figure 1: A directed monograph G
1
.
By Theorem 1 and in order to maximize the cer-
tainty probabilities of an acceptable overall yield of
Π, X can find the shortest path in the monograph
G
2
minimize the uncertainty probabilities. Such that
S
2
= S
1
. For each valuation α in G
1
we associate a
valuation β in G
2
such that β = α = 1 − α
α ⊕ β = α × (1 − α) ⇒ S
1
and S
2
are different
from the semiring or diod structures.
b d
c e
0.1
a f
0.3
0.5
0.9
0.02
0.8
0.03
0.01
0.5
0.4
0.05
Figure 2: A directed monograph G
2
.
3.3 Optimality Notion
The dynamic programming repose on the fundamen-
tal principle of optimality:
Given a directed graph G, a sub-path of a shortest path
µ ∈ G is a shortest path in G
s
a sub-graph of G.
Theorem 2. Let:
• A directed graph G = (E
S
,E
~
A
),
• A valuation function of G ϕ : E
S
× E
S
→ E with a
fire and strictly monotone valuation structure S,
• a shortest path µ(x
1
,x
k
) from x
1
∈ E
S
to x
k
∈ E
S
µ(x
1
,x
k
) = x
1
→ x
2
→ .. . → x
k
= x
1
∗
→ x
k
,
• A sub-path CH(x
i
,x
j
) of µ(x
1
,x
k
) from x
i
to x
j
:
CH(x
i
,x
j
) = x
i
→ .. . → x
j
such as x
i
∗
→ x
j
1
.
Then CH(x
i
,x
j
) = µ(x
i
,x
j
) is the shortest path from
x
i
∗
→ x
j
.
Proof Theorem 2. We proceed by absurd reasoning.
Assume that:
1. µ(x
1
,x
k
) is a shortest path
2. CH(x
i
,x
j
) is a sub path of µ(x
1
,x
k
)
3. It ∃ CH’(x
i
,x
j
) of G such as Φ(CH’(x
i
,x
j
)) ≺
Φ(CH(x
i
,x
j
)).
We proceed to get a contradiction.
Decompose µ(x
1
,x
k
) in CH(x
1
,x
i
), CH(x
i
,x
j
) and
CH(x
j
,x
k
)
then
Φ(µ(x
1
,x
k
)) = Φ(CH(x
1
,x
i
)) ⊕ Φ(CH(x
i
,x
j
)) ⊕
Φ(CH(x
j
,x
k
)).
As it ∃ CH’(x
i
,x
j
) such as Φ(CH’(x
i
,x
j
)) ≺
Φ(CH(x
i
,x
j
)) and given that ⊕ is strictly monotone
then
Φ(µ(x
1
,x
k
)) Φ(CH(x
1
,x
i
)) ⊕ Φ(CH’(x
i
,x
j
)) ⊕
Φ(CH(x
j
,x
k
)), which is a contradiction by the
fact that the path µ(x
1
,x
k
) is a shortest path then
CH(x
i
,x
j
) = µ(x
i
,x
j
).
4 GENERALIZATION OF
DIJKSTRA-MOORE AND
BELLMAN-FORD
ALGORITHMS
4.1 Common Functions
The generalized Dijkstra-Moore and Bellman-Ford
algorithms presented in this paper use
1. Algorithm 1 is an initialization marker algorithm
of all nodes of G that we will denote
INITMARK(G,s);
2. Algorithm 2 is an initialization finding shortest
path algorithm that we will denote
INITSPP(G, s);
1
– x
i
is an immediate predecessor or a non immediate of x
j
(it
exists a path from x
i
to x
j
).
– x
i
is an immediate successor or a non immediate of x
1
or x
i
= x
1
– x
j
is an immediate predecessor or a non immediate of x
k
or
x
j
= x
k
Extended Shortest Path Problem - Generalized Dijkstra-Moore and Bellman-Ford Algorithms
309

3. The updating shortest path Algorithm, denoted
UPDATESPP(x
i
,x
j
,ϕ).
Updating the shortest path between two nodes x
i
and x
j
consists in updating the valuation of one
of the arcs ~x
i
x
j
:
(a) The valuation spv[x
j
] of the shortest path until
x
j
;
(b) The predecessor of x
j
predspp[x
j
] in the short-
est path until x
j
.
Algorithm 1: InitMark(G, s):Mark.
for (x
i
= s Nbr
Sommets
G
) do
Mark[x
i
] ← 0;
Mark[s] ← 2;
Algorithm 2: InitSpp(G, s):spv,predspp.
for (x
i
= s Nbr
Sommets
G
) do
spv[x
i
] ← >;
predspp[x
i
] ← 0;
spv[s] ← α
0
;
The updating process is based on the Theorem 2
where each sub-path of the shortest path is a shortest
path in the sub-graph involving this sub-path.
The UpdateSpp(x
i
,x
j
,ϕ) function update the shortest
path from one origin node to all other one if a shortest
path is detected.
Algorithm 3: UpdateSpp(x
i
,x
j
,ϕ):spv,predspp.
if (spv[x
j
] spv[x
i
] ⊕ ϕ[x
i
][x
j
]) then
spv[x
j
] ← spv[x
i
] ⊕ ϕ[x
i
][x
j
];
predspp[x
j
] ← x
i
;
In the DIJKSTRA-MOORE Algorithm 4, each arc
is updated exactly one way. In BELLMAN-FORD Al-
gorithm, each arc can be updated many way.
4.2 Generalization of the
Dijkstra-Moore Algorithm
If the arcs valuation, is in R, can model for example
• A distance (kilometers)
• A cost (e)
In this case, the classic Dijkstra-Moore Algorithm can
be used.
In this paper, we present a generalization of Dijkstra-
Moore Algorithm 4 for a graph G with a S
⊕
valuation
structure.
Let G a valued directed graph given a valuation struc-
ture S
⊕
. We denote by s the origin node of G and x
i
the destination node. For each node x
i
of G, the Al-
gorithm 4 associate
• The valuation spv[x
j
] for the shortest sub-path un-
til x
i
;
• The predecessor of x
i
predspp[x
i
] in the shortest
sub-path until x
i
.
• The marker of x
i
denoted Mark[x
i
] verifying if the
distance from s to x
i
has been updated.
Principe of the Algorithm:
1. initialization:
For the node s
• Mark[s] ← 2
• predspp[s] ← 0
• spv[s] ← α
0
for all other nodes x
i
• Mark[x
i
] ← 0
• predspp[x
i
] ← 0
• spv[x
i
] ← >
2. Let X = the set of non marked nodes;
Do
• For each non marked node i successor of y
– UpdateSpp(y,i, ϕ)
• Mark the node y if spv[y] = min
x∈X
pcc[x].
While X 6=
/
0
b d
c e
β
a f
λ
λ β
T
β
λ β
α
α
α
λ λ
λ
β
Figure 3: A directed monograph G.
Example 2. Let the directed monograph G presented
by Figure 3. And let a valuation structure S
⊕
(can be
6= to the semiring or diod structures) such that
• {α, β, λ, γ, >} ⊂ E
⊕
• α ≺ β ≺ λ
• β = α ⊕ α
• λ = α ⊕ β
• if γ λ ⊕ λ ⊕ λ ⊕ β then γ = >
1. We apply the principle of Generalized Dijkstra al-
gorithm on G: Figure 4
2. We present an algorithmic solution: Algorithm 4.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
310
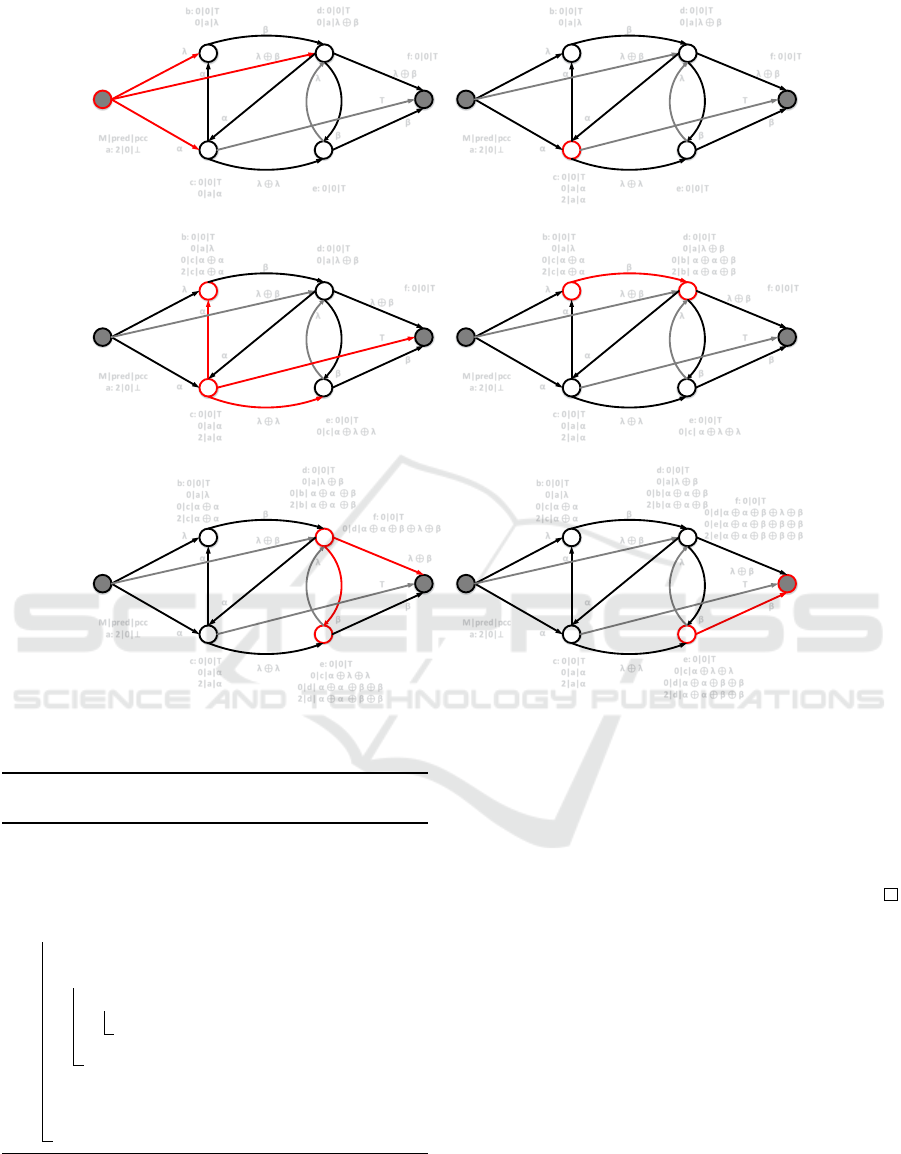
b d
c e
β
a f
λ
λ β
T
β
λ β
α
α
α
λ λ
λ
β
M|pred|pcc
a: 2|0|
b: 0|0|T
0|a|λ
c: 0|0|T
0|a|α
d: 0|0|T
0|a|λ β
e: 0|0|T
f: 0|0|T
b d
c e
β
a f
λ
λ β
T
β
λ β
α
α
α
λ λ
λ
β
M|pred|pcc
a: 2|0|
b: 0|0|T
0|a|λ
c: 0|0|T
0|a|α
2|a|α
d: 0|0|T
0|a|λ β
e: 0|0|T
f: 0|0|T
b d
c e
β
a f
λ
λ β
T
β
λ β
α
α
α
λ λ
λ
β
M|pred|pcc
a: 2|0|
b: 0|0|T
0|a|λ
0|c|α α
2|c|α α
c: 0|0|T
0|a|α
2|a|α
d: 0|0|T
0|a|λ β
e: 0|0|T
0|c|α λ λ
f: 0|0|T
b d
c e
β
a f
λ
λ β
T
β
λ β
α
α
α
λ λ
λ
β
M|pred|pcc
a: 2|0|
b: 0|0|T
0|a|λ
0|c|α α
2|c|α α
c: 0|0|T
0|a|α
2|a|α
d: 0|0|T
0|a|λ β
0|b| α α β
2|b| α α β
e: 0|0|T
0|c| α λ λ
f: 0|0|T
b d
c e
β
a f
λ
λ β
T
β
λ β
α
α
α
λ λ
λ
β
M|pred|pcc
a: 2|0|
b: 0|0|T
0|a|λ
0|c|α α
2|c|α α
c: 0|0|T
0|a|α
2|a|α
d: 0|0|T
0|a|λ β
0|b| α α β
2|b| α α β
e: 0|0|T
0|c|α λ λ
0|d| α α β β
2|d| α α β β
f: 0|0|T
0|d|α α β λ β
b d
c e
β
a f
λ
λ β
T
β
λ β
α
α
α
λ λ
λ
β
M|pred|pcc
a: 2|0|
b: 0|0|T
0|a|λ
0|c|α α
2|c|α α
c: 0|0|T
0|a|α
2|a|α
d: 0|0|T
0|a|λ β
0|b|α α β
2|b|α α β
e: 0|0|T
0|c|α λ λ
0|d|α α β β
2|d|α α β β
f: 0|0|T
0|d|α α β λ β
0|e|α α β β β
2|e|α α β β β
Figure 4: Applying Generalized-Dijkstra-Moore on G.
Algorithm 4: Generalized-Dijkstra-Moore(G, ϕ,s,t):
spv,predspp.
InitMark(G,s);
InitSpp(G,s);
recent ← s;
t ← f ;
while (Mark[t] = 0) do
j ← 0;
while (succ[recent][ j]) do
if (Mark[ j] = 0) then
UpdateSpp(recent, j, ϕ);
j ← j + 1;
y ← min(spv);
Mark[y] ← 2;
recent ← y;
Theorem 3. Given a directed monograph G with n
nodes and a valuation structure S
⊕
, the shortest path
from one started node to all others can be done in
O(n
2
).
Proof Theorem 3. Given a directed monograph G
with n nodes and a valuation structure S
⊕
, and re-
ferred to Theorem 2, the shortest path from one
started node to all others can be done by applying
Algorithm 4 to G. And the Algorithm 4 run in O(n
2
).
4.3 Generalization of Bellman-Ford
Algorithm
Given a fire and strictly monotone valuation structure
S we can model as example earnings and bounded
costs!
Unfortunately, as nodes may be marked only once,
the DIJKSTRA-MOORE algorithm does not guarantee
the optimal solution if we consider the valuation
structure not a subset of S
⊕
(For example the bounded
negative arcs). In fact, once the node is marked we
cannot change the marking in subsequent iterations.
Fortunately, we can present an algorithm that ensures
marking update until the program is not determined:
Extended Shortest Path Problem - Generalized Dijkstra-Moore and Bellman-Ford Algorithms
311
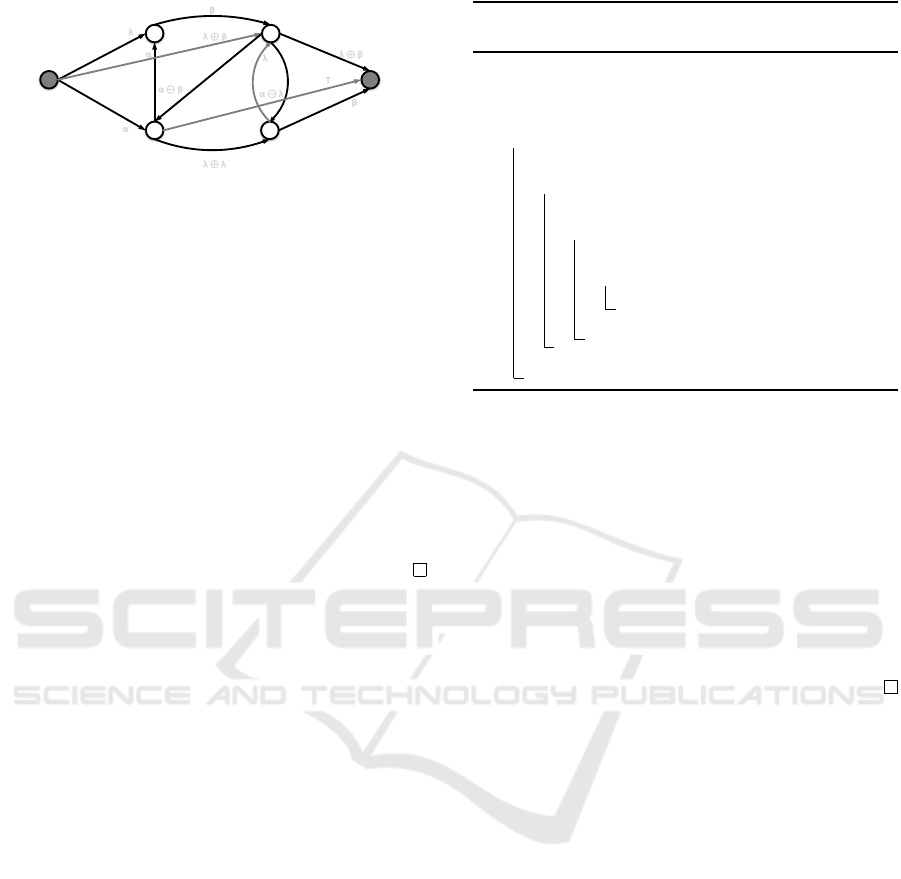
b d
c e
β
a f
λ
λ β
T
β
λ β
α β
α
α
λ λ
λ
α λ
Figure 5: A directed monograph G
0
.
a generalization of the BELLMAN-FORD Algorithm
can be used for a fire and strictly monotone valuation
structure S.
Theorem 4. Given a fire and strictly monotone
valuation structure S, the final values of the shortest
paths are obtained by at most n − 1 iterations.
Proof Theorem 4. In the absence of absorbing cir-
cuitry, a shortest path from s to all other nodes is an
element path, that is to say a path of at most n − 1
arcs. By consulting the predecessors of all nodes Al-
gorithm 5 must obtain the final values of the shortest
paths by at most n − 1 iterations.
Corollary 1. If after n iterations, the values spv[i]
continue to be modified, is that the graph has an
absorbent circuitry.
Based on the results of Theorem 4 and Corollary 1 we
can introduce the principle of the BELLMAN-FORD
generalization algorithm.
Principle of the BELLMAN-FORD generalization
algorithm:
1. InitSpp(G, s)
2. Do
UpdateSpp(i, j,ϕ)
While there is an edge to decrease spv[i].
Algorithm 5 presents an algorithmic solution for the
generalized BELLMAN-FORD algorithm.
Example 3. Let the directed monograph G
0
given by
Figure 5. And let a valuation structure S (can be 6= to
the semiring or diod structures) such that
• {α, β, λ, γ, >} ⊂ E
• α ≺ β ≺ λ
• β = α ⊕ α
• λ = α ⊕ β
• if γ λ ⊕ λ ⊕ λ ⊕ β then γ = >
1. Present an algorithmic solution: Algorithm 5.
Algorithm 5: Generalized-Bellman-Ford(G,ϕ, s):
spv,predspp.
InitSpp(G,s);
k ← 0;
t ← 1;
while (t ou k > N
Sommet
G
− 1) do
t ← 0;
for (i de 1 N
Sommet
G
) do
j ← 0;
while (predspp[i][ j]) do
UpdateSpp( j,i,ϕ);
if (spv[i] spv[ j] ⊕ ϕ[ j][i]) then
t ← 1;
j ← j + 1;
k ← k + 1;
Theorem 5. Given a directed monograph G with n
nodes and a fire and strictly valuation structure S, the
shortest path from one started node to all others can
be done in O(n
3
).
Proof Theorem 5. Given a directed monograph G
with n nodes and a fire and strictly valuation structure
S, and referred to Theorem 2, Theorem 4 and Corol-
lary 1, the shortest path from one started node to all
others can be done by applying Algorithm 5 to G. And
the Algorithm 5 run in O(n
3
).
5 CONCLUSION
This paper addressed combinatorial problems that
can be expressed as shortest path solution but use a
set of valuation not a subset of R and/or a combining
operator not equal to the classic sum (+).
Firstly, we have modeled the valuations of a graph G
by using a general valuation structure S.
Secondly, given a general valuation structure S, we
have discussed the equivalence between longest path
and shortest path problem.
And finally, we have discussed the generalization
of the shortest path algorithms according to the
properties of the graph G and the valuation structure
S:
1. The valuation structure of G is S
⊕
.
2. The graph G and the valuation structure S are ar-
bitrary.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
312

REFERENCES
Allouche, D., de Givry, S., Sanchez, M., and Schiex, T.
(2009). Tagsnp selection using weighted csp and rus-
sian doll search with tree decomposition 1. In In Pro-
ceedings of the WCB09. Lisbon Portugal, 1–8.
Bellman, R. (1958). On a routing problem. In Quarterly of
Applied Mathematics. 16: 87–90.
Cohen, D. A., Cooper, M. C., Jeavons, P. G., and Krokhin,
A. A. (2004). A maximal tractable class of soft con-
straint satisfaction. In Journal of Artificial Intelligence
Research 22, 1–22.
Cooper, M. C. (2003). Reduction operations in fuzzy or val-
ued constraint satisfaction. In Fuzzy Sets and Systems
134 311–342.
Cooper, M. C. (2004). Arc consistency for soft constraints.
In Artificial Intelligence 154, 199–227.
Erickson, J. (2010). Maximum flows and parametric short-
est paths in planar graphs. In In Proceedings of the
21st Annual ACM-SIAM Symposium on Discrete Al-
gorithms, 794–804.
Ford, J. and Lester, R. (1956). Network flow theory. In
RAND Corporation, 923, Santa Monica, California.
Ford, L. R. and Fulkerson, D. R. (1955). A simple algorithm
for finding maximal network flows and an application
to the hitchock problem. In In Rand Report Rand Cor-
poration, Santa Monica, California.
Ford, L. R. and Fulkerson, D. R. (1962). Flows in networks.
In In Princeton University Press.
Gondran, M. and Minoux, M. (2008). Graphs, dioids
and semirings: New models and algorithms (opera-
tions research/computer science interfaces series). In
Springer Publishing Company.
Helaoui, M., Naanaa, W., and Ayeb, B. (2013).
Submodularity-based decomposing for valued csp. In
International Journal on Artificial Intelligence Tools.
Schiex, T., Fargier, H., and Verfaillie, G. (1995). Valued
constraint satisfaction problems: hard and easy prob-
lems. In In Proceedings of the 14
th
IJCAI, 631–637,
Montr
´
eal, Canada.
Sedgewick, R. and Wayne, K. D. (2011). Algorithms (4th
ed.). In Addison-Wesley Professional, 661–666.
Shimbel, A. (1955). Structure in communication nets. In
Proceedings of the Symposium on Information Net-
works, 199–203, New York, NY: Polytechnic Press of
the Polytechnic Institute of Brooklyn.
Extended Shortest Path Problem - Generalized Dijkstra-Moore and Bellman-Ford Algorithms
313
