Optimal Price Reaction Strategies in the Presence of Active and Passive

Competitors

Rainer Schlosser and Martin Boissier

Hasso Plattner Institute, University of Potsdam, Potsdam, Germany

Keywords:

Dynamic Pricing, Competition, Optimal Control, Response Strategies, Reaction Time, Price Cycles.

Abstract:

Many markets are characterized by pricing competition. Typically, competitors are involved that adjust their

prices in response to other competitors with different frequencies. We analyze stochastic dynamic pricing

models under competition for the sale of durable goods. Given a competitor’s pricing strategy, we show how

to derive optimal response strategies that take the anticipated competitor’s price adjustments into account. We

study resulting price cycles and the associated expected long-term proﬁts. We show that reaction frequencies

have a major impact on a strategy’s performance. In order not to act predictable our model also allows to

include randomized reaction times. Additionally, we study to which extent optimal response strategies of

active competitors are affected by additional passive competitors that use constant prices. It turns out that

optimized feedback strategies effectively avoid a decline in price. They help to gain proﬁts, especially, when

aggressive competitors are involved.

1 INTRODUCTION

In many markets, ﬁrms have to deal with competition

and stochastic demand. Sellers are required to choose

appropriate pricing decisions to maximize their ex-

pected proﬁts. In E-commerce, it has become easy to

observe and to change prices. Hence, dynamic pric-

ing strategies that take the competitors’ strategies into

account will be used increasingly. However, optimal

price reactions are not easy to ﬁnd. While some mar-

ket participants use mostly constant prices others use

automated price adjustment strategies. Applications

can be found in a variety of contexts that involve per-

ishable (e.g., fashion goods, seasonal products, event

tickets) as well as durable goods (e.g., books, natu-

ral resources, gasoline). In many markets, it can be

observed, that the application of response strategies

typically leads to cyclic price patterns over time, cf.

Edgeworth cycles, see, e.g., Maskin, Tirole (1988),

Noel (2007). We want to explain such effects from a

theoretical perspective.

In this paper, we study oligopoly pricing models

in a stochastic dynamic framework. In our model, the

sales probabilities are allowed to be an arbitrary func-

tion of time and the competitors’ prices. Our aim is to

take into account (i) various competitors’ strategies,

(ii) different (randomized) reaction times, and (iii) ad-

ditional passive competitors that use constant prices.

Selling products is a classical application of rev-

enue management theory. The problem is closely

related to the ﬁeld of dynamic pricing, which is

summarized in the books by Talluri, van Ryzin

(2004), Phillips (2005), and Yeoman, McMahon-

Beattie (2011). The survey by Chen, Chen (2015)

provides an excellent overview of recent pricing mod-

els under competition.

In the article by Gallego, Wang (2014) the authors

consider a continuous time multi-product oligopoly

for differentiated perishable goods. They use op-

timality conditions to reduce the multi-dimensional

dynamic pricing problem to a one-dimensional one.

Gallego, Hu (2014) analyze structural properties of

equilibrium strategies in more general oligopoly mod-

els for the sale of perishable products. The solution

of their model is based on a deterministic version of

the model. Martinez-de-Albeniz, Talluri (2011) con-

sider duopoly and oligopoly pricing models for iden-

tical products. They use a general stochastic counting

process to model customer’s demand.

Further related models are studied by Yang, Xia

(2013) and Wu, Wu (2015). Dynamic pricing mod-

els under competition that also include strategic cus-

tomers are analyzed by Levin et al. (2009) and Liu,

Zhang (2013). Dynamic pricing competition mod-

els with limited demand information are analyzed by

Tsai, Hung (2009), Adida, Perakis (2010) and Chung

Schlosser R. and Boissier M.

Optimal Price Reaction Strategies in the Presence of Active and Passive Competitors.

DOI: 10.5220/0006118200470056

In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 47-56

ISBN: 978-989-758-218-9

et al. (2012) using robust optimization and learning

approaches. Many models consider continuous time

models with ﬁnite horizon and limited inventory. In

most existing models, discounting is not included and

the demand is assumed to be of a special functional

form. We consider inﬁnite horizon models with un-

limited inventory (i.e., products can be reproduced or

reordered). Demand is allowed to depend generally

on time as well as the prices of all market participants.

While many publications concentrate on (the ex-

istence of) equilibrium strategies, we do not assume

that all market participants act rationally. In many

markets it can be observed that automated strategies

that are used by ﬁrms are relatively simple and aggres-

sive. The most common strategy is to slightly under-

cut the competitor’s price, cf. Kephart et al. (2000).

In order to be able to respond to various potentially

suboptimal pricing strategies we provide applicable

solution algorithms that allow to compute optimal re-

sponse strategies.

The main contribution of this paper is threefold.

We (i) derive optimal price response strategies that

anticipate competitors’ prices, (ii) we quantify the im-

pact of different (randomized) reaction times on ex-

pected long-term proﬁts of all market participants,

and (iii) we are able to explain different types of price

cycles.

This paper is organized as follows. In Section 2,

we describe the stochastic dynamic oligopoly model

with inﬁnite time horizon (durable goods). We allow

sales probabilities to depend on competitor prices as

well as on time (seasonal effects). The state space

is characterized by time and the actual competitors’

prices. The stochastic dynamic control problem is ex-

pressed in discrete time. In Section 3, we consider

a duopoly competition. The competitor is assumed

to frequently adjust its prices using a predetermined

strategy. We assume that the price reactions of com-

petitors as well as their reaction times can be antic-

ipated. We set up a ﬁrm’s Hamilton-Jacobi-Bellman

equation and use recursive methods (value iteration)

to approximate the value function. We are able to

compute optimal feedback prices as well as expected

long-term proﬁts of the two competing ﬁrms. Evalu-

ating price paths over time, we are able to explain spe-

ciﬁc price cycles. Furthermore, the results obtained

are generalized to scenarios with randomized reaction

times and mixed strategies.

In Section 4, we analyze optimal response strate-

gies in the presence of active and passive competi-

tors. We study how the duopoly game of two active

competitors is affected by additional passive competi-

tors. We show how to compute optimal pricing strate-

gies and to evaluate expected proﬁts. We also illus-

trate how the cyclic price paths of the active competi-

tors are affected by different price levels of passive

competitors. Finally, we evaluate the expected prof-

its when different strategies are played against each

other. Conclusions and managerial recommendations

are offered in ﬁnal Section 5.

2 MODEL DESCRIPTION

We consider the situation where a ﬁrm wants to sell

goods (e.g., gasoline, groceries, technical devices) on

a digital market platform (e.g., Amazon, eBay). We

assume that several sellers compete for the same mar-

ket, i.e., customers are able to compare prices of dif-

ferent competitors.

We assume that the time horizon is inﬁnite. We

assume that ﬁrms are able to reproduce or reorder

products (promise to deliver), and the ordering is de-

coupled from pricing decisions. If a sale takes place,

shipping costs c have to be paid, c ≥ 0. A sale of one

item at price a, a ≥ 0, leads to a net proﬁt of a − c.

Discounting is also included in the model. For the

length of one period, we will use the discount factor

δ, 0 < δ < 1.

Since in many practical applications prices cannot

be continuously adjusted, we consider a discrete time

model. The sales intensity of our product is denoted

by λ. Due to customer choice, the sales intensity will

particularly depend on our offer price a and the com-

petitors’ prices. We also allow the sales intensity to

depend on time, e.g., the time of the day or the week.

We assume that the time dependence is periodic and

has an integer cycle length of J periods. In our model,

the sales intensity λ is a general function of time, our

offer price a and the competitors’ prices ~p. Given the

prices a and ~p in period t, the jump intensity λ satis-

ﬁes, t = 0, 1,2,..., a ≥ 0, ~p ≥

(a,~p) = λ

t mod J

(a,~p). (1)

In our discrete time model, we assume the sales

probabilities (for one period) to be Poisson dis-

tributed. I.e., the probability to sell exactly i items

within one period of time is given by, t = 0,1,2, ...,

a ≥ 0, ~p ≥

0, i = 0, 1,2,...,

(i,a,~p) =

(a,~p)

· e

−λ

(a,~p)

. (2)

For each period t, a price a has to be chosen. We

call strategies (a

)

admissible if they belong to the

class of Markovian feedback policies; i.e., pricing de-

cisions a

≥ 0 may depend on time t and the current

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

prices of the competitors. By A we denote the set of

admissible prices. A list of variables and parameters

is given in the Appendix, cf. 3.

By X

we denote the random number of sales in

period t. Depending on the chosen pricing strategy

)

, the random accumulated proﬁt from time/period

t on (discounted on time t) amounts to, t = 0, 1,2,...,

∞

∑

s=t

s−t

· (a

− c) · X

. (3)

The objective is to determine a non-anticipating

(Markovian) pricing policy that maximizes the ex-

pected total proﬁt E(G

In the following sections, we will solve dynamic

pricing problems that are related to (1) - (3). In the

next section, we study a duopoly situation. We as-

sume that the competitor frequently adjusts his/her

prices and show how to derive optimal response

strategies. We analyze the impact of different reac-

tion times as well as randomized reaction times. We

also consider the case in which the competitor plays

mixed strategies. In Section 4, we compute pricing

strategies for oligopoly scenarios with active and pas-

sive competitors.

3 OPTIMAL REACTION

STRATEGIES IN A DUOPOLY

3.1 Fixed Reaction Times

In some applications, sellers are able to anticipate

transitions of the market situation. Such information

can be used to optimize expected proﬁts. In particu-

lar, the price responses of competitors as well as their

reaction time can be taken into account. In this case, a

change of the market situation ~p can take place within

a period. A typical scenario is that a competitor ad-

justs its price in response to our price with a certain

delay. In this section, we assume that the pricing strat-

egy and the reaction time of the competitor is known;

i.e., we assume that choosing a price a at time t is fol-

lowed by a state transition (e.g., a competitor’s price

reaction) and the current market situation ~p changes

to a subsequent state described by a transition func-

tion F, which can depend on ~p and a.

In the following, we want to derive optimal price

response strategies to a given competitor’s strategy.

For simplicity, we consider the sale of one type of

product in a duopoly situation. We assume that the

state of the system (the market situation) is one-

dimensional and simply characterized by the competi-

tor’s price p, i.e., we let ~p := p.

In real-life applications, a ﬁrm is not able to ad-

just its prices immediately after the price reaction of

the competing ﬁrm. Hence, we assume that in each

period the price reaction of the competing ﬁrm takes

place with a delay of h periods, h < 1. I.e., after an

interval of size h the competitor adjusts its price from

p to F(a), see Figure 1.

R. Schlosser: Dynamic Pricing under Competition: Evidence from the Amazon Marketplace

Sequence of Events (Duopoly Price Reactions)

Phase

()

adjusted competitor s price F a

′

competitor s price p

′

our price a

Phase

Figure 1: Sequence of price reactions in case of a duopoly.

Thus in period t, the probability to sell ex-

actly i items during the ﬁrst interval of size h

is P

(h)

(i,a, p) := Pois (h · λ

(a, p)), while for the

rest of the period the sales probability changes to

(1−h)

(i,a, F(a)) = Pois((1 − h) · λ

(a,F(a))).

We will use value iteration to approximate the

value function, which represents the present value

of future proﬁts. For a given ”large” number T ,

T  J, we let V

(p) = 0 for all p, and compute,

t = 0, 1,2,...,T − 1, 0 < h < 1, p ∈ A,

(p) = max

a∈A

(

∑

≥0

(h)

,a, p)

∑

≥0

(1−h)

t+h

,a, F(a))



(a − c) · (i

+ i

) + δ ·V

t+1

(F(a))



. (4)

The associated pricing strategy a

∗

(p), t =

0,1, 2,...,J − 1, p ∈ A, is determined by the argmax

∗

(p) = argmax

a∈A

(

∑

≥0

(h)

,a, p)

∑

≥0

(1−h)

t+h

,a, F(a))



(a − c) · (i

+ i

) + δ ·V

t+1

(F(a))



. (5)

In case a

∗

(p) is not unique, we choose the largest

one.

Remark 3.1. Our recursive solution approach also

allows to solve problems with perishable products and

ﬁnite horizons T . Equations (4)-(5) just have to be

evaluated for all t = 0,1,2, ...,T − 1.

Optimal Price Reaction Strategies in the Presence of Active and Passive Competitors

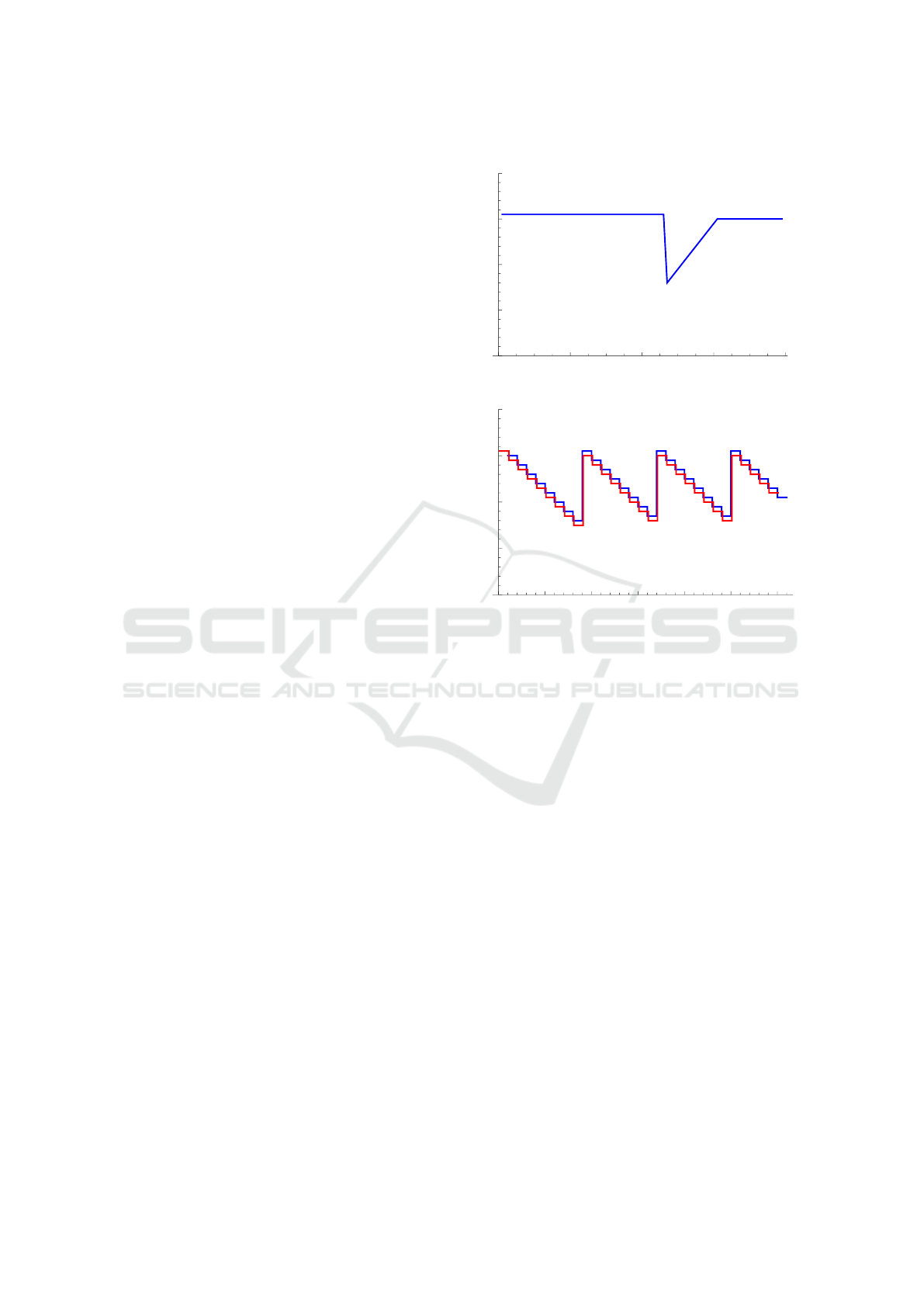
To illustrate our approach we will consider a nu-

merical example for durable goods. We assume

that the competitor applies one of the most common

strategies: the competitor undercuts our current price

by ε down to a certain minimum (e.g., the shipping

costs c). The sales dynamics of the following example

above are based on a large data set from the Amazon

market for used books, see Schlosser et al. (2016).

Deﬁnition 3.1. We deﬁne the sales probabil-

ities P

(h)

(i,a, p) := Pois



h · e

~x(a,p)

/(1 + e

~x(a,p)

)



using linear combinations of the following ﬁve regres-

sors ~x =~x(a, p) given coefﬁcients

β = (β

,..., β

(i) constant / intercept

(a, p) = 1

(ii) rank of price a compared to price p

(a, p) = 1 +



{p<a}

+ 1

{p≤a}



(iii) price gap between price a and price p

(a, p) = a − p

(iv) total number of competitors

(a, p) = 1

(v) average price level

(a, p) = (a + p)/2

Example 3.1. We assume a duopoly. Let c = 3,

δ = 0.99, 0 ≤ h ≤ 1, and let F(a) := max(a − ε,c),

ε=1, a ∈ A :=

{

1,2, ...,100

}

. For the computation

of the value function, we let T := 1000. We assume

the sales probabilities P

(h)

(·,a, p), see Deﬁnition 3.1,

where

β = (−3.89,−0.56,−0.01,0.07,−0.02).

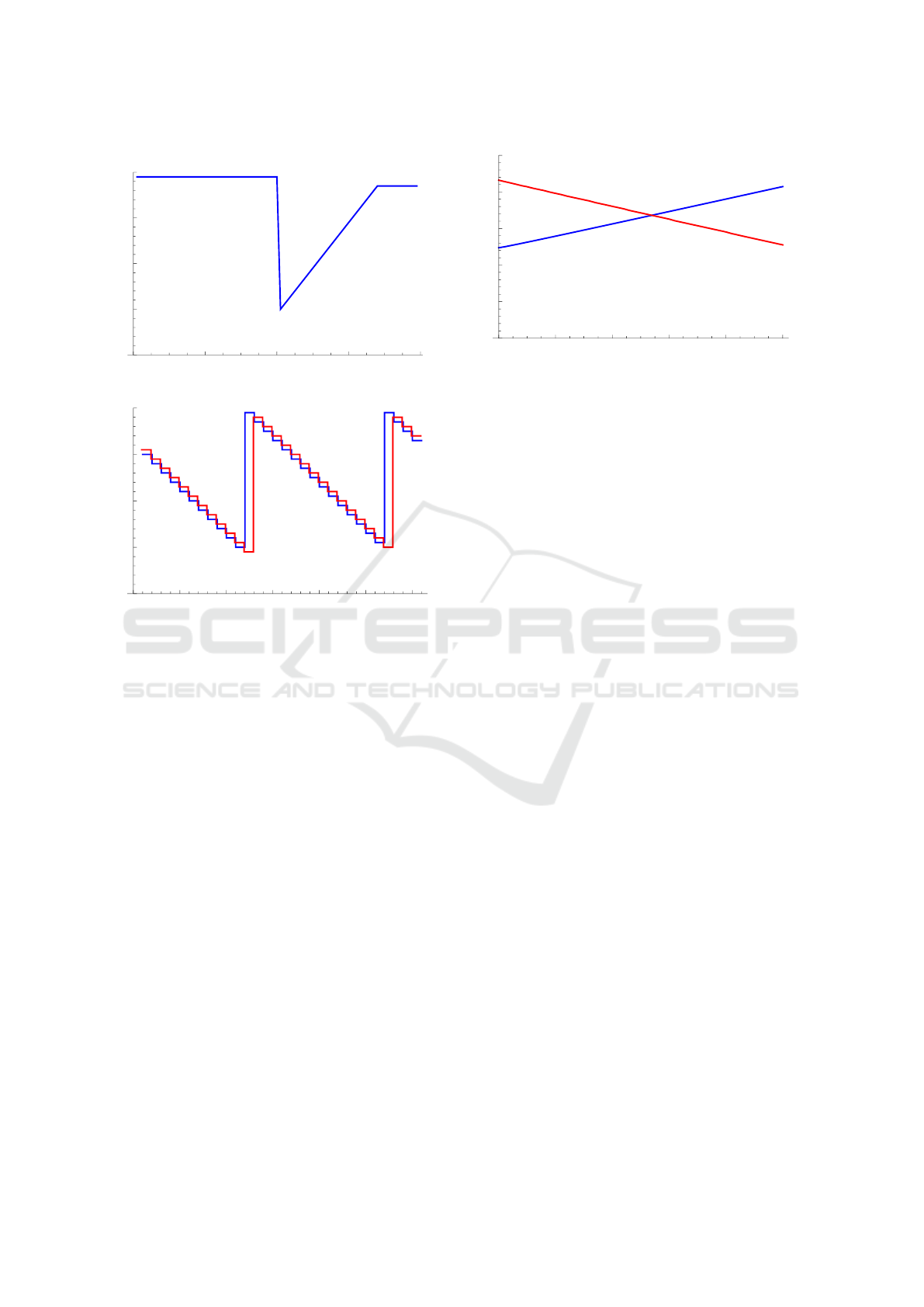
Figure 2a and Figure 3a show optimal response

strategies for different reaction times h=0.1 and

h=0.9. The case h = 0.1 illustrates a fast reaction time

of the competitor; h = 0.9 represents a slow reaction

of the competitor. If h = 0.5 both competing ﬁrms re-

act equally fast. In all three cases the optimal response

strategy are of similar shape. If the competitor’s price

is either very low or very large, it is optimal to set the

price to a certain moderate level. If the competitor’s

price is somewhere in between (intermediate range),

it is best to undercut that price by one price unit ε. If

h is larger, the upper price level is increasing and the

intermediate range is bigger.

The application of optimal response strategies

leads to cyclic price patterns over time, cf. Edgeworth

cycles, see, e.g., Maskin, Tirole (1988), Kephart et al.

0 20 40 60 80

a(p)

(a) Optimal response policy.

0 5 10 15 20 25 30

(b) Evaluated price paths over time.

Figure 2: Optimal response policy and price paths for Ex-

ample 3.1 with h = 0.1.

(2000), or Noel (2007). The resulting price paths are

shown in Figure 2b and Figure 3b. If the reaction time

of the competitor is longer, we observe that the cycle

length and the amplitude of the price patterns are in-

creasing. Note, roughly h · 100% of the time our ﬁrm

is offering the lowest price; i.e., the parameter h can

also be used to model situations in which one ﬁrm is

able to adjust its prices more often than another ﬁrm.

In addition, we are able to analyze the impact

of the reaction time on expected long-term proﬁts

of our ﬁrm as well as the competitor. We assume

that the competitor faces the same sales probabilities

and shipping costs as we do. The competitor’s ex-

pected proﬁts can be recursively evaluated by, cf. (4),

t = 0, 1,2,...,T − 1, 0 < h < 1, a ∈ A, V

(c)

T +h

(a) = 0,

(c)

t+h

(a) =

∑

≥0

(1−h)

t+h

,F(a),a)

∑

≥0

(h)

t+1



,F(a),a

∗

t+1 mod J

(F(a))





(F(a) − c) · (i

+ i

) + δ ·V

(c)

t+h+1



∗

t+1 mod J

(F(a))





(6)

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

0 20 40 60 80

a(p)

(a) Optimal response policy.

0 5 10 15 20 25 30

(b) Evaluated price paths over time.

Figure 3: Optimal response policy and price paths for Ex-

ample 3.1 with h = 0.9.

Due to the cyclic price paths, the expected future

proﬁts V

(p) and V

(c)

(a) are (almost) independent of

the initial states/prices. Figure 4 depicts V as well

as the competitor’s expected proﬁts V

(c)

as a function

of h. We observe that the expected proﬁt V is lin-

ear increasing in the competitor’s reaction time; the

competitor’s proﬁt V

(c)

is decreasing in h. Note, the

impact of h is substantial. The disadvantage of the

player that stops the undercutting phase can already

be compensated if our reaction time is smaller than

0.46, i.e., if h exceeds the value 0.54.

3.2 Randomized Reaction Times

Due to the signiﬁcant impact of reaction times, ﬁrms

will try to minimize their reaction times by anticipat-

ing their competitor’s time of adjustment. In order not

to act predictable, ﬁrms will randomize their reaction

times. Moreover, ﬁrms will try to gain advantage by

updating their prices more frequently.

In case the reaction time is not deterministic, the

model can be adjusted. If the distribution of the re-

action time of competitors is known, the Hamilton-

Jacobi-Bellman (HJB) equation, cf. (4), can be mod-

0.0 0.2 0.4 0.6 0.8 1.0

(c)

Figure 4: Expected proﬁt for different reaction times of the

competitor; Example 3.1.

iﬁed. The different reaction scenarios just have to be

considered with the corresponding probability. Note,

the reaction times of different competitors can be ob-

served in the long run.

Strategic ﬁrms will try to optimally time their

price adjustments. In order not to act predictable,

ﬁrms might use randomized strategies. In the fol-

lowing, we consider such a scenario. We assume

that each ﬁrm adjusts its price with a certain intensity

(e.g., on average once a period of size 1). We model

that approach as follows: we assume that at each point

in time d, d = t + ∆,t + 2∆,...,t + 1, 0 < ∆  1, our

ﬁrm adjusts its price with probability q, 0 < q  1;

i.e., on average we adjust our price q/∆ times a pe-

riod of size 1. Similarly, the competitor adjusts its

price with probability q

(c)

, 0 < q

(c)

 1.

The competitor applies a certain strategy F(a). By

−

we denote our current price at time d, the be-

ginning of the sub-period (d,d + ∆). With proba-

bility q

(c)

, the competitor adjusts its price from p to

F(a

−

). With probability q, we adjust the price a

−

price a. Since q and q

(c)

are assumed to be ”small”

we do not consider the case in which both ﬁrms ad-

just their prices at the same time. The related value

function is given by, a

−

, p ∈ A, t = 0, ∆,2∆, ...,T −∆,

−

, p) = 0,

−

, p) = (1 − q − q

(c)

)

∑

i≥0

(∆)

(i,a

−

, p)·



−

− c) · i + δ

∆

t+∆

−

, p)



(c)

∑

i≥0

(∆)

(i,a

−

,F(a

−

))



−

− c) · i + δ

∆

t+∆

−

,F(a

−

))



+q · max

a∈A

(

∑

i≥0

(∆)

(i,a, p)



(a − c) · i + δ

∆

t+∆

(a, p)

o

. (7)

Optimal Price Reaction Strategies in the Presence of Active and Passive Competitors

The optimal price ˜a

∗

−

, p), t = 0,∆, 2∆,...,J −∆,

is determined by the arg max of (7). The competitor’s

expected proﬁt corresponds to, t = 0,∆, 2∆,...,T − ∆,

(c)

−

, p) = 0,

(c)

−

, p) = (1 − q − q

(c)

)

∑

i≥0

(∆)

(i, p,a

−

) ·



(p − c) · i + δ

∆

(c)

t+∆

−

, p)



(c)

∑

i≥0

(∆)

(i,F(a

−

),a

−

)



(F(a

−

) − c) · i + δ

∆

(c)

t+∆

−

,F(a

−

))



+q ·

∑

i≥0

(∆)



i, p, ˜a

∗

t mod J

−

, p)





(p − c) · i + δ

∆

(c)

t+∆



˜a

∗

t mod J

−

, p), p





. (8)

Example 3.2. We assume the duopoly setting of

Example 3.1. We let c = 3, F(a) := max(a − ε, c),

ε = 1, a ∈ A :=

{

1,2, ...,100

}

, δ=0.99, ∆=0.1. We use

T := 1000. We consider different reaction probabili-

ties q and q

(c)

1 contains the expected proﬁts (

V ,

(c)

) of the

two competing ﬁrms for different reaction probabili-

ties. We observe that

V is increasing in q and decreas-

ing in q

(c)

. For

(c)

it is the other way around. It turns

out, that the ratio q/q

(c)

of the adjustment frequencies

is a critical quantity.

Table 1: Expected proﬁts

V and

(c)

for different reaction

probabilities q, q

(c)

= 0.05,0.1,0.2, δ = 0.99, ∆ = 0.1; Ex-

ample 3.2.

(c)

\q 0.05 0.1 0.2

0.05 (16.53, 17.07) (16.80, 16.81) (17.01, 16.62)

0.1 (16.26, 17.36) (16.48, 17.09) (16.75, 16.84)

0.2 (16.03, 17.59) (16.22, 17.37) (16.48, 17.12)

The overall adjustment frequency plays a minor

role as long as the ratio q/q

(c)

is the same. Hence, the

expected proﬁts of both ﬁrms can be approximated by

the proﬁts from the model with deterministic reaction

time, cf. Section 3.1, where h = q/q

(c)

, i.e., the per-

centage of time our ﬁrm has the most recent price.

Figure 5b illustrates the (simulated) price paths

for the parameter setting of Example 3.2. Figure

5a shows the deterministic case of Example 3.1 for

h = 0.5. We observe that overall the price patterns

have similar characteristics. However, in the random-

ized case, the timing of the price reactions is not pre-

dictable. While in the deterministic h = 0.5 case (cf.

0 5 10 15 20 25 30

(a) Deterministic reaction times h = 0.5, Example 3.1.

0 5 10 15 20 25 30

(b) Randomized reaction times for ∆ = 0.1, q = q

(c)

= 0.1;

Example 3.2.

Figure 5: Evaluated price paths over time.

Section 3.1) we have

V = 16.44 and

(c)

= 17.13, in

the randomized case (∆ = 0.1, q = q

(c)

= 0.1) the ex-

pected proﬁts are

V = 16.48 and

(c)

= 17.09. I.e.,

in both models the advantage of the aggressive player

is basically the same; in the model with randomized

reaction times the advantage is slightly smaller.

3.3 Mixed Competitors’ Strategies

Our results show that if the competitor’s strategy is

known, suitable response strategies can be computed.

Hence, ﬁrms might try to randomize their strategies.

In this section, we will analyze scenarios in which

competitors play a mixed pricing strategy.

We assume that the competitor plays strategy

(a), a ∈ A, with probability π

, 1 ≤ k ≤ K < ∞,

∑

= 1.

We assume deterministic reaction times. We ad-

just our model, cf. Section 3.1, by using a weighted

sum of the potential price reactions. The Hamilton-

Jacobi-Bellman (HJB) equation can be written as,

t = 0, 1,2,...,T − 1, 0 < h < 1, p ∈ A,

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

(p) = max

a∈A

(

∑

≥0

(h)

,a, p)

∑

≥0

(1−h)

t+h

,a, F

(a))



(a − c) · (i

+ i

) + δ ·V

t+1

(a))



, (9)

where V

(p) = 0 for all p. The associated pric-

ing strategy a

∗

(p), t = 0, 1,2, ...,J − 1, 0 < h < 1,

p ∈ A, is determined by the argmax of (9). The result-

ing competitor’s expected proﬁts can be computed by

(starting from, e.g., V

(c)

T +h

(a) = 0), t = 0, 1,2,...,T −1,

0 < h < 1, a ∈ A,

(c)

t+h

(a) =

∑

≥0

(1−h)

t+h

(a),a)

∑

≥0

(h)

t+1



(a),a

∗

t+1 mod J

(a))





(a) − c) · (i

+ i

) + δ ·

(c)

t+h+1



∗

t+1 mod J

(a))





(10)

The models described above allow computing

suitable pricing strategies in various competitive mar-

kets. As long as the number of competing ﬁrms is

small, the value function and the optimal prices can be

computed. Note, due to the coupled state transitions

in general the value function has to be computed for

all states in advance. When the number of competitors

is large this can cause serious problems since the state

space can grow exponentially (curse of dimensional-

ity). Hence, the approach is suitable, if the number of

competitors is small and their strategies are known.

If the number of competitors is large and the ﬁrm’s

strategies are unknown, we recommend using simple

but robust strategies, see Schlosser et al. (2016).

4 COMPETITION WITH ACTIVE

AND PASSIVE SELLERS

If the pricing strategies and the reaction times of dif-

ferent competitors are known the model can be ex-

tended to an oligopoly setting. For each additional

competitor the state space of the model has to be ex-

tended by one dimension. Note, only active competi-

tors that frequently adjust their prices should be taken

into account. Inactive customers will be treated as ex-

ternal ﬁxed effects.

In the following, we assume one active competi-

tor and Z passive competitors. The prices of the pas-

sive competitors are denoted by~z = (z

,..., z

), z

≥ 0,

j = 1, ...,Z, and assumed to be constant over time.

The active competitor plays a (non-randomized) strat-

egy F(a) that refers to our price a (not the passive

one). The Hamilton-Jacobi-Bellman (HJB) equation

can be written as, t = 0,1, 2,...,T − 1, 0 < h < 1,

p ≥ 0, V

(p,~z) = 0 for all p,~z,

(p,~z) = max

a∈A

(

∑

≥0

(h)

,a, p,~z)

∑

≥0

(1−h)

t+h

,a, F(a),~z)



(a − c) · (i

+ i

) + δ ·V

t+1

(F(a),~z)



. (11)

The associated pricing strategy amounts to, t =

0,1, 2,...,J − 1, 0 < h < 1, p ∈ A,

∗

(p,~z) = arg max

a∈A

(

∑

≥0

(h)

,a, p,~z)

∑

≥0

(1−h)

t+h

,a, F(a),~z)



(a − c) · (i

+ i

) + δ ·V

t+1

(F(a),~z)



. (12)

The competitor’s proﬁts can be computed by

(starting from, e.g., V

T +h

(a,~z) = 0 for all a,~z), t =

0,1, 2,...,T − 1, 0 < h < 1, a ≥ 0,

(c)

t+h

(a,~z) =

∑

≥0

(1−h)

t+h

,F(a),a,~z)

∑

≥0

(h)

t+1



,F(a),a

∗

t+1 mod J

(F(a),~z),~z





(F(a) − c) · (i

+ i

) + δ ·V

(c)

t+h+1



∗

t+1 mod J

(F(a),~z),~z





(13)

Note, the value function does not need to be com-

puted for all price combinations of passive competi-

tors in advance. The value function and the associated

pricing policy can be computed separately for speciﬁc

market situations (e.g., just when they occur).

In the following, we consider an example with ac-

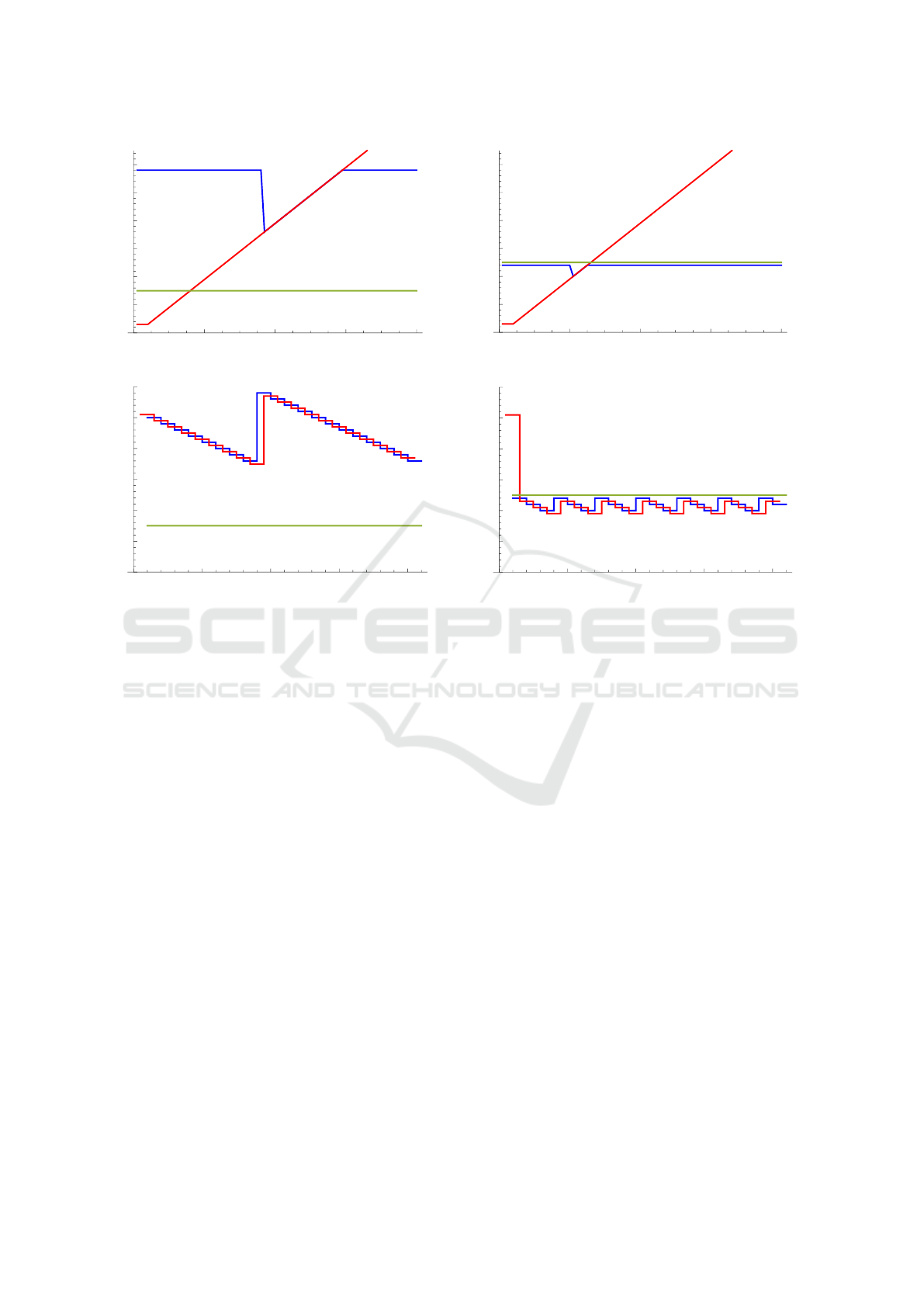
tive and passive competitors.

Example 4.1. We assume the duopoly setting of

Example 3.1. We let F(a) := max(a−ε,c), ε = 1, c =

3, h = 0.5, a ∈ A :=

{

1,2, ...,100

}

, δ = 0.99, and T =

1000. Furthermore, we consider an additional passive

competitor with the constant price z, z = 15, 20,25.

Optimal Price Reaction Strategies in the Presence of Active and Passive Competitors

0 20 40 60 80

(p,z)

p= F(a)

z=15

(a) Optimal response strategy.

0 5 10 15 20

z=15

(b) Evaluated price paths over time.

Figure 6: Optimal response strategy and evaluated price

paths for Example 4.1; h = 0.5, z = 15.

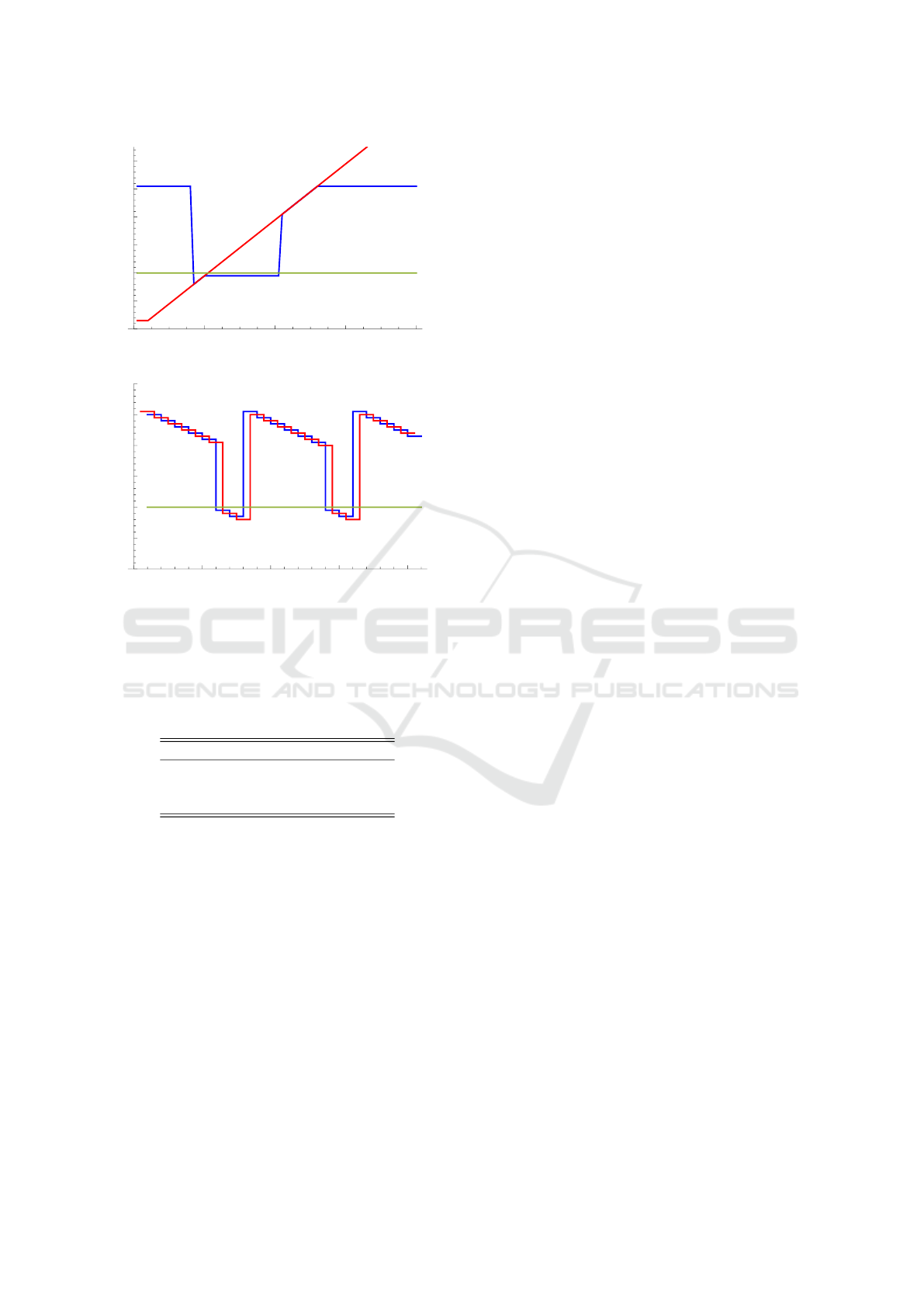
The results of the three cases z = 15, z = 20, and

z = 25 are illustrated in Figure 6, 7 and 8. We observe

three different characteristics. If the passive competi-

tor’s price is low (z = 15) the cyclic price battle be-

tween our ﬁrm and the aggressive ﬁrm takes place at a

higher price level, see Figure 6b. The response strate-

gies of the three ﬁrms are displayed in Figure 6a.

If the price of passive ﬁrm is sufﬁciently high

(z = 20), then the cyclic price paths of the two active

ﬁrms take place below that level. If the constant price

is ”moderate” (z = 20), then a mixture of the charac-

teristics shown in Figure 6 and 7 is optimal. We also

observe that it is not advisable to place price offers

that slightly exceed competitors’ prices, cf. Figure 8.

At the end of this section, we want to generally

evaluate the outcome when different (time homoge-

neous) strategies are played against each other. We

assume time homogeneous demand and h = 0.5. If

ﬁrm 1 plays a pure strategy S

and ﬁrm 2 plays the

pure strategy S

then the associated expected proﬁts

can be computed by, t = 0, 1,2,...,T − 1, V

(1)

(a) =

(2)

(a) = 0, for all a ≥ 0,

(1)

(a) =

∑

≥0

(0.5)

(a),a)

0 20 40 60 80

(p,z)

p=F(a)

z=25

(a) Optimal response strategy.

0 5 10 15 20

z=25

(b) Evaluated price paths over time.

Figure 7: Optimal response strategy and evaluated price

paths for Example 4.1; h = 0.5, z = 25.

∑

≥0

(0.5)

(a),S

(a)))



(a) − c) · (i

+ i

) + δ ·V

(1)

t+1

(a)))



(14)

(2)

(a) =

∑

≥0

(0.5)

(a),a)

∑

≥0

(0.5)

(a),S

(a)))



(a) − c) · (i

+ i

) + δ ·V

(2)

t+1

(a)))



(15)

By S

we denote the response strategy F(a) :=

max(a − ε,c), which slightly undercuts the competi-

tor’s price. By S

we denote the optimal response

strategy to S

. By S

RRU

we denote the optimal re-

sponse strategy to S

, cf. (11)-(12). Considering

Example 4.1 with z = 20, the expected proﬁts of the

different strategy combinations are summarized in 2.

We observe that the aggressive strategy S

yields

very good results with the exception when the com-

petitor also plays S

. The strategy S

yields good

results in all three constellations. Strategy S

RRU

is ex-

cellent when played against S

but yields only mod-

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

0 20 40 60 80

(p,z)

p= F(a)

z=20

(a) Optimal response strategy.

0 5 10 15 20

z=20

(b) Evaluated price paths over time.

Figure 8: Optimal response strategy and evaluated price

paths for Example 4.1; h = 0.5, z = 20.

Table 2: Expected proﬁts V

(1)

(50) of ﬁrm 1 when its

strategy S

{

RRU

}

is played against a strategy

{

RRU

}

, z = 20, Example 4.1.

RRU

1.69 9.85 9.91

9.42 9.66 9.58

RRU

8.76 10.62 8.76

erate results in the other two cases. For other z val-

ues, cf. Example 4.1, the results are similar. Iterating

mutual strategy responses further is a way to identify

equilibrium strategies.

Finally, our example shows that optimal response

strategies have a signiﬁcant impact on expected prof-

its. They help to gain proﬁts, especially, when aggres-

sive competitors are involved. On the other hand, we

learn that it is also important to know the competitors’

strategies. In practical applications, the competitors’

price reactions can be inferred from market data over

time.

5 CONCLUSION

With a rise in E-commerce it has become easier to ob-

serve and to adjust prices automatically. As a result,

dynamic pricing strategies are applied by an increas-

ing number of ﬁrms. This paper analyzes stochastic

dynamic inﬁnite horizon oligopoly models character-

ized by active and passive competitors. We set up

a dynamic pricing model including discounting and

shipping costs. The sales probabilities are allowed

to depend on time and can arbitrarily depend on our

price as well as the competitors’ prices. Hence, our

model is suitable for practical applications. Data-

driven estimations of sales intensities under pricing

competition can be used to calibrate the model.

Given a competitor’s response strategy, we are

able to compute optimal reaction strategies that take

the anticipated competitors’ price adjustments into

account. In general, it is optimal to slightly undercut

competitor’s prices. However, when the price falls be-

low a certain lower bound it is advisable to raise the

price to an optimally chosen upper level. Our exam-

ples show that the model can be used to explain and

to study Edgeworth price cycles.

We also verify that reaction times have a signif-

icant impact on long-term proﬁts. Hence, ﬁrms will

try to strategically time their price adjustments. In or-

der not to act predictable ﬁrms might use randomized

strategies. Using a generalized version of our model,

we show how to derive optimal response strategies

when reaction times are randomized. We observe that

the ratio of frequencies of the competitors’ prices ad-

justments is crucial for the ﬁrm’s expected proﬁts, i.e.,

to be able to adjust prices more often than the com-

petitors do is an important competitive advantage.

In an extension of the model, we have considered

additional players with ﬁxed price strategies. We have

presented a solution approach that allows deriving op-

timal response strategies. We have analyzed how the

presence of additional passive competitors affects the

price battle of active players that frequently adjust

their prices. The solution approach is even applica-

ble when the number of passive competitors is large.

Our technique to compute prices remains simple and

is easy to implement.

Moreover, we have evaluated the outcome when

different reaction strategies are played against each

other. It turned out that our optimized feedback strate-

gies effectively avoid a decline in price. Especially,

when competitors play aggressive strategies it is im-

portant to react in a reasonable way in order not to

loose potential proﬁts. Our approach allows to derive

and to study price response strategies for various real-

life applications especially in E-commerce.

Optimal Price Reaction Strategies in the Presence of Active and Passive Competitors

Iterating mutual strategy responses, cf. Table 2,

may also be the key to identify equilibrium strategies.

Note, mutual strategy responses do not necessarily

have to converge as pure strategy equilibria might not

exist, see Kephart et al. (2000). In such cases, the

approach used in Section 3.3 might help to identify

equilibria in mixed strategies.

In future research we will use market data to es-

timate competitors’ response strategies. We will also

extend the model to study the sale of perishable prod-

ucts with ﬁnite initial inventory levels.

REFERENCES

Adida, E., G. Perakis. 2010. Dynamic Pricing and Inven-

tory Control: Uncertainty and Competition. Opera-

tions Research 58 (2), 289–302.

Chen, M., Z.-L. Chen. 2015. Recent Developments in Dy-

namic Pricing Research: Multiple Products, Compe-

tition, and Limited Demand Information. Production

and Operations Management 24 (5), 704–731.

Chung, B. D., J. Li, T. Yao, C. Kwon, T. L. Friesz. 2012.

Demand Learning and Dynamic Pricing under Com-

petition in a State-Space Framework. IEEE Transac-

tions on Engineering Management 59 (2), 240–249.

Gallego, G., M. Hu 2014. Dynamic Pricing of Perishable

Assets under Competition. Management Science 60

(5), 1241–1259.

Gallego, G., R. Wang. 2014. Multi-Product Optimization

and Competition under the Nested Logit Model with

Product-Differentiated Price Sensitivities. Operations

Research 62 (2), 450–461.

Kephart, J. O., J. E. Hanson, A. R. Greenwald. 2000. Dy-

namic Pricing by Software Agents. Computer Net-

works 32, 731-752.

Levin, Y., J. McGill, M. Nediak. 2009. Dynamic Pricing in

the Presence of Strategic Consumers and Oligopolistic

Competition. Operations Research 55, 32–46.

Liu, Q., D. Zhang. 2013. Dynamic Pricing Competition

with Strategic Customers under Vertical Product Dif-

ferentiation. Management Science 59 (1), 84–101.

Martinez-de-Albeniz, V., K. T. Talluri. 2011. Dynamic Price

Competition with Fixed Capacities. Management Sci-

ence 57 (6), 1078–1093.

Maskin, E., J. Tirole. 1988. A Theory of Dynamic

Oligopoly, II: Price Competition, Kinked Demand

Curves and Edgeworth Cycles. Econometrica 56 (6),

571–599.

Noel, M. D. 2007. Edgeworth Price Cycles, Cost-Based

Pricing, and Sticky Pricing in Retail Gasoline Mar-

kets. The Review of Economics and Statistics 89 (2),

324–334.

Phillips, R. L. 2005. Pricing and Revenue Optimization.

Stanford University Press.

Schlosser, R., M. Boissier, A. Schober, M. Uﬂacker. 2016.

How to Survive Dynamic Pricing Competition in

E-commerce. Poster Proceedings of the 10th ACM

Conference on Recommender Systems, RecSys 2016,

Boston, MA, USA.

Talluri, K. T., G. van Ryzin. 2004. The Theory and Practice

of Revenue Management. Kluver Academic Publish-

ers.

Tsai, W.-H., S.-J. Hung. 2009. Dynamic Pricing and Rev-

enue Management Process in Internet Retailing under

Uncertainty: An Integrated Real Options Approach.

Omega 37 (2-37), 471–481.

Wu, L.-L., D. Wu. 2015. Dynamic Pricing and Risk Analyt-

ics under Competition and Stochastic Reference Price

Effects. IEEE Transactions on Industrial Informatics

12 (3), 1282–1293.

Yang, J., Y. Xia. 2013. A Nonatomic-Game Approach to

Dynamic Pricing under Competition. Production and

Operations Management 22 (1), 88–103.

Yeoman, I., U. McMahon-Beattie. 2011. Revenue Man-

agement: A Practical Pricing Perspective. Palgrave

Macmillan.

APPENDIX

Table 3: List of variables and parameters.

t time / period

X random number sold items

G random future proﬁts

c shipping costs

δ discount factor

F competitor’s reaction strategy

Z number of passive competitors

A set of admissible prices

V,V

(c)

value functions

a offer price

~p,~z competitors’ prices

λ sales intensity

P sales probability

J cycle length

h reaction time

q,q

(c)

reaction probabilities

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems