
Land Cover Clustering based on Improved Dictionary Learning Method
from Modis Data
Mariem Zaouali, Sonia Bouzidi and Ezzeddine Zagrouba
1
RIADI Laboratory, Research Team on Intelligent Systems in Image and Artificial Vision, ISI,
University of Tunis El Manar, Tunis, Tunisia
Keywords:
k-Means Clustering Algorithm, Discriminative Temporal Behavior, Dictionary Learning, Coarse Spatial
Resolution Images, Remote Sensing, Sparse Representation.
Abstract:
An approach based on k-means clustering algorithm combined with the concept of sparse representation is
proposed in this paper. We intend to discriminate, each vegetation type, by its temporal behavior. Our method
is composed of two main parts : The first part consists of designing the dictionary that we are going to use.
For this reason, we propose a modification of the k-svd algorithm by switching the use of OMP algorithm
by the SunSAL algorithm. Then we carry on an unsupervised clustering process using k-means algorithm on
sparse vectors. As a result, we found that SunSAL algorithm outperforms the OMP algorithm and we succeed
to elaborate discriminative temporal behaviors of the vegetation in our region of study. As perspectives, our
approach could be considered as an attempt to overcome the shortage of high spatial resolution data since we
are relying only on coarse remote sensing images like MODIS to monitor Land Cover dynamics.
1 INTRODUCTION
Over the past decades, remote sensing measurements
have played a key role in analyzing climate changes
and dynamics of ecosystem, in order to protect the
Earth surface from environmental disasters. Nowa-
days, thanks to the development of aerospace tech-
nologies, a great number of satellite sensors has been
launched, which has increased incredibly the amount
of available data. The use of multitemporal coarse
resolution satellite imagery has shown potentials but
requires a considerable amount of data, especially
ground truth, to monitor land cover change (Zhan
et al., 2002; Morton et al., 2005). Thus, unsuper-
vised methods give a more attractive solution to that.
In this work, we explore a coarse spatial resolution
data but highly frequent in time. We estimate that
the temporal features is interesting to model the land
cover and could improve vegetation cover classifica-
tion (Jia et al., 2013). Indeed, time series vegetation
index (eg. NDVI or EVI) are approved to well de-
scribe vegetation growth as well as revealing the veg-
etation type information since it represents the phe-
nology cycle (Brown et al., 2013). Whereas, the main
issue comes to how surpass dimensionality of time se-
ries data and limited availability of labeled samples
to improve land cover classification accuracy. In a
recent work (Yang et al., 2014), an approach is pro-
posed based on NDVI, PCA and ISODATA cluster-
ing algorithm (which groups pixels with similar spa-
tial and spectral characteristics into classes (Moham-
mady et al., 2015)). However, in practical application,
the quality of this classification is often not enough
(Guha and Ward, 2012). Recently, sparse model-
ing has proven fruitful application in various fields
such as signal, image, compression and others (Lim
et al., 2012; Mahmoudi and Sapiro, 2012; Wright
et al., 2009). It also provides a useful tool for ma-
chine learning. In fact, sparse representation can clas-
sify any samples based on the concept that it is a lin-
ear combination of labeled prototype samples (Chen
and Donoho, 1994). In this work, we tried to exploit
sparse representation paradigm since it is a tool for
dimensionality reduction, in order to conduct unsu-
pervised clustering. The idea is to find a dictionary
that can well approximate NDVI temporal behavior
without the requirement of labeled samples. The fi-
nal result is a discriminant temporal behavior of each
land cover and a labeled data. This paper is organized
as follows: Section II presents Related concepts, Sec-
tion III describes the proposed approach, Section IV
presents the Study area, Section V describes experi-
mental protocol and results. Finally the last Section is
the conclusion.
Zaouali, M., Bouzidi, S. and Zagrouba, E.
Land Cover Clustering based on Improved Dictionary Learning Method from Modis Data.
DOI: 10.5220/0005851006970704
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 697-704
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
697

2 RELATED CONCEPTS
Sparse representation helps having compact represen-
tation of images by using a reduced set of coefficients
from a basis of elements, i.e dictionary, which is a
matrix whose columns d
k
are called atoms. This tech-
nique has been applied in various fields including re-
mote sensing. In our case, we want to exploit sparse
representation in order to improve land cover classifi-
cation and then use it for changes detection. We aim
to discriminate classes by their temporal behavior in
order to make detecting changes easier. This would
be an attempt to deal with limited availability of la-
beled samples. Our approach is based on considering
temporal patches as dictionary atoms This means that
we track the temporal behavior of a pixel through the
time series images. In this section, we present the def-
inition of sparse representation and its classifier logic.
2.1 Sparse Representation
Let the dictionary D ∈ R
n×p
be a base containing p
atoms, , each one composed of n rows, with n < p.
This dictionary contains a set of temporal behaviors
chosen randomly from the study area. For a given sig-
nal Y, it is demanded to find a sparse vector X, having
only few non zeros coefficients, combining linearly
the atoms of dictionary D. This problem could be pre-
sented in equation 1:
argminkX k
0
sub ject to kY − DXk
2
≤ δ (1)
with Y is the signal to represent via X from D and δ
is the level of sparsity. Due to the presence of pos-
sible modeling error and noise, equation (1) is often
replaced by
argminkX k
1
sub ject to kY − DXk
2
≤ δ (2)
where kX k
1
=
∑
n
i=1
|x
i
|. This is due to the difficulty
to resolve l
0
norm, which is considered as NP-hard
problem. In fact, several algorithms have been pro-
posed to solve equation (1) such as Basis pursuit BP
(Chen and Donoho, 1994), Orthogonal Matching Pur-
suit OMP (Tropp et al., 2007) and Sparse UNmixing
by variable Splitting and Augmented Lagrangian Sun-
SAL (Bioucas-Dias and Figueiredo, 2010). BP re-
places the l
0
norm with l
1
norm as mentioned in equa-
tion (2). However, OMP proposes a greed strategy. In
the first iteration, OMP takes the test sample Y as an
initial residual, then, through each iteration, OMP has
to recognize the atom that could best approximate the
residual. Using the selected atoms, OMP re-estimates
X. This algorithm will stop once if one of the fol-
lowing conditions are met: Approximation error is
less than a certain threshold or a predefined number
of atoms have been selected. However SunSAL pro-
poses another approach. It is based on the fact that
the equation (1) is equivalent to the following uncon-
strained optimization problem:
min
1
2
ky − Dxk
2
2
+ λkxk
1
(3)
where λ is a Lagrangian multiplier. SunSAL provides
an efficient solution form l
2
− l
1
norm problem. It is
considered more efficient and less complex with equal
accurate solution as an alternate of LASSO-(least ab-
solute shrinkage and selection operator)(Xue et al.,
2015). In this work, we deal with OMP and SunSAL
and compare their performance in designing dictio-
nary. In next section, we describe how, with the help
of dictionary and sparse representation, we can clas-
sify training samples.
2.2 Sparse Representation based
Classifier
Sparse representation relies on the idea that any signal
is a linear combination of atoms belonging to a class.
That is mean that any signal representing a class C
i
could be sparsely composed by remarkable coefficient
of class C
i
while for the other class, are barely zeros.
Indeed, for a set of k objects of classes : v
i,1
, ...v
i,k
with v
i, j
is the j
th
sample of the i
th
class, let consider
D
i
= [v
i,1
, ...v
i,k
] as the matrix representing the i
th
. Let
D= [D
1
, D
2
, ...D
p
] be a dictionary. The resolution of
Y = DX with X = [0, ....0, x
i,1
, x
i,2
, ..., x
i, j
, 0.....0]
T
is
the sparse vector, gives us the label of the sample Y .
In fact X would have only few non zero coefficients
which refer to the class of Y . Thanks to the residual
base criterion formula :
class(y
i
) = arg min
j∈1...c
kY − DXk
2
(4)
where class(y
i
) is the class label affected to y, we can
measure the accuracy of the classification result. In
our case, we cannot determine the label of samples y
i
because the dictionary atoms’ are anonymous. They
just were extracted from the study region without any
further information pertaining to its type. The pro-
posed solution to this point, is described in the next
section.
3 PROPOSED APPROACH
In this work, we try to classify vegetation based on its
discriminant behavior using NDVI (Normalized Dif-
ferential Vegetation Index) profiles. This index is de-
fined as the difference between the visible (red) and
RGB-SpectralImaging 2016 - Special Session on RBG and Spectral Imaging for Civil/Survey Engineering, Cultural, Environmental,
Industrial Applications
698

near-infrared (nir) bands, over their sum. It is directly
related to the amount of photo synthetically-active ra-
diation intercepted by the vegetation canopy, and thus
it is widely used for differentiating areas that contain
healthy vegetation. We aim, in this paper, to charac-
terize the phenology of vegetation through its NDVI
profiles. To reach this goal, we propose, an approach
based on sparse representation and dictionary learn-
ing. In literature, dictionary could be pre-designed or
resulting from training process. The choice of which
dictionary to use, is established according to the appli-
cation context. In our work, we have chosen to con-
Sequence of
images - MODIS
Dictionary learning
NDVI Temporal
Behavior of pixels
K-means performed on sparse vectors
Number of clusters fixed by Silhouette method
Mean of Temporal Profiles of each cluster
dates
dates
NDVI
NDVI
NDVI
NDVI
Extract temporal
patches to plot
NDVI Temporal
behavior
Dictionary initialization : atoms are NDVI Temporal Behavior
dates
dates
Figure 1: Proposed approach.
duct a dictionary learning process in order to fit the
data and to characterize it only through its temporal
behavior not through its spatial characteristics. Thus,
in our case, we edit the K-SVD algorithm (Aharon
et al., 2006) to do this learning: The first step is the
dictionary initialization, we choose randomly samples
from the study area which would be used as the atoms
of dictionary. The design of the dictionary consists of
two steps:
• Sparse coding where we determine the dictionary
atoms’ fitting given samples
• Dictionary update where we edit the atoms of
dictionary in order to minimize approximation er-
ror.
In this paper, we propose an amelioration of the K-
SVD algorithm consisting of substituting the OMP
algorithm in sparse coding step, by the SunSAL algo-
rithm. Thus, Algorithm 1 presents the usual K-SVD
and Algorithm 2 presents its modification. We used
them in our experimentation in order to compare their
performance.
Since we don’t have labeled data, we cannot deter-
mine the classes’ labels of the samples using residual-
based criterion of formula (4) described in previous
section. Thus, we perform k-means algorithm to re-
group signals having similar linear atoms combina-
tion into clusters. We vary the cluster’s number in
Algorithm 1: Dictionary Design - K-SVD.
Data: Test Samples Y, initial dictionary D
Result: The learned dictionary D’
• Sparse Coding solving
argminkxk
1
sub ject to ky − Dxk
2
≤ δ (5)
• Dictionary Update minimmize E : E = Y -
∑
d
j
x
i
using SVD, repeat until error E remains
unchanged, where d
j
is the jth atom of the
dictionary and x
i
is the ith element of a
column of the sparse vector x.
Algorithm 2: Dictionary Design - K-SVD modified.
Data: Test Samples Y, initial dictionary D
Result: The learned dictionary D”
• Sparse Coding solving
min
1
2
ky − Dxk
2
2
+ λkxk
1
(6)
• Dictionary Update minimmize E : E = Y -
∑
d
j
x
i
using SVD, repeat until error E remains
unchanged, where d
j
is the jth atom of the
dictionary and x
i
is the ith element of a
column of the sparse vector x.
order to find which of them gives the best silhouette
values(Rousseeuw, 1987). The silhouette value can
be calculated for each point and represents a measure
of similarity of a given point to the other points in
its own cluster (intra cluster distance), compared to
points belonging to other clusters (inter cluster dis-
tance). For the i
th
point, Si, is defined as:
Si =
b
i
− a
i
max(a
i
, b
i
)
(7)
where a
i
is the average distance from the i
th
point to
the other points in the same cluster as i, and b
i
is
the minimum average distance from the i
th
point to
points in a different cluster, minimized over clusters.
Si value varies from -1 to 1. High values indicate that
a given point fits its own cluster and weakly matched
to others. If we have many negative Silhouette values,
this means that the clustering process has whether de-
composed the samples in too many or few clusters.
Whereas, if we get many positive Silhouette values,
this means that the result of the clustering process is
appropriate.
The following Algorithm 3 exhibits the unsuper-
vised clustering process :
After running this algorithm, we compute the dis-
Land Cover Clustering based on Improved Dictionary Learning Method from Modis Data
699

Algorithm 3: Unsupervised Clustering.
Data: Time series images T, learned
dictionaries D’ and D” obtained from the
previous algorithms
Result: Clusters of training samples
• Step 1: Extract randomly temporal samples from T
and reconstruct it using OMP or
SunSAL over respectively D’ and D” dictionaries
• Step 2: Calculate the Silhouette value of the sparse
vectors resulting from the previous step, in order to
determine the number of clusters
• Step 3: K means clustering algorithm on sparse
vectors using the number of clusters found in step 2
criminant temporal behavior of each cluster which is
the mean of all intra-cluster temporal behavior. This
procedure helps us to reduce dimensionality since we
conduct clustering process on sparse vectors instead
of large signals. The Figure 1 exhibits an overview
of the proposed approach.
4 STUDY AREA AND DATA
The study area corresponds to Taquari basin, located
almost entirely in the state of Mato Grosso do Sul in
the Center-West of Brazil - Figure 2.
Figure 2: The state of Mato Grosso do Sul in the Center-
West of Brazil.
We have a time-series data from MODIS-Terra
satellite, ”Vegetation Indices 16 days L3 Global 250
m” product which has two indices and ten other chan-
nels for each image: the NDVI and EVI (Enhanced
Vegetation Index). We have used only the NDVI
channel thanks to its relevance (Jonathan et al., 2005).
The used time series contains 26 acquisitions, span-
ning a period from August 2000 to July 2001 which
considered as significant to track vegetation evolution
(complete phenology cycle). For the validation phase,
we have a classification image at MODIS scale - Fig-
ure 3, elaborated from a Landsat image and expert
validation. We have to emphasize that having a well
documented study region is considered challenging.
Table 1: Silhouette values resulted from the variation of
cluster number which are the input of kmeans algorithm.
The data to be clustered are sparse vectors resulted from the
two algorithms of Dictionary Learning: Algo1(K-SVD) and
Algo2(K-SVD modified).
nb clus DL:Algo1 DL:Algo2
1 NaN NaN
2 0.5809 0.8489
3 0.3581 0.7364
4 0.2247 0.7331
5 0.1802 0.6881
6 0.1813 0.7059
7 0.1611 0.6208
8 0.1949 0.6792
9 0.1361 0.6287
10 0.1768 0.6589
11 0.1125 0.6529
12 0.1737 0.6694
13 0.1142 0.6623
14 0.1065 0.5945
15 0.0882 0.6521
20 0.1042 0.5400
5 EXPERIMENTAL PROTOCOL
AND RESULTS
In this section, we evaluate the proposed approach by
using MODIS time series data which contain 26 ac-
quisitions. We focussed on the following parameters
because they have a significant impact on the result:
• Since the temporal profiles of the pixels were
noisy which could probably affect the final clas-
sification result, we proceeded to filter them by
applying discrete wavelet transform (Daubechies
functions)
• Dictionary: In order to consider all the possible
types of vegetation, when creating our dictionary,
we chose atoms from different regions that cover
most of the studied area
• For the level of sparsity δ mentioned in equation
(2), we varied δ empirically, until reaching a min-
imum value of MSE. This value was fixed to δ =
13
This experiment is conducted on two dictionaries.
The size of each one of them is 26 × 4868 where 26
is the number of dates, 4868 is the number of atoms.
They are trained using both K-SVD and K-SVD mod-
ified algorithm as mentioned in Algorithm 1 and 2 re-
spectively. Next, we run kmeans using different num-
ber of clusters : 1,2,3..to 20. To find out which is the
RGB-SpectralImaging 2016 - Special Session on RBG and Spectral Imaging for Civil/Survey Engineering, Cultural, Environmental,
Industrial Applications
700
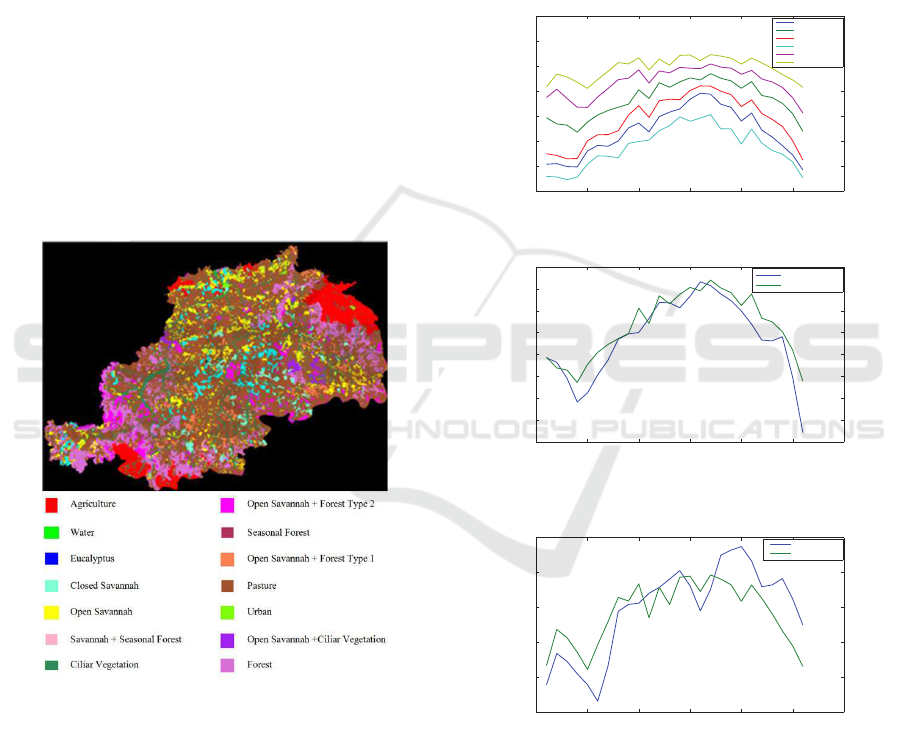
appropriate number, we calculate the silhouette value
of each resulted cluster. This value indicates whether
the cluster needs to be further divided or not. The
results are illustrated in Table 1 showing silhouette
values’ variation according to the number of clusters.
The lines correspond to the number of clusters used
in kmeans, and columns correspond to the algorithm
used to train the dictionary.
According to Table 1, the use of SunSAL as clas-
sifier, has led to better silhouette values. In fact, all
the SunSAL’s silhouette values are near to 1 which
means we have a good segregation ratio. Here Sun-
SAL suggests that the data could be divided in k = 6
clusters while OMP suggests that k = 8. Thanks to
this table, we discard the classifier OMP because of
its very low silhouette values and we keep SunSAL
classifier since it grants better results. So with k = 6,
we obtain 6 clusters where the mean profiles are rep-
resented in Figure 4. To evaluate our experimental
result, we use a ground truth of the studied region de-
scribed in (Jonathan et al., 2005) (Figure 3).
Figure 3: Reference Classes (Jonathan et al., 2005).
Our aim is to match the clusters found by kmeans to
the classes of ground truth in order to identify the
land cover types. So we calculate the Mean Square
Error (MSE) between the estimated temporal behav-
iors and the reference classes. The Table 2 presents
in columns the ground truth classes and in lines the
label of clusters belonging to kmeans algorithm re-
sult. This table helps us finding the land cover types
corresponding to clusters. For example, according to
Table 2, cluster 2 corresponds to Ciliar Vegetation
and Open Savannah, while cluster 6 corresponds to
Forest. This is confirmed in Figure 5 where we su-
perpose the mean profile in cluster 2 with the mean of
Ciliar Vegetation and Open Savannah. We have done
the same thing to cluster 6 by superposing it with the
Forest profile of ground truth in Figure 6.
Whereas cluster 5 is confused with several classes
: Closed Savannah, Seasonal Forest and Open Savan-
nah + Forest Type 1. This could be explained by the
fact that those 3 classes have close temporal profiles
and thus we could regroup all of them in a one single
profile.
0 5 10 15 20 25 30
0.4
0.5
0.6
0.7
0.8
0.9
1
Dates
NDVI values
X1 = Cluster 1
X2 = Cluster 2
X3 = Cluster 3
X4 = Cluster 4
X5 = Cluster 5
X6 = Cluster 6
Figure 4: Mean profiles of the 6 found clusters.
0 5 10 15 20 25 30
0.4
0.45
0.5
0.55
0.6
0.65
0.7
0.75
0.8
Dates
NDVI values
X1 = Class 2
X2 = Cluster 2
Figure 5: A: Superposition of Cluster 2 mean profile with
the mean profile of Ciliar Vegetation and Open Savannah.
0 5 10 15 20 25 30
0.65
0.7
0.75
0.8
0.85
0.9
Dates
NDVI values
X1 = Class 6
X2 = Cluster 6
Figure 6: Superposition of Cluster 6 mean profile with the
Forest profile.
So, thanks to our approach, we have found clusters
that gather more than one ground truth classes. Table
3 shows matching result of our clusters with ground
truth classes. By this way, based on information in
Table 3, we can generate labeled dictionary by deter-
mining to which class, each atom belongs.
We succeed to identify the majority of classes, but
we estimate that some of them are not well recognized
Land Cover Clustering based on Improved Dictionary Learning Method from Modis Data
701

Table 2: Table 2 of MSE values of Sunsal classifier, where A=Argriculture, B=Water,C=Eucalyptus,D=Open Savannah,
E=Closed Savannah, F=Forest, G=Seasonal Forest, H=Ciliar Vegetation I= Open Savanah+ciliar vegetation, J=Open Sa-
vanah+Forest type 1, K= Open Savanah+Forest type 2, L= Savannah+ Seasonal Forest, M=Pasture, N=Urban.
A B C D E F
1 0,013702123 0,014358648 0,00394132 0,014724775 0,045046558 0,072690414
2 0,043921584 0,022896723 0,031124566 0,002306937 0,007234252 0,019553144
3 0,020523329 0,016096906 0,010706222 0,007059779 0,026975737 0,049272183
4 0,01338676 0,017668488 0,002655275 0,029399763 0,072473686 0,105373549
5 0,076233369 0,042593683 0,060901952 0,009707884 0,001062428 0,005719512
6 0,110176038 0,065631921 0,09301972 0,023370714 0,004278307 0,001799481
G H I J K L
1 0,056415746 0,011683206 0,006053524 0,052763398 0,005628253 0,003442471
2 0,01302728 0,001776301 0,006218013 0,010195047 0,012103119 0,008181732
3 0,037179256 0,00419623 0,002892844 0,033783286 0,003984626 0,00177814
4 0,084818225 0,027074711 0,015296688 0,081290543 0,011946412 0,011910625
5 0,005061559 0,010941475 0,021002377 0,001024141 0,031136352 0,025381872
6 0,005089482 0,026979652 0,041094464 0,001690714 0,05498827 0,047385143
M N
1 0,008173389 0,017284448
2 0,004114109 0,066694088
3 0,002740651 0,032219417
4 0,020860182 0,005923803
5 0,015761101 0,108046735
6 0,033708819 0,149705802
Table 3: New classes elaborated after conducting our ap-
proach.
Clusters Ground truth classes
1 Water (B)
2 OpenSav and CiliarVeg (D+H)
3 OpenSav+CiliarVeg, Forest+OpenSav
Type 2 and Sav+SeasonForest (I+K+L)
4 Agriculture, Eucalyptus and Urban
(A,C,N)
5 OpenSav+Forest Type 1 and ClosedSav
and SeasonForest (J+E+G)
6 Forest (F)
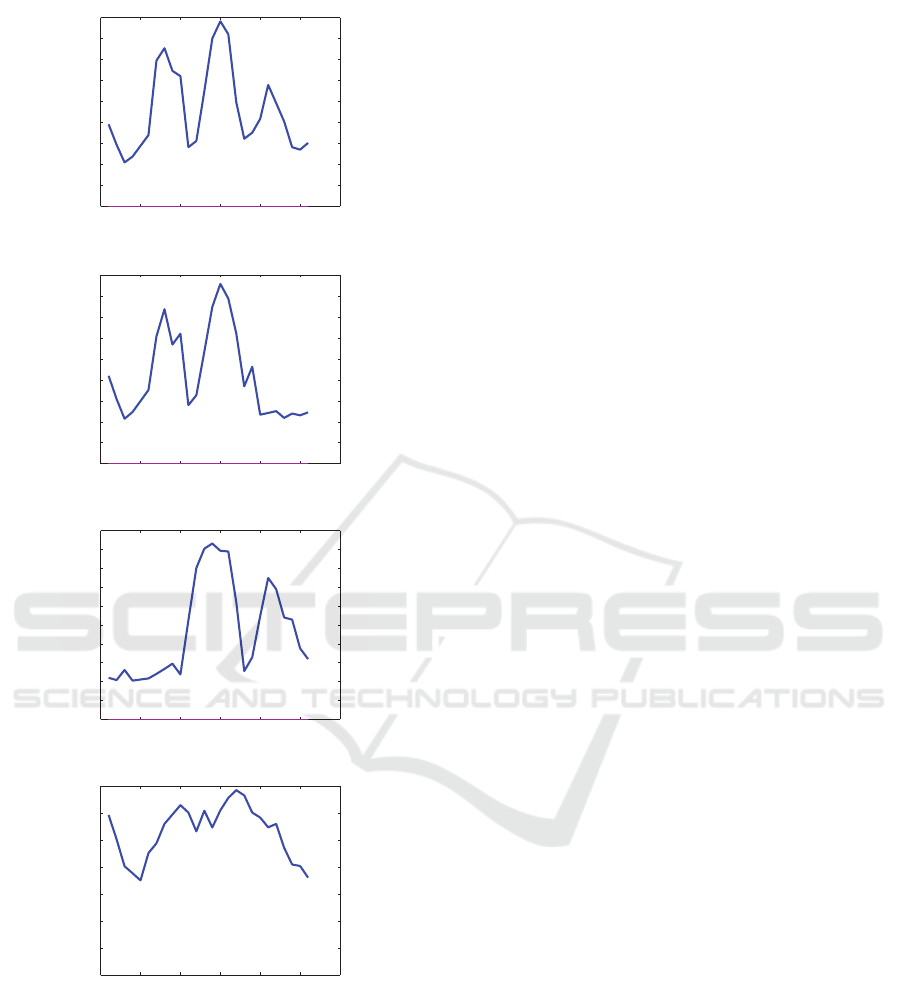
such as Agriculture. This deduction comes from the
fact that its MSE is relatively high (0.013) and this can
be explained by the heterogeneity of its class: it rep-
resents three behavior’s types as illutrated in Figure 7
and (Jonathan et al., 2005).
6 CONCLUSION
Thanks to coarse data, we conducted a clustering pro-
cess and generated ”labeled” dictionary. We explored
the sparse representation and its capabilities to fit the
data, to reduce dimensions in order to improve clus-
tering results. We compared two classifiers : OMP
and SunSAL and found that SunSAL outperforms
OMP. But here some critics must be mentioned : al-
though MODIS images provide coverage at continen-
tal and global scales, the ability to reveal specific de-
tails of the region study remains difficult. Many of
pixels generated by coarse resolution sensors are not
characteristic of only one vegetation but represent a
mixture as we mentioned in the experimentation sec-
tion. Therefore, for this study, we consider that the
pixel refers to one type of vegetation. So, in perspec-
tives, we aim to accurate our results by finding a way
to tradeoff multi-sensor data in order to enhance class
discrimination to monitor land cover change. This
would be done by the mean of merging multi-source
images with different spatial, spectral and temporal
resolutions.
RGB-SpectralImaging 2016 - Special Session on RBG and Spectral Imaging for Civil/Survey Engineering, Cultural, Environmental,
Industrial Applications
702
0 5 10 15 20 25 30
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Dates
NDVI values
Agriculture
(a)
0 5 10 15 20 25 30
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Dates
NDVI values
Agriculture
(b)
0 5 10 15 20 25 30
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Dates
NDVI values
Agriculture
(c)
0 5 10 15 20 25 30
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Dates
NDVI values
Agriculture
(d)
Figure 7: Ground truth temporal behaviors of Agriculture
Class. (a): Agriculture Temporal Behavior with 3 modes.
(b) and (c): Agriculture temporal behavior with 2 modes.
(d) : Agriculture Temporal Behavior with 1 mode.
ACKNOWLEDGEMENTS
The authors would thank the anonymous reviewers
for their helpful comments.
REFERENCES
Aharon, M., Elad, M., and Bruckstein, A. (2006). K-svd:
An algorithm for designing overcomplete dictionaries
for sparse representation. Signal Processing, IEEE
Transactions on, 54(11):4311–4322.
Bioucas-Dias, J. M. and Figueiredo, M. A. (2010). Alternat-
ing direction algorithms for constrained sparse regres-
sion: Application to hyperspectral unmixing. In Hy-
perspectral Image and Signal Processing: Evolution
in Remote Sensing (WHISPERS), 2010 2nd Workshop
on, pages 1–4. IEEE.
Brown, J. C., Kastens, J. H., Coutinho, A. C., de Castro Vic-
toria, D., and Bishop, C. R. (2013). Classifying mul-
tiyear agricultural land use data from mato grosso us-
ing time-series modis vegetation index data. Remote
Sensing of Environment, 130:39–50.
Chen, S. and Donoho, D. (1994). Basis pursuit. In Sig-
nals, Systems and Computers, 1994. 1994 Conference
Record of the Twenty-Eighth Asilomar Conference on,
volume 1, pages 41–44. IEEE.
Guha, T. and Ward, R. K. (2012). Learning sparse represen-
tations for human action recognition. Pattern Analy-
sis and Machine Intelligence, IEEE Transactions on,
34(8):1576–1588.
Jia, K., Wu, B., and Li, Q. (2013). Crop classification using
hj satellite multispectral data in the north china plain.
Journal of Applied Remote Sensing, 7(1):073576–
073576.
Jonathan, M., Meirelles, M. S. P., Berroir, J.-P., Herlin,
I., and da Costa Coutinho, H. L. (2005). Regional
scale land use/land cover classification using tempo-
ral series of modis data at the high taquari basin, ms,
brazil. Simp
´
osio Brasileiro de Sensoriamento Remoto,
12:579–581.
Lim, Y., Shinn-Cunningham, B., and Gardner, T. J. (2012).
Sparse contour representations of sound. Signal Pro-
cessing Letters, IEEE, 19(10):684–687.
Mahmoudi, M. and Sapiro, G. (2012). Sparse representa-
tions for range data restoration. IEEE transactions on
image processing: a publication of the IEEE Signal
Processing Society, 21(5):2909–2915.
Mohammady, M., Moradi, H., Zeinivand, H., and Temme,
A. (2015). A comparison of supervised, unsupervised
and synthetic land use classification methods in the
north of iran. International Journal of Environmental
Science and Technology, 12(5):1515–1526.
Morton, D. C., DeFries, R. S., Shimabukuro, Y. E., An-
derson, L. O., Del Bon Esp
´
ırito-Santo, F., Hansen,
M., and Carroll, M. (2005). Rapid assessment of
annual deforestation in the brazilian amazon using
modis data. Earth Interactions, 9(8):1–22.
Rousseeuw, P. J. (1987). Silhouettes: a graphical aid to
the interpretation and validation of cluster analysis.
Journal of computational and applied mathematics,
20:53–65.
Tropp, J., Gilbert, A. C., et al. (2007). Signal recovery
from random measurements via orthogonal matching
pursuit. Information Theory, IEEE Transactions on,
53(12):4655–4666.
Land Cover Clustering based on Improved Dictionary Learning Method from Modis Data
703

Wright, J., Yang, A. Y., Ganesh, A., Sastry, S. S., and Ma,
Y. (2009). Robust face recognition via sparse repre-
sentation. Pattern Analysis and Machine Intelligence,
IEEE Transactions on, 31(2):210–227.
Xue, Z., Li, J., Cheng, L., and Du, P. (2015). Spectral–
spatial classification of hyperspectral data via mor-
phological component analysis-based image separa-
tion. Geoscience and Remote Sensing, IEEE Trans-
actions on, 53(1):70–84.
Yang, X., Yang, T., Ji, Q., He, Y., and Ghebrezgabher,
M. G. (2014). Regional-scale grassland classifica-
tion using moderate-resolution imaging spectrometer
datasets based on multistep unsupervised classifica-
tion and indices suitability analysis. Journal of Ap-
plied Remote Sensing, 8(1):083548–083548.
Zhan, X., Sohlberg, R., Townshend, J., DiMiceli, C.,
Carroll, M., Eastman, J., Hansen, M., and DeFries,
R. (2002). Detection of land cover changes using
modis 250 m data. Remote Sensing of Environment,
83(1):336–350.
RGB-SpectralImaging 2016 - Special Session on RBG and Spectral Imaging for Civil/Survey Engineering, Cultural, Environmental,
Industrial Applications
704
