Semantic Social Network Analysis Foresees Message Flows

Matteo Cristani, Claudio Tomazzoli and Francesco Olivieri

Dipartimento di Informatica, University of Verona, Strada le Grazie 15, Verona, Italy

Keywords:

Social Network Analysis, Information Flow, Semantics of Data Flow.

Abstract:

Social Network Analysis is employed widely as a means to compute the probability that a given message

ﬂows through a social network. This approach is mainly grounded upon the correct usage of three basic

graph- theoretic measures: degree centrality, closeness centrality and betweeness centrality. We show that, in

general, those indices are not adapt to foresee the ﬂow of a given message, that depends upon indices based

on the sharing of interests and the trust about depth in knowledge of a topic. We provide an extended model,

that is a simpliﬁed version of a more general model already documented in the literature, the Semantic Social

Network Analysis, and show that by means of this model it is possible to exceed the drawbacks of general

indices discussed above.

1 INTRODUCTION

Social Networks are considered, on the current

panorama of web applications, as the principal vir-

tual space for online communication. Therefore, it is

of strong relevance for practical applications to un-

derstand how strong a member of the network is with

respect to the others.

Traditionally, sociological investigations have

dealt with problems of deﬁning properties of the users

that can value their relevance (sometimes their impor-

tance, that can be considered different, the ﬁrst denot-

ing the ability to emerge, and the second the relevance

perceived by the others). Scholars have developed

several measures and studied how to compute them

in different types of graphs, used as models for so-

cial networks. This ﬁeld of research has been named

Social Network Analysis. Sometimes the same name

is attributed to a wider context, where we also mean

to include analysis of the ways in which such values

arise (for instance, processes able to change impor-

tance of members), or to provide methods for employ-

ing these measures in applications.

Majorly, scholars dealt with the Social Network

Analysis from the viewpoint of information ﬂow,

namely they provide models of importance (and other

aspects as well) to understand how probable would

be that a piece of information passed through a given

node. Mainly, the information ﬂow has been stud-

ied for propagation of viruses (both in medical and

in computer security contexts), news spread-out (and

hence, studies about viral marketing as well), and

message passing in certain application contexts.

Three basic measures have been developed that

belong to the family of centrality measures: degree

centrality, closeness centrality and betweeness cen-

trality. In this paper we criticize the models of so-

cial network analysis developed for these measures,

showing that there are cases in which these measures

are not adapt. The criticism arises mainly as related

to the absence of semantic aspects in measures. To

show what we mean with these limits, let us introduce

a general example.

Example 1. Consider two users of facebook, Alice

and Bob, and assume that the measures of importance

is settled to coincide with the number of friends, the

distance to non-friends, and the probability of being

in common between two non-friends. Alice results to

be much more important in the network than Bob, un-

der all the three measures. However, to a closer ob-

servation we notice that this result is deﬁnitely true for

certain topics whilst it results false for other ones. In

particular, Alice is much more expert than Bob about

Geography and History, equivalent with respect to

Sport and weaker for Cuisine. When someone passes

a message to Alice and the message regards Geogra-

phy, she is much more likely to pass the message than

Bob. Conversely, when a message regards Sport the

opposite case holds. Cuisine information ﬂow is bet-

ter when passes through Bob.

The above described example shows that it can be the

case that two members of a social network can ex-

hibit different orders of prevalence in terms of central-

ity depending on the topic we refer the prevalence to.

296

Cristani, M., Tomazzoli, C. and Olivieri, F.

Semantic Social Network Analysis Foresees Message Flows.

DOI: 10.5220/0005832902960303

In Proceedings of the 8th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2016) - Volume 1, pages 296-303

ISBN: 978-989-758-172-4

This may produce effects that cannot be reproduced

by a single index, as shown in the example below.

Example 2. Consider ﬁve individuals: Alice, Bob,

John, Annie and Charlie.Alice is connected to Bob

and John; John connects also to Bob and Charlie and

also Annie is connected to Bob and Charlie, while

Bob is connected directly to everyone and is person

who loathes gossips when the others like or accept it.

If we don’t consider topics we would say that

dropping a gossip in the network, the right person to

deliver it to have it spread is of course Bob.

Unfortunately, the message has contents of a topic

which probably will see Bob cancel it, instead of for-

warding it, while both John and Charlie are good

choices because they are directly connected to three

people each and they have a different attitude toward

gossip than Bob.

The purpose of this paper is to give account to the

aspects showed in the example above. We provide a

model of Social Network Analysis that takes into ac-

count topics, and show that it can foresee information

ﬂow for message treating those topics in a more accu-

rate way than classical topic-free social network anal-

ysis. We also name Semantic Social Network Anal-

ysis the techniques we studied in this investigation to

cover a part of research that some previous studies did

not cover satisfacorily.

The rest of the paper is organised as follows: in

Section 2 we provide the actual technical part of the

paper. Further we employ Section 3 to discuss related

work. Finally Section 4 takes some conclusions and

sketches further work.

2 SEMANTIC SOCIAL

NETWORK ANALYSIS

In this section we introduce two distinct themes of

graph theory: Social Network Analysis and Informa-

tion Flow. The basis of both is the very general notion

of a labelled graph, that we assume to be known to the

reader, and specify in terms of form of the labels in

Subsection 2.1. Social Network Analysis is extended

in semantic terms in Subsection 2.2 and analysed in

computational details in Subsection 2.3. The ability

of the introduced modiﬁed measures to foresee Infor-

mation Flow is discussed in Subsection 2.4.

2.1 Graph Theory Preliminaries and

Social Network Analysis

A graph is a pair G = hV , E i, where V is a ﬁnite

set of vertices, and E is a set of edges. A graph G is

labelled when to each vertex or to each edge is associ-

ated a label, determined by Λ, a function that associ-

ated vertices and edges to the label sets (that are thus

denoted by ∆(V ) and ∆(E), or simply by ∆, meant to

be the union of the above). We use the term node and

the term vertex indifferenty.

In this paper we concentrate ourselves onto in-

directed graphs, and delay the investigation on di-

rected graphs to further work. We also assume that the

graphs we deal with have no circular edge (although

we do not assume them to be acyclic).

We name incident edges of a node v, the set of

nodes that are on one extreme of an edge that has v

as opposite extreme. We use the term path between

two vertices v and w, to denote a sequence of nodes

p = {v = v

, v

, ..., v

= w} that connects v to w, so

that every pair (v

, v

i+1

) is an edge of the graph. We

call length of p the number n. We say that a vertex v

is between two nodes v

and v

when v belongs to the

shortest path from v

to v

The number n of vertices in a graph is named the size

of the graph. Given a graph G of size n, if e is the

number of edges in G, then the ratio δ =

is named

the density of G. When a graph G

is denser than

another graph G

, we also say that G

is sparser than

To treat the notion of distance we employ no-

tions derived from classic algorithmic graph theory,

as widely discussed in (Eppstein, 1999). The distance

between two vertices v

and v

, denoted by δ(v

, v

in a graph, is the length of the shortest path connect-

ing v

and v

We now introduce three basic measures of social

network analysis, and discuss several ﬂaws they ex-

hibit.

Deﬁnition 1. A node v of a graph is said to have ab-

solute degree centrality k when the number of edges

incident to v is k.

From absolute degree centrality we can easily derive

relative degree centrality, as the absolute degree cen-

trality weighted by the size of the graph. In other

terms, if a graph has n vertices, and a node v has abso-

lute degree centrality k, the relative degree centrality

of v is

The absolute degree centrality clearly depends on

the size of the graph. In a graphs with n vertices abso-

lute degree centrality can vary from 0 to n − 1, and

therefore if a graph is larger than another, vertices

may have greater degree centrality.

Relative degree centrality does not suffer of this

ﬂaw. On the other hand, if you consider two graphs

of the same size, where one is denser than the other, in

the denser one the relative degree centrality varies less

than in the sparser one. A way to reduce this effect is

Semantic Social Network Analysis Foresees Message Flows

297

to consider a third variant of the degree centrality: the

graded degree centrality. This variant considers the

relative degree of each vertex and compares it to the

corresponding values of the other vertices. A vertex

v has a graded degree centrality δ =

where n is the

size of the graph and k is the number of vertices in the

graph with a relative degree centrality less than the

relative degree centrality of v.

We now introduce the second measure of social

network analysis.

Deﬁnition 2. A node v of a graph is said to have far-

ness f such that:

f (v

) =

∑

k=1,k6=i

δ(v

, v

)

The closeness centrality of a vertex is the reciproce of

the farness of v:

c(v) =

f (v)

Closeness centrality only works for connected graphs.

Conceptually, however, two vertices that are not con-

nected ar as far as inﬁnite, thus being closeness cen-

trality of these equivalent to 0. This is clearly faulty.

There have been several proposals to solve this aspect,

mainly by means of techniques that are based upon

weights. For the purpose of this research we assume

that networks are connected.

For comparison purposes closeness centrality suf-

fers of the same ﬂaws of degree centrality. Larger

graphs have potentially longer paths, and thus longer

distances, consequenly closeness centrality can vary

signiﬁcantly. In particular, since the distance between

two vertices in our graphs is at least one (we exclude

networks with self-cycles), and at most is the length of

the longest possible connection path that is as long as

the size (speciﬁcally n − 1), the farness of a vertex is

obtained as the sum of the lenghts n − 1 for each other

vertex connected to it, that sums to (n − 1) · (n − 1).

Therefore, the closeness varies from a minimum of

to a maximum of

. To normalize this and make

it indipendent from the size we cannot use fractions,

as we did for degree centrality. A possible approach

is to employ a logarithmic measure, and then normal-

ize it by n. In other terms we can measure farness as

the sum of the logarithmic measure of shortest paths,

weighted by the size of the graph itself. Formally

f (v

) = n ·log(

∑

k=1,k6=i

δ(v

, v

))

The above introduced measure does not suffer of de-

pendence on either size or density of the graph, and its

reciproce varies from 0 to 1. More precisely, it varies

from

and 1, evidently. We can obtain a normalised

measure by using

) = ()

f (v

) −

) · 2

The third measure we consider here is betweeness

centrality. It is obtained as the number of pairs of ver-

tices that are traversed by a path containing the mea-

sured vertex, or such that the vertex is between the

elements of the pair.

Deﬁnition 3. The betweeness centrality of a vertex v

is the number K of pairs in the graph for which v is

between.

Analogously to the previous analysis about degree

centrality we can note that large networks may exhibit

wider spectrum of betweeness centrality than smaller

ones, and conversely, less wide

2.2 Semantic Social Network Analysis

Social network Analysis starts from unlabelled and

for the settings of this investigation indirected graphs

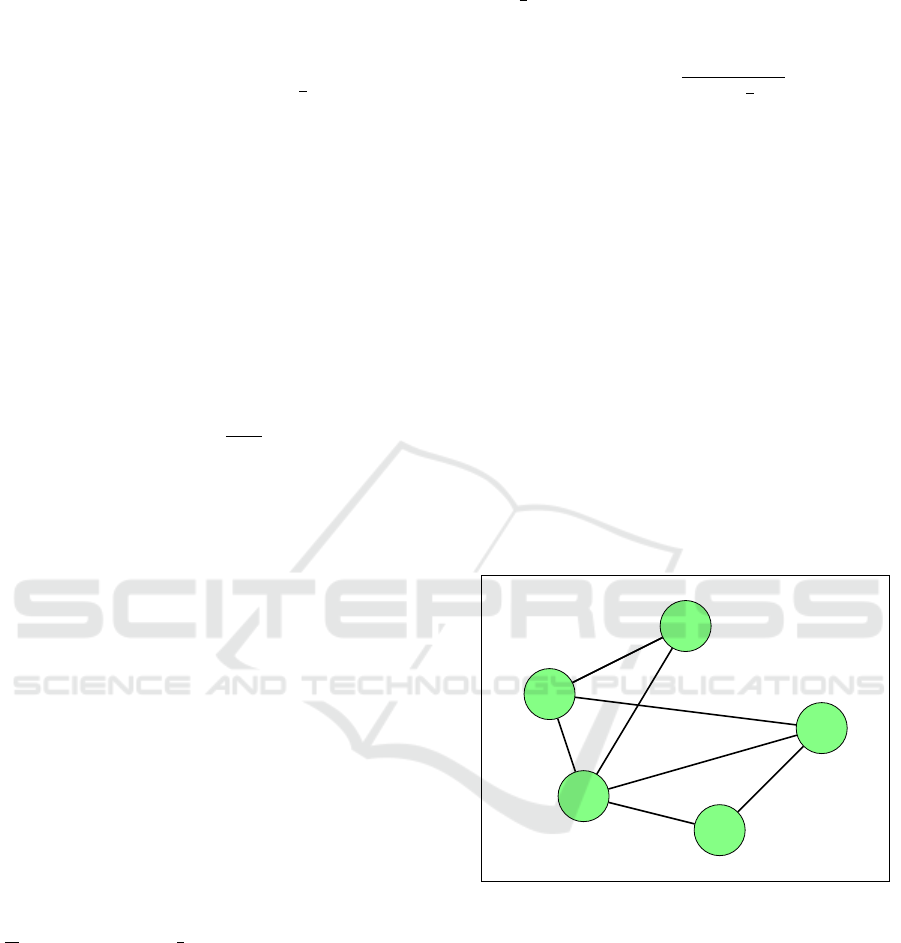
John

Alice

Bob

Annie

Charlie

Figure 1: Representing a social network by an unlabelled

indirected graph.

This, as discussed in Section 1 is unrealistic. An

individual can be connected to another over a cer-

tain topic, but deﬁnitively disconnected over another

topic. Moreover, the link between individuals can be

indipendent from the shared topics. This concepts are

known as homophily and have been discussed in Sec-

tion 3.

If we measure centralities by means of unlabelled

graphs, we may be rather misleading in deﬁning the

relevance (or importance, in some sense) of a vertex

in the graph, since an individual can exhibit strong

connections on one speciﬁc topic and weak ones

on other topics, providing therefore a differentiated

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

298

degree centrality, in particular, and analogously for

closeness and betweeness measures.

Consider two individuals John and Alice belong-

ing to the same school but not sharing a hobby like

music. A message regarding a class has a good prob-

ability of being forwarded from John to Alice while

one regarding the hobby hasn’t.

So we can say that John and Alice are connected

over a topic school but are disconnected over topic

music.

A method to provide this is to add a label to

vertices in the graph with label corresponding to a

measure of depths relative to a set of topics T =

, . . . ,t

}. The label will be vector D = {d

, . . . d

}

whose component d

is the depth over the topic t

the individual represented by vertex i as can be seen

in Figure 2.

, d

Figure 2: Introducing labels for depth in topics.

The goal of centrality measures is to provide a tool

for foreseeing information ﬂow. The basic assump-

tion we make here is that when someone is not in-

volved in a speciﬁc topic, it is rather unlikely that she

promotes the ﬂow of a piece of information through

the vertex she occupies.

Considering the aforementioned two individuals

John and Alice, their interests in the set of topics

T = {gossip, music, sport, cooking, politics} can be

expressed as D

= (0.3, 0.5, 0.5, 0.0, 0.0) for Alice

and D

= (0.9, 0.7, 0.0, 0.5, 0.0) for John, meaning

that while both are interested in gossip and music and

not interested in politics, Alice is keen to sport and

John is not but he likes cooking while Alice does not,

as is expressed in Figure 3.

An individual has depth on a certain topic mea-

suring the degree of involvement on it; an individ-

ual has also an activation threshold which describes

the inverse of the likelihood of that individual of be-

coming active when “hit” by a message. The notion

introduced here is inspired by that used in scientiﬁc

John

Alice

Bob

Annie

Charlie

(0.9, 0.7, 0.0, 0.5, 0.0)

(0.3, 0.5, 0.5, 0.0, 0.0)

(0.5, 0.7, 0.9, 0.3, 0.0)

(0.3, 0.0, 0.7, 0.0, 0.0)

(0.9, 0.5, 0.7, 0.3, 0.0)

Figure 3: An Example of a social network with labels on

topics gossip, music, sport, cooking, politics.

evalutation as proposed in (Tonta and Darvish, 2010).

, a

, d

, a

, d

, a

, d

, a

, d

, a

, d

Figure 4: Activation thresholds: a means for representing

sensitivity to information ﬂows.

A method to express this is to add another label

to vertices in the graph with label corresponding to

a measure of activation threshold relative to a set of

topics T = {t

, . . . ,t

} as can be seen in Figure 4.

The label will be vector A = {a

, . . . a

} whose

component a

is the activation threshold over the

topic t

of the individual represented by vertex i, with

a higher threshold meaning that it is less probable to

see that individual i activated on topic t

Considering the aforementioned two individuals

John and Alice, their activation in the set of top-

ics T = {gossip, music, sport, cooking, politics} can

be expressed as A

= (0.6, 0.3, 0.7, 0.5, 0.8) for Alice

and A

= (0.3, 0.6, 0.3, 0.5, 0.9) for John meaning that

while both are equally active in music and cooking,

Alice is more reactive to gossip than John while he is

probably forwarding more messages over topic sport

than Alice and both will probably stop messages re-

Semantic Social Network Analysis Foresees Message Flows

299

garding politics, as is expressed in Figure 5.

John

Alice

Bob

Annie

Charlie

(0.3, 0.6, 0.3, 0.5, 0.9)

(0.9, 0.7, 0.0, 0.5, 0.0)

(0.6, 0.3, 0.7, 0.5, 0.8)

(0.3, 0.5, 0.5, 0.0, 0.0)

(0.9, 0.4, 0.5, 0.5, 0.6)

(0.5, 0.7, 0.9, 0.3, 0.0)

(0.3, 0.3, 0.3, 0.3, 0.8)

(0.3, 0.0, 0.7, 0.0, 0.0)

(0.3, 0.9, 0.9, 0.9, 0.9)

(0.9, 0.5, 0.7, 0.3, 0.0)

Figure 5: An example of a social network with topic depths

and activation thresholds on topics gossip, music, sport,

cooking, politics.

2.3 Computational Analysis of

Semantic Social Network Analysis

Computation of degree centrality is straightforwardly

obtained from the basic algorithm for Social Net-

works, that simply counts the number of incident

edges of each vertex, and then derives the consequent

computations for relative and graded variants. In Se-

mantic Social Network Analysis, we sum the weights,

instead of counting the incident edges.

The base for computing both closeness and be-

tweeness centrality is the labelling of edges by the

graph distance, meant as shortest path. We extend

here the method known as Floyd Warshall Algorithm.

In indirected unlabelled graphs, the algorithm com-

putes just the incident edges to obtain the correct

value of distances. We use the vectorial min() func-

tion both to initialize the distance matrix and to give

a the value of the distance between two vertices in the

core of the algorithm.

The distance of two vertices v

, v

with corre-

sponding labels λ

, λ

will be δ[i, j] = min(λ

, λ

The sum in Floyd Warshall will be substituted

with the min()in our vectorial case.

As the minimum function is compliant with the tri-

angle inequality the algorithm still holds.

It is easy to show that the method is polynomial and

that the resulting labels provide an Euclidean distance

between vertices in the graph.

Theorem 1. FWSSNA terminates labelling of the

input graph in O(n

) where n is the size of the graph.

Algorithm 1: ALGORITHM FWSSNA. Given a graph G

with vertices V , returns matrix of distances.

1: Input: a graph G of vertices V = v

, . . . , v

with

corresponding labes Λ = λ

, . . . , λ

;

2: Output: a matrix of distances ∆;

3: i ← 1, j ← 1;

4: ∆ ←

5: for i < |V | do

6: for j < |V | do

7: δ[i, j] ← min(λ

, λ

);

8: end for

9: end for

10: i ← 1, j ← 1, k ← 1;

11: for k < |V | do

12: for j < |V | do

13: for i < |V | do

14: δ[i, j] ← min(δ[i, j], min(δ[i, k], δ[k, j]));

15: end for

16: end for

17: end for

Theorem 2. FWSSNA returns a labelling that is a

Euclidean distance between vertices.

As a consequence, we can employ FWSSNA to pro-

vide semantic closeness centrality, and semantic be-

tweeness centrality.

Closeness centrality is obtained by simply la-

belling vertices in the graph with the minimum of the

computed distance from the node to the other nodes.

Minimum is well known to respect Euclidean distance

properties as well. Once we have executed the algo-

rithm FWSSNA, every other node is connected to a

given node, and thus we can consider the closeness

computation as a second step. We say, in particular

that an algorithm A

is in overhead computational cost

C with respect to another algorithm A

, when the cost

of executing A

is C, after A

has been executed as a

preliminary step wrt A

Theorem 3. Computing semantic closeness central-

ity is in overhead O(n) wrt FWSSNA.

Betweeness centrality can be obtained by modifying

the method of FWSSNA with the introduction of a la-

bel reporting the shortest path, or better, the internal

nodes of the path. If the shortest path connecting two

vertices x and y is the sequence x = x

, x

, ..., x

= y,

then the computed set of internal nodes is formed by

, x

, ..., x

n−1

}. To obtain, therefore, the correct be-

tweeness it is sufﬁcient to compute those labels (that

is with no overhead wrt to FWSSNA) and then, for a

vertex v determine the number of shortest paths that

pass through v by counting the number of appearances

of v in the labels of the vertices. This can obviously

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

300

be done in a number of steps that is equivalent to the

number of edges, giving the result below.

Theorem 4. Computing semantic betweeness cen-

trality is in overhead O(n

) wrt FWSSNA.

2.4 Forecasting the Information Flow

with Semantic Social Network

Analysis

A message injected in a social network, i.e. sent to

a person, has a higher probability of being forwarded

if the person has a low activation threshold and if the

content of the messages catches the attention of the

person, or in other word if the information content

of the message is higher or equal to the depth of the

person on the topic.

In particular we assume that every information

piece, that we name a message passing through the

network, is associated with depth measures for the

same topic vector employed to label the vertices of

the network itself.

Therefore, we can say that the probability of a

message m of topics t

, ...,t

to be forwarded by

an individual i can be expressed as a function of

the depth on the topics, the information content over

those topics of the message and the reactivity of the

member. We denote by t

the vector of topic depths of

the message m, by d

the vector of topic depths of the

member i and by a

the vector of activation threshold

of the member i.

P(m, i) = Ψ(t

, d

, a

)

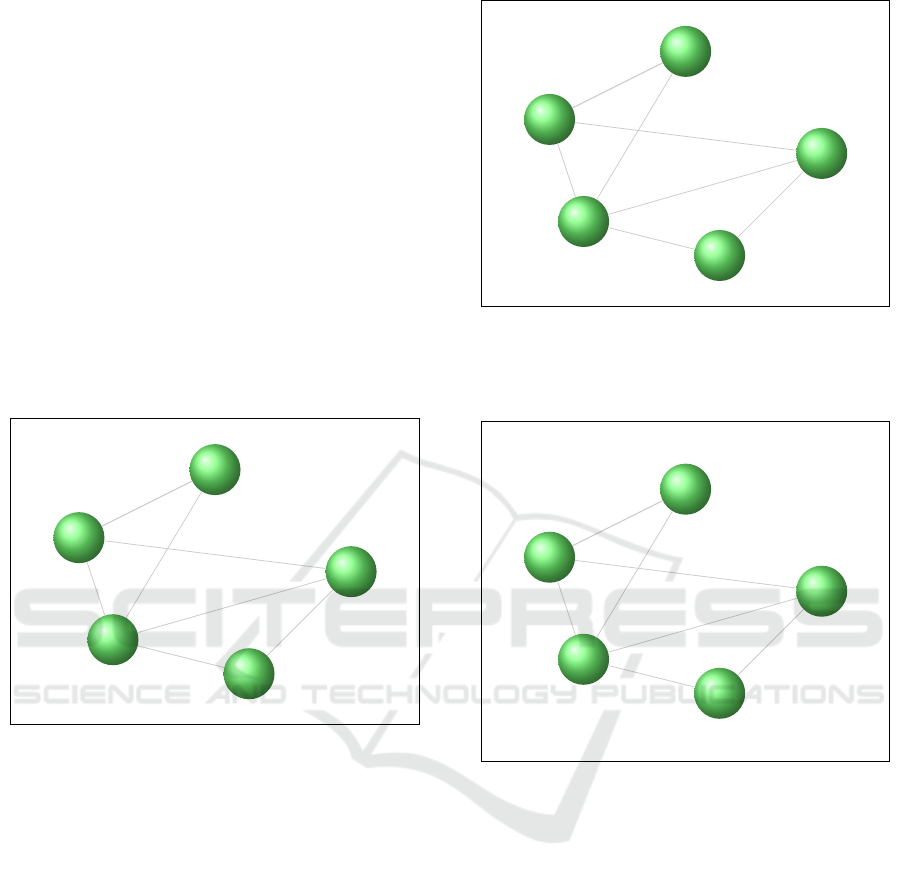
If we consider a message of the topic gossip when

this hits John or Charlie is is less likely that it will be

forwarded, as shown in Figure 6.

John

Alice

Bob

Annie

Charlie

Figure 6: Our representation of a social network.

To introduce the notion we need, let us recall the

idea of probablistic complement. When an event has

the probability p, the proablistic complement of p,

namely 1 − p is the probability of the opposite event.

When two events can occur, the probablity of the oc-

currence of some of them is the probablistic comple-

ment of the conjunction of the opposite events. For in-

stance, if two events have probabilities p

and p

, the

probability of the occurrence of some of them is the

probabilistic complement 1 − (1 − p

)(1 − p

), to be

read as the probability that among all cases it would

not be the case that none of the two events occur. For a

set of values between 0 and 1 we P = {p

, p

, ..., p

we denote by P

the probablistic complement

= 1 −

∏

i=1

1 − p

The simplest function we can promote, when as-

suming that one message only deals with a single

topic, is the direct product of the probabilistic com-

plement of the activation threshold, the depth of the

member in that topic and the depth of the message in

the topic itself. When the topics involved are more

than one, then the above is poor, and we need to work

on the probablistic complement for the depths of the

involved topics.

P(m, i) = (t

)

· (d

)

· (a

)

On a purely theoretical basis, it is clear that when two

members of a network have a good activation thresh-

old on a given topic, when a message on that topic

reaches the vertex, and the message has a high depth

in that topic, then the message has a good probability

of being passed.

The ability of the above mentioned index to fore-

see correctly the information ﬂow is under experimen-

tal evaluation and the ﬁrst preliminary results are very

encouraging.

3 RELATED WORK

The reference literature can be considered as articu-

lated in three themes:

• Studies about implicit social links that exist

among users of the internet (or of an internet ap-

plication), or about enrichment of social web;

• Investigations of the semantics of social networks;

• Research about Social Network Analysis and re-

lationships to semantic issues.

Regarding the ﬁrst topic, we can look at meth-

ods for social link extraction, as discussed below, as

one of the best structured investigations on the theme.

This speciﬁc method for extracting social networks

Semantic Social Network Analysis Foresees Message Flows

301

from the web using similarity between collective con-

texts is proposed in (Alguliev et al., 2011). The au-

thors construct three social networks on the same set

of named entities. They use Jaccard, overlap and

Normalized Google Distance (NGD) (Cilibrasi and

Vit

anyi, 2007) coefﬁcients to retrieve degree of close-

ness between entities. They show how actors may be

assigned different relevance degrees and that actors

having higher ranking results may be assigned lower

ranks and inversely by choosing another measure to

perform the ranking. In our perspective their work is

solid, but lacks in one important aspect, the authors

build homophily on the based of the contents.

This is a technique to build a network, and not an

analysis of the network itself, as we do in this work.

Suffering the same issue is the work of (Er

eo et al.,

2009), where the authors present a new framework

for applying Social Netork Analysis to RDF repre-

sentations of social data. In particular, the use of

graph models underlying RDF and SPARQL exten-

sions enables us to extract efﬁciently and to param-

eterize the classic Social Network Analysis features

directly from these representations.

The main criticisms to the proposed approach lie

on the fact that, as already shown in many practical

cases, it makes a lot of difference, in terms of under-

stading of the structure of similarity between nodes,

to know the relevance of the two nodes. In fact, sim-

ilarity can be used, as done, for instance in (Cruz

et al., 2014), for community detection, where mem-

bers are related to each other based on their similarity

in semantic terms. This is different in terms of rela-

tionship, with respect to measuring the relevance and

study attactivity. Clearly, being interested in Football

lies on liking it, but the community is formed around

authoritative persons, for instance journalists.

A more practical research has been documented in

(Yuan and Fei, 2010) where an application of seman-

tic social networks and attraction theory to web based

services is carried out.

The relation between trust and Social Network

Analysis has been investigate in (Zhang et al., 2006)

and speciﬁed as a means for understanding deeply the

meaning of centrality and other measures as related to

authority. The same concept is employed to provide a

framework for the general interpretation of the logic

bases of recommendation systems in (Davoodi et al.,

2013).

The studies cited above all aim at discovering net-

work links by means of mining techniques. On the

other hand, the introduction of notions derived from

semantic web into social networks is the core quest

of many recent studies, including (Zhou et al., 2011).

As a complete reference to the current literature about

meaning of social links, and relationships between so-

cial web and semantics, readers can look at (Leydes-

dorff, 2012).

More deeply, in (Mika, 2004) a direct and ex-

plicit comparison between social networks and the

semantic web is carried out. This paper proposes a

parallel between networked knowledge of members

in a network and the basic notions of semantic web.

The same issue is dealt with, with the speciﬁcity of a

known technique, the semantic networks, in (Downes,

2005). More generally, the semantic web methods

are employed for understanding the meaning of social

networks as sharing platforms for common knowl-

edge, in (Mika, 2005).

The idea of using Social Network Analysis as a

means for forecasting the probability of a message to

pass through a given member of the network itself is

not novel at all. Base of our analysis is the criticisms

to the roughness of the employed measures, criticisms

that are not novel anyhow.

This has been dealt in two distinct ways: by us-

ing semantic methods for habilitating the forecast pro-

cesses: in particular in (Zywica and Danowski, 2008),

authors use semantic networks for foreseeing the be-

haviour in facebook.

On the other hand, many criticisms are applied to

centrality measures ((Landherr et al., 2010), (Kang,

2007)). The main criticisms, that are met by the above

mentioned investigations as well as by researches

tending to correct the ﬂaws of the general methods

for centrality measures, and the measures themselves,

lie on the weakness of the notion of similarity derived

from the notion of centrality.

The above mentioned notion of similarity as de-

rived from centrality measures, and its applications to

the notion of reciprocity, a concept that has a crucial

importance, for instance, in asymmetric social net-

works (Instagram, Twitter) are dealt with in (A. Ra-

machandra Rao, 1987). Authors show that centrality

measures as used so far are unsuccessful in forecast-

ing the information ﬂows.

4 CONCLUSIONS

In this paper we investigated an extension to Social

Network Analysis based upon the usage of a network

model that includes the notion of topic. This leads to

a further model that incorporates the notion of sensi-

tivity, by means of a value, called activation threshold

that is meant to denote the probability of a member of

the network to be active in an information ﬂow. Algo-

rithms for computing extended notions of centrality

are provided, and proved to be correct, complete and

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

302

computationally efﬁcient. We provide examples that

show that our approach can fruitfully solve few ev-

ident drawbacks of the general model, as applied to

information ﬂow forecast.

There are at least three different ways in which

this investigation can be extended. First of all we aim

at formalising a problem of dissemination of informa-

tion pieces throughout a network. The problem can be

formulated as follows: given a social network, a num-

ber k and a probability value p, select k members in

such a way that the set of members reached by an in-

formation piece sent to the members in the selection

and dissemintated by them and the chains of mem-

bers generated therefore, has a probability of being

total (namely to cover the entire network) of at least

A second study investigates ways of providing

reacher models of topics. In particular, we aim at in-

vestigating topics with sub-topics.

A third investigation will introduce the notion of

orientation. Foir instance two persons can be both

interested in football, but one may support Juventus

F.C., whilst the other one may support A.C. Chievo

Verona. These studies are taken into a track of re-

search for viral marketing purposes, including meth-

ods to evaluate networks for advertisment, alerts, and

emergencies.

REFERENCES

A. Ramachandra Rao, S. B. (1987). Measures of reciprocity

in a social network. Sankhy: The Indian Journal of

Statistics, Series A (1961-2002), 49(2):141–188.

Alguliev, R., Aliguliyev, R., and Ganjaliyev, F. (2011). In-

vestigation of the role of similarity measure and rank-

ing algorithm in mining social networks. Journal of

Information Science, 37(3):229–234.

Cilibrasi, R. and Vit

anyi, P. M. B. (2007). The google

similarity distance. IEEE Trans. Knowl. Data Eng.,

19(3):370–383.

Cruz, J. D., Bothorel, C., and Poulet, F. (2014). Commu-

nity detection and visualization in social networks: In-

tegrating structural and semantic information. ACM

Trans. Intell. Syst. Technol., 5(1):11:1–11:26.

Davoodi, E., Kianmehr, K., and Afsharchi, M. (2013). A se-

mantic social network-based expert recommender sys-

tem. Applied Intelligence, 39(1):1–13.

Downes, S. (2005). Semantic networks and social networks.

The Learning Organization, 12(5):411–417.

Eppstein, D. (1999). Finding the k shortest paths. SIAM J.

Comput., 28(2):652–673.

eo, G., Gandon, F. L., Corby, O., and Buffa, M.

(2009). Semantic social network analysis. CoRR,

abs/0904.3701.

Kang, S. M. (2007). A note on measures of similarity based

on centrality. Social Networks, 29(1):137 – 142.

Landherr, A., Friedl, B., and Heidemann, J. (2010). A

critical review of centrality measures in social net-

works. Business and Information Systems Engineer-

ing, 2(6):371–385.

Leydesdorff, L. (2012). Advances in science visualiza-

tion: Social networks, semantic maps, and discursive

knowledge. CoRR, abs/1206.3746.

Mika, P. (2004). Social networks and the semantic web.

In Web Intelligence, 2004. WI 2004. Proceedings.

IEEE/WIC/ACM International Conference on, pages

285–291.

Mika, P. (2005). Flink: Semantic web technology for the

extraction and analysis of social networks. Web Se-

mantics: Science, Services and Agents on the World

Wide Web, 3(2):211 – 223. Selcted Papers from

the International Semantic Web Conference, 2004

ISWC, 20043rd. International Semantic Web Confer-

ence, 2004.

Tonta, Y. and Darvish, H. R. (2010). Diffusion of latent

semantic analysis as a research tool: A social network

analysis approach. Journal of Informetrics, 4(2):166

– 174.

Yuan, S.-T. and Fei, Y.-L. (2010). A synthesis of seman-

tic social network and attraction theory for innovating

community-based e-service. Expert Systems with Ap-

plications, 37(5):3588 – 3597.

Zhang, Y., Chen, H., and Wu, Z. (2006). A social network-

based trust model for the semantic web. In Yang,

L., Jin, H., Ma, J., and Ungerer, T., editors, Au-

tonomic and Trusted Computing, volume 4158 of

Lecture Notes in Computer Science, pages 183–192.

Springer Berlin Heidelberg.

Zhou, L., Ding, L., and Finin, T. (2011). How is the se-

mantic web evolving? a dynamic social network per-

spective. Computers in Human Behavior, 27(4):1294

– 1302. Social and Humanistic Computing for the

Knowledge Society.

Zywica, J. and Danowski, J. (2008). The faces of facebook-

ers: Investigating social enhancement and social com-

pensation hypotheses; predicting facebook and ofﬂine

popularity from sociability and self-esteem, and map-

ping the meanings of popularity with semantic net-

works. Journal of Computer-Mediated Communica-

tion, 14(1):1–34.

Semantic Social Network Analysis Foresees Message Flows

303