
Large Scale Petrol Station Replenishment Problem with Time Windows:
A Real Case Study
Pablo A. Villegas and V´ıctor M. Albornoz
Departamento de Industrias, Universidad T´ecnica Federico Santa Mar´ıa, Av. Santa Mar´ıa 6400, 7660251, Santiago, Chile
Keywords:
Petrol Station Delivery Problem, Time Windows, Trip Packing, Scheduling, Heuristic.
Abstract:
In this study we deal with a real case of the problem known as Petrol Station Replenishment Problem with
Time Windows arising in Chile. The company involved is one of the biggest actors in the country, and every
day must schedule a series of trips from their depots to their clients, delivering different kinds of fuel. This
specific case has some differences from prior formulations of this problem (e.g. trucks works in shifts with
hard time windows). Also, another challenge is the high number of orders and trucks involved in everyday
planning. To solve this problem in reasonable computing times we propose a sequential insertion heuristic.
Finally, we present results over a month of data.
1 INTRODUCTION
Oil companies have the duty to supply their clients
(gas stations and industrial clients) with different
kinds of fuel, that is why every day they are con-
fronted with the challenge of arranging a schedule
program for the next day. This work is motivated by
the challenge that one of the biggest oil companies
in Chile faces when dealing with this scheduling pro-
gram.
The problem known as Petrol Station Replenish-
ment Problem with Time Windows (Cornillier et al.,
2008a; Cornillier et al., 2012) or PSRPTW, corre-
sponds to a specific multi-compartment vehicle rout-
ing problem or MCVRP, which includes time win-
dows constraints. This problem consists in assigning
a series of products demanded by clients to available
truck compartments and schedule their delivery time.
Thus, trips must be defined and assigned to trucks
considering time windows constraints.
In this case we deal with trucks that are without
flow meters, thus, every truck compartment must be
delivered to no more than one client. Also, trucks
are able to make more than one trip during their work
shift.
The contribution of this work comes in two as-
pects. First, we deal with a real case which has some
slight differences over the ones previously worked,
for instance, trucks works in shifts with defined
time windows. Shift starting and ending times vary
from truck to truck, different from prior formulations
(Benantar and Ouafi, 2012; Cornillier et al., 2009;
Cornillier et al., 2012; Surjandari et al., 2011) that
considered either maximum worktime or closing time
windows at the depot. Here, the final objective is to
maximize compliance with customer orders, follow-
ing a certain priority, with a limited heterogeneous
fleet. Also, costs do not change based on the lapsed
time from the start of the first trip till the end of the
last, as every trip has its own cost. Client priority
could have been addressed by forcing orders fulfill-
ment, however, orders may focus on a certain time
lapse making it an infeasible problem, while posing
this problem as the maximization of dispatched prod-
uct by priority enable us to get the best possible so-
lution, assuming the possibility that not every order
will be delivered in the agreed time window. Our
second contribution consists on a proposed heuris-
tic for this specific case, which main feature is get-
ting a relatively good operational solution in a short
time frame, so that people in charge of scheduling can
work over this proposal. This heuristic consist on an
adapted version of the insertion heuristic proposed by
(Solomon, 1987) for a vehicle routing or scheduling
problem with time windows.
The view from the standpoint of compliance with
customer brings a wider view than just minimizing
costs, as there is value associated with each client that
is not necessarily reflected by the net profit of a trans-
action. This is very important in the case of fuels, as
the profit per transaction is relatively low, and the gain
is in the quantity sold. Therefore, it may be important
408
Villegas, P. and Albornoz, V.
Large Scale Petrol Station Replenishment Problem with Time Windows: A Real Case Study.
DOI: 10.5220/0005823604080415
In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 408-415
ISBN: 978-989-758-171-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

to give preference to a client making large quantities
of orders.
The remainder of this papers is organized as fol-
lows. In Section 2, we address some relevant litera-
ture related to previous works dealing with this prob-
lem. In section 3 we formally define the problem ad-
dressed in this work and introduce some assumptions
and characteristics that have impact in our solution
approach. In Section 4 we introduce the solution strat-
egy, including our proposed heuristic. In Section 5 we
present results obtained over a month of data on one
of the company depots. In Section 6 we provide some
final conclusions and future research.
2 LITERATURE REVIEW
In this section we provide a brief overview of pub-
lished literature concerning the Petrol Station Replen-
ishment Problem (PSRP) over the last few decades.
(Brown and Graves, 1981) were the first to pub-
lish an article dealing with the PSRP. They were faced
with a situation involving more than 80 depots and
300 tank trucks. The main features of the problem
was that all the orders corresponded to full truck-
loads, so each trip could only reach one customer.
To solve this case, they proposed an integer program-
ming model to assign commands to different trucks,
in order to minimize the amount of travel costs, es-
tablishing a penalty if the need for overtime or idle
time existed.
(Brown et al., 1987) described a decision-making
support system, where they focused on the possibility
to add more than one customer per trip to their previ-
ous work. The distribution network involved was 120
tanks and 430 tanker trucks.
(Van der Bruggen et al., 1995) in a counseling pro-
cess to a Netherlands company, proposed some sim-
ple models: assign customers to depots, determining
fleet size and composition, and restructure the net-
work of depots. The problem considered five depots,
20-30 tanker trucks and about 800 customers.
(Ronen, 1995) described some of the features
present in the operating environment of this problem
and presented three models that can be applied to it:
The set partitioning model, the elastic set partitioning
model, and the set packing model.
(Taqa allah et al., 2000) addressed the problem
dealing with one tank and a homogeneous tank truck
fleet. They proposed four original heuristics, three
which visited one client by lap while the fourth allows
more than one client in every trip, and stations can re-
ceive multiple visits. They showed results for cases
up to 75 clients with different evaluation horizons.
(Mal`epart et al., 2003) worked with the problem of
supply over a time horizon of several business days.
This problem stems from the notion that in some cases
the fueling stations are managed by the company, so
they can decide at their convenience which day they
will be supplied. They proposed four heuristics to
solve this problem.
(Avella et al., 2004) studied the case of one de-
pot and heterogeneous tank truck fleet, where orders
were integral multiples of m
3
and truck compartments
leave either full or empty. They proposed a set parti-
tioning formulation and developeda branch-and-price
algorithm that could solve the problem up to 6 trucks
and 25 customers. They also proposed a heuristic to
select a promising set of columns.
(Ng et al., 2008) studied two distribution networks
in Hong Kong. The resulting problem corresponds
to a model of supply over several working days, as
stations inventories were managed by the company.
They proposed a model to assign trips to trucks and
stations simultaneously. The model does not guaran-
tee that the stations are not left without fuel. Between
the two areas studied, the number of stations was 48
and had a fleet of 8 tank trucks.
(Cornillier et al., 2008a) worked with the problem
of one depot and unlimited heterogeneous fleet. They
proposed an exact algorithm and conducted a test with
an instance of 42 stations and 8 types of vehicles.
Same year, (Cornillier et al., 2008b) treated the multi-
period case with limited heterogeneous fleet, where
they proposed a multiple phase heuristic. They con-
ducted tests for this heuristic with instances up to 200
customers and a 28 days planning horizon.
(Cornillier et al., 2009) proposed two heuristics
for the case of limited heterogeneous fleet and cus-
tomer time windows. To verify the performance
of these heuristics, they used instances of up to 50
clients.
(Boctor et al., 2011) addressed the trip packing
problem arising in the PSRP. They proposed a formu-
lation for the generalized version of that problem and
four heuristics to solve it.
(Surjandari et al., 2011) worked a real case with
time windows, multi-depot, split-deliveries and a lim-
ited heterogeneous fleet of tank trucks. As a solution
they proposed a tabu search algorithm. In their work
they show results for that particular case, which had
two depots and a fleet of 76 tank trucks.
(Benantar and Ouafi, 2012) discussed the case
with time windows, one depot and a limited hetero-
geneous fleet. They presented an algorithm based on
tabu search, solving instances of over 100 customers
and 20 trucks.
(Cornillier et al., 2012) proposed a heuristic for
Large Scale Petrol Station Replenishment Problem with Time Windows: A Real Case Study
409

the multi-depot problem with time windows. This
heuristic included the generation of all possible trips
visiting less than three clients and then selecting the
most promising one and solve the allocation problem.
In their work they show results of instances up to 6
depots, 10 trucks and 50 customers.
(Wang et al., 2014) presented the results of a meta-
heuristic called ”guided reactive tabu search” applied
to the problem of a single depot with heterogeneous
fleet. They addressed instances up to 200 orders.
(Coelho and Laporte, 2015) defined and com-
pared four categories of the single period multi-
compartment vehicle routing problem. This problem
is one of the possible variants that appears when ad-
dressing the PSRP. For each of the particular cases
they proposed a mathematical model and a ”branch-
and-cut” algorithm that is applicable to all of them.
Largest instances that could be solved accurately con-
tained 50 clients in the single period case and 20 for
the multi-period version.
To the best of our knowledge there has not been
addressed a real case with instance sizes bigger than
the ones presented in this work or time windows as-
sociated with truck shifts. The challenge is to get an
acceptable solution (proposal) for planners in a rea-
sonably short time, as they will work over this so-
lution. To this effect, we followed the strategy used
by (Cornillier et al., 2012) separating routes creation,
their allocation to the various truck shifts and finally
defining their schedule.
3 PROBLEM DEFINITION
The PSRPTW used in this real case can be defined
as follows. Let G = ({0, n+ 1} ∪C, A) be a directed
graph, where {0, n + 1} corresponds to the depot,
C = {1, ..., n} is the set of clients, and A = {(i, j) :
i, j ∈ {0, n+ 1} ∪C, i6= j} is the set of arcs. Every arc
(i, j) has associated a travel time t
i, j
. Also, service
time s
i
at depot or station i, where i ∈ {0, n + 1} ∪C,
is known. The set of trucks associated to the depot is
denoted by K. Client i orders are composed of P
i
or-
der lines, where every line specifies a different kind of
product and which type of compartment will be filled
with that order, also, every order specifies an ideal
time window. Trucks must get to the client i inside
the proposed time window [a
i
, b
i
]. Furthermore, ev-
ery truck must comply with their shift time window
[α
′
k
, β
′
k
].
The real nature of the problem leads to many sit-
uations where theory differs from reality, so it is im-
portant to make a balance between which elements
of reality we will model and those we will simplify
through assumptions.
One of the most important simplifications of the
model is present in the step of route generation.
Clients are grouped by zones, so travel time is di-
rectly associated to the zone they are into. As a rule of
thumb, routes visiting more than one client shall only
visit clients inside the same zone. For this and some
other restrictions, orders may be grouped in a way so
that they will be assigned to one and just one possi-
ble route. Resulting routes will have just one kind of
truck assigned (capacity related), letting us solve the
problem for every truck type separately. Orders that
do not comply to these rules are left outside this prob-
lem, as the compliance decision is in the schedulers’
hands. As an interesting fact, volume of discarded
orders is often below 1% of total volume transported
during a work day.
Next, other important assumptions are noted for
this particular problem:
• Orders are composed of order lines, every client
may generate orders lines till they fill a truck. This
orders may contain more than one kind of product,
but no more than one by compartment.
• Every client is free to generate more than one or-
der. Every one of such is treated separately as they
have their own requirements and time windows.
• Every order must be complied with just one trip.
• A route may include more than one client, but no
more than two.
• Trucks may have more than one shift during the
working day. As they are independent, they are
treated as different trucks.
• There exists relevance associated to the priority of
an order, this will be represented by constant ρ.
4 SOLUTION STRATEGY
To solve this problem in reasonably low computing
times, we have separated this problem in two phases,
addressed separately:
• Phase I: Route generation
• Phase II: Route assignment & Scheduling
We have developed a heuristic which follows the
same idea used by the sequential insertion heuristics
proposed by (Solomon, 1987). It also shows some
similarities with the construction heuristics proposed
by (Boctor et al., 2011).
In addition to parameters already defined, the fol-
lowing notation will be used:
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
410

Indices:
t, l: route index
k: truck index
v: trip position index
Sets:
T: set of routes
T
k
: set of routes associated to truck k
V: set of possible trip indices.
V = {1, 2, ..., N}
V
k
: set of possible trip indices for truck k
Parameters:
N: maximum number of possible trips
during a shift
ρ
t
: route t’s priority associated value
α
t
: starting time of route t’s time window
β
t
: ending time of route t’s time window
λ
t
: route t’s time duration
α
k
: starting time of truck k’s time window
β
k
: ending time of truck k’s time window
Next, we describe the two phases of this problem
and how we address them.
4.1 Phase I: Route Generation
This first phase is considered an initialization process.
It consist on the generation of the set of routes T. As
said in section 3, order aggregation in routes must fol-
low certain company rules. This allows us to group
orders in a way so that they will be assigned to one
and just one possible route. Resulting routes will have
just one kind of truck assigned, letting us solve the as-
signment problem for every truck type separately.
4.2 Phase II: Assignment & Scheduling
The main objective of the company is to maximize the
routes to be performed, weighted by their respective
priority, while complying with their time windows.
The objective function of the assignment problem can
be expressed as follows:
Maximize:
∑
t∈T
∑
v∈V
∑
k∈K
ρ
t
x
tvk
, (1)
where x
tvk
corresponds to a binary variable that takes
value 1 if route t corresponds to the v-th trip of truck
k, 0 otherwise. The complete assignment model can
be checked in the appendix section. As solving this
problem by exact methods proves to be difficult with
high number of trucks and routes, we used a sequen-
tial insertion heuristic, which will assign routes to one
truck at a time until the truck can not take in another
route.
For every route in the truck, the position and start-
ing time must be defined, thus leading to the Schedul-
ing problem. The next model deals with the Schedul-
ing of routes for every truck k:
Variables:
x
tv
: binary that takes value 1 if route t
corresponds to the v-th trip of truck k; 0
otherwise
d
v
: starting time of v-th trip of truck k
Minimize:
∑
v∈V
k
d
v
(2)
Subject to:
∑
v∈V
k
x
t,v
= 1, ∀t ∈ T
k
(3)
∑
t∈T
k
x
t,v
= 1, ∀v ∈ V
k
(4)
∑
t∈T
k
α
t
x
t,v
≤ d
v
≤
∑
t∈T
k
β
t
x
t,v
, (5)
∀v ∈ V
k
d
v
≥ d
v−1
+
∑
t∈T
k
λ
t
x
t,v−1
, (6)
∀v ∈ V
k
| v 6= 1
α
′
k
≤ d
1
(7)
d
n(V
k
)
≤ β
′
k
−
∑
t∈T
k
λ
t
x
t,n(V
k
)
(8)
x
t,v
∈ {0, 1} , ∀t ∈ T
k
, ∀v ∈ V
k
(9)
d
v
∈ R, ∀v ∈ V
k
(10)
Objective function (2) minimizes starting times
while privileging shorter trips before longer ones if
possible, this function corresponds to a secondary op-
timization criteria. Restrictions of type (3) ensures
that every route assigned to truck k will be performed
once. Type (4) restrictions states that every trip posi-
tion will host one route, no more, no less. Restrictions
of type (5) ensures that every route must comply their
time window if they correspond to the v-th trip. Type
(6) restrictions states that v-th trip starting time will
occur after the end of the previous one. Restriction
(7) ensures that the first trip must comply with truck’s
starting time. Restriction (8) states that the last trip
must finish before the ending time window of truck
k. Finally, restrictions of type (9) and (10) show vari-
ables’ nature.
Our proposed sequential insertion heuristic can be
expressed as follows:
For every truck:
1. Fill a list with the set of unassigned routes.
2. Sort routes in descending order by priority.
Large Scale Petrol Station Replenishment Problem with Time Windows: A Real Case Study
411

Table 1: Main test results.
Day NR NT T (sec) T
AMPL
(sec) T
CPLEX
(sec) OF COF COF1
1 195 142 44.9 3.3 41.6 109678 83224 84849
2 207 97 42.6 2.8 39.8 80577 63613 69163
3 47 50 5.8 0.4 5.5 15647 14011 14811
4 272 142 67.6 5.2 62.4 113129 98638 103721
5 238 150 50.0 4.0 46.0 87056 66270 69610
6 294 158 81.0 6.2 74.8 117471 96616 99563
7 236 153 51.7 3.8 47.9 81992 69319 72674
8 297 156 86.8 6.1 80.6 118004 98471 99303
9 260 111 59.2 4.2 55.0 92722 74538 78578
10 62 47 7.8 0.6 7.2 15961 16013 17988
11 279 150 86.8 6.8 80.1 115868 101731 105428
12 286 154 77.2 6.0 71.2 96268.5 73765 78488
13 299 156 99.6 7.0 92.6 114833 94907 96577
14 268 154 98.8 7.0 91.8 83135 65521 66696
15 312 157 100.6 7.0 93.6 123246 108039 111279
16 261 111 53.3 3.6 49.7 88379 70378 73412
17 58 48 7.3 0.5 6.9 16342 15103 16735
18 287 141 78.8 6.0 72.9 114749.5 98706.5 110828.5
19 273 148 60.6 4.3 56.3 90570 76992 79452
20 318 152 101.5 6.9 94.5 116170 91926 101455
21 190 148 37.3 2.4 34.8 78426 61614 62914
22 255 155 58.7 4.5 54.2 121452.5 98923.5 99753.5
23 251 112 39.7 2.8 36.9 90362 71204 77964
24 58 53 8.5 0.5 8.0 19889 17900 18700
25 282 144 81.0 5.5 75.5 112043 101201 105358
26 280 154 58.3 4.2 54.1 90863.5 70729.5 75139.5
27 300 152 89.7 6.9 82.8 121682 95812 99022
28 260 153 56.2 3.4 52.8 83511.75 67608.75 72073.75
29 310 158 105.5 7.5 98.1 127477.5 105188.5 109408.5
30 282 105 58.1 4.1 54.0 88796 67359 69930
31 80 56 15.9 1.2 14.7 20518 16650 17495
3. Filter routes by truck’s time window compatibil-
ity.
4. Assign a route from the list, which complies to a
certain starting criteria, to the truck and extract it
from the list.
5. For every element in the list:
(a) Verify compatibility with current routes as-
signed. If verification is positive, then solve the
scheduling problem including the current route.
Else, move onto the next element of the list.
(b) If scheduling problem is correctly solved, as-
sign current route to the truck, extract it from
the list and check for potential remaining
routes. Else, move onto the next element of the
list.
(c) If there are potential routes, move onto the next
element of the list. Else, move onto the next
truck.
The process ends once we have been through every
truck or all routes have been assigned.
5 RESULTS
We tested our heuristic against a month of real data.
Each day presented different number of orders and
trucks involved, so a wide variety of possibilities are
covered. The route start criteria used was: any route
that holds the highest priority on the list. As for the
main parameters used, we set the maximum number
of trips per shift to 4, and ρ(i) takes values from table
3.
Our heuristic was coded in AMPL language, using
CPLEX 12.1, in a computer with O.S. Windows 8,
Intel Core i5-4200U 1.6 - 2.3 GHz processor and 8
GB of RAM.
As shown in table 1, the objective function ob-
tained by our heuristic (OF) outperforms the ones
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
412
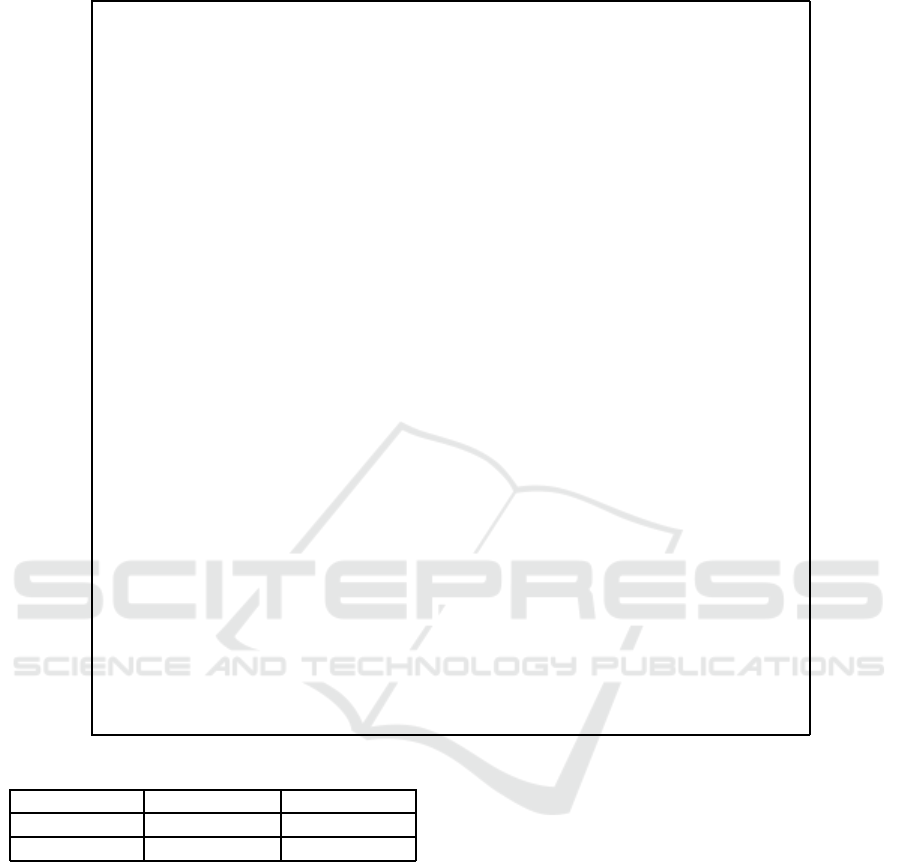
Table 2: Detailed Compliance Level.
Day NR NT T (sec) C CC CC1 CCCL CCCL1 CCT
1 195 142 44.9 97.9% 77.4% 79.0% 90.3% 92.8% 86.2%
2 207 97 42.6 89.9% 81.2% 86.0% 91.3% 98.1% 87.9%
3 47 50 5.8 87.2% 83.0% 85.1% 93.6% 95.7% 89.4%
4 272 142 67.6 93.4% 83.5% 87.1% 94.1% 98.2% 88.6%
5 238 150 50.0 97.1% 81.9% 84.9% 93.3% 96.6% 88.2%
6 294 158 81.0 98.6% 85.0% 87.8% 94.9% 97.6% 90.1%
7 236 153 51.7 99.2% 87.3% 91.5% 92.4% 96.6% 94.9%
8 297 156 86.8 98.0% 84.2% 84.8% 96.3% 97.3% 87.5%
9 260 111 59.2 98.1% 85.0% 88.1% 94.2% 98.8% 89.2%
10 62 47 7.8 72.6% 82.3% 87.1% 93.5% 98.4% 88.7%
11 279 150 86.8 93.9% 83.5% 86.4% 96.4% 99.3% 87.1%
12 286 154 77.2 99.3% 83.9% 87.8% 93.0% 96.9% 90.6%
13 299 156 99.6 97.3% 85.3% 87.0% 96.3% 98.3% 88.6%
14 268 154 98.8 99.3% 83.6% 84.3% 96.3% 97.4% 86.6%
15 312 157 100.6 98.4% 86.5% 88.1% 96.2% 98.1% 89.4%
16 261 111 53.3 98.1% 82.8% 85.4% 94.6% 97.7% 87.4%
17 58 48 7.3 77.6% 81.0% 86.2% 93.1% 98.3% 86.2%
18 287 141 78.8 94.8% 81.9% 89.2% 88.9% 98.3% 89.9%
19 273 148 60.6 96.7% 81.7% 87.9% 90.1% 96.3% 91.6%
20 318 152 101.5 93.7% 83.3% 87.4% 92.1% 96.2% 91.2%
21 190 148 37.3 100.0% 83.7% 85.8% 95.3% 97.4% 88.4%
22 255 155 58.7 99.2% 85.5% 86.7% 96.5% 98.0% 88.6%
23 251 112 39.7 96.8% 85.7% 90.4% 92.8% 99.2% 91.2%
24 58 53 8.5 96.6% 89.7% 91.4% 94.8% 96.6% 94.8%
25 282 144 81.0 90.8% 81.9% 86.5% 92.2% 98.2% 87.2%
26 280 154 58.3 99.6% 82.1% 86.8% 91.4% 97.1% 88.9%
27 300 152 89.7 99.0% 84.7% 87.0% 93.7% 96.0% 91.0%
28 260 153 56.2 99.2% 83.8% 87.3% 93.1% 96.9% 90.0%
29 310 158 105.5 97.7% 81.0% 84.2% 94.8% 98.1% 85.8%
30 282 105 58.1 94.7% 78.4% 81.2% 92.9% 96.5% 84.4%
31 80 56 15.9 92.5% 85.0% 90.0% 91.3% 96.3% 92.5%
Table 3: ρ values.
Type A Client Type B Client
Type A Order 125 25
Type B Order 5 1
from the company (COF) in 30 out of 31 cases. There
is a second acceptance criteria which states that any
order may have plus/less one hour of error. Consider-
ing this criteria, our heuristic gets a higher objective
function than the ones from the company (COF1) in
29 out of 31 cases. Looking deeper within these two
cases, it is important to state that few of the routes
were made by a truck with higher capacity, action that
needs further confirmation and is not included in the
set obtained in Phase I. Overall, our heuristic is able
to find good solutions despite being simple and fast.
The average increase in the objective function respect
COF is of 22%.
The lowest computing times (T) are reported on
days 3, 10, 17, 24 and 31, which corresponds to
Sundays, where there is little movement compared to
other working days. Time required to solve this prob-
lem on these days ranges from 6 to 16 seconds. In-
terestingly, the only two days where our heuristic’s
resulting objective function was lower than the com-
pany’s one are present in this group. There is no clear
difference between other days of the week.
Excluding Sundays, the number of routes (NR)
ranges from 190 to 318, the number of trucks (NT)
ranges from 97 to 158 and solution time ranges from
37 to 106 seconds. An increase in any of them, routes
and trucks, have a negative impact in computing time,
although it is expected that a higher number of routes
encourages the company to try and get enough truck
shifts to perform them, so they often grow together.
Breaking down total computing time in time used
by CPLEX solver (T
CPLEX
) and the rest of the phases
(T
AMPL
), it is possible to see that most of the time
is used to solve the single truck scheduling problem
with tentative sets of routes assigned. Any improve-
Large Scale Petrol Station Replenishment Problem with Time Windows: A Real Case Study
413

ment to the selection of routes to be included or to the
model itself is expected to have a huge impact on total
computing time.
Table 2 shows compliance levels. We can see that
our heuristic is capable of obtaining a proposal with a
really high number of trips while fulfilling all restric-
tions proposed, even outperforming the compliance
of the company (CC), even considering the error ac-
ceptance criteria (CC1) in most of the cases. We can
see that the compliance of the company with clients’
time windows is really high (CCCL), their main prob-
lem resides in being able to manage compliance with
trucks’ time windows (CCT). If we go by the criteria
of an acceptable error of plus/less one hour, the com-
pany compliance with the clients (CCCL1) is higher
than our heuristic in 18 out of the 31 days.
In average our heuristic got a 95.1% compliance
level, which correspond to an increase of 14% with
respect of the current compliance level of the com-
pany over that month.
The CCT column in table 2 shows that truck com-
pliance is fairly lower when comparing it to client
compliance or our heuristic’s result. This means that
truck compliance is one of the key points that can be
drastically improved in practice.
6 CONCLUSIONS AND FUTURE
RESEARCH
From the results obtained, we can say it is possible
to include trucks shifts’ time windows in the schedul-
ing problem faced by the company, as it is possible to
reach at least the same compliance level the company
already has without considering it, for most of cases.
The end result from our heuristic correspond to a
proposal which schedulers usually request at the start
of their day or along it, specially when big changes
to the current schedule plan is required, so it must be
able to present a good starting plan in a short span
of time. As stated in results section, the heuristic is
able to handle the biggest instances of this problem in
at most 2 minutes, which is a fairly good time span
considering the compliance yielded.
Future research will be focused on the impact of
including more real life aspects to the two phases
mentioned in 3, and test different aspects of the
heuristic so it can solve them, such as: the efficiency
of using a parallel insertion heuristic for this case; the
impact on time solution of the secondary optimization
criteria; and lastly, test different route starting criteria,
as they might boost the heuristic performance.
ACKNOWLEDGEMENTS
This research was partially supported by Direccion
General de Investigacion y Postgrado (DGIP) from
Universidad Tecnica Federico Santa Maria, Grant
USM 28.15.20. Pablo Villegas also wishes to ac-
knowledge the Graduate Scholarship also from DGIP.
REFERENCES
Avella, P., Boccia, M., and Sforza, A. (2004). Solving a fuel
delivery problem by heuristic and exact approaches.
European Journal of Operational Research, 152:170–
179.
Benantar, A. and Ouafi, R. (2012). Optimization of ve-
hicle routes: an application to logistic and transport
of the fuel distribution. In 9th International Confer-
ence on Modeling, Optimization and Simulation, Bor-
deaux, France.
Boctor, F., Renaud, J., and Cornillier, F. (2011). Trip
packing in petrol stations replenishment. Omega,
39(1):86–98.
Brown, G., Ellis, C., Graves, G., and D., R. (1987). Real-
time, wide area dispatch of mobil tank trucks. Inter-
faces, 17:107–120.
Brown, G. and Graves, G. (1981). Real-time dispatch of
petroleum tank trucks. Management Science, 27:19–
32.
Coelho, L. and Laporte, G. (2015). Classification, mod-
els and exact algorithms for multi-compartment deliv-
ery problems. European Journal of Operational Re-
search, 242:854–864.
Cornillier, F., Boctor, F., and Renaud, J. (2008a). An exact
algorithm for the petrol station replenishment prob-
lem. Journal of the Operational Research Society,
59:607–615.
Cornillier, F., Boctor, F., and Renaud, J. (2008b). A heuris-
tic for the multi-period petrol station replenishment
problem. European Journal of Operational Research,
191:295–305.
Cornillier, F., Boctor, F., and Renaud, J. (2009). The petrol
station replenishment problem with time windows.
Computers and Operations Research, 36:919–935.
Cornillier, F., Boctor, F., and Renaud, J. (2012). Heuristics
for the multi-depot petrol station replenishment prob-
lem with time windows. European Journal of Opera-
tional Research, 220:361–369.
Mal`epart, V., Boctor, F., and Renaud, J.and La-
bilois, S. (2003). Nouvelles approches pour
l’approvisionnement des stations d’essence. Revue
Francaise de Gestion Industrielle, 22:15–31.
Ng, W., Leung, S., Lam, J., and Pan, S. (2008). Petrol de-
livery tanker assignment and routing: a case study in
hong kong. Journal of the Operational Research So-
ciety, 59:1191–1200.
Ronen, D. (1995). Dispatching petroleum products. Oper-
ations Research, 43(3):379–387.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
414

Solomon, M. (1987). Algorithms for the vehicle routing and
scheduling problems with time window constraints.
Operations Research, 35(2):254265.
Surjandari, I., Rachman, A., Dianawati, F., and Wibowo,
R. (2011). Petrol delivery assignment woth multi-
product, multi-depot, split deliveries and time win-
dows. International Journal of Modeling and Opti-
mization, 1(5):375–379.
Taqa allah, D., Renaud, J., and Labilois, S. (2000).
Le probl`eme d’approvisionnement des stations d’
essence. APII-JESA, Journal Europ´een des Syst`emes
Automatis´es, 34:11–33.
Van der Bruggen, L., Gruson, R., and Salomon, M. (1995).
Reconsidering the distribution structure of gasoline
products for a large oil company. European Journal
of Operation Research, 81:460–473.
Wang, Q., Qingkai, J., and Chun-Hung, C. (2014). Op-
timal routing for heterogeneous fixed fleets of multi-
compartment vehicles. Mathematical Problems in En-
gineering, 2014. Article ID 847630.
APPENDIX
Assignment Model
Variables:
x
tvk
: binary that takes value 1 if route t
corresponds to the v-th trip of truck k; 0
otherwise
d
tvk
: starting time of route t if it corresponds
to the v-th trip of truck k
Maximize:
∑
t∈T
∑
v∈V
∑
k∈K
ρ
t
x
tvk
(11)
Subject to:
∑
v∈V
∑
k∈K
x
tvk
≤ 1, ∀t ∈ T (12)
∑
t∈T
k
x
tvk
≤ 1, ∀v ∈ V, ∀k ∈ K (13)
∑
t∈T
k
x
t,v−1,k
≥
∑
t∈T
k
x
t,v,k
, (14)
∀v ∈ V | v 6= 1, ∀k ∈ K
α
t
x
tvk
≤ d
tvk
≤ β
t
x
tvk
, ∀t ∈ T, (15)
∀v ∈ V, ∀k ∈ K
α
′
k
x
tvk
≤ d
tvk
≤
β
′
k
− λ
t
x
tvk
, (16)
∀t ∈ T, ∀v ∈ V, ∀k ∈ K
d
tvk
≥
∑
l∈T
k
,l6=t
d
l,v−1,k
+ λ
l
x
l,v−1,k
,
(17)
∀t ∈ T, ∀v ∈ V | v 6= 1,
∀k ∈ K
x
t,v,k
∈ {0, 1} , d
t,v,k
∈ R, (18)
∀t ∈ T, ∀v ∈ V, ∀k ∈ K
Objective function (11) maximizes priority as-
signed. Restrictions of type (12) ensures that routes
can be performed at most once. Type (13) restrictions
ensures that at most one route can be performed as
v-th trip of truck k. Restrictions of type (14) ensures
that in truck k, the v-th trip exists just if trip v-1 also
exists. Type (15) restrictions states that if route t is
the v-th trip of truck k, its departing time must be
inside the route’s time window. Restrictions of type
(16) states that if route t corresponds to the v-th trip
of truck k, its departing and arriving time must be in-
side truck’s time window. Type (17) restrictions states
that starting time of route t in truck k must be higher
than the arrival time of the previous trip. Finally, type
(18) restrictions show variables’ nature.
ρ
t
constant is calculated as follows:
ρ
t
=
∑
i∈C
t
ρ
i
∗ Q
i
(19)
Where C
t
is the set of orders involved in route t, ρ
i
is the priority modifier of order i, and finally Q
i
is the
quantity of product to be delivered in order i.
Large Scale Petrol Station Replenishment Problem with Time Windows: A Real Case Study
415
