
A Robust Pixel ECC based Algorithm for Occluded Image Alignment
Nefeli Lamprinou and Emmanouil Z. Psarakis
Department of Computer Engineering and Informatics, University of Patras, 26504 Rio-Patras, Greece
Keywords:
Image Alignment, Occluded Images, Correlation Coefficient.
Abstract:
The alignment of occluded images constitutes a common and difficult problem. In this paper we propose a
new method based on ECC algorithm tailored to occluded image alignment problem which enjoy a simple
closed-form solution with low computational cost. Moreover, the use of a proper subset of the region of
interest that limits the impact of the outliers in the estimation of the parameters is proposed. The use of this set
seems to make the proposed method insensitive to the use of the occluded image as template or as warped in
the alignment process. The proposed method is compared against two well known Gradient Corellation based
methods by its application in several image alignment problems and in all cases outperforms its rivals in terms
of accuracy and percentage of convergence.
1 INTRODUCTION
Image registration methods aim at finding the corre-
sponding points in two or more images and align them
by moving their data to a common coordinate system.
So alignment means to restore the geometric defor-
mations that exist between the images. Solving the
alignment problem is essencial to many different high
level applications such as face or object recognition,
motion analysis and medical imaging. A demanding
problem is face alignment, especially in cases where
real images are considered, due to many different con-
ditions during image capture such as face expressions,
lighting conditions and occlusions (sunglasses, scarf
etc.).
Alignment methods aim to estimate the parame-
ters of the geometric trasformation between a tem-
plate and an observation image, which can be
achieved through the optimization of a cost or simi-
larity function. Refering to area based techiques LK
algorithm (Lucas and Kanade, 1981) is the most pop-
ular method based on the minimization of the l
2
norm
of the error between the images. The original LK
algorithm, however, is inefficient in the presence of
outliers, which constitutes a very common problem
when using real images with ucontrolled lighting con-
ditions and occlusions. So numerous variations and
extensions of the LK algorithm have been proposed
through the years to address this problem such as FM
(Fuh and Maragos, 1991), weighted LK (Baker and
Matthews, 2004), Fourier LK (S. Lucey and Sridha-
ran, 2012) and (A.B. Ashraf and Chen, 2010).
A different approach in solving the alignment
problem is the maximization of a similarity func-
tion with the most known one being the correlation
coefficient. Existing similarities and differencies of
the above mentioned approach with l
2
based one can
be found in (Evangelidis and Psarakis, 2008) where
the ECC, an algorithm that uses the above similarity
measure on image intensities, was introduced. Simi-
rarly, Gradient Correlation algorithm (G. Tzimiropou-
los and Pantic, 2011) maximizes the correlation of
image gradient orientations (G.Tzimiropoulos, 2010),
an approach that is able to address the problem of
non uniform photometric distortions and occlusions,
although the use of face features reduces its perfor-
mance in images with different content.
In this paper we focus on the alignment of oc-
cluded images, that constitutes a common and diffi-
cult problem (F. Yang and Metaxas, 2011), (G. Yang
and Lu, 2015), and the use of an ECC based algo-
rithm, applied in each pixel is proposed. Specifically,
we propose the maximization of the correlation be-
tween the image gradients at every pair of correspond-
ing pixels separately, leading to a global estimation
of the distortion parameters. Since in the problem we
address, there is a large number of outliers, not all pix-
els must be used during the optimization. To this end
we propose a criterion that excludes a large number
or even all of the pixels within the occluded regions,
ensuring that the outliers have a minimum contribu-
tion in the final estimation. In addition, the proposed
Lamprinou, N. and Psarakis, E.
A Robust Pixel ECC based Algorithm for Occluded Image Alignment.
DOI: 10.5220/0005788202790284
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 279-284
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
279

closed form solution results in a computational effi-
cient, as well as robust, algorithm.
The paper is organized as follows. In Section 2 the
problem formulation is presented and the pixel-ECC
approach is introduced . In Section 3 the image align-
ment problem is formulated and the proposed opti-
mization problem is solved. In Section 4 the results
we obtained from the application of the proposed al-
gorithm in the experiments we have contacted, are
presented. Finally, Section 5 contains our conclusions
and future directions.
2 PROBLEM FORMULATION
Let us consider that the photometric distortions are
local and they can be modeled as follows;
g(x
i
) = α
i
f (x
i
) + β
i
, i = 1, 2,·· · , N (1)
where f (.), g(.) denote the intensities of the x
i
-th
pixel of the template and the warped and photomet-
rically distorted image respectively, and N is the total
number image’s pixel.
As it is clear from (1), the photometric distortion
is modeled by the use of the multiplicative and the ad-
ditive parameter α
i
and β
i
respectively. Actually, we
can easily remove the effects of the additive param-
eter by evaluating the gradient of the intensity func-
tion at each one pixel. Moreover, in order to remove
the effects of the multiplicative parameter we are go-
ing to use the cost function introduced in (Evangelidis
and Psarakis, 2008), but by defining it using a pair of
corresponding pixels. To this end let us define the fol-
lowing quantity:
t
i
= ∇ f (x
i
) = [
∂ f (x
i
)
∂x
i1
∂ f (x
i
)
∂x
i2
]
t
and its normalized counterpart:
t
i
=
∇ f (x
i
)
||∇ f (x
i
)||
2
(2)
where ||x||
2
denotes the l
2
norm of vector x.
Then, for the i-th pair of the corresponding pixels
we define the following cost function:
ε
i
(p) = ||t
i
− q
i
(p)||
2
2
(3)
and we would like to minimize it w.r.t. the vector ge-
ometric distortion parameters p. The above defined
minimization problem, as it was proved in (Evange-
lidis and Psarakis, 2008), is equivalent with the max-
imization of the following quantity which is known
in the literature as Enchanced Correlation Coefficient
(ECC):
ρ(p) =< t
i
, q
i
(p) > (4)
where < x, y > denotes the inner product of the vec-
tors x, y. Since, the similarity function defined by (4)
is a nonlinear function of the parameter vector p, we
are going to linearize it and thus replacing the original
optimization problem with a sequence of secondary
ones. To this end we adopt the forward additive up-
dating rule expessed by the followign equation:
p
n
← p
n−1
+ ∆p
n
(5)
and use the Taylor expansion of the warped image,
i.e.:
q
i
(p
n
) = q
i
(p
n−1
+ ∆p
n
)
= q
i
(p
n−1
) + H
i
(I
2
⊗
˜
x
t
i
)∆p
n
(6)
where H
i
is the 2× 2 Hessian matrix of warped inten-
sity function on the i-th pixel having homogeneous
coordinates
˜
x
i
, I
2
the 2 × 2 eye matrix and ⊗ is de-
noting the kronecker product operator. For simplicity
reasons we drop the depedency of the warped vectors
on the parameter vector p and the dependency of the
updating rule on n.
By setting:
z
i
= H
i
(I
2
⊗
˜
x
t
i
)∆p (7)
and substituting it into (6), Equation (4) can be ex-
pressed as follows:
ρ(z
i
) =
t
t
i
q
i
+ t
t
i
z
i
q
||q
i
||
2
2
+ 2q
t
i
z + ||z
i
||
2
2
(8)
and our goal is to maximize it w.r.t. z
i
. This is
achieved by the next lemma.
Lemma 1. Let us consider that we would like to
maximize the similarity function defined by (8) w.r.t.
the vector z
i
. Assuming the invertibility of matrix H
i
,
the similarity function attains its maximum value, i.e.
ρ(z
i
) = 1, iff vector z
?
i
is of the following form:
z
?
i
= λ
i
t
i
− q
i
(9)
where λ
i
is a positive number.
Proo f : The proof of the lemma is simple and is
ommited.
As it is clear from Lemma 1, the parameter λ
i
models the photometric distortion related to the i-th
pixel of the photometrically distrorted image. We
must stress at this point that the only constraint that
must be imposed, is the positivity of the parameter λ
i
.
Concluding, we would like to remove the local
photometric distortions existing in corresponding pix-
els by using their gradients denoted by the vectors t
i
and q
i
) respectively and the vector z
i
defined by (7).
This is exactly our goal in the next section.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
280

3 THE ALIGNMENT PROBLEM
Let us now reformulate the image matching problem
by taking into account all the quantities defined in the
previous section. To this end let us consider that for
each member of the following pixel subset of the re-
gion of interest R :
P = {x
k
∈ R , k = 1, · ·· , K} (10)
there is λ
k
> 0 such that equation (9) can be satis-
fied (i.e. pixels x
k
and W(x
k
; p), associated with
the template and the warped intensities f (x
k
) and
g(W(x
k
; p)) respectively, constitute a pair of corre-
sponding pixels, where W(x; p) denotes a geomet-
ric transformation parametrized by vector p). Then,
using Lemma 1 in each pair of corresponding pixels
contained in the above defined set and by taking into
account that in the general case K >> 6, we obtain the
following overdetermined linear system of equations:
(I
2
⊗
˜
x
t
k
)∆p = H
−1
k
(λ
k
t
k
− q
k
), k = 1, 2, · ·· , K (11)
whose the solution we are going to investigate in the
next paragraph.
3.1 An l
2
based Solution
As it was already mentioned, the linear system of
equations defined by (11) is overdetermined and thus,
in the general case, it has not an exact solution. In or-
der to overcome this obstacle we are going to find an
approximate solution which will be optimum in the l
2
sense.
To this end let us define the following quantities:
X = {I
2
⊗
˜
x
t
k
}
K
k=1
D = −diag{H
−1
k
t
k
}
K
k=1
b = −{H
−1
k
q
k
}
K
k=1
λ = {λ
k
}
K
k=1
(12)
where X is a 2K × 6 matrix, D is a 2K × K block di-
agonal matrix and b, λ column vectors of length 2K
and K respectively.
Then, the linear system defined by (11) can be
rewritten as follows:
X D
∆p
λ
= b. (13)
and we would like to solve the following optimization
problem:
min
∆p λ
||
X D
∆p
λ
− b||
2
2
(14)
whose the optimal solution can be easily proved that
is given by the following relation:
∆p
?
λ
?
=
X
T
X X
T
D
D
T
X D
T
D
−1
X
T
D
T
b. (15)
To avoid numerical problems and reduce the com-
putational cost, we exploit the special form of the
above linear system and propose to use instead the
following equations:
X
T
X∆p + X
T
Dλ = X
T
b (16)
D
T
X∆p + D
T
Dλ = D
T
b. (17)
Solving (17) for λ and substituting into (16) we ob-
tain:
∆p
?
=
X
T
(I
2K
− P
D
)X
−1
X
T
(I
2K
− P
D
)b (18)
where matrix P
D
is the following projection matrix:
P
D
= D(D
T
D)
−1
D
T
.
Note that the matrix D
T
D is diagonal and conse-
quently its inverse is easily computed.
3.2 Defining Subset P
In order to complete the proposed technique, we have
yet to define the pixel subset of (10). To achieve our
goal we are going to exploit the special form of the
linear system (17). To this end we use the quantities
defined in (12), and re-express it as follows:
−t
t
k
H
−1
k
(I
2
⊗
˜
x
t
k
)∆p + ||H
−1
k
t
k
||
2
2
λ
k
= t
t
k
H
−2
k
q
k
(19)
where k = 1, 2, ·· ·K.
As we can see, when we are close to the optimum
warp (i.e. ∆p → 0
6
) each one of the above mentioned
equation can be written as follows:
t
t
k
H
−1
k
(H
−1
k
t
k
λ
k
− H
−1
k
q
k
) ≈ 0
2
. (20)
Since H
−1
k
t
k
, in the general case is not equal to zero,
we have that the vector H
−1
k
t
k
λ
k
− H
−1
k
q
k
must be
close to 0
2
. Note that in the ideal case
H
−1
k
t
k
λ
k
= H
−1
k
q
k
and the above equations have a unique solution for the
parameter λ
k
, that is λ
k
= ||q
k
||
2
and this in turn en-
sures the desired positivity of λ. However, when we
are not close to the optimal solution the above men-
tioned equality does not hold for any pair of corre-
sponding pixels and as an alternative we propose to
define the pixel subset P as follows:
P = ∩
3
i=1
R
i
, (21)
where:
R
1
= {
ˆ
x
k
∈ R : sign(H
−1
k
t
k
) = sign(H
−1
k
q
k
)}
R
2
= {
ˆ
x
k
∈ R : sign(H
−1
f
k
t
k
) = sign(H
−1
f
k
q
k
)}
R
3
= {
ˆ
x
k
∈ R : sign(H
−1
k
t
k
) = sign(H
−1
f
k
t
k
)}
A Robust Pixel ECC based Algorithm for Occluded Image Alignment
281

and H
f
k
denotes the 2 × 2 Hessian matrix of the tem-
plate intensity function on the k−th pixel with coor-
dinates x
k
. Note that through the use of sets R
2
and
R
3
we impose, in some sense, the desired insensitiv-
ity of the proposed algorithm independently if we use
the occluded image in the alignment process as the
template or as the warped one.
It is clear that the above defined set P changes in
each iteration of the algorithm. In Figure 1 instances
of the evolution of the set P for four different exam-
ples are shown. From this figure it is clear that the car-
dinality of of these sets is an increasing sequence of
the iteration number. Note also the impact of the pro-
posed constraints in the formation of the set. Pixels
that belong into occluded regions, with high probabil-
ity, are not members of the aformentioned sets. This
is apparent in the last three rows of Figure 1 where
the proposed technique is applied for the alignment
of occluded images.
The outline of the proposed algorithm follows.
Algorithm 1 : Pixel Based ECC Image Alignment Algo-
rithm. Input: Template f (.) and Warped g(.) Images.
1: Compute the gradient of the template image f (.)
and its hessian.
2: repeat
3: Compute the gradient of the warped image
g(.) and its hessian.
4: Using (21) define the pixel subset P .
5: Using (18) compute ∆p
?
.
6: Use (5) to update the parameter vector p.
7: Update the warped image
8: until convergence
9: Output: The warp.
Having completed the presentation of the pro-
posed technique, we are going to apply it in the next
section.
4 EXPERIMENTS
In this section we are going to apply the proposed
alignment technique by conducting a couple of ex-
periments. In addition we will compare its per-
formance in terms of the achieved alignment error,
as well as its frequency of convergence against the
methods proposed in (G. Tzimiropoulos and Pan-
tic, 2011); namely GradientImages and Gradient-
Corr. We assessed the performance of rivals by using
the performance evaluation framework proposed in
(Baker and Matthews, 2004) that has been adopted by
other researchers (Evangelidis and Psarakis, 2008),
(A.B. Ashraf and Chen, 2010) as a stantard for that
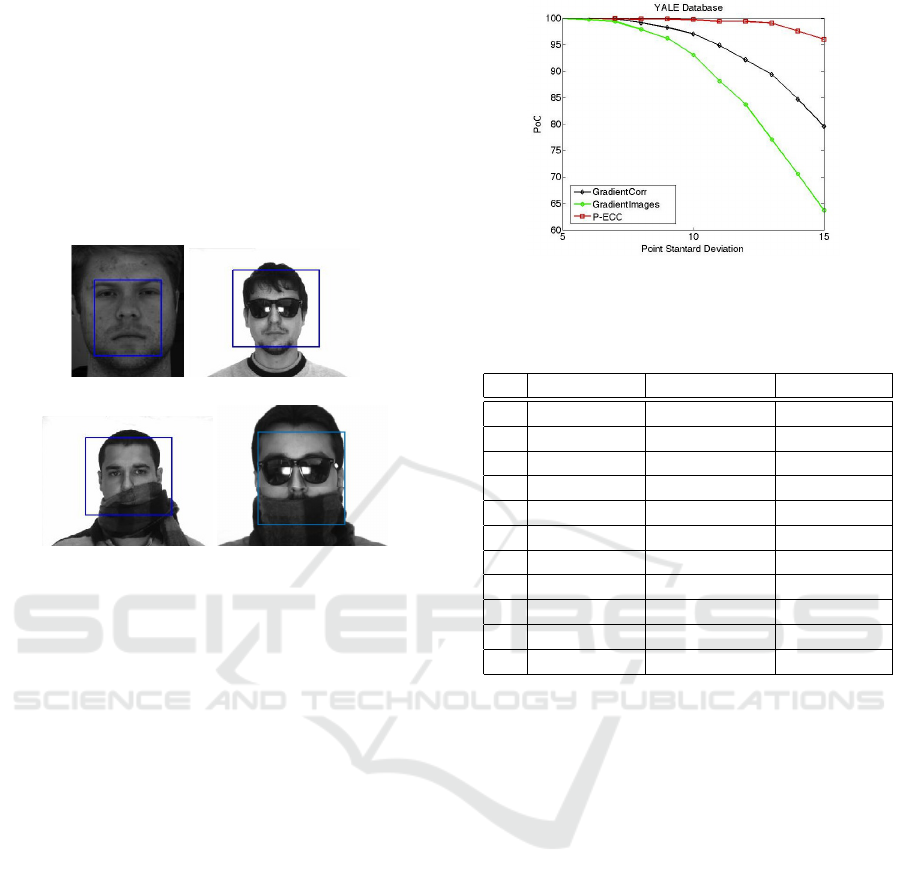
Figure 1: Pixel subset P defined in (21). First line: Subset
P for a nonoccluded image with σ = 5 in the 1−st, 5−th and
10−th iteration. Second line: Subset P for the same image
but with σ = 15 in the 1−st, 40−th and 60−th iteration.
Third line: The template image with σ = 10 aligned with
sunglasses occluded image and the pixel subset P in the
1−st and 30−th iteration. Fourth line: The template image
with σ = 10 aligned with scarf occluded image and the pixel
subset P in the 1−st and 30−th iteration. Fifth line: The
template image with σ = 10 aligned with mixed sunglasses
and scarf occluded image and the pixel subset P in the 1−st
and 30−th iteration.
purpose. This framework is briefly summarized in the
next paragraph.
4.1 Experimental Setup
The evaluation in (Baker and Matthews, 2004) is as
follows. We select a Region of Interest (RoI) (please
see Figure 2) and three canonical points in this region.
We perturb these points using Gaussian noise of stan-
dard deviation σ and compute the initial RMS Dis-
tance (RMSD) between the canonical and perturbed
points. Using the affine warp that the original and per-
turbed points define, we generate the affine distorted
image. Given a warp estimate, we compute the desti-
nation of the three canonical points and, then, the final
RMSD between the estimated and correct locations.
We use RMSD for a fixed Point Stantard Deviation σ
and the Percentage of Converging (POC) runs for sev-
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
282
eral values of σ as figures of merit for the performance
evaluation. An algorithm is considered as converged
if the final RMSD was less than 3 pixels after 60 it-
erations in total. In particular, for the efficient imple-
mentation of the proposed algorithm we have used a
three level pyramid dividing the above mentioned iter-
ations into 30, 20 and 10 in each level of the pyramid
respectively. In all experiments we used the Matlab
code provided by the authors of (G. Tzimiropoulos
and Pantic, 2011).
(a) (b)
(c) (d)
Figure 2: Different forms of Regions of interest (RoI) which
are used in our experiments (please see the text for the de-
tails).
4.2 Experiment I
In this experiment we are going to apply the rivals
on geometrically distorted images without photomet-
ric distortions or occlusions by using the RoI shown
in Figure 2.a. For all the results we obtained we used,
for each σ, 30 randomly generated warps in ten differ-
ent images from Yale B database (A.S. Georghiades
and Kriegman, 2001) . The resulting Percentange of
Converging runs of the rivals with the size of the ge-
ometric distortion σ ∈ [5, 15] from their application
on face images from the Yale B database are shown
in Figure 3. As we can see the proposed technique
outperforms its rivals.
In addition, Table 1 contains the RMS Distances
achieved by the rivals, in converging runs, with the σ
taking the above mentioned values. As it is clear from
this table, the proposed technique achieves the small-
est RMSD even in the strongest geometric distortions.
4.3 Experiment II
In addition to the standard Yale B based Experiment
I, we considered the problem of face alignment in the
presence of real strong occlusions by using face im-
ages from the AR database (Martinez and Benavente,
Figure 3: Frequency of Convergence versus Point Standard
Deviation σ ∈ [5, 15] for images from Yale B database.
Table 1: RMS Distances obtained from the application of
the rivals on images from Yale B database.
σ GradientIm GradientCorr P-ECC
5 6.0 × 10
−02
3.0 × 10
−02
1.9 × 10
−10
6 7.0 × 10
−02
5.0 × 10
−02
1.9 × 10
−10
7 1.0 × 10
−01
6.0 × 10
−02
1.7 × 10
−09
8 1.1 × 10
−01
6.0 × 10
−02
2.3 × 10
−09
9 1.5 × 10
−01
1.1 × 10
−01
3.0 × 10
−07
10 1.7 × 10
−01
1.3 × 10
−01
1.0 × 10
−04
11 2.1 × 10
−01
1.3 × 10
−01
6.3 × 10
−03
12 7.1 × 10
−01
6.8 × 10
−01
6.4 × 10
−03
13 8.8 × 10
−01
7.8 × 10
−01
6.4 × 10
−03
14 1.02 8.8 × 10
−01
5.1 × 10
−02
15 1.21 9.1 × 10
−01
5.8 × 10
−02
1998). More specifically, we applied the rivals on the
sunglasses and scarf occluded images contained in the
AR database and on mixed sunglasses and scarf im-
ages we created. The Regions of Interest we have
used for the above mentioned categories are shown in
Figures 2.(b), 2.(c) and 2.(d) respectively. Note that in
this database the sunglasses and scarf images are al-
ready geometrically distorted w.r.t. the template ones,
occasionaly including large rotation and/or translation
distortions. In order to be able to correctly measure
RMSD we estimated the original transform and then
subtracted it from the final estimations. Thus, in this
experiment we have used only the images where we
were able to achieve a high quality original alignment.
This is also the reason why the RoI we have used in
this case is larger than the corresponding one in Yale
B (see Figure 2).
For the results we obtained for the sunglasses im-
ages we used, for each σ, 25 randomly generated
warps in 24 different images, for the scarf images we
used, for each σ, 20 randomly generated warps in 26
different images while for the mixed sunglasses and
scarf images we used, for each σ, 30 randomly gen-
erated warps in 12 different images.
The resulting Percentange of Converging runs of
A Robust Pixel ECC based Algorithm for Occluded Image Alignment
283

the rivals with the size of the geometric distortion
σ ∈ [1, 10] are shown in Figures 4, 5 and 6 respec-
tively. As we can see from these figures the proposed
technique outperforms again its rivals.
Figure 4: Frequency of Convergence versus Point Standard
Deviation σ ∈ [1, 10] for Sunglasses images from AR
database.
Figure 5: Frequency of Convergence versus Point Standard
Deviation σ ∈ [1, 10] for Scarf images from AR Database.
Figure 6: Frequency of Convergence versus Point Standard
Deviation σ ∈ [1, 10] for the mixed Sunglasses and Scarf
images from AR database.
5 CONCLUSIONS
In this paper a new occluded image alignment method
based on ECC algorithm was proposed. The optimal
parameters were obtained by iteratively solving a se-
quence of approximate nonlinear optimization prob-
lems which enjoy a simple closed-form solution with
low computational cost. The proposed method was
compared against two well known Gradient Corella-
tion methods through two experiments. In all cases,
the proposed algorithm was outperforming its rivals
in terms of accuracy and percentage of convergence.
The extension of the proposed algorithm for the prob-
lem of image alignment under strong photometric dis-
tortions is under investigation.
REFERENCES
A.B. Ashraf, S. L. and Chen, T. (2010). Fast image align-
ment in the fourier domain. Proceedings of CVPR,
pages 2480–2487.
A.S. Georghiades, P. B. and Kriegman, D. (2001). From few
to many: Illumination cone models for face recogni-
tion under variable lighting and pose.
Baker, S. and Matthews, I. (2004). Lucas-kanade 20 years
on: A unifying framework. International Journal in
Computer Vision, 56, no. 3:221 255.
Evangelidis, G. and Psarakis, E. (2008). Parametric image
alignment using enhanced correlation coefficient max-
imization. IEEE Transactions on Pattern Analysis and
Machine Intelligence, pages 1858–1865.
F. Yang, J. H. and Metaxas, D. (2011). Sparse shape regis-
tration for occluded facial feature localization. IEEE
Conference on Automatic Face and Gesture Recogni-
tion.
Fuh, C. and Maragos, P. (1991). Motion displacement es-
timation using an affine model for image matching.
Optical Eng., 30, no. 7:881 887.
G. Tzimiropoulos, S. Z. and Pantic, M. (2011). Robust
and efficient parametric face alignment. IEEE Inter-
national Conference on Computer Vision (ICCV).
G. Yang, Y. F. and Lu, H. (2015). Sparse error via
reweighted low rank representation for face recogni-
tion with various illumination and oclusion. Interna-
tional Journal for light and electron optics.
G.Tzimiropoulos, V.Argyriou, S. a. T. (2010). Robust fft-
based scale-invariant image registration with image
gradients. IEEE Transactions on Pattern Analysis and
Machine Intelligence, pages 1899–1906.
Lucas, B. and Kanade, T. (1981). An iterative image regis-
tration technique with an application to stereo vision.
Proc. Seventh Intl Joint Conf. Artificial Intelligence.
Martinez, A. and Benavente, R. (1998). The Book. CVC
Technical Report 24.
S. Lucey, R. Navarathna, A. B. A. and Sridharan, S. (2012).
Fourier lucas-kanade algorithm. IEEE Transactions
on Pattern Analysis and Machine Intelligence, 6, no.
1.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
284
