
World Model for Testing Urban Search and Rescue (USAR) Robots using
Petri Nets
Anneliese Andrews, Mahmoud Abdelgawad and Ahmed Gario
Department of Computer Science, University of Denver, Denver, CO 80208, U.S.A.
Keywords:
Model-based Testing, Behavioral Models, Petri Nets, USAR Robots.
Abstract:
This paper describes a model-based test generation approach for testing Urban Search and Rescue (USAR)
robots interacting with their environment (i.e., world). Unlike other approaches that assume a static world
with attributes and values, we present and test a dynamic world. We use Petri Nets to illustrate a world
model that describes behaviors of environmental entities (i.e., actors). The Abstract World Behavioral Test
Cases (AWBTCs) are generated by covering the active world model using graph coverage criteria. We also
select test-data by input-space partitioning to transform the generated AWBTCs into executable test cases.
Reachability of the active world model and efficiency of coverage criteria are also discussed.
1 INTRODUCTION
According to (Williamson and Carnegie, 2007),
Search and Rescue (SAR) refers to rescue activities
in high-risk emergency situations. The 2001 World
Trade Center (WTC) collapse, the 2005 Hurricanes
Katrina, Rita, and Wilma in the United States, the
2011 Tohoku earthquake and Tsunami in Japan, are
examples of emergency situations. (Murphy et al.,
2008) report that over 900,000 people were reported
killed by disasters from 1995 to 2004, with the to-
tal amount of disaster related damage estimated at
738 billion US dollars. Urban Search and Rescue
(USAR) robotics aims at minimizing human involve-
ment in these emergency situations. In a USAR mis-
sion, the USAR robots explore unknown urban dis-
aster scenes providing real-time video and other sen-
sory data about the situation while searching for vic-
tims (Liu and Nejat, 2013). Urban disaster scenes are
often inaccessible for rescue workers due to poten-
tial collapses, poisonous gases, hazardous materials,
radiation or extreme temperatures. Testing the inter-
actions between the USAR robots and urban disaster
actors- victims, rubble, debris, bricks, mobile objects,
and unknown obstacles- poses a series of challenges,
due to the complexity and uncertainty of these ac-
tors. Model-based Testing (MBT) is able to leverage
behavioral models, such as CEFSM (Li and Wong,
2002), Coloured Petri Nets (CPN) (Lill and Saglietti,
2012), and Labelled Transition Systems (LTS) (Tret-
mans, 2008), to describe the behavioral scenarios that
can occur between the USAR robots and the disaster
actors. This requires testing solutions that deal with
the large number of possible behaviors. Current MBT
approaches for testing Real-time Embedded Systems
(RTES) interacting with their worlds assume a static
world model (Iqbal et al., 2012) and (Hessel et al.,
2008) . However, for USAR robots, the world cannot
be described only statically with attributes and val-
ues, the world should also be presented and tested a
dynamically. To address these challenges, we use a
systematic MBT approach, World Model-based Test
Generation (WMBTG), that identifies what, where
and how to test USAR robots interacting with their
surroundings. Test cases are generated by aggregating
test paths in the individual models. These test paths
are grouped as concurrent test paths which can be
used with simulators or test-harnesses to validate the
USAR robots. WMBTG has been introduced, in our
previous work, and was applied to Unmanned Ground
Vehicle (UGV) domain (Andrews et al., 2015). This
paper extends the applicability of WMBTG to USAR
robots. We also evaluate the efficiency of test path
coverage criteria used to generate Abstract World Be-
havioral Test Cases (AWBTs). We evaluate input-
space partitioning coveragecriteria (Ammann and Of-
futt, 2008) used to generate test-data. We use UML
class diagrams to construct the structural model of
disaster actors and their relationships. We also use
Petri Nets (PNs) (Murata, 1989) to represent the be-
haviors of urbandisaster actors that are involvedinthe
disaster scenes (snippets). These snippets are used to
Andrews, A., Abdelgawad, M. and Gario, A.
World Model for Testing Urban Search and Rescue (USAR) Robots using Petri Nets.
DOI: 10.5220/0005782106630670
In Proceedings of the 4th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2016), pages 663-670
ISBN: 978-989-758-168-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
663

link the behavioral models of disaster actors. This pa-
per explores the applicability of the MBT technique
for testing USAR robot behaviors in dynamic worlds
alongside behavioral testing that is systematic, scal-
able, and shows that this technique is extendable to
other domains of autonomous systems.
The remainder of this paper is organized as fol-
lows. Section 2 discuses the state of research related
to MBT, testing USAR robots, and World Model-
based Testing. Section 3 describes a case study. Sec-
tion 4 presents our approach and applies it to the case
study. We analyze and discuss reachability and effi-
ciency issues in section 5. Section 6 draws conclu-
sions and future work.
2 STATE OF RESEARCH
2.1 Model-based Testing (MBT)
According to (Dias-Neto et al., 2007), MBT uses var-
ious models to automatically generate tests. MBT in-
cludes three key elements: models that describe soft-
ware behavior, criteria that guide the test-generation
algorithms, and tools that generate supporting infras-
tructure for the tests. (Zander et al., 2012) define
MBT as an algorithm that generates test cases auto-
matically from models instead of creating them man-
ually. (Utting et al., 2012) define six dimensions of
MBT approaches (a taxonomy): model scope, charac-
teristics, paradigm, test selection criteria, test genera-
tion technology and test execution. (Shirole and Ku-
mar, 2013) also present a survey on model-based test
generation. They define the process of test case gen-
eration from graphs as follows: build a graph model,
identify test requirements, select test paths to cover
those requirements, and derive test data. (Lill and
Saglietti, 2012) use Coloured Petri Nets (CPNs) for
testing a factory robot that carries a load from one
place to another. The authors define coverage criteria
for CPNs, such as color-based and event-based cov-
erage criteria. This work does not provide validation,
nor does it address dynamic worlds.
2.2 World Model-based Testing
Most approaches in the literature for modeling the
world of autonomous systems aim at improve the un-
derstandability of the decision-making module to the
surroundings, but not for testing. (Furda and Vlacic,
2010) present an object-oriented world model ap-
proach for the road traffic environment of autonomous
vehicles. The approach uses UML class diagrams to
represent the structure of the world actors. The au-
thors conducted a field trial using two autonomous
vehicles. The experiment illustrates that the world
model strongly supports the decision-making module
for making appropriate driving decisions in real-time.
This work neither intends to be a testing technique for
autonomous systems nor does it handle the dynamic
aspect of world actors. A closely related approach
for world model-based testing is presented in (Iqbal
et al., 2010). The approach generates black-box test
cases automatically based on a static world model for
real-time embedded systems. The main characteris-
tics of the approach are: 1) An extension of UML
(MARTE) is used for modeling the structural and be-
havioralworld properties, especially real-time proper-
ties. 2) Test oracles are then generated automatically
from these models. 3) To identify feasible test cases
and maximize possibilities of fault detection, heuristic
algorithms are used as test generation strategies. An
empirical study shows that Adaptive Random Testing
(ART) is more satisfactory than the others. This ap-
proach limits the world model to a static world, there-
fore it is not applicable for autonomous systems be-
cause their worlds are dynamic.
2.3 Testing USAR Robots
The literature of testing USAR robots shows that
the techniques for testing USAR robots are mostly
computer-based simulation and test fields/arenas. (Ja-
coff et al., 2003), by the National Institute of Stan-
dards and Technology (NIST), introduce a standard
for designing and evaluating test arenas (Reference
Test Arena for Autonomous Mobile Robots). The
test arenas consist of collapsed structures that are de-
signed from buildings in various stages of the col-
lapse. The authors classify the test arenas into three
categories, each labelled by a specific color (Yellow,
Orange, and Red). The Yellow arena consists of a
planar maze with isolated test sensors in the form of
obstacles, simulated victims, doors that can be closed,
blinds that can be raised or lowered, and simple col-
lapses that can block passages. The Orange arena
provides more difficult challenges by adding an ele-
vated floor, holes, ramps, and stairs. The Red arena is
composed of unstable floors, harsh rubble, and piled
debris. Thirty simulated victims can be placed over
these test arenas. Each victim displays up to five signs
of life (form, motion, body heat, sound, and/or CO
2
emission). (Chiou and Wynn, 2009) also provide a
small test arena that is portable and can be placed in a
laboratory. Although test fields/arenas provide phys-
ical fidelity, they do not fully represent the physical
conditions of actual disasters (Murphy et al., 2008).
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
664

(Pepper et al., 2007) illustrate a computer-based sim-
ulation technique for evaluating USAR robots us-
ing USARSim, a robot simulation tool. (Ferworn
et al., 2013) also provide virtual urban disaster mod-
els for simulating USAR robots. These models are
extracted from actual urban disaster scenes. The
computer-based simulation is flexible, repeatable, and
accurate compared with physical test fields/arenas;
however, it lacks physical fidelity. Both techniques,
test fields/arenas and computer-based simulation, also
limit possible behavioral scenarios that may occur in
urban disasters.
3 CASE STUDY DESCRIPTION
For modeling an urban disaster world, we use the
Reference Test Arena for Autonomous Mobile Robots
(Jacoff et al., 2003) because it provides a clear de-
scription for urban disaster actors. The urban disaster
actors include victims, constructions, rubble, debris,
and hazards. The victims include humans and ani-
mals. They can be survivors or non-survivors. These
victims can be visual, not visual, accessible, inac-
cessible, trapped, and entombed. Only the survivors
show signs of life (motion, body heat, sound, CO
2
emission). The survivors have different conditions,
aware, semi-conscious, and unconscious. The non-
survivors do not stimulate any signs but can be recog-
nized visually. The constructions are infrastructural
objects including posts, stairs, elevators, walls, doors,
windows, and ramps. These constructions may be in-
accessible. They also have changeable states such as
unsteady posts, loose walls, sloppy stairs, unsafe el-
evators. The posts can be placed as flat, hill, and di-
agonal. The ramps can also be pitch and roll. The
Figure 1: Urban disaster, Kathmandu, Nepal, May 2015.
rubble consist of rocks, bricks, and concretes. The de-
bris are furniture, woods, ropes, wires, pipes, papers,
glasses, and plastics. These debris are usually piled
together. The rubble and debris block passages and
increase orientation complexity. These rubble and de-
bris also have changeable states as well. For example,
a brick tumbles over a collapse then stops. An urban
disaster scene may include all of these urban disaster
actors as showing in Figure 1. The hazards also can
occur when a collapse happens. Examples of the haz-
ards are high temperature, electricity, and explosion.
Regarding to the hazard severity, these hazards may
not be manipulatable. The hazard severity has five
levels (minimal, slight, moderate, serious, and sever).
4 APPROACH
Our objective is to apply a systematic model-based
test generation approach (Andrews et al., 2015) to
generate test cases from an active world model that
represents urban disaster actors of USAR robots. We
build the active world model in two steps. First, we
construct a structural model of disaster actors to rep-
resent their attributes, functions and relations. Sec-
ond, we construct the behavioral model to describe
the disaster actors’ possible states and transitions and
their interactions. Each disaster actor is presented by
Figure 2: World Behavioral Test Generation Process.
one behavioral model showing its behaviors. The in-
teractions between these disaster actors represent the
active world model. Since the disaster actors are inter-
acting simultaneously, the active world model should
cover not only the internal transitions of these disas-
ter actors, but also the interactions between them. The
active world model can then be leveraged to generate
world behavioral test cases. Once we build the active
world model, any member of the graph-based testing
criteria from (Ammann and Offutt, 2008) and (Lill
and Saglietti, 2012) can be used to generate abstract
behavioral test paths, which are AWBTCs. Finally,
we generate test-data by input-space partitioning to
transform the generated AWBTCs into executable test
cases. The test generation process is illustrated in Fig-
World Model for Testing Urban Search and Rescue (USAR) Robots using Petri Nets
665

ure 2. The World Model-based Test Generation pro-
cess follows three phases:
• Model the active world by constructing structural
and then behavioral models.
• Select proper graph-based coverage criteria for
test-path generation and proper input-space par-
titioning coverage criteria for test-data.
• Generate AWTCs which are concurrent test paths
and then generate test-data to transform these
concurrent test paths into executable test cases.
4.1 Phase 1: World Models
4.1.1 Structural Model
The structural model is constructed using a UML
class diagram, where classes represent the urban dis-
aster actors including their important characteristics,
behavioral messages, and relationships. An urban dis-
Figure 3: Structural Model for Urban Disaster Scenes.
aster scene can be represented by a single snippet
”Urban Disaster Scene”. The urban disaster actors
are of six types: survivors, non-survivors, construc-
tions, rubble, debris, and hazards. The UML class
diagram that represents the urban disaster scene is
shown in Figur 3. The urban disaster actors are ag-
gregated into a Urban Disaster Scene snippet. Similar
actors are generalized to a single class. For instance,
Survivors and Non-survivors are generalized into Vic-
tim class. The number of involved disaster actors in
the Urban Disaster Scene is determined by their mul-
tiplicity relationship. Instances of the urban disaster
actors and examples of their behavioral messages are
illustrated in Table 1. We assume that only the USAR
robots perform in a snippet; these robots are not con-
sidered world actors as they are the SUT.
4.1.2 Behavioral Model
Although a wide range of behavioral models ex-
ists, we illustrate the behavioral model using Petri
Nets (PNs). The strength of PNs is that they can
Table 1: Instances of Urban Disaster Actors.
Class Actor Instance Behavioral Messages
Survivor human (child,
adult, and el-
derly) and an-
imal (pets)
child.stimulate(){return CO
2
}
child.isVisual(){return true}
child.getCondition(){return
trapped}
child.isAccessible(){return
true}
Non-
survivor
human body
and part.
body.isVisual(){return true}
body.isAccessible(){return
false}
body.getDescription(){return
”entombed body”}
Construction post, wall,
stair, elevator,
door, window,
and ramp
post.getState(){return ”hill &
safe”}
post.change(”diagonal &
unsafe”)
stairs.getState(){return
”sloppy”}
door.getState(){return ”acces-
sible”}
Rubble rock, brick,
and concrete.
rock.getState(){return ”tum-
bling”}
rock.getState(){return
”steady”}
concrete.getState(){return
”sloppy”}
Debris furniture,
pipe, wood,
rope, paper,
glass, and
plastic
table.getState(){return
”steady”}
pipe.getState(){return ”un-
steady”}
wood.getState(){return ”un-
steady”}
Hazard temperature,
electricity,
fire, and
explosion
temp.getSeverity(){return
”slight”}
elect.isManipulatable(){return
true}
model the functional behaviors of systems that are
characterized as being concurrent, asynchronous, dis-
tributed, parallel, nondeterministic, and/or stochastic
(Murata, 1989) and (David and Alla, 1994). For-
mally, a Petri Net is a 5-tuple, PN = (P, T, F, W,
M
0
) where P = {p
1
, p
2
, . . . , p
m
} is a finite set of
places, T = {t
1
, t
2
, . . . , t
n
} is a finite set of transitions,
F ⊆ (P× T)∪ (T × P) is a set of arcs (flow relation),
W : F → {1, 2, 3, . . . } is a weight function, M
0
: P ⊆
{0, 1, 2, 3, . . . } is the initial marking (the initial sys-
tem state), P ∩ T = φ and P ∪ T 6= φ. A Petri Net
structure N = (P, T, F, W) without any specific initial
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
666
marking is denoted by N. A Petri Net with the given
initial marking is denoted by (N, M
0
). Modeling be-
havioral models follows two steps. First, each urban
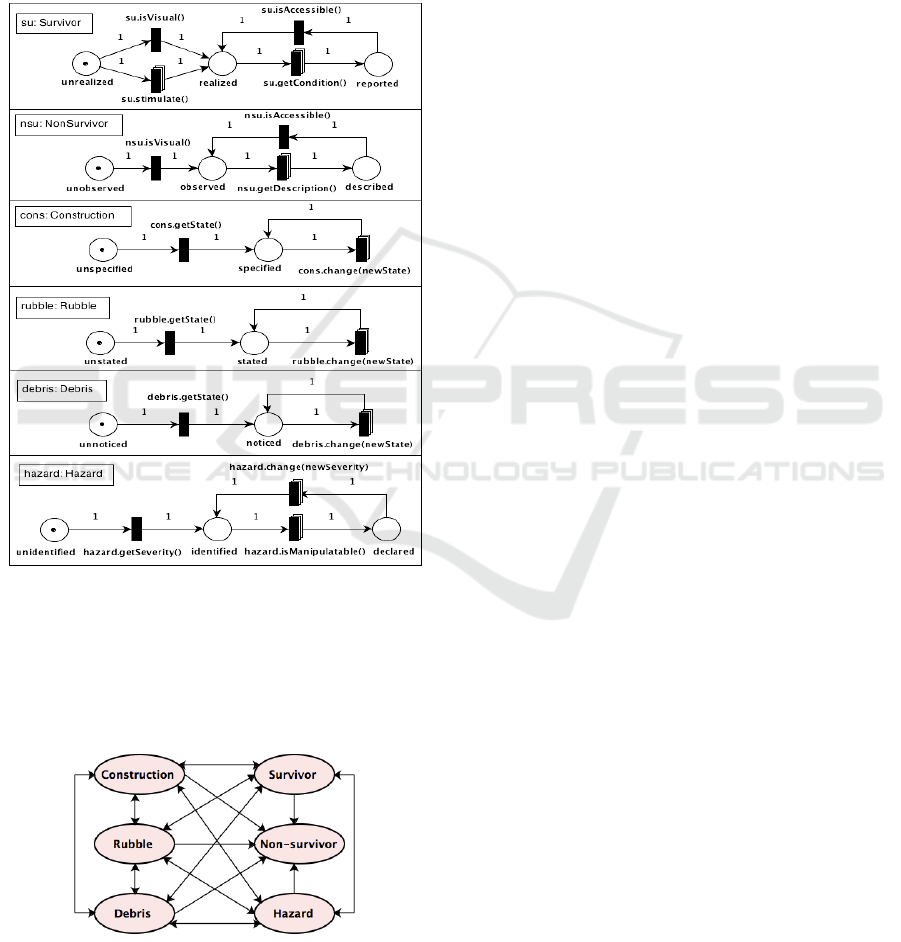
disaster actor is modeled individually. Figure 4 shows
a set of PNs that represent a group of urban disaster
actors, so-called actors processes. It is clear that these
actors processes act independently and concurrently.
As shown in Figure 4, in the top model, the survivor
process stimulates signs of life, or visuality. The non-
Figure 4: Behavioral Models for Urban Disaster Actors.
survivor process stimulates only visuality. The con-
struction process displays its state. The construction
state changes unpredictably. It is similar to other ac-
tors’ processes. The key difference is that the behav-
ioral messages of these processes are dissimilar. All
Figure 5: Behavioral Model (High-Level).
actor processes also report either the actors are acces-
sible or inaccessible. The hazard process reports the
hazard severity. The hazard also is considered as ma-
nipulatable or not manipulatable. Secondly, these be-
havioral models that represent the disaster actors are
linked together into a higher level behavioral model
which describes the interactions among these actors.
Figure 5 illustrates the high level behavioral model.
All disaster actors can interact with each other except
the non-survivor, it can only be affected by others.
4.2 Phase 2: Coverage Criteria
An active world behavioral model is de-
fined as a collection of concurrent processes
AWM = {PN
1
, PN
2
, . . . , PN
i
} where i is the number
of actors that share a snippet. Model-flow coverage
criteria such as node coverage and edge coverage
(Ammann and Offutt, 2008) and (Lill and Saglietti,
2012), can be applied. Using any of a number of
test path generation techniques, test paths that fulfill
these coverage criteria can be generated. Let TP
i
=
(tp
i1
, tp
i2
, ..., tp
ik
) be a set of such internal test paths
that cover a process, PN
i
, and k is the number of
these paths. These internal paths describe the internal
execution of the processes. We use transition-based
coverage (Lill and Saglietti, 2012) to generate inter-
nal paths that cover the processes of disaster actors.
The internal test paths that cover the disaster actors
processes are illustrated in Table 2. Transition-based
Coverage Criterion (TBCC) is defined as that given
a set of input-places P
in
and output-places P
out
for
TBCC, a test set TP
i
satisfies TBCC on a process PN
i
if and only if every p
in
i
∈ P
in
and p
out
j
∈ P
out
, there
is at least one internal test path tp
ij
∈ TP
i
such that
tp
ij
enables a sequence of transitions involved in the
execution of process PN
i
to be fired. The internal test
path sets, (TP
1
, TP
2
, TP
3
, TP
4
, TP
5
, TP
6
), interact
concurrently with each other via the exchange of
behavioral messages (i.e., interaction messages).
These interaction messages represent the high level
of execution behavior of the active world model, as
shown in behavioral model (High-Level), in Figure
5. The interaction among the processes can be
covered by interaction test paths which represent the
possibilities of execution behavior of these processes.
To avoid cyclic paths, simple-path coverage criterion
(Ammann and Offutt, 2008), is used to generate the
interaction test paths that cover the high level of
the behavioral model. The high level of the active
world model of the disaster actors is covered by 12
interaction test paths (ITP
1
, ITP
2
, . . . , ITP
12
). Each
interaction test path combines the internal test paths
of the processes that are involved in the interaction
scenario. For instance, the interaction test path
ITP
1
= (Construction : TP
3
) −→ (Hazard : TP
6
) −→
World Model for Testing Urban Search and Rescue (USAR) Robots using Petri Nets
667

Table 2: Internal Test Path Sets.
1. survivor process, TP
1
= {tp
11
, tp
12
}
tp
11
: unrealized
su.isVisual()
−−−−−−−→ realized
su.getCondition()
−−−−−−−−−−→
reported
su.isAccessible()
−−−−−−−−−→ realized
tp
12
: unrealized
su.stimulate()
−−−−−−−−→ realized
su.getCondition()
−−−−−−−−−−→
reported
su.isAccessible()
−−−−−−−−−→ realized
2. non-survivor process, TP
2
= {tp
21
}
tp
21
: unobserved
nsu.isVisual()
−−−−−−−→ observed
nsu.getDescription()
−−−−−−−−−−−→
described
nsu.isAccessible()
−−−−−−−−−−→ observed
3. construction process, TP
3
= {tp
31
}
tp
31
: unspecified
cons.getState()
−−−−−−−−→ specified
cons.change(newState)
−−−−−−−−−−−−−→
specified
4. rubble process, TP
4
= {tp
41
}
tp
41
: unstated
rubble.getState()
−−−−−−−−−→ stated
rubble.change(newState)
−−−−−−−−−−−−−−→
stated
5. debris process, TP
5
= {tp
51
}
tp
51
: unnoticed
debris.getState()
−−−−−−−−−→ noticed
debris.change(newState)
−−−−−−−−−−−−−−→
noticed
6. hazard process, TP
6
= {tp
61
}
tp
61
: unidenti fied
hazard.getSeverity()
−−−−−−−−−−−→
identified
hazard.isManipulatable()
−−−−−−−−−−−−−−→
declared
hazard.change(newSeverity)
−−−−−−−−−−−−−−−→ identified
(Survivor : TP
1
) covers the interaction between
the construction process, the hazard process, and
the survivor process. Thus, the internal paths
of this interaction are (tp
31
→ tp
61
→ tp
11
) and
(tp
31
→ tp
61
→ tp
12
). The interaction test paths
are considered concurrent paths. Therefore, the
concurrent interaction between internal test paths that
represent multiple processes produces an arbitrary
combination of internal paths. In order to cover all
possible combinations of internal paths, path combi-
nation coverage criteria should determine what com-
binations are required. Let (TP
1
, TP
2
, . . ., TP
n
) be
sets of internal test paths (nodes in ITP
i
) where TP
1
=
{tp
11
, tp
12
, . . ., tp
1k
}, TP
2
= {tp
21
, tp
22
, . . ., tp
2k
},
. . . , and TP
j
= {tp
j1
, tp
j2
, . . ., tp
jk
}. Then, the
selection of tp
1i
from TP
1
and tp
2j
from TP
2
is called a path combination. Let len(tp) be the
number of nodes in tp, the length of tp. The
combination set for interaction test path ITP
i
,
Comb
ITP
i
= {(tp
jk
, . . ., p
mn
)|tp
mn
∈ TP
m
, m =
len(ITP
i
), n = |TP
i
|, 1 ≤ j ≤ m, 1 ≤ k ≤ n}. The
number of all path combinations of ITP
i
will be
the product of the number of internal paths of
each TP
i
. Each combination introduces a set of
concurrent test paths. The path combination sets
do not show how these paths interact concurrently.
Therefor, we use the Rendezvous coverage crite-
rion (RCC), as in (Yang and Chung, 1990). The
test requirements contain a set of all paths that
have rendezvous nodes. The possible number of
rendezvous-paths of the interaction test path ITP
i
is
n
∏
i=1
(TP
i
+ 1) − 1. However, the generated concur-
rent test paths are still abstract. To transform
these concurrent test paths into executable test cases,
test-data coverage criteria, i.e. input-space parti-
tioning (Ammann and Offutt, 2008), are required.
We divide a collection of values (input-domain) into
test-data blocks that make the concurrent test paths
executable. The input-domain is the possible values
that input parameters (tokens in Petri Nets) can have.
The urban disaster snippet has ten input-domains:
survivor stimuli, survivor conditions, construction
types, construction states, rubble types, rubble states,
debris types, debris states, hazard types, and hazard
severity. The survivorstimuli block includes {motion,
body heat, sound, and CO
2
emission}. The survivor
conditions block consists of {aware, semi-conscious,
and unconscious}. The construction types block
consists of {posts, stairs, elevators, walls, doors,
windows, and ramps} while the rubble types block
consists of {rocks, bricks, and concretes}. The debris
types block includes {furniture, woods, ropes, wires,
pipes, papers, glasses, and plastics}. The construc-
tion states block consists of {flat, hill, diagonal,
pitch, roll, steady, unsteady, loose, sloppy, safe, and
unsafe}. In addition to the construction states block
values, the rubble and debris states blocks contain
{piled, scattered, tumbled}. The hazards block
includes {exothermic-fire, high-temperature, high-
voltage, and gas explosion}. The hazard severity
block consists of {minimal, slight, moderate, serious,
and sever}. We use All Combinations Coverage
(ACoC) which exercises all possible combinations
of test-data. The number of the test-data sets that
satisfy ACoC is
Q
∏
i=1
(B
i
), where B
i
is a block of values
for a parameter and Q is the number of parameters.
To compare with ACoC, we also use Each Choice
Coverage (ECC) that selects one value only from
each block of values. The number of the test-data
sets that satisfy ECC is MAX
Q
i=1
(B
i
) (Ammann and
Offutt, 2008).
4.3 Phase 3: Test Generation
The path combinations are represented as an ordered
references of internal test paths of the processes in-
volved in the execution. These combinations may
result in a huge number of concurrent test paths,
AWBTCs, although not all of these concurrent test
paths are feasible. We used the serialization algo-
rithm in (Yang and Chung, 1990) to generate these
concurrent test paths. The concurrent test paths
are serialized nodes of the internal paths. We ex-
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
668

pressed the concurrency of test paths using double-
bar ”||” as used in LOTOS for defining concurrent
function (Sighireanu et al., 2000). For instance,
ITP
1
= (Construction : TP
3
) −→ (Hazard : TP
6
) −→
(Survivor : TP
1
) generates two AWBTCs. When we
impose the RCC on these AWBTCs, it produces 11
rendezvous-path. We apply ACoC and ECC coverage
criteria to select test-data that fulfill these AWBTCs.
For each interaction test path ITP
i
, a set of test-data
is selected from blocks that are only related to the
actor processes involved in this ITP
i
. For instance,
for ITP
1
, six blocks (construction types, construction
states, hazard types, hazard severity, survivor stimuli,
and survivor conditions) are used to select test-data.
The ACoC results 18480 test-data set while the ECC
produces 11 test-data set. When this 18480 test-data
set is fulfilled in the 11 rendezvous-paths, this trans-
formation results 203280 executable test cases. Nev-
ertheless, the number of executable test cases gener-
ated by ECC with RCC is 121 test cases.
5 REACHABILITY & CRITERIA
EFFICIENCY
To perform reachability analysis on the behavioral
models, we use Platform-Independent Petri Net Ed-
itor (PIPE) (Dingle et al., 2009). For reachability
analysis, the reachability graph module that PIPE pro-
vides is used to generate all possible states that a sys-
tem can reach. For six disaster actor processes, the
generated reachability graph consists of 216 states in-
tensively interconnected by 1161 arcs. However, the
number of reachable states grows exponentially as the
number and the size of processes increase. For in-
stance, when these six processes are replicated to 12
processes, the number of reachable states expended to
13824 states with 161280 arcs which displaying them
in PIPE may not be feasible. However, CADP (Con-
struction and Analysis of Distributed Processes) tool-
box (Garavel et al., 2013) is more practicable due to
its scalability. CADP is scalable up to 10
13
node. In-
stead of investigating reachability, one can also use
Markov chain techniques for probabilistic. For cov-
erage criteria efficiency, we exercise all interaction
test paths, (ITP
1
, ITP
2
, . . . , ITP
12
). The total number
of executable test cases generated by the RCC with
ACoC is 58841115 test case while the RCC with ECC
generates 1878 test case. It is clear that using RCC
with ACoC is not feasible but it is considered as an
upper bound. Nevertheless, exploiting RCC on ECC
shows feasibility and efficiency.
6 CONCLUSION AND FUTURE
WORK
This paper presented the applicability of a model-
based test generation approach (Andrews et al., 2015)
that allows testing of autonomous systems in their ac-
tive world. We modeled an active world of the USAR
robots. A test generation process is applied. RCC
is used to generate AWBTCs. To transform the gen-
erated AWBTCs into executable test cases, we also
exploited ACoC and ECC coverage criteria to gener-
ate test-data. The findings show that exploiting RCC
on ECC is practically feasible. The PIPE tool is used
for reachability analysis. However, a display in PIPE
is no longer easily readable. Future work will ex-
periment using the CADP (Construction and Analy-
sis of Distributed Processes) toolbox (Garavel et al.,
2013). Future work will also explore other testing
techniques that can handle the scalability of concur-
rent processes. Comparison between experiments will
also be provided.
ACKNOWLEDGEMENTS
This work was supported, in part, by NSF IUCRC
grant # 0934413, 1127947, and 1332078 to the Uni-
versity of Denver.
REFERENCES
Ammann, P. and Offutt, J. (2008). Introduction to Software
Testing. Cambridge University Press, 32 Avenue of
the Americas, New York, NY 10013, USA, first edi-
tion.
Andrews, A., Abdelgawad, M., and Gario, A. (2015).
Towards world model-based test generation in au-
tonomous systems. In Proceedings of the 3rd In-
ternational Conference on Model-Driven Engineer-
ing and Software Development (MODELSWARD)
2015, MODELSWARD 2015, pages 165–176.
SCITEPRESS Digital Library.
Chiou, A. and Wynn, C. (2009). Urban search and res-
cue robots in test arenas: Scaled modeling of dis-
asters to test intelligent robot prototyping. In Sym-
posia and Workshops on Ubiquitous, Autonomic and
Trusted Computing, UIC-ATC, pages 200–205.
David, R. and Alla, H. (1994). Petri nets for modeling of dy-
namic systems: Survey. Automatica, 30(2):175–202.
Dias-Neto, A., Subramanyan, R., Vieira, M., and Travas-
sos, G. H. (2007). A survey on model-based test-
ing approaches: A systematic review. In Proceedings
of the 1st ACM International Workshop on Empirical
Assessment of Software Engineering Languages and
Technologies, WEASELTech ’07, pages 31–36. ACM.
World Model for Testing Urban Search and Rescue (USAR) Robots using Petri Nets
669

Dingle, N. J., Knottenbelt, W. J., and Suto, T. (2009).
PIPE2: A tool for the performance evaluation of gen-
eralised stochastic petri nets. SIGMETRICS Perform.
Eval. Rev., 36(4):34–39.
Ferworn, A., Herman, S., Tran, J., Ufkes, A., and Mcdon-
ald, R. (2013). Disaster scene reconstruction: Mod-
eling and simulating urban building collapse rubble
within a game engine. In Proceedings of the 2013
Summer Computer Simulation Conference, SCSC ’13,
pages 18:1–18:6, Vista, CA. Society for Modeling
& Simulation International.
Furda, A. and Vlacic, L. (2010). An object-oriented de-
sign of a world model for autonomous city vehicles.
In Intelligent Vehicles Symposium (IV), IEEE, pages
1054–1059.
Garavel, H., Lang, F., Mateescu, R., and Serwe, W. (2013).
CADP 2011: a toolbox for the construction and anal-
ysis of distributed processes. International Journal
on Software Tools for Technology Transfer, 15(2):89–
107.
Hessel, A., Larsen, K., Mikucionis, M., Nielsen, B., Pet-
tersson, P., and Skou, A. (2008). Formal methods and
testing. chapter Testing real-time systems using UP-
PAAL, pages 77–117. Springer-Verlag, Berlin, Hei-
delberg.
Iqbal, M., Arcuri, A., and Briand, L. (2010). Environ-
ment modeling with UML/MARTE to support black-
box system testing for real-time embedded systems:
Methodology and industrial case studies. In Model
Driven Engineering Languages and Systems, volume
6394 of Lecture Notes in Computer Science, pages
286–300. Springer Berlin Heidelberg.
Iqbal, M., Arcuri, A., and Briand, L. (2012). Empiri-
cal investigation of search algorithms for environment
model-based testing of real-time embedded software.
In Proceedings of the 2012 International Symposium
on Software Testing and Analysis, ISSTA 2012, pages
199–209, New York, NY, USA. ACM.
Jacoff, A., Messina, E., Weiss, B., Tadokoro, S., and Naka-
gawa, Y. (2003). Test arenas and performance metrics
for urban search and rescue robots. In Proceedings
of the IEEE International Conference on Intelligent
Robots and Systems (IROS), volume 4, pages 3396–
3403 vol.3.
Li, J. and Wong, W. (2002). Automatic test generation
from communicating extended finite state machine
(CEFSM)-based models. In Proceedings of 5th IEEE
International Symposium on Object-Oriented Real-
Time Distributed Computing. (ISORC 2002), pages
181–185.
Lill, R. and Saglietti, F. (2012). Model-based testing of
autonomous systems based on coloured petri nets. In
ARCS Workshops (ARCS), pages 1–5.
Liu, Y. and Nejat, G. (2013). Robotic urban search and res-
cue: A survey from the control perspective. Journal
of Intelligent and Robotic Systems, 72(2):147–165.
Murata, T. (1989). Petri nets: Properties, analysis and ap-
plications. Proceedings of the IEEE, 77(4):541–580.
Murphy, R., Tadokoro, S., Nardi, D., Jacoff, A., Fiorini,
P., Choset, H., and Erkmen, A. (2008). Search and
rescue robotics. In Siciliano, B. and Khatib, O., ed-
itors, Springer Handbook of Robotics, pages 1151–
1173. Springer Berlin Heidelberg.
Pepper, C., Balakirsky, S., and Scrapper, C. (2007). Robot
simulation physics validation. In Proceedings of the
2007 Workshop on Performance Metrics for Intelli-
gent Systems, PerMIS ’07, pages 97–104, New York,
NY, USA. ACM.
Shirole, M. and Kumar, R. (2013). Uml behavioral model
based test case generation: A survey. Softw. Eng.
Notes, SIGSOFT, 38(4):1–13.
Sighireanu, M., Chaudet, C., Garavel, H., Herbert, M., Ma-
teescu, R., and Vivien, B. (2000). Lotos NT user man-
ual.
Tretmans, J. (2008). Model based testing with labelled
transition systems. In Hierons, R., Bowen, J., and
Harman, M., editors, Formal Methods and Testing,
volume 4949 of Lecture Notes in Computer Science,
pages 1–38. Springer Berlin Heidelberg.
Utting, M., Pretschner, A., and Legeard, B. (2012). A
taxonomy of model-based testing approaches. Softw.
Test. Verif. Reliab., 22(5):297–312.
Williamson, D. and Carnegie, D. (2007). Toward hierar-
chical multi-robot urban search and rescue: Develop-
ment of a ’mother’ agent. In Mukhopadhyay, S. and
Gupta, G., editors, Autonomous Robots and Agents,
volume 76 of Studies in Computational Intelligence,
pages 1–7. Springer Berlin Heidelberg.
Yang, R. and Chung, C.-G. (1990). A path analysis ap-
proach to concurrent program testing. In Proceedings
of the 9th Annual International Phoenix Conference
on Computers and Communications, pages 425–432.
Zander, J., Schieferdecker, I., and Mosterman, P. J. (2012).
Model-based testing for embedded systems. CRC
Press, 6000 Broken Sound Parkway NW,Boca Raton,
FL 3348, USA, first edition.
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
670
