
Exploiting the Kinematic of the Trajectories of the Local Descriptors to
Improve Human Action Recognition
Adel Saleh
1
, Miguel Angel Garcia
2
, Farhan Akram
1
, Mohamed Abdel-Nasser
1
and Domenec Puig
1
1
Department of Computer Engineering and Mathematics, Rovira i Virgili University, Tarragona, Spain
2
Department of Electronic and Communications Technology, Autonomous University of Madrid, Madrid, Spain
Keywords:
Activity Recognition, Kinematic Features, Classification.
Abstract:
This paper presents a video representation that exploits the properties of the trajectories of local descriptors in
human action videos. We use spatial-temporal information, which is led by trajectories to extract kinematic
properties: tangent vector, normal vector, bi-normal vector and curvature. The results show that the pro-
posed method provides comparable results compared to the state-of-the-art methods. In turn, it outperforms
compared methods in terms of time complexity.
1 INTRODUCTION
Human action recognition is still an open challeng-
ing problem in computer vision community. The per-
formance of applications, such as surveillance sys-
tems (Ben Aoun et al., 2011) and human-computer
interaction (Bouchrika et al., 2014) mainly depend
on the accuracy of human activity recognition sys-
tems. Several methods were proposed to improve the
performance of human action recognition in uncon-
trolled videos. Bag of words (BOW) based on a set
of low level features, such as histogram of optical
flow (HOF), histogram of oriented gradients (HOG)
and motion boundary histograms (MBH) have be-
come very common video representation for action
recognition (Laptev et al., 2008). These models are
insensitive to the position and orientation of the ob-
jects in the image. In addition, they have fixed length
vectors irrespective to the number of objects and num-
ber of frames in each video. These aforementioned
methods are independent of usage of explicit config-
uration of visual word. Moreover, they have a poor
localization of the objects and actions in the videos.
The use of the local information is very useful to im-
prove the recognition rate (Peng et al., 2014).
In this paper we used the kinematic features of
the trajectories of the local descriptors to improve the
performance of the current super-vector based activ-
ity recognition methods. For each local descriptor, a
trajectory is defined, then a set of kinematic features
are calculated, such as tangent vector, normal vector,
bi-normal vector and curvature. The steps of the pro-
posed method are shown in Figure 1. The rest of the
paper is organized as follows. In Section 2 we review
related work. In section 3 the mathematical formula-
tions and functioning of the proposed method are ex-
plained. Section 4 includes the experimental results
and discussion. Finally, the conclusion of this paper
is given in section 5.
2 RELATED WORK
Several works showed that the performance of human
recognition methods can be improved significantly
while using the trajectory of the spatio-temporal inter-
est points (Wang et al., 2009). In (Wang et al., 2011)
trajectories were used as features to build a code-
book of visual words. They proposed a robust method
Figure 1: The proposed approach.
182
Saleh, A., Garcia, M., Akram, F., Abdel-Nasser, M. and Puig, D.
Exploiting the Kinematic of the Trajectories of the Local Descriptors to Improve Human Action Recognition.
DOI: 10.5220/0005781001800185
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 182-187
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

to get information of trajectory shape by tracking
densely sampled points using the optical flow fields.
In (Wang et al., 2013) Fisher coding is compared with
other encoding methods. It provided better results
in action recognition. In (Jain et al., 2013) an im-
proved method using motion stabilization and person
trajectories is demonstrated. In (Raptis and Soatto,
2010) parts from different grouping trajectories were
embedded into a graphical model. In (Sekma et al.,
2013) the Delaunay triangulation method is applied
on the trajectories of each video to get geometric re-
lationship of objects. A graph is built for trajectories
and then encoded (this method is also known as bag-
of-graphs).
Many works were dedicated to describe the shape
of the area around the trajectory, local motion and
appearance pattern. The common methods are:
histograms of optical flow (HOF) (Laptev et al.,
2008), motion boundary histograms (MBH) (Dalal
et al., 2006) and histograms of oriented gradients
(HOG) (Dalal and Triggs, 2005). After extracting the
features and encoding them, a codebook is built using
a clustering algorithm, such as k-means. In (Wang
and Schmid, 2013) the authors showed that camera
motion compensation and removal of the inconsistent
matches generated by human motion can greatly im-
prove the performance of the dense trajectories. They
used the Fisher vector (FV) (S
´
anchez et al., 2013) to
generate a representation for each video. However,
the previous approaches only consider simple trajec-
tory information. The proposed method uses the kine-
matic features of trajectories to improve the perfor-
mance of activity recognition methods.
The proposed work is inspired by (Wang et al.,
2015) in which they extracted Frenet-Serret frames
(see Section 3.5 for its definition) from the trajecto-
ries then histograms of tangent vector and normal,
bi-normal vector were used to overcome the depen-
dency on the trajectory length. After that they clus-
tered videos using histograms. In their work, they did
not discuss the performance of these features in ac-
tivity recognition. In (Jain et al., 2013) the authors
used kinematic features of the flow field to capture
additional information about motion patterns. The
proposed method is different from the technique dis-
cussed in (Wang et al., 2015) because in it kinematic
features of the trajectory (tangent vector, binormal
vector an curvature) is applied rather than histograms.
The proposed method exploits the improved trajec-
tories of the same length and then combines them
with low level features like HOF, HOG and MBH.
Compared to the proposed method, the CNN based
method (Simonyan and Zisserman, 2014) is better in
terms of accuracy but it has high time complexity be-
cause it needs a large number of training samples with
supervised labels.
3 PROPOSED APPROACH
The main idea of the proposed approach is that we are
getting complementary information like motion, ac-
celeration and curvature, which gives useful descrip-
tion of the trajectory. The improvements in results
leads to the conclusion that modeling the trajectories
of low-level features statistically enhance the recog-
nition performances of the concepts in videos.
3.1 Improved Dense Trajectories
In the proposed method, the low-level motion features
are calculated using the same configuration proposed
in (Wang and Schmid, 2013). It uses dense sampled
features for several spatial scales, estimate a homog-
raphy with RANSAC using the SURF feature match-
ing between two consecutive frames. Then it warps
optical flow with the estimated homography. The
calculated low-level descriptor is computed on the
warped optical flow to capture motion patterns. Ad-
ditional improvement is obtained by using a human
detector because it removes the trajectories which are
consistent with camera motion compensation.
Default parameters are supposed to extract all
low-level feature descriptors, such as HOG, HOF,
MBHx, MBHy and trajectory. The length of utilized
trajectories is 15 frames. The dimensions of descrip-
tors are : 96 for HOG, 108 for HOF, 96 for MBHx ,
96 for MBHy and 30 for trajectory.
3.2 Gradient and Optical Flow
Histograms
According to (Wang et al., 2009), HOG and HOF de-
scriptors show good results on a different data-sets
compared to classical descriptors for activity recog-
nition. Unlike HOG descriptor which captures infor-
mation about the appearance, HOF captures the lo-
cal motion information. The proposed method com-
puted the HOG and HOF descriptors using the same
approach proposed in (Wang and Schmid, 2013). To
calculate HOG, the proposed method computed gra-
dient magnitude responses in the horizontal and ver-
tical directions. To calculate HOF, optical flow dis-
placement vectors in horizontal and vertical direc-
tions were determined. As a result we have a 2D
vector field per frame. Then for each response the
magnitude is quantized in number of orientations.
For HOG descriptor, orientations are quantized into
Exploiting the Kinematic of the Trajectories of the Local Descriptors to Improve Human Action Recognition
183

8 bins, while they are quantized into 9 bins for HOF
as given in (Laptev et al., 2008). We used l2-norm
to normalize the descriptors. The length of HOG and
HOF is 96 (2 ×2 ×3 ×8) and 108 (2 ×2 ×3 ×9),
respectively.
3.3 Motion Boundary Histograms
Descriptor
MBH is popular descriptor for video classification
tasks (Dalal et al., 2006). In their work, they showed
the robustness of the descriptor against camera and
background motion. The intuition behind MBH is
computing oriented gradients over the vertical and the
horizontal optical flow displacements. The superi-
ority of this representation is that camera and opti-
cal flow differences between frames (motions bound-
aries) boosted in the same time. Actually, the opti-
cal flow’s horizontal and vertical displacements are
mapped, so they can be treated as gray-level images
of the motion displacements. For each of the two
optical flow component images, histograms of ori-
ented gradients are computed using the same config-
uration used for still images. Information related to
motion changes in the boundaries is attained using
the flow difference, while information with constant
scene from the camera is discarded.
3.4 Theoretical Background to
Calculate Moving Frames
Suppose that we have a curve which describes a tra-
jectory, as follows:
r(t) = (x(t), y(t),z(t)) (1)
Then the tangent vector to the curve at the point where
is:
v(t) = r
0
(t) = (x
0
(t),y
0
(t),z
0
(t)) (2)
Some researchers call it velocity vector and length of
it is called speed (Figure 2). Derivative vector of unit
length is especially important. It is called the unit tan-
gent vector and is obtained by dividing the derivative
vector by its length:
T (t) =
(x
0
(t),y
0
(t),z
0
(t))
r
0
(t)
(3)
also,
T (t) =
v(t)
|v(t)|
(4)
Since T (t) is a unit vector, then
T (t)T (t) = 1 (5)
Figure 2: The velocity vector.
Figure 3: The osculating plane defined by tangent and nor-
mal vectors and the direction of binormal vector.
For all values of t, if we calculate the differentia-
tion of both sides of this equation we find that
2T
0
(t)T (t) = 0 (6)
Thus T
0
(t) and T (t) are always orthogonal for
each value of t. We define that unit normal as follows.
N(t) =
T
0
(t)
|T
0
(t)|
(7)
For each point we can span a plane using T and
N, this plane called osculating plane (see Figure 3). If
we are dealing with 2D motion, then z(t) = 0. Obvi-
ously, that normal vector and osculating plane are not
defined when T
0
(t) = 0. The derivative of the velocity
vector is called acceleration vector.
a(t) = a
T
(t)T (t) + a
N
(t)N(t) (8)
This vector has the same direction as the force
needed to keep the particle on the track of the curve.
This force makes a particle traveling along curve to
stay on this course. Without this force, such particle
would continue the motion as indicated by the veloc-
ity vector and not stay on the course of r(t). The ac-
celeration vector lies on the osculating plane too.
Suppose that r (t) is a circle of radius ρ centered at
(0,0).
r(t) = ρ(cos(ωt), sin(ωt)) (9)
The velocity is v(t) = pω(−sin(ωt), cos(ωt)), the
speed is |v(t)| = pω = v
0
, the unit tangent vector is
T (t) = v(t)/|v(t)| = (−sin(ωt), cos(ωt)) and the unit
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
184
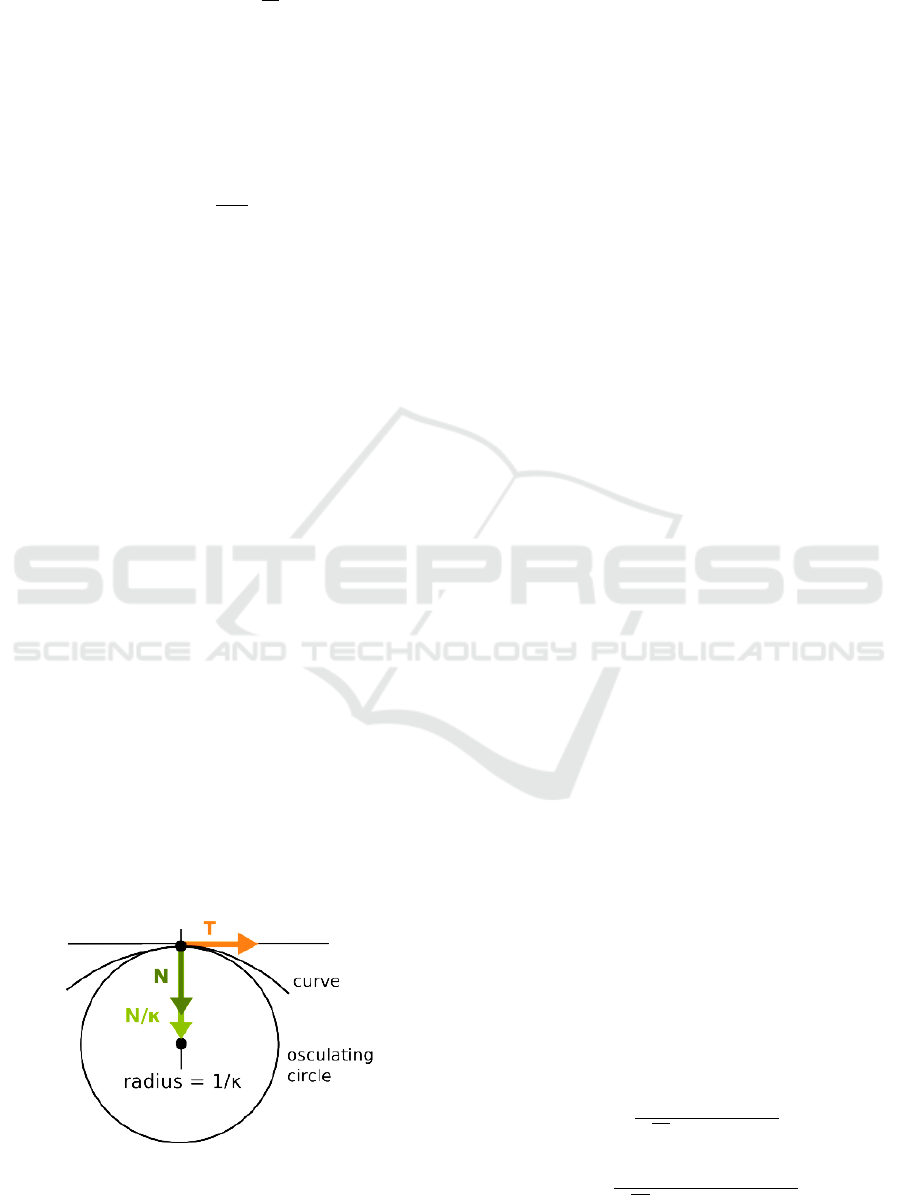
normal vector is N = (−sin(ωt),cos(ωt)). Since the
speed is constant, then a
T
(t) =
d
dt
v(t) = 0. There is
no acceleration in the tangential direction. Hence, the
whole acceleration should be in the normal direction,
which can be described with the following two equa-
tions.
a = ρω
2
(−cos(ωt),−sin(ωt)) = ρω
2
N (10)
and
a =
Nv
2
0
ρ
(11)
Hence a
N
(t) = v
2
0
/ρ. One can get ρ at t = t
0
as
follows.
ρ = |r
0
(t
0
)|/|T
0
(t
0
)| (12)
The radius of the circle of the motion can be found
from Eq. 12. The circle of the motion is called oscu-
lating circle. The reciprocal of the radius is called
curvature at t = t
0
(see Figure 4). The curvature can
be defined as follows.
k = |T
0
(t
0
)|/|r
0
(t
0
)| (13)
3.5 Moving Frame
Bi-normal vector is defined as cross product of T and
N. Obviously, B is perpendicular to both T and N and
its unit vector since T and N are of have length 1. N
and B determine a plane which is called the normal
plane (see Figure 4). All lines in the normal plane are
perpendicular to the tangent vector T.
In literature, it is agreed to call the triple (T, N,
B) moving frame (it is also known as FrenetSerret
frame). The moving frame (T,N,B) is an orthonormal
basis, that means that each vector is of unit length,
and each pair of them are perpendicular, so every
three dimensions vector can be represented using a
linear combination of these three components. Con-
sequently, they take over the role of the usual basis
vectors k = (0,0,1), i = (1,0,0), j = (0,1, 0) at a point
on the curve.
Figure 4: The relation between osculating circle and curva-
ture.
3.6 From Trajectories to Moving
Frames
Let r = {r(1),.. ., r(t), ... ,r(n)} be a trajectory in 2D
space in which r(t) represents the positions of a mov-
ing point in t
th
video frame and n is the length of the
trajectory. Since we exploit improved dense trajecto-
ries (Wang and Schmid, 2013), all trajectories have
the same length. For each trajectory, the proposed
method calculates the moving frame (T, N,B) and the
curvature k. Then it builds a codebook for the con-
catenated vectors of (T,N, B,k). Likewise, it does
with HOF, HOG and MBH.
Obviously, the calculated descriptors extract
meaningful information from the trajectory which
does not depend on the original location of tracked
point. The good thing that information which is ex-
tracted from trajectory can cover descriptions in both
3D and 2D spaces. Furthermore, the 3D trajectory is
able to accurately describe the spatial and temporal
relations among the multiple trajectories. Generally,
image data suffers from the motion confusion caused
by the possibly different viewpoints in visual pro-
jection but it is still very useful for 2D applications.
Therefore, the overall descriptor consists of concate-
nation of HOF, HOG, MBH and kinematic features
(moving frame + curvature).
3.7 Fisher Vector
In pattern recognition, Fisher vector (FV) coding was
derived from well know Fisher Kernel, which is based
on the assumption that generation process of local
descriptor X can be modeled by a probability den-
sity function p(X,θ). Using the gradient of the log-
likelihood it is possible to describe the way that pa-
rameters contribute to the generation process of X.
Then the sample can be described as:
G
X
θ
= ∇
θ
log(p(X; θ))/N (14)
The dimensionality of this vector depends on the
number of parameters in θ. Gaussian mixture model
(GMM) is used to model the probability density func-
tion, and θ = {π
1
,µ
1
,σ
1
.. ., π
K
,µ
K
,σ
K
} contains the
parameters of the model,were π,µ,σ are Gaussian
mixture weights, means and diagonal covariance, re-
spectively. An improved Fisher Vector (Perronnin
et al., 2010) was proposed as follows.
ρ
k
=
1
√
π
k
γ
k
(x −µ
k
)/σ
k
(15)
τ
k
=
1
√
π
k
((x −µ
k
)
2
/σ
2
k
−1)
(16)
Exploiting the Kinematic of the Trajectories of the Local Descriptors to Improve Human Action Recognition
185

where γ
k
is the weight of local descriptor x to k
th
Gaussian component, so
m = π
1
N(x; µ
1
;σ
1
) + ···+ π
k
N(x; µ
k
;σ
k
) (17)
The parameter γ can be determined as follows.
γ
k
= π
k
N(x; µ
k
;σ
k
)/m (18)
FV is a result of concatenation of the gradients of
Eq 15 and 16 as follows.
FV = [ρ
1
,τ
1
,. .. ,ρ
K
,τ
K
] (19)
4 EXPERIMENTAL RESULTS
AND DISCUSSION
4.1 Data-set
HMDB51 data-set, which is a generic action classifi-
cation data-set (Kuehne et al., 2011) is used in this pa-
per. Videos in this data-set were collected from differ-
ent sources: YouTube and movies. It contains around
6670 videos, which are further grouped in 51 action
classes in which each class contains around 100. To
measure the performance we follow the original eval-
uation protocol. We used three training and testing
splits and the average accuracy over the three splits is
computed.
4.2 Experiments Setup
In our experiments, we adopt improved dense trajec-
tory features used in (Wang and Schmid, 2013). To
implement the kinematic model, we build 256 Gaus-
sian mixture models and use them to cluster randomly
taken 250,000 samples for each type separately. The
resulting GMM models were used to build a FV for
each descriptors type of low level vectors. The fisher
vectors were concatenated and send to a classifier. We
use a SVM classifier with RBF (χ
2
kernel) for classi-
fication. Since, the motion is 2D, we took first two
dimensions from tangent and normal vectors and the
third dimension from bi-normal vector for each tra-
jectory. Since, the improved length of trajectory is
15 (by default), therefore; trajectory descriptor has
90 dimensions (30 from the tangent vector, 30 from
the normal, 15 from the bi-normal and 15 from the
curvature). For dimension reduction and correlation
removal an algorithm based on principle component
analysis (PCA) before building FV. The PCA factor
is set to 0.5.
In this work a complementary descriptor is de-
signed by using the trajectories of the local descrip-
tors. It utilizes the spatio-temporal data of the tra-
jectories, and extracts additional information about
Table 1: Comparison of the baseline methods with the pro-
posed approach using the HMDB51 data-set.
Method Accuracy
(Yang and Tian, 2014) 26.90%
(Wang and Schmid, 2013) 57.20%
(Hou et al., 2014) 57.88%
(Simonyan and Zisserman, 2014) 59.50%
Proposed approach 58.20%
the shape of trajectories. The proposed method en-
hances the recognition performance of concepts in
videos. CNN based model has a better performance
because it represents higher level semantic concept
but it has high time complexity and requires compli-
cated training passes in the training step. In turn, the
proposed method is faster than (Simonyan and Zis-
serman, 2014). It took approximately 1 day for one
temporal CNN on a system with four NVIDIA Titan
cards (it took 3.1 times the aforementioned training
time on single GPU). In turn, our approach took ap-
proximately 14 hours on Core i7 2.5GHz CPU with
16 GB RAM. This certifies that our approach gives
comparable results with small training time.
5 CONCLUSION
In this paper a new method to recognize human ac-
tion in videos is proposed. It exploits the trajecto-
ries information extracted from the motion frames.
The proposed method calculates tangent, normal, bi-
normal and curvature then combines them with clas-
sical low level features. The proposed approach gives
better description for geometrical shape of the trajec-
tories and shows comparable results with the stateof-
the-art. The performance of the proposed method is
evaluated by using a complex and large-scale action
data-set HMDB51. Experimental results demonstrate
that the proposed approach is comparable with several
state-of-the-art methods as shown in Table 1.
ACKNOWLEDGMENTS
This work was partially supported by Hodeida Uni-
versity, Yemen and Univesity Rovira i Virgili, Tarrag-
ona, Spain.
REFERENCES
Ben Aoun, N., Elghazel, H., and Ben Amar, C. (2011).
Graph modeling based video event detection. In 2011
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
186

International Conference on Innovations in Informa-
tion Technology (IIT), pages 114–117. IEEE.
Bouchrika, T., Zaied, M., Jemai, O., and Amar, C. B.
(2014). Neural solutions to interact with computers
by hand gesture recognition. Multimedia Tools and
Applications, 72(3):2949–2975.
Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-
dients for human detection. In IEEE Computer Society
Conference on Computer Vision and Pattern Recogni-
tion (CVPR), volume 1, pages 886–893. IEEE.
Dalal, N., Triggs, B., and Schmid, C. (2006). Human de-
tection using oriented histograms of flow and appear-
ance. In Computer Vision–ECCV 2006, pages 428–
441. Springer.
Hou, R., Zamir, A. R., Sukthankar, R., and Shah, M.
(2014). Damn–discriminative and mutually nearest:
Exploiting pairwise category proximity for video ac-
tion recognition. In Computer Vision–ECCV 2014,
pages 721–736. Springer.
Jain, M., J
´
egou, H., and Bouthemy, P. (2013). Better ex-
ploiting motion for better action recognition. In 2013
IEEE Conference on Computer Vision and Pattern
Recognition (CVPR), pages 2555–2562. IEEE.
Kuehne, H., Jhuang, H., Garrote, E., Poggio, T., and Serre,
T. (2011). Hmdb: a large video database for human
motion recognition. In IEEE International Conference
on Computer Vision (ICCV), pages 2556–2563. IEEE.
Laptev, I., Marszałek, M., Schmid, C., and Rozenfeld,
B. (2008). Learning realistic human actions from
movies. In IEEE Conference on Computer Vision and
Pattern Recognition (CVPR), pages 1–8. IEEE.
Peng, X., Wang, L., Wang, X., and Qiao, Y. (2014). Bag of
visual words and fusion methods for action recogni-
tion: Comprehensive study and good practice. arXiv
preprint arXiv:1405.4506.
Perronnin, F., S
´
anchez, J., and Mensink, T. (2010). Improv-
ing the fisher kernel for large-scale image classifica-
tion. In Computer Vision–ECCV 2010, pages 143–
156. Springer.
Raptis, M. and Soatto, S. (2010). Tracklet descriptors for
action modeling and video analysis. In Computer
Vision–ECCV 2010, pages 577–590. Springer.
S
´
anchez, J., Perronnin, F., Mensink, T., and Verbeek, J.
(2013). Image classification with the fisher vector:
Theory and practice. International journal of com-
puter vision, 105(3):222–245.
Sekma, M., Mejdoub, M., and Amar, C. B. (2013). Hu-
man action recognition using temporal segmentation
and accordion representation. In Computer Analysis
of Images and Patterns, pages 563–570. Springer.
Simonyan, K. and Zisserman, A. (2014). Two-stream con-
volutional networks for action recognition in videos.
In Advances in Neural Information Processing Sys-
tems, pages 568–576.
Wang, H., Kl
¨
aser, A., Schmid, C., and Liu, C.-L. (2011).
Action recognition by dense trajectories. In IEEE
Conference on Computer Vision and Pattern Recog-
nition (CVPR), pages 3169–3176. IEEE.
Wang, H. and Schmid, C. (2013). Action recognition with
improved trajectories. In IEEE International Confer-
ence on Computer Vision (ICCV), pages 3551–3558.
IEEE.
Wang, H., Ullah, M. M., Klaser, A., Laptev, I., and Schmid,
C. (2009). Evaluation of local spatio-temporal fea-
tures for action recognition. In British Machine Vision
Conference (BMVC), pages 124–1. BMVA Press.
Wang, L., Qiao, Y., and Tang, X. (2013). Motionlets: Mid-
level 3d parts for human motion recognition. In IEEE
Conference on Computer Vision and Pattern Recogni-
tion (CVPR), pages 2674–2681. IEEE.
Wang, W.-C., Chung, P.-C., Cheng, H.-W., and Huang, C.-
R. (2015). Trajectory kinematics descriptor for trajec-
tory clustering in surveillance videos. In IEEE Inter-
national Symposium on Circuits and Systems (ISCAS),
pages 1198–1201. IEEE.
Yang, X. and Tian, Y. (2014). Action recognition using su-
per sparse coding vector with spatio-temporal aware-
ness. In Computer Vision–ECCV 2014, pages 727–
741. Springer.
Exploiting the Kinematic of the Trajectories of the Local Descriptors to Improve Human Action Recognition
187
