
Towards High-Quality Parallel Stabilization
Abdelrahman Ahmed and Mohamed S. Shehata
Department of Electrical and Computer Engineering, Memorial University of Newfoundland, St. John’s, Canada
Keywords:
Stabilization, Parallel Architecture, Handheld Devices, UAV.
Abstract:
With the widespread use of handheld devices and unmanned aerial vehicles (UAVs) that has the ability to
record video sequences. Digital video stabilization becomes more important as these sequences are usually
shaky undermining the visual quality of the video. Digital video stabilization has been studied for decades
yielding an extensive amount of literature in the field. However, most of them are highly sequential. In this
paper, we present a new parallel technique that exploits the parallel architecture found in modern day devices.
The algorithm divides the frame into blocks and estimates a camera path for each block to better enhance the
estimation of the transformation needed to adjust for the shakiness of the video.
1 INTRODUCTION
The introduction of digital cameras in cell phones and
the spread of unmanned aerial vehicles (UAVs) made
the capture of video sequences much easier. How-
ever, these sequences usually suffer from undesired
high frequency jittering due to the movement of the
camera holder or the movement of the UAV platform.
This jittering result in video sequences with poor vi-
sual quality, plus it undermines the use of other algo-
rithms used for object detection and tracking which
are vital in many video applications (e.g., surveillance
systems, search and rescue .. etc.). The aim of digital
video stabilization is to remove the unwanted jittering
producing sequences with better quality.
Digital video stabilization has been studied for years
in the field of computer vision. Generally, Stabiliza-
tion algorithms perform three main operations: 1) Es-
timating the camera motion (shaky path), 2) Estimate
new smooth camera path, 3) Refine the original shaky
path using the smoothed one. Digital video stabi-
lization approaches fall broadly into two categories
based on the motion estimation model: 1) 2D Stabi-
lization, 2) 3D Stabilization. The 2D methods (Mat-
sushita et al., 2006; Grundmann et al., 2011) estimate
a linear transformation either affine or homography
between successive frames. And the camera path is
formed by the concatenation of the linear transfor-
mations. In general these methods are robust and
fast. However, they suffer a limitation as they can-
not deal with the parallax caused by depth informa-
tion in the scene. 3D methods (Liu et al., 2012; Liu
Figure 1: Block diagram of the proposed algorithm.
et al., 2009)on the opposite hand can handle the par-
allax induced by the depth information and produce
highly stable sequences. However, their motion esti-
mation model is complex and less robust than the 2D
methods. Recent approaches tried to combine both
benefits of the 2D and 3D as shown in (Goldstein and
Fattal, 2012) by employing the concepts of epipolar
geometry. However, these methods require tracking
features for long period of time which can be difficult
in sequences with rapid motion or occlusion.
This paper falls in the first category aiming to pro-
vide robust and high quality stable sequences from 2D
linear transformations. This paper contribution is in
two folds. 1) We propose a novel algorithm in the
estimation of the frame trajectory. Specifically, the
proposed algorithm divides the image into blocks and
maintains the trajectory for each block so that each
block has its own camera path, then for any given
frame the paths of its blocks are combined to give
a better estimation for its transformation. Figure 1
summarizes the proposed algorithm. 2) Unlike, most
of the algorithms in the literature, the proposed al-
Ahmed, A. and Shehata, M.
Towards High-Quality Parallel Stabilization.
DOI: 10.5220/0005765306650670
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 667-672
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
667
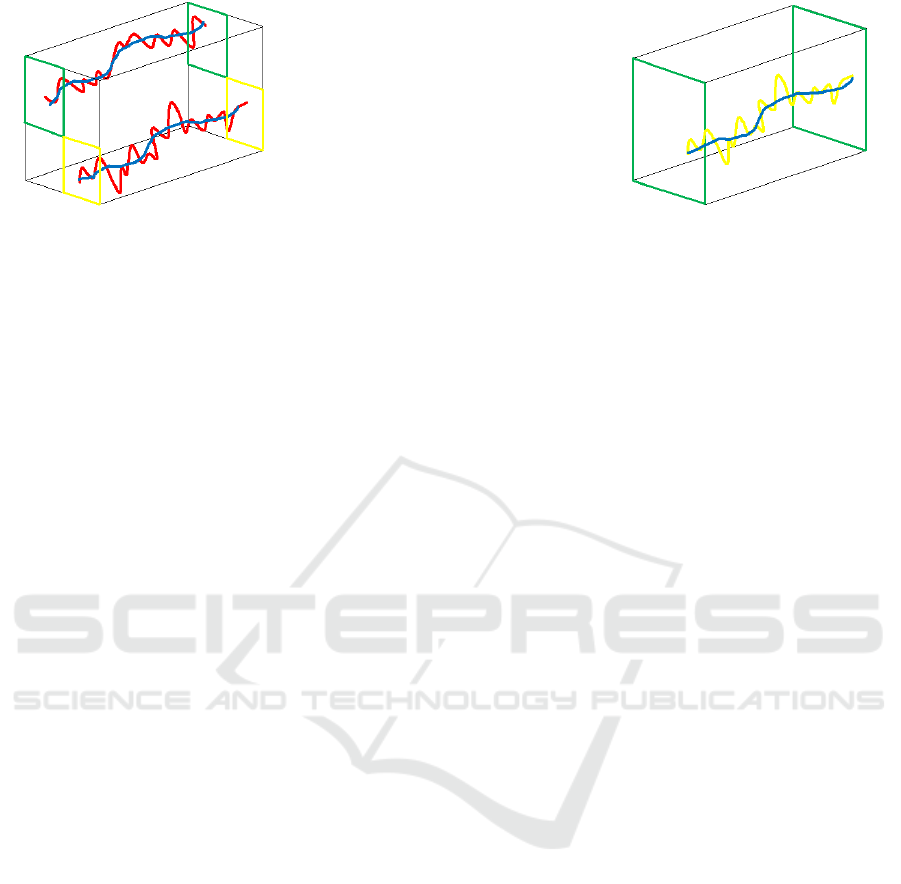
(a) Original block shaky path in red,
smoothed path for the block in blue.
(b) Original frame path in yellow,
smoothed path for the frame in blue.
Figure 2: Camera paths.
gorithm is highly parallelizable exploiting the paral-
lel architecture found in modern computers and hand-
held devices ensuring real time performance. The re-
mainder of this paper is organized as follows: related
work is presented in section 2; a detailed description
of the proposed algorithm is presented in Section 3,
followed by the evaluation criteria and results in Sec-
tion 4. A discussion of the results is presented in sec-
tion 5. Finally, Section 6 concludes the paper and di-
rects future work.
2 RELATED WORK
Stabilization methods can be categorized into two
main categories: 1) 2D Methods, 2) 3D methods.
The 2D methods estimates linear transformations
(affine or homography) between successive frames
and smooth the trajectory over time to produce a sta-
bilized video. Wang et al.(Wang et al., 2011) as-
sumes the motion model fit a polynomial curve e.g.
a cubic curve to smooth the parameters. Irani et
al. (Irani et al., 1994) deals with complex video se-
quences and attempts to estimate a homography trans-
formation which stabilizes a dominant planar region
in the video. Matsushita et al.(Matsushita et al., 2006)
extends the stabilized frames to become full frames
and apply low pass filter for smoothing the parame-
ters over time. Grundmann et al. (Grundmann et al.,
2011) proposes the application of L1- norm optimiza-
tion model to smooth the camera path to follow cin-
ematography rules. This technique was integrated
into Googles YouTube. 3D methods require the re-
covery of structure from the video sequence includ-
ing 3D camera poses and depth structures. These
structures can computed using Structure from motion
(SFM) techniques (Agarwal et al., 2011; Furukawa
et al., 2010; Jiang et al., 2012; Wu, 2013). Buehler
et al.(Buehler et al., 2001) computes SFM in a gen-
eral un-calibrated camera setting and solved using the
bundle adjustment method (Triggs et al., 2000). Liu
et al. (Liu et al., 2009) proposes a full 3D stabiliza-
tion method by introducing content-preserving warps
for the novel view synthesis. Liu et al. (Liu et al.,
2012) uses a depth camera to recover depth infor-
mation and perform 3D video stabilization. Since
3D reconstruction of a full video is still challenging.
Goldstein and Fattal (Goldstein and Fattal, 2012) uses
the concepts of epipolar geometry to avoid 3D recon-
struction. Wang et al.(Wang et al., 2013) proposes
a new representation of each feature trajectory as a
Bezier curve and then smoothed over time. Liu et
al. (Liu et al., 2011) choose to smooth basis trajecto-
ries of the subspace (Irani, 2002) which are extracted
from long feature tracks of 50 frames or more. This
method achieves high quality stabilization that is sim-
ilar to the full 3D methods, while avoiding the need
of a full 3D reconstruction and using long feature tra-
jectories instead. This technique has been integrated
in Adobe After Effects as a video stabilization func-
tion named Warp Stabilizer. Recently, Liu et al.(Liu
et al., 2013) proposes an extension of the method to
cope with stereoscopic videos. However, the need of
long feature trajectories is difficult to achieve espe-
cially in videos with quickly changing scenes or a lot
of occlusions. Regardless if the algorithms are 2D or
3D, almost all of them are either highly sequential or
offline stabilizers. Previous work on real-time stabi-
lization as in Wang et al. work (Wang et al., 2011)
the motion model was restricted to translation only.
Litvin et al.(Litvin et al., 2003) the algorithm used
Kalman filtering to extend the model to be a full 2D
affine model with translation and rotation. However,
these techniques sacrifice much of the robustness and
visual quality to achieve real time performance. The
proposed method aims at providing parallel, real time
performance without sacrificing loss in the robustness
or the visual quality provided by the offline stabiliz-
ers. By dividing the frame into blocks and smoothing
their trajectory over time allowing better estimation
for the frame transformation that can adopt with vari-
ous videos.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
668

3 PROPOSED ALGORITHM
The proposed method uses a novel technique to esti-
mate the transformation parameters for a video frame
and smooth the parameters over time in two phases,
as illustrated in Figure 1. The algorithm description
is discussed in the next sections.
3.1 Algorithm Description
Phase I: At each frame, the frame is divided into N
blocks with window overlap of 60% that has been
defined empirically through experiments on various
videos some of which are shown in Figure 4. The
overlap ensures that the features are well tracked
along the boundaries. Then, for each block features
are extracted using good features to track(Shi and
Tomasi, 1994). These features are then tracked in
the same block in the next frame using optical flow
method. An affine transformation denoted by H is
then estimated for each block. The camera path of the
block is then smoothed over time using a Gaussian
low pass filter with sigma σ
0
producing a more stable
camera path for that block. So let P
t
denotes the origi-
nal shaky block path, which is formed by the concate-
nation of the blocks affine transformations over time
as defined by equation 1. The desired (smoothed)
camera path for the block C
t
is calculated based on
equation 2.
P
t
=
i
∏
i=0
H
i
. (1)
C
t
= P
t
∗ G
t
(2)
where G
t
is the Gaussian low pass filter function with
sigma σ
0
. Phase II: With each block camera path
smoothed individually from phase I. these paths are
then combined to form an estimate for the transfor-
mation parameters for their corresponding frame. The
paths are combined using another low pass 2D Gaus-
sian with sigma σ
1
which gives more weight to the
central blocks of the frame as the central blocks of
the frame should contain the dominant motion in the
frame. Let C
t,i
represent the smoothed block path the
frame estimation
´
P
t
is derived by equation 3.
´
P
t
= C
t
∗W (X, Y ) (3)
where W (X, Y) is the 2D Gaussian window function
with sigma σ
1
. Then as a final step the final camera
path for that frame is smoothed within a window of
neighbouring frames using a third low pass Gaussian
filter with sigma σ
2
to produce the final transforma-
tion parameters for the frame in a similar procedure
to the smoothing of the block path defined by equa-
tion 2. As seen the algorithm is highly parallelizable
as the estimation of the block transformation does not
need any communication or dependency between data
needed by different processors to produce results so
the process can be easily parallelized.
Algorithm 1: The Proposed Algorithm.
1: Input: Input Frame.
2: Divide the frame into blocks(Input frame).
3: for each block i ∈ N Parallel do
4: Extract good features to track.
5: Track the features into previous block.
6: Evaluate good matches.
7: Estimate affine transformation.
8: In case no good transformation can be calcu-
lated, the estimation is replaced by the transfor-
mation of the same block from previous frame.
9: For each block in the neighborhood window,
the trajectory is smoothed using a low pass Gaus-
sian filter.
10: A new transformation is estimated based on
the smoothed trajectory.
11: end for
12: For each block in the frame, their estimation is
smoothed using a 2D Gaussian kernel to estimate
the transformation for the frame.
13: The trajectory of the frame is then smoothed
based on the Gaussian filter with the neighboring
frame in the window.
14: The final transformation is then estimated based
on the smoothed trajectory of the whole frame.
15: The final stabilized frame is computed through
warping the input frame.
16: Output: Stabilized Frame.
3.2 Implementation
In the implementation of the proposed algorithm, the
number of blocks N =16 for videos with frame height
of 720 and width of 1280. The size of the neighbor-
hood used for smoothing was set to 30 in both cases
of smoothing on block and frame level. The sigma of
the Gaussian filter used in block smoothing is small
σ
0
=0.3 and σ
1
= 0.5. Only σ
2
is set to larger value to
suppress any fluctuations and enforce more smooth-
ness on the path of the camera, so σ
2
is set to 10.
All the values were set empirically based on experi-
menting with different video sequences. Then Using
OpenMp directives the estimation of the transforma-
tion for each block is done in parallel. The rest of
the implementation for feature extraction, matching
and estimation of transformation and warping of the
frames is based on OpenCV implementation. Algo-
rithm 1 shows a pseudo-code of the implementation.
Towards High-Quality Parallel Stabilization
669

(a) Original Mean of Sequence (b) Our Stabilized Sequence Mean (c) Google’s Youtube Stabilized
Sequence Mean
Figure 3: Sequence Mean Comparison.
4 RESULTS
The proposed algorithm has been tested on both the
datasets provided by (of Central Florida, ) (Grund-
mann et al., 2011) and (Liu et al., 2009). The evalu-
ation criteria are based on (Morimoto and Chellappa,
1998) measuring the average fidelity with equation 4,
the mean of the sequence to assess the visual quality
improvement and also the path of the camera.
PSNR
dB
(I
1
, I
0
) = 10 log
(255)
2
MSE(I
1
, I
0
)
(4)
where MSE is the mean squared error measuring the
error per pixel from the optimal stabilized result, and
the 255 represents the maximum intensity a pixel may
have. Figure 3 shows a comparison of the mean of
the stabilized sequence from the results from Googles
YouTube stabilizer at the right and the result from our
proposed algorithm at the middle. by examining the
images, it can be seen that our proposed method can
produce results that are comparable to one the state
of the art stabilization algorithms. However, in se-
quences with high jitter as in the fourth sequence, our
algorithm performs poorly which will be discussed
later in the upcoming section. In Table 1 the value
of the fidelity after the stabilization is significantly
higher. In Figures 4-6 the trajectory of the sequence
in Y-axis, X-axis and the rotation angle respectively
plotted with the original trajectory in blue and the
smoothed version in green, it can be clearly seen that
the smoothed trajectory does not suffer the high fluc-
tuations found on the original trajectory.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
670
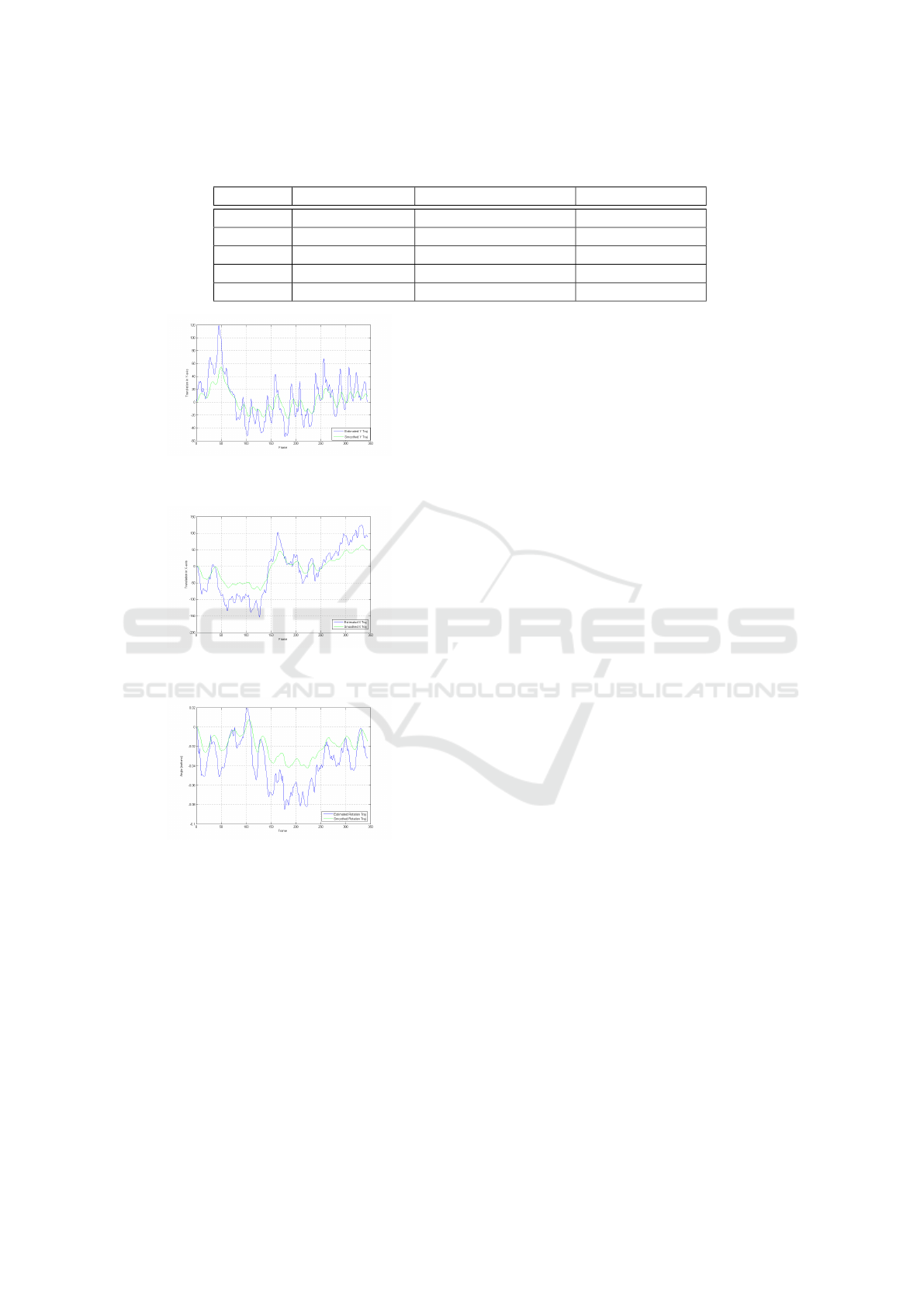
Table 1: Comparison between the fidelity of the original sequence (left) ,using our method (middle) and Stabilized Fidelity
from Google’s Youtube(right).
Sequence Original Fidelity Our Stabilized Fidelity Google’s Youtube
Seq. 1 40 dB 56 dB 53 dB
Seq. 2 45 dB 50 dB 66 dB
Seq. 3 42 dB 60 dB 59 dB
Seq. 4 42 dB 53 dB 77 dB
Seq. 5 34 dB 45 dB 50 dB
Figure 4: Comparison between the original trajectory (blue)
and the smoothed trajectory (green) for Y-direction.
Figure 5: Comparison between the original trajectory (blue)
and the smoothed trajectory (green) for X-direction.
Figure 6: Comparison between the original trajectory (blue)
and the smoothed trajectory (green) for the angle of rota-
tion.
5 DISCUSSION AND
PERFORMANCE ANALYSIS
5.1 Discussion
The proposed algorithm does perform well on short
sequences, However as seen in Figure 3 the mean
sequence still suffers some jittering especially in se-
quence with extreme jittering as maintaining the cam-
era path for each block will tend to make some drifts
in the estimations this can be seen also in Figure 5. as
the smoothing of the X-direction drifting away from
the estimation and instability in both the estimation
and the smoothing increases over time. To overcome
this drawback more constraints will be added to the
system to ensure the calculations in both the block
and frame level. Generally, we find that the 3D recon-
struction method gives the best results when success-
ful. However, the proposed method produces videos
with high visual quality and takes benefit of the ro-
bustness and simplicity of 2D methods and not re-
stricted to one type of transformation.
5.2 Runtime Analysis
The proposed algorithm has been tested on the follow-
ing configurations: Intel Quad Core processor @2.20
GHz. The average running time for the whole algo-
rithm is around 20 fps, taking around more than half
the time needed to process one frame in Phase I. Typ-
ically the running time for this phase increases with
increasing the number of blocks in the frame and with
extending the size of the window used for smoothing.
6 CONCLUSION AND FUTURE
WORK
This paper presented a parallel technique in stabiliza-
tion based on 2D linear transformations with running
time suitable for real time systems and with high vi-
sual quality compared to offline and 3D stabilizers.
In the future, the algorithm will be tested in more
datasets, plus extending the work to handle feature-
less scenes and longer sequences. Also, the addition
of new constraints on the smoothing function to allow
the process of longer sequences to produce the highest
stabilization quality.
REFERENCES
Agarwal, S., Furukawa, Y., Snavely, N., Simon, I., Cur-
less, B., Seitz, S. M., and Szeliski, R. (2011). Build-
Towards High-Quality Parallel Stabilization
671

ing rome in a day. Communications of the ACM,
54(10):105–112.
Buehler, C., Bosse, M., and McMillan, L. (2001). Non-
metric image-based rendering for video stabilization.
In Computer Vision and Pattern Recognition, 2001.
CVPR 2001. Proceedings of the 2001 IEEE Computer
Society Conference on, volume 2, pages II–609. IEEE.
Furukawa, Y., Curless, B., Seitz, S. M., and Szeliski, R.
(2010). Towards internet-scale multi-view stereo. In
Computer Vision and Pattern Recognition (CVPR),
2010 IEEE Conference on, pages 1434–1441. IEEE.
Goldstein, A. and Fattal, R. (2012). Video stabilization us-
ing epipolar geometry. ACM Transactions on Graph-
ics (TOG), 31(5):126.
Grundmann, M., Kwatra, V., and Essa, I. (2011). Auto-
directed video stabilization with robust l1 optimal
camera paths. In Computer Vision and Pattern Recog-
nition (CVPR), 2011 IEEE Conference on, pages 225–
232. IEEE.
Irani, M. (2002). Multi-frame correspondence estimation
using subspace constraints. International Journal of
Computer Vision, 48(3):173–194.
Irani, M., Rousso, B., and Peleg, S. (1994). Recovery of
ego-motion using image stabilization. In Computer
Vision and Pattern Recognition, 1994. Proceedings
CVPR’94., 1994 IEEE Computer Society Conference
on, pages 454–460. IEEE.
Jiang, N., Tan, P., and Cheong, L.-F. (2012). Seeing
double without confusion: Structure-from-motion in
highly ambiguous scenes. In Computer Vision and
Pattern Recognition (CVPR), 2012 IEEE Conference
on, pages 1458–1465. IEEE.
Litvin, A., Konrad, J., and Karl, W. C. (2003). Probabilis-
tic video stabilization using kalman filtering and mo-
saicing. In Electronic Imaging 2003, pages 663–674.
International Society for Optics and Photonics.
Liu, F., Gleicher, M., Jin, H., and Agarwala, A. (2009).
Content-preserving warps for 3d video stabilization.
In ACM Transactions on Graphics (TOG), volume 28,
page 44. ACM.
Liu, F., Gleicher, M., Wang, J., Jin, H., and Agarwala, A.
(2011). Subspace video stabilization. ACM Transac-
tions on Graphics (TOG), 30(1):4.
Liu, F., Niu, Y., and Jin, H. (2013). Joint subspace sta-
bilization for stereoscopic video. In Computer Vi-
sion (ICCV), 2013 IEEE International Conference on,
pages 73–80. IEEE.
Liu, S., Wang, Y., Yuan, L., Bu, J., Tan, P., and Sun,
J. (2012). Video stabilization with a depth camera.
In Computer Vision and Pattern Recognition (CVPR),
2012 IEEE Conference on, pages 89–95. IEEE.
Matsushita, Y., Ofek, E., Ge, W., Tang, X., and Shum, H.-Y.
(2006). Full-frame video stabilization with motion in-
painting. Pattern Analysis and Machine Intelligence,
IEEE Transactions on, 28(7):1150–1163.
Morimoto, C. and Chellappa, R. (1998). Evaluation of
image stabilization algorithms. In Acoustics, Speech
and Signal Processing, 1998. Proceedings of the 1998
IEEE International Conference on, volume 5, pages
2789–2792. IEEE.
of Central Florida, U. Ucf aerial action data set.
http://crcv.ucf.edu/data/UCF
Aerial Action.php.
Shi, J. and Tomasi, C. (1994). Good features to track.
In Computer Vision and Pattern Recognition, 1994.
Proceedings CVPR’94., 1994 IEEE Computer Society
Conference on, pages 593–600. IEEE.
Triggs, B., McLauchlan, P. F., Hartley, R. I., and Fitzgibbon,
A. W. (2000). Bundle adjustmenta modern synthesis.
In Vision algorithms: theory and practice, pages 298–
372. Springer.
Wang, Y., Hou, Z., Leman, K., and Chang, R. (2011). Real-
time video stabilization for unmanned aerial vehicles.
In MVA, pages 336–339.
Wang, Y.-S., Liu, F., Hsu, P.-S., and Lee, T.-Y. (2013). Spa-
tially and temporally optimized video stabilization.
Visualization and Computer Graphics, IEEE Transac-
tions on, 19(8):1354–1361.
Wu, C. (2013). Towards linear-time incremental structure
from motion. In 3D Vision-3DV 2013, 2013 Interna-
tional Conference on, pages 127–134. IEEE.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
672
