
Recursive Reductions of Internal Dependencies in Multiagent Planning
Jan To
ˇ
zi
ˇ
cka, Jan Jakub
˚
uv and Anton
´
ın Komenda
Agent Technology Center, Department of Computer Science, Czech Technical University in Prague,
Karlovo namesti 13, 121 35, Prague, Czech Republic
Keywords:
Automated Planning, Multiagent Systems, Problem Reduction.
Abstract:
Problems of cooperative multiagent planning in deterministic environments can be efficiently solved both by
distributed search or coordination of local plans. In the current coordination approaches, behavior of other
agents is modeled as public external projections of their actions. The agent does not require any additional
information from the other agents, that is the planning process ignores any dependencies of the projected ac-
tions possibly caused by sequences of other agents’ private actions.
In this work, we formally define several types of internal dependencies of multiagent planning problems and
provide an algorithmic approach how to extract the internally dependent actions during multiagent planning.
We show how to take an advantage of the computed dependencies by means of reducing the multiagent plan-
ning problems. We experimentally show strong reduction of majority of standard multiagent benchmarks and
nearly doubling of solved problems in comparison to a variant of a planner without the reductions. The effi-
ciency of the method is demonstrated by winning in a recent competition of distributed multiagent planners.
1 INTRODUCTION
Cooperative intelligent agents acting in a shared en-
vironment have to coordinate their steps in order to
achieve their goals. A well-established model for
multiagent planning in deterministic environments
was described by (Brafman and Domshlak, 2008)
as MA-STRIPS, which is a minimal extension of
classical planning model STRIPS (Fikes and Nilsson,
1971). MA-STRIPS provides problem partitioning in
form of separated sets of actions of particular agents,
and notion of local private information the agents are
not willing to share. By definition, private actions and
facts about the environment do not affect other agents
and cannot be affected by other agents. Shared facts
and actions which can influence more than one agent
are denoted as public.
In multiagent planning modeled as MA-STRIPS,
agents can either plan only with their own actions
and facts and inform the other agents about public
achieved facts, as for instance in the MAD-A* plan-
ner (Nissim and Brafman, 2012). Or, agents can also
use other agents’ public actions provided that the ac-
tions are stripped of the private facts in preconditions
and effects. Thus agents plan actions, in a sense, for
other agents and then coordinate the plans (To
ˇ
zi
ˇ
cka
et al., 2014b).
Only a complete stripping of all private informa-
tion from public actions was used in literature so far.
Such approach can, however, lead to tangible loss of
information on causal dependencies of the actions de-
scribed by the private actions. A seeming remedy is
to borrow techniques from classical planning on prob-
lem reduction (e.g., in (Haslum, 2007; Chen and Yao,
2009; Coles and Coles, 2010)). As our motivation is
to “pack” sequences of public and private actions, the
most suitable are recursive macro actions as proposed
by (Jonsson, 2009; B
¨
ackstr
¨
om et al., 2012). A macro
action can represent a sound sequence of actions and,
provided that it allows for recursive reductions, it can
be used repeatedly with possibly radical downsizing
of the reduced planning problem.
In a motivation logistic problem, when an agent
transports a package from one city to another and
wants to keep its current load internal, it is not prac-
tical to publish two actions: load(package, fromC-
ity) and unload(package, toCity). Instead it should
publish action transport(package, fromCity, toCity),
which is capturing the hidden (private) relation be-
tween this pair of actions while it is not disclosing it
in an explicit way.
We propose to keep the pair of actions and to add
new public predicate that says that some action re-
quires another action to precede it (because it better
fits the proposed coordination algorithm). In the sim-
Toži
ˇ
cka, J., Jakub˚uv, J. and Komenda, A.
Recursive Reductions of Internal Dependencies in Multiagent Planning.
DOI: 10.5220/0005754901810191
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 2, pages 181-191
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
181

plest case, the new public fact would directly corre-
spond to the internal fact isLoaded(package), but in
realistic cases, it could also capture more complex de-
pendencies, for example, the transshipment between
different vehicles belonging to the transport agent.
In this paper, we build on our previous
work (To
ˇ
zi
ˇ
cka et al., 2015a) where internal depen-
dencies of public actions where studied with a restric-
tion that every action consumes all of its precondi-
tions. This restriction no longer applies here because
it can be very limiting in practice. Furthermore, we
demonstrate the effect of our approach on a bench-
mark set from the CoDMAP competition held on In-
ternational Conference on Automated Planning and
Scheduling (ICAPS’15). Our planner, employing the
theory from this paper, won the distributed track of
CoDMAP 2015.
2 MULTIAGENT PLANNING
This section provides condensed formal prerequisites
of multiagent planning based on the MA-STRIPS for-
malism (Brafman and Domshlak, 2008). Refer to
(To
ˇ
zi
ˇ
cka et al., 2014a) for more details.
An MA-STRIPS planning problem Π is a quadru-
ple Π = hP,{α
i
}
n
i=1
,I, Gi, where P is a set of
facts, α
i
is the set of actions of i-th agent
1
I ⊆
P is an initial state, and G ⊆ P is a set of
goal facts. We define selector functions facts(Π),
agents(Π), init(Π), and goal(Π) such that Π =
hfacts(Π),agents(Π),init(Π),goal(Π)i. An action
a ∈ α, the agent α can perform, is a triple of subsets
of P called preconditions, add effects, delete effects.
Selector functions pre(a), add(a), and del(a) are de-
fined so that a = hpre(a),add(a),del(a)i. Note that
an agent is identified with the actions the agent can
perform in an environment.
In MA-STRIPS, out of computational or privacy
concerns, each fact is classified either as public or as
internal. A fact is public when it is mentioned by
actions of at least two different agents. A fact is in-
ternal for agent α when it is not public but mentioned
by some action of α. A fact is relevant for α when it
is either public or internal for α. MA-STRIPS further
extends this classification of facts to actions as fol-
lows. An action is public when it has a public (add-
or delete-) effect, otherwise it is internal. An action
from Π is relevant for α when it is either public or
owned by (contained in) α.
1
Whereas, in STRIPS, the second parameter is a set of
actions, in MA-STRIPS, the second parameter is actually a
set of sets of actions.
We use int-facts(α) and pub-facts(α) to denote in
turn the sets internal facts and the set of public facts
of agent α. Moreover, we write pub-facts(Π) to de-
note all the public facts of problem Π. We write
pub-actions(α) to denote the set of public actions of
agent α. Finally, we use pub-actions(Π) to denote all
the public actions of all the agents in problem Π.
In multiagent planning with external actions, a lo-
cal planning problem is constructed for every agent
α. Each local planning problem for α is a classical
STRIPS problem where α has its own internal copy
of the global state and where each agent is equipped
with information about public actions of other agents
called external actions. These local planning prob-
lems allow us to divide an MA-STRIPS problem into
several STRIPS problems which can be solved sepa-
rately by a classical planner.
The projection F .α of a set of facts F to agent
α is the restriction of F to the facts relevant for α,
representing F as seen by α. The public projection
a.? of action a is obtained by restricting the facts in
a to public facts. Public projection is extended to sets
of actions element-wise.
A local planning problem Π.α of agent α, also
called projection of Π to α, is a classical STRIPS
problem containing all the actions of agent α together
with external actions, that is, public projections of
other agents’ public actions. The local problem of α is
defined only using the facts relevant for α. Formally,
Π.α = hP .α,α ∪ exts(α),I . α, Gi
where the set of external actions exts(α) is defined as
follows.
exts(α) =
[
β6=α
(pub-actions(β).?)
In the above, β ranges over all the agents of Π. The set
exts(α) can be equivalently described as exts(α) =
(pub-actions(Π) \α) . ?. To simplify the presenta-
tion, we consider only problems with public goals and
hence there is no need to restrict goal G.
3 PLANNING WITH EXTERNAL
ACTIONS
The previous section allows us to divide an MA-
STRIPS problem into several classical STRIPS local
planning which can be solved separately by a classi-
cal planner. Recall that the local planning problem
of agent α contains all the actions of α together with
α’s external actions, that is, with projections of public
actions of other agents. This section describes con-
ditions which allow us to compute a solution of the
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
182

Algorithm 1:Distributed MA planning algorithm.
1 Function MaPlanDistributed(Π . α) is
2 Φ
α
←
/
0;
3 loop
4 generate new π
α
∈ sols(Π.α);
5 Φ
α
← Φ
α
∪ {π
α
.?};
6 exchange public plans Φ
α
with other
agents;
7 Φ ←
T
β∈agents(Π)
Φ
β
;
8 if Φ 6=
/
0 then
9 return Φ;
10 end
11 end
12 end
original MA-STRIPS problem from solutions of local
problems.
A plan π is a sequence of actions. A solution of Π
is a plan π whose execution transforms the initial state
to a subset of the goals. A local solution of agent α is
a solution of Π.α. Let sols(Π) denote the set of all
the solutions of MA-STRIPS or STRIPS problem Π.
A public plan σ is a sequence of public actions. The
public projection π.? of plan π is the restriction of π
to public actions.
A public plan σ is extensible when there is π ∈
sols(Π) such that π . ? = σ. Similarly, σ is α-
extensible when there is π ∈ sols(Π.α) such that
π.? = σ. Extensible public plans give us an order of
public actions which is acceptable for all the agents.
Thus extensible public plans are very close to solu-
tions of Π and it is relatively easy to construct a so-
lution of Π once we have an extensible public plan.
Hence our algorithms will aim at finding extensible
public plans.
The following theorem (To
ˇ
zi
ˇ
cka et al., 2014a) es-
tablishes the relationship between extensible and α-
extensible plans. Its direct consequence is that to find
a solution of Π it is enough to find a local solution
π
α
∈ sols(Π.α) which is β-extensible for every agent
β.
Theorem 1. Public plan σ of Π is extensible if and
only if σ is α-extensible for every agent α.
The theorem above suggests the distributed mul-
tiagent planning algorithm described in Algorithm 1.
Every agent executes the loop from Algorithm 1, pos-
sibly on different machine. Every agent keeps gener-
ating new solutions of its local problem and stores so-
lution projections in set Φ
α
. These sets are exchanged
among all the agents so that every agent can com-
pute their intersection Φ. Once the intersection Φ is
non-empty, the algorithm terminates yielding Φ as the
result. Theorem 1 ensures that every public plan in
the resulting Φ is extensible. Consult (To
ˇ
zi
ˇ
cka et al.,
2014a) for more details on the algorithm.
4 INTERNAL DEPENDENCIES
OF ACTIONS
One of the benefits of planning with external ac-
tions is that every agent can plan separately its local
problem which involves planning of actions for other
agents (external actions). Other agents can then only
verify whether a plan generated by another agent is
α-extensible for them. A con of this approach is that
agents have only a limited knowledge about external
actions because internal facts are removed by projec-
tion. Thus it can happen that an agent plans exter-
nal actions inappropriately in a way that the resulting
public plan is not α-extensible for some agent α.
In the rest of this paper we try to overcome the
limitation of partial information about external ac-
tions. The idea is to equip agents with additional in-
formation about external actions without revealing in-
ternal facts. The rest of this section describes depen-
dency graphs which are used in the following sections
as a formal ground for our analysis of public and ex-
ternal actions.
4.1 Dependency Graphs
Local planning problem Π . α of agent α contains in-
formation about external actions provided by the set
exts(α). The idea is to equip agent α with more in-
formation described by a suitable structure. A depen-
dency graphs is a structure we use to encapsulate in-
formation about public actions which an agent shares
with other agents.
Dependency graphs are known from litera-
ture (Jonsson and B
¨
ackstr
¨
om, 1998; Chrpa, 2010). In
our context, a dependency graph ∆ is a bipartite di-
rected graph defined as follows.
Definition 1. A dependency graph ∆ is a bipartite di-
rected graph whose nodes are actions and facts. We
write actions(∆) and facts(∆) to denote action and
fact nodes respectively. Given the nodes, graph ∆
contains the following three kinds of edges.
(a → f ) ∈ ∆ iff f ∈ add(a) (a produces f )
( f → a) ∈ ∆ iff f ∈ pre(a) \ del(a) (a requires f )
( f 99K a) ∈ ∆ iff f ∈ pre(a) ∩ del(a) (a consumes f )
Additionally, a fact can be marked as initial in ∆. The
set of states marked as initial is denoted init(∆).
Hence edges of a dependency graph ∆ are
uniquely determined by the set of nodes. Note that
Recursive Reductions of Internal Dependencies in Multiagent Planning
183

action nodes are themselves actions, that is, triples of
fact sets. These action nodes can contain additional
facts other than fact nodes facts(∆). We use depen-
dency graphs to represent internal dependencies of
public actions. Dependencies determined by public
facts are known to other agents and thus we do not
need them in the graph as fact nodes. From now on
we suppose that facts(∆) contains no public facts as
fact nodes. Action nodes, however, can contain public
facts in their public actions.
Definition 2. Let an MA-STRIPS problem Π be
given. The minimal dependency graph MD(α)
of agent α ∈ agents(Π) is the dependency graph
uniquely determined by the following set of nodes.
actions(MD(α)) = pub-actions(α)
facts(MD(α)) =
/
0
init(MD(α)) =
/
0
Hence MD(α) has no edges as there are no fact
nodes. Thus the graph contains only separated public
action nodes. Furthermore, the set exts(α) of exter-
nal actions of agent α can be trivially expressed as
follows.
exts(α) =
[
β6=α
(actions(MD(β)).?)
Thus we see that dependency graphs can carry the
same information as provided by exts(α).
Definition 3. The full dependency graph FD(α) of
agent α contains all the actions of α and all the in-
ternal facts of α.
actions(FD(α)) = α
facts(FD(α)) = int-facts(α)
init(FD(α)) = init(Π) ∩ int-facts(α)
Hence FD(α) contains all the information known
by α. By publishing FD(α), an agent reveals all his
internal dependencies which might be a potential pri-
vacy risk. On the other hand, other agents are by
FD(α) provided the most precise information about
dependencies of public actions of α. Every plan of
another agent, computed with FD(α) in mind, is auto-
matically α-extensible. Thus we see that dependency
graphs can carry dependencies information with a var-
ied precision.
4.2 Dependency Graph Collections
A dependency graph represents information about
public actions of one agent. Every agent needs to
know information from all the other agents. We use
dependency graph collections to represent all the re-
quired information. A dependency graph collection
D of an MA-STRIPS problem Π is a set of depen-
dency graphs which contains exactly one dependency
graph for every agent of Π. We write D(α) to denote
the graph of α. We write actions(D ), facts(D), and
init(D ) to denote in turn all the action, fact, and initial
fact nodes from all the graphs in D.
Definition 4. Given problem Π, we can define the
minimal collection MD(Π) and the full collection
FD(Π) as follows.
MD(Π) = {MD(α) : α ∈ agents(Π)}
FD(Π) = {FD(α) : α ∈ agents(Π)}
Later we shall show some interesting properties of
the minimal and full collections.
4.3 Local Problems and Dependency
Collections
In order to define local problems informed by D, we
need to define facts and action projections which pre-
serve information from D . We use symbol .
D
to de-
note projections accordingly to D. Recall that the
public projection a.? of action a is the restriction of
the facts of a to pub-facts(Π). The public projection
a.
D
? of action a accordingly to D is the restriction
of the facts of a to pub-facts(Π) ∪ facts(D). Pub-
lic projection is extended to sets of actions element-
wise. Furthermore, external actions of α according
to D, denoted exts
D
(α), contain public projections
(according to D) of actions of other agents. In other
words, exts
D
(α) carries all the information published
by other agents for agent α. It is computed as follows.
exts
D
(α) =
[
β6=α
(actions(D(β)).
D
?)
This equation captures distributed computation
of exts
D
(α) where every agent β separately com-
putes published actions, applies public projection, and
sends the result to α.
In order to define a local planning problem of
agent α which would take information from D into
consideration, we need to extract from D facts and
initial facts of other agents. Below we define sets
facts
D
(α) and init
D
(α) which contain those facts and
initial facts published by other agents, that is, all the
facts from D except of the facts of α.
facts
D
(α) = facts(D) \ facts(D(α))
init
D
(α) = init(D )\ init(D (α))
Now we are ready to define local planning problems
according to D which extends local planning prob-
lems by the information contained in D.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
184

Definition 5. Let Π be MA-STRIPS problem. The
local problem Π.
D
α of agent α ∈ agents(Π) accord-
ingly to D is the classical STRIPS problem Π .
D
α =
hP
0
,A
0
,I
0
,G
0
i where
(1) P
0
= facts (Π .α)∪ facts
D
(α),
(2) A
0
= α ∪ exts
D
(α),
(3) I
0
= init(Π . α) ∪ init
D
(α), and
(4) G
0
= goal(Π).
We can see that a local problem Π.
D
α according
to D extends the local problem Π.α by the facts and
actions published by D.
Let us consider two boundary cases of depen-
dency collections MD(Π) and FD(Π). Given an MA-
STRIPS problem Π, we can construct local problems
using the minimal dependency collection MD(Π). It is
easy to see that Π.
MD(Π)
α = Π . α for every agent α.
With the full dependency collection FD(Π) we obtain
equal projections, that is, Π .
FD(Π)
α = Π .
FD(Π)
β for
all agents α and β. Moreover, local solutions equal
MA-STRIPS solutions, that is, sols(Π .
FD(Π)
α) =
sols(Π) for every α.
4.4 Publicly Equivalent Problems
We have seen that dependency collections can pro-
vide information about internal dependencies with a
varied precision. Given two different collections, two
different local problems can be constructed for every
agent. However, when the two local problems of the
same agent equal on public solutions, we can say that
they are equivalent because their public solutions are
equally extensible.
In order to define equivalent collections, we first
define public equivalence on problems. Two planning
problems Π
0
and Π
1
are publicly equivalent, denoted
Π
0
'Π
1
, when they have equal public solutions. For-
mally as follows.
Π
0
'Π
1
⇔ sols(Π
0
).? = sols(Π
1
).?
Public equivalence can be extended to dependency
graph collections as follows. Two collections D
0
and
D
1
of the same MA-STRIPS problem Π are equiva-
lent, written D
0
'D
1
, when for any agent α, it holds
that the local problems Π.
D
0
α and Π.
D
1
α are pub-
licly equivalent. Formally as follows.
D
0
'D
1
⇔ (Π.
D
0
α)'(Π.
D
1
α) (for all α)
Example 1. Given an MA-STRIPS problem Π, with
the full dependency collection FD(Π) we can see that
Π'Π.
FD(Π)
α holds for any agent. Hence to find
a public solution of Π it is enough to solve the lo-
cal problem (accordingly to FD(Π)) of an arbitrary
agent. The same holds for any dependency collection
D such that D 'FD(Π). Note that D can be much
smaller and provide less private information than the
full dependency collection.
The above definitions allow us to recognize prob-
lems without any internal dependencies which we can
define as follow.
Definition 6. An MA-STRIPS problem Π is internally
independent when MD(Π)'FD(Π).
In order to solve an internally independent prob-
lem, it is enough to solve the local problem Π .α of
an arbitrary agent. Any local public solution is exten-
sible which makes internally independent problems
easier to solve because there is no need for interac-
tion and negotiation among the agents. Later we shall
show how to algorithmically recognize internally in-
dependent problems. The following formally captures
the above properties.
Lemma 2. Let Π be an internally independent MA-
STRIPS problem. Then (Π . α) ' Π.
Proof. (Π.α)'(Π.
MD(Π)
α)'(Π.
FD(Π)
α)'Π
5 SIMPLE ACTION
DEPENDENCIES
Let us consider dependency collections without inter-
nal actions, that is, collections D where actions(D )
contains no internal actions. When D is published,
then no agent publishes actions additional to exts(α)
which is desirable out of privacy concerns. Further-
more, the plan search space of Π.
D
α is not increased
when compared to Π . α. Even more, every addition-
ally published fact in D providing a valid dependency
prunes the search space. Action dependencies cap-
tured by collections without internal actions can be
expressed by requirements on the order of actions in a
plan. This further abstracts the published information
providing privacy protection. Thus it seems reason-
able to publish dependency collections without inter-
nal actions.
5.1 Simply Dependent Problems
The following defines simply dependent MA-STRIPS
problems, where internal dependencies of public ac-
tions can be expressed by a dependency collection
free of internal actions.
Definition 7. An MA-STRIPS problem Π is simply
dependent when there exists D such that actions(D )
contains no internal actions and D 'FD(Π).
Recursive Reductions of Internal Dependencies in Multiagent Planning
185

Suppose we have a simply dependent MA-
STRIPS problem and a dependency collection D
which proves the fact. In order to solve Π, once again,
it is enough to solve only one local problem Π.
D
α
(of an arbitrary agent α).
Lemma 3. Let Π be a simply dependent MA-
STRIPS problem. Let D be a dependency collec-
tion which proves that Π is simply dependent. Then
(Π.
D
α)'Π holds for any agent α ∈ agents(Π).
Proof. (Π.
D
α)'(Π.
FD(Π)
α)'Π
The above method requires all the agents to pub-
lish the information from D . However, the informa-
tion does not need to be published to all the agents as
it is enough to select one trusted agent and send the
information only to him. Hence it is enough for all
the agents to agree on a single trusted agent.
5.2 Dependency Graph Reductions
Recognizing simply dependent MA-STRIPS prob-
lems might be difficult in general. That is why we
define an approximative method which can provably
recognize some simply dependent problems. We
define a set of reduction operations on dependency
graphs and we prove that the operations preserve rela-
tion '. Then we apply the reductions repeatedly start-
ing with FD(∆) obtaining a dependency graph which
can not be reduced any further. This is done by every
agent. When the resulting graphs contain no internal
actions, then we know that the problem is simply de-
pendent. Additionally, when the resulting graphs con-
tain no internal facts, then we know that the problem
is independent.
Our previous work (To
ˇ
zi
ˇ
cka et al., 2015a) was re-
stricted to problems where pre(a) = del(a) holds for
every action a. This impractical limitation is removed
here. We still restrict our attention to problems where
del(a) ⊆ pre(a) holds for every action a. This is not
considered limiting because a problem not meeting
this requirement can be easily transformed to a per-
missible equivalent problem.
Finally, to abstract from the set of initial facts of
a dependency graph ∆, we introduce to the graph a
special initial action h
/
0,init(∆),
/
0i. We suppose that
every dependency graph has exactly one initial action
and hence we do not need to remember the set of ini-
tial facts. The initial action is handled as public even
when it has no public effect. Both definitions of de-
pendency graphs are trivially equivalent but the one
with an initial action simplifies the presentation of re-
duction operations.
We proceed by informal descriptions of depen-
dency graph reductions. The formal definition is
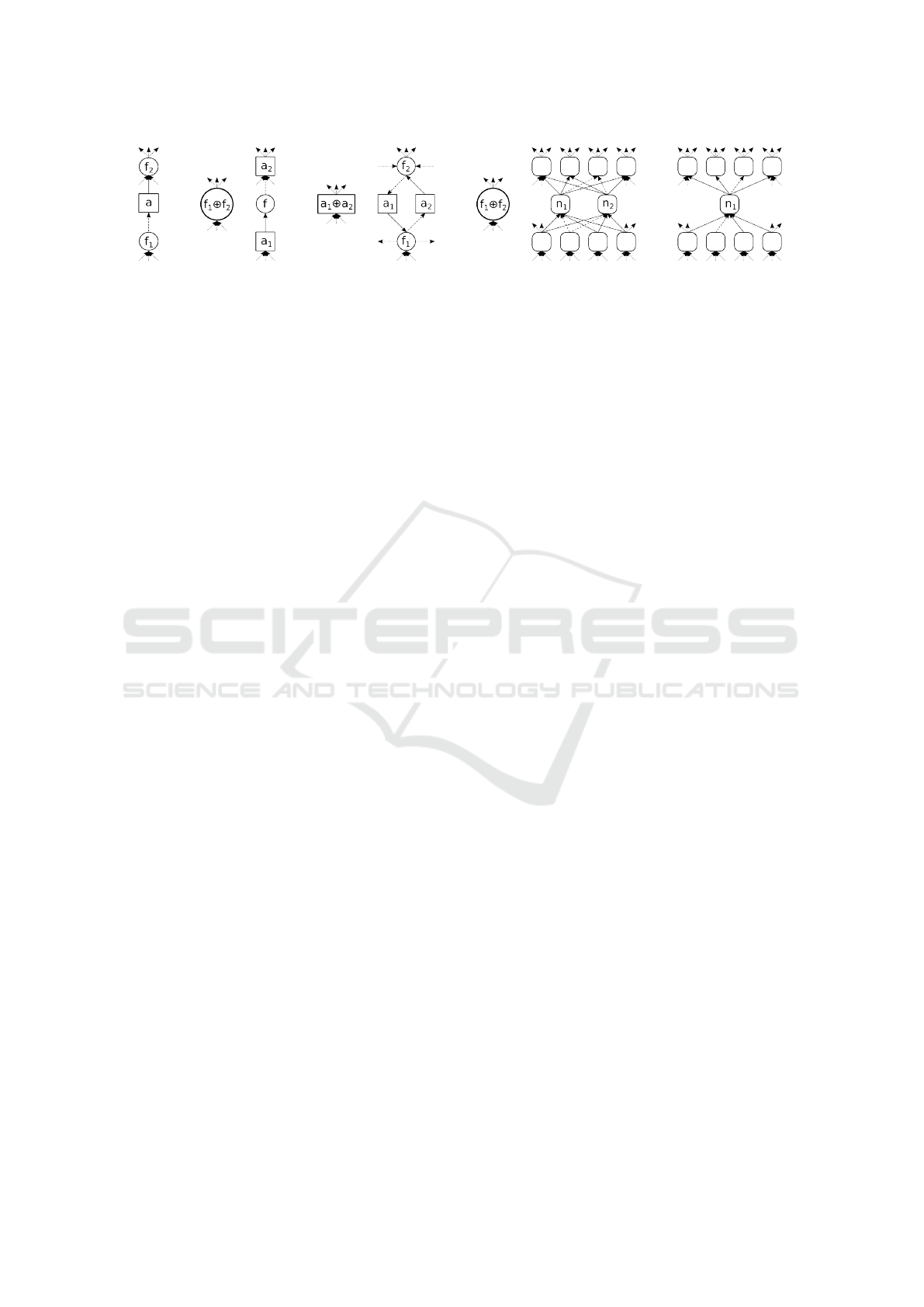
given below. The operations are depicted in Figure 1.
(R1) Remove Simple Action Dependency. If some
internal action has only one delete effect and one
add effect and there is no other action depending
on f
1
we can merge both facts into one and re-
move that action.
(R2) Remove Simple Fact Dependency. If some
fact is the only effect of some action and there is
only one action that consumes this effect without
any side effects, we can remove this fact and
merge both actions.
(R3) Remove Small Action Cycle. In many do-
mains, there are reversible internal actions that
allow transitions between two (or more) states.
All these states can be merged into a single state
and the actions changing them can be omitted.
(R4) Merge Equivalent Nodes. If two nodes (facts
or actions) equal on incoming and outgoing edges,
then we can merge these two nodes. Mostly this is
not directly in the domain but this structure might
appear when we simplify a dependency graph us-
ing the other reductions.
(R5) Remove Invariants. After several reduction
steps, it can happen that all the delete effects on
some fact are removed and the fact is always ful-
filled from the initial state. This happens, for
example, in Logistics, where the location of a
vehicle is internal knowledge and can be freely
changed as described by reduction (R3). Once
these cycles are removed, only one fact remains.
The remaining fact represents that the vehicle is
somewhere, which is always true. This fact can be
freely removed from the dependency graph.
In order to formally define the above reductions
we first define operator [F]
f
1
→ f
2
which renames fact
f
1
to f
2
in the set of facts F ⊆ P.
[F]
f
1
→ f
2
=
(
F if f
1
6∈ F
(F \ { f
1
}) ∪ { f
2
} otherwise
Similarly, we define operator [F]
- f
= F \ { f } which
removes fact f from the set of facts F. These oper-
ators are extended to actions (applying the operator
to preconditions, add, and delete effects) and to ac-
tion sets (element-wise). The operators can be fur-
ther extended to dependency graphs, where [∆]
- f
is
the dependency graph determined by [actions(∆)]
- f
and [facts(∆)]
- f
. Finally, for two actions a
1
and a
2
we define the merged action a
1
⊕a
2
as the action ob-
tained by unifying separately preconditions, add, and
delete effects of both the actions.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
186
(R1) (R2) (R3) (R4)
Figure 1: Graphical illustration of reduction operations (R1)–(R4). Circles represent fact nodes and rectangles represent
action nodes. Rounded boxes in (R4) represent any node (either fact or action node).
The following formally defines reduction relation
∆
0
→ ∆
1
which holds when ∆
0
can be transformed to
∆
1
using one of the reduction operations.
Definition 8. The reduction relation ∆
0
→ ∆
1
on
dependency graphs is defined by the following four
rules.
(R1) Rule (R1) is applicable to ∆
0
when
(1) ∆
0
contains edges ( f
1
99K a → f
2
),
(2) a is internal, and
(3) there are no other edges from/to a, and
(4) there are no other edges from f
1
.
Then ∆
0
→ ∆
1
where ∆
1
is defined as ∆
1
=
[∆
0
]
f
1
→ f
2
. The initial action is preserved.
(R2) Rule (R2) is applicable to ∆
0
when
(1) ∆
0
contains edges (a
1
→ f 99K a
2
),
(2) there are no other edges from/to f , and
(3) there are no other edges from a
1
, and
(4) a
2
has no other delete effects, and
(5) a
2
is internal action.
Then ∆
0
→ ∆
1
where ∆
1
is given by the following.
actions(∆
1
) = {[a
1
⊕a
2
]
- f
} ∪ (actions(∆
0
) \ {a
1
,a
2
})
facts (∆
1
) = [facts(∆
0
)]
- f
If a
1
is the initial action of ∆
0
then the new merged
action becomes the initial action of ∆
1
. Other-
wise, the initial action is preserved.
(R3) Rule (R3) is applicable to ∆
0
when
(1) ∆
0
contains edges ( f
1
99K a
1
→ f
2
), and
(2) ∆
0
contains edges ( f
2
99K a
2
→ f
1
), and
(3) a
1
and a
2
are both internal, and
(4) there are no other edges from/to a
1
or a
2
.
Then ∆
0
→ ∆
1
where ∆
1
is given by the following.
actions(∆
1
) = [actions(∆
0
) \ {a
1
,a
2
}]
f
2
→ f
1
facts (∆
1
) = [facts(∆
0
)]
f
2
→ f
1
The initial action is preserved as it is public.
(R4) Rule (R4) is applicable to ∆
0
when ∆
0
contains
two nodes n
1
and n
2
(either action or fact nodes)
such that
(1) nodes n
1
and n
2
have equal sets of incoming
and outgoing edges, and
(2) n
1
and n
2
are not public actions.
Then ∆
0
→ ∆
1
where, in the case n
1
and n
2
are
actions, ∆
1
is given by the following.
actions(∆
1
) = {n
1
⊕n
2
} ∪ (actions(∆
0
) \ {n
1
,n
2
})
facts (∆
1
) = facts(∆
0
)
When n
1
or n
2
is the initial action of ∆
0
then the
new merged action becomes the initial action of
∆
1
. Otherwise, the initial action is preserved.
In the case n
1
and n
2
are facts, ∆
1
= [∆
0
]
n
2
→n
1
.
(R5) Let a
init
be the initial action of ∆
0
. Rule (R5) is
applicable to ∆
0
when there exists fact f such that
(1) ∆
0
contains edge (a
init
→ f ), and
(2) ∆
0
contains no edge ( f 99K a) for any a.
Then ∆
0
→ ∆
1
where ∆
1
is defined as ∆
1
= [∆
0
]
- f
.
The initial action of ∆
1
is [a
init
]
- f
.
The following defines reduction equivalence re-
lation ∆
0
∼∆
1
as a reflexive, symmetric, and transi-
tive closure of →. In other words, ∆
0
and ∆
1
are re-
duction equivalent when one can be transformed to
another using the reduction operations. Dependency
collections D
0
and D
1
are reduction equivalent when
graphs of corresponding agents are reduction equiva-
lent.
Definition 9. Dependency graphs reduction equiva-
lence relation, denoted ∆
0
∼∆
1
, is the least reflexive,
symmetric, and transitive closure generated by the re-
lation →.
Given MA-STRIPS problem Π, dependency col-
lections D
0
and D
1
of Π are reduction equivalent,
written D
0
∼D
1
, when D
0
(α)∼D
1
(α) for any agent
α ∈ agents(Π).
The following theorem formally states that reduc-
tion operations preserves public equivalence.
Theorem 4. Let Π be an MA-STRIPS problem and
let pre(a) ⊆ del(a) hold for any internal action. Let
D
0
and D
1
be dependency collections of problem Π.
Then D
0
∼D
1
implies D
0
'D
1
.
Proof sketch. It can be shown that none of the re-
duction operations changes the set of public plans
sols(D
0
(α)).? of any agent α ∈ agents(Π). There-
fore repetitive application of reductions assures that
D
0
'D
1
.
Recursive Reductions of Internal Dependencies in Multiagent Planning
187

Algorithm 2: Compute the dependency graph to
be published by agent α.
1 Function ComputeSharedDG(α) is
2 ∆
0
← FD(α);
3 loop
4 if ∃∆
1
: ∆
0
→ ∆
1
then
5 ∆
0
← ∆
1
;
6 else
7 break;
8 end
9 end
10 if ∆
0
contains only public actions then
11 return ∆
0
;
12 else
13 return MD(α);
14 end
15 end
To avoid possible action confusion caused by
value renaming, we suppose that actions are assigned
unique ids which are preserved by the reduction, and
that plans are sequences of these ids.
The consequences of the theorem are discussed in
the following section.
5.3 Recognizing Simply Dependent
Problems
Let us have an MA-STRIPS problem Π where
pre(a) ⊆ del(a) holds for every internal action a. Sup-
pose that every agent α can reduce its full dependency
collection FD(α) to a state where it contains no inter-
nal action. Then there is D such that D ∼FD(Π) and
hence D 'FD(Π) by Theorem 4. Hence Π is sim-
ply dependent and its public solution can be found
without agent interaction, provided all the agents al-
low to publish D . Important idea here is that publicly
equivalent dependency graphs do not need to reveal
the same amount of sensitive information. Moreover
when D ∼MD(α) then Π is independent and can be
solved without any interaction and without revealing
other than public information. This gives us an algo-
rithmic approach to recognize some independent and
simply dependent problems.
6 PLANNING WITH
DEPENDENCY GRAPHS
This section describes how agents use dependency
graphs in order to solve MA-STRIPS problem Π (Al-
gorithm 3). At first, every agent computes the de-
Algorithm 3: Distributed planning with depen-
dency graphs.
1 Function DgPlanDistributed(α) is
2 ∆ ← ComputeSharedDG(α);
3 send ∆ to other agents;
4 construct D from other agent’s graphs;
5 compute local problem Π.
D
α;
6 return MaPlanDistributed(Π.
D
α);
7 end
pendency graph it is willing to share using function
ComputeSharedDG described by Algorithm 2. Ev-
ery agent α starts with the full dependency graph
FD(α) and tries to apply reduction operations repeat-
edly as long as it is possible. When the resulting re-
duced dependency graph ∆
0
contains only public ac-
tions, then the agent publishes ∆
0
. Otherwise, the
agent publishes only the minimal dependency graph
MD(α). Algorithm 2 clearly terminates for every in-
put because every reduction decreases the number of
nodes in the dependency graph. Hence the algorithm
loop (lines 3–9 in Algorithm 2) can not be iterated
more than n times when n is the count of nodes in
FD(α). Moreover, every reduction operation can be
performed in a time polynomial to the size of the
problem, and thus the whole algorithm is polynomial-
time.
Once the shared dependency graph ∆ is computed,
Algorithm 3 continues by sending ∆ to other agents.
Then shared dependency graphs of other agents are
received. This allows every agent to complete the
dependency collection D , and to construct the local
problem Π.
D
α. The rest of the planning procedure
is the same as in the case of Algorithm 1.
The algorithm can be further simplified when all
the agents succeeds in reducing FD(α) to an equiva-
lent dependency graph without internal actions, that
is, when Π is provably simply dependent. Then it is
enough to select one agent to compute public solu-
tion of Π. When at least one agent α fails to share
dependency collection equivalent to the full depen-
dency collection FD(α) then iterated negotiation is re-
quired. When some agent α (but not all the agents)
succeeds in reducing FD(α) then every plan created
by any other agent will be automatically α-extensible.
7 EXPERIMENTS
For experimental evaluation we use benchmark prob-
lems from the CoDMAP’15 competition
2
. The
2
See http://agents.fel.cvut.cz/codmap
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
188
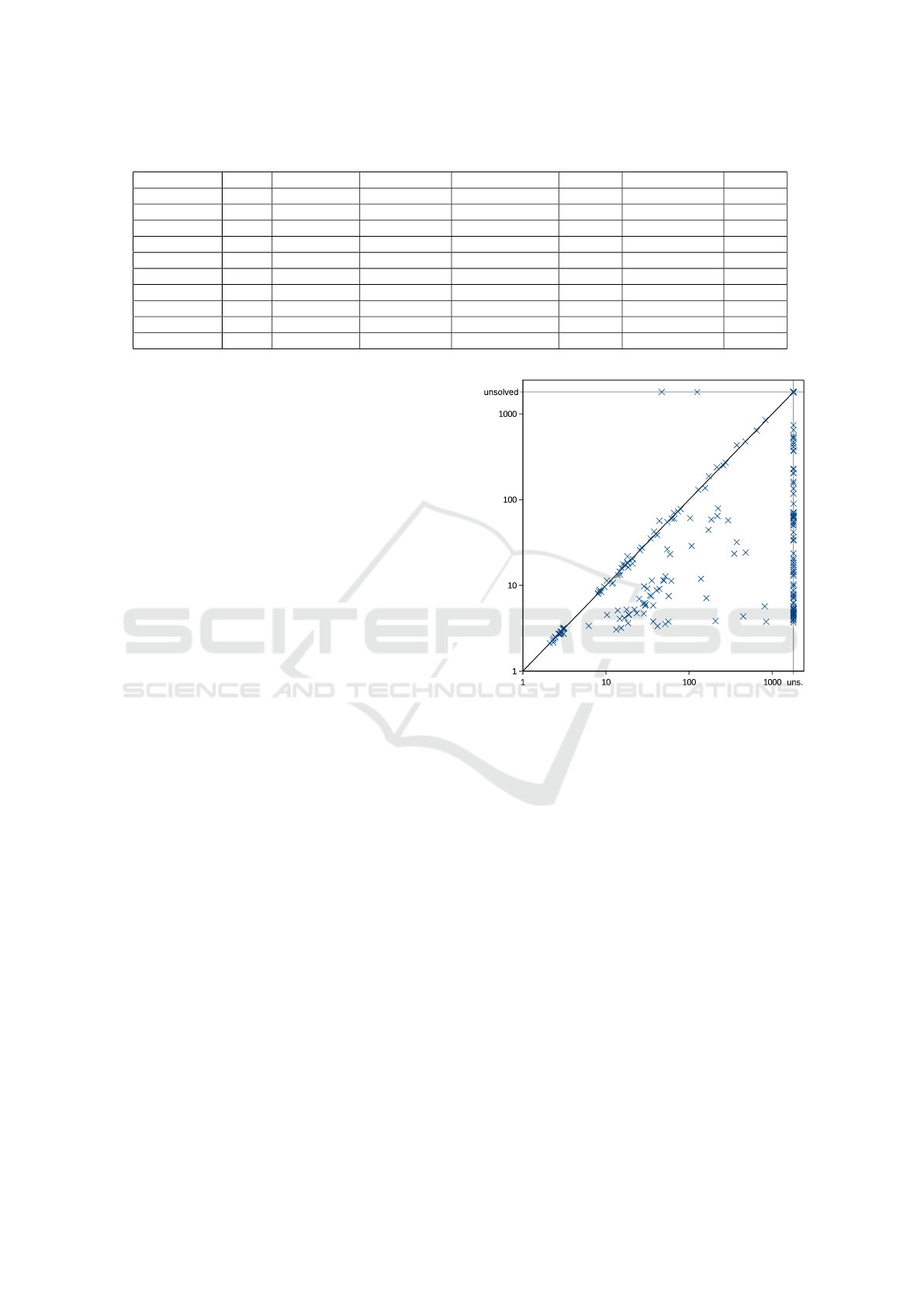
Table 1: Results of the analysis of internal dependencies of public actions in benchmark domains.
Domain Facts Public facts Merge facts Fact disclosure Actions Public actions Success
Blocksworld 787 733 53 100 % 1368 1368 100 %
Depots 1203 1139 56 85 % 2007 2007 100 %
Driverlog 1532 1419 16 25 % 7682 7426 100 %
Elevators 509 343 43 29 % 2060 1767 70 %
Logitics 240 154 56 63 % 342 298 100 %
Rovers 2113 1251 31 3 % 3662 1555 13 %
Satellite 846 578 0 0 % 8839 914 1 %
Taxi 177 173 0 0 % 107 107 100 %
Woodworing 1448 1425 7 27 % 4126 4126 100 %
Zenotravel 1349 1204 0 0 % 13516 2364 0 %
benchmark set contains 12 domains with 20 problems
per domain. Each agent has its own domain and prob-
lem files containing description of known facts and
actions. Additionally, some facts/predicates are spec-
ified as private and thus should not be communicated
to other agents. The privacy classification roughly
corresponds to MA-STRIPS.
We firstly present analysis of internal dependen-
cies and their reductions in Section 7.1. In Sec-
tion 7.2, we present results independently evaluated
by organizers of the CoDMAP’15 competition.
7.1 Domain Analysis
In this section we present analysis of internal depen-
dencies of public action in the benchmark problems.
We have evaluated internal dependencies of pub-
lic actions within benchmark problems by construct-
ing full dependency graph for every agent in every
benchmark problem. We have applied Algorithm 2 to
reduce full dependency graphs to an irreducible pub-
licly equivalent dependency graph. The results of the
analysis are presented in Table 1. The table columns
have the following meaning. Column (Facts) repre-
sents an average number of all facts in a domain prob-
lem. Column (Public facts) represents an average
number of public facts in a domain problem. Column
(Merge facts represents an average size of facts(∆)
in the resulting irreducible dependency graph. Col-
umn (Fact disclosure) represents the percentage of
published merge facts with respect to all the internal
facts. Column (Actions) represents an average num-
ber of all actions in a domain problem. Column (Pub-
lic actions) represents an average number of public
actions in a domain problem. Column (Success) rep-
resents the percentage of agents capable of reducing
their full dependency graph to to a publicly equivalent
graph without internal actions.
We can see that five of the benchmark domains,
namely Blocksworld, Depots, Driverlog, Logistics,
Taxi, Wireless, and Woodworking were found simply
dependent. All the problems in these domains can be
Figure 2: Comparison of planning times (in seconds) of
PSM-VR algorithm without (X axis) and with (Y axis) in-
ternal problem reduction.
solved by solving a local problem of a single agent.
On the contrary, in most problems of domains Rovers,
Satellite, and Zenotravel, none of the agents were able
to reduce its full dependency graph so that it con-
tains no internal actions. Hence the agents in these
domain publish only the minimal dependency graphs
and hence the analysis does not help in solving them.
Finally, in Elevators domain, some of the agents suc-
ceeded in reducing their full dependency graphs and
thus the analysis can partially help to solve them.
7.2 Experimental Results
To evaluate the impact of dependency analysis, we
use our PSM-based planners (To
ˇ
zi
ˇ
cka et al., 2014b)
submitted to the CoDMAP’15 competition. Namely,
we use planner PSM-VR (To
ˇ
zi
ˇ
cka et al., 2015b) and
its extension with dependency analysis PSM-VRD.
Figure 2 evaluates the impact of the dependency
analysis on CoDMAP benchmark problems. For each
Recursive Reductions of Internal Dependencies in Multiagent Planning
189
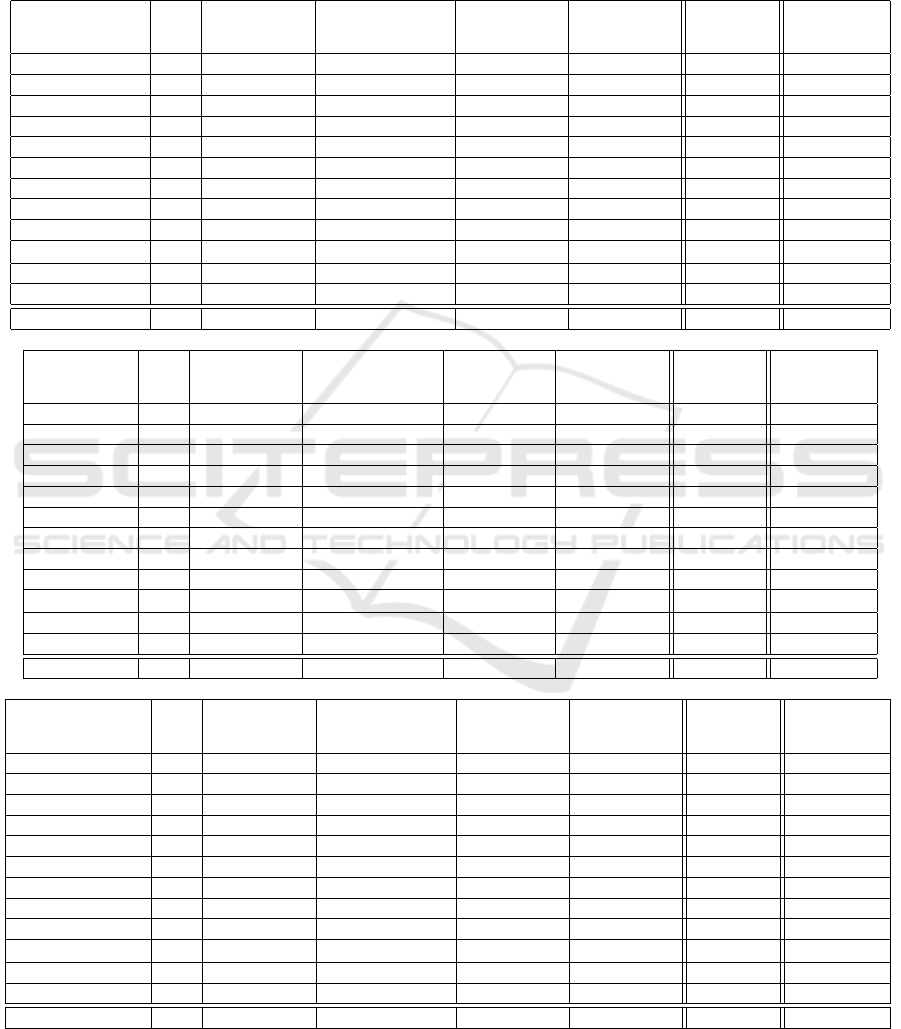
Table 2: Results at CoDMAP competition (http://agents.fel.cvut.cz/codmap/results/). Top table shows overall
coverage of solved problem instances. Middle table shows IPC score over the plan quality Q (a sum of Q
∗
/Q over all
problems, where Q
∗
is the cost of an optimal plan, or of the best plan found by any of the planners for the given problem
during the competition). Bottom table shows IPC Agile score over the planning time T (a sum of 1/(1 + log
10
(T /T
∗
)) over
all problems, where T
∗
is the runtime of the fastest planner for the given problem during the competition).
‡
This is optimal
planner.
†
This post-submission domain was not supported by the planner parser. These results are presented with the consent
of CoDMAP organizers.
Domain #
MAPlan
LM-Cut
‡
MAPlan
MA-LM-Cut
‡
MH-FMAP
MAPlan
FF+DTG
PSM-VR PSM-VRD
Blocksworld 20 2 1 0 14 12 20
Depots 20 5 2 2 10 1 16
Driverlog 20 15 9 18 18 16 20
Elevators 20 2 0 9 9 2 5
Logitics 20 4 5 4 16 0 16
Openstacks 20 1 1 8 18 14 18
Rovers 20 2 4 18 19 13 13
Satellite 20 13 4 4 14 7 17
Taxi 20 19 14 20 19 9 20
Wireless 20 3 2 0 4 0
†
0
†
Woodworing 20 3 4 8 14 9 19
Zenotravel 20 6 6 16 19 16 16
Total Coverage 240 75 52 107 174 99 180
Domain #
MAPlan
LM-Cut
‡
MAPlan
MA-LM-Cut
‡
MH-FMAP
MAPlan
FF+DTG
PSM-VR PSM-VRD
Blocksworld 20 2 1 0 7 11 17
Depots 20 5 2 2 6 1 15
Driverlog 20 15 9 17 12 14 16
Elevators 20 2 0 8 6 1 4
Logitics 20 4 5 4 13 0 15
Openstacks 20 1 1 8 18 9 12
Rovers 20 2 4 18 16 5 5
Satellite 20 13 4 4 10 6 13
Taxi 20 19 14 17 15 6 16
Wireless 20 3 2 0 4 0
†
0
†
Woodworing 20 3 4 7 13 8 17
Zenotravel 20 6 6 15 15 10 10
IPC Score 240 75 52 100 135 72 140
Domain #
MAPlan
LM-Cut
‡
MAPlan
MA-LM-Cut
‡
MH-FMAP
MAPlan
FF+DTG
PSM-VR PSM-VRD
Blocksworld 20 1 0 0 14 5 14
Depots 20 3 1 1 9 0 14
Driverlog 20 10 4 11 17 7 14
Elevators 20 1 0 4 8 1 4
Logitics 20 3 2 2 13 0 14
Openstacks 20 0 0 3 18 7 8
Rovers 20 1 1 7 19 6 6
Satellite 20 10 2 1 13 3 12
Taxi 20 14 7 10 19 3 15
Wireless 20 3 2 0 2 0
†
0
†
Woodworing 20 2 3 4 9 5 18
Zenotravel 20 5 4 10 18 8 8
IPC Agile Score 240 52 27 52 159 45 127
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
190

problem, a point is drawn at the position correspond-
ing to the runtime without dependency analysis (x-
coordinate) and the runtime with dependency analy-
sis (y-coordinate). Hence the points below the diag-
onal constitute improvements. Results show that the
dependency analysis decreases overall planning time
of PSM algorithm. We can see that in few cases the
time increases which is caused by the time consumed
by reduction process. Also, by publishing additional
facts, the problem size can grow and thus it can be-
come harder to solve.
Table 2 shows official results of the CoDMAP
competition. We can see that the dependency anal-
ysis significantly improved the performance of PSM-
VR planner. Moreover, PSM-VRD achieved the over-
all best coverage in 8 out of 12 domains. As expected,
the highest coverage directly corresponds to the suc-
cess of dependency analysis. The table also shows
results of two additional criteria comparing the qual-
ity (IPC Score) of solutions and the time (IPC Agile
Score) need to find the solution. In both criteria PSM-
VRD performed very well even though it was outper-
formed by MAPlan-FF+DTG planner in the IPC Ag-
ile Score.
8 CONCLUSIONS
We have formally and semantically defined inter-
nally independent and simply dependent MA-STRIPS
problems and proposed a set of reduction rules utiliz-
ing the underlying dependency graph. To identify in-
ternally independent and simply dependent problems,
we have proposed technique which can build a full de-
pendency graph and try to reduce it to an irreducible
publicly equivalent dependency graph. This provides
an algorithmic procedure for recognizing provably in-
ternally independent and simply dependent problems.
We have shown that provably independent and sim-
ply dependent problems can be solved easily without
agent interaction. The proposed reduction rules were
defined over structural information of the dependency
graph and provided possibly recursive removal of su-
perfluous facts and actions by analysis of simple de-
pendency, cycles, equivalency, and state invariants.
We experimentally showed that reduction of the
standard multiagent planning benchmarks using the
dependencies provides overall 71% downsizing and
nearly doubled the number of solved problems in
comparison to the same algorithm used without the
reductions. Finally, in comparison with the latest dis-
tributed multiagent planners the proposed approach
outperformed all and won the distributed track of the
recent multiagent planning competition CoDMAP.
ACKNOWLEDGEMENTS
This research was supported by the Czech Sci-
ence Foundation (no. 13-22125S and 15-20433Y)
and by the Czech Ministry of Education (no.
SGS13/211/OHK3/3T/13). Access to computing and
storage facilities owned by parties and projects con-
tributing to the National Grid Infrastructure MetaCen-
trum, provided under the program ”Projects of Large
Infrastructure for Research, Development, and Inno-
vations” (LM2010005), is greatly appreciated.
REFERENCES
B
¨
ackstr
¨
om, C., Jonsson, A., and Jonsson, P. (2012).
Macros, reactive plans and compact representations.
In ECAI 2012, pages 85–90.
Brafman, R. I. and Domshlak, C. (2008). From one to
many: Planning for loosely coupled multi-agent sys-
tems. In ICAPS’08, pages 28–35.
Chen, Y. and Yao, G. (2009). Completeness and optimal-
ity preserving reduction for planning. Proceedings of
21st IJCAI, pages 1659–1664.
Chrpa, L. (2010). Generation of macro-operators via inves-
tigation of action dependencies in plans. Knowledge
Eng. Review, 25(3):281–297.
Coles, A. and Coles, A. (2010). Completeness-preserving
pruning for optimal planning. In Proceedings of 19th
ECAI, pages 965–966.
Fikes, R. and Nilsson, N. (1971). STRIPS: A new approach
to the application of theorem proving to problem solv-
ing. In IJCAI’71, pages 608–620.
Haslum, P. (2007). Reducing Accidental Complexity in
Planning Problems. In Proceedings of 20th IJCAI,
pages 1898–1903.
Jonsson, A. (2009). The role of macros in tractable plan-
ning. Journal of Artificial Intelligence Research,
36:471–511.
Jonsson, P. and B
¨
ackstr
¨
om, C. (1998). Tractable plan exis-
tence does not imply tractable plan generation. Annals
of Mathematics and Artificial Intelligence, 22:281–
296.
Nissim, R. and Brafman, R. I. (2012). Multi-agent A* for
parallel and distributed systems. In Proceedings of
AAMAS’12, pages 1265–1266.
To
ˇ
zi
ˇ
cka, J., Jakub
˚
uv, J., Durkota, K., Komenda, A., and
P
ˇ
echou
ˇ
cek, M. (2014a). Multiagent Planning Sup-
ported by Plan Diversity Metrics and Landmark Ac-
tions. In Proceedings ICAART’14.
To
ˇ
zi
ˇ
cka, J., Jakub
˚
uv, J., and Komenda, A. (2014b). Gener-
ating multi-agent plans by distributed intersection of
finite state machines. In ECAI2014, pages 1111–1112.
To
ˇ
zi
ˇ
cka, J., Jakub
˚
uv, J., and Komenda, A. (2015a). On
internally dependent public actions in multiagent
planning. In Proceedings of DMAP Workshop of
ICAPS’15.
To
ˇ
zi
ˇ
cka, J., Jakub
˚
uv, J., and Komenda, A. (2015b). PSM-
based Planners Description for CoDMAP 2015 Com-
petition. In CoDMAP-15.
Recursive Reductions of Internal Dependencies in Multiagent Planning
191
