
A Complementarity Problem Formulation for Chance-constraine Games
Vikas Vikram Singh
1
, Oualid Jouini
2
and Abdel Lisser
1
1
Laboratoire de Recherche en Informatique, Universit
´
e Paris Sud XI, B
ˆ
at 650, 91405, Orsay, France
2
Laboratoire G
´
enie Industriel, Ecole Centrale Paris, Grande Voie des Vignes, 92290, Ch
ˆ
atenay-Malabry, France
Keywords:
Chance-Constrained Game, Nash Equilibrium, Normal Distribution, Cauchy Distribution, Nonlinear Com-
plementarity Problem, Linear Complementarity Problem.
Abstract:
We consider a two player bimatrix game where the entries of each player’s payoff matrix are independent ran-
dom variables following a certain distribution. We formulate this as a chance-constrained game by considering
that the payoff of each player is defined by using a chance-constraint. We consider the case of normal and
Cauchy distributions. We show that a Nash equilibrium of the chance-constrained game corresponding to nor-
mal distribution can be obtained by solving an equivalent nonlinear complementarity problem. Further if the
entries of the payoff matrices are also identically distributed with non-negative mean, we show that a strategy
pair, where each player’s strategy is the uniform distribution on his action set, is a Nash equilibrium of the
chance-constrained game. We show that a Nash equilibrium of the chance-constrained game corresponding to
Cauchy distribution can be obtained by solving an equivalent linear complementarity problem.
1 INTRODUCTION
It is well known that there exists a mixed strategy sad-
dle point equilibrium for a two player zero sum ma-
trix game (Neumann, 1928). John Nash (Nash, 1950)
showed that there exists a mixed strategy equilibrium
for the games with finite number of players where
each player has finite number of actions. Later such
equilibrium was called Nash equilibrium. For two
player case the game considered in (Nash, 1950) can
be represented by m ×n matrices A and B. The matri-
ces A = [a
i j
] and B = [b
i j
] denote the payoff matrices
of player 1 and player 2 respectively, and m, n denote
the number of actions of player 1 and player 2 respec-
tively. Let I = {1,2,··· ,m}, and J = {1,2,··· ,n}
be the action sets of player 1 and player 2 respec-
tively. The sets I and J are also called the sets of pure
strategies of player 1 and player 2 respectively. The
set of mixed strategies of each player is defined by
the set of all probability distributions over his action
set. Let X = {x = (x
1
,x
2
,··· , x
m
)|
∑
m
i=1
x
i
= 1, x
i
≥
0, ∀ i ∈ I} and Y = {y = (y
1
,y
2
,··· , y
n
)|
∑
n
j=1
y
j
=
1,y
j
≥ 0, ∀ j ∈ J} be the sets of mixed strategies of
player 1 and player 2 respectively. For a given strat-
egy pair (x,y), the payoffs of player 1 and player 2
are given by x
T
Ay and x
T
By respectively; T denotes
the transposition. For a fixed strategy of one player,
another player seeks for a strategy that gives him the
highest payoff among all his other strategies. Such a
strategy is called the best response strategy. The set of
best response strategies of player 1 for a fixed strategy
y of player 2 is given by
BR(y) =
¯x|¯x
T
Ay ≥x
T
Ay, ∀ x ∈X
.
The set of best response strategies of player 2 for a
fixed strategy x of player 1 is given by
BR(x) =
¯y|x
T
B ¯y ≥ x
T
By, ∀ y ∈Y
.
A strategy pair (x
∗
,y
∗
) is said to be a Nash equilib-
rium if and only if x
∗
∈ BR(y
∗
) and y
∗
∈ BR(x
∗
). A
Nash equilibrium of above bimatrix game can be ob-
tained by solving a linear complementarity problem
(LCP) (Lemke and Howson, 1964).
Both (Nash, 1950) and (Neumann, 1928) consid-
ered the games where the payoffs of the players are
exact real values. In some cases the payoffs of play-
ers may be within certain ranges. In (Collins and Hu,
2008) these situations are modeled as interval val-
ued matrix game using fuzzy theory. The compu-
tational approaches have been proposed to solve in-
terval valued matrix game
see (Deng-Feng Li and
Zhang, 2012), (Li, 2011), (Mitchell et al., 2014)
.
However, in many situations payoffs are random vari-
ables due to uncertainty which arises from various
external factors. The wholesale electricity markets
are the good examples
see (Mazadi et al., 2013),
(Couchman et al., 2005), (Valenzuela and Mazum-
dar, 2007), (Wolf and Smeers, 1997)
. One way to
58
Singh, V., Jouini, O. and Lisser, A.
A Complementarity Problem Formulation for Chance-constraine Games.
DOI: 10.5220/0005754800580067
In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 58-67
ISBN: 978-989-758-171-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

handle this type of game is by taking the expecta-
tion of random payoffs and consider the correspond-
ing deterministic game
see (Valenzuela and Mazum-
dar, 2007), (Wolf and Smeers, 1997)
. Some recent
papers on the games with random payoffs using ex-
pected payoff criterion include (Ravat and Shanbhag,
2011), (Xu and Zhang, 2013), (Jadamba and Raciti,
2015), (DeMiguel and Xu, 2009).
The expected payoff criterion does not take a
proper account of stochasticity in the cases where
the observed sample payoffs are large amounts with
very small probabilities. These situations are bet-
ter handled by considering a satisficing payoff crite-
rion that uses chance-constrained programming
see
(Charnes and Cooper, 1963), (Cheng and Lisser,
2012), (Pr
´
ekopa, 1995)
. Under satisficing payoff
criterion the payoff of a player is defined using a
chance-constraint and for this reason these games are
called chance-constrained games. There are few pa-
pers on zero sum chance-constrained games available
in the literature
see (Blau, 1974), (Cassidy et al.,
1972), (Charnes et al., 1968), (Song, 1992)
. Re-
cently, a chance-constrained game with finite num-
ber of players is considered in (Singh et al., 2015a),
(Singh et al., 2015b) where authors showed the exis-
tence of a mixed strategy Nash equilibrium. In (Singh
et al., 2015a), the case where the random payoff vec-
tor of each player follows a certain distribution is con-
sidered. In particular, the authors considered the case
where the components of the payoff vector of each
player are independent normal random variables, and
they also consider the case where the payoff vector
of each player follows a multivariate elliptically sym-
metric distribution. In (Singh et al., 2015b), the case
where the distribution of payoff vector of each player
is not known completely is considered. The authors
consider a distributionally robust approach to handle
these games. In application regimes some chance-
constrained game models have been considered, e.g.,
see (Mazadi et al., 2013), (Couchman et al., 2005).
In (Mazadi et al., 2013), the randomness in payoffs is
due to the installation of wind generators on electric-
ity market, and they consider the case of independent
normal random variables. Later, for better represen-
tation and ease in computation the authors, in detail,
considered the case where only one wind generator
is installed in the electricity market. In (Couchman
et al., 2005), the payoffs are random due to uncertain
demand from consumers which is assumed to be nor-
mally distributed.
In this paper, we consider the case where the en-
tries of the payoff matrices are independent random
variables following the same distribution (possibly
with different parameters). For a given strategy pair
(x,y), the payoff of each player is a random vari-
able which is a linear combination of the indepen-
dent random variables. We consider the distributions
that are closed under a linear combination of the in-
dependent random variables. The normal and Cauchy
distributions satisfy this property. We consider each
distribution separately. We show that a Nash equi-
librium of the chance-constrained game correspond-
ing to normal distribution can be obtained by solv-
ing an equivalent nonlinear complementarity problem
(NCP). Further we consider a special case where the
entries of the payoff matrices are also identically dis-
tributed with non-negative mean. We show that a
strategy pair, where each player’s strategy is a uni-
form distribution over his action set, is a Nash equilib-
rium. We show that a Nash equilibrium of the chance-
constrained game corresponding to Cauchy distribu-
tion can be obtained by solving an equivalent LCP.
Now, we describe the structure of rest of the pa-
per. Section 2 contains the definition of a chance-
constrained game. Section 3 contains the comple-
mentarity problem formulation of chance-constrained
game. We conclude the paper in Section 4
2 THE MODEL
We consider two player bimatrix game where the en-
tries of the payoff matrices are random variables. We
denote the random payoff matrices of player 1 and
player 2 by A
w
and B
w
respectively, where w denotes
the uncertainty parameter. Let (Ω,F ,P) be a proba-
bility space. Then, for each i ∈ I, j ∈ J, a
w
i j
: Ω → R,
and b
w
i j
: Ω → R. For each (x,y) ∈ X ×Y , the payoffs
x
T
A
w
y and x
T
B
w
y of player 1 and player 2 respec-
tively would be random variables. We assume that
each player uses satisficing payoff criterion, where
the payoff of each player is defined using a chance-
constraint. At strategy pair (x,y), each player is in-
terested in the highest level of his payoff that he can
attain with at least a specified level of confidence.
The confidence level of each player is given a pri-
ori. We assume that the confidence level of one
player is known to another player. Let α
1
∈ [0,1]
and α
2
∈ [0,1] be the confidence levels of player 1
and player 2 respectively. Let α = (α
1
,α
2
) be a con-
fidence level vector. For a given strategy pair (x, y)
and a given confidence level vector α, the payoff of
player 1 is given by
u
α
1
1
(x,y) = sup{u|P(x
T
A
w
y ≥ u) ≥ α
1
}, (1)
and the payoff of player 2 is given by
u
α
2
2
(x,y) = sup{v|P(x
T
B
w
y ≥ v) ≥ α
2
}. (2)
A Complementarity Problem Formulation for Chance-constraine Games
59

We assume that the probability distributions of the en-
tries of the payoff matrix of one player are known to
another player. Then, for a given α the payoff func-
tion of one player defined above is known to another
player. That is, for a given α the chance constrained
game is a non-cooperative game with complete infor-
mation. For a given α, the set of best response strate-
gies of player 1 against the fixed strategy y of player
2 is given by
BR
α
1
(y) =
¯x ∈X|u
α
1
1
( ¯x,y) ≥ u
α
1
1
(x,y), ∀ x ∈ X
,
and the set of best response strategies of player 2
against the fixed strategy x of player 1 is given by
BR
α
2
(x) =
¯y ∈Y |u
α
2
2
(x, ¯y) ≥u
α
2
2
(x,y), ∀ y ∈Y
.
Next, we give the definition of Nash equilibrium.
Definition 2.1 (Nash equilibrium). For a given con-
fidence level vector α, a strategy pair (x
∗
,y
∗
) is said
to be a Nash equilibrium of the chance-constrained
game if the following inequalities hold:
u
α
1
1
(x
∗
,y
∗
) ≥ u
α
1
1
(x,y
∗
), ∀ x ∈ X ,
u
α
2
2
(x
∗
,y
∗
) ≥ u
α
2
2
(x
∗
,y). ∀ y ∈Y.
3 COMPLEMENTARITY
PROBLEM FOR
CHANCE-CONSTRAINED
GAME
In this section, we consider the case where the en-
tries of payoff matrix A
w
of player 1 are independent
random variables following a certain distribution, and
the entries of payoff matrix B
w
of player 2 are inde-
pendent random variables following a certain distri-
bution. Then, at strategy pair (x,y) the payoff of each
player is a linear combination of the independent ran-
dom variables. We are interested in those probabil-
ity distributions that are closed under a linear com-
bination of the independent random variables. That
is, if Y
1
,Y
2
,··· ,Y
k
are independent random variables
following the same distribution (possibly with differ-
ent parameters), for any b ∈ R
k
, the distribution of
∑
k
i=1
b
i
Y
i
is same as Y
i
up to parameters. The normal
and Cauchy distributions satisfy the above property
(Johnson et al., 1994). We discuss each probability
distribution mentioned above separately. For the case
of normal distribution we show that a Nash equilib-
rium of the chance-constrained game can be obtained
by solving an equivalent NCP, and for the case of
Cauchy distribution we show that a Nash equilibrium
of the chance-constrained game can be obtained by
solving an equivalent LCP.
3.1 Payoffs Following Normal
Distribution
We assume that all the components of matrix A
w
are independent normal random variables, where the
mean and variance of a
w
i j
, i ∈ I, j ∈ J, are µ
1,i j
and
σ
2
1,i j
respectively, and all the components of ma-
trix B
w
are independent normal random variables,
where the mean and variance of b
w
i j
, i ∈ I, j ∈ J,
are µ
2,i j
and σ
2
2,i j
respectively. For a given strat-
egy pair (x,y), x
T
A
w
y follows a normal distribution
with mean µ
1
(x,y) =
∑
i∈I, j∈J
µ
1,i j
x
i
y
j
and variance
σ
2
1
(x,y) =
∑
i∈I, j∈J
x
2
i
y
2
j
σ
2
1,i j
, and x
T
B
w
y follows a nor-
mal distribution with mean µ
2
(x,y) =
∑
i∈I, j∈J
µ
2,i j
x
i
y
j
and variance σ
2
2
(x,y) =
∑
i∈I, j∈J
x
2
i
y
2
j
σ
2
2,i j
. Then,
Z
N
1
=
x
T
A
w
y−µ
1
(x,y)
σ
1
(x,y)
and Z
N
2
=
x
T
B
w
y−µ
2
(x,y)
σ
2
(x,y)
follow a
standard normal distribution. Let F
−1
Z
N
1
(·) and F
−1
Z
N
2
(·)
be the quantile functions of a standard normal distri-
bution. From (1), for a given strategy pair (x,y) and
a given confidence level α
1
, the payoff of player 1 is
given by
u
α
1
1
(x,y) = sup{u|P(x
T
A
w
y ≥u) ≥ α
1
}
= sup{u|P(x
T
A
w
y ≤u) ≤ 1 −α
1
}
= sup
u|F
Z
N
1
u −µ
1
(x,y)
σ
1
(x,y)
≤ 1 −α
1
= sup
n
u|u ≤ µ
1
(x,y) + σ
1
(x,y)F
−1
Z
N
1
(1 −α
1
)
o
.
That is,
u
α
1
1
(x,y) =
∑
i∈I, j∈J
µ
1,i j
x
i
y
j
+
∑
i∈I, j∈J
x
2
i
y
2
j
σ
2
1,i j
!
1/2
F
−1
Z
N
1
(1 −α
1
).
(3)
Similarly, from (2) for a given strategy pair (x,y) and
a given confidence level α
2
, the payoff of player 2 is
given by
u
α
2
2
(x,y) =
∑
i∈I, j∈J
µ
2,i j
x
i
y
j
+
∑
i∈I, j∈J
x
2
i
y
2
j
σ
2
2,i j
!
1/2
F
−1
Z
N
2
(1 −α
2
).
(4)
Theorem 3.1. Consider a bimatrix game (A
w
,B
w
).
If all the components of matrix A
w
are independent
normal random variables, and all the components
of matrix B
w
are also independent normal random
variables, there exists a Nash equilibrium for the
chance-constrained game in mixed strategies for all
α ∈ [0.5,1]
2
.
Proof. The proof follows from (Singh et al., 2015a)
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
60

3.1.1 Nonlinear Complementarity Problem
Formulation
The payoff function of player 1 defined by (3) can be
written as follows:
u
α
1
1
(x,y) = x
T
µ
1
(y) + ||Σ
1/2
1
(y)x||F
−1
Z
N
1
(1 −α
1
), (5)
where || · || is the Euclidean norm, and
µ
1
(y) =
µ
1,i
(y)
i∈I
is an m × 1 vector where
µ
1,i
(y) =
∑
j∈J
µ
1,i j
y
j
, and Σ
1
(y) is an m × m
diagonal matrix whose ith diagonal entry
Σ
1,ii
(y) =
∑
j∈J
σ
2
1,i j
y
2
j
. Similarly, the payoff
function of player 2 defined by (4) can be written as
follows:
u
α
2
2
(x,y) = y
T
µ
2
(x) + ||Σ
1/2
2
(x)y||F
−1
Z
N
2
(1 −α
2
), (6)
where µ
2
(x) =
µ
2, j
(x)
j∈J
is an n ×1 vector where
µ
2, j
(x) =
∑
i∈I
µ
2,i j
x
i
, and Σ
2
(x) is an n × n diag-
onal matrix whose jth diagonal entry Σ
2, j j
(x) =
∑
i∈I
σ
2
2,i j
x
2
i
. For fixed y ∈ Y and α
1
∈ [0.5, 1], the
payoff function u
α
1
1
(·,y) of player 1 defined by (5)
is a concave function of x because F
−1
Z
N
1
(1 −α
1
) ≤ 0
for all α
1
∈ [0.5,1]. Similarly, for fixed x ∈ X and
α
2
∈ [0.5, 1], the payoff function u
α
2
2
(x,·) of player 2
defined by (6) is a concave function of y.
Then, for a fixed y ∈Y and α
1
∈[0.5, 1], a best re-
sponse strategy of player 1 can be obtained by solving
the convex quadratic program [QP1] given below:
[QP1] max
x
x
T
µ
1
(y) + ||Σ
1/2
1
(y)x||F
−1
Z
N
1
(1 −α
1
)
s.t
(i)
∑
i∈I
x
i
= 1
(ii) x
i
≥ 0, i ∈ I.
It is easy to see that a feasible solution of [QP1]
satisfies the linear independence constraint qualifica-
tion. Then, Karush-Kuhn-Tucker (KKT) conditions
of [QP1] will be necessary and sufficient conditions
for optimal solution
for details see (Nocedal and
Wright, 2006), (Bazaraa et al., 2006)
. For a given
vector ν, ν ≥ 0 means ν
k
≥ 0, for all k. The equal-
ity constraint of [QP1] can be replaced by two equiv-
alent inequality constraints, and the free Lagrange
multiplier corresponding to equality constraint can be
replaced by the difference of two nonnegative vari-
ables. By using these transformations, the best re-
sponse strategy of player 1 can be obtained by solving
the following KKT conditions of [QP1]:
0 ≤ x ⊥−µ
1
(y) −
Σ
1
(y)x ·c
α
1
||Σ
1/2
1
(y)x||
−λ
1
e
m
+ λ
2
e
m
≥ 0,
0 ≤ λ
1
⊥
∑
i∈I
x
i
−1 ≥0,
0 ≤ λ
2
⊥ 1 −
∑
i∈I
x
i
≥ 0,
(7)
where e
m
is the m × 1 vector of ones, and
c
α
1
= F
−1
Z
N
1
(1 − α
1
), and ⊥ means that element-
wise equality must hold at one or both sides. For
fixed x ∈ X and α
2
∈ [0.5,1], a best response strat-
egy of player 2 can be obtained by solving the convex
quadratic program [QP2] given below:
[QP2] max
y
y
T
µ
2
(x) + ||Σ
1/2
2
(x)y||F
−1
Z
N
2
(1 −α
2
)
s.t
(i)
∑
j∈J
y
j
= 1
(ii) y
j
≥ 0, j ∈J.
From the similar arguments used in previous case, the
best response strategy of player 2 can be obtained by
solving the following KKT conditions of [QP2]:
0 ≤ y ⊥−µ
2
(x) −
Σ
2
(x)y ·c
α
2
||Σ
1/2
2
(x)y||
−λ
3
e
n
+ λ
4
e
n
≥ 0,
0 ≤ λ
3
⊥
∑
j∈J
y
j
−1 ≥0,
0 ≤ λ
4
⊥ 1 −
∑
j∈J
y
j
≥ 0,
(8)
where c
α
2
= F
−1
Z
N
2
(1 −α
2
).
Nonlinear Complementarity Problem: By combin-
ing the KKT conditions given by (7) and (8), a Nash
equilibrium (x, y) can be obtained by solving the fol-
lowing NCP:
0 ≤ ζ ⊥ G(ζ) ≥ 0, (9)
where ζ,G(ζ) ∈ R
m+n+4
are given below:
ζ
T
= (x
T
,y
T
,λ
1
,λ
2
,λ
3
,λ
4
),
G(ζ) =
−µ
1
(y) −
Σ
1
(y)x·c
α
1
||Σ
1/2
1
(y)x||
−λ
1
e
m
+ λ
2
e
m
−µ
2
(x) −
Σ
2
(x)y·c
α
2
||Σ
1/2
2
(x)y||
−λ
3
e
n
+ λ
4
e
n
∑
i∈I
x
i
−1
1 −
∑
i∈I
x
i
∑
j∈J
y
j
−1
1 −
∑
j∈J
y
j
.
A Complementarity Problem Formulation for Chance-constraine Games
61

For given k, l, 0
k×l
is a k ×l zero matrix and 0
k
is a
k ×1 zero vector. Define,
Q =
0
m×m
−µ
1
−e
m
e
m
0
m
0
m
−µ
T
2
0
n×n
0
n
0
n
−e
n
e
n
e
T
m
0
T
n
0 0 0 0
−e
T
m
0
T
n
0 0 0 0
0
T
m
e
T
n
0 0 0 0
0
T
m
−e
T
n
0 0 0 0
,
where µ
1
= (µ
1,i j
)
i∈I, j∈J
, µ
2
= (µ
2,i j
)
i∈I, j∈J
are m ×n
matrices. Define,
R(ζ) =
−c
α
1
·Σ
1
(y)
||Σ
1/2
1
(y)x||
0
m×n
0
m×4
0
n×m
−c
α
2
·Σ
2
(x)
||Σ
1/2
2
(x)y||
0
n×4
0
4×m
0
4×n
0
4×4
, r =
0
m
0
n
−1
1
−1
1
.
Then, G(ζ) =
Q + R(ζ)
ζ + r.
Theorem 3.2. Consider a bimatrix game (A
w
,B
w
)
where all the components of matrix A
w
are indepen-
dent normal random variables, and all the compo-
nents of matrix B
w
are also independent normal ran-
dom variables. Let ζ
∗T
= (x
∗T
,y
∗T
,λ
∗
1
,λ
∗
2
,λ
∗
3
,λ
∗
4
) be
a vector. Then, the strategy part (x
∗
,y
∗
) of ζ
∗
is a
Nash equilibrium of the chance-constrained game for
a given α ∈ [0.5,1]
2
if and only if ζ
∗
is a solution of
NCP (9).
Proof. Let α ∈ [0.5,1]
2
, then (x
∗
,y
∗
) is a Nash equi-
librium of the chance-constrained game if and only if
x
∗
is an optimal solution of [QP1] for fixed y
∗
and y
∗
is an optimal solution of [QP2] for fixed x
∗
. Since,
[QP1] and [QP2] are convex optimization problems
and linear independence constraint qualification holds
at all feasible points, then the KKT conditions (7) and
(8) are both necessary and sufficient conditions for
optimality. Then, the proof follows by combining the
KKT conditions (7), (8).
For computational purpose freely available
solvers for complementarity problems can be used,
e.g., see (Schmelzer, 2012), (Ferris and Munson,
2000), (Munson, 2000).
3.1.2 Special Case
Here we consider the case where the components of
payoff matrices A
w
and B
w
are independent as well
as identically distributed. We assume that the com-
ponents of matrix A
w
are independent and identi-
cally distributed (i.i.d.) normal random variables with
mean µ
1
≥ 0 and variance σ
2
1
, and the components
of matrix B
w
are i.i.d. normal random variables with
mean µ
2
≥ 0 and variance σ
2
2
.
Theorem 3.3. Consider a bimatrix game (A
w
,B
w
)
where all the components of matrix A
w
are i.i.d. nor-
mal random variables with mean µ
1
≥0 and variance
σ
2
1
, and all the components of matrix B
w
are also i.i.d.
normal random variables with mean µ
2
≥0 and vari-
ance σ
2
2
. The strategy pair (x
∗
,y
∗
), where,
x
∗
i
=
1
m
, ∀ i ∈ I, y
∗
j
=
1
n
,∀ j ∈J, (10)
is a Nash equilibrium of the chance-constrained game
for all α ∈ [0.5,1]
2
.
Proof. Fix α ∈ [0.5,1]
2
. From Theorem 3.2, it is
enough to show that there exist (λ
∗
1
,λ
∗
2
,λ
∗
3
,λ
∗
4
) which
together with (x
∗
,y
∗
) defined by (10) is a solution
of NCP (9). For all (x, y), we have µ
1
(y) = µ
1
e
m
and µ
2
(x) = µ
2
e
n
because µ
1,i j
= µ
1
and µ
2,i j
= µ
2
for all i ∈ I, j ∈ J, and Σ
1
(y) = σ
2
1
||y||
2
I
m×m
and
Σ
2
(x) = σ
2
2
||x||
2
I
n×n
because σ
2
1,i j
= σ
2
1
and σ
2
2,i j
= σ
2
2
for all i ∈I, j ∈J; I
k×k
is a k ×k identity matrix. Using
above expressions, we have
G(ζ) =
−µ
1
e
m
−
σ
1
||y||x·c
α
1
||x||
−(λ
1
−λ
2
)e
m
−µ
2
e
n
−
σ
2
||x||y·c
α
2
||y||
−(λ
3
−λ
4
)e
n
∑
i∈I
x
i
−1
1 −
∑
i∈I
x
i
∑
j∈J
y
j
−1
1 −
∑
j∈J
y
j
.
Consider the Lagrange multipliers (λ
∗
1
,λ
∗
2
,λ
∗
3
,λ
∗
4
) as
follows:
λ
∗
1
= −
σ
1
·c
α
1
√
mn
, λ
∗
2
= µ
1
, λ
∗
3
= −
σ
2
·c
α
2
√
mn
, λ
∗
4
= µ
2
.
Since, µ
1
≥ 0, µ
2
≥ 0, and for α ∈ [0.5,1]
2
, c
α
1
≤ 0
and c
α
2
≤0, then, λ
∗
1
≥0, λ
∗
2
≥0, λ
∗
3
≥0, λ
∗
4
≥0. It is
easy to check that (x
∗
,y
∗
,λ
∗
1
,λ
∗
2
,λ
∗
3
,λ
∗
4
) is a solution
of NCP (9). That is, (x
∗
,y
∗
) defined by (10) is a Nash
equilibrium of chance-constrained game.
3.2 Payoffs Following Cauchy
Distribution
We assume that all the components of matrix A
w
are independent Cauchy random variables, where the
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
62

location and scale parameters of a
w
i j
, i ∈ I, j ∈ J,
are µ
1,i j
and σ
1,i j
respectively, and all the compo-
nents of matrix B
w
are independent Cauchy ran-
dom variables, where the location and scale param-
eters of b
w
i j
, i ∈ I, j ∈ J, are µ
2,i j
and σ
2,i j
re-
spectively. Since, a linear combination of the in-
dependent Cauchy random variables is a Cauchy
random variable (Johnson et al., 1994), then, for
a given strategy pair (x,y), the payoff x
T
A
w
y of
player 1 follows a Cauchy distribution with location
parameter µ
1
(x,y) =
∑
i∈I, j∈J
x
i
y
j
µ
1,i j
and scale pa-
rameter σ
1
(x,y) =
∑
i∈I, j∈J
x
i
y
j
σ
1,i j
, and the payoff
x
T
B
w
y of player 2 follows a Cauchy distribution with
location parameter µ
2
(x,y) =
∑
i∈I, j∈J
x
i
y
j
µ
2,i j
and
scale parameter σ
2
(x,y) =
∑
i∈I, j∈J
x
i
y
j
σ
2,i j
. Then,
Z
C
1
=
x
T
A
w
y−µ
1
(x,y)
σ
1
(x,y)
and Z
C
2
=
x
T
B
w
y−µ
2
(x,y)
σ
2
(x,y)
follow a
standard Cauchy distribution. Let F
−1
Z
C
1
(·) and F
−1
Z
C
2
(·)
be the quantile functions of a standard Cauchy dis-
tribution. For more details about Cauchy distribution
see (Johnson et al., 1994). Similar to the normal dis-
tribution case, for a given strategy pair (x,y) and a
given α the payoff of player 1 is given by
u
α
1
1
(x,y) = sup
u|F
Z
C
1
u −µ
1
(x,y)
σ
1
(x,y)
≤ 1 −α
1
= sup
n
u|u ≤ µ
1
(x,y) + σ
1
(x,y)F
−1
Z
C
1
(1 −α
1
)
o
.
That is,
u
α
1
1
(x,y) =
∑
i∈I, j∈J
x
i
y
j
µ
1,i j
+ σ
1,i j
F
−1
Z
C
1
(1 −α
1
)
!
.
(11)
Similarly, the payoff of player 2 is given by
u
α
2
2
(x,y) =
∑
i∈I, j∈J
x
i
y
j
µ
2,i j
+ σ
2,i j
F
−1
Z
C
2
(1 −α
2
)
!
.
(12)
The quantile function of a standard Cauchy distribu-
tion is not finite at 0 and 1. Therefore, we consider
the case of α ∈ (0,1)
2
, so that payoff functions de-
fined by (11) and (12) have finite values. Define, a
matrix
˜
A(α
1
) = ( ˜a
i j
(α
1
))
i∈I, j∈J
, where
˜a
i j
(α
1
) = µ
1,i j
+ σ
1,i j
F
−1
Z
C
1
(1 −α
1
), (13)
and a matrix
˜
B(α
2
) =
˜
b
i j
(α
2
)
i∈I, j∈J
, where
˜
b
i j
(α
2
) = µ
2,i j
+ σ
2,i j
F
−1
Z
C
2
(1 −α
2
). (14)
Then, we can write (11) as
u
α
1
1
(x,y) = x
T
˜
A(α
1
)y,
and we can write (12) as
u
α
2
2
(x,y) = x
T
˜
B(α
2
)y.
Then, for a given α ∈ (0, 1)
2
, the chance-
constrained game is equivalent to the bimatrix game
˜
A(α
1
),
˜
B(α
2
)
.
Theorem 3.4. Consider a bimatrix game (A
w
,B
w
). If
all components of matrix A
w
are independent Cauchy
random variables, and all components of matrix B
w
are also independent Cauchy random variables, there
exists a Nash equilibrium for the chance-constrained
game in mixed strategies for all α ∈ (0,1)
2
.
Proof. For each α ∈ (0, 1)
2
the chance-constrained
game is equivalent to the bimatrix game
˜
A(α
1
),
˜
B(α
2
)
. Hence, the existence of a Nash
equilibrium in mixed strategies follows from (Nash,
1950).
Remark 3.5. For case of i.i.d. Cauchy random vari-
ables each strategy pair (x, y) is a Nash equilibrium
because from (11), (12) the payoff functions of both
the players are constant.
3.2.1 Linear Complementarity Problem
For a given matrix N = [N
i j
], N > 0 means that N
i j
> 0
for all i, j. Let E be the m×n matrix with all 1’s. Let k
be the large enough such that kE
T
−(
˜
B(α
2
))
T
> 0 and
kE −
˜
A(α
1
) > 0. Then, from (Lemke and Howson,
1964), (Lemke, 1965) it follows that for a given α, a
Nash equilibrium of the chance-constrained game can
be obtained by following LCP:
0 ≤ z ⊥Mz + q ≥ 0, (15)
where
z =
x
y
, M =
0
m×m
kE −
˜
A(α
1
)
kE
T
−(
˜
B(α
2
))
T
0
n×n
!
,
q =
−e
m
−e
n
.
Theorem 3.6. Consider a bimatrix game (A
w
,B
w
)
where all the components of matrix A
w
are indepen-
dent Cauchy random variables, and all the compo-
nents of matrix B
w
are also independent Cauchy ran-
dom variables, then,
1. For a α ∈ (0,1)
2
, if (x
∗
,y
∗
) is a Nash equi-
librium of the chance-constrained game, z
∗T
=
x
∗T
k−x
∗T
˜
B(α
2
)y
∗
,
y
∗T
k−x
∗T
˜
A(α
1
)y
∗
is a solution of LCP
(15) at α.
2. For a α ∈ (0,1)
2
, if ¯z
T
= ( ¯x
T
, ¯y
T
) is a solution
of LCP (15), (x
∗
,y
∗
) =
¯x
∑
i∈I
¯x
i
,
¯y
∑
i∈I
¯y
j
is a Nash
equilibrium of the chance-constrained game at α.
A Complementarity Problem Formulation for Chance-constraine Games
63
Proof. For a α ∈(0,1)
2
, the chance-constrained game
corresponding to Cauchy distribution is equivalent
to a bimatrix game
˜
A(α
1
),
˜
B(α
2
)
, where
˜
A(α
1
)
and
˜
B(α
2
) is defined by (13) and (14) respectively.
Then, the proof follows from (Lemke and Howson,
1964).
3.2.2 Numerical Results
We consider few instances of random bimatrix game
of different sizes. We compute the Nash equilib-
ria of corresponding chance-constrained game by us-
ing Lemke-Howson algorithm (Lemke and Howson,
1964). We use the MATLAB code of Lemke-Howson
algorithm given in (Katzwer, 2013).
(i) 3 ×3 random bimatrix game: We consider five
instances of random bimatrix game of size 3 ×3. The
datasets consisting of location parameters µ
1
= [µ
1,i j
],
µ
2
= [µ
2,i j
], and scale parameters σ
1
= [σ
1,i j
], σ
2
=
[σ
2,i j
] of independent Cauchy random variables that
characterizes chance-constrained game are follows:
1. µ
1
=
1 2 1
2 3 1
1 2 3
, σ
1
=
1 1 2
1 2 3
2 1 2
,
µ
2
=
2 1 2
3 2 1
1 2 3
, σ
2
=
1 2 3
3 1 2
2 3 1
.
2. µ
1
=
1 1 2
2 1 1
2 1 3
, σ
1
=
2 2 3
3 2 1
1 2 3
,
µ
2
=
2 2 1
3 2 3
2 1 2
, σ
2
=
1 2 2
2 3 1
2 1 3
.
3. µ
1
=
2 1 3
3 2 1
1 3 2
, σ
1
=
2 3 1
3 1 2
1 2 3
,
µ
2
=
1 2 3
2 1 3
3 1 2
, σ
2
=
1 1 2
1 2 1
3 1 1
.
4. µ
1
=
3 1 2
2 1 3
1 2 3
, σ
1
=
2 4 1
1 2 3
3 2 1
,
µ
2
=
4 1 3
3 2 4
2 1 3
, σ
2
=
5 2 3
3 2 1
4 2 3
.
5. µ
1
=
1 2 1
2 3 1
1 2 3
, σ
1
=
2 2 3
3 2 1
1 2 3
,
µ
2
=
1 2 3
2 1 3
3 1 2
, σ
2
=
5 2 3
3 2 1
4 2 3
.
The entries of µ
1
, σ
1
, µ
2
, σ
2
defined above are the
location and scale parameters of corresponding in-
dependent Cauchy random variables. For example,
in dataset 1 random payoff a
11
is a Cauchy random
variable with location parameter 1 and scale param-
eter 1. The Table 1 summarizes the Nash equilibria
of chance-constrained game corresponding to datasets
given for five instances of 3 ×3 random bimatrix
game.
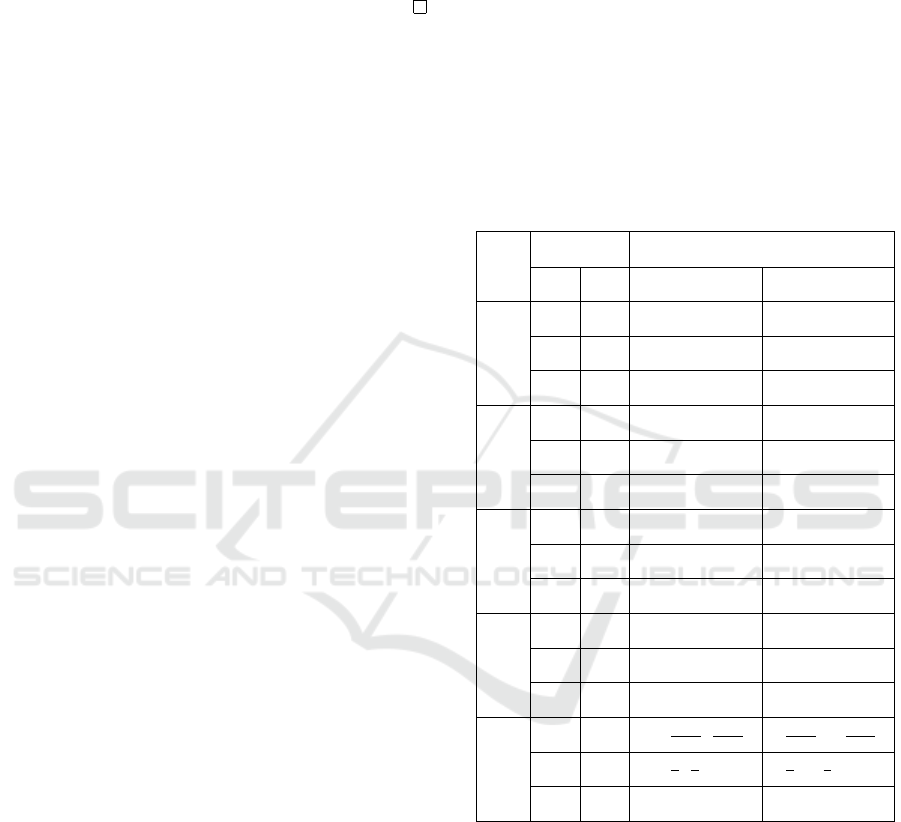
Table 1: Nash equilibria for various values of α.
No.
α Nash Equilibrium
α
1
α
2
x
∗
y
∗
1
0.4 0.4 (0, 0, 1) (0, 0, 1)
0.5 0.5 (0, 1, 0) (1, 0, 0)
0.7 0.7 (0, 1, 0) (0, 1, 0)
2
0.4 0.4 (1, 0, 0) (0, 1, 0)
0.5 0.5 (0, 1, 0) (1, 0, 0)
0.7 0.7 (0, 0, 1) (1, 0, 0)
3
0.4 0.4 (1, 0, 0) (0, 0, 1)
0.5 0.5 (1, 0, 0) (0, 0, 1)
0.7 0.7 (1, 0, 0) (0, 0, 1)
4
0.4 0.4 (1, 0, 0) (1, 0, 0)
0.5 0.5 (1, 0, 0) (1, 0, 0)
0.7 0.7 (0, 0, 1) (0, 0, 1)
5
0.4 0.4
0,
791
1000
,
209
1000
616
1000
,0,
384
1000
0.5 0.5
0,
1
2
,
1
2
2
3
,0,
1
3
0.7 0.7 (0, 0, 1) (1, 0, 0)
(ii) 5 ×5 random bimatrix game: We consider two
instances of random bimatrix game of size 5 ×5. The
location parameters µ
1
, µ
2
, and scale parameters σ
1
,
σ
2
of independent Cauchy random variables are as
follows:
1. µ
1
=
1 2 1 1 3
2 3 1 1 2
1 2 3 2 3
2 1 3 4 2
1 2 4 5 2
,σ
1
=
2 2 3 2 1
1 2 3 2 1
1 2 3 3 1
2 1 3 4 2
3 1 2 5 2
,
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
64
µ
2
=
1 2 3 2 1
3 2 2 1 3
1 2 3 1 2
2 1 4 2 1
1 1 2 1 3
, σ
2
=
5 2 3 2 3
2 4 3 2 1
1 3 4 2 3
2 1 3 5 1
2 1 2 3 4
.
2. µ
1
=
1 2 2 4 3
2 1 3 2 2
1 2 4 2 1
2 2 3 4 1
1 2 4 5 2
,σ
1
=
2 3 1 2 1
1 1 3 1 2
3 1 3 3 1
2 2 5 4 2
3 1 3 5 2
,
µ
2
=
1 2 3 2 1
3 1 2 1 4
2 1 3 4 2
3 2 4 2 1
2 4 2 1 3
, σ
2
=
5 2 4 2 1
2 4 3 2 1
4 3 3 2 3
2 1 3 5 3
1 3 4 3 4
.
The Table 2 summarizes the Nash equilibria of
chance-constrained game corresponding to datasets
given for two instances of 5 × 5 random bimatrix
game.
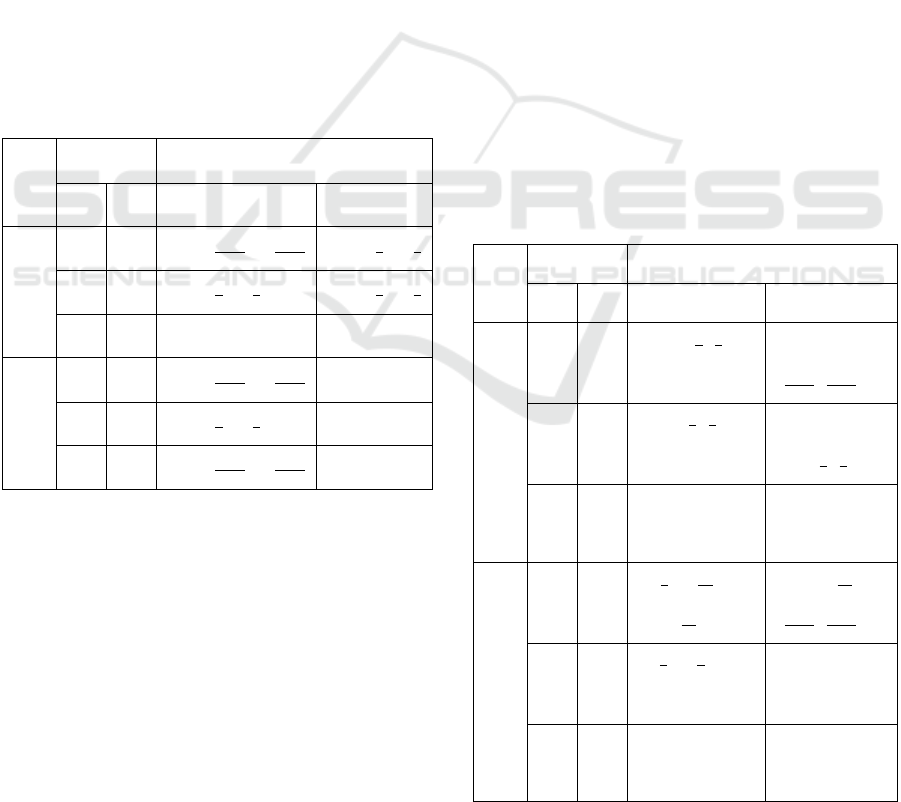
Table 2: Nash equilibria for various values of α.
No.
α Nash Equilibrium
α
1
α
2
x
∗
y
∗
1
0.4 0.4
0,0,
555
1000
,0,
445
1000
0,0,
1
2
,0,
1
2
0.5 0.5
0,0,
1
2
,0,
1
2
0,0,
1
2
,0,
1
2
0.7 0.7 (0,0,0,0,1) (0,0,1,0,0)
2
0.4 0.4
0,0,
663
1000
,0,
337
1000
(0,0,1,0,0)
0.5 0.5
0,0,
1
2
,0,
1
2
(0,1,0,0,0)
0.7 0.7
0,0,
446
1000
,0,
554
1000
(0,1,0,0,0)
(iii) 7 ×7 random bimatrix game: We consider two
instances of random bimatrix game of size 7 ×7. The
location parameters µ
1
, µ
2
, and scale parameters σ
1
,
σ
2
of independent Cauchy random variables are as
follows:
1. µ
1
=
1 2 2 4 3 2 1
1 1 2 1 3 2 2
3 2 1 2 4 2 1
2 4 2 2 3 4 1
1 2 4 5 2 2 3
1 3 4 3 2 2 3
2 1 4 2 3 2 1
,σ
1
=
2 3 1 2 1 1 2
1 1 3 1 2 2 4
2 1 3 1 3 3 1
2 2 5 4 2 1 3
2 1 3 1 3 5 2
1 2 3 1 2 3 2
2 1 4 2 3 1 2
,
µ
2
=
1 2 3 2 3 2 1
1 2 3 1 2 1 4
2 1 2 1 3 4 2
1 2 3 2 4 2 1
2 3 1 4 2 1 3
1 2 3 2 1 3 4
2 3 1 2 3 4 2
, σ
2
=
5 2 4 2 1 2 3
1 2 2 4 3 2 1
2 3 4 3 3 2 3
2 3 2 1 3 5 3
2 1 2 3 4 3 4
1 2 2 3 1 3 1
2 4 1 2 3 1 2
.
2. µ
1
=
1 2 3 1 3 4 1
2 1 2 1 2 4 2
1 2 1 5 3 2 1
1 3 2 2 3 2 1
2 3 4 5 2 1 3
1 3 2 1 2 4 3
2 1 3 2 1 2 1
,σ
1
=
1 3 1 2 1 2 2
2 1 3 1 2 2 4
2 1 3 2 3 4 1
2 2 3 4 2 1 3
2 4 3 1 3 2 2
1 2 3 2 2 4 2
2 3 4 1 3 1 2
,
µ
2
=
2 1 3 4 3 2 1
1 2 3 3 2 1 4
2 1 2 1 3 4 2
1 2 3 2 4 2 1
2 3 2 4 2 1 3
1 2 1 2 5 3 4
2 3 1 2 1 4 2
, σ
2
=
5 2 4 3 1 2 3
1 2 3 4 3 2 3
1 3 4 2 1 2 3
2 3 2 2 3 4 3
2 1 2 2 4 1 4
2 3 2 3 4 3 1
2 4 3 2 3 1 2
.
The Table 3 summarizes the Nash equilibria of
chance-constrained game corresponding to datasets
given for two instances of 7 × 7 random bimatrix
game.
Table 3: Nash equilibria for various values of α.
No.
α Nash Equilibrium
α
1
α
2
x
∗
y
∗
1
0.4 0.4
0,0,
2
3
,
1
3
,
0,0,0
0,0,0,0,
505
1000
,
495
1000
,0
0.5 0.5
0,0,
2
3
,
1
3
,
0,0,0
0,0,0,0,
2
3
,
1
3
,0
0.7 0.7
1,0,0,0,
0,0,0
0,0,0,0,
1,0,0)
2
0.4 0.4
1
5
,0,
13
25
,0,
7
25
,0,0
0,0,
13
50
,0,
675
1000
,
65
1000
,0
0.5 0.5
1
2
,0,
1
2
,0,
0,0,0
0,0,0,0,
1,0,0
0.7 0.7
1,0,0,0,
0,0,0
0,0,0,0,
1,0,0
A Complementarity Problem Formulation for Chance-constraine Games
65

4 CONCLUSIONS
We formulate the bimatrix game with random payoffs
as a chance-constrained game. We consider the case
where the entries of payoff matrices are independent
random variables following a certain distribution. In
particular, we discuss the case of normal and Cauchy
distributions. We show that the chance-constrained
game corresponding to normal distribution can be for-
mulated as an equivalent NCP. Further if the entries of
payoff matrices are also identically distributed with
non-negative mean, a uniform strategy pair is a Nash
equilibrium. We show that the chance-constrained
game corresponding to Cauchy distribution can be
formulated as an equivalent LCP. Recently, the elec-
tricity markets over the past few years have been
transformed from nationalized monopolies into com-
petitive markets with privately owned participants.
The uncertainties in electricity markets are present
due to various external factors. These situations can
be modeled as chance-constrained games and the ap-
proaches developed in this paper can be applied to
compute the Nash equilibrium.
REFERENCES
Bazaraa, M., Sherali, H., and Shetty, C. (2006). Nonlinear
Programming Theory and Algorithms. John Wiley and
Sons, Inc., U.S.A, Third ed.
Blau, R. A. (1974). Random-payoff two person zero-sum
games. Operations Research, 22(6):1243–1251.
Cassidy, R. G., Field, C. A., and Kirby, M. J. L. (1972). So-
lution of a satisficing model for random payoff games.
Management Science, 19(3):266–271.
Charnes, A. and Cooper, W. W. (1963). Determinis-
tic equivalents for optimizing and satisficing under
chance constraints. Operations Research, 11(1):18–
39.
Charnes, A., Kirby, M. J. L., and Raike, W. M. (1968).
Zero-zero chance-constrained games. Theory of Prob-
ability and its Applications, 13(4):628–646.
Cheng, J. and Lisser, A. (2012). A second-order cone
programming approach for linear programs with joint
probabilistic constraints. Operations Research Let-
ters, 40(5):325–328.
Collins, W. D. and Hu, C. (2008). Studying interval val-
ued matrix games with fuzzy logic. Soft Computing,
12:147–155.
Couchman, P., Kouvaritakis, B., Cannon, M., and Prashad,
F. (2005). Gaming strategy for electric power with
random demand. IEEE Transactions on Power Sys-
tems, 20(3):1283–1292.
DeMiguel, V. and Xu, H. (2009). A stochastic multiple
leader stackelberg model: analysis, computation, and
application. Operations Research, 57(5):1220–1235.
Deng-Feng Li, J.-X. N. and Zhang, M.-J. (2012). Inter-
val programming models for matrix games with in-
terval payoffs. Optimization Methods and Software,
27(1):1–16.
Ferris, M. C. and Munson, T. S. (2000). Complementarity
problems in GAMS and the PATH solver. Journal of
Economic Dynamics and Control, 24:165–188.
Jadamba, B. and Raciti, F. (2015). Variational inequality ap-
proach to stochastic nash equilibrium problems with
an application to cournot oligopoly. Journal of Opti-
mization Theory and Application, 165(3):1050–1070.
Johnson, N. L., Kotz, S., and Balakrishnan, N. (1994). Con-
tinuous Univariate Distributions, volume 1. John Wi-
ley and Sons Inc., 2nd edition.
Katzwer, R. (2013). Lemke-Howson Algorithm for 2-Player
Games. File ID: #44279 Version: 1.3.
Lemke, C. and Howson, J. (1964). Equilibrium points of
bimatrix games. SIAM Journal, 12:413–423.
Lemke, C. E. (1965). Bimatrix equilibrium points and
mathematical programming. Management Science,
11(7):681–689.
Li, D.-F. (2011). Linear programming approach to solve
interval-valued matrix games. Journal of Omega,
39(6):655–666.
Mazadi, M., Rosehart, W. D., Zareipour, H., Malik, O. P.,
and Oloomi, M. (2013). Impact of wind integration
on electricity markets: A chance-constrained Nash
Cournot model. International Transactions on Elec-
trical Energy Systems, 23(1):83–96.
Mitchell, C., Hu, C., Chen, B., Nooner, M., and Young,
P. (2014). A computational study of interval-valued
matrix games. In International Conference on Com-
putational Science and Computational Intelligence.
Munson, T. S. (2000). Algorithms and Environments for
Complementarity. PhD thesis, University of Wiscon-
sin - Madison.
Nash, J. F. (1950). Equilibrium points in n-person games.
Proceedings of the National Academy of Sciences,
36(1):48–49.
Neumann, J. V. (1928). Zur theorie der gesellschaftsspiele.
Math. Annalen, 100(1):295–320.
Nocedal, J. and Wright, S. J. (2006). Numerical Optimiza-
tion. Springer Science + Business Media LLC, New
York, 2 edition.
Pr
´
ekopa, A. (1995). Stochastic Programming. Springer,
Netherlands.
Ravat, U. and Shanbhag, U. V. (2011). On the characteriza-
tion of solution sets of smooth and nonsmooth convex
stochastic Nash games. Siam Journal of Optimization,
21(3):1168–1199.
Schmelzer, S. (2012). COMPASS: A free solver for mixed
complementarity problems. Master’s thesis, Univer-
sit
¨
at Wien.
Singh, V. V., Jouini, O., and Lisser, A. (2015a).
Existence of nash equilibrium for chance-
constrained games. http://www.optimization-
online.org/DB FILE/2015/06/4977.pdf.
Singh, V. V., Jouini, O., and Lisser, A. (2015b). Exis-
tence of nash equilibrium for distributionally robust
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
66

chance-constrained games. http://www.optimization-
online.org/DB FILE/2015/09/5120.pdf.
Song, T. (1992). Systems and Management Science by
Extremal Methods, chapter On random payoff matrix
games, pages 291–308. Springer Science + Business
Media, LLC.
Valenzuela, J. and Mazumdar, M. (2007). Cournot prices
considering generator availability and demand un-
certainty. IEEE Transactions on Power Systems,
22(1):116–125.
Wolf, D. D. and Smeers, Y. (1997). A stochastic version of a
Stackelberg-Nash-Cournot equilibrium model. Man-
agement Science, 43(2):190–197.
Xu, H. and Zhang, D. (2013). Stochastic nash equilibrium
problems: sample average approximation and applica-
tions. Computational Optimization and Applications,
55(3):597–645.
A Complementarity Problem Formulation for Chance-constraine Games
67
