High-performance FPGA Implementation of Elliptic Curve
Cryptography Processor over Binary Field GF(2
163
)
Md Selim Hossain, Ehsan Saeedi and Yinan Kong
Department of Engineering, Macquarie University, Sydney, NSW-2109, Australia
Keywords:
Elliptic Curve Cryptography (ECC), Finite/Galois Field Arithmetic, Elliptic Curve Point Multiplication
(ECPM), Field-programmable Gate Array (FPGA).
Abstract:
Elliptic curve cryptography (ECC) plays a vital role in passing secure information among different wireless
devices. This paper presents a fast, high-performance hardware implementation of an ECC processor over
binary field GF(2
m
) using a polynomial basis. A high-performance elliptic curve point multiplier (ECPM) is
designed using an efficient finite-field arithmetic unit in affine coordinates, where ECPM is the key operation of
an ECC processor. It has been implemented using the National Institute of Standards and Technology (NIST)
recommended curves over the field GF(2
163
). The proposed design is synthesized in field-programmable
gate array (FPGA) technology with the VHDL. The delay of ECPM in a modern Xilinx Kintex-7 (28-nm)
technology is 1.06 ms at 306.48 MHz. The proposed ECC processor takes a small amount of resources on the
FPGA and needs only 2253 slices without using any DSP slices. The proposed design provides nearly 50%
better delay performance than recent implementations.
1 INTRODUCTION
With the swift growth of mobile devices and com-
puter applications, cryptography has become a vital
tool to ensure the security of data communications
and network services. Secret-key cryptography and
public-key cryptography (PKC) are two main fami-
lies of cryptography used for different data-security
purposes. ECC (Miller, 1986; Koblitz, 1987) and the
RSA cryptosystem (Rivest et al., 1978) are the most
popular PKCs. The elliptic curve system as applied
to cryptography was first proposed in the mid 80s by
Koblitz and Miller. This cryptosystem became pop-
ular because it offers equivalent security to the tradi-
tional RSA with significantly smaller keys. For in-
stance, 163-bit ECC provides equivalent security to
1024-bit RSA (Koblitz et al., 2000; SEC2, 2000).
This feature makes ECC very popular for resource-
constrained environments such as pagers, PDAs, cel-
lular phones, smart cards and so on (Sutter et al.,
2013). The IEEE (IEEE, 2000) and National Institute
of Standards and Technology (NIST) (NIST, 2000)
have standardized elliptic curve (EC) parameters for
GF(p) and GF(2
m
). Certicom has provided NIST-
recommended EC domain parameters, standard for
efficient cryptography in SEC2 (SEC2, 2000).
Several FPGA-based efficient ECC hardware ar-
chitectures and elliptic curve cryptographic proces-
sors have been presented in the literature (Sutter et al.,
2013; Chelton and Benaissa, 2008; Reaz et al., 2012;
Hassan and Benaissa, 2010; Machhout et al., 2010;
Ghanmy et al., 2014; Shieh et al., 2009; Smyth
et al., 2006; Park and Hwang, 2005). In (Ghanmy
et al., 2014), Ghanmy proposed ECC processor over
GF(2
163
) on a FPGA platform for wireless sensor
networks (WSN). Reaz’s design (Reaz et al., 2012)
can perform ECC over GF(2
131
) and GF(2
163
) on Al-
tera FPGAs. Hasan and Benaissa (Hassan and Be-
naissa, 2010) implemented their ECC processor using
the µ-coding technique on Xilinx Spartan-3 FPGAs
over GF(2
131
), GF(2
163
), GF(2
283
) and GF(2
571
). A
coupled FPGA/ASIC implementation of an elliptic
curve crypto-processor over GF(2
163
) is presented
in (Machhout et al., 2010), and they used Xilinx Vir-
tex Pro FPGAs and ASIC CMOS 45 nm technology
as a hardware platform. Shieh (Shieh et al., 2009),
Park et al. (Park and Hwang, 2005) also proposed
their ECC processor over a binary field using Xilinx
FPGAs. An ASIC-based ECC processor is presented
over GF(2
m
) in (Smyth et al., 2006).
The optimization aim is generally to reduce the
latency of an ECPM in terms of the number of re-
quired clock cycles. For this, we have concentrated
on efficient algorithms and mathematical reformula-
tions for improving finite-field arithmetic operations
which are required for ECPM (Sutter et al., 2013;
Hossain, M., Saeedi, E. and Kong, Y.
High-performance FPGA Implementation of Elliptic Curve Cryptography Processor over Binary Field GF(2
163
).
DOI: 10.5220/0005741604150422
In Proceedings of the 2nd International Conference on Information Systems Security and Privacy (ICISSP 2016), pages 415-422
ISBN: 978-989-758-167-0
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
415

Chelton and Benaissa, 2008; Kong and Phillips, 2009;
Phillips et al., 2010). The arithmetic includes opera-
tions defined in finite (Galois) fields, namely GF(p)
and GF(2
m
) (Hankerson et al., 2003). To the best of
the authors’ knowledge, there have been few high-
speed hardware implementations of an ECC proces-
sor in the literature. Thus an efficient design of an
ECC processor is still mandatory for modern crypto-
graphic applications.
In this paper an efficient ECC processor is de-
veloped in which ECPM operations are achieved in
a very low area (around 2.25K slices without using
any DSP slices) and latency (almost 50% less than re-
cent implementations). For this, efficient algorithmic
reformulations underlying binary finite field and ar-
chitectural optimization schemes are explored to im-
prove the operating speed. We propose a data-flow
architecture of elliptic curve point doubling (ECPD)
and elliptic curve point addition (ECPA) that are re-
quired for the ECC processor. An efficient field inver-
sion and multiplication algorithms over GF(2
m
) are
employed to implement high-performance ECPD and
ECPA. Finally, an FPGA-based high-performance
hardware implementation over GF(2
163
) is proposed,
which is the fastest implementation in an affine coor-
dinate system.
The rest of this paper is organized as follows. Sec-
tion II introduces a background of groups and fields,
Galois finite fields (GF(p) and GF(2
m
)), and ECC the-
ories related to this work. Section III describes an effi-
cient finite-field algorithm over GF(2
m
), elliptic curve
group operations (PD and PA) and hardware architec-
tures. An elliptic curve point multiplication algorithm
and cryptographic processor are given in Section IV.
FPGA implementation results and comparisons with
related designs are given in Section V. Finally this pa-
per is summarized in Section VI.
2 BACKGROUND
In this section, a brief introduction to abstract algebra,
field and group theories relevant to ECC designs used
in our hardware implementation is presented.
2.1 Groups and Fields
An abelian group (G,∗) consists of a set of elements
together with a binary operation ∗ which satisfies the
following properties :
1. (Associativity) a ∗(b ∗c) = (a∗b)∗c for all a, b,c ∈
G.
2. (Identity) There is an element e ∈ G such that
a ∗ e = e ∗ a for all a ∈ G.
3. (Inverse) for each a ∈ G, there is an element b ∈ G,
called the inverse of a, such that a ∗ b = b ∗ a = e.
The group operation is generally called addition (+)
or multiplication (.). The group is finite if G is a fi-
nite set, in which case the number of elements in G is
called the order of G.
Fields are abstractions of familiar number systems
and their essential properties. A field (F, +, ×) is
a set of numbers F with two operations, addition and
multiplication, satisfying the following properties:
1. (F, +) is an abelian group with (additive) identity
0.
2. (F \{0}) is an abelian group with (mult.) identity
1.
Division of field elements is represented in terms of
multiplication (mult.): for a,b ∈ F with b 6= 0, a/b =
a.b
−1
where b.b
−1
= 1. (b
−1
is called the inverse of
b) (Hankerson et al., 2003).
2.2 Elliptic Curve Cryptography (ECC)
ECC is the most popular public-key encryption tech-
nique. To encrypt data in ECC, it is denoted as a point
on an elliptic curve (EC) over a Galois field. A Galois
field denoted normally as GF(q = p
m
) is said to be a
binary field or characteristic-two finite field if q = 2
m
.
A elliptic curve defined over a Galois field provides
a group structure that is used to implement crypto-
graphic systems. The group operations are EC point
addition (ECPA) and EC point doubling (ECPD).
There are various coordinate systems to represent el-
liptic curve points. They vary in the number and type
of field operations required to implement PA/PD. In
our work, we implement all elliptic curve operations
in an affine coordinate system. A non-supersingular
elliptic curve E over GF(2
m
) in affine coordinates is
the set of solutions to the equation
y
2
+ xy = x
3
+ ax
2
+ b (1)
where x,y,a,b ∈ GF(2
m
),b 6= 0. The coefficients a,b
∈ F
2
m
specifying an elliptic curve E(F
2
m
) are defined
by the NIST standard and then the elliptic curve is
defined by (1). The number of points on an elliptic
curve E is represented by #E(F
2
m
). It is defined over
F
2
m
as nh, where n is the prime order of the curve,
and h is an integer called the co-factor.
If P = (x
1
,y
1
) ∈ E and Q = (x
2
,y
2
) ∈ E (points on the
EC), then summing PA and PD can be respectively
derived as
R(x
3
,y
3
) = P(x
1
,y
1
) + Q(x
2
,y
2
) ∈ E,
x
3
= λ
2
+ λ + x
1
+ x
2
+ a,
y
3
= λ(x
1
+ x
3
) + x
3
+ y
1
,
where λ = (y
2
+ y
1
)/(x
2
+ x
1
)andP 6= Q;
(2)
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
416

R(x
3
,y
3
) = 2P(x
1
,y
1
) ∈ E,
x
3
= λ
2
+ λ + a = x
2
1
+ b/x
2
1
,
y
3
= x
2
1
+ λx
3
+ x
3
,
where λ = x
1
+ y
1
/x
1
andP = Q;
(3)
where R = 0 when x
1
= x
2
and y
2
6= y
1
, or x
1
= x
2
= 0.
Hence, when P 6= Q we have the PA operation in
(2) and when P = Q we have the PD operation in
(3). Using these operations, EC point multiplication
kP will be implemented using an ECC- based algo-
rithm (Hankerson et al., 2003; Sutter et al., 2013;
Miller, 1986; Koblitz, 1987).
Table 1: Comparison of Key length for equivalent security
of Symmetric-key and public-key Cryptography (Hanker-
son et al., 2003).
Symmetric key Example- RSA and ECC in ECC in
algorithm DH GF(p) GF(2
m
)
80 SKIPJACK 1024 160 163
112 Triple-DES 2048 224 233
128 AES Small 3072 256 283
192 AES Medium 8192 384 409
256 AES Large 15360 521 571
In 2000, FIPS-2 was recommended with 10 finite
fields: 5 prime fields, and 5 binary fields. The binary
fields are F
2
163
,F
2
233
,F
2
283
,F
2
409
and F
2
571
(NIST,
2000). Prime fields GF(p) and binary fields GF(2
m
)
of similar size are considered to provide almost the
same level of security (Koblitz et al., 2000). Ta-
ble 1 compares symmetric cipher key length, and key
lengths for PKC such as RSA, Diffie-Hellman (DH),
and ECC (both prime and binary fields). It demon-
strates that smaller field sizes can be used in ECC
than in RSA and DH systems at a given security level.
ECC is many times more efficient than RSA and DH
for either private-key operations (such as signature
generation and decryption) or public-key operations
(such as signature verification and encryption). This
makes ECC a promising branch of public-key cryp-
tography (Hankerson et al., 2003).
3 HARDWARE
IMPLEMENTATION FOR
FINITE FIELD
This section presents all arithmetic algorithms and op-
erations for hardware implementation which are im-
portant for ECC. All parameters for NIST elliptic
curves over GF(2
163
) are listed in Table 2. The ir-
reducible polynomial is f (x) = x
163
+x
7
+x
6
+x
3
+1
given for the field GF(2
163
). A modern Xilinx Kintex-
7 (XC7K325T-2FFG900) FPGA with VHDL (VH-
SIC Hardware Description Language) is used for this
hardware implementation. The main components in
this ECC design are: polynomial-basis modular addi-
tion or field addition, field multiplication, field squar-
ing, field inversion, and elliptic curve group opera-
tions (PD and PA).
3.1 Polynomial Basis Representation
A polynomial basis (or standard basis) is an extension
field used to represent field elements and is very pop-
ular. PB is used in our hardware design for the repre-
sentation of numbers. For the PB representation, the
elements F
2
m
are the binary polynomials of degree at
most m − 1, i.e.
F
2
m
= u
m−1
.x
m−1
+ u
m−2
.x
m−2
+ · · · + u
1
.x + u
0
=
m−1
∑
i=0
u
i
x
i
: u
i
∈ {0, 1}
For instance, x
3
+ x + 1 is a polynomial-basis rep-
resentation for the 4-bit number 1011
2
. For a reduc-
tion polynomial or irreducible polynomial, ( f (x) be
an irreducible binary polynomials of degree m), and
f (x) = x
m
+ G(x) = x
m
+
∑
m−1
i=0
g
i
x
i
where g
i
∈ {0, 1}
for i = 1,...,m − 1 and g
0
= 1 (Hankerson et al.,
2003). For example, f (x) = x
4
+ x + 1 = 10011
2
is
an irreducible polynomial of the finite field GF(2
4
).
Table 2: NIST-recommended elliptic curves over F
2
163
.
K-163: m = 163, f (x) = x
163
+ x
7
+ x
6
+ x
3
+ 1, a, b = 1, h = 2
n=0x 4 00000000 00000000 00020108 A2E0CC0D 99F8A5EF
x=0x 2 FE13C053 7BBC11AC AA07D793 DE4E6D5E 5C94EEE8
y=0x 2 89070FB0 5D38FF58 321F2E80 0536D538 CCDAA3D9
3.2 Addition in GF(2
m
)
Addition is the simplest operation in GF(2
m
). It
is simply a bit-wise exclusive-or (xor (⊕)) in ei-
ther hardware or software. Addition in F
2
m
can be
achieved as shown in (4) (Wolkerstorfer, 2002):
Z(x) = U (x) +V (x) =
m−1
∑
i=0
u
i
x
i
+
m−1
∑
i=0
v
i
x
i
=
m−1
∑
i=0
(u
i
+ v
i
)x
i
=
m−1
∑
i=0
z
i
x
i
(4)
where z
i
= (u
i
+ v
i
) mod 2 = u
i
⊕ v
i
. The subtrac-
tion operation in GF(2
m
) is the same as addition be-
cause the additive inverse of an element is its identity
: U(x) +U(x) = 0.
High-performance FPGA Implementation of Elliptic Curve Cryptography Processor over Binary Field GF(2
163
)
417

For example, if U = 1100
2
and V = 0110
2
over
the finite field GF(2
4
) then Z = U + V = U ⊕ V =
(1100
2
⊕ 0110
2
) = 1010
2
.
3.3 Multiplication in GF(2
m
)
Polynomial multiplication or multiplication in
GF(2
m
) with the interleaved modular reduction
algorithm is a well-known algorithm for hardware
implementation (Wolkerstorfer, 2002). It computes
the product of two polynomials then applies modular
reduction, and its operation is different from simple
integer multiplication. Multiplication in F
2
m
can be
achieved as shown in (5):
Z(x) = U(x).V (x) = U(x).
m−1
∑
i=0
v
i
.x
i
=
m−1
∑
i=0
(U(x).v
i
).x
i
(5)
Multiplication by x
i
can easily be calculated by the
binary left-shift operation. From polynomial multi-
plication in algorithm 1, we check whether the result
is an element of GF(2
m
) with degree < m. A modu-
lar reduction step is only necessary if the polynomial
multiplication result Z
v
has degree m or higher. This
condition is checked by the Z
v
(m) = 1 command.
Algorithm 1: Mult. in GF(2
m
) with interleaved modular
reduction.
Input: U (x),V (x) ∈ GF(2
m
), irreducible polynomials of degree m
Output: Z(x) = U(x) . V (x) mod f (x)
Z
v
= 0 ; U
v
= ’0’ & U(x) ;
for i = m - 1 to 0 do
if V (i) = ’1’ then
Z
v
= Z
v
. x + U
v
; else Z
v
= Z
v
. x ;
end if
if Z
v
(m) = ’1’ then
Z
v
= Z
v
+ f (x) ;
end if
end for
Return (Z(x) = Z
v
(m-1 downto 0)) (At this instance,
Z(x) is the result of U(x) . V (x) mod f (x))
The result of polynomial multiplication Z(x) =
U(x).V (x) mod f (x), is achieved after m iterations.
Algorithm 1 (Wolkerstorfer, 2002), named multipli-
cation (Mult.) in GF (2
m
) with interleaved modular
reduction, takes just four steps to find the solution of
polynomial multiplication over GF(2
4
). The polyno-
mial multiplication result should be reduced to a de-
gree < 4 by irreducible polynomial f (x) = x
4
+x + 1.
3.4 Squaring in GF(2
m
)
A PB squarer is simpler than and closely related to
multiplication. But squaring in GF(2
m
) has less dif-
ficulty than polynomial multiplication because U(x)
2
mod f (x) is a linear operation. It can be computed as
shown in (6):
Z(x) = U (x)
2
= u
m−1
.x
2m−2
+···+u
2
.x
4
+u
1
.x
2
+u
0
=
m−1
∑
i=0
u
i
x
2i
(6)
The squaring operation in GF(2
m
) of Z(x) =U(x)
2
is achieved by setting a 0 bit between consecutive bits
of the binary representation of U (x) as shown in Fig-
ure 1 (Hankerson et al., 2003; Wolkerstorfer, 2002).
U
m-1
U
m-2
….
U
1
U
0
0
U
m-1
0
U
m-2
0
….
0
U
1
0
U
0
U(x
U(x)
2
Figure 1: Squaring a binary polynomial U(x).
3.5 Inversion in GF(2
m
)
Inversion in GF(2
m
) is the most expensive operation
for implementing ECC over a binary field. Algorithm
2 computes the field inversion of a non-zero field ele-
ment U(x) ∈ F
2
m
using the modified Euclidean algo-
rithm (Guo and Wang, 1998). We used this inversion
algorithm for our hardware implementation because it
is easy to implement on a FPGA.
Algorithm 2: Inversion in GF(2
m
) with Modified Euclide-
an Algorithm.
Input: U (x) ∈ GF(2
m
), irreducible polynomial of degree m
Output: Z(x) = 1/U(x) mod f (x)
P
v
= ’0’ & U(x) ; Q
v
= f (x); Z
v
= 00001; V = 0 ; cnt = 0 ;
for i = 1 to 2m do
if P
v
(m) = ’0’ then
P
v
= x . P
v
; Z
v
= x . Z
v
;
if Z
v
(m) = ’1’ then
Z
v
= Z
v
+ f (x) ;
end if
cnt = cnt + 1 ;
else
if Q
v
(m) = ’1’ then
Q
v
= Q
v
+ P
v
; V = V + Z
v
mod f (x) ;
end if
Q
v
= x . Q
v
;
if cnt = 0 then
P
v
= Q
v
; Q
v
= P
v
; (P
v
↔ Q
v
)
Z
v
= V ; V = Z
v
; (Z
v
↔ V , exchange operations)
Z
v
= x . Z
v
mod f (x); cnt = cnt + 1 ;
else
Z
v
= Z
v
/x mod f (x) ; cnt = cnt − 1 ;
end if
end if
end for
Return (Z(x) = Z
v
(m-1 downto 0)) (At this case,
Z(x) is the result of 1/U(x) mod f (x))
The result of field inversion Z(x) = 1/U(x) mod
f (x) or multiplicative inversion of U(x) is achieved
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
418

after 2m iterations (i = 1to 2m) and the value of cnt
is always equal to zero at the end of the last itera-
tion (Guo and Wang, 1998).
3.6 Proposed EC Group Operations
The elliptic curve group operations in GF(2
m
) are
the PD and PA operations. These are the building
blocks of finite-field arithmetic operations such as ad-
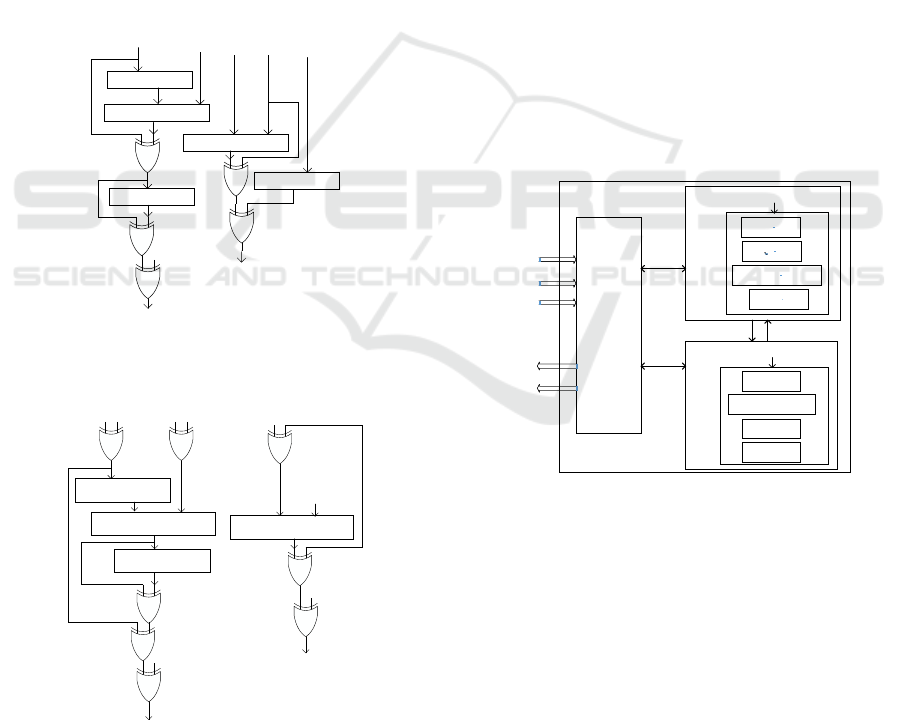
dition, multiplication, squaring and inversion. Fig-
ures 2 and 3 show the data-flow architecture of the
proposed ECPD and ECPA operations, correspond-
ing to (2) and (3) respectively. The ECPD operation
in affine coordinates requires one field inversion, five
field additions, two field multiplications, and two field
squarings. Similarly, the ECPA operation in affine co-
ordinates requires one field inversion, eight field ad-
ditions, two field multiplications, and one field squar-
ing.
Inversion
a

2

3
x
1
x
1
y
1
x
ax  
2
3
33
2
1
3
. xxxy  

Squaring
Squaring
Multiplication
Multiplication

Figure 2: Hardware architecture of the elliptic curve point
doubling (ECPD) operation.
Multiplication
Inversion
Squaring
1
x
1
y


3
x
1
x
2

a
1
y
axxx 
21
2
3

13313
)( yxxxy




2
x
2
y
Multiplication
Figure 3: Hardware architecture of the elliptic curve point
addition (ECPA) operation.
4 PROPOSED ECPM
Elliptic curve point multiplication (ECPM) is the
main operation of an ECC processor; it is compu-
tationally the most expensive. However, we have
designed a high-performance ECPM using efficient
group operations and FFMA units. The building
block of an elliptic curve cryptosystem contains
ECC protocols such as ECDH (elliptic curve Diffie-
Hellman) key exchange, ECDSA (EC digital signa-
ture algorithm) at the top level, point multiplication
in the second level, group operations in the third
level, and field arithmetic operations in the bottom
level. The basic operation of ECPM is defined as
kP, where k is a positive integer and P is a point on
the elliptic curve E defined over a field F
2
m
. The
proposed ECPM architecture over GF(2
m
) is pre-
sented in Figure 4. Various methods exist for imple-
menting ECPM: the binary method, the Non-adjacent
form (NAF) method, and the Montgomery method.
The easiest way to implement ECPM is the binary
method (left to right) (Hankerson et al., 2003). Fi-
nally, we present the ECPM Algorithm 3 using the
binary method. It is implemented using the “Double-
and-Add” algorithm concept.
Inversion
Addition
Squaring
Multiplication
FiniteFieldArithmetic
PA
Inversion
Addition
Squaring
Multiplication
FiniteFieldArithmetic
PD
Control
Unit
k
x
P
y
P
x
Q
y
Q
Figure 4: Hardware architecture of Elliptic Curve Point
Multiplication (ECPM) processor.
High-performance FPGA Implementation of Elliptic Curve Cryptography Processor over Binary Field GF(2
163
)
419

Table 3: Synthesis Results of the finite-field arithmetic for GF(2
163
) in Kintex-7.
Arithmetic FF LUTS LUT-FF CC Frequency Time
Opn (Pairs) (MHz) (µs)
Mult./SQ 335 385 335 163 388.83 0.419
Inversion 1479 2007 1315 327 431.71 0.757
Table 4: Elliptic curve Group Operation Results for GF(2
m
) in Kintex-7.
Group FF LUTs LUT-FF CC Frequency Time
Operation Pairs (MHz) (µs)
PD 3484 4264 3037 1636 331.76 4.930
PA 6587 8347 5664 1636 331.58 4.934
Algorithm 3: Binary method (Left to right) for point mul-
tiplication.
Input: k = (k
m−1,...,k
1
,k
0
)
2
, P(x, y) ∈ E(F
2
m
)
Output: Q(x,y) = k.P(x, y), where Q(x, y),P(x,y) ∈ E(F
2
m
)
Q = 0 ;
for i = m - 1 to 0 do
Q = 2Q;
if k(i) = ’1’ then
Q = Q + P ;
end if
end for
Return (Q(x,y))
5 FPGA IMPLEMENTATION
RESULTS AND
PERFORMANCE ANALYSIS
This section presents the hardware implementation
results of this design. We have implemented and
tested our design on a modern 28-nm Xilinx Kintex-
7 (XC7K325T-2FFG900) FPGA. All VHDL modules
are extensively simulated using both Isim and Model-
Sim, and synthesized using Xilinx ISE 14.7 synthesis
technologies.
Table 3 depicts the synthesis results of the finite-
field arithmetic operations such as field multiplica-
tion/squaring and field inversion over GF(2
163
). Mul-
tiplication or squaring over GF(2
163
) takes the same
area (FF and LUTS), the same number of clock cycles
and the same computation time. On the other hand,
the clock cycles, flip-flops (FFs), and LUTs (look-up
tables) ratio of inversion to multiplications are about
2, 4.45, and 5.2 respectively. Only inversion con-
sumes more clock cycles, area, and timing. The mul-
tiplication/squaring (SQ) over GF(2
163
) is performed
in Xilinx Kintex-7 in 419 ns but inversion takes 757
ns. From our implementation results, we notice that
field inversion is the most time-consuming operation
over the binary field because an inversion takes the
same number of clock cycles as 2 multiplications.
The hardware implementation results of proposed
elliptic curve group operations are presented in Ta-
ble 4. The major building block of the elliptic
curve group operations (PD and PA) contains addi-
tion, multiplication, squaring and inversion. These
operations were defined over the binary finite field
GF(2
m
). The PA operation occupies almost dou-
ble the area of the PD operation, but the number
of clock cycles and the computation time are iden-
tical for both operations. The ECPM results for the
NIST-recommended field (GF(2
163
) is shown in Ta-
ble 6. We achieve a point multiplication in 1.06 ms
at a frequency of 306.48 MHz in Xilinx Kintex-7
(XC7K325T-2FFG900) FPGA.
Table 5: Synthesis results for elliptic curve point multipli-
cation (ECPM) over F
2
163
.
Logic Utilization Used Available Used
(%)
Numbers of Slice Registers 6620 407600 1
Number of Slice LUTs 7963 203800 3
Numbers of Fully Used LUT-FF Pairs 5712 8871 66
Numbers of BUFG/BUFGCTRLs 2 32 6
Numbers of Bonded IOBs 330 500 66
Numbers of occupied Slices 2253 50950 4
Table 5 represents the summary of estimated val-
ues of device utilization. The implemented design
over the binary field F
2
163
takes a small amount of re-
sources on the FPGA. The synthesis report shows that
our design is area-efficient as it contains only 2253
slices (4% utilization of total available resources).
The hardware implementation results and perfor-
mance comparisons with related cryptographic pro-
cessors are listed in Table 6, which tries to give all the
frequencies, number of clock cycles, and the compu-
tation time of the designs to make a fair comparison
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
420

Table 6: Comparison between our ECC design and related work over GF(2
163
).
References Technology Frequency Clock cycles Time
(MHz) (ms)
This work Kintex-7 306.48 325564 1.06
Ghanmy (Ghanmy et al., 2014) Virtex-II 24 54138 2.26
Reaz (Reaz et al., 2012) FLEX10KE 43 640700 14.9
Hasan (Hassan and Benaissa, 2010) Spartan-3 76 205200 2.7
Machhout (Machhout et al., 2010) Virtex-II 167.84 347425 2.07
Shieh (Shieh et al., 2009) V1000E - - 2.55
Park (Park and Hwang, 2005) V1000E 44 134090 3.05
Smyth (Smyth et al., 2006) 0.13µmASIC 166 526280 3.17
on the performance between them. An ECC processor
over GF(2
163
) for wireless sensor networks (WSN)
is proposed in (Ghanmy et al., 2014), and it requires
2.26 ms to achieve a point multiplication. The ECC
processor proposed by Reaz (Reaz et al., 2012) pro-
vides a result for the field GF(2
163
), and their de-
sign takes 14.9 ms to compute a point multiplica-
tion. Our implemented result is almost 14 times the
speed of Reaz (Reaz et al., 2012) but our presented
result is not in the same platform. Hasan (Hassan and
Benaissa, 2010), Machhout (Machhout et al., 2010),
and Sheih (Shieh et al., 2009) implemented ECC pro-
cessors over GF(2
163
), and their designs require 2.7
ms, 2.07 ms, and 2.55 ms respectively. Our imple-
mented result is almost double the speed of that of
Hasan, Maccout, and Sheih. Park (Park and Hwang,
2005) and Smyth (Smyth et al., 2006) developed ECC
processors over GF(2
163
) in different platforms but
their cryptographic processors require more compu-
tation time than our design. Our ECC processor over
GF(2
163
) takes 1.06 ms to accomplish a point multi-
plication. We have also achieved a higher frequency
than other cryptographic processors. From the com-
parison and performance analysis in Table 6, our ECC
processor over GF(2
163
) provides better performance
than others.
6 CONCLUSIONS
A high-performance ECC processor over GF(2
163
)
has been implemented using FPGA technology. The
binary method (double-and-add) point-multiplication
algorithm using an affine coordinate system was
used for this hardware implementation. An efficient
polynomial-basis multiplication and inversion algo-
rithm was developed for performing elliptic curve PD
and PA operations and hence ECC processor. The
implemented design is optimized by using different
optimization techniques such as balancing the PD
and PA architecture, parallelization in operations, and
pre-computations for obtaining high performance on
an FPGA compared to other designs. In GF(2
163
),
we can achieve a point multiplication in 1.06 ms at
306.48 MHz in Kintex-7 (28-nm) devices, which is
the fastest hardware implementation result. The pro-
posed design provides nearly 50% better delay per-
formance than recent implementations. Our imple-
mented design is also area-efficient as it contains only
2253 slices without using any DSP slices. Based on
the overall performance analysis and comparisons of
different ECC processors over the binary field F
163
,
it can be concluded that this design provides better
performance than others in terms of the area and the
timing.
REFERENCES
Chelton, W. and Benaissa, M. (2008). Fast elliptic curve
cryptography on FPGA. IEEE Transactions on Very
Large Scale Integration (VLSI) Systems, 16(2):198–
205.
Ghanmy, N., Fourati, L. C., and Kamoun, L. (2014). El-
liptic curve cryptography for WSN and SPA attacks
method for energy evaluation. Journal of Networks,
9(11):2943–2950.
Guo, J.-H. and Wang, C.-L. (1998). Systolic array imple-
mentation of euclid’s algorithm for inversion and divi-
sion in GF(2
m
). IEEE Trans. Comput., 47(10):1161–
1167.
Hankerson, D., Menezes, A. J., and Vanstone, S. (2003).
Guide to Elliptic Curve Cryptography. Springer-
Verlag New York, Inc., Secaucus, NJ, USA.
Hassan, M. N. and Benaissa, M. (2010). Efficient time-area
scalable ECC processor using µ-coding technique. In
Third International Workshop, WAIFI, Arithmetic of
Finite Fields, LNCS 6087, pages 250–268.
IEEE (2000). IEEE standard specifications for public-key
cryptography. IEEE Std 1363-2000, pages 1–228.
Koblitz, N. (1987). Elliptic curve cryptosystems. In Math.
Computation, volume 48 (177), pages 203–209.
High-performance FPGA Implementation of Elliptic Curve Cryptography Processor over Binary Field GF(2
163
)
421

Koblitz, N., Menezes, A., and Vanstone, S. (2000). The
state of elliptic curve cryptography. Des. Codes Cryp-
tography, 19(2-3):173–193.
Kong, Y. and Phillips, B. (2009). Fast scaling in the residue
number system. Very Large Scale Integration (VLSI)
Systems, IEEE Transactions on, 17(3):443–447.
Machhout, M., Guitouni, Z., Torki, K., Khriji, L., and
Tourki, R. (2010). Coupled FPGA/ASIC implemen-
tation of elliptic curve crypto-processor. Interna-
tional Journal of Network Security & its Applications
(IJNSA), 2(2):100–112.
Miller, V. S. (1986). Use of elliptic curves in cryptography.
In Lecture Notes in Computer Sciences; 218 on Ad-
vances in cryptology—CRYPTO 85, pages 417–426,
New York, NY, USA. Springer-Verlag New York, Inc.
NIST (2000). NIST- National Institute of Standards and
Technology, Digital Signature Standard, FIPS Publi-
cation 186-2.
Park, J. and Hwang, J.-T. (2005). FPGA and ASIC im-
plementation of ECC processor for security on med-
ical embedded system. In Proceedings of the Third
International Conference on Information Technology
and Applications (ICITA’05) Volume 2 - Volume 02,
ICITA ’05, pages 547–551, Washington, DC, USA.
IEEE Computer Society.
Phillips, B., Kong, Y., and Lim, Z. (2010). Highly paral-
lel modular multiplication in the residue number sys-
tem using sum of residues reduction. Applicable Alge-
bra in Engineering, Communication and Computing,
21(3):249–255.
Reaz, M. B. I., Jalil, J., Husian, H., and Hasim, F. H. (2012).
FPGA implementation of elliptic curve cryptography
engine for personal communication systems. WSEAS
Tran. on Circuits and Systems, 11(3):82–91.
Rivest, R. L., Shamir, A., and Adleman, L. (1978). A
method for obtaining digital signatures and public-key
cryptosystems. Commun. ACM, 21(2):120–126.
SEC2 (2000). SEC 2: Recommended elliptic curve domain
parameters, standards for efficient cryptography, Cer-
ticom Research.
Shieh, M.-D., Chen, J.-H., Lin, W.-C., and Wu, C.-M.
(2009). An efficient multiplier/divider design for el-
liptic curve cryptosystem over GF(2
m
). Journal of In-
formation Science and Engineering, 25:1555–1553.
Smyth, N., McLoone, M., and McCanny, J. V. (2006). An
adaptable and scalable asymmetric cryptographic pro-
cessor. In ASAP, pages 341–346. IEEE Computer So-
ciety.
Sutter, G., Deschamps, J., and Imana, J. (2013). Efficient
elliptic curve point multiplication using digit-serial bi-
nary field operations. IEEE Transactions on Industrial
Electronics, 60(1):217–225.
Wolkerstorfer, J. (Springer, 2002). Dual-field arithmetic
unit for GF(p) and GF(2
m
). In CHES, Lecture Notes
in Computer Science, pages 500–514.
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
422