Quantitative Evaluation of Security on Cryptographic ICs against

Fault Injection Attacks

C. Shao, H. Li and G. Xu

Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, The Chinese University of Hong Kong,

518055, Shenzhen, China

Keywords: Fault Injection Attacks, DFST, Security Evaluation, Quantitative Evaluation, RSA.

Abstract: Fault injection attacks have become a serious threat against cryptographic ICs. However, the traditional

security evaluation often demands experienced engineers repeatedly scan the IC under test for a few hours to

a few days, and take the workload statistics and experiences as qualitative indexes. This paper proposes a

quantitative model to evaluate security based Design for Security Test (DFST), considering both the sensitive

time during the algorithm operation and the sensitive area of the cryptographic IC against fault injection

attacks. The case study on two RSA implementations demonstrates the feasibility of the quantitative

evaluation of security model.

1 INTRODUCTION

Cryptographic integrated circuits (ICs) are dedicated

semiconductor implementations of various

cryptographic algorithm and have been employed in

an increasing number of consumer products, e.g.,

smart cards, cell phones, and set-top boxes, to provide

security and privacy protection. In order to ensure that

the confidential information in cryptographic ICs will

be generated, stored, transmitted and processed safely,

we define security for its information assurance

capabilities with the ability to resist attacks.

Cryptographic modules as one of the information

security products, how to timely and efficiently

evaluate its security to complete their functions, has

issued the relevant international standards and many

scholars have made a research in this are a(Su et al.,

2011).

Cryptographic ICs inevitably become the targets

of numerous attacks, including fault injection attacks.

The fault injection may cause transient logic errors

during the execution of cryptographic algorithms.

The transient errors may bypass the security condition

checks, or be used for differential fault analysis(DFA)

(Barenghi et al., 2012).There are multiple methods to

invoke faults such as variations in supply voltage,

variations in the external clock, temperature

variation, white light, laser, and X-rays and ion beams

(Kim and Quisquater, 2007). The RSA

implementation with Chinese Remainder Theorem

(CRT-RSA) was reported broken by fault attacks with

only one faulty computation (Boneh et al., 2001).

Similarly the secret keys could be compromised from

ECC, DES, AES and RC5 crypto modules etc. (Bar-

El et al., 2006).

The key point of fault injection attack is injecting

a fault in correct location and correct time. Therefore

security evaluation must be done in both time and

space domains. The security evaluation in space

domain is to locate the vulnerable region of

cryptographic ICs under test. The security evaluation

in time domain is to identify the sensitive time period

on the vulnerable region.

The traditional security evaluation often demands

experienced engineers repeatedly scan the IC under

test for a few hours to a few days to obtain effective

results. Take the smart card test for example, it

usually takes 1-5 days for security evaluation against

laser beam attacks (MasterCard International

Incorporated, 2005). On one hand, this is due to the

niche probability of effective fault injection both on

the temporal and the spatial domain. On the other

hand, the traditional way of fault injection test cannot

effectively detect the internal logic errors due to the

limited IO numbers. The requirement on specific and

profound knowledge of cryptographic ICs also makes

it difficult for successful evaluation both in space and

time domains. Besides, location of the vulnerable

region is affected by the attack time, which will cause

Shao, C., Li, H. and Xu, G.

Quantitative Evaluation of Security on Cryptographic ICs against Fault Injection Attacks.

DOI: 10.5220/0005686300970104

In Proceedings of the 2nd International Conference on Information Systems Security and Privacy (ICISSP 2016), pages 97-104

ISBN: 978-989-758-167-0

inaccurate evaluation results if security evaluation in

space and time are separated.

Motivated by these challenges, we develop a

quantitative model to evaluate the security

considering both the sensitive time and space during

the algorithm operation for cryptographic ICs, which

is based on the proposed design for security test

(DFST) in (Shao et al., 2014) against fault injection

attacks with industrial automatic test equipment

(ATE). A three dimensions (3D) fault map in time

and space can be quickly and accurately obtained,

which helps to locate the error-prone region of

cryptographic ICs. The value representing the

security level can be calculated by the quantitative

model.

Compared to the existing security evaluation, the

main contributions of the proposed security

evaluation method are as follows:

 Security evaluation is performed based DFST,

which helps to diagnose the fault occurrence

locations with high accuracy and fault occurrence

time period with high efficiency.

 The quantitative model considers both the space

domain and the time domain, which could provide

intuitive understanding and comprehensive

evaluation of cryptographic ICs security against

fault injection attacks.

The rest of the paper is organized as follows. We

briefly introduce the background of fault injection

attacks on cryptographic ICs and security test of

cryptographic ICs with DFST in Section II. In Section

III, we present the evaluation flow based on DFST

method and present the quantitative model

considering both the space and the operation time. In

Section IV, a case study on two RSA implementations

is demonstrated to validate the effectiveness of the

quantitative evaluation model. The study is concluded

in Section V.

2 BACKGROUND

2.1 Fault Injection Attacks

Fault injection attackers aim to maliciously alter the

correct functioning of computing devices, and

analyze the faulty output to retrieve the secret

information, which been listed into Federal

Information Processing Standard FIPS 140-3,

Security Requirements for Cryptographic Modules

(NIST, 2009), generally accepted as one of the

standard security evaluation methods. Fault injection

techniques can be classified in two main categories:

hardware fault injection, and software fault injection

(Ningfang et al., 2011).The hardware fault injection

are of the main interest in this paper, which include

variations in the external clock, variations in supply

voltages, laser illumination, X-rays and ion beams

radiation etc.

The hardware fault injection tools can be

classified by their (temporal and spatial) precision

and the cost (Kim and Quisquater, 2007).

With well-timed power spikes or dropdowns into

the supply line, it is possible to for the device to skip

specific instruction execution. The temporal precision

depends on the voltage drop/spike duration and

synchronization with the target device. Similarly,

altering the length of a single clock cycle may corrupt

data storage, which also requires relatively high

temporal precision.

Electromagnetic (EM) disturbances near the

device may induceddy currents in the circuit, causing

temporary alterations of the signal voltage level.

Laser beam and heavy ion micro beam can cause

abnormal behaviors on semiconductor devices

through single event effects (SEE), where a strong

radiation of a transistor may form a temporary

conductive channel in the dielectric, which, in turn,

may cause the logic circuit to switch state in a precise

and controlled manner.

2.2 Fault Attacks to Break

Cryptosystems

Fault injection has been reported effective on various

crypto modules. DES (Data Encryption Standard)

was reported vulnerable against fault injection attacks

at the15

round, an exclusive-OR (XOR) operation

between the correct and faulty cipher text will yield

the 15

round-sub keys. An exhaustive search of the

64 possible values of the corresponding substitution

will reveal the left 6-bitsubkey and thus the entire key

(Bar-El et al., 2006). A fault occurs on the 9

round

of AES (Advanced Encryption Standard) before Mix

Column operation will also yield the round key

(Moradi et al., 2006).This paper will take the right-to-

left RSA binary implementation with Montgomery

modular multiplication as the example to illustrate the

principle of fault injection attacks.

RSA is one of the first practicable public-key

cryptosystems and is widely used for secure data

transmission, named after Ron Rivest, Adi Shamir

and Leonard Adleman (Rivest et al., 1978). In such a

crypto system, the encryption key is public and differs

from the decryption key which is private and kept

secret. Two distinct and large odd prime numbers p

and q are used to generate two key-pair values: the

ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy

public key-pair (e,N), and the private key-pair (d,N)

(Wang, 2006; Zhang, 2005). The RSA algorithm can

be described as follows:

The modulus N is the product of two large primes

p and q.

Computes e through

()()

()

,111gcd e p q−−=

, where

gcd refers to the function of greatest common divisor

(Hardy and Wright, 1979).

Computes d through

()

1 mod( 1)( 1)de p q⋅= − −

The RSA encryption is performed using the public

key e:

mod

cm=

(1)

Where m is the plaintext,0<m<N, and c is the

ciphertext which can be decrypted using the secret

key d:

mod

mc=

(2)

An effective fault induced in one of the RSA private

key bits in the binary RSA implementation will result

in a faulty decryption result. With detailed fault

analysis, one can extract the key bit (Bar-El et al.,

2006). The procedure is as following. An attacker

arbitrarily chooses a plaintext m and computes the

cipher-text c. Let us assume there is one bit in secret

key d flipping from 1 to 0 or vice versa with a fault

injection, and the position of the flipped bit is

randomly located, then the attacker obtains a faulty

plaintext

as the decryption result. Since there is

only one bit flipped, let it be

[]di

flipped to

[]di

]

[id

then the division between the faulty and the correct

plaintext will yield:

2[]

(mod )

(3)

Obviously, if

(mod ) [ ] 1

Ndi

= →=

(4)

And if

(mod ) [ ] 0

cNdi

= →=

(5)

This process is repeated until enough information is

obtained about the secret key d.

RSA using the Chinese Remainder Theorem

(CRT-RSA) is also vulnerable to fault attacks (Kim

and Quisquater, 2007). Let a and b be the pre-

computed values required by the CRT-RSA, there is:

{

1mod() 0mod()

0mod( ) 1mod( )

ap b p

and

aq bq

≡≡

(6)

And define:

mod ( 1)

dd p

dd q

−

(7)

The RSA signature s is the sum as:

(mod )

sas bs N=+⋅⋅

(8)

Where:

(mod )

sm p

sm q

(9)

If there is a fault injected during the computation of

, then the faulty signature

(mod )

as bs N

′′

=⋅ +⋅

. The subtraction between

the correct and the faulty signature will yield:

()

()mod

sbs s N

′′

Δ= − = ⋅ −

(10)

A simple gcd (greatest common divisor) calculation

will factor N:

gcd( , )NpΔ=

(11)

This will compromise the RSA secret key, since we

can easily obtain d with known two large primes p

and q.

2.3 Security Test of Cryptographic ICs

with DFST

Quantitative Evaluation of Security is based on the

proposed design for security test (DFST). In this

section we demonstrate design for security test

(DFST) method and the consequent security test with

ATE on cryptographic ICs proposed in (Shao et al.,

2014), combining DFT and fault injection techniques

to facilitate a fast security test against fault injection

with a low IC area overhead.

Figure 1 demonstrates the relation of different

phases of cryptographic ICs from design to test. The

cryptographic ICs are designed with the proposed

DFST. Security test of cryptographic ICs is

performed by an engineer in a third authentication

party. The designers of cryptographic ICs should

provide the test patterns to the security authentication

party.

Quantitative Evaluation of Security on Cryptographic ICs against Fault Injection Attacks

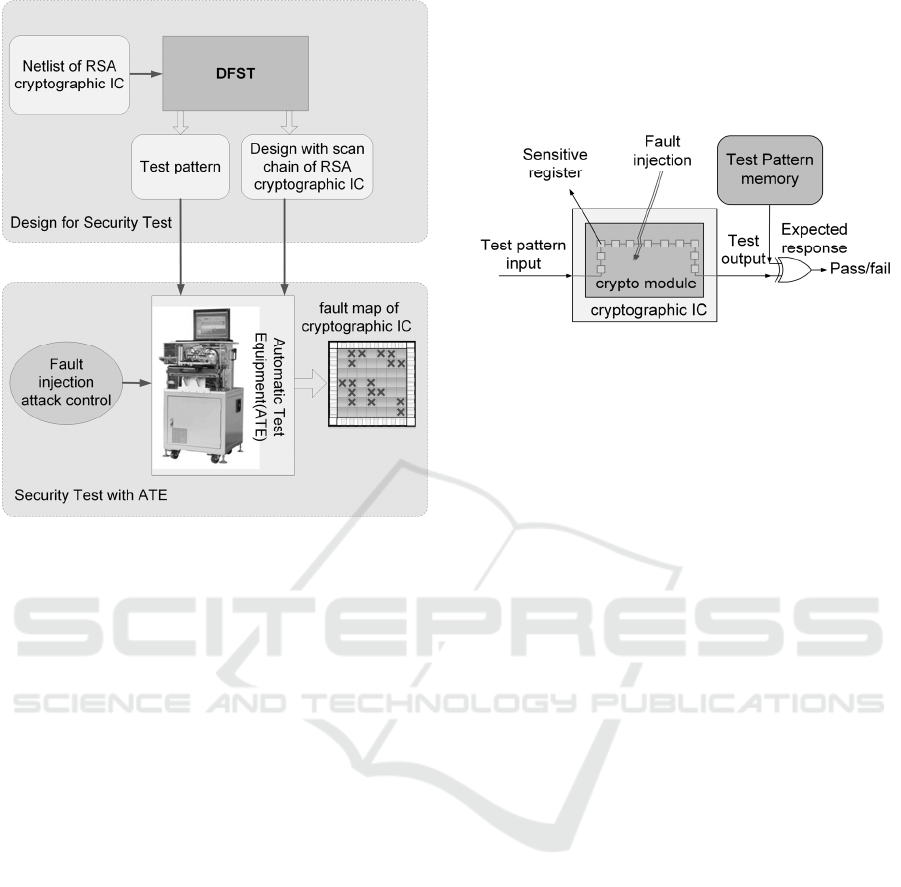
Figure 1: Design for security test (DFST) and Security test

of cryptographic ICs.

The security test only concerns a small fraction of

the internal circuit states, on which an injected fault

will result in an effective faulty

encryption/decryption result. With careful

differential fault analysis, the effective faulty result

will largely reduce the search space of the secret key.

The principle idea of DFST is to observe the internal

states of those vulnerable cells.

The flowchart of DFST is as follows: Firstly, we

identify the sensitive registers with SER analysis as

previously described. Secondly, we mark the

sensitive registers in Register Transfer Level (RTL)

design netlist by prefixing sensitive registers. For

example, in the cryptographic algorithm of the right-

to-left RSA binary implementation with Montgomery

modular multiplication, all the sensitive registers

d[i]are beginning with ‘e_or_d_reg_’. Thirdly, we

only insert those marked registers into scan chains.

Finally, the test patterns are generated with the

commercial Automatic Test Pattern Generation

(ATPG) tools. The test pattern will be used during the

security test.

Once cryptographic ICs are designed for security

test with the proposed DFST, the security test could

be performed with the industrial ATE equipment. The

test structure is illustrated in Figure 2.

The procedures of the security test are as follows:

1) Set the device under test (DUT) in test mode; 2)

Run the test repeatedly with fault injection scanning

the DUT; 3) Compare the test result to the golden

references. If the two results are inconsistent, mark

the area being attacked as the sensitive area; 4) Scan

the whole DUT and form a fault map.

Figure 2: Security test on the cryptographic ICs with DFST.

3 QUANTITATIVE SECURITY

EVALUATION BASED ON DFST

Since the attacks are sensitive in both time and space

domains. We develop the quantitative security

evaluation model accordingly. We first locate the

vulnerable region of the IC under test. Then we

further identify the sensitive time period on the

vulnerable region. Thus we can plot the three-

dimensional (3D) map indicating the vulnerability.

Each fault is represented with a cuboid, the bottom

area stands for the fault injection spot on the chip

layout, and the height stands for the sensitive time

period of the spot. The volume of all the cuboids is

then calculated for quantitative evaluation.

3.1 Security Evaluation in Space

Domain

The aim of security evaluation in space domain is to

locate the vulnerable region of ICs under test. The

cryptographic ICs designed by DFST can facilitate

fast and automatic security test in space domain

against fault injection. The flow of security test with

the DFST is displayed in Figure3.

The procedures of the security evaluation in space

are as follows:

1) Set the security chip designed by DFST in test

mode;

2) Make a scan test of the security chip under fault-

attack;

3) Judge the sensitive area by comparing the scan

output to the expected value and compute number

of fault occurrences n. If the two results are

ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy

100

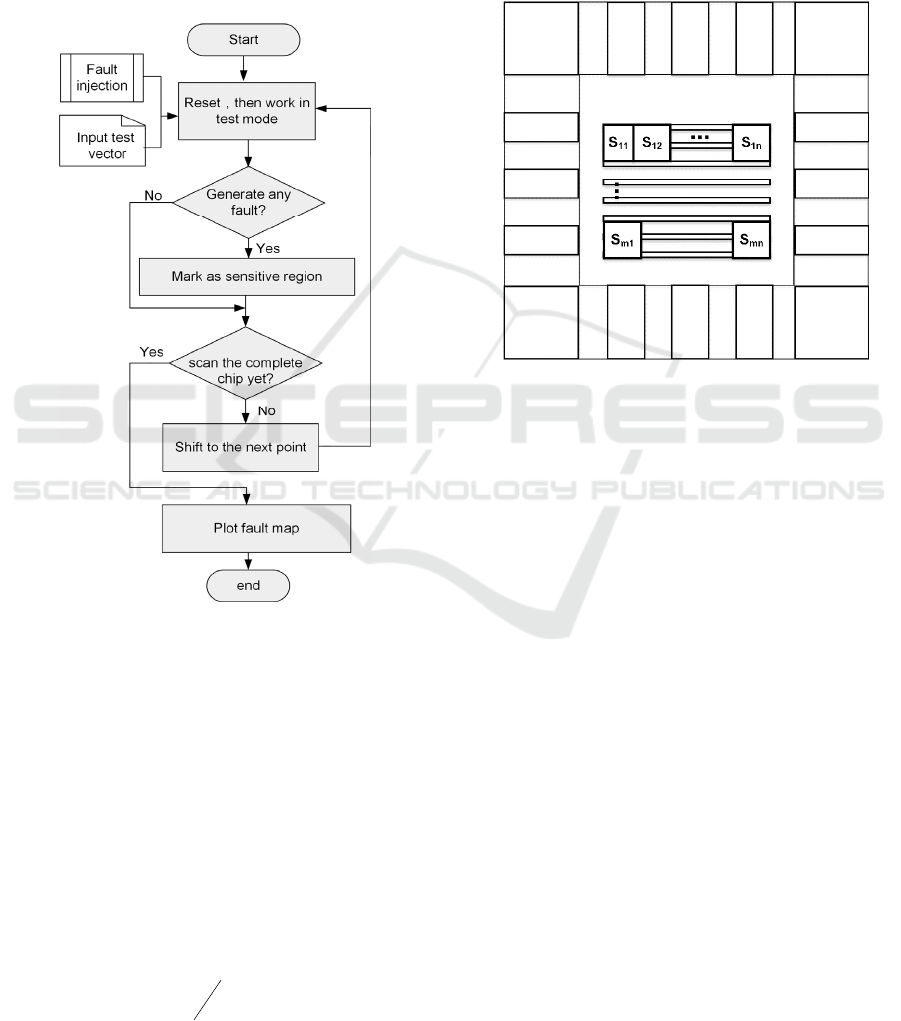
inconsistent, mark the area being attacked as the

sensitive area.

4) Scan the whole chip layout and form a 2D fault

map.

The Security evaluation based DFST can determine

the sensitive region exactly by the output vector and

has nothing to do with the output analysis, which is

much more efficient than security chip without scan

chain.

Figure 3: The flow of security test.

During the security test, the chip surface will be

scanned with various fault injection tools, such as

laser illumination and ion beam irradiation. The chip

can be scanned with any size of fault injection attack

(FIA) spot, which can target from a single transistor

to hundreds of transistors, depending on the

equipment used by the attackers as described in

Section II. Figure 4 illustrates scanning in the security

test, where each scan (S

, S

…, S

) is scan spot,

which corresponds to scan step and scan precision of

fault injection tool.

The equation for quantitative security in space

domain

for the entire chip is as:

(12)

Where N denotes the total number of the fault

injection evenly traversing the entire IC, which

depends on the entire chip area, each injection spot

size and scan step; n denotes the number of fault

occurrences;

denotes the percentage of the

sensitive area in the whole chip. A larger value of

indicates a lower security level.

Figure 4: Fault injection scan on the cryptographic ICs with

DFST.

3.2 Security Evaluation in Time

Domain

Since security evaluation in time domain aims to

locate the vulnerable time regions of marked

vulnerable locations during the cryptographic

algorithm execution, the cryptographic IC should

work in function mode. In order to flexible control

fault injection, security evaluation in time domain is

operated by the method of function simulation. The

procedures are as follows:

1) Select a sensitive logic cell from marked

vulnerable locations and inject faults at certain

time intervals. Fault can be injected by the

simulation tools. The time interval of fault

injection is flexible. A short interval usually

means finer operation but longer evaluation cycle.

We recommend one clock cycle as the time

interval for the simulation of each fault injection.

2) Analysis the encryption/decryption results and

judge the sensitive time. If the result generates a

valid error, mark the time interval as the

Quantitative Evaluation of Security on Cryptographic ICs against Fault Injection Attacks

101

sensitive time.

3) Traverse the entire encryption/decryption period

under fault injection at certain time intervals.

4) Move to the next a sensitive point and repeat the

above steps.

5) Traverse all sensitive logic cells from marked

vulnerable locations of 2D fault map. Then plot

the sensitive time period for corresponding

sensitive logic cells and form 3D fault map. Each

fault is represented with a cuboid.

The volume V of the sensitive regions is calculated as:

)()(

isitV



⋅=

(13)

Where n denotes the total number of the sensitive

spots in space; i denotes the ith spot that exhibits a

fault; s(i) denotes the area of the i

fault injection

spot; t(i) denotes the time during of the fault on the i

spot.

Eq. (13) does not take into account of the parallel

and the serial implementations of the same

cryptographic algorithm. A parallel implementation

usually occupies larger IC footprint than the serial

implementation, but takes shorter time. To eliminate

the effect from parallel and serial operation of the

same function, Eq. (13) could be updated through

normalization:

isit

∗

⋅



)()(

(14)

Where S denotes the entire IC area, T denotes the

entire time for each cryptographic execution cycle. A

bigger value of

indicates a lower security level.

4 CASE STUDY

4.1 Security Quantitative Evaluation

Method Based RSA

In this section, we demonstrate the quantitative

evaluation with the implementation of a 1024-bit

RSA cryptosystem. The RSA module is the right-to-

left binary algorithm with Montgomery modular

multiplication. The design mainly includes an 8051

microprocessor, memory, a bus controller, a random

number generator (RNG), the RSA encryption and

the decryption module. The procedure of security

quantitative evaluation for the RSA cryptographic IC

is divided into two steps: design for security test and

security quantitative evaluation. The detailed flow is

as follows:

1) Design for Security Test:

 The key registers d[i] are identified as the

sensitive registers.

 Mark the sensitive registers by defining the

registers’ names with the prefix “e_or_d_reg_” in

the netlist.

 Insert the scan-chain around the marked sensitive

registers and output the original DFT gate-level

netlist. The DFT commands such as

“set_scan_path” and “set_scan_element

true/false” are able to separate the sensitive

registers from other registers.

 Generate the test patterns out of TetraMax

, a

commercial ATPG tool.

 Generate the physical layout of the RSA

implementation t.

2) Quantitative Evaluation of Security:

 Set the RSA cryptographic IC designed by DFST

in test mode.

 Make a scan test of the RSA cryptographic IC

under fault-attack in Automatic Test Equipment.

 Perform the quantitative security evaluation in

space domain by simulating the fault injection

test, and plot the 2D fault map.

 Perform the quantitative security evaluation in

time domain, and plot the 3D fault map.

4.2 Experimental Results

In our simulation, the scan registers are synthesized

with Synopsys Design Compiler™, the scan chains

are inserted with DFT Complier™, the test patterns

are generated from the ATPG tool TetraMax™, and

the circuit simulator is chosen to be VCS™. Other

similar tools can also be used. We identify 2048

sensitive registers and insert 6 scan-chains, which

accounts for an area overhead of 0.6%. For our RSA

implementation and the necessary peripheral circuits

of 740,000 logic gates, the area of cryptographic IC

design of RSA is 36mm

, with the technology

of0.18um GSMC. Laser illumination is selected as

fault injection source, and a laser spot size is selected

to be 10umx 10umlarge.

Figure 5 demonstrates the 2D fault map of the

RSA cryptographic IC design. The crosses indicate

the faults (not one by one indication due to the image

resolution limit). The sensitive registers contain two

types: key_ed[i] and e_or_d[i]. The total number of

laser illumination traversing the entire chip is 360000,

ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy

102

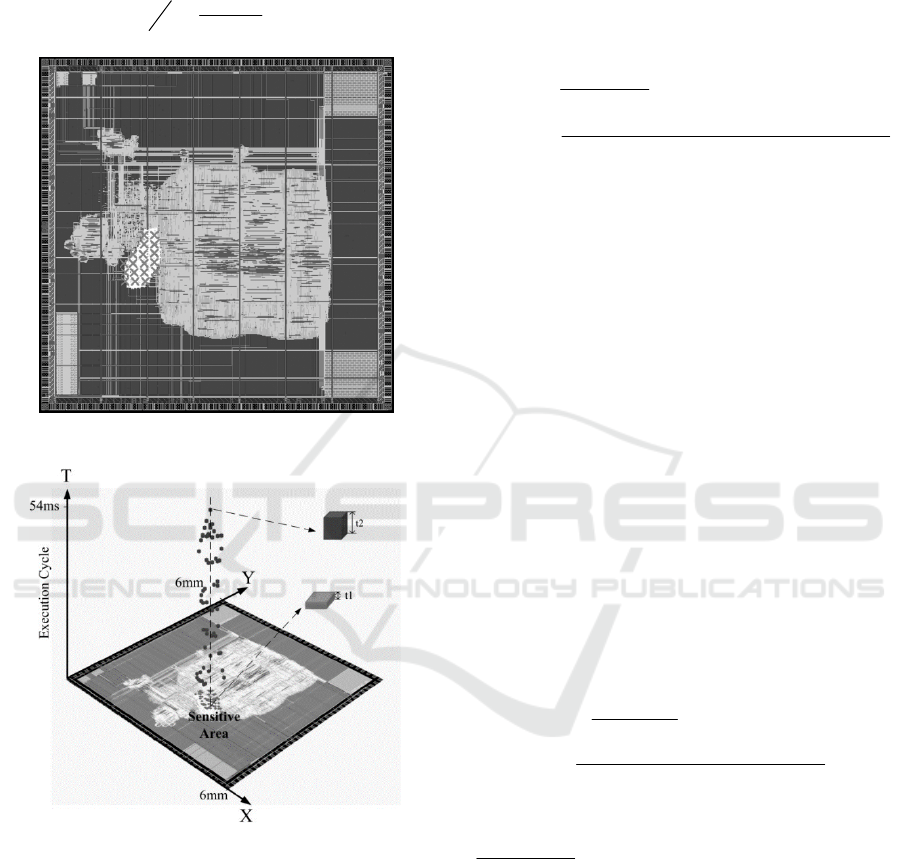
among which the number to successfully inject faults

is 4248. Then the quantitative security evaluation of

our test chip in space domain for the entire chip is

calculated as:

%18.1

360000

4248

===

Figure 5: 2D fault map of the binary RSA design.

Figure 6: 3D fault map of the binary RSA design.

Figure 6 demonstrates the of the 3D fault map of

the cryptographic IC design of the binary RSA

implementation. The die area of cryptographic IC

design of RSA is 36mm

and the length of the RSA

decryption time is about 54ms. The number of

sensitive spots related to the registers key_ed[i] is

2016, shown with the pink short blocks at the bottom.

The sensitive time interval for key_ed[i] is 50ns, as

‘t1’exemplifies. The number of sensitive spots related

to the registers e_or_d[i] is 2232, shown with the blue

blocks along the time axis. The sensitive time interval

for e_or_d[i] is 51400ns, as ‘t2’exemplifies. The area

of each register in technology library of0.18um

GSMC is 66.5um

The quantitative security evaluation of the right-

to-left binary implementation of RSA is then

calculated as:

62 6

() ()

(50 2016 51400 2232) 66.5

36 10 54 10

3.9 10

Q binary

ti si

ns ns um

um ns

−

⋅

∗

×+ × ×

×∗×

=×



Various implementations will have different values of

quantitative security evaluation. The CRT-RSA has

much larger value than the binary RSA, since CRT-

RSA has much larger sensitive area: the whole sub-

modules computing

and

.Furthermore, each

sensitive spot will be vulnerable for a long time along

the execution cycle, since the fault injection attack

works on binary RSA if and only if one bit is changed,

but there is no such limit on CRT-RSA.

For our CRT-RSA implementation and the

necessary peripheral circuits of 983,000 logic gates,

there are 21633 sensitive registers. The total layout

area is 72mm

, the number of sensitive logic cells in

sub-modules computing sp or sq is 519401. The area

of a standard cell in technology library of0.18um

GSMC is 13.5um

.Each of the computation of s

and

roughly takes 27ms. Then the quantitative security

evaluation of the CRT-RSA implementation is

calculated as:

62 6

() ()

2(27 10 519401) 13.5

0.19

72 10 27 10

Q CRT RSA

ti si

ns um

um ns

−

⋅

∗

×× ×

×∗×



This indicates that CRT-RSA is almost

48717

Q CRT RSA

Q binary

−

times more vulnerable against

the fault injection attacks. The result is quite contrary

to previous observation that CRT-RSA is superior

compared to the right-to-left binary implementation,

in terms of better security against simple power

analysis etc. This quantitative evaluation model can

help the product designers to select the appropriate

implementation, considering potential attack

environments.

Quantitative Evaluation of Security on Cryptographic ICs against Fault Injection Attacks

103

5 CONCLUSIONS

The security evaluation against fault injection attacks

is challenging due to the niche probability of effective

fault injection both on the temporal and spatial

domain and the difficulty in observing internal

transient logic errors. This paper proposes a

quantitative model to evaluate security based DFST

against fault injection attacks, considering both the

operation time and the sensitive area of the

cryptographic ICs. Simulation results on two RSA

implementations demonstrate the feasibility of the

design for security test method and the evaluation

model, which can be easily extend to implementation

of other cryptographic algorithms. Further work is to

improve the efficiency of the security evaluation

with automated scripts.

ACKNOWLEDGEMENTS

This work was supported by Shenzhen S&T Funding

with Grant No. JCYJ20140417113430591,

GJHZ20140417113430584,

CXZZ20140527172356968,

JSGG20150511104613104, Guangdong S&T

Funding 2013B050800003, 2015B010106004 and

China National S&T Major Project with Grant No.

2014ZX01032401-001.

REFERENCES

Su, D., Xu, K. and Gao, Y., 2011. The Evaluation Model

and Index System of Cryptographic Modules Security

Assurance Ability. Proceedings of Third International

Conference on Multimedia Information Networking

and Security, pp. 448-452.

Barenghi, A., Breveglieri, L., Koren, I. and Naccache, D.,

2012. Fault injection attacks on cryptographic devices:

Theory, practice, and countermeasures. Proceedings of

the IEEE, vol. 100, no. 11, pp. 3056—3076.

Kim, C.H. and Quisquater, J. J., 2007. Fault attacks for CRT

based RSA: New attacks, new results, and new

countermeasures. In: Information Security Theory and

Practices. Smart Cards, Mobile and Ubiquitous

Computing Systems, pp. 215—228.

Boneh, D., De Millo, R. A. and Lipton, R. J., 2001. On the

importance of eliminating errors in cryptographic

computations. Journal of cryptology, vol. 14, no. 2, pp.

101—119.

Bar-El, H., Choukri, H., Naccache, D., et al, 2006. The

sorcerer's apprentice guide to fault attacks. Proceedings

of the IEEE, vol. 94, no.2, pp. 370—382.

MasterCard International Incorporated, 2005. Security

Guidelines for Smart Card Integrated Circuits.

Shao, C., Li, H., Xu, G., et al, 2014. Design for security test

against fault injection attacks. Electronics Letters. vol.

50, no. 23, pp. 1677-1678.

The National Institute of Standards and Technology

(NIST), 2009. Security Requirements for

Cryptographic Modules. FIPSPUB140-3 Draft.

Ningfang, S., Jiaomei, Q., Xiong, P., et al, 2011. Fault

Injection Methodology and Tools. Electronics and

Optoelectronics (ICEOE), pp. 47—50.

Moradi, A., Shalmani, M. T. M., and Salmasizadeh, M.,

2006. A generalized method of differential fault attack

against AES cryptosystem. In Proc. Cryptographic

Hardware and Embedded Systems-CHES, Springer

Berlin Heidelberg, pp. 91-100.

Rivest, R. L., Shamir, A., and Adleman, L., 1978. A method

for obtaining digital signatures and public-key

cryptosystems.in Communications of the ACM, vol. 21,

pp.120-126.

Wang, J., 2006. Research of RSA Encryption Algorithm.

Shenyang University thesis.

Zhang, L., 2005. Research and Implementation of RSA

Cryptography. Shandong University of Science and

Technology thesis.

Hardy, G. H., and Wright, E. M., 1979. An introduction to

the theory of numbers. The Clarendon Press Oxford

University Press, fifth edition.

ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy

104