
A Simple Algorithm for Topographic ICA
Ewaldo Santana
1
, Allan Kardec Barros
1
, Christian Jutten
2
, Eder Santana
1
and Luis Claudio Oliveira
1
1
Federal University of Maranhao, Dept. Electrical Engineering, Sao Luis, Maranhao, Brazil
2
GIPSA-lab, Department Images et Signal, Saint Martin d’Heres Cedex, France
Keywords:
Independent Component Analysis (ICA), Topographic ICA, Receptive Fields.
Abstract:
A number of algorithms have been proposed which find structures that resembles that of the visual cortex.
However, most of the works require sophisticated computations and lack a rule for how the structure arises.
This work presents an unsupervised model for finding topographic organization with a very easy and local
learning algorithm. Using a simple rule in the algorithm, we can anticipate which kind of structure will result.
When applied to natural images, this model yields an efficient code for natural images and the emergence
of simple-cell-like receptive fields. Moreover, we conclude that the local interactions in spatially distributed
systems and local optimization with norm L2 are sufficient to create sparse basis, which normally requires
higher order statistics.
1 INTRODUCTION
Perhaps the most productive set of self-organizing
principles are information theoretic in nature. Shan-
non in his seminal work showed how to optimally de-
sign communication systems by manipulating the two
fundamental descriptors of information: entropy and
mutual information Shannon (1948). Inspired by this
achievement, Linsker proposed the “infomax" prin-
ciple, which shows that maximization of mutual in-
formation for Gaussian probability density functions
comes to correlation minimization Linsker (1992).
Using correlation as the basis of learning, some re-
searchers have developed several algorithms to mimic
the process of learning Oja (1989); Ray et al. (2013).
Bell and Sejnowski applied this same principle for
independent component analysis (ICA) with a very
clever local learning rule taking advantage of the sta-
tistical properties of the input data Bell and Sejnowski
(1995). Barlow hypothesized that the role of the vi-
sual system is exactly to minimize the redundancy in
real world scenes Barlow (1989).
Finding the maximum entropy distribution, one
of the principles of redundancy reduction when per-
formed with the constraint of a fixed mean, provides
probability density functions with sharp peaks at the
mean and heavy tails, i.e. sparse distributions Si-
moncelli and Olshausen (2001). Thus, assuming that
the goal of the primary visual (V1) cortex of mam-
mals is to obtain a sparse representation of the natu-
ral scenes, Olshausen and Field derived a neural net-
work that self-organizes into oriented, localized and
bandpass filters reminiscent of receptive fields in V1
Olshausen and Field (1996). Exploiting V1, Vinje
and Gallant Vinje and Gallant (2000) experimentally
proved the sparse representations in natural vision. In
modeling natural scenes, Hyvarinen et al Hyvarinen
and Hoyer (2000) defined an Independent Component
Analysis (ICA) generative model in which the com-
ponents are not completely independent but have a
dependency that is defined in relation to some topog-
raphy. Components close to one another in this to-
pography have greater co-dependence than those that
are further away. Using a similar rationale, Osindero
et al Osindero (2006) presented a hierarchical energy-
based density model that is applicable to data-sets that
have a sparse structure, or that can be well character-
ized by constraints that are often well-satisfied, but
occasionally violated by a large amount. Moreover,
there have been a number of studies on sparse coding
and ICA that match rather well the receptive fields
of the visual cortex, and also a number of algorithms
which finds excellent organization that resembles that
of the visual cortex, i.e., Olshausen and Field (1996).
One of the difficulties faced by all these stud-
ies is the sophisticated computation required to ob-
tain sparse representations and the generative models
which are generally derived with several constraints
to conform with mathematical analysis. Analyzing
sensory coding in a supervised framework, Barros et
al Barros and Ohnishi (2002) proposed the minimiza-
tion of a nonlinear version of the local discrepancy
between the sensory input and a neuron internal ref-
erence signal which also yields wavelet like recep-
150
Santana, E., Barros, A., Jutten, C., Santana, E. and Oliveira, L.
A Simple Algorithm for Topographic ICA.
DOI: 10.5220/0005683501500155
In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 4: BIOSIGNALS, pages 150-155
ISBN: 978-989-758-170-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
tive fields when applied to natural images. In this
work we propose an unsupervised model for find-
ing topographic organization using convex nonlinear-
ities with a very easy and local learning algorithm.
Our development is based on the fact that most non-
linearities yield higher order statistical properties in
modeling. In our context, we model the neuron as
a system which performs non-linear stimuli filtering
Barros and Ohnishi (2002), and use its output as in-
put signals from neighboring neurons. This arrange-
ment gives spatially coherent responses. This paper
is organized as follows: In Section 2, we present the
model and develop methods for obtaining the algo-
rithm. Section 3 shows simulations and results. Dis-
cussions and conclusions are proposed in section 4.
2 METHODS
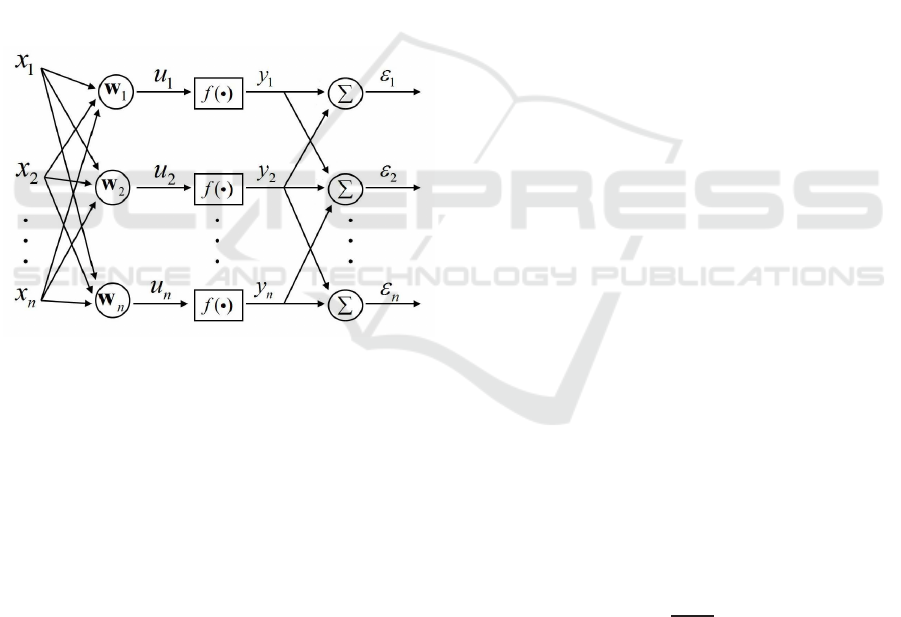
Figure 1: Proposed model, which works in parallel fashion.
First layer: input vector x; second layer: the input vector
are locally linearly combined by synaptic weights vector w
yielding the signal u; Third layer: the signal u pass through
a non-linearity, f(.) to get higher order characteristics of
input signal; Fourth layer: the local discrepancy.
Input signals, x
k
= [x
1
(k),...,x
n
(k)], are assumed gen-
erated by a linear combination of real world source
signals, s(k) = [s
1
(k),..., s
n
(k)]
T
, x = As, where A is
an unknown basis functions set.
In order to facilitate further development, we
also assume that the input signals are preprocessed
by whitening Hyvarinen and Hoyer (2000). In the
demixing model each signal, x
j
, at the input of
synapse j connected to neuron k will be multiplied
by the synaptic weight w
kj
and summed to produce
the linear combined output signal of neuron k, which
is an estimation of s
k
,
u
k
=
n
∑
j=1
w
kj
x
j
,y
k
= f(u
k
), (1)
where f is an even symmetric non-linear function,
which is chosen to exploit the higher order statisti-
cal information from the input signal Hyvarinen and
Hoyer (2000). This signal, y
k
, interacts with neigh-
boring outputs, since in the nervous system the re-
sponse of a neuron tends to be correlated with the re-
sponse of its neighboring area Durbin and Mitchison
(2007). So, y
k
is used to generate a signal to adapt w
kj
and make its output coherent with the response of its
neighbors.
We define the neighborhood of neuron k, all neu-
rons i that are close to neuron k in a matrix representa-
tion, and define the action of a neuron’s neighborhood
as a weighted sum of output signals from all neurons
in the neighborhood,
v
k
=
∑
i
y
ik
=
∑
i
f(u
ik
), (2)
where i are the indices of the neighboring outputs k
and v
k
interacts with y
k
to generate a self reference
signal, ε
k
= y
k
+ αv
k
, where α determines the neigh-
borhood influence on neuron’s activation. This self
reference signal must be minimized in order to reduce
the local redundancy. Thus, we define the following
local cost,
J
k
= E[ε
2
k
] = E[(y
k
+ αv
k
)
2
], (3)
which should be minimized with respect to all
weights of neuron k. Taking the partial derivative of
Eq.(3) with respect to the parameters and equating it
to zero we obtain the following equation:
2E
f
′
(u
k
)(y
k
+ αv
k
)x
= 0, (4)
where we used the fact that f
′
(u
ik
), with respect to
w
k
, is zero for i 6= k.
In order to avoid the trivial solution of zero
weight, we utilize the Lagrange multipliers to mini-
mize J
k
under constraint kw
k
k = 1 and observe that
the derivative of
∑
i
f
′
(u
ik
) with respect to w
k
is zero.
With this, we obtain the following two step algorithm,
w
k
= E
f
′
(u
k
)ε
k
x
w
k
=
w
k
kw
k
k
. (5)
This procedure is accomplished in parallel to ad-
just all weights for each neuron in the network,
where we include orthogonalization steps taken from
Foldiák (1990). In this way a matrix W is obtained.
Moreover, we can show that the proposed algo-
rithm converges as given in the theorem below.
Theorem: Assume that the observed stimuli fol-
low the ICA model and that the whitened version of
A Simple Algorithm for Topographic ICA
151

those signals are x=VAs, where A is an invertible ma-
trix and V is an orthogonal matrix, and s is the source
vector. Suppose that J(w
k
) = E{[ f(w
T
k
v)+α.v
k
]
2
} is
an appropriate smoothing even function. Moreover,
suppose that any source signal s
k
is statistically inde-
pendent from s
j
, for all i 6= j. This way, the local min-
imum of J(w
k
), under restriction k w
k
k = 1 describes
one line of the matrix (VA)
−1
and the correspondent
separated signal obeys
E[s
2
i
( f
′
(s
k
))
2
+ s
2
i
f(s
k
) f
′′
(s
k
) +
+ s
i
f(s
k
) f
′
(s
k
) −s
k
f(s
k
) f
′
(s
k
)] +
+E[( f
′
(s
k
))
2
+ f(s
k
) f
′′
(s
k
) −
− s
k
f(s
k
) f
′
(s
k
)] < 0, ∀i ∈v
k
, (6)
We show the proof in the appendix.
3 SIMULATIONS AND RESULTS
We performed simulations with the closest eight neu-
rons neighbors, as defined in Appendix A. We chose
the following even symmetric non-linearity: f(u
k
) =
u
k
.atan(0.5u
k
) −ln(1 + 0.25u
2
k
)). This function has
some advantages in terms of information transmission
between input and outputButko and Triesch (2007).
Moreover, this function will work on all statistics of
the signal, yielding therefore a better approximation
to the probability density function (pdf) of it Bell and
Sejnowski (1995). This can be intuitively understood
by expanding the sigmoidal function into a Taylor se-
ries, whereas one can easily notice that f(u
k
) can be
written as a linear combination of u
2
k
. That function
also satisfies the requirement of a unique minimum as
shown by Gersho Gersho (1969).
We applied the algorithm given by Equation (5)
to encode natural images, in a way similar to that
carried out in the literature Olshausen and Field
(1996). We take random samples of 16 x 16
pixel image patches from a set of 13 wild life pic-
tures,(http://www.naturalimagestatistics.net/) and put
each sample into a column vector of dimension
256x1. We used 200,000 whitened versions of those
samples as stimuli. For each set of 200,000 points the
algorithm runs over 20,000 times in order to obtain
a good estimation for matrix A. In this case we have
also 16 x 16 units in the network. We varied α from
0.005 to 1.0 to highlight the influence of the neigh-
borhood in the results.
In Fig.2, one can see the obtained basis vectors
(columns of matrix A) for α = 0.1 and 0.9, respec-
tively. The clustered topographical organization can
be easily seen taking one little square (receptive field)
and considering its eight closest neighbors.
(a)
(b)
Figure 2: The topographic basis functions (columns of ma-
trix A) estimated from natural image data when f(u
k
) =
u
k
·atan(0.5u
k
) −Ln(1+ 0.25u
2
k
) was the non-linearity uti-
lized and neighborhood consisting of the 8 closest neigh-
bors.. (a) α = 0.005; (b) α = 0.9.
In these figures one can observe that basis vec-
tors which are similar in location, orientation and fre-
quency are close to each other. Moreover, we see the
importance of neighbours contribution on organiza-
tion: increasing α, the filters became more correlated.
In Figure 3 , one can see the α values and correspond-
ing mean of correlation coefficients of all neurons in
neighborhood.
4 DISCUSSIONS AND
CONCLUSIONS
In this paper we have presented a model for unsuper-
vised neural network adaptation. In (5) we have a
very simple unsupervised rule to update the weights
in a neural network. In topographic organization lit-
erature, as far as we know, this is the simplest ever
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
152
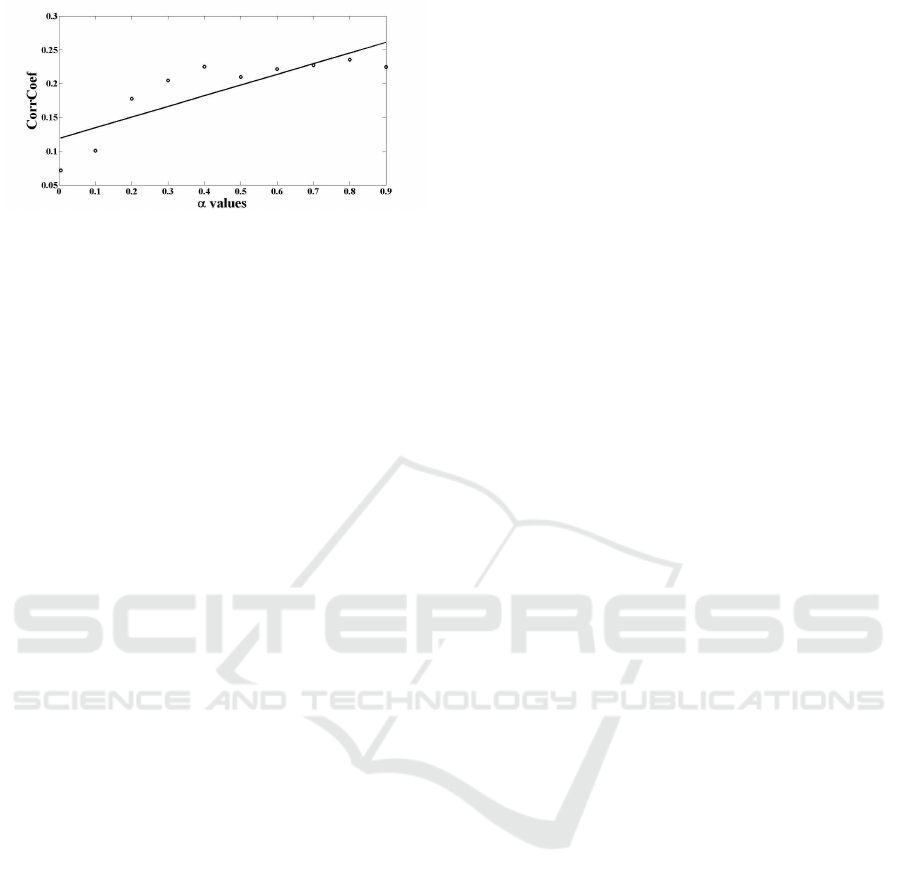
(a)
Figure 3: Mean of correlation coefficient between pair of
basis functions as a function of α values.
suggested, when compared to others in the literature-
Hyvarinen et al. (2000); Hyvarinen and Hoyer (2000);
Osindero (2006). Besides, we have proven mathemat-
ically that the adaptation converges. One possible ap-
plication of this method is to image/signal recogni-
tion, as for each α in (3), we can adjust the character-
istics of the topological structure in order to fit more
closely to the desired image.
There are at least two advantages in this model:
it organizes the resulting filters topographically and
it may be regarded as biologically plausible. Firstly,
we can see in Fig. 2 (a) that a small α results
in no organization at all, while in Fig. 2 (b), we
can see that an α = 0.9 causes the filters to ap-
pear organized. Moreover, we have found the cor-
relation in neighborhood filters. By using equation
Cov(a
i
,a
j
)/(std(a
i
)std(a
)
), where a
i
and a
j
are two
basis functions in the neighborhoodof one neuron, we
can see that the correlation is directly proportional to
the value of α, as shown in Fig. 3. The correlation
between α and Cov(a
i
,a
j
)/(std(a
i
)std(a
)
) was 0.88.
Secondly, it is well known that receptive fields in
the mammalian visual cortex resemble Gabor filters
Laughlin (1981), Linsker (1992). This way, the infor-
mation about the visual world would excite different
cells Laughlin (1981). In Figure 2 (a) and (b), we can
see that the estimation of matrix A is a bank of local-
ized, oriented and frequency selective Gabor-like fil-
ters. Each little square, in the figures above, represent
one receptive field. By visual inspection of Fig. 2 (b),
one can see that the orientation and location of each
visual field mostly change smoothly as a function of
position on the topographic grid. Thus, the emergence
of organized Gabor-like receptive fields can be under-
stood as a biologically plausibility of our model.
This model can be regarded also as biologically
plausible as it works in an unsupervised fashion with
local adaptation rules Olshausen and Field (1996). To
do this, we had chosen some even symmetric non-
linearities which were applied upon a neuron inter-
nal signal.This signal interacts with similar ones from
neighborhoods neurons to generate its output. This
model mimics the V1 cells by an interaction between
neighborhood signals, which is possible due to the
fact that signals from neighborhood neurons are ref-
erence to the activation of one specific neuron Field
(1987). In addition, our method extracts oriented, lo-
calized and bandpass filters as basis functions of nat-
ural scenes without restricting the probability density
function of the network output to exponential ones,
as the IP algorithm of Butko et al Butko and Triesch
(2007). Moreover, Stork and WilsonStork and Wil-
son (1990) proposed an architecture very similar to
the one proposed here, which is largely based on neu-
ral architecture.
ACKNOWLEDGEMENTS
The authors would like to thank Brazilian Agency
FAPEMA for continued support.
REFERENCES
Barlow, H. B., Unsupervised learning, Neural Computa-
tion,v.01, pp. 295-311, 1989.
Barros, A. K. and Ohnishi, N., Wavelet like Receptive fields
emerge by non-linear minimization of neuron error,
International Journal of Neural Systems,v.13, n. 2, pp.
87-91, 2002.
Bell, Anthony J. and Sejnowski, Terrence J., An
Information-Maximixation Approach to Blind Sepa-
ration and Blind Deconvolution, Neural Computation,
n. 7, pp. 61-72, 1995.
Butko, N. J. and Triesch, J., Learning sensory representa-
tions with intrinsic plasticity, Neurocomputing, v. 70,
pp. 1130-1138, 2007.
Comon, Pierre. Independent component analysis, A new
concept?. Signal Processing, v.36,p 287-314, 1994.
Durbin, R and Mitchison, G., A dimension reduction frame-
work for understanding cortical maps, Nature, n.343,
pp. 644-647, 2007.
Field, David J., Relation between the statistics of natural
images and the response properties of cortical cells.
J. Optical Society of America, v. 04, n.12, pp. 2379 -
2394, 1987.
Foldiák, P., Some Aspects of Linear Estimation wiht Non-
Mean Squares error Criteria. Biological Cybernetics,
v. 64, pp. 165 - 170, 1990.
Gersho, A., Forming sparse representations by local anti-
Hebbian learning., Proc. Asilomar Ckts. and Systemas
Conf. (1969).
Hyvarinen, Aapo; Hoyer, Patrik O. and Inki, Mika., Topo-
graphic ICA as a Model of V1 Receptive Fields. Proc.
of International Joint Conference on Neural Networks,
v.03, pp 83-88, 2000.
A Simple Algorithm for Topographic ICA
153

Hyvarinen, Aapo and Hoyer, Patrik O., Topographic In-
dependent Component Analysis. Neural Computation,
v.13, pp 1527-1558. (2000).
Kohonen, T., Self-Organizing Maps. Springer, 2000.
Linsker, R., Local Synaptic Rules Suffice to maximize Mu-
tual Information in a Linear Network. Neural Compu-
tation, v.04, pp 691-702, 1992.
Laughlin, Simon., A Simple Coding Procedure Enhances a
Neuron’s Information Capacity. Z. Naturforsch, v.36,
pp 910-912, 1981.
Oja, E., Neural Networks,Principal Components and Linear
Neural Networks. Neural Networks, v.05, pp 27-935,
1989.
Olshausen, B. A. and Field, D. J., Emergence of Simple-
Cell Receptive Field Properties by Learning a Sparse
Coding for natural Images. Nature, v.381, pp 607-609,
1996.
Osindero, Simon; Welling, Max and Hinton, Geoffrey
E., Topographic Products Models Applied to Natural
Scene Statistics. Neural Computation, v.18, pp 381-
414, 2006.
Ray, K. L., McKay, D. R., Fox, P. M., Riedel, M. C.,
Uecker, A. M., Beckmann, C. F., Smith, S. M., Fox,
P. T., Laird, A. ICA model order selection of task co-
activation networks. Front. Neurosci. 7:237; 2013
Simoncelli, E. P and Olshausen, B. A., Natural Image
Statistics and Neural representations. Annu. Rev. Neu-
roscience, n. 24, pp 1193-1216, 2001.
Shannon C. E., A Mathematical Theory of Communica-
tion. Bell Systems Technical Journal, v. 27, pp 379-
423, 1948.
Stork, D.G. and Wilson, H.R. Do Gabor functions pro-
vide appropriate descriptions of visual cortical recep-
tive fields? J Opt Soc Am A7, 1362-1373, 1990.
Vinje, W. E. and Gallant, J. L., Sparse Coding and Decorre-
lation in Primary Visual Cortex During natural Vision.
Vision Science, v. 287, pp 1273-1276, 2000.
APPENDIX
Take an indexed set of N neurons, as one can see in table 1,
and put them into a
√
N ×
√
N matrix (let’s suppose N=64,
Table 1: A set of N neurons.
1 2 3 4 5 6 7 8 ··· N
for example), as one can see in table 2
We define the neighborhood of neuron k, all neurons i
that are close to the neuron k in the matrix representation.
In other words, neurons i are neighbors of neuron k if the
coordinates of neuron i obeys the following relation
D(i,k) =
q
(a
i
−a
k
)
2
+ (b
i
−b
k
)
2
6 T, (7)
where (a
k
,b
k
) and (a
i
,b
i
) are the coordinates of neuron
k and neuron i, respectively, in the matrix representa-
tion, T is a constant that defines the neighborhood size.
For example, for T = 1, the neighborhood of neuron 28
as highlighted in the table below. In this case v
28
=
{19,20,21,27,29, 35, 36,37}.
Table 2: One neighborhood of neuron 28.
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
49 50 51 52 53 54 55 56
57 58 59 60 61 62 63 64
With this definition of neighborhood, we are able to an-
alyze the algorithm stability in the following steps:
Assume that signal x can be modeled as x=As, where A
is an invertible matrix;
Let us make the following change in coordinates, p
k
=
[p
1
, p
2
,··· , p
n
]
T
= A
T
V
T
w
k
, where V is the whitening ma-
trix to obtain the signals x;
In this new coordinates basis, we define the cost func-
tion as
J(p
k
) = E[ε
2
k
] = E{[ f (p
t
k
s) +α·v
k
]
2
}; (8)
One can analyze, without loss of generality, the stabil-
ity of J(p
k
) at point p
k
= [0,··· , p
k
,··· , 0]
T
= e
k
. In this
case, p
k
= 1 and than w
k
is one row of the inverse of VA.
For assumption, J(p
k
) is an even function and this analysis
applies for p
k
= −1;
Let d = [d
1
,··· , d
n
]
T
be a small perturbation on e
k
. Ex-
pressing J(e
k
+ d) into a Taylor series expansion about e
k
,
we obtain
J(e
k
+d) = J(e
k
)+d
T
∂J(e
k
)
∂p
+
1
2
d
T
∂
2
J(e
k
)
∂p
2
d
T
+o(kd
2
k).
(9)
∂J(p)
∂p
k
= s
k
f
′
(p
T
s)[ f(p
T
s) +v
k
], (10)
∂J(p)
∂p
2
k
= s
2
k
f
′′
(p
T
s)[ f(p
T
s) +v
k
] + s
2
k
f
′
(p
T
s) f
′
(p
T
s)
(11)
and
∂J(p)
∂p
2
k
= s
k
s
j
f
′′
(p
T
s)[ f(p
T
s) +v
k
] + s
k
s
j
f
′
(p
T
s) f
′
(p
T
s)
(12)
Taking in account that signals out of neighborhood are
statistically independent, we have
d
T
∂(e
k
)
∂p
= 2{E
s
k
f(s
k
) f
′
(s
k
)
d
k
+
+ α
∑
i∈v
k
E
s
i
f(s
k
) f
′
(s
k
)
d
i
}, (13)
because in consequence of independency,
E[s
j
f(s
k
) f
′
(s
k
)] = 0, if j /∈ v
k
.
BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing
154

In the same way, using the assumption of independence,
one can obtain
1
2
d
T
∂
2
J((e)
k
)
∂p
2
d =
= E
h
s
2
k
( f
′
(s
k
))
2
+ s
2
k
f(s
k
) f
′′
(s
k
)
i
d
2
k
+ α
∑
i∈v
k
{E
h
s
2
i
( f
′
(s
k
))
2
f
′′
(s
k
)
i
d
2
i
+ E
h
s
k
s
i
( f
′
(s
k
))
2
+ s
k
s
i
f(s
k
) f
′′
(s
k
)
i
d
k
d
i
},
+
∑
i/∈v
k
E
h
( f
′
(s
k
))
2
+ f(s
k
) f
′′
(s
k
)
i
d
2
j
+ o(kdk
2
).
(14)
Supposing kwk = 1 and VA being orthogonal, we have
kpk = kA
T
V
T
wk = 1. Consequently, ke
i
+ dk = 1, which
implies d
k
=
q
1−
∑
∀l6=i
d
2
l
−1.
Remembering that
p
1−β = 1−
β
2
+o(β), one can dis-
card the terms which contains d
2
k
and d
k
d
i
in step 8 above,
because they are okd
2
k .
Now we can take the following approximation: d
k
≈
∑
∀l6=i
d
2
l
= −
∑
i
d
2
i
−
∑
j
d
2
j
.
Using the above approximation in step 11, and using
equation 13 and equation 14, in equation 9, one get
J(e
k
+ d) = J(e
i
)
+ α
∑
i
{E[s
2
i
( f
′
(s
k
))
2
+ s
2
i
f(s
k
) f
′′
(s
k
)
+ s
i
f(s
k
) f
′
(s
k
) −s
k
f(s
k
) f
′
(s
k
)]d
2
i
}
+
∑
j
E[( f
′
(s
k
))
2
+ f(s
k
) f
′′
(s
k
)
− s
k
f(s
k
) f
′
(s
k
)]d
2
j
. (15)
Choosing properly a function f so that E[s
2
i
( f
′
(s
k
))
2
+
s
2
i
f(s
k
) f
′′
(s
k
) + s
i
f(s
k
) f
′
(s
k
) − s
k
f(s
k
) f
′
(s
k
)] +
E[( f
′
(s
k
))
2
+ f(s
k
) f
′′
(s
k
) − s
k
f(s
k
) f
′
(s
k
)] < 0,∀i ∈ v
k
,
we obtain that J(e
i
+ d) will be always small that J(e
i
) in
equation 9.
A Simple Algorithm for Topographic ICA
155
