
Novel Ways to Estimate Homography from Local Affine Transformations
Daniel Barath and Levente Hajder
MTA SZTAKI, Distributed Event Analysis Research Laboratory, Budapest, Hungary
Keywords:
Homography Estimation, Affine Transformation, Perspective-invariance, Stereo Vision, Epipolar Geometry,
Planar Reconstruction.
Abstract:
State-of-the-art 3D reconstruction methods usually apply point correspondences in order to compute the 3D
geometry of objects represented by dense point clouds. However, objects with relatively large and flat surfaces
can be most accurately reconstructed if the homographies between the corresponding patches are known. Here
we show how the homography between patches on a stereo image pair can be estimated. We discuss that these
proposed estimators are more accurate than the widely used point correspondence-based techniques because
the latter ones only consider the last column (the translation) of the affine transformations, whereas the new
algorithms use all the affine parameters. Moreover, we prove that affine-invariance is equivalent to perspective-
invariance in the case of known epipolar geometry. Three homography estimators are proposed. The first
one calculates the homography if at least two point correspondences and the related affine transformations
are known. The second one computes the homography from only one point pair, if the epipolar geometry is
estimated beforehand. These methods are solved by linearization of the original equations, and the refinements
can be carried out by numerical optimization. Finally, a hybrid homography estimator is proposed that uses
both point correspondences and photo-consistency between the patches. The presented methods have been
quantitatively validated on synthesized tests. We also show that the proposed methods are applicable to real-
world images as well, and they perform better than the state-of-the-art point correspondence-based techniques.
1 INTRODUCTION
Although computer vision has been an intensively
researched area in computer science from many
decades, several unsolved problems exist in the field.
The main task of the research behind this paper is to
discover the relationship among the affine transfor-
mation, the homography, the epipolar geometry, and
the projection matrices using the fundamental formu-
lation introduced in the pioneering work of Molnar
at al. (Moln
´
ar and Chetverikov, 2014) in 2014. The
aim of this study is to show how this theory can be
applied to solve real-life computer vision tasks like
estimating the homography and affine transformation
between planar patches more accurately than it can
be done by classical methods (Hartley and Zisserman,
2003).
A two-dimensional point in an image can be rep-
resented as a 3D vector, it is called the homogeneous
representation of the point. It lies on the projective
plane P
2
. The homography is an invertible mapping
of points and lines on the projective plane P
2
. Other
terms for the transformation include collineation, pro-
jectivity, and planar projective transformation. (Hart-
ley and Zisserman, 2003) provide a specific defini-
tion: A mapping P
2
→ P
2
is a projectivity if and only
if there exists a non-singular 3× 3 matrix H such that
for any point in P
2
represented by vector x it is true
that its mapped point equals Hx.
The correspondence can also be formalized for 2D
lines as l
0
H
−T
l where line parameters can be written
as vectors l and l
0
on the first and second images, re-
spectively. If a point p lies on line l, the transformed
location x
0
must lie on the corresponding line l
0
.
It is a very exciting fact that the concept of ho-
mography was already known in the middle of the last
century (Semple and Kneebone, 1952).
There are many approaches in the field to esti-
mate homography between two images as it is sum-
marized in (Agarwal et al., 2005). At first, we have
to mention the simplest method called Direct Linear
Transform (Hartley and Zisserman, 2003) (DLT). In
that case one wishes to estimate 8 unknown param-
eters of the homography H based on known point
correspondences by solving an overdetermined sys-
tem of equations generated from the linearization of
the basic relationship x
0
∼ Hx, where the operator ∼
means equality up to scale. The linearization itself
434
Barath, D. and Hajder, L.
Novel Ways to Estimate Homography from Local Affine Transformations.
DOI: 10.5220/0005674904320443
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 434-445
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

distorts the noise, therefore optimization for the orig-
inal nonlinear projective equations gives more accu-
rate results. This can be done by numerical optimiza-
tion techniques such as the widely used Levenberg-
Marquardt (Marquardt, 1963) optimization. How-
ever, the linear algorithms can also be enhanced if
data normalization (Hartley and Zisserman, 2003) is
applied first.
(Kanatani, 1998) proposed a method to minimize
the estimation error within the Euclidean framework
since the noise occurs in image coordinates and not in
abstract higher dimensional algebraic spaces.
Obviously, there are many other ways to esti-
mate the homography: line-based (Murino et al.,
2002), conic-based (Kannala et al., 2006; Mudigonda
et al., 2004), contour-based (Kumar et al., 2004) and
patch-based (Kruger and Calway, 1998) methods ex-
ist. However, the matching of these features is not as
easy as that of points. Nowadays, there are very effi-
cient feature point matchers (Morel and Yu, 2009).
Despite the fact that so many kind of homography
estimation techniques available in the field, we have
not find any dealing with local affine transformation-
based homography estimation.
Application of Homographies. There are many
cases in computer vision where homography is re-
quired. First of all, one has to write about camera
calibration (Zhang, 2000). If the homographies be-
tween the 3D chessboard coordinates and the pro-
jected ones is computed for several images, then the
intrinsic camera parameters can be computed as it is
proved by (Zhang, 2000).
Camera calibration is the process of determining
the intrinsic and extrinsic parameters of the camera,
where intrinsic parameters are camera-specific: focal
length, lens distortion, and the principal point. Extrin-
sic parameters describe the camera orientation, and its
location in 3D space.
Estimation of surface normals is also an impor-
tant application of plane-plane homographies. If the
homography is known between the images of a plane
taken by two perspective cameras, then the homog-
raphy can be decomposed into camera extrinsic pa-
rameters, the plane normal, and the distance of the
plane w.r.t. the first camera (Faugeras and Lustman,
1988; Malis and Vargas, 2007). Molnar et al. (Moln
´
ar
et al., 2014) and Barath et al. (Barath et al., 2015)
showed that the affine transformation is enough in or-
der to compute the surface normal, and it can be com-
puted from the homography by derivating that as it is
described in the appendix.
A very important application area of homography
estimation is to build 3D models of scenes where
relatively large flat planes are present. Typical ex-
ample for such tasks is the reconstruction of urban
scenes that is a challenging and long-researched prob-
lem (Musialski et al., 2012; Tan
´
acs et al., 2014).
Nowadays, 3D reconstruction pipelines uses point
correspondences to compute the sparse (Agarwal
et al., 2011; Pollefeys et al., 2008) or dense (Fu-
rukawa and Ponce, 2010; Vu et al., 2012) reconstruc-
tion of the scenes. However, patch-based approaches
has recently proposed (B
´
odis-Szomor
´
u et al., 2014;
Tan
´
acs et al., 2014).
The main contributions of the paper are as follows.
The first part of the paper deals with homography es-
timation when the fundamental matrix is unknown.
In this case, the affine parameters can be calculated
from corresponding patches in stereo images. (i) It is
described that the homography can robustly be esti-
mated using the affine transformations. In the second
part, we focus on the presence of the known funda-
mental matrix. (ii) It is proven that the homography
can be calculated only from one point correspondence
and the related affine transformation if the epipolar
geometry is known. Finally, a novel algorithm is de-
scribed. (iii) We show here that homography can be
estimated using only two point correspondences and
the neighboring image patches if the cameras are fully
calibrated.
2 METHODS TO ESTIMATE
HOMOGRAPHY FROM AFFINE
TRANSFORMATION
The main contribution of this paper is to introduce dif-
ferent techniques in order to estimate the homography
if affine transformations are known at different loca-
tions. We also show here that more efficient estima-
tors can be formed if the epipolar geometry is known
as well. The main geometric terms and concepts are
summarized in this section first.
2.1 THEORETICAL BACKGROUND
Homography and Affine Transformation. The
standard definition of homography is applied here
which was mentioned in the introduction: a homog-
raphy H is the mapping P
2
→ P
2
which maps each
vector x
(1)
i
= [u
(1)
i
v
(1)
i
]
T
to its corresponding location
x
(2)
i
= [u
(2)
i
v
(2)
i
]
T
as [u
(2)
i
v
(2)
i
,1]
T
∼ H[u
(1)
i
v
(1)
i
,1]
T
.
(The upper and lower indices denote the index of the
current image, and the number of the current feature
point, respectively.) (Moln
´
ar and Chetverikov, 2014)
Novel Ways to Estimate Homography from Local Affine Transformations
435

showed that the affine transformation
A =
a
11
a
12
a
13
a
21
a
22
a
23
(1)
can be expressed from the parameters of the homo-
graphies as it is discussed in the appendix. These four
parameters are responsible for horizontal and verti-
cal scales, shear and rotation. The last column of the
affine transformation A gives the offset.
Extracting Homography with Fundamental Ma-
trix. Relationship, which is well-known from epipo-
lar geometry (Hartley and Zisserman, 2003) led us to
make estimation process easier, and decrease the DoF
of the problem if the fundamental matrix is known.
This relationship is formulated as follows (Hartley
and Zisserman, 2003):
h
e
(2)
i
×
H = λF (2)
where e
(2)
= [e
(2)
x
,e
(2)
y
,1]
T
denotes the epipole in the
second image, and λ is the scale of the fundamental
matrix F. The operator [v]
×
is the well-known matrix
formula representing the cross product with vector v.
Remark that the rank of matrix [v]
×
is two, therefore
the third row of the matrix can be determined as the
linear combination of the first two ones.
The basic relationship defined in Eq. 2 shows how
the knowledge of fundamental matrix decreases the
DoF of the estimation problem. The last row is re-
dundant as the rank of [e
(2)
]
×
is two. Therefore, only
the first two rows contain useful information. They
can be written as
0 −1 e
y
1 0 −e
x
h
11
h
12
h
13
h
21
h
22
h
23
h
31
h
32
h
33
= (3)
λ
f
11
f
12
f
13
f
21
f
22
f
23
This equation shows that the DoF can be reduced
to 3 since the elements in the first two rows of the
homography can be expressed by those in the third
one (h
31
,h
32
, and h
33
), if the fundamental matrix is
known:
h
11
= e
x
h
31
+ λ f
21
h
12
= e
x
h
32
+ λ f
22
h
13
= e
x
h
33
+ λ f
23
h
21
= e
y
h
31
− λ f
11
(4)
h
22
= e
y
h
32
− λ f
12
h
23
= e
y
h
33
− λ f
13
Remark that both the fundamental matrix and the
homography are determined up to an arbitrary scale.
Therefore, one scale is allowed to be set to an arbi-
trary value. In our algorithms, λ = 1.
If Equation 4 is substituted into the relationship
of the DLT method (p
(2)
∼ H p
(1)
), then the homog-
raphy can be computed. Remark that one point pair
gives only one equation as the fundamental matrix re-
duces the DoF of the correspondence problem to one
since the point pairs have to lie on the related epipolar
lines. This homography estimation method is called
3PT in this study because the estimation can be car-
ried out if at least three point correspondences (and
the fundamental matrix) are given.
2.2 Homography Estimation from
Affine Transformation (HA)
Based on the elements of the affine matrix a linear
system of equations can be formed. The relationship
between the affine transformation A
i
belonging to the
i-th point pair and the corresponding homography is
discussed in the appendix. For the linearization, the
Eqs. 9, 11- 13 have to be multiplied by the projective
depth s (see Eq. 10). The obtained linear equations
are as follows:
h
11
− h
31
u
(2)
i
+ a
i,11
u
(1)
i
(5)
−h
32
a
i,11
v
(1)
i
− h
33
a
i,11
= 0
h
12
− h
32
u
(2)
i
+ a
i,12
v
(1)
i
−h
31
a
i,12
u
(1)
i
− h
33
a
i,12
= 0
h
21
− h
31
v
(2)
i
+ a
i,21
u
(1)
i
−h
32
a
i,21
v
(1)
i
− h
33
a
i,21
= 0
h
22
− h
32
v
(2)
i
+ a
i,22
v
(1)
i
−h
31
a
i,22
u
(1)
i
− h
33
a
i,22
= 0
Thus, the estimation can be written as a homoge-
nous system of linear equations. However, all the el-
ements of homography H cannot be estimated since
elements h
13
, and h
23
are not present in the equations.
This is trivial as these elements code the offset of the
planes. Fortunately, the well-known (Hartley and Zis-
serman, 2003) Direct Linear Transformation (DLT)
method can compute the offset as well. It gives two
additional linear equations for the elements of the ho-
mography. They are as follows:
h
11
u
(1)
i
+ h
12
v
(1)
i
+ h
13
− h
31
u
(1)
i
u
(2)
i
− (6)
h
32
v
(1)
i
u
(2)
i
− h
33
u
(2)
i
= 0
h
21
u
(1)
i
+ h
22
v
(1)
i
+ h
23
− h
31
u
(1)
i
v
(2)
i
−
h
32
v
(1)
i
v
(2)
i
− h
33
v
(2)
i
= 0
Equations 5, and 6 give the linear relationship among
the elements of the affine transformation, homogra-
phy, and point locations. Six equations are obtained
for each point correspondence. They can be written
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
436

B =
1 0 0 0 0 0 −
u
(2)
i
+ a
i,11
u
(2)
i
a
i,11
v
(1)
i
−a
i,11
0 1 0 0 0 0 −a
i,12
u
(1)
i
−
u
(2)
i
+ a
i,12
v
(2)
i
−a
i,12
0 0 0 1 0 0 −
v
(2)
i
+ a
i,21
u
(1)
i
−a
i,21
v
(1)
i
−a
i,21
0 0 0 0 1 0 −a
i,11
u
(1)
i
−
v
(2)
i
+ a
i,22
v
(1)
i
−a
i,22
u
(1)
i
v
(1)
i
1 0 0 0 −u
(1)
i
u
(2)
i
−v
(1)
i
u
(2)
i
−u
(2)
i
0 0 0 u
(1)
i
v
(1)
i
1 −u
(1)
i
v
(2)
i
−v
(1)
i
v
(2)
i
−v
(2)
i
(7)
h = [h
11
,h
12
,h
13
,h
21
,h
22
,h
23
,h
31
,h
32
,h
33
]
T
as a homogeneous linear form Bh = 0 where the vec-
tor h, and matrix B contain the elements of the ho-
mography, and the corresponding coefficients, respec-
tively. They are expressed in Eq. 7. The optimal so-
lution (Bj
¨
orck, 1996) subject to |h| = 1 is obtained as
the eigenvalue of B
T
B corresponding to the smallest
eigenvalue. If at least two point correspondences are
given, the homography can be estimated. This is a
notable advantage of HA algorithm compared to the
classical DLT one as the latter one requires at least
four correspondences.
2.3 Homography Estimation from
Affine Transformation with Known
Fundamental Matrix (HAF)
In this section, we show that the estimation method
becomes much simpler if the epipolar geometry is
known. Equation 4 shows the basic relationship of
the plane-plane homography and the epipolar geom-
etry of the stereo camera setup. The affine transfor-
mation can be computed from the homography. (It
is written in the appendix in detail.) By considering
both relationship, the estimation of homography can
also be written in a linear form even if the epipolar
geometry is known. It is as follows:
h
31
a
i,11
u
(1)
i
+ u
(2)
i
− e
x
+
h
32
a
i,11
v
(1)
i
+ h
33
a
i,11
= f
21
h
32
a
i,12
v
(1)
i
+ u
(2)
i
− e
x
+
h
31
a
i,12
u
(1)
i
+ h
33
a
i,12
= f
22
h
31
a
i,21
u
(1)
i
+ v
(2)
i
− e
y
+
h
32
a
i,21
v
(1)
i
+ h
33
a
i,21
= − f
11
h
32
a
i,22
v
(1)
i
+ v
(2)
i
− e
y
+
h
31
a
i,22
u
(1)
i
+ h
33
a
i,22
= − f
12
This is an inhomogeneous system of linear equations,
thus it can be formed as Cy = d , where matrix C
consists of the coefficients, d = [ f
21
, f
22
,− f
11
,− f
12
]
while y = [h
31
,h
32
,h
33
]
T
is the vector of the unknown
parameters. The optimal solution in the least squares
sense is given by y = C
†
d where C
†
is the Moore-
Penrose pseudo-inverse of matrix C. The elements of
matrix C are as follows:
C
11
=
a
i,11
u
(1)
i
+ u
(2)
i
− e
x
C
12
= a
i,11
v
(1)
i
C
13
= a
i,11
C
21
= a
i,12
u
(1)
i
C
22
=
a
i,12
v
(1)
i
+ u
(2)
i
− e
x
C
23
= a
i,12
C
31
=
a
i,21
u
(1)
i
+ v
(2)
i
− e
y
C
32
= a
i,21
v
(1)
i
C
33
= a
i,21
C
41
= a
i,22
u
1
i
C
42
=
a
i,22
v
(1)
i
+ v
(2)
i
− e
y
C
43
= a
i,22
(8)
This method gives an overdetermined system for only
one corresponding point pair, and an affine transfor-
mation. More equations can be added trivially to the
system. It means, that if one has only a single point
pair and the related affine transformation, one is able
to compute the homography. Of course, it can be eas-
ily completed by other methods (e.g. DLT algorithm)
exactly the same way as we showed in the previous
section.
2.4 Improvements
Nonlinear Refinement. The methods proposed here
are solved by linear algorithms since the original
problems are linearized by multiplying with the de-
nominator. However, this multiplication distorts the
original signal-noise ratio. If the denominator is rel-
atively small, the distortion can be significant. For
this reason, the nonlinear version of the proposed al-
gorithms have to be formed. We used the classi-
cal Levenberg-Marquardt (Marquardt, 1963) numeri-
cal technique in order to compose nonlinear methods.
To distinguish the linear and nonlinear versions of the
methods, the names of the linear versions begin with
’LIN’.
Normalization. Normalization of the input data is
usual in homography estimation (Hartley and Zisser-
Novel Ways to Estimate Homography from Local Affine Transformations
437
man, 2003). Here we show how the normalized coor-
dinates and the normalized affine transformation can
be obtained.
Let us denote the normalizing transformations
which are applied to the 2D point clouds in each im-
age with T
1
, and T
2
. The normalized points are calcu-
lated on the first, and second images as p
(1)
0
i
= T
1
p
(1)
i
,
and p
(2)
0
i
= T
2
p
(2)
i
, respectively.
It is not enough to normalize only the points, both
the fundamental matrix and the affine transformations
have to be normalized. The normalization formula for
the fundamental matrix can be written (Hartley and
Zisserman, 2003) as F
0
= T
−T
2
FT
−1
1
.
The affine transformations can also be normalized,
as it is described in the appendix in details.
To distinguish the normalized versions of the
methods, the names of the normalized algorithms be-
gin with ’Norm.’.
Robustification. It is unavoidable in real application
that the input dataset contains both inliers and out-
liers. We apply the RANSAC (Fischler and Bolles,
1981) paradigm in order to make the proposed meth-
ods robust. The names of RANSAC-based methods
contain the word ’RSC’.
2.5 Theoretical Contribution
It can be seen from the theory of HAF algorithm
that if the fundamental matrix is known, then the ho-
mography and the affine transformation can unequiv-
ocally be calculated from each other in an observed
point. This property of perspective projection states
that affine-invariance is equivalent to perspective-
invariance if the epipolar geometry is known between
stereo images. In order to take the advantages of this
property, fully calibrated camera setup is not needed,
only the fundamental matrix between the cameras is
required.
3 Homography Estimation based on
Photo-consistency and Point
Correspondences (RHE – Rotary
Homography estimation)
The homography estimation (Agarwal et al., 2005)
can be carried out using usual features in images such
as point or line correspondences. Another approach
is to use pixel intensities to estimate the plane-plane
transformation between image patches (Habbecke
and Kobbelt, 2006; Z. Megyesi and D.Chetverikov,
2006; Tan
´
acs et al., 2014). The study of (Habbecke
Figure 1: Rotating plane.
and Kobbelt, 2006) proposes to estimate the four
spatial plane parameters, while (Z. Megyesi and
D.Chetverikov, 2006) and (Tan
´
acs et al., 2014) reduce
the DoF of plane estimation problem to three using
rectified images. Remark that rectification can be car-
ried out if the fundamental matrix is known, the two
projection matrices themselves does not have to be
known.
Other possible solution is to use point correspon-
dences in order to compute the homography (Hart-
ley and Zisserman, 2003). If the fundamental ma-
trix is known, the estimation can be calculated from
three correspondences. If the epipolar geometry is not
known, four points are required at least.
We show here that homography can also be es-
timated if both point correspondences and photo-
consistency are considered. For the algorithm pro-
posed in this section, two point correspondences are
taken. The projection matrices of the stereo images
are known, therefore, the spatial coordinates of the
two points can be calculated via triangulation (Hart-
ley and Sturm, 1997).
It is trivial that three spatial points determine the
plane as they are enough to determine the homogra-
phy. Two of those are calculated by triangulation, the
remaining task is to determine the third one. The
DoF of the problem is only one since an angle α
(∈ (0,π]) determines the plane as it is visualized in
Fig. 1. This angle is determined via a brute-force (ex-
haustive) search in our approach. For each candidate
value α, a spatial patch can be formed that consists of
the two triangulated points p
1
and p
2
, and the angle
of the patch is α. The cameras are calibrated, there-
fore the homographies between the projected patches
can be calculated. Then this homography is evalu-
ated. Its score is calculated as the similarity
1
of the
corresponding pixels around the projected locations
of points p
1
and p
2
. (The pixel correspondences are
obtained by the homography.) The 3D patch with the
highest similarity score gives the best estimation for
1
We use normalized cross correlation (Sonka et al.,
2007) (NCC) for this purpose.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
438
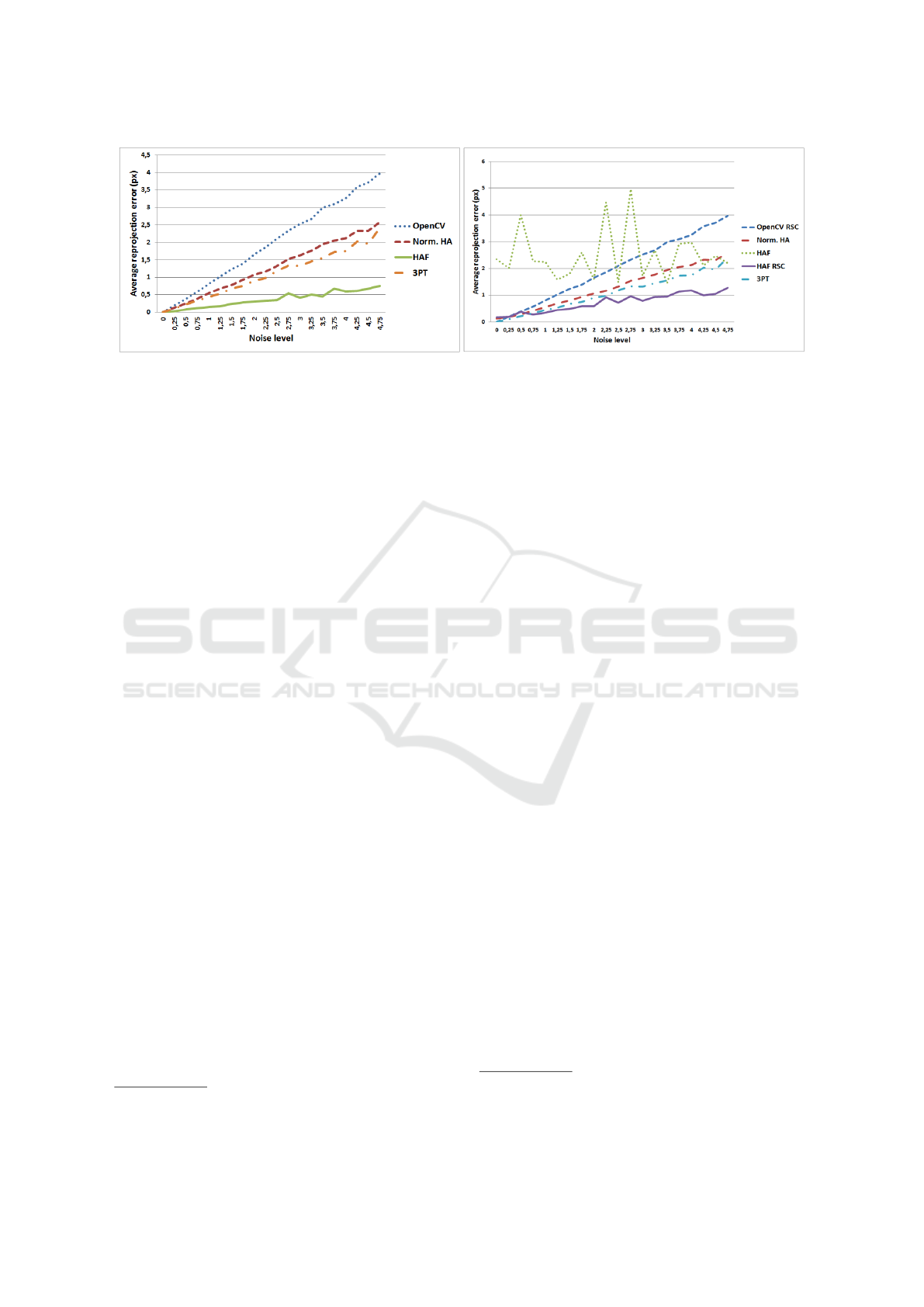
Figure 2: The left and right plots shows the average errors of the methods with noisy point coordinates and noisy affine trans-
formation, respectively. The vertical axis are the average reprojections errors in pixels. The horizontal ones are the σ (spread)
of the Gaussian-noise added to point coordinates. Affine error appears by multiplying the original affine transformation with
a relatively small random transformation.
the 3D patches. The obtained homography is deter-
mined by this 3D patch.
The proposed algorithm is as follows:
1. Calculate point p
3
related to the current α value,
and the homography H
α
. Then for the i-th (i ∈
[1,2]) point pair compute A
α,i
between the vicini-
ties of the point projection using H
α
.
2. Compute the similarity (NCC) related to each
point and affine transformation. If the sum of the
similarities in the two observed points is greater
than the currently best candidate then α
opt
:= α.
3. If α < π increase α, and continue from Step 2.
Otherwise, terminate with H
α
.
4 EXPERIMENTAL RESULTS
The proposed homography estimators are tested both
on synthesized data and real world images.
4.1 Test on Synthesized Data
The main goal of the tests is to generate different
cases where homographies have to be estimated. For
this reason, a stereo image pair represented by pro-
jection matrices is generated first. Their orientation
are constrained, and the positions are randomized
2
on
a 30 × 30 plane that is 60 unit far from the origin on
axis Z. The generated cameras look at the origin. The
remaining one DoF of the camera orientation is ran-
domized as well. Then a 3D plane is generated at the
origin with a random normal vector. Then 50 points
2
We applied zero-mean Gaussian noise for random num-
ber generation.
are randomly sampled, and they are perspectively pro-
jected onto the two cameras. The ground truth ho-
mography between the projections of the plane is cal-
culated as well.
The error values are defined as the average/median
reprojection errors of the points.
All the proposed methods are tested
3
in the syn-
thesized environment except for the RHE which re-
quires real images for photo-consistency calculation.
For each test, 100 different planes are generated on
every noise level.
The proposed methods are compared to the
OpenCV-implemented ‘findHomography’ function,
which is a normalized DLT algorithm (Hartley and
Zisserman, 2003) and a refinement stage using
Levenberg-Marquardt algorithm (Marquardt, 1963)
that minimizes the reprojection error. The other ri-
val method is the normalized 3PT. The latter one is
implemented by us.
Test with Noisy Point Coordinates. In the first
test case, 2D point coordinates are contaminated by
zero-mean Gaussian noise, but the affine transforma-
tions do not. Two kinds of methods can be seen in
the left plot of Fig 2: the first one uses the funda-
mental matrix, the second one does not. Within the
first group, it can be observed that normalized HA
performs better than OpenCV implementation. The
second group which uses the fundamental matrix con-
sists of HAF algorithm and the normalized three point
(3PT) method. It can be seen that HAF performs sig-
nificantly better.
Test with Noisy Affine Transformations. The
next test case (left plot of Fig. 2) is with noisy affine
transformations. Noise in the affine transformation
3
All the tests have been implemented both on Mat-
lab, and C++. It can be downloaded from webpage
http://web.eee.sztaki.hu
Novel Ways to Estimate Homography from Local Affine Transformations
439

appeares as a nearly identity random transformation.
Every affine matrix is multiplied with such a trans-
formation. Note that the horizontal axis in the charts
shows only the noise of point coordinates. It can be
seen that the original HAF is very sensitive to the
affine noise, however, its RANSAC version balances
this behaviour.
Figure 3: The average reprojection errors of the variants
of HA, and HAF method are shown in the top, and bot-
tom rows, respectively. The point are contaminated by
Gaussian-noise, which σ value is denoted by the horizon-
tal axis. The vertical one shows the average error in pixels.
In the top plot of Fig 3, the variants of HA can
be seen with contaminated point coordinates. It is
evident that the normalized, numerically refined ver-
sion gives the most accurate result. The bottom figure
shows the different versions of the HAF. The normal-
ized HA is also visualized for the sake of comparison.
The average error seems to be very chaotic, however,
the numerically refined version seems to be the best.
It is unequivocal that the proposed methods give
more accurate results than the rival ones. Without
the knowledge of the epipolar geometry, the normal-
ized version of HA method performs better than the
numerically refined normalized DLT. All methods is
outperformed by HAF.
4.2 Test on Real Data
Our algorithms are tested on the sequences of Oxford
dataset
4
.
Calculation of the Affine Transformation for Real
Tests. In order to apply the proposed algorithms to
real data, the knowledge of the affine transforma-
tion is required between every single point correspon-
dences. There are several ways to compute the affine
transformation: brute-force algorithms, or affine in-
variant feature trackers (Mikolajczyk and Schmid,
2004). During our experiments the following method
is used:
(1.) Big planar surfaces are segmented using se-
quential RANSAC. For each planar patch the con-
tained 2D point cloud are triangulated by Delaunay
triangulation (B., 1934; Lee and Schachter, 1980).
(2.) Then, for each point pair we iterate through all
the corresponding triangles. The homography is com-
puted between every triangle pair (on the first and
the second images) using 3PT method, then the affine
transformation is decomposed from that as it is de-
scribed in the appendix. (3.) This method computes
many slightly different affine transformations for ev-
ery single point pair. Remark that all of them are used
during the homography estimation as an overdeter-
mined system of equations.
To visualize the quality of the proposed algo-
rithms, the surface normals are computed, and they
are drawn into the images. There are several normal
estimators (Faugeras and Papadopoulo, 1998; Malis
and Vargas, 2007; Barath et al., 2015) in the field,
we choose the method of Barath et al. (Barath et al.,
2015) due to its efficiency and simplicity. This es-
timator calculates the surface normal from the affine
transformation related to the observed point instead
of the homography in order to avoid the ambiguity of
the homography decomposition (He, 2012).
The Oxford data set contain point correspon-
dences, but we use ASIFT method (Morel and Yu,
2009) to detect and track points instead of the original
data. The Hartley-Sturm triangulation (Hartley and
Sturm, 1997) is applied to each point pair first. Pla-
nar regions are selected using sequential RANSAC,
however, it could be done by J-Linkage (Toldo and
Fusiello, 2010), or other multi-homography fitting al-
gorithm as well. Then fundamental matrix are cal-
culated by the RANSAC 8-point technique (Hart-
ley and Zisserman, 2003). The tests are both qual-
itatively and quantitatively evaluated. For the latter
one, the error values are calculated as follows: 50%
of the point correspondences are separated, and the
4
Dataset can be downloaded from http://www.robots.
ox.ac.uk/∼vgg/data/data-mview.html
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
440

homography is computed using only them. Then the
reprojection error of the homography is computed for
all the features. The final value was the RMS (Root
Mean Squares) of the errors.
Another error metric have to be used for testing
the RHE method. RHE computes the homography
from only two feature correspondences. Therefore,
the edges of the mentioned Delaunay triangulation
are chosen as point pairs, and the homography related
to the pair is computed by RHE. Then the reprojec-
tion error of every homography is calculated for all
the feature points. The final reprojection error of the
method is calculated as the average of these errors.
In the following comparisons, the minimum reprojec-
tion error is also shown. Note that photo-consistency
calculation processed on patches are of sizes from
60 × 60 up to 120 × 120.
Figure 4 shows an example that demonstrates how
the homography can be estimated by the proposed
methods using many feature points. In this example,
the baseline of the stereo setup is short, and the two
main walls are segmented. The list of the obtained re-
projection errors is written in Table 1. It is clear that
the proposed algorithms (HA and HAF) outperform
the rival ones (robust version of 3PT and OpenCV
methods). HAF gives more accurate reconstruction
than HA since it uses the fundamental matrix as ad-
ditional information for the estimation. The obtained
surface normals are perpendicular to each other (see
the bottom of Fig. 4) as it is expected.
Delaunay triangulation is applied to the points of
each wall (see the top of Fig. 4). Then RHE algo-
rithm runs on every edge. The reprojection error of
each estimated homography is calculated w.r.t. to ev-
ery point pair selected from the current planar patch
(both for the walls ’Left’ and ’Right’). From the aver-
age of these reprojection errors, this algorithm yields
less accurate results since it is calculated using only
two point pairs. Even so, we have many estimated ho-
mographies (one for each edge of the triangulation)
and we choose the one with the lowest reprojection
error. It is turned out that it provides accurate estima-
tion. Its results are the best and second one among
all the other methods for the ’Left’ and ’Right’ walls,
respectively.
The next two examples are seen in Figures 5 and 6.
The first one is the sequence ’Model House’. The
segmentation finds two large planes on the scene: the
wall and the ground. The next normal reconstruction
example is called the sequence ’Library’. Two large
planes are found in this scene: the wall and the roof.
Then the proposed and rival homography estimators
are applied. The normals reconstructed by the RHE
algorithm are visualized in these figures, therefore the
Figure 4: The top row visualize the delaunay triangulation
of the points. The bottom row shows reconstructed surface
normals using homography of large walls on sequence ’Col-
lege’.
Table 1: Reprojection errors (px) for sequence ’College’.
Left Right
OpenCV RSC 3.824 2.668
3PT RSC 3.586 2.604
HA RSC 3.589 1.759
HAF RSC 3.585 1.677
RHE AVG 7.881 8.768
RHE MIN 3.442 1.692
estimated normals are independent of each other.
The proposed and rival homography estimators
are compared in Table 2. (Note that the patch size of
the RHE algorithm was set to 60 × 60 for sequences
’Building’ and ’Model House’.) It is clear that the
proposed methods outperform the rival ones in these
cases. The HAF algorithm yields the best results ex-
cept for only one example when HA method is the
most accurate.
Table 2: Reprojection errors (px) for sequences ’Model
House’ and ’Library’.
Model House Library
Wall Ground Wall Roof
OpenCV RSC 1.554 2.750 1.422 1.693
3PT RSC 1.400 1.569 1.513 1.399
HAF RSC 0.864 1.635 1.317 1.320
HA RSC 0.759 1.736 1.338 1.422
RHE Avg. 2.911 4.819 7.889 2.445
RHE Min. 0.780 2.378 1.384 1.514
The proposed methods are tested on 60 different
planes, as it is shown in Table 3. The showed value is
as follows: for every test plane homography is calcu-
lated by all the examined methods. Then the reprojec-
Novel Ways to Estimate Homography from Local Affine Transformations
441

Figure 5: Reconstructed surface normals using RHE algo-
rithm on sequence ’Model House’. Left: reconstructed wall
Right: reconstructed floor. Top: first image. Bottom: sec-
ond image.
Figure 6: Reconstructed surface normals using RHE al-
gorithm on sequence ’Library’. Left: reconstructed wall
Right: reconstructed roof. Top: first image. Bottom: sec-
ond image.
tion error of the homography computed by OpenCV
is labeled with 100%. Other values in the table such
as 66% related to HAF, means that the ratio of the
average reprojection errors of HAF and OpenCV is
0.66.
4.3 Processing Times
The processing time of each method is discussed here.
HA and HAF methods are based on the solution of a
homogeneous, and inhomogeneous linear system of
equations, respectively. These systems consists of 6
and 4 equations per point pair. Therefore, HA is a bit
slower than DLT, however, not significantly. HAF is
as fast as DLT since the equation number per point is
equal.
Even though, RHE is a numerical optimization in
a 1-DoF search space, our implementation is not ap-
plicable to online tasks since its processing time is
Table 3: Error percentage compared to OpenCV on 60 dif-
ferent planes.
OpenCV 3PT HA HAF RHE
Avg.
RHE
Min.
100% 79% 67% 66% 119% 57%
around half a second. However, it could be paral-
lelised on GPU straighforwardly.
5 CONCLUSION
Novel homography estimator methods (HA and HAF)
have been proposed here that can estimate the homog-
raphy if the affine transformations are known between
the surrounding regions of the corresponding point
pairs. We have also proposed an algorithm to estimate
the homography based on both point correspondences
and photo-consistency.
HA method does not need the knowledge of
epipolar geometry, however, it gives better results
than the standard homography estimation techniques
in most of the situations. As a minimal problem, it
is computable from only two point correspondences
and the related affine transformations. The HAF al-
gorithm requires the knowledge of the fundamental
matrix, and at least one point correspondence and the
related affine transformation have to be known to cal-
culate the homography. It is usually the most effi-
cient method. Their RANSAC variants are recom-
mended to use for contaminated input data, because
affine transformations are significantly more sensitive
to noise than point correspondences.
It is proven that affine-invariance is equivalent to
perspective-invariance in the case of known funda-
mental matrix. We think it is a significant contribution
to the theory of 3D stereo vision.
The novelty of the proposed RHE algorithm is to
reduce homography estimation to a one-dimensional
search in a half unit circle when both point correspon-
dences and camera parameters are known. The simi-
larity function for the minimization problem is based
on photo-consistency.
The synthetic and real tests have shown that all
the proposed methods (HA and HAF) give more ac-
curate results and use similar amount of resources as
the state-of-the-art point correspondence-based tech-
niques. Therefore the novel and standard algorithms
can be easily replaced for each other. RHE algorithm
also gives appropriate results using only two corre-
sponding point pairs. Moreover, RHE gives accurate
estimation in offline applications by repeating the op-
timization for many possible pairings. Then the point
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
442

pair which supplies the best homography by RHE are
usually more accurate than the results of all the other
methods. It is important to note that if many point
correspondences (hundreds of points) are given from
the observed plane, the original point-based homog-
raphy estimation methods give nearly the same result
as the proposed ones.
ACKNOWLEDGEMENTS
The research was partially supported by the Hungar-
ian Scientific Research Fund (OTKA No. 106374).
REFERENCES
Agarwal, A., Jawahar, C., and Narayanan, P. (2005). A Sur-
vey of Planar Homography Estimation Techniques.
Technical report, IIT-Hyderabad.
Agarwal, S., Furukawa, Y., Snavely, N., Simon, I., Curless,
B., Seitz, S. M., and Szeliski, R. (2011). Building
rome in a day. Commun. ACM, 54(10):105–112.
B., D. (1934). Sur la sphere vide. Izvestia Akademii
Nauk SSSR, Otdelenie Matematicheskikh i Estestven-
nykh Nauk, 7:793–800.
Barath, D., Molnar, J., and Hajder, L. (2015). Optimal Sur-
face Normal from Affine Transformation. In VISAPP
2015, pages 305–316.
Bj
¨
orck,
˚
A. (1996). Numerical Methods for Least Squares
Problems. Siam.
B
´
odis-Szomor
´
u, A., Riemenschneider, H., and Gool, L. V.
(2014). Fast, approximate piecewise-planar modeling
based on sparse structure-from-motion and superpix-
els. In IEEE Conference on Computer Vision and Pat-
tern Recognition.
Faugeras, O. and Lustman, F. (1988). Motion and struc-
ture from motion in a piecewise planar environment.
Technical Report RR-0856, INRIA.
Faugeras, O. D. and Papadopoulo, T. (1998). A Nonlin-
ear Method for Estimating the Projective Geometry of
Three Views. In ICCV, pages 477–484.
Fischler, M. and Bolles, R. (1981). RANdom SAmpling
Consensus: a paradigm for model fitting with appli-
cation to image analysis and automated cartography.
Commun. Assoc. Comp. Mach., 24:358–367.
Furukawa, Y. and Ponce, J. (2010). Accurate, dense, and
robust multi-view stereopsis. IEEE Trans. on Pattern
Analysis and Machine Intelligence, 32(8):1362–1376.
Habbecke, M. and Kobbelt, L. (2006). Iterative multi-view
plane fitting. In Proceeding of Vision, Modelling, and
Visualization, pages 73–80.
Hartley, R. I. and Sturm, P. (1997). Triangulation. Computer
Vision and Image Understanding: CVIU, 68(2):146–
157.
Hartley, R. I. and Zisserman, A. (2003). Multiple View Ge-
ometry in Computer Vision. Cambridge University
Press.
He, L. (2012). Deeper Understanding on Solution Ambigu-
ity in Estimating 3D Motion Parameters by Homogra-
phy Decomposition and its Improvement. PhD thesis,
University of Fukui.
Kanatani, K. (1998). Optimal homography computation
with a reliability measure. In Proceedings of IAPR
Workshop on Machine Vision Applications, MVA,
pages 426–429.
Kannala, J., Salo, M., and Heikkil, J. (2006). Algorithms for
computing a planar homography from conics in cor-
respondence. In Proceedings of the British Machine
Vision Conference.
Kruger, S. and Calway, A. (1998). Image registration using
multiresolution frequency domain correlation. In Pro-
ceedings of the British Machine Vision Conference.
Kumar, M. P., Goyal, S., Kuthirummal, S., Jawahar, C. V.,
and Narayanan, P. J. (2004). Discrete contours in mul-
tiple views: approximation and recognition. Image
and Vision Computing, 22(14):1229–1239.
Lee, D.-T. and Schachter, B. J. (1980). Two algorithms
for constructing a delaunay triangulation. Interna-
tional Journal of Computer & Information Sciences,
9(3):219–242.
Malis, E. and Vargas, M. (2007). Deeper understanding of
the homography decomposition for vision-based con-
trol. Technical Report RR-6303, INRIA.
Marquardt, D. (1963). An algorithm for least-squares esti-
mation of nonlinear parameters. SIAM J. Appl. Math.,
11:431–441.
Mikolajczyk, K. and Schmid, C. (2004). Scale & affine in-
variant interest point detectors. International journal
of computer vision, 60(1):63–86.
Moln
´
ar, J. and Chetverikov, D. (2014). Quadratic transfor-
mation for planar mapping of implicit surfaces. Jour-
nal of Mathematical Imaging and Vision, 48:176–184.
Moln
´
ar, J., Huang, R., and Kato, Z. (2014). 3d recon-
struction of planar surface patches: A direct solution.
ACCV Big Data in 3D Vision Workshop.
Morel, J.-M. and Yu, G. (2009). Asift: A new framework for
fully affine invariant image comparison. SIAM Jour-
nal on Imaging Sciences, 2(2):438–469.
Mudigonda, P. K., Kumar, P., Jawahar, M. C. V., and
Narayanan, P. J. (2004). Geometric structure compu-
tation from conics. In In ICVGIP, pages 9–14.
Murino, V., Castellani, U., Etrari, A., and Fusiello, A.
(2002). Registration of very time-distant aerial im-
ages. In Proceedings of the IEEE International Con-
ference on Image Processing (ICIP), volume III, pages
989–992. IEEE Signal Processing Society.
Musialski, P., Wonka, P., Aliaga, D. G., Wimmer, M., van
Gool, L., and Purgathofer, W. (2012). A survey of
urban reconstruction. In EUROGRAPHICS 2012 State
of the Art Reports, pages 1–28.
Pollefeys, M., Nist
´
er, D., Frahm, J. M., Akbarzadeh, A.,
Mordohai, P., Clipp, B., Engels, C., Gallup, D., Kim,
S. J., Merrell, P., Salmi, C., Sinha, S., Talton, B.,
Wang, L., Yang, Q., Stew
´
enius, H., Yang, R., Welch,
G., and Towles, H. (2008). Detailed real-time urban
3d reconstruction from video. Int. Journal Comput.
Vision, 78(2-3):143–167.
Novel Ways to Estimate Homography from Local Affine Transformations
443

Semple, J. and Kneebone, G. (1952). Algebraic Projective
Geometry. Oxford University Press.
Sonka, M., Hlavac, V., and Boyle, R. (2007). Image Pro-
cessing, Analysis, and Machine Vision. CENGAGE-
Engineering, third edition edition.
Tan
´
acs, A., Majdik, A., Hajder, L., Moln
´
ar, J., S
´
anta, Z.,
and Kato, Z. (2014). Collaborative mobile 3d recon-
struction of urban scenes. In Computer Vision - ACCV
2014 Workshops - Singapore, Singapore, November 1-
2, 2014, Revised Selected Papers, Part III, pages 486–
501.
Toldo, R. and Fusiello, A. (2010). Real-time incremen-
tal j-linkage for robust multiple structures estimation.
In International Symposium on 3D Data Processing,
Visualization and Transmission (3DPVT), volume 1,
page 6.
Vu, H.-H., Labatut, P., Pons, J.-P., and Keriven, R. (2012).
High accuracy and visibility-consistent dense multi-
view stereo. IEEE Trans. Pattern Anal. Mach. Intell.,
34(5):889–901.
Z. Megyesi, G. and D.Chetverikov (2006). Dense 3d re-
construction from images by normal aided matching.
Machine Graphics and Vision, 15:3–28.
Zhang, Z. (2000). A flexible new technique for camera cal-
ibration. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 22(11):1330–1334.
APPENDIX
Affine Transformation from
Homography
The affine parameters can be obtained from homog-
raphy between corresponding patches in stereo image
pairs. Let us assume that the homography H is given.
Then the correspondence between the coordinates in
the first (u and v) and second (u
0
and v
0
) images is
written as
u
0
=
h
T
1
[u,v, 1]
T
h
T
3
[u,v, 1]
T
v
0
=
h
T
2
[u,v, 1]
T
h
T
3
[u,v, 1]
T
where the 3 × 3 homography matrix H is written as
H =
h
T
1
h
T
2
h
T
3
=
h
11
h
12
h
13
h
21
h
22
h
23
h
31
h
32
h
33
The affine parameters come from the partial deriva-
tives of the perspective plane-plane transformation.
The top left element a
11
of affine transformation ma-
trix is as follows:
a
11
=
∂u
0
∂u
=
h
11
h
T
3
[u,v,1]
T
−h
31
h
T
1
[u,v,1]
T
(
h
T
3
[u,v,1]
T
)
2
= (9)
h
11
−h
31
u
0
s
,
where
s = h
T
3
[u,v, 1]
T
(10)
The other components of affine matrix are obtained
similarly
a
12
=
∂u
0
∂v
=
h
12
− h
32
u
0
s
(11)
a
21
=
∂v
0
∂u
=
h
21
− h
31
v
0
s
(12)
a
22
=
∂v
0
∂v
=
h
22
− h
32
v
0
s
. (13)
Normalization of Affine
Transformation
Given corresponding point pairs x
(1)
and x
(2)
, the
goal is to determine the related affine transforma-
tions if the points are normalized as x
0(2)
= T
2
x
(2)
and
x
0(1)
= T
1
x
(1)
. The normalization is the concatenation
of a scale and a translation. Therefore, the transfor-
mation matrices can be written as
T
1
=
s
(1)
x
0 t
(1)
x
0 s
(1)
y
t
(1)
y
0 0 1
,T
2
=
s
(2)
x
0 t
(2)
x
0 s
(2)
y
t
(2)
y
0 0 1
. (14)
For an arbitrary 2D point x
(i)
= [u
(i)
,v
(i)
] on the i-
th image, the transformed coordinates can be written
as
x
0(i)
=
s
(i)
x
0 t
(i)
x
0 s
(i)
y
t
(i)
y
0 0 1
u
(i)
v
(i)
1
=
s
(i)
x
u
(i)
+t
(i)
x
s
(i)
y
v
(i)
+t
(i)
y
1
.
If the homography of a plane is denoted by H using
the original coordinates, it connects the coordinates
on the first and second image as x
2
∼ Hx
1
. If the nor-
malized coordinates are used, the relationship modi-
fies as T
−1
2
x
0(2)
∼ HT
−1
1
x
0(1)
.
Therefore, the homography using the normalized
coordinates is H
0
= T
2
HT
−1
1
. The deviations are writ-
ten in Eqs.15 – 18.
For the sake of simplicity, we do not determine the
last two elements of the first row as they do not affect
the affine transformation. They are denoted by stars
(’*’). The elements of the affine transformation are
written in Eqs. 9 – 13. The normalized scale s
0
is
written as
s
0
=
1
s
(1)
x
h
31
u
0(1)
−t
(1)
x
+
1
s
(1)
y
h
32
v
0(1)
−t
(1)
y
+
h
33
= u
(1)
h
31
+ v
(1)
h
32
+ h
33
= s
Therefore, the normalization does not modify the
scale as it is expected. Now, the numerator for the first
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
444

T
−1
1
=
1/s
(1)
x
0 −t
(1)
x
/s
(1)
x
0 1/s
(1)
y
−t
(1)
y
/s
(1)
y
0 0 1
(15)
H
0
= T
2
HT
−1
1
=
s
(2)
x
0 t
(2)
x
0 s
(2)
y
t
(2)
y
0 0 1
h
11
h
12
h
13
h
21
h
22
h
23
h
31
h
32
h
33
1/s
(1)
x
0 −t
(1)
x
/s
(1)
x
0 1/s
(1)
y
−t
(1)
y
/s
(1)
y
0 0 1
(16)
H
0
=
s
(2)
x
h
11
+t
(2)
x
h
31
s
(2)
x
h
12
+t
(2)
x
h
32
s
(2)
x
h
13
+t
(2)
x
h
33
s
(2)
y
h
21
+t
(2)
y
h
31
s
(2)
y
h
22
+t
(2)
y
h
32
s
(2)
y
h
23
+t
(2)
y
h
33
h
31
h
32
h
33
1/s
(1)
x
0 −t
(1)
x
/s
(1)
x
0 1/s
(1)
y
−t
(1)
y
/s
(1)
y
0 0 1
(17)
H
0
=
s
(2)
x
s
(1)
x
h
11
+
t
(2)
x
s
(1)
x
h
31
s
(2)
x
s
(1)
y
h
12
+
t
(2)
x
s
(1)
y
h
32
∗
s
(2)
y
s
(1)
x
h
21
+
t
(2)
y
s
(1)
x
h
31
s
(2)
y
s
(1)
y
h
22
+
t
(2)
y
s
(1)
y
h
32
∗
1
s
(1)
x
h
31
1
s
(1)
y
h
32
−h
31
t
(1)
x
/s
(1)
x
− h
32
t
(1)
y
/s
(1)
y
+ h
33
(18)
affine transformation can be expressed as follows:
h
0
11
− h
0
31
u
0(2)
=
s
(2)
x
s
(1)
x
h
11
+
t
(2)
x
s
(1)
x
h
31
−
1
s
(1)
x
h
31
s
(2)
x
u
(2)
+t
(2)
x
=
s
(2)
x
s
(1)
x
h
11
−
s
(2)
x
s
(1)
x
u
(2)
h
31
The other three components of the transformation can
be computed similarly:
h
0
12
− h
0
32
u
0(2)
=
s
(2)
x
s
(1)
y
h
12
−
s
(2)
x
s
(1)
x
u
(2)
h
32
h
0
21
− h
0
31
v
0(2)
=
s
(2)
y
s
(1)
x
h
21
−
s
(2)
y
s
(1)
x
v
(2)
h
31
h
0
22
− h
0
32
v
0(2)
=
s
(2)
y
s
(1)
y
h
22
−
s
(2)
y
s
(1)
y
v
(2)
h
32
By rearranging the equations the following formulas
are given:
h
31
u
(1)
+ h
32
v
(2)
+ h
33
a
0
11
=
s
(2)
x
s
(1)
x
h
11
−
s
(2)
x
s
(1)
x
u
(2)
h
31
(19)
h
31
u
(1)
+ h
32
v
(1)
+ h
33
a
0
12
=
s
(2)
x
s
(1)
y
h
12
−
s
(2)
x
s
(1)
x
u
(2)
h
32
h
31
u
(1)
+ h
32
v
(1)
+ h
33
a
0
21
=
s
(2)
y
s
(1)
x
h
21
−
s
(2)
y
s
(1)
x
v
(2)
h
31
h
31
u
(1)
+ h
32
v
(1)
+ h
33
a
0
22
=
s
(2)
y
s
(1)
y
h
22
−
s
(2)
y
s
(1)
y
v
(2)
h
32
These equations are linear w.r.t. the elements of the
homography. Therefore, these formulas compose a
homogeneous, linear system of equations. In order
to apply affine normalization to the proposed meth-
ods, the equations refer to the affine transformations
have to be replaced in the coefficient matrix of each
method. For HAF a few modifications are required
beforehand. Formulas, which describe the connection
to the fundamental matrix (Eq. 4) have to substituted
into Eq. 19. The given equations are inhomogeneous
due to the elements of matrix F. After a few modifica-
tions these can also be substituted into the coefficient
matrix of HAF (Eq. 8).
Novel Ways to Estimate Homography from Local Affine Transformations
445
