
The Challenges and Advantages with a Parallel Implementation of
Feature Matching
Anders Hast
1
and Andrea Marchetti
2
1
Department of Information Technology, Division of Visual Information and Interaction,
Uppsala University, Uppsala, Sweden
2
Istituto di Informatica e Telematica, Consiglio Nazionale delle Ricerche, Pisa, Italy
Keywords:
Feature Matching, RANSAC, Interest Points, Parallel Implementation.
Abstract:
The number of cores per cpu is predicted to double every second year. Therefore, the opportunity to parallelise
currently used algorithms in computer vision and image processing needs to be addressed sooner rather than
later. A parallel feature matching approach is proposed and evaluated in Matlab
r
. The key idea is to use
different interest point detectors so that each core can work on its own subset independently of the others.
However, since the image pairs are the same, the homography will be essentially the same and can therefore
be distributed by the process that first finds a solution. Nevertheless, the speedup is not linear and reasons why
is discussed.
1 INTRODUCTION
An efficient parallel implementation of feature match-
ing is proposed and discussed. Especially it will be
shown how the different steps of matching can be im-
plemented and that the problem itself, when solved in
parallel, not only can be computed faster, but in part
also becomes simpler.
Research in such areas as image processing, com-
puter vision and pattern recognition, still mainly fo-
cus on sequential algorithms even though parallelism
have been at hand for many years. Today, most lap-
tops have two or more cores and desktop computers
have even more. Not surprisingly, even some cell
phones have more than one core nowadays. More-
over, multithreading makes it possible to run more
than one program per core. It has been suggested that
the number of cores will double every two years (Va-
jda, 2011) and therefore the communities in the afore-
mentioned research areas have to, sooner rather than
later, deal with parallel implementations of the most
commonly used algorithms. Among these are cer-
tainly feature matching, including interest key point
detection, matching, outlier removal using some vari-
ant of Random sample consensus (RANSAC) (Fis-
chler and Bolles, 1981) and homography computa-
tion. Besides this, what is the fastest method for a
sequential approach may not necessarily be the fastest
in parallel and methods that were considered too slow
in the past might be used in the future when making
use of the multicore capacity.
It will be shown how feature matching can be im-
plemented to benefit from the available parallelism
and it will be shown how different types of interest
points can be extracted in parallel together with the
respective matching. Moreover, a parallel implemen-
tation of RANSAC is presented that works on each
set of matches. Whenever, one of the processes finds
a good solution, it is shared among the other processes
so that the whole procedure will theoretically be just
as fast as the one finding the solution first.
2 FEATURE MATCHING
Feature matching is important for applications like
image stitching (Szeliski, 2006) and registration (Zi-
tova and Flusser, 2003). The feature vector is usually
a visual descriptor of the area around key points in
the image. Many different descriptors have been pro-
posed in literature and severals overviews have been
published (Gauglitz et al., 2011). In the performed
tests a Fourier based descriptor was used (Hast, 2014).
However, the implementation discussed could use any
kind of descriptor. More importantly is the fact that
different different interest point detectors can be used
and not only one, as usually is the case. Some of them
will be mentioned in the following section as they will
be used for the parallel implementation.
Hast, A. and Marchetti, A.
The Challenges and Advantages with a Parallel Implementation of Feature Matching.
DOI: 10.5220/0005674501010106
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 101-106
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
101

2.1 Interest Point Detectors
The detector proposed by Harris and Stephens (Harris
and Stephens, 1988) is based on the so called struc-
ture tensor, S of an image I , which is defined as
S =
"
I
2
x
I
x
I
y
I
x
I
y
I
2
y
#
(1)
where I
x
and I
y
are image derivatives in the x and y
directions, respectively.
In order to detect corners it was proposed to com-
pute the response using the trace and determinant of
the matrix as
R = det(S)− k · tr
2
(S) (2)
where k is a constant, typically set to 0.04. However,
the formulation by Noble (Noble, 1989) will be used
herein since it has no such ad hoc constant and is
therefore, in some sense, more general. Noble pro-
posed to use
R
H
= det(S)/(tr(S)+ ε) (3)
where ε is a small constant used to avoid division by
zero.
A Gaussian window is generally used to compute
isotropic responses, i.e. each one of the elements
in the tensor in equation 1 are all filtered separately
using a Gaussian kernel. This was an improvement
compared to the early detector by Moravec (Moravec,
1980), which used a square window, yielding non
isotropic responses. This Gaussian convolution is
omitted in the equations above for clarity.
Furthermore, the trace R
t
= tr(S ) can also be used
for interest point detection and will find edges rather
than corners. The Hessian matrix used for SURF by
Bay et al. (Bay et al., 2008), on the other hand will
find blobs and is defined as
H =
"
I
xx
I
xy
I
xy
I
yy
#
(4)
They proposed to use the determinant of H
R
+
= det(H ) = I
xx
I
yy
− I
2
xy
(5)
By changing the sign of R
+
so that R
−
= −R
+
a blob detector that will find dark blobs instead of
bright blobs is obtained. Once again, the trace R
t+
=
tr(H )can also be used for interest point detection.
Moreover, the inverted sign R
t−
= −R
t+
can be used
for the Hessian. The trace of the structure tensor can-
not be inverted as the sign does not matter, since it
contains squares of derivatives.
Many other detectors have been proposed in liter-
ature (Smith and Brady, 1997; Obdrz
´
alek and Matas,
2006; Hast and Marchetti, 2014; Hast, 2015), as
discussed in the aforementioned overviews. How-
ever the six rather different detectors discussed above
(R
H
,R
t
,R
−
,R
+
,R
t−
,R
t+
) will be used for the pro-
posed parallel implementation of feature matching.
2.2 Nearest Neighbour Search
By comparing the feature vectors extracted for key
points in image A with the points in image B, tenta-
tive correspondences are obtained. A distance mea-
sure is used to determine how similar these feature
vectors are and the pair of features having the smallest
distance is consequently considered as nearest neigh-
bours. If there are few points and the feature vectors
themselves are rather small, then an exhaustive search
can be applied where each of the features in one set is
compared to all of the features in the other set. This
is often a rather time consuming approach that can be
improved by some kind of partitioning method such
as kd-trees (Friedman et al., 1977) or k-means clus-
tering (Fukunage and Narendra, 1975) and a short
overview of such approximating approaches is given
by (Muja and Lowe, 2009). Nevertheless, a proof of
concept is given herein using the exhaustive search
and therefore the choice of approximate algorithms
are left to the reader.
2.3 RANSAC
RANSAC is one of the most used algorithms for out-
lier removal, i.e. removing false positives among
the tentative correspondeces, even though other ap-
proaches exist (Enqvist and Kahl, 2008). The main
idea is to generate a hypothesis from random samples
and then verifying it using all the data. In practice, it
first starts by selecting the minimal number of points
required to determine the model parameters, i.e. find-
ing the homography (Brown and Lowe, 2007), which
is the projective transformation between the images.
Then the set is rescored using this transformation, in
the way that the number of inliers that falls below
a certain predefined tolerance ε, are counted. This
means that when transformed, these points are be-
ing close enough to its corresponding match and are
hence regarded as true inliers.
If the number of inliers is large enough or more
commonly when the probability of finding a bet-
ter model becomes lower than some threshold, then
the algorithm terminates, otherwise it starts all over
again. RANSAC generally treats all correspondences
equally and draws random samples uniformly from
the full set.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
102

2.4 Parallel RANSAC
MultiRANSAC (M. Zuliani and Manjunath, 2005) is
a parallel extension of the sequential RANSAC that
allows to deal simultaneously with multiple models,
which have the advantage of being able to cope with
a high percentage of outliers. Nevertheless, running
the algorithms on several cores is only proposed for
further research. GASAC (Rodehorst and Hellwich,
2006) is another parallel algorithm using a genetic
algorithm approach. Neither this approach is imple-
mented for several processors, instead it is parallel in
the sense that several evaluated solutions exists simul-
taneously.
There are very few attempts to parallelise
RANSAC in literature as noted by Hidalgo et al.
(Hidalgo-Paniagua et al., 2014), who make a com-
parative study of parallel versions using OpenMP and
CUDA. The algorithm starts by clustering points and
each thread is then working on a subset of the original
set. The overhead for this type of approach is there-
fore the clustering of these subsets. They refer to what
they claim to be the only other parallel implementa-
tion by Iser et al.(Iser et al., 2009). This approach
lets several threads be divided into two groups which
samples the two point sets, in each image, and up-
dates a hash table to establish correspondences. Nev-
ertheless, Fijany and Diotalevi (Fijany and Diotalevi,
2012) propose a variant of RANSAC that was imple-
mented on a many-core architecture and is based on
cooperative search, where a global broadcast is done,
if and when a better partial solution is found. In this
way the best solution is known to all processes that
draw samples from the whole dataset, which resides
in shared memory.
In conclusion, RANSAC is close to embarrass-
ingly parallel, as each process can work on the whole
data, drawing samples and scoring in parallel, and the
only thing needed is to distribute the best result to all
processors in order to keep track of the best homog-
raphy. Alternatively, it can work on a clustered sub-
set of the data, with the overhead of performing such
clustering.
3 PARALLELISATION OF
FEATURE MATCHING
In this paper a rather different approach is taken, even
if some details are similar, as parallelisation is pro-
posed not only for RANSAC, but also for interest
point extraction. The idea is to let several processes
extract interst points that by definition are different
and thus, to some extent, the clustering for near-
est neighbour search comes for free. This can be
achieved by using the previously explained interest
point detectors that generally finds different features,
such as corners, dark and white blobs, and lines (or
ridges). Another advantage is that only the strongest
responses (interest points with high contrast (Lowe,
2004)) are useful, as low contrast points often are
more sensitive to noise. This implies that it theoreti-
cally could be better to use the top n responses from
k number of detectors than m number of points from
any single detector, where m = n · k. Then each pro-
cess performs matching within its own set only. Es-
pecially, if an exhaustive search for true matches is
used for comparing feature point neighbourhoods, it
is an advantage to use several detectors (k) and fewer
points within them (n), than using one detector and
many points (m). Hence, the exhaustive search is de-
limited to be performed only on the points from each
detector and the matching will therefore be faster. The
number of comparisons will therefore be k ·n
2
instead
of m
2
= (n · k)
2
= k · (k · n
2
), which means that the to-
tal work done in the exhaustive search will be scaled
down with a factor of k.
Furthermore, since these different detectors gener-
ally find different interest points, then RANSAC can
be run in parallel, where each thread or process com-
putes the homographies for each such set. If a true
homography is found for one set then it should also
be possible to use for the other sets. If this is the case,
then a true solution is found and all sets can be com-
bined to a single set and the homography can be com-
puted for the resulting set. The advantage is that the
sets the different processes are working on are smaller
(n < m) than what would be the case if only one detec-
tor was used. Hence, n points are evaluated using the
homography in each thread instead of m points. If, on
the other hand kd-trees or similar are used to speed up
the matching, the above reasoning must be changed
accordingly. However, the overhead of making such
trees might not be worth the extra work needed, as the
matching is divided into k sets anyway and are there-
fore smaller from the start.
Whenever a process i finds a transformation giv-
ing more inliers than the maximum so far, the homog-
raphy H
i
is broadcasted to all other processes. They,
in their turn probe for such messages and try out the
homography on their set of matches. In this way, if
some process finds a good homography it is shared
and the other processes will test how well the model
works on their data. One advantage is that if some
processes are having trouble finding a good homogra-
phy, they will automatically get help from those who
are more successful. The result will be a more con-
sistent result as they are helping each other. Another
The Challenges and Advantages with a Parallel Implementation of Feature Matching
103
advantage is that the total speed of the whole proce-
dure will in principle be just as fast as the process that
finds the best homography first, with the added over-
head of distributing the homography and scoring it.
In this paper the RANSAC used (Hast et al., 2013)
for the suggested parallel implementation stops when
two identical sets are found after local optimisation,
re-estimation and pruning. Whenever this occurs, the
homography is broadcasted to all processes, which in
their turn scores their sets, computes the homography
and then terminates.
Pisa, The Duomo
Pisa, The Duomo and the city centre
Pisa, Fields north of the river Arno
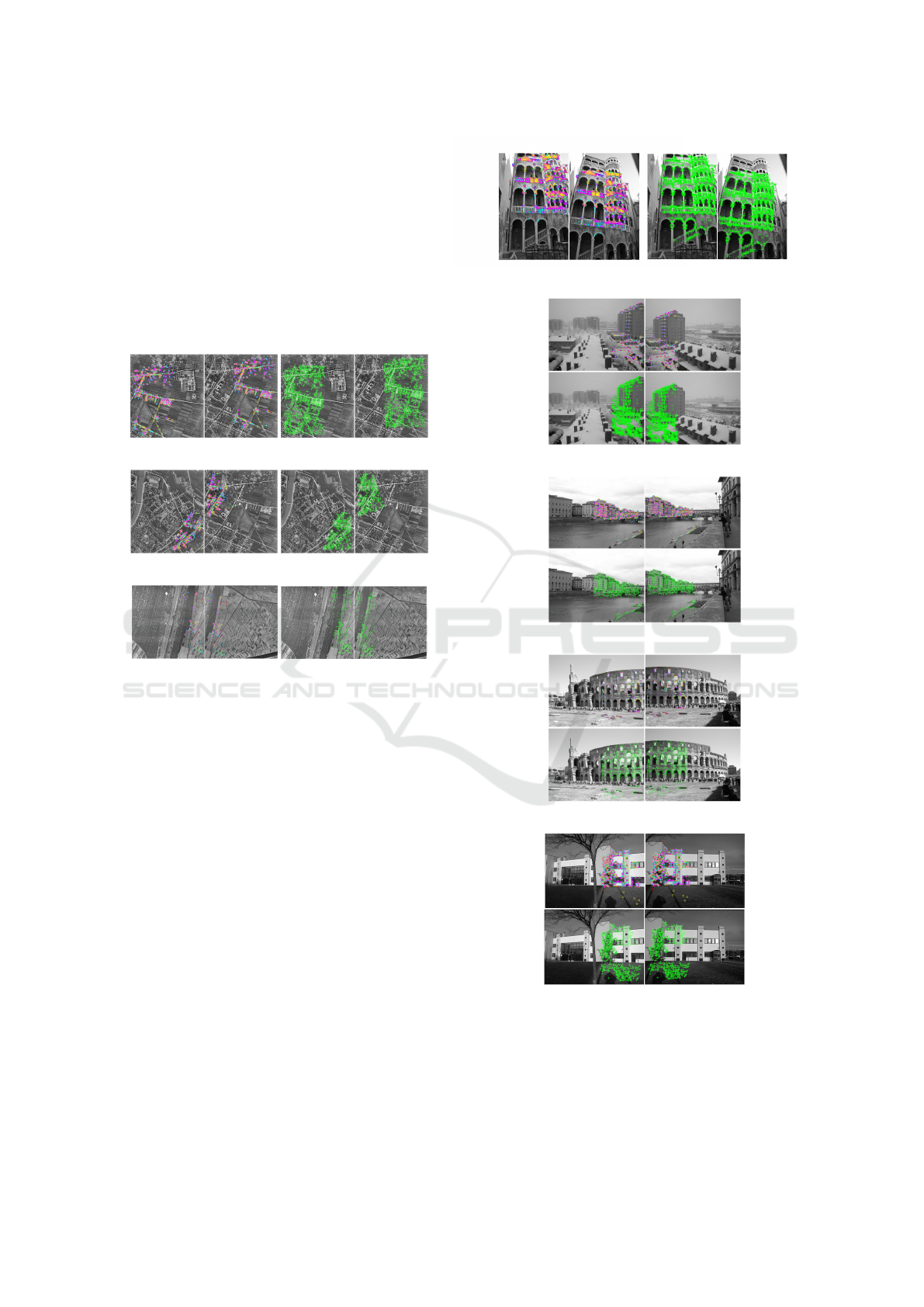
Figure 1: Illustration of corresponding pairs (inliers only)
for a set of images. The six different detectors are visualised
using individual colours and glyphs, while the case of one
detector (DoH) using 6 times more key points is depicted
using green ’+’.
c
MiBAC-ICCD, Aerofototeca Nazionale,
fondo RAF.
4 RESULTS
A proof of concept was performed on a set of images
shown in figure 1. Six cores were used to compute
the aforementioned interest points and matched us-
ing a simple invariant matching procedure (Hast and
Marchetti, 2013; Hast, 2014). A parallel version was
compared to a ordinary sequential version in 1000
test runs. The results are shown in figure 1 and 2.
In each pair of images, to the left, the resulting in-
liers are depicted using different glyphs in different
colours: R
H
(blue), R
t
(green), R
−
(red), R
+
(cyan),
R
t−
(magenta), R
t+
(yellow). The top 500 points were
chosen from each detector, giving a total of 3000
points. When one detector only was used, depicted
in the right image pairs with green ’+’, the top 3000
were chosen using R
H
, just for comparison.
Venice, Palazzo Contarini del Bovolo
Bologna, Snowfall in Casalecchio di Reno
Florence, Ponte Vecchio
Rome, Colloseum
Pisa, CNR
Figure 2: Illustration of corresponding pairs (inliers only)
for a set of images. The six different detectors are visualised
using individual colours and glyphs, while the case of one
detector (DoH) using 6 times more key points is depicted
using green ’+’. All images
c
Anders Hast.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
104
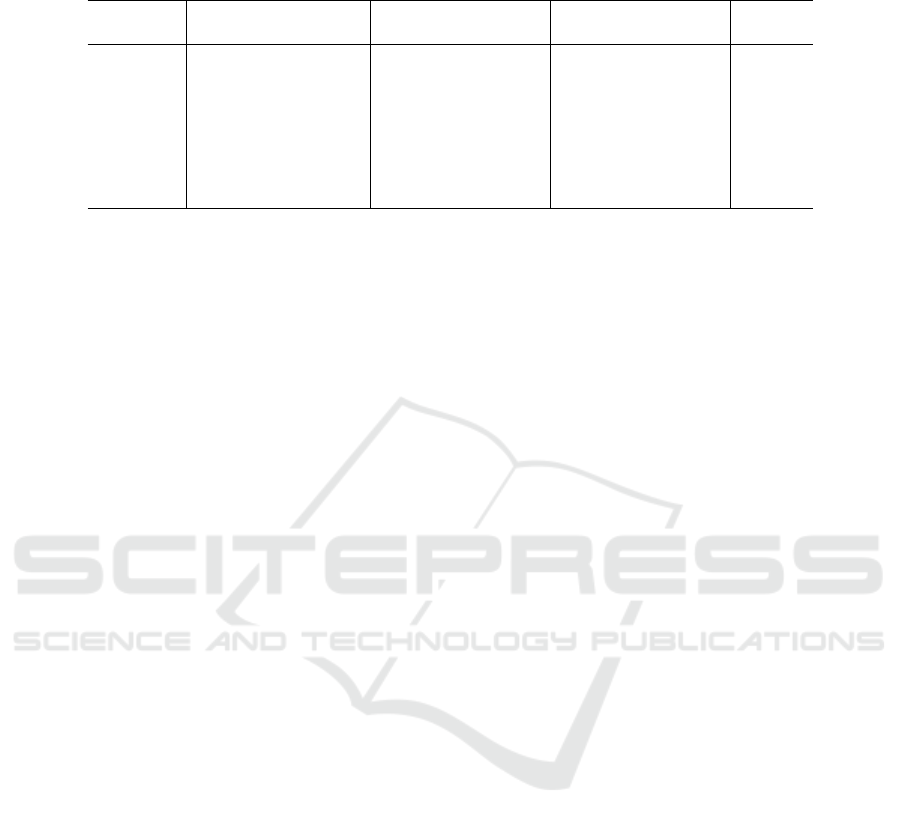
Table 1: Comparison between a parallel and sequential implementation of feature matching, showing inliers after matching
and after RANSAC, as well as wall clock time and speedup (ratio).
image Inliers matching Inliers RANSAC Time Speedup
parallel sequential parallel sequential parallel sequential ratio
Pisa 1 613 509 443 352 1,99 5,24 2,64
Pisa 2 1046 1211 932 1146 2,08 6,29 3.03
Pisa 3 453 454 273 330 3,63 5,74 1,58
Venice 1835 2139 1728 2078 7,74 18,36 2,37
Bologna 1160 1048 1008 908 3,28 10,65 3,25
Florence 1443 1090 1365 1014 4,75 6,75 1,42
Rome 702 985 532 893 4,54 6,43 1,42
Pisa 1172 848 944 542 5,14 35,96 7,00
In table 1 the results are shown for each image
pair and the number of inliers, after matching and af-
ter RANSAC, measured wall clock time and speedup
is reported for both the parallel and sequential imple-
mentation.
5 DISCUSSION
The results in table 1 reveals that the speedup varies
noticeably for these few examples, when one could
expect close to six times speedup. The implementa-
tion in Matlab
r
seem to have a rather high overhead
when using the smpd command for launching the pro-
gram on several cores. Another reason for the results
might be that interest points are found in parallel and
then a barrier waits for all processes to return their
result. In the next step feature extraction and match-
ing is done followed by a barrier. Finally the paral-
lel RANSAC is called and the whole procedure ends
when all processes terminates. The reason for the bar-
riers is simply that different parallel functions were
made so that the user easily can change each one of
them. By incorporating all steps into one continuous
process, the time to finish would be decreased, but
the parallel program would be more complex. It is
of course not enough to use only eight image pairs to
draw decisive conclusions. However, the images are
from two different types of applications (aerial pho-
tography and outdoor scenes) and the idea is just to
give a proof of the concept. We strongly believe that
an entire implementation in OpenMP or MPI, using
C++ instead of Matlab would get better results. In
any case, the results obtained show that a parallel ap-
proach is possible and will always be faster than a
sequential approach.
In the performed test runs, six cores were avail-
able and used. However, there is nothing that pre-
vents from using fewer or more cores. For the latter
case more interest point detectors are necessary and
several have, as mentioned, been proposed in litera-
ture. Alternatively one could use different σ for the
gaussian in order to detect points of different sizes.
One advantage is that more cores means less points
to handle per core and only the strongest responses
are used, which prevents from using noisy data. This
is also clearly visible in the images as the different
detectors finds points only in interesting areas where
there are large changes in derivatives. It can be noted
that many points lie close to each other, but at least in
theory they are most of the time different. In any case
it is an advantage that they find the strongest points
and points that are resulting from noise are therefore
reduced.
6 CONCLUSION AND FUTURE
WORK
The main idea proposed is to use different interest
point detectors for image matching and distributing
each set to different cores or processes. Moreover,
each core works on its own data and shares the ho-
mography to the other processes whenever a probable
transformation is found. In this way several things
can be done independently, such as obtaining inter-
est points, descriptor extraction, matching and finally
outlier removal. Another advantage is that the nearest
neighbour search is automatically clustered into indi-
vidual sets that are not dependent of each other, other
than that they share the same transformation, and this
will in itself reduce the computational cost with a fac-
tor corresponding to the number of cores. The draw-
back is that distributing data over several processes
and communicating between them has its own cost
and reduces the theoretical gain.
For future work it is proposed to incorporate all
steps necessary, from interest point detection and
matching to outlier removal, into one single proce-
dure without any barriers. Furthermore, the imple-
mentation should benefit from using C++ together
with OpenMP or MPI. It should also be examined
The Challenges and Advantages with a Parallel Implementation of Feature Matching
105

how the parallel algorithm could be distributed over
more cores by using other kinds of interest point de-
tectors and feature descriptors than the ones used in
the experiments, such as SURF (Bay et al., 2008) and
SIFT (Lowe, 2004).
REFERENCES
Bay, H., Ess, A., Tuytelaars, T., and Gool, L. V. (2008).
Speeded-up robust features (surf). Comput. Vis. Image
Underst., 110(3):346–359.
Brown, M. and Lowe, D. G. (2007). Automatic panoramic
image stitching using invariant features. International
Journal of Computer Vision, 74(1):59–73.
Enqvist, O. and Kahl, F. (2008). Robust optimal pose esti-
mation. In ECCV.
Fijany, A. and Diotalevi, F. (2012). A cooperative search
algorithm for highly parallel implementation of ransac
for model estimation on tilera mimd architecture. In
Aerospace Conference, 2012 IEEE, pages 1–14.
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: A paradigm for model fitting with appli-
cations to image analysis and automated cartography.
Communications of the ACM, 24:381–395.
Friedman, J. H., Bentley, J. L., and Finkel, R. A. (1977).
An algorithm for finding best matches in logarithmic
expected time. ACM Trans. Math. Softw., 3(3):209–
226.
Fukunage, K. and Narendra, P. M. (1975). A branch and
bound algorithm for computing k-nearest neighbors.
IEEE Trans. Comput., 24(7):750–753.
Gauglitz, S., H
¨
ollerer, T., and Turk, M. (2011). Evaluation
of interest point detectors and feature descriptors for
visual tracking. Int. J. Comput. Vision, 94(3):335–360.
Harris, C. and Stephens, M. (1988). A combined corner
and edge detection. In Alvey Vision Conference, pages
147–151.
Hast, A. (2014). Robust and invariant phase based local fea-
ture matching. In ICPR 2014, pages 809–814. Poster
with Paper.
Hast, A. (2015). Interest point detection based on the ex-
tended structure tensor with a scale space parameter.
In VISAPP, pages 1–8. Short Paper.
Hast, A. and Marchetti, A. (2013). Rotation invariant fea-
ture matching - based on gaussian filtered log polar
transform and phase correlation. In ISPA 2013, pages
100–105.
Hast, A. and Marchetti, A. (2014). Invariant interest point
detection based on variations of the spinor tensor. In
WSCG 2014, pages 49–56. Short Paper.
Hast, A., Nysj
¨
o, J., and Marchetti, A. (2013). Optimal
ransac - towards a repeatable algorithm for finding the
optimal set. In WSCG, pages 21–30.
Hidalgo-Paniagua, A., Vega-Rodrguez, M., Pavn, N., and
Ferruz, J. (2014). A comparative study of parallel
ransac implementations in 3d space. International
Journal of Parallel Programming, pages 1–18.
Iser, R., Kubus, D., and Wahl, F. M. (2009). An ef-
ficient parallel approach to random sample match-
ing (pransam). In Proceedings of the 2009 IEEE
International Conference on Robotics and Automa-
tion, ICRA’09, pages 655–662, Piscataway, NJ, USA.
IEEE Press.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International Journal of Com-
puter Vision, 60(2):91–110.
M. Zuliani, C. K. and Manjunath, B. (2005). The multi-
ransac algorithm and its application to detect planar
homographies. In The International Conference on
Image Processing (ICIP), volume 3, pages 153–156.
Moravec, H. P. (1980). Obstacle avoidance and navi-
gation in the real world by a seeing robot rover.
PhD thesis, Stanford University, Stanford, CA, USA.
AAI8024717.
Muja, M. and Lowe, D. G. (2009). Fast approximate near-
est neighbors with automatic algorithm configuration.
In In VISAPP International Conference on Computer
Vision Theory and Applications, pages 331–340.
Noble, J. A. (1989). Descriptions of image surfaces. PhD
thesis, Oxford University, St Hugh’s College, Oxford,
GB. Ph. D. : Engineering sci. : April.
Obdrz
´
alek, S. and Matas, J. (2006). Object recognition us-
ing local affine frames on maximally stable extremal
regions. In Ponce, J., Hebert, M., Schmid, C., and
Zisserman, A., editors, Toward Category-Level Object
Recognition, volume 4170 of Lecture Notes in Com-
puter Science, pages 83–104. Springer.
Rodehorst, V. and Hellwich, O. (2006). Genetic algorithm
sample consensus (gasac) - a parallel strategy for ro-
bust parameter estimation. In IEEE Computer Society
Conference on Computer Vision and Pattern Recogni-
tion Workshop (CVPRW), pages 1–8.
Smith, S. M. and Brady, J. M. (1997). Susan - a new ap-
proach to low level image processing. Int. J. Comput.
Vision, 23(1):45–78.
Szeliski, R. (2006). Image alignment and stitching: a tuto-
rial. Found. Trends. Comput. Graph. Vis., 2(1):1–104.
Vajda, A. (2011). Programming Many-Core Chips.
Springer.
Zitova, B. and Flusser, J. (2003). Image registration meth-
ods: a survey. Image and Vision Computing, 21:977–
1000.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
106
