
A Multiresolution 3D Morphable Face Model and Fitting Framework
Patrik Huber
1
, Guosheng Hu
2
, Rafael Tena
1∗
, Pouria Mortazavian
3
, Willem P. Koppen
1
,
William Christmas
1
, Matthias R
¨
atsch
4
and Josef Kittler
1
1
Centre for Vision, Speech & Signal Processing, University of Surrey, Guildford, U.K.
2
LEAR Group, INRIA Grenoble Rh
ˆ
one-Alpes, Montbonnot, France
3
Samsung Electronics Research Institute, London, U.K.
4
Reutlingen University, Reutlingen, Germany
Keywords:
3D Morphable Face Model, 3D Face Reconstruction, Face Model Fitting, Pose Estimation, Shape Recon-
struction, Open Source Software.
Abstract:
3D Morphable Face Models are a powerful tool in computer vision. They consist of a PCA model of face
shape and colour information and allow to reconstruct a 3D face from a single 2D image. 3D Morphable
Face Models are used for 3D head pose estimation, face analysis, face recognition, and, more recently, facial
landmark detection and tracking. However, they are not as widely used as 2D methods - the process of building
and using a 3D model is much more involved.
In this paper, we present the Surrey Face Model, a multi-resolution 3D Morphable Model that we make
available to the public for non-commercial purposes. The model contains different mesh resolution levels
and landmark point annotations as well as metadata for texture remapping. Accompanying the model is a
lightweight open-source C++ library designed with simplicity and ease of integration as its foremost goals. In
addition to basic functionality, it contains pose estimation and face frontalisation algorithms. With the tools
presented in this paper, we aim to close two gaps. First, by offering different model resolution levels and fast
fitting functionality, we enable the use of a 3D Morphable Model in time-critical applications like tracking.
Second, the software library makes it easy for the community to adopt the 3D Morphable Face Model in their
research, and it offers a public place for collaboration.
1 INTRODUCTION
3D face models and in particular 3D Morphable Mod-
els are a powerful tool for computer vision. They
have applications in 2D face processing such as track-
ing, face analysis, recognition, pose estimation and
pose normalisation. 3D Morphable Models (3DMM)
were proposed by Blanz and Vetter in 1999 (Blanz
and Vetter, 1999) and since then have been applied
to a variety of these tasks. However they are not as
widespread in use as their 2D counterparts (for exam-
ple Active Appearance Models (Cootes et al., 2001)),
yet they have certain distinct advantages over 2D
methods. In a 3D model, the pose of a face is clearly
separated from the shape. Its projection to 2D is mod-
eled by a physical camera model, such as a perspec-
tive or affine camera model. Also, the use of a 3D face
model allows to model the light explicitly since 3D
surface normals, self-occlusion and depth information
are available. The illumination model separates light
from the face appearance and is not encoded in the
∗
now at Disney Research
texture parameters, as is for example the case in 2D
AAMs. The most prominent approaches to modelling
the environment or light sources in conjunction with
3DMMs are spherical harmonics (Aldrian and Smith,
2013; Zivanov et al., 2013) and the Phong illumina-
tion model (Romdhani and Vetter, 2005; Hu et al.,
2012).
Furthermore, a 3D Morphable Model can be used
in a generative way to create specific faces or to gen-
erate annotated training data for other algorithms that
e.g. covers a large variety of pose angles, including
more extreme poses like profile views. For exam-
ple, R
¨
atsch et al. (R
¨
atsch et al., 2012) used 3DMM-
generated data to improve the performance of a 2D
pose regressor, while Feng et al. (Feng et al., 2015)
augment the training data of their facial landmark
detection with 3DMM data to make it more robust
on larger pose angles. Very recently, 3DMMs have
also been used directly with regression-based meth-
ods (Huber et al., 2015; Zhu et al., 2015) with aspira-
tions to provide a unified solution to landmark detec-
tion and 3D model fitting.
Huber, P., Hu, G., Tena, R., Mortazavian, P., Koppen, W., Christmas, W., Rätsch, M. and Kittler, J.
A Multiresolution 3D Morphable Face Model and Fitting Framework.
DOI: 10.5220/0005669500790086
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 79-86
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
79

On the other hand, a 3D Morphable Face Model
is comparatively hard to obtain and use. To train a
model, a number of good quality 3D scans are needed.
These scans then need to be brought into dense corre-
spondence with a mesh registration algorithm. After
building a model, a model-to-image fitting algorithm
is required, and these fitting algorithms are often very
complex, slow, and are easily trapped in local min-
ima. The non-trivial training and fitting is in our opin-
ion one of the main reasons for the limited adoption
of 3D Morphable Face Models, and there is a lack of
readily available 3D face model fitting frameworks.
In 2009, Vetter et al. published the Basel Face
Model (BFM, (Paysan et al., 2009)) to spur research
with Morphable Models. It surpassed existing mod-
els (Sarkar, 2005; Blanz and Vetter, 1999) by the
accuracy of the scanner used and the quality of the
registration algorithm, and their multi-segment face
model, along with fitting results and various metadata,
can be obtained after signing a licence agreement.
While this led to some adoption by other research
groups (e.g. (van Rootseler et al., 2012; Aldrian and
Smith, 2013)), the adoption is still limited. Addition-
ally, while the BFM provides the model, they only
provide fitting results for limited databases and do not
provide algorithms to apply the model to novel im-
ages. With the model and software framework pub-
lished in this paper, we aim to go one step further and
make our model available as well as a lightweight fit-
ting framework promoting the use of the model.
This paper introduces the Surrey Face Model
(SFM), a multi-resolution 3D Morphable Face Model.
The model consists of three different resolution lev-
els of shape and colour, a pose-invariant image tex-
ture representation and metadata such as landmark
point information. The model is available freely for
non-commercial purposes. Alongside the model, we
present a library to interface with the model and per-
form basic pose and shape fitting. The main focus
of the software is its ease of use and interoperability
with the popular OpenCV library. The library is open
source, available under Apache License, Version 2.0,
and actively developed on GitHub, creating a public
place for exchange and contributions. In addition to
the full 3DMM being available via the University, we
release a low-resolution shape-only model distributed
within the software. In contrast to the Basel Face
Model, we offer the models at lower resolutions as
well, which are much more practical for many appli-
cations. We focus on ease of use of the framework
for vision tasks such as face tracking, pose estimation
and face frontalisation, and hope to further pave the
way to make 3DMMs more widely adopted. Table 1
summarises how the different parts are available.
Table 1: Availability of the different components.
Component Availability & Licence
Software library GitHub, Apache License Version 2.0
Low-resolution
shape model
GitHub, free for non-commercial
purposes
†
Full Surrey Face
Model
After signing licence agreement, free
for non-commercial purposes
†
†
For commercial purposes, contact us via
http://cvssp.org/facemodel.
The contributions of this work are threefold. First,
we present the Surrey Face Model, a multi-resolution
3D Morphable Face Model that we make available to
the public for non-commercial purposes. Second, we
present a lightweight open-source Morphable Model
software framework written in modern C++ that is
designed with simplicity and ease of integration as
its primary goals. Lastly, we make a low resolution
shape model available together with the software to
allow an immediate start with the framework. With
this whole package, our aim is to make 3D Mor-
phable Models easily available and to encourage re-
search with 3D face models.
In the rest of this paper, we first describe the acqui-
sition and the building process as well as the metadata
of the Surrey Face Model in detail (Section 2). We in-
troduce the resolution levels and show visualisations
of the model and its PCA components. In Section 3,
we then present the accompanying software frame-
work and demonstrate its ease of use and flexibility
by means of a 3D pose estimation and face frontalisa-
tion example. Section 4 concludes the paper.
2 THE SURREY FACE MODEL
The Surrey Face Model consists of a 3D Morphable
Model, that is, a PCA shape model and a PCA colour
model, each in different resolution levels, and accom-
panying metadata, like a 2D texture representation
and landmark annotations. The following sections
will describe each part in detail.
2.1 3D Morphable Models
A 3D Morphable Model is based on three dimensional
meshes of faces that have been registered to a refer-
ence mesh, i.e. are in dense correspondence. A face
is represented by a vector S ∈R
3N
, containing the x, y
and z components of the shape, and a vector T ∈ R
3N
,
containing the per-vertex RGB colour information. N
is the number of mesh vertices. The 3DMM consists
of two PCA models, one for the shape and one for the
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
80
colour information. Each PCA model
M := (
¯
v, σ, V) (1)
consists of the components
¯
v ∈ R
3N
, which is the
mean of the example meshes, a set of principal com-
ponents V = [v
1
, . . . , v
n−1
] ∈ R
3N×n−1
, and the stan-
dard deviations σ ∈ R
n−1
. n is the number of scans
used to build the model. Novel faces can be gener-
ated by calculating
S =
¯
v +
M
∑
i
α
i
σ
i
v
i
(2)
for the shape, where M ≤ n − 1 is the number of
principal components and α ∈ R
M
are the 3D face
instance coordinates in the shape PCA space. The
same is calculated for the colour (or so-called albedo)
model.
2.2 3D Scan Data
The Surrey Face Model is built using a number of
high-resolution 3D scans that were acquired at our
lab. The scans were captured using a 3dMDface
2
camera system that consists of two structured light
projectors, 4 infrared cameras that capture the light
pattern and are used to reconstruct the 3D shape, and
two RGB cameras recording a high-resolution face
texture. Half the cameras record the face from the
left side, the other half from the right side, resulting
in a 180
◦
view of the face. The images are acquired
under uniform illumination to ensure that the model
texture is representative of face skin albedo only. The
3dMDface software reconstructs a textured 3D mesh
from this information.
These scans can then be brought into dense corre-
spondence using a 3D to 3D registration algorithm, in
our case the Iterative Multi-resolution Dense 3D Reg-
istration (IMDR) method (Tena et al., 2006). Figure 1
shows an example scan with the captured mesh on the
left, the RGB texture in the middle, and the scan after
registration to the 3D model. The registration process
is described in more detail in the next section together
with how we built the multi-resolution model.
Figure 1: (left): Raw mesh output from the 3dMDface soft-
ware. (middle): Texture image from two angles captured
by the 3dMDface cameras. (right): The scan and texture
densely registered to the 3D model.
2
http://www.3dmd.com/
Our recorded subjects represent a diverse range of
skin tones and face shapes to well represent the mul-
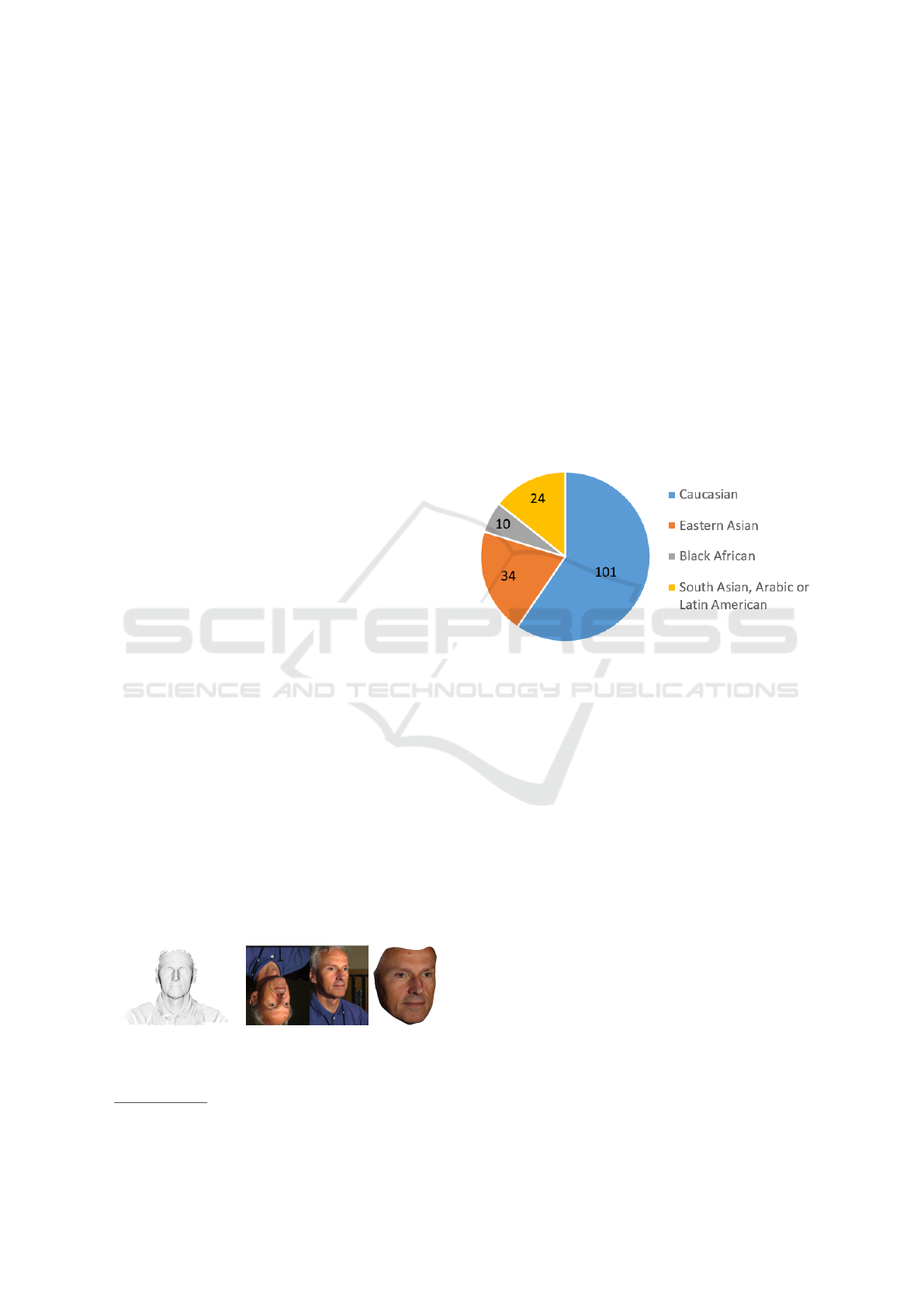
ticultural make up of many modern societies. Fig-
ure 2 shows the perceived racial distribution of the
169 scans used to build the model. Non-Caucasian
people are well-represented and significant numbers
of subjects from other races are included allowing
the model to generalise well to people from various
backgrounds. This is in stark contrast to the BFM,
which only contains a very insignificant number of
non-Caucasian people.
The age of the recorded people was categorised
into 5 groups. 9 are teens (age 0-19), 106 young
adults (20-29), 33 adults (30-44), 13 mature (45-59)
and 8 seniors (60+). Similar to the BFM, most peo-
ple are in the young-adult range, but the Surrey Face
Model contains more people in the 30+ groups.
Figure 2: Racial distribution of the 169 scans used to train
the Surrey Face Model. Our model is generated from a sig-
nificant number of non-Caucasian people.
2.3 Multi-resolution Model Generation
The Surrey Face Model comes in three different res-
olution levels. After obtaining the full set of scans,
they are registered using the Iterative Multi-resolution
Dense 3D Registration (IMDR) algorithm. It uses a
deformable reference 3D face model and performs a
combination of global mapping, local matching and
energy-minimisation to establish dense correspon-
dence among all the scans at different resolution lev-
els. The generic reference face we used has 845 ver-
tices and 1610 triangles. The following is a high-level
overview of the process:
1. The target scan is denoised using Gaussian and
median filtering if spikes and noise are present.
2. Perform a global mapping from the generic
model to the target scan using facial landmarks,
smoothly deforming the generic model.
3. Do a local matching on the current resolution
level based on the distances between reference
and target vertices. If a particular vertex cannot
A Multiresolution 3D Morphable Face Model and Fitting Framework
81
be matched, its mirrored counterpart is used (and
if that fails as well, the algorithm interpolates us-
ing the neighbouring matches).
4. The final set of matches guides an energy min-
imisation process that conforms the model to the
target scan. Steps 3 and 4 are iterated.
5. The generic face model is subdivided using the 4-
8 mesh subdivision algorithm (Velho and Zorin,
2001).
6. Steps 3 to 5 are repeated until the desired highest
mesh resolution is achieved.
Table 2 shows the three constructed resolution lev-
els with their number of vertices and triangles. The
smallest model consists of 3448 vertices and the full
model consists of 29587 vertices. Figure 3 depicts the
three mesh resolutions with a close-up on the model’s
mesh. Note that the higher resolution meshes are built
upon the lower resolutions, and therefore each ver-
tex from a lower resolution mesh is also present in
all higher resolution meshes, and has the same vertex
index.
Table 2: The different model resolution levels.
Model name No. vertices No. triangles
sfm 29587 29587 59763
sfm 16759 16759 33211
sfm 3448 3448 6736
Figure 3: Close-up of the different mesh resolutions of the
Surrey Face Model. (left): The low-resolution model with
3448 vertices. (middle): Medium-resolution model (16759
vertices) (right): The full resolution model (29587 vertices).
2.4 Shape and Colour Model
The shape and colour PCA models are built using
aforementioned 169 registered scans. Of the result-
ing PCA basis matrix, we keep 63 shape eigenvectors
and 132 colour eigenvectors so that 99% of the origi-
nal variation of the data is preserved after reconstruc-
tion. To analyse the variations in the face model, we
can visualise the directions of largest variance in the
PCA space by taking the formula in Equation 2 and
setting a specific α
i
to a fixed value while setting all
others to zero. The resulting face mesh S can then
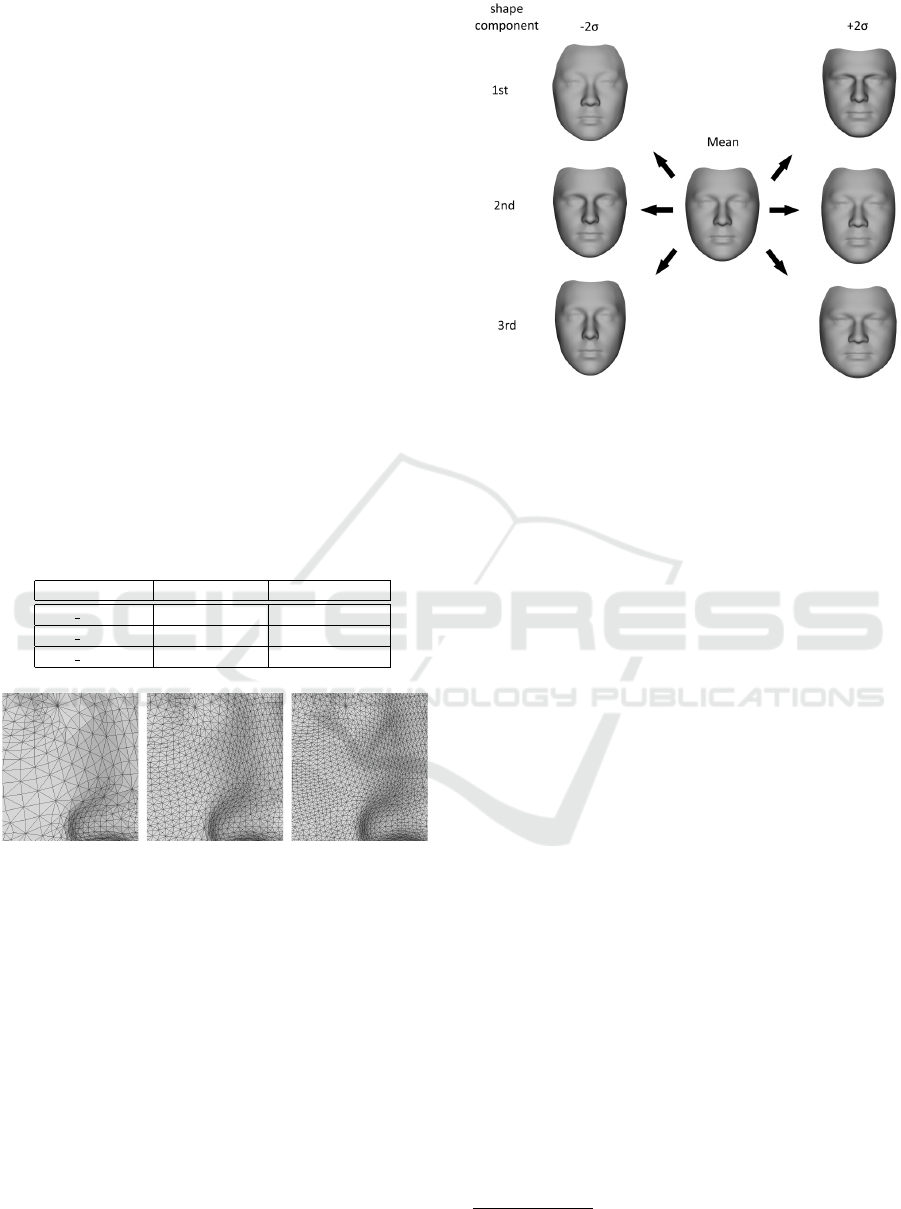
be rendered. Figure 4 shows the mean of the model
Figure 4: The mean face and shape variation of the high-
resolution Surrey Face Model. The figure shows the first
three PCA shape coefficients at -2 and +2 standard devia-
tions.
and the first three shape components set to ±2 stan-
dard deviations. The first components mainly account
for global structure of the face, like global face shape
(more round or square, slim or chubby) and size of
the face. Later components model the finer structures
of the face.
Figure 5 depicts the colour PCA model with the
colour coefficients set to ±2 standard deviations.
Varying the first component of the colour model re-
sults mainly in a change of global skin colour from
black to white, while the second component models
more diverse changes relating to the gender. The third
component encodes a mixture of skin colour and pos-
sibly gender.
Along with the model, we publish annotations of
the most commonly used facial landmark points for
all resolution levels. When using the model, it is use-
ful to have a standardised and known set of the loca-
tion (i.e. vertex index) of certain points like the eye
corners or the tip of the nose on the mesh. We pro-
vide such metadata with the model. Whenever pos-
sible, the points are defined on the generic reference
face or in the lowest model resolution and valid on
all model levels. Some points are only defined on the
higher mesh resolutions because the mesh resolution
at a lower level is too coarse and does not have a ver-
tex at the landmark location. Figure 6 shows a set of
manually selected landmark points on the mesh that
correspond to a subset of the popular ibug facial point
annotations
3
.
3
http://ibug.doc.ic.ac.uk/resources/
facial-point-annotations/
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
82

Figure 5: The mean face and colour variation of the high-
resolution Surrey Face Model. The figure shows the first
three PCA colour coefficients at -2 and +2 standard devia-
tions.
Figure 6: The facial landmark points that are annotated on
the mesh and available as metadata together with the model.
2.5 Texture Representation
The PCA colour model is a useful representation for
the appearance of a face, but in some cases it is desir-
able to use the pixel colour information (texture) from
the image or a combination of the two. The texture
from the input image remapped onto the mesh pre-
serves all details of a face’s appearance, while some
high-frequency information can be lost if a face is
only represented using the PCA colour model. An-
other reason to use the texture is to avoid a colour
and light model fitting, for example in consideration
of run-time. Therefore, we would like a 2D represen-
tation of the whole face mesh that we can use to store
the remapped texture. We create such a generic rep-
resentation with the isomap algorithm (Tenenbaum
et al., 2000): it finds a projection from the 3D vertices
to a 2D plane that preserves the geodesic distance be-
tween the mesh vertices. Our mapping is computed
with the algorithm from Tena (Rodr
´
ıguez, 2007).
Figure 7: Texture representation in the form of an isomap.
The 3D mesh vertices are projected to 2D with an algo-
rithm that preserves the geodesic distance between ver-
tices, resulting in a pose-independent, detail-preserving tex-
tural representation of a face. Shown is the isomap of the
sfm 3448.
In contrast to other representations, like for exam-
ple cube mapping, this isomap has the advantage that
it can be stored as a single 2D image, and it has face-
like appearance, i.e. it can be easily used with ex-
isting face recognition and face analysis techniques.
The isomap coordinates are only generated once, that
is the isomaps of different people are in dense cor-
respondence with each other, meaning each location
in the map corresponds to the same physical point in
the face of every subject (for example, a hypothetical
point x = [100, 120] is always the center of the right
eye). This makes the isomap especially suitable for
processing with further algorithms.
Figure 7 shows the isomap of the low-resolution
model as a wireframe. The isomap captures the whole
face, while for example a rendering of the mesh would
always only show parts of the face.
We provide texture coordinates generated with the
isomap algorithm for each model resolution level.
3 SOFTWARE FRAMEWORK
The Surrey Face Model is accompanied by an
open source software framework that is available on
GitHub under Apache License, Version 2.0. It is
a lightweight and cross-platform header-only library
built using modern C++, which makes it very flex-
ible, easy to use and simple to include into exist-
ing software. The library requires no other depen-
dency than applications developed using it linking
to OpenCV-core. The software framework includes
a low-resolution shape-only model (sfm shape 3448)
to facilitate immediate use.
This section will first give a brief introduction
A Multiresolution 3D Morphable Face Model and Fitting Framework
83

about the core functionality of the framework and
then present the pose and landmark fitting algorithms
included in the software and a basic use case example.
The library, low-resolution shape model, example ap-
plications and a complete documentation are available
at https://github.com/patrikhuber/eos.
4
3.1 Core Functionality
A 3D Morphable Model is represented using a thin
layer on top of OpenCV. A PcaModel class contains
a mean, the PCA basis vectors and eigenvalues, and
a MorphableModel class contains a shape and colour
PCA model and texture coordinates, along with the
functionality to retrieve a mesh that can be rendered.
Figure 8 shows an UML-like overview of this basic
functionality.
Figure 8: UML-like diagram of the MorphableModel and
PcaModel classes, which are simple wrappers for the un-
derlying PCA and model metadata (diagram slightly sim-
plified).
A model can be loaded as simple as:
MorphableModel model =
load_model("sfm_shape_3448.bin");→
The semantic landmark information (see end of
Section 2.4) is stored separately as it differs depend-
ing on the use-case and it can be accessed through
a LandmarkMapper class. In the following, we will
extend this code snippet and build a 3D face frontal-
isation example with the software framework in only
a few lines of code.
5
In addition to loading the Surrey Face Models, we
provide a script to convert and load the Basel Face
Model.
3.2 Landmark Fitting
The library includes methods to fit the pose and shape
of a model and perform face frontalisation. This sec-
tion describes the individual components and how
they fit together.
4
The functionality described in this paper is based on
v0.5.0. Naturally, software evolves, and certain parts might
be slightly different in future versions. We encourage users
to look at the example app of the most current version.
5
For the sake of brevity, we omit namespaces in the code
examples. Where not otherwise indicated, types and func-
tions are either in the std or our library’s namespace.
3.2.1 Pose Estimation
The first component presented here is pose (camera)
fitting. Given a set of 2D landmark locations and their
known correspondences in the 3D Morphable Model,
the goal is to estimate the pose of the face (or the po-
sition of the camera, which in this case is the identical
problem). We assume an affine camera model and
implement the Gold Standard Algorithm of Hartley
& Zisserman (Hartley and Zisserman, 2004), which
finds a least squares approximation of a camera ma-
trix given a number of 2D - 3D point pairs.
First, the detected or labeled 2D landmark points
in the image x
i
∈R
3
and the corresponding 3D model
points X
i
∈ R
4
(both represented in homogeneous
coordinates) are normalised by similarity transforms
that translate the centroid of the image and model
points to the origin and scale them so that the Root-
Mean-Square distance from their origin is
√
2 for the
landmark and
√
3 for the model points respectively:
˜x
i
= Tx
i
with T ∈R
3×3
, and
˜
X
i
= UX
i
with U ∈R
4×4
.
Using ≥ 4 landmark points, we then compute a nor-
malised camera matrix
˜
C ∈R
3×4
using the Gold Stan-
dard Algorithm (Hartley and Zisserman, 2004) and
obtain the final camera matrix after denormalising:
C = T
−1
˜
CU.
Computing the camera matrix C involves solving
a linear system of equations - the algorithm calculates
the least squares solution, so any number of corre-
sponding points can be given. This process is also
very fast, taking only a few milliseconds to compute.
The function in our library can be run by simply
loading and defining point correspondences and then
calling the algorithm:
vector<cv::Vec2f> image_points = ...;
vector<cv::Vec3f> model_points = ...;
Mat affine_camera =
estimate_affine_camera(image_points,
model_points);
→
→
which returns the estimated 3×4 affine camera matrix
that can subsequently be used in the next steps.
3.2.2 Shape Fitting
The second component in our face frontalisation ex-
ample consists of reconstructing the 3D shape using
the estimated camera matrix. We implement a sim-
ple shape-to-landmarks fitting similar to the algorithm
from Aldrian & Smith (Aldrian and Smith, 2013). We
find the most likely vector of PCA shape coefficients
α by minimising the following cost function:
E =
3N
∑
i=1
(y
m2D,i
−y
i
)
2
2σ
2
2D
+ kαk
2
2
, (3)
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
84

where N is the number of landmarks, y are detected or
labelled 2D landmarks in homogeneous coordinates,
σ
2
2D
is an optional variance for these landmark points,
and y
m2D
is the projection of the 3D Morphable Model
shape to 2D using the estimated camera matrix. More
specifically, y
m2D,i
= P
i
·(
ˆ
V
h
α +
¯
v), where P
i
is the
i-th row of P and P is a matrix that has copies of the
camera matrix C on its diagonal, and
ˆ
V
h
is a modi-
fied PCA basis matrix that consists of a sub-selection
of the rows that correspond to the landmark points
that the shape is fitted to. Additionally, a row of
zeros is inserted after every third row to accommo-
date for homogeneous coordinates, and the basis vec-
tors are multiplied with the square root of their re-
spective eigenvalue. The cost function in (3) can be
brought into a standard linear least squares formula-
tion. For details of the algorithm, we refer the reader
to (Aldrian and Smith, 2013).
This functionality is directly mapped into code.
The shape coefficients can be estimated as:
vector<float> shape_coefficients =
fit_shape_to_landmarks_linear(model,
affine_camera, image_points,
vertex_indices, lambda);
→
→
→
The first three parameters are given from the previ-
ous step. The vertex_indices are obtained with the
supplied landmark annotation metadata and the map-
ping facilities of the library - we refer to the online
material for the full documentation. lambda is an op-
tional regularisation parameter to constrain the opti-
misation to plausible shapes.
The pose estimation and shape fitting steps can be
iterated if desired to refine the estimates. The pose es-
timation can make use of the shape estimate (instead
of using the mean face) to refine the face pose. The
shape estimate can in turn use the refined camera ma-
trix to improve the shape fitting. The shape estimation
is as fast as the pose estimation: each of them only in-
volves solving a small linear system of equations and
runs in the order of milliseconds.
3.2.3 Texture Representation
After obtaining the pose and shape coefficients, there
is a dense correspondence between mesh vertices and
the face in the input image. We can then remap the
texture onto the model, and store it, and re-render it
in arbitrary poses, e.g. frontalise it. The texture can
be extracted and stored in the isomap introduced in
Section 2.5 with another simple call to the library:
Mesh model_instance =
model.draw_sample(shape_coefficients);→
Mat isomap = extract_texture(model_instance,
affine_camera, input_image);→
Note that, in addition to being used to remap the
texture or visualise the model, draw sample allows
drawing arbitrary samples from the model, for exam-
ple to generate artificial training data from the 3D face
model.
Figure 9 shows an example fitting with the input
image, the resulting shape and camera model fitting,
and the extracted face texture as an isomap. In the
figure, regions of self-occlusion are depicted as white
spots; however, in the isomap, they are identified by
the alpha channel.
Figure 9: An example result of the landmark fitting. (left):
Input image from LFPW. (middle): The extracted face tex-
ture as isomap. Regions of self-occlusion are depicted in
white. (right): Resulting shape and camera model fitting.
This section presented how the proposed
lightweight library makes it possible to build a
real-time 3D pose estimation and face frontalisation
system with little effort. The example code snippets
from these sections can be combined into a fully
working application with not many more lines than
presented here. The pose estimation and landmark
fitting run in a matter of milliseconds, while the
texture remapping is the slowest component taking
around 100 milliseconds (measured on an Intel Core
i7-4700MQ). That is, to reduce dependencies of the
framework and to make it run on any environment,
it is not using OpenGL or any other acceleration
technique. The main goals of the library are that it
is simple, easy to use, easy to integrate into existing
software and extensible. The full documentation,
which includes additional functionality not presented
here, as well as the complete and documented
example application from this section, are available
in the library repository.
4 CONCLUSIONS
We presented the Surrey Face Model, a multi-
resolution 3D Morphable Face Model that is pub-
licly available for non-commercial purposes. The
model is available in three different resolution lev-
els and accompanied by isomap coordinates and land-
mark metadata. We introduced a lightweight header-
only library written in modern C++ that accompanies
A Multiresolution 3D Morphable Face Model and Fitting Framework
85

the model and is actively developed on GitHub at
https://github.com/patrikhuber/eos. The software fea-
tures real-time shape model fitting and face frontalisa-
tion functionality and interoperability with OpenCV.
In contrast to existing work, the Surrey Face
Model is available in multiple resolution levels and
is built from racially diverse scans. Furthermore,
a model-fitting software is available alongside the
model to fit the model to novel images and videos.
By designing the whole framework with simplicity
as its foremost goal and using a public place for de-
velopment and interaction, we hope to spur research
with 3D Morphable Face Models in the community
and encourage new parties to tackle their challenges
with 3D face models. In addition to the full 3DMM
being available via the University, we release a low-
resolution shape model distributed directly within the
public repository so that interested researchers can be
ready-to-go in a matter of minutes.
Instructions to acquire the full model are available
at http://cvssp.org/facemodel.
ACKNOWLEDGEMENTS
Partial support from the BEAT project (Euro-
pean Union’s Seventh Framework Programme, grant
agreement 284989) and the EPSRC Programme Grant
EP/N007743/1 is gratefully acknowledged.
REFERENCES
Aldrian, O. and Smith, W. A. P. (2013). Inverse rendering
of faces with a 3D Morphable Model. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
35(5):1080–1093.
Blanz, V. and Vetter, T. (1999). A Morphable Model for the
synthesis of 3D faces. In Proceedings of the 26th An-
nual Conference on Computer Graphics and Interac-
tive Techniques (SIGGRAPH), pages 187–194. ACM
Press/Addison-Wesley Publishing Co.
Cootes, T., Edwards, G., and Taylor, C. (2001). Active ap-
pearance models. IEEE Transactions on Pattern Anal-
ysis and Machine Intelligence, 23(6):681 –685.
Feng, Z.-H., Huber, P., Kittler, J., Christmas, W., and Wu,
X.-J. (2015). Random cascaded-regression copse for
robust facial landmark detection. IEEE Signal Pro-
cessing Letters, 22(1):76–80.
Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-
ometry in Computer Vision. Cambridge University
Press, second edition.
Hu, G., Chan, C.-H., Kittler, J., and Christmas, W. (2012).
Resolution-aware 3D Morphable Model. In British
Machine Vision Conference (BMVC), pages 1–10.
Huber, P., Feng, Z., Christmas, W., Kittler, J., and R
¨
atsch,
M. (2015). Fitting 3D Morphable Models using local
features. In IEEE International Conference on Image
Processing (ICIP).
Paysan, P., Knothe, R., Amberg, B., Romdhani, S., and Vet-
ter, T. (2009). A 3D face model for pose and illumi-
nation invariant face recognition. In Proceedings of
the 6th IEEE International Conference on Advanced
Video and Signal based Surveillance (AVSS).
R
¨
atsch, M., Huber, P., Quick, P., Frank, T., and Vetter,
T. (2012). Wavelet reduced support vector regres-
sion for efficient and robust head pose estimation. In
IEEE Ninth Conference on Computer and Robot Vi-
sion (CRV), pages 260–267.
Rodr
´
ıguez, J. R. T. (2007). 3D Face Modelling for 2D+3D
Face Recognition. PhD thesis, University of Surrey.
Romdhani, S. and Vetter, T. (2005). Estimating 3D shape
and texture using pixel intensity, edges, specular high-
lights, texture constraints and a prior. In IEEE Con-
ference on Computer Vision and Pattern Recognition
(CVPR), volume 2, pages 986–993. IEEE.
Sarkar, S. (2005). USF HumanID 3D face dataset.
Tena, J. R., Hamouz, M., Hilton, A., and Illingworth, J.
(2006). A validated method for dense non-rigid 3D
face registration. In Advanced Video and Signal Based
Surveillance, 2006 IEEE International Conference on
Video and Signal Based Surveillance (AVSS’06), 22-
24 November 2006, Sydney, Australia., page 81. IEEE
Computer Society.
Tenenbaum, J. B., de Silva, V., and Langford, J. C. (2000).
A global geometric framework for nonlinear dimen-
sionality reduction. Science, 290:2319–2323.
van Rootseler, R. T. A., Spreeuwers, L. J., and Veldhuis, R.
N. J. (2012). Using 3D Morphable Models for face
recognition in video. In Proceedings of the 33rd WIC
Symposium on Information Theory in the Benelux.
Velho, L. and Zorin, D. (2001). 4-8 subdivision. Computer
Aided Geometric Design, 18(5):397–427.
Zhu, X., Yan, J., Yi, D., Lei, Z., and Li, S. Z. (2015).
Discriminative 3D Morphable Model fitting. In In-
ternational Conference on Automatic Face and Ges-
ture Recognition, FG 2015, 4-8 May, 2015, Ljubljana,
Slovenia. IEEE.
Zivanov, J., Forster, A., Sch
¨
onborn, S., and Vetter, T.
(2013). Human face shape analysis under spherical
harmonics illumination considering self occlusion. In
International Conference on Biometrics, ICB 2013, 4-
7 June, 2013, Madrid, Spain, pages 1–8. IEEE.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
86
