
ACO and CP Working Together to Build a Flexible Tool for the VRP
Negar ZakeriNejad
1
, Daniel Riera
1
and Daniel Guimarans
2,3
1
Computing, Multimedia and Telecommunication Department, Universitat Oberta de Catalunya (UOC), Barcelona, Spain
2
Optimisation Research Group, National ICT Australia (NICTA), Sydney, Australia
3
Aviation Academy, Amsterdam University of Applied Sciences, Amsterdam, The Netherlands
Keywords:
Ant Colony Optimisation, Constraint Programming, Vehicle Routing Problem, Optimisation.
Abstract:
In this paper a flexible hybrid methodology, combining Ant Colony Optimisation (ACO) and Constraint Pro-
gramming (CP), is presented for solving Vehicle Routing Problems (VRP). The stress of this methodology is
on the word ‘flexible’: It gives reasonably good results to changing problems without high solution redesign
efforts. Thus a different problem with a new set of constraints and objectives requires no changes to the search
algorithm. The search part (driven by ACO) and the model of the problem (included in the CP part) are sep-
arated to take advantage of their best attributes. This separation makes the application of the framework to
different problems much simpler. To assess the feasibility of our approach, we have used it to solve different
instances of the VRP family. These instances are built by combining different sets of constraints. The results
obtained are promising but show that the methodology needs deeper communication between ACO and CP to
improve its performance.
1 INTRODUCTION
Vehicle Routing Problems (VRPs) are an optimisa-
tion problem in the field of transportation and logis-
tics. It involves routing a fleet of vehicles to serve
several customers. This problem is difficult not only
because it is NP-hard but also for having many diverse
forms (Laporte et al., 2000; Golden et al., 2008)
Exact methods exist to solve VRPs optimally, but
they become computationally prohibitive for large
problem sizes. On the other hand approximate meth-
ods trade off optimality for feasibility of solving large
problem instances.
Also, hybridised methods, combining different al-
gorithms, have been developed to tackle VRPs (La-
porte et al., 2013; C´aceres-Cruz et al., 2014). One
successful hybridised approach has been combining
Constraint Programming (CP) with metaheuristics
(Solnon, 2010; Talbi, 2013; Shaw, 2011; Berbeglia
et al., 2012; Blum et al., 2011; Khichane et al., 2008;
Meyer and Ernst, 2004). CP is an exact method that
models a problem as a Constraint Satisfaction Prob-
lem (CSP) which can be solved using general purpose
solvers (Rossi et al., 2006; Khichane et al., 2010).
Metaheuristic algorithms are approximate methods
that explore the most promising regions of the solu-
tion space to find a sufficiently good solutions (La-
porte, 2009).
Unfortunately, most of the research efforts for de-
veloping effective hybrid approaches are focused on
specific problems and are not easily extensible to oth-
ers (Vidal et al., 2013; Pisinger and Ropke, 2007) .
Accordingly, a fruitful challenge for researchers is de-
veloping a framework hybridising optimisation algo-
rithms and methods to address a large class of VRPs.
This would be useful because real-life applications
vary greatly and such a framework reduces design
costs. To satisfy this challenge a methodology is re-
quired that allows easy modeling (and re-modeling)
of different problems and a fast and effective search
engine.
The aim of our methodology is to maximise flex-
ibility in terms of quick adaptation to different vari-
ants of VRPs, while staying reasonably close to the
optimal solutions. Our design hypothesis is based on
the high modelling power of Constraint Programming
(CP) and the ease of metaheuristics to explore search
spaces and quickly generate fairly good solutions. In
this case, Ant Colony Optimisation (ACO) (Dorigo
and Birattari, 2010) has been chosen as a metaheuris-
tic because of the closeness of the VRP instance rep-
resentations to the representation of the problems that
ACO solves.
The proposed approach has the merit of not de-
122
ZakeriNejad, N., Riera, D. and Guimarans, D.
ACO and CP Working Together to Build a Flexible Tool for the VRP.
DOI: 10.5220/0005668101220129
In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 122-129
ISBN: 978-989-758-171-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

pending on the form of the problem and thus allow-
ing extensibility to a wide variety of VRPs, includ-
ing the ones that capture the high complexities, large
data sizes, uncertainties, and dynamisms that exist in
real-life. These kind of VRPs are called Rich Vehicle
Routing Problems (RVRPs) and are even more dif-
ficult to solve than simpler VRPs (Drexl, 2012). The
final aim of this work is to deal with RVRPs, although
for the initial assessment of the methodology we have
chosen classical VRP variants and incrementally con-
structed more complex problems.
In order to assess these goals, first the collabora-
tion of two main parts of the framework needs to be
explored, which is the objective of this paper. This
is carried out by generating solutions using ACO as
a search algorithm and verifying their feasibility us-
ing CP. We aim to reduce the development time by
using the CP to model the constraints and check their
feasibility, and thus guide the approximate algorithm
towards better results.
The paper is organised as follows. In Section 2,
we propose our general framework by describing its
main two parts and how they cooperate to build feasi-
ble solutions. The experimental setup and the results
of the experiments are shown in Sections 3 and 4. Fi-
nally, the last section states the conclusions and some
future research ideas.
2 PROPOSED FRAMEWORK
The proposed framework is made up of two main ele-
ments: the CP and theselected heuristic/metaheuristic
(in this specific case, a basic version of the ACO).
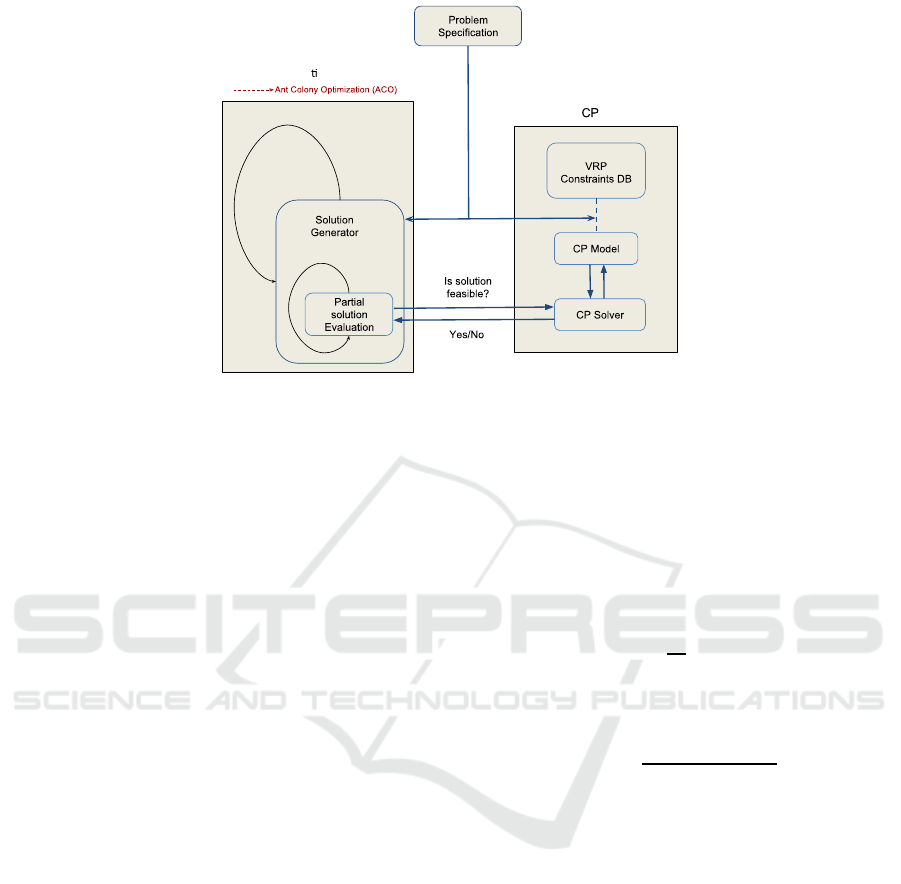
The cooperation between these two parts is depicted
in Fig.1.
The aim of the CP part of the framework is
twofold. First, it provides a clear and powerful for-
mulation to encode any constraints relevant to a given
routing problem. Thus, different VRPs can be quickly
modelled and re-modelled as CSPs without the need
of changing the architecture of the framework. Sec-
ond, it encompasses a CP solver, which provides eval-
uations of solutions’ feasibility and also global search
information given partial solutions. This informa-
tion helps the metaheuristic to avoid exploring search
spaces with no feasible solutions.
The metaheuristic part of the framework is where
the main search through the solution space takes
place. In the proposed framework the metaheuristic
part is implemented in two distinct loops as shown in
figure 1. While the outer loop is mostly concerned
with the logic of the metaheuristic, the inner one uses
the interaction with the CP solver to guide the con-
struction of solutions.
The inner loop of the metaheuristic is effectively a
random construction algorithm. That is, in each iter-
ation the solution is augmented with a new part. The
selection of the new part is guided according to the
mechanism of the metaheuristic.
Because the metaheuristic is oblivious to the na-
ture of the problem, it frequently asks CP to verify the
solution. This is done by sending a partial solution to
the CP and having CP check that no constraints are
broken given the current assignment. As we will later
explain in more details, the CP checking performed in
the internal loop is allowed to ignore serving all cus-
tomers in a way that makes construction of a feasible
solution always possible. Therefore, in the outer loop
each solution is checked one last time to compute the
fitness of the solution according to the objective func-
tion and possible unsatisfied customers.
The outer loop starts by constructing a new solu-
tion using the inner loop iterations. Then, it evalu-
ates the new solution quality and updates the state of
the metaheuristic according to the quality of the solu-
tion. For example in the case of ACO, it updates the
pheromone matrix.
2.1 CP Model
As said before there are many different problem sub-
classes (defined by the specific active constraints) in
VRP, most of which have already been studied. This
makes it possible to build a constraint and objective
library and activate only the needed parts for solving
the given problem. In our case, we are working with
a CP-VRP library (Riera et al., 2009), built for the
ECLiPSe
1
CP system. This library allows the use of
constraints for capacity, distance, heterogeneous ve-
hicles, asymmetric routes, time windows, and pick up
and delivery, among others.
2.2 Search Algorithm
ACO is a well-known nature inspired metaheuristic
algorithm used for solving combinatorial optimisa-
tion problems. In particular, ACO is a probabilistic
technique which builds a solution iteratively through
a stochastic construction procedure. This class of
optimisation algorithms follows simple rules based
on a collective behaviour of the self-organised sim-
ple agents with no centralised control structure dictat-
ing how individual agents should behave (Dorigo and
Birattari, 2010; Yu and Yang, 2011; Balseiro et al.,
2011).
1
http://eclipseclp.org/
ACO and CP Working Together to Build a Flexible Tool for the VRP
123
Metaheuris c algorithm
Figure 1: Main parts of the proposed framework and the relationship between them.
At the moment, we use a basic version of the ACO
algorithm: Each ant constructs a solution determining
the trips for all vehicles in an iterative fashion. To
do this, it selects a path through a graph of nodes.
Each node corresponds to one customer, except for
the initial-final node which corresponds to the depot.
Choosing the depot signals the route completion for
the current vehicle and the start of the journey of the
next vehicle.
At each iteration, the ant chooses a random node,
according to the distance of the nodes to the current
one and the amount of pheromone on the edge lead-
ing to the neighbours. Then a partial solution corre-
sponding with the current partial path is constructed
and passed to the CP checker. If the CP checker finds
the solution infeasible, the ant backtracks one step and
returns to the depot, ending the planning for the cur-
rent vehicle. If the CP checker finds no problem with
the current partial path (i.e. there might be feasible
solutions containing this partial one), the construction
of the path continues normally. These iterations ter-
minate when all vehicles have been planned for. Note
that, after termination some costumers may not have
been serviced.
After an ant constructs one solution, the CP solver
is invoked one last time to check the feasibility of the
solution found by the ant. We calculate the total dis-
tance of the trip as an objective function and use it
along with the number of unserviced customers to as-
sign a quality value to the solution found. The amount
of pheromone for each section of the solution is then
updated according to this computed quality. In Fig.2,
the flowchart of the search procedure for one ant is
presented.
2.2.1 Ant Route Selection
An ant constructs its route by selecting nodes one by
one, in a stochastic manner. The probability of a node
being selected is computed according to two factors.
The first factor is the amount of pheromone deposited,
τ
ij
, for the transition between the current node i and
the prospective node j. The second factor is the vis-
ibility heuristic defined as the inverse of the distance
between nodes i and j,
1
d
ij
, and denoted by η
ij
. The
probability of choosing next node, P
ij
, can be stated
as follows:
P
ij
=
[τ
ij
]
α
· [η
ij
]
β
∑
l∈N
[τ
il
]
α
· [η
il
]
β
(1)
where α and β are parameters to tune the relative in-
fluence of pheromone trail and heuristic information,
and N is the set of all nodes yet to be visited.
2.2.2 Pheromone Update
The process of updating pheromone trail consists of
two mechanisms. The first is pheromone evaporation
which decreases the amount of pheromone values de-
posited on each edge in predefined intervals. By ap-
plying this mechanism, the algorithm can avoid con-
vergence to sub-optimal solutions rapidly.
The second mechanism is pheromone deposition
which increases the pheromone trails of solution
edges according to the quality of the solution. The
aim of this mechanism is to make better solutions
more attractive for other ants and guide them towards
more promising regions.
The pheromoneupdate for each edge is commonly
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
124
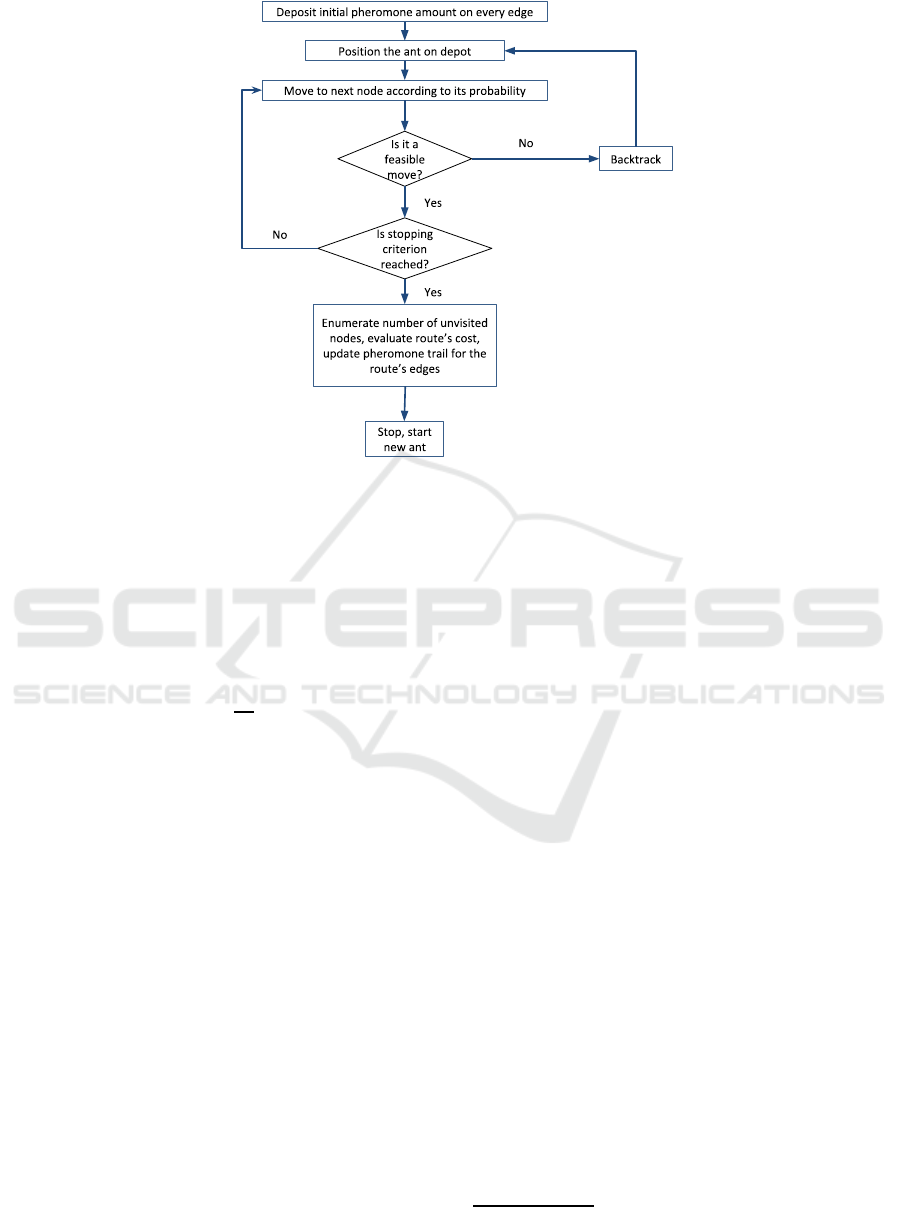
Figure 2: Flowchart of the search procedure for a single ant.
implemented as:
τ
ij
← (1− ρ)· τ
ij
+
∑
k
∆τ
k
ij
(2)
In this formula, ρ is the pheromone evaporation
rate, and ∆τ
ij
is the amount of pheromone deposited
by ant k ant, computed as:
∆τ
k
ij
=
Q
L
k
(3)
where Q is a constant (problem-specific parameter
to tune), and L
k
determines the quality of a solution
found by ant k. In this case, it is equal to the total
distance travelled by the ant.
According to the type of a given problem and its
complexity, the process of updating pheromone trail
can be applied in different ways. In this work, we ap-
ply both pheromone evaporation and pheromone de-
position mechanisms simultaneously in predefined in-
tervals.
3 EXPERIMENTAL SETUP
3.1 Problem Instances
In this paper, we study the interactions between the
two main parts of the framework and also the exten-
sibility aspect of the approach to adapt to newer in-
cremental problems without extra development. For
this, we have selected four VRP variants (C´aceres-
Cruz et al., 2014):
• Capacitated VRP (CVRP). It is one of the ear-
lier and most studied VRPs, where all vehicles
have the same capacity which cannot be exceeded.
The data used for CVRP is taken from a stan-
dard benchmark set proposed by Augerat et al.
(Augerat et al., 1995), where instance sizes are
between 15 and 100 customers.
• Heterogeneous fleet VRP (HVRP). This is an ex-
tension of the CVRP with the difference that the
capacity and cost of vehicles are not homoge-
neous. To test the HVRP, eight problem instances
developed by Taillard (1999) (Imran et al., 2009)
are used. In this dataset, the number of customers
varies from 50 to 100 and the number of vehicle
types varies from 3 to 6.
• Distance-Constrained VRP (DCVRP). It is an ex-
tension of the CVRP with the difference that both
vehicle capacity and a maximum distance (for
each vehicle) are imposed as constraints. For
preliminary experiments, six problem instances
of the CVRP dataset
2
have been adapted for the
DCVRP.
• Asymmetric cost matrix VRP (AVRP). In this
type of problems the distance between each pair
of locations in the two directions is not the
same in both ways. Fourteen problem instances
based on realistic scenarios are selected from
AVRP benchmark proposed by Rodriguez and
2
Problem instances P-n16-k8, P-n20-k2, P-n40-k5, P-
n50-k7, P-n55-k10, and P-n101-k4.
ACO and CP Working Together to Build a Flexible Tool for the VRP
125
Ruiz (Rodr´ıguez and Ruiz, 2012)
3
. Because this
dataset provides a diverse number of tests, in-
stances were chosen so their sizes were between
50 and 100 customers. We also limited the dataset
to those instances that have higher demand and
nodes’ locations were randomly chosen within an
intra-city area.
4
3.2 Computational Setting
The metaheuristics part of the framework has been
implemented in Java. For the CP part, we chose the
ECLiPSe platform. A CP-VRP library (Riera et al.,
2009) has been used as a constraints pool. All experi-
ments were ran on a system with an Intel core i5-3470
CPU and 4GB RAM.
The performance of the ACO-based algorithms re-
lies on a set of correlated parameters and the values
chosen for them. Tuning the parameters is a time-
consuming process and can lead to a diverse set of pa-
rameters depending on the given problem. As the aim
of this experiment is to show the ability of the frame-
work to adapt to different types of VRPs, devoting
time to adjust parameters is not indispensable. As a
matter of fact, the need of adjusting parameters when
adding new constraints would be considered a penalty
for the methodology. Table 1 summarises the values
chosen for the ACO parameters used indistinctly in
all the experiments.
Table 1: Parameters used for conducting the tests.
Parameters Value
No of ants 2500
Pheromone update interval 50
Initial pheromone 2
α 3
β 3
ρ 0.0001
Q 100
4 EXPERIMENTAL RESULTS
In order to assess the efficiency of the proposed
framework, two different kinds of experiments are
considered. In the first one, a small-sized example
is used as a preliminary test instance to show how the
3
http://soa.iti.es/problem-instances
4
Problem instances G-A-CAA0501, G-A-CAA0502,
G-A-CAA0503, G-A-CAA0504, G-A-CAA0505, G-
A-CAA1003, G-A-CAA1004, G-C-CAA0501, G-
C-CAA0502, G-C-CAA0503, G-C-CAA0504, G-C-
CAA0505, G-C-CAA1001, G-C-CAA1002.
framework behaves when solving different types of
VRPs (by adding constraints one by one). In the sec-
ond experiment, the framework is applied over four
classical benchmark sets, each related to a different
type of VRP, to check the quality of the solutions
found by the algorithm compared to the best known
5
.
The experimental results are given in detail below.
4.1 Laboratory Incremental Example
The flexibility of the proposed method has been as-
sessed through a small-sized experimental test de-
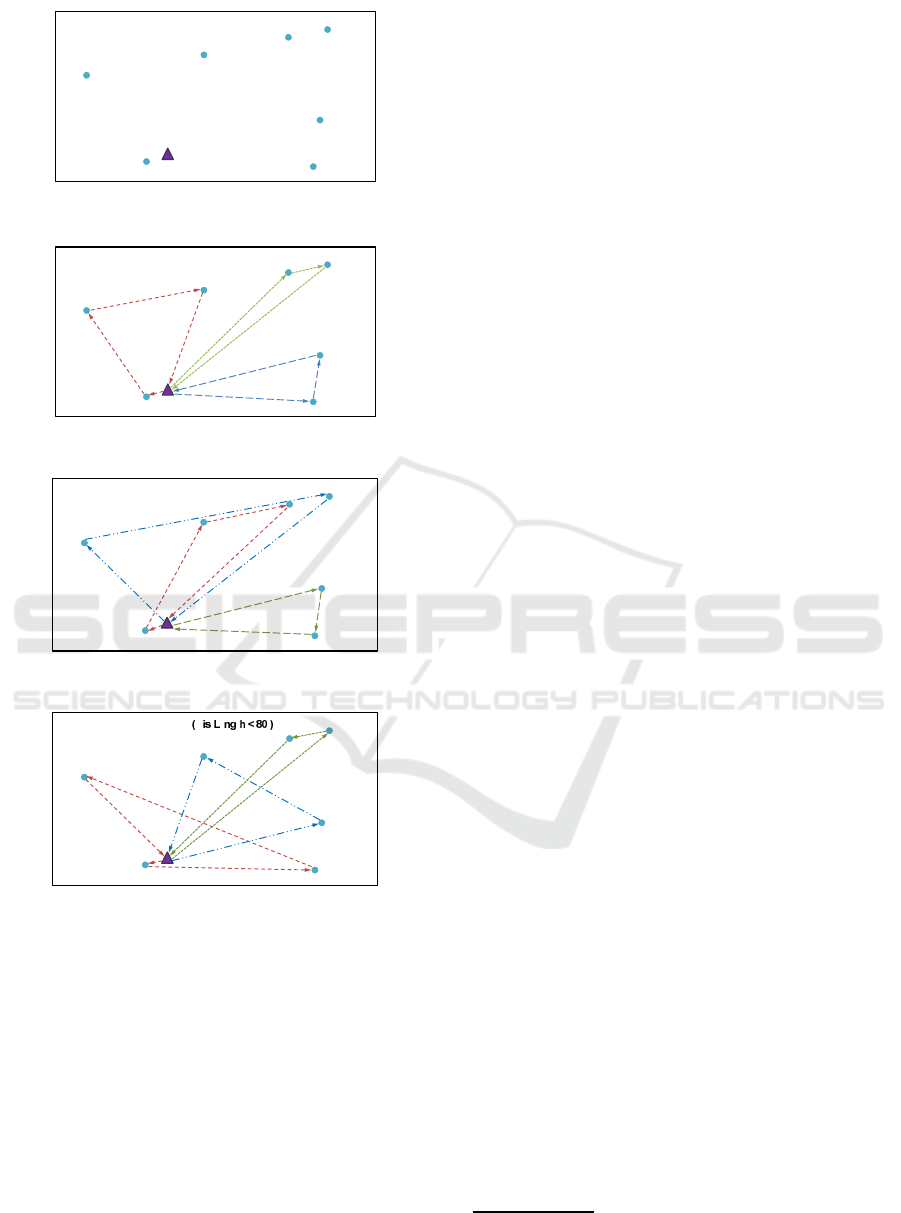
scribed as follows. Table 2 shows the coordinates
of the depot and the coordinates and demand of the
clients to be served. The corresponding map can be
seen in Fig.3.
Table 2: summary of the simple model used for the test.
Node [X,Y] Demand (units)
Depot [40.348, -3.851] 0
C
1
[40.372, -3.593] 59
C
2
[40.295, -3.645] 64
C
3
[40.448, -3.760] 84
C
4
[40.444, -3.879] 70
C
5
[40.427, -3.548] 80
C
6
[40.335, -3.866] 69
C
7
[40.453, -3.528] 75
Furthermore, we have pre-calculated the (asym-
metric) distance matrix for the nodes, containing the
depot and the clients:
0 16 20 33 9 30 13 28 28 28
15 0 23 33 22 25 26 25 25 25
26 23 0 14 22 20 24 18 18 18
37 33 16 0 35 15 36 14 14 14
15 21 21 35 0 34 5 32 32 32
33 24 22 15 34 0 36 3 3 3
19 26 23 36 6 36 0 34 34 34
31 25 19 15 32 4 33 0 0 0
We have got three vehicles to design the routes.
In the homogeneous cases their capacity is 195 units,
while for the heterogeneous instances their capacities
are 210, 160, and 145.
Figures 3-6 show how the methodology adapts
from one kind of problem to another by only enabling
or disabling constraints. Notice that, as said before,
no changes in the search algorithm parameters have
been made for any experiment.
4.2 VRP Benchmarks
The second set of tests were performed to assess
the quality of the solutions found by the proposed
5
http://neo.lcc.uma.es/vrp/
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
126
C1
C2
C3
C4
C5
C6
C7
Depot
Figure 3: Configuration of the small-sized instance.
C1
C2
C3
C4
C5
C6
C7
Depot
CVRP
d
5
=80
d
2
=64
d
1
=59
d
6
=69
d
7
=75
d
3
=84
d
4
=70
Figure 4: Solution found for CVRP/AVRP.
C1
C2
C3
C4
C5
C6
C7
Depot
HVRP
d
2
= 64
d
1
= 59
d
3
= 84
d
4
= 70
d
5
= 80
d
7
= 75
d
6
= 69
Figure 5: Solution found for HVRP.
C1
C2
C3
C4
C5
C6
C7
Depot
DCVRP D t e t
Figure 6: Solution found for DCVRP.
methodology. Although this is not the main aim, we
consider it important to not be very far from the state-
of-the-art best-known solutions. Note that we use the
same framework for solving different types of prob-
lems while the best-known solutions are specific for
that kind of problem.
For this, for every instance of each classical
benchmark set mentioned in Section 3, 50 runs with
different random seeds have been carried out. The
results are summarised in Table 3, where the compar-
isons between our methodology and the best-known
solutions are shown. For each benchmark, the num-
ber of problem instances and their size, according to
the number of customers and vehicles, has been indi-
cated. In the column “CSTR”, the type of constraints
activated for that benchmark is mentioned.
In the last two columns, we compare the quality of
the solutions found by our methodology with the best-
known solutions. We calculate the difference between
the average values of 50 runs and the best-known for
each instance. Then, we present the percentage gap
calculated over all instances for the given benchmark
set. In the same way, the difference is calculated by
consideringthe best of our solutions for each instance.
In this work, the computational time is not compared
because the methods used to obtain the best-known
solutions are vastly different from each other and in
some cases the timing is unknown.
In the CVRP experiment, the fleet size of each
problem instance was fixed to the minimum feasible
value specified in that instance. However, five in-
stances were too complex to be solved in a limited
time. For these instances
6
, the computations were
based on solutions using an additional vehicle.
To evaluate the results for HVRP, we compared
our results with the best-known solutions published
in (C´aceres Cruz, 2013) which are obtained in the
same situation according to the same objective func-
tion. Except the problem instance 13, all instances
were tested with the same type of vehicles introduces
in the standard benchmark.
Although our results are far from the best-known
solutions, the flexibility of the approach is promising.
We hope that using the CP solver to search the solu-
tion space as opposed to just verifying the feasibility
of the solutions, would improve the quality of the re-
sults.
The aim in the DCVRP experiment was to show
that the framework could work properly and find an
acceptable solution by adding a new constraint to the
problem. We selected six problems from the same
data set used for the CVRP tests ranging from small
to large size instances and imposed capacity and dis-
tance limitations. The results are summarised in Table
4. The best values of 50 runs for each instances are
shown in the table for both DCVRP and CVRP. The
results show that the algorithm can adapt to the new
situation without any modification in the ACO part.
5 CONCLUSIONS AND FUTURE
WORK
In this work we have presented a flexible hybrid
methodology to solve VRPs. The methodology fol-
6
P-n23-k8, P-n50-k8, P-n51-k10, P-n55-k15, P-n60-
k15.
ACO and CP Working Together to Build a Flexible Tool for the VRP
127
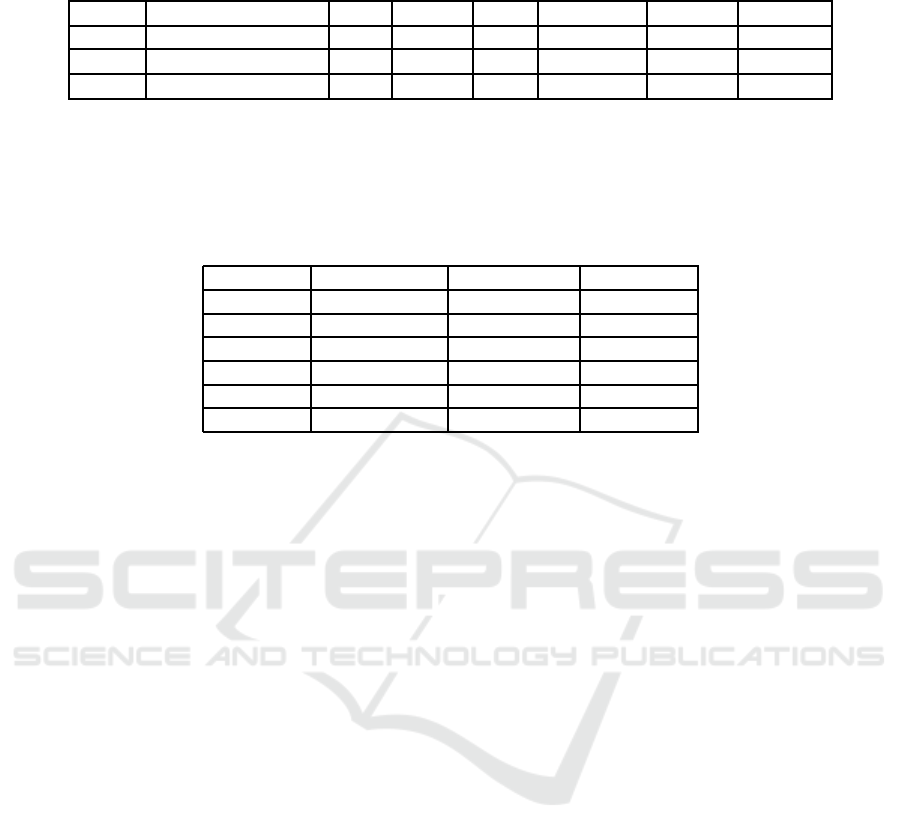
Table 3: Comparison between the proposed framework and the best-known solutions for three types of VRPs.
Prob Bench #Inst #Cust #Veh CSTR
a
Avg (%)
b
Best (%)
CVRP Augerat et al. setP 23 15-100 2-15 C 12.37%
c
6.68%
HVRP Taillard 8 50-100 7-17 C+H 26.89%
d
18.82%
AVRP Rodrguez et al. 14 50-100 2-6 C+A 13.26%
d
8.36%
a
The abbreviations are as follows: C = Capacity constraint, H = Heterogeneous fleet of vehicles, D = Distance
constraint, A = Asymmetric cost matrix.
b
Avg.(%), means the average of the solution deviations, each defined as ((AverageValue
50
runs− BKS)/BKS) × 100.
c
The fleet size was increased by one for five problem instances of the benchmark set.
d
The results were compared with the best solutions found in (C´aceres Cruz, 2013).
Table 4: Computational results for DCVRP.
Instances Distance limit DCVRP-Best CVRP-Best
P-n16-k8 < 70 451 452
P-n20-k2 < 125 217 219
P-n40-k5 < 135 538 497
P-n50-k7 < 130 618 600
P-n55-k10 < 120 734 632
P-n101-k4 < 330 804 760
lows a constructive strategy, building partial solutions
through the collaboration of a metaheuristic/heuristic
and a CP solver. This provides a straightforward way
to share the search space between the two approaches
and take advantage of the characteristics of both ap-
proaches.
The methodology has been tested on different
VRP benchmarks, and also with combinations built
by mixing a set of constraints. The results show the
flexibility of the framework in satisfying new con-
straints.
Currently we are including new constraints related
to time windows and the order clients are visited.
Once these constraints are added, the question that
we aim to answer is how to best share the problem
space between the CP solver and the metaheuristic
framework. More specifically, we would like to get
more feedbacks from the CP solver to guide the meta-
heuristic algorithm towards better solutions.
Other future work to be considered is the union of
ACO and CP in a single platform to avoid commu-
nication leaks, the inclusion of clustering techniques
in the problem, and an automatic ACO parameters’
tuning in order to improve its performance without
requiring additional effort from the final user.
ACKNOWLEDGEMENTS
The authors would like to thank Amir Hossein
Bakhtiary Davijani for his kind help and collabora-
tion during the experiments. This work has been
partially supported by the Spanish Ministry of Econ-
omy and Competitiveness (grant TRA2013-48180-
C3-P), FEDER, and the Department of Universities,
Research & Information Society of the Catalan Gov-
ernment (Grant 2014-CTP-00001).
NICTA is funded by the Australian Government
through the Department of Communications and the
Australian Research Council through the ICT Centre
of Excellence Program.
REFERENCES
Augerat, P., Belenguer, J. M., Benavent, E., Corbern, A.,
Naddef, D., and Rinaldi, G. (1995). Computational
results with a branch and cut code for the capacitated
vehicle routing problem. IMAG.
Balseiro, S. R., Loiseau, I., and Ramonet, J. (2011). An ant
colony algorithm hybridized with insertion heuristics
for the time dependent vehicle routing problem with
time windows. Computers & Operations Research,
38(6):954–966.
Berbeglia, G., Cordeau, J.-F., and Laporte, G. (2012). A
hybrid tabu search and constraint programming algo-
rithm for the dynamic dial-a-ride problem. INFORMS
Journal on Computing, 24(3):343355.
Blum, C., Puchinger, J., Raidl, G. R., and Roli, A. (2011).
Hybrid metaheuristics in combinatorial optimization:
A survey. Applied Soft Computing, 11(6):4135–4151.
C´aceres-Cruz, J., Arias, P., Guimarans, D., Riera, D., and
Juan, A. A. (2014). Rich Vehicle Routing Problem:
Survey. ACM Computing Surveys (CSUR), 47(2):32.
C´aceres Cruz, J. d. J. (2013). Randomized Algorithms for
Rich Vehicle Routing Problems: From a Specialized
Approach to a Generic Methodology. Doctoral thesis.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
128

Dorigo, M. and Birattari, M. (2010). Ant colony optimiza-
tion. In Encyclopedia of machine learning, pages 36–
39. Springer.
Drexl, M. (2012). Rich vehicle routing in theory and prac-
tice. Logistics Research, 5(1-2):4763.
Golden, B. L., Raghavan, S., and Wasil, E. A. (2008). The
Vehicle Routing Problem: Latest Advances and New
Challenges: latest advances and new challenges, vol-
ume 43. Springer.
Imran, A., Salhi, S., and Wassan, N. A. (2009). A variable
neighborhood-based heuristic for the heterogeneous
fleet vehicle routing problem. European Journal of
Operational Research, 197(2):509–518.
Khichane, M., Albert, P., and Solnon, C. (2008). Integration
of ACO in a constraint programming language. In Ant
Colony Optimization and Swarm Intelligence, pages
84–95. Springer.
Khichane, M., Albert, P., and Solnon, C. (2010). Strong
combination of ant colony optimization with con-
straint programming optimization. In Integration of
AI and OR Techniques in Constraint Programming for
Combinatorial Optimization Problems, pages 232–
245. Springer.
Laporte, G. (2009). Fifty years of vehicle routing. Trans-
portation Science, 43(4):408416.
Laporte, G., Gendreau, M., Potvin, J.-Y., and Semet, F.
(2000). Classical and modern heuristics for the ve-
hicle routing problem. International transactions in
operational research, 7(4-5):285300.
Laporte, G., Toth, P., and Vigo, D. (2013). Vehicle routing:
historical perspective and recent contributions. EURO
Journal on Transportation and Logistics, 2(1-2):14.
Meyer, B. and Ernst, A. (2004). Integrating ACO and con-
straint propagation. In Ant Colony Optimization and
Swarm Intelligence, pages 166–177. Springer.
Pisinger, D. and Ropke, S. (2007). A general heuristic for
vehicle routing problems. Computers & operations
research, 34(8):24032435.
Riera, D., Juan, A., Guimarans, D., and Pagans, E. (2009).
A constraint programming-based library for the vehi-
cle routing problem. In Proceedings of the 21st Eu-
ropean Modeling and Simulation Symposium (EMSS
2009), pages 261–266.
Rodr´ıguez, A. and Ruiz, R. (2012). A study on the ef-
fect of the asymmetry on real capacitated vehicle rout-
ing problems. Computers & Operations Research,
39(9):2142–2151.
Rossi, F., Van Beek, P., and Walsh, T. (2006). Handbook of
constraint programming. Elsevier.
Shaw, P. (2011). Constraint programming and local search
hybrids. In Hybrid Optimization, pages 271–303.
Springer.
Solnon, C. (2010). Ant colony optimization and constraint
programming. Wiley Online Library.
Talbi, E.-G. (2013). Hybrid metaheuristics. Springer.
Vidal, T., Crainic, T. G., Gendreau, M., and Prins, C.
(2013). A unified solution framework for multi-
attribute vehicle routing problems. European Journal
of Operational Research.
Yu, B. and Yang, Z. Z. (2011). An ant colony optimization
model: The period vehicle routing problem with time
windows. Transportation Research Part E: Logistics
and Transportation Review, 47(2):166181.
ACO and CP Working Together to Build a Flexible Tool for the VRP
129
