
Integer Linear Programming Approach to Median and Center Strings
for a Probability Distribution on a Set of Strings
Morihiro Hayashida
1
and Hitoshi Koyano
2
1
Bioinformatics Center, Institute for Chemical Research, Kyoto University, Gokasho, Uji, Kyoto 611-0011, Japan
2
Graduate School of Medicine, Kyoto University, 54 Kawahara-cho, Shogoin, Sakyo-ku, Kyoto 606-8397, Japan
Keywords:
Median String, Center String, Integer Linear Programming.
Abstract:
We address problems of finding median and center strings for a probability distribution on a set of strings
under Levenshtein distance, which are known to be NP-hard in a special case. There are many applications in
various research fields, for instance, to find functional motifs in protein amino acid sequences, and to recognize
shapes and characters in image processing. In this paper, we propose novel integer linear programming-based
methods for finding median and center strings for a probability distribution on a set of strings under Leven-
shtein distance. Furthermore, we restrict several variables to a region near the diagonal in the formulation,
and propose novel integer linear programming-based methods also for finding approximate median and center
strings for a probability distribution on a set of strings. For evaluation of our proposed methods, we perform
several computational experiments, and show that the restricted formulation reduced the execution time.
1 INTRODUCTION
It is a fundamental statistical method for understand-
ing a data set to take an average. In this paper, we
focus on a set of strings. For instance, nucleotide
sequences of DNAs and RNAs are represented by
strings as well as protein amino acid sequences. The
number of such sequences has rapidly increased, and
analytical methods are required. In the field of evo-
lutionary studies of organisms, it would be an aim
to find genetic information, nucleotide sequences of
common ancestors. In the field of protein science, it
is essential to find functional motifs in protein amino
acid sequences. Also in the field of image recog-
nition, there are several applications such as post-
processing of optical character recognition (OCR) re-
sults (Bunke et al., 2002) and shape recognition(Chen
et al., 1998). Furthermore, it can be applied to clas-
sification and clustering of strings and biological se-
quences (Mart´ınez-Hinarejos et al., 2003).
Several definitions have been proposed for repre-
senting an average of strings because the average is
not uniquely determined. One is a median string,
which is defined as a string that minimizes the sum
of distances with strings included in a set (Koho-
nen, 1985). One is a center string, which is de-
fined as a string that minimizes the maximum of dis-
tances with strings (Gusfield, 1997). As distances be-
tween two strings, several distances such as Leven-
shtein distance (Levenshtein, 1965), Hamming dis-
tance (Hamming, 1950), and Jaro-Winkler distance
(Winkler, 1990) have been proposed, where the Jaro-
Winkler distance is known not to obey the triangle in-
equality. The Levenshteindistance between two given
strings s and t allows three types of edit operations,
insertion, deletion, substitution, and can be calculated
in polynomial time O(|s||t|) using dynamic program-
ming, where |s| denotes the length of s. The Hamming
distance has been also used for closest strings and re-
lated problems (Gramm, 2003; Gramm et al., 2003).
Data reduction techniques that reduce candidates of
a center string under the Hamming distance were de-
veloped (Hufsky et al., 2011). However, they men-
tioned that their parameterized methods would be not
applicable for finding center strings under the Leven-
shtein distance. A genetic algorithm for finding clos-
est strings under rank distance was developed (Dinu
and Ionescu, 2012), where the rank distance has been
applied in biology, natural language processing, and
authorship attribution.
The problems of finding the median and center
strings for a finite set of strings under the Levenshtein
distance have been proved to be NP-complete for
an unbounded alphabet (de la Higuera and Casacu-
berta, 2000), and even for a binary alphabet (Nicolas
and Rivals, 2003; Nicolas and Rivals, 2005). It has
Hayashida, M. and Koyano, H.
Integer Linear Programming Approach to Median and Center Strings for a Probability Distribution on a Set of Strings.
DOI: 10.5220/0005666400350041
In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 3: BIOINFORMATICS, pages 35-41
ISBN: 978-989-758-170-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
35

been proved that a related problem CSCE is also NP-
complete when a penalty matrix is a metric (Sim and
Park, 2003). An exact algorithm for finding the me-
dian string under the Levenshtein distance using dy-
namic programming was proposed (Kruskal, 1983),
which requires N-dimensional array and O(n
N
) time
and space for a set of N strings with length n, for
example, it requires 10
10
· 4 bytes = 40GB memory
for n = N = 10. For computing approximate me-
dian strings in practical time, several methods have
been proposed. If given strings are all quite similar,
the path by the optimal dynamic programming should
be close to the main diagonal. Hence, the method
to restrict candidate paths to a region near the di-
agonal was proposed (Lopresti and Zhou, 1997). A
greedy algorithm starts from an empty string, and se-
lects a letter that minimizes the exact consensus error
(Casacuberta and de Antoni, 1997). An online algo-
rithm takes the current approximate median string and
a new string, and calculates a weighted mean of these
strings (Jiang et al., 2003). In a stochastic approach,
some conditional probability from a string to an-
other was defined, and an approximate median string
was obtained by expectation maximization technique
(Olivares-Rodr´ıguez and Oncina, 2008). An iterative
algorithm applies the edit operation with some high-
est score to the current string until a better solution is
not found (Abreu and Rico-Juan, 2014). These meth-
ods output approximate median strings, and there are
a few methods to output optimal median strings. As
far as we know, methods for finding optimal cen-
ter strings have not been developed. In this paper,
hence, we propose an approach using integer linear
programming for finding optimal median and center
strings because efficient solvers for integer linear pro-
gramming problems have been developed. In addi-
tion, we introduce a probability distribution on a set
of strings (Koyano and Kishino, 2010), and propose
methods for finding median and center strings of such
a probability distribution under the Levenshtein dis-
tance. Furthermore, we propose integer linear pro-
gramming formulations restricted to a region near the
diagonal for finding approximate median and center
strings. We perform several computational experi-
ments and verify the efficiency of our methods.
2 METHODS
We use the Levenshtein distance because it is often
used and a fundamental edit distance. In this sec-
tion, we briefly review the computation of the Lev-
enshtein distance, median, center strings, and pro-
pose integer linear programming formulations for ex-
act and approximate median and center strings. Let
A = {a
1
,... ,a
z
} be an alphabet composed of z letters,
for instance, A = {A,T,G,C} for DNA nucleotide se-
quences. We define A
∗
to be the set of all strings on
A with varying lengths, and for a string s ∈ A
∗
, |s|
denotes the length of s.
2.1 Levenshtein Distance
The Levenshtein distance d(s,t) between two strings
s and t is defined as the minimum cost of sequences
of edit operations transforming s = s
1
·· ·s
n
into t =
t
1
·· ·t
m
, and can be calculated by the following dy-
namic programming (Wagner and Fischer, 1974).
D[0,0] = 0, (1)
D[i, j] = min
D[i− 1, j − 1] + γ(s
i
→ t
j
)
D[i− 1, j] + γ(s
i
→ ε)
D[i, j− 1] + γ(ε → t
j
)
(2)
where ε denotes an empty letter, γ(s
i
→ t
j
), γ(s
i
→ ε),
and γ(ε → t
j
) denote the costs of substitution, dele-
tion, and insertion, respectively. Then, D[n,m] is the
Levenshtein distance d(s,t).
2.2 Median and Center Strings
Given N strings s
(k)
with length n
k
(k = 1,..., N) on
A
∗
, the median string is defined by
argmin
t∈A
∗
N
∑
k=1
d(t,s
(k)
). (3)
Similarly, the center string is defined by
argmin
t∈A
∗
max
k∈{1,...,N}
d(t,s
(k)
). (4)
For a given probability distribution p(s) on A
∗
, we
define median and center strings by
argmin
t∈A
∗
∑
s∈A
∗
p(s)d(t,s), (5)
argmin
t∈A
∗
max
s∈A
∗
p(s)d(t,s), (6)
respectively. If p(s
(k)
) =
1
N
for k = 1,. .. , N and
p(s) = 0 for all s /∈ {s
(k)
}, Eqs (3) and (4) are equiva-
lent to Eqs (5) and (6), respectively.
2.3 Integer Linear Programming
Formulation
Since it is known that problems of finding median and
center strings under the Levenshtein distance are NP-
hard (Nicolas and Rivals, 2003; Nicolas and Rivals,
2005), we make use of integer linear programming
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
36

x
k,1,0
x
k,i+1,j
x
kij
y
k,i,j+1
y
kij
z
kij
z
k,i+1,j+1
y
k,0,1
x
kn
k
m
y
kn
k
m
z
k,1,1
s
1
(k)
s
n
k
(k)
t
1
t
j
t
m
z
kn
k
m
s
i
(k)
t
l
t
m
y
kn
k
j
=1
s
n
k
(k)
Figure 1: Illustration on variables appeared in our integer
linear programming formulation. (Left) Variables x
ki j
, y
ki j
,
and z
ki j
represent a path in dynamic programming for calcu-
lating the Levenshtein distance if the value of its variable is
equal to 1. (Right) Variable l represents the length of string
t. For all j > l, y
kn
k
j
is forced to be 1.
which efficient solvers have been developed. We can
find a median string t by integer linear programming
if the Levenshtein distance d(t,s
(k)
) between t and
s
(k)
can be calculated in linear formulas. It, however,
is difficult to directly represent the array D[i, j] in
the dynamic programming by integer linear program-
ming because it includes the selection of the mini-
mum value in Eq. (2).
Suppose that a probability distribution p(s) on A
∗
is given, where the number of strings s satisfying
p(s) > 0 is finite, N, that is, p(s
(k)
) > 0 (k = 1, .. ., N).
We use integer numbers 1,...,|A | instead of letters
in A because a variable takes a value in linear pro-
gramming. s
(k)
i
(i = 1, .. .,n
k
) is given as a constant
value of 1,. .. ,|A |, and represents the i-th letter in
s
(k)
. t
j
( j = 1,..., m) is a variable taking a value of
1,..., |A|. Then, we propose the following integer
linear programming formulation, called ILPMed, for
finding the median string for p(s) under the Leven-
shtein distance with costs C
sub
, C
del
, C
ins
of substitu-
tion, deletion, insertion (see Fig. 1).
min
N
∑
k=1
p(s
(k)
)
n
n
k
∑
i=1
C
del
x
k,i,0
+
m
∑
j=1
C
ins
y
k,0, j
+
n
k
∑
i=1
m
∑
j=1
(C
del
x
kij
+C
ins
y
kij
+C
sub
h
kij
)
o
−C
ins
(m− l)
subject to
for all k = 1, .. ., N,
1 = x
k,1,0
+ y
k,0,1
+ z
k,1,1
, (a1)
x
k,i,0
= x
k,i+1,0
+ y
k,i,1
+ z
k,i+1,1
for all i < n
k
, (a2)
x
k,n
k
,0
= y
k,n
k
,1
, (a3)
y
k,0, j
= x
k,1, j
+ y
k,0, j+1
+ z
k,1, j+1
for all j < m, (a4)
y
k,0,m
= x
k,1,m
, (a5)
x
kij
+ y
kij
+ z
kij
= x
k,i+1, j
+ y
k,i, j+1
+ z
k,i+1, j+1
for all i < n
k
, j < m, (a6)
x
kn
k
j
+ y
kn
k
j
+ z
kn
k
j
= y
k,n
k
, j+1
for all j < m, (a7)
x
kim
+ y
kim
+ z
kim
= x
k,i+1,m
for all i < n
k
, (a8)
x
kn
k
m
+ y
kn
k
m
+ z
kn
k
m
= 1, (a9)
y
kn
k
j
≥
1
m
( j − l) for all j, (b)
for all k, i, j,
s
(k)
i
− t
j
≤ |A |g
kij
, (c1)
t
j
− s
(k)
i
≤ |A |g
kij
, (c2)
h
kij
≥ z
kij
+ g
kij
− 1, (d1)
h
kij
≤
1
2
(z
kij
+ g
kij
), (d2)
x
kij
,y
kij
,z
kij
,g
kij
,h
kij
∈ {0,1},
t
j
∈ {1,...,|A|}, 0 ≤ l ≤ m,
where m is a sufficient large constant integer, that is,
the sum of n
k
, and l is the variable representing the
length of median string.
In the formulation, variable x
kij
takes 1 if s
(k)
i
is
deleted, otherwise 0. y
kij
takes 1 if t
j
is inserted, oth-
erwise 0. z
kij
takes 1 if s
(k)
i
is substituted with t
j
, oth-
erwise 0. There must be exactly one path from the
upper left to the lower right for each string s
(k)
. If ei-
ther of x
kij
, y
kij
, and z
kij
is 1, either of x
k,i+1, j
, y
k,i, j+1
,
and z
k,i+1, j+1
must be 1, which is represented by Eq.
(a6). According to the position (i, j), Eqs (a1-9) are
constructed. Eq. (b) represents the constraint that the
length of median string t is l, and y
kn
k
j
is forced to be
1 if j > l. It is difficult to represent the Levenshtein
distance d(t,s
(k)
) =
∑
n
k
i=1
C
del
x
k,i,0
+
∑
l
j=1
C
ins
y
k,0, j
+
∑
n
k
i=1
∑
l
j=1
(C
del
x
kij
+C
ins
y
kij
+C
sub
h
kij
) in the formu-
lation because l is also a variable to be found. Hence,
we use a constant integer m instead of l. Then, the
sum includes the extra cost of C
ins
(m− l). We reduce
the cost such that the objective function represents the
sum in Eq. (5). It should be noted that for all j > l,
y
kn
k
j
is forced to be 1. Eqs (c1-2) represent that g
kij
becomes 1 if s
(k)
i
is the same as t
j
. Eqs (d1-2) repre-
sent that h
kij
becomes 1 if and only if both of z
kij
and
g
kij
are 1. It means that the substitution cost from s
(k)
i
to t
j
is C
sub
if s
(k)
i
6= t
j
, otherwise 0.
It is guaranteed that we can find the median string
for p(s) under the Levenshtein distance by solving
this integer linear programming formulation because
the objective function is equivalent to the sum in Eq.
(5), t can be any string with length up to m =
∑
N
k=1
n
k
,
and the sum for a string with length more than m is
larger than that for the concatenated string of all s
(k)
.
In a similar way to median strings, we propose
the following integer linear programming formula-
Integer Linear Programming Approach to Median and Center Strings for a Probability Distribution on a Set of Strings
37
tion, called ILPCen, for finding the center string for
a probability distribution p(s).
min d
subject to
for all k = 1, .. ., N,
p(s
(k)
)
n
n
k
∑
i=1
C
del
x
k,i,0
+
m
∑
j=1
C
ins
y
k,0, j
+
n
k
∑
i=1
m
∑
j=1
(C
del
x
kij
+C
ins
y
kij
+C
sub
h
kij
) −C
ins
(m− l)
o
≤ d,
1 = x
k,1,0
+ y
k,0,1
+ z
k,1,1
,
x
k,i,0
= x
k,i+1,0
+ y
k,i,1
+ z
k,i+1,1
for all i < n
k
,
x
k,n
k
,0
= y
k,n
k
,1
,
y
k,0, j
= x
k,1, j
+ y
k,0, j+1
+ z
k,1, j+1
for all j < m,
y
k,0,m
= x
k,1,m
,
x
kij
+ y
kij
+ z
kij
= x
k,i+1, j
+ y
k,i, j+1
+ z
k,i+1, j+1
for all i < n
k
, j < m,
x
kn
k
j
+ y
kn
k
j
+ z
kn
k
j
= y
k,n
k
, j+1
for all j < m,
x
kim
+ y
kim
+ z
kim
= x
k,i+1,m
for all i < n
k
,
x
kn
k
m
+ y
kn
k
m
+ z
kn
k
m
= 1,
y
kn
k
j
≥
1
m
( j − l) for all j,
for all k, i, j,
s
(k)
i
− t
j
≤ |A |g
kij
,
t
j
− s
(k)
i
≤ |A |g
kij
,
h
kij
≥ z
kij
+ g
kij
− 1,
h
kij
≤
1
2
(z
kij
+ g
kij
),
x
kij
,y
kij
,z
kij
,g
kij
,h
kij
∈ {0,1},
t
j
∈ {1,. .. ,|A |},
0 ≤ l ≤ m, d ≥ 0.
Here, d is a variable that represents the minimum in
Eq.(6).
If strings s
(k)
are similar to each other, we can
restrict candidate paths to a region near the diago-
nal without loss of optimality. We introduce an con-
stant positive integer w, and propose integer linear
programming formulations, called ILPMedDiag and
ILPCenDiag, by reducing variables, x
kij
, y
kij
, z
kij
,
g
kij
, and h
kij
with |i− j| > w from ILPMed and ILP-
Cen, respectively.
3 COMPUTATIONAL
EXPERIMENTS
For the evaluation of our methods, we performed
several computational experiments. We used C
del
=
C
ins
= C
sub
= 1 to calculate the Levenshtein distance,
and used an alphabet A with 4 letters as DNA and
RNA nucleotide sequences. We randomly gener-
ated two types of probability distributions, p
1
(s) and
p
2
(s), on A
∗
. In p
1
(s), N strings s
(k)
with length n
k
were generated as strings satisfying p
1
(s) > 0 while
varying N = 2, .. ., 10 and n
k
= 2,. .. ,10, where n
k
was the same for all k = 1,. .. ,N. Each s
(k)
i
was gen-
erated as min(1 + ⌊|α|⌋, |A|), where α followed the
normal distribution with mean 0 and variance 1, and
⌊α⌋ is the largest integer not greater than α. The prob-
ability of p
1
(s
(k)
) was generated uniquely at random
such that
∑
N
k=1
p
1
(s
(k)
) = 1 holds. In p
2
(s), N strings
s
(k)
were generated from a string of a
1
·· ·a
1
(a
1
∈ A )
with length n by applying randomly selected edit op-
erations of substitution, insertion, and deletion, three
times, where we examined N = 2,. .. , 10 and n =
5,...,10, and the length n
k
of s
(k)
could be different
according to k. The probability of p
2
(s
(k)
) was gener-
ated uniquely at random such that
∑
N
k=1
p
2
(s
(k)
) = 1
holds. For each case of p
1
(s), p
2
(s), n
k
, and N,
we generated a set of N strings s
(k)
with p
1
(s
(k)
) or
p
2
(s
(k)
) ten times, and took the average of execution
times. We used CPLEX (version 12.5) as the inte-
ger linear programming solver under a linux operat-
ing system with Xeon 2.9GHz processor and 35GB
memory.
2
3
4
5
6
7
8
9
10
2
3
4
5
6
7
8
9
10
0.01
0.1
1
10
100
1000
10000
100000
Elapsed time (sec)
ILPMed
ILPMedDiag
Length
# strings
Elapsed time (sec)
(a) median string
2
3
4
5
6
7
8
9
10
2
3
4
5
6
7
8
9
10
0.01
0.1
1
10
100
1000
10000
Elapsed time (sec)
ILPCen
ILPCenDiag
Length
# strings
Elapsed time (sec)
(b) center string
Figure 2: Results on the average execution time in seconds
on a log scale by ILPMed, ILPMedDiag with w = 2, ILP-
Cen, and ILPCenDiag with w = 2 for probability distribu-
tions p
1
(s) for N = 2, ... ,10 and n
k
= 2, ..., 10. (a) For
finding median strings. (b) For finding center strings.
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
38
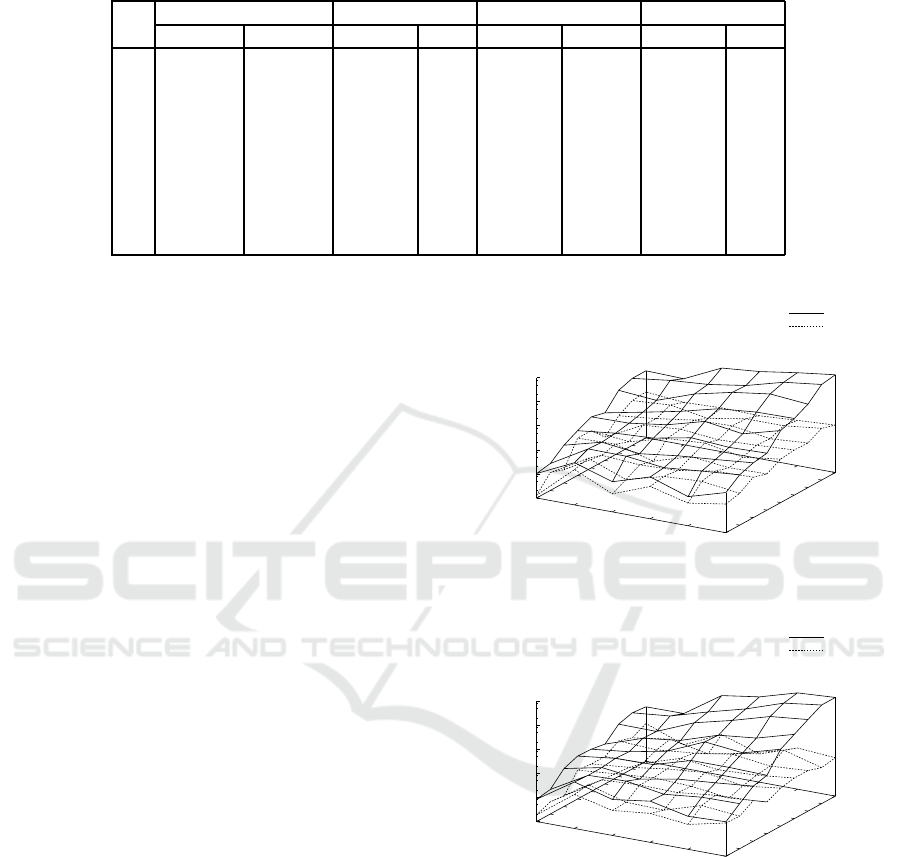
Table 1: Results on the average and standard deviation of execution time in seconds by ILPMed, ILPMedDiag with w = 2,
ILPCen, and ILPCenDiag with w = 2 for probability distributions p
1
(s) for n = 10 and N = 2,. ..,10.
N ILPMed ILPMedDiag ILPCen ILPCenDiag
average s.d. average s.d. average s.d. average s.d.
2 14.4 6.8 1.7 1.8 6.4 1.9 3.8 2.5
3 21.5 10.5 7.0 4.4 18.1 7.4 7.0 5.1
4 23.7 15.3 7.0 4.5 72.1 27.2 5.5 4.0
5 168.0 69.0 15.7 3.6 464.8 312.8 8.8 4.8
6 798.6 280.4 21.7 8.3 1015.6 580.6 6.9 3.0
7 1400.6 773.3 41.6 20.5 2810.3 1218.8 10.7 4.4
8 11269.8 9074.5 61.0 39.2 5936.2 3522.8 20.4 9.5
9 22438.1 16417.6 37.7 17.9 5086.0 1358.6 23.9 10.5
10 18467.8 16625.5 67.4 22.8 8120.3 4336.0 41.1 29.5
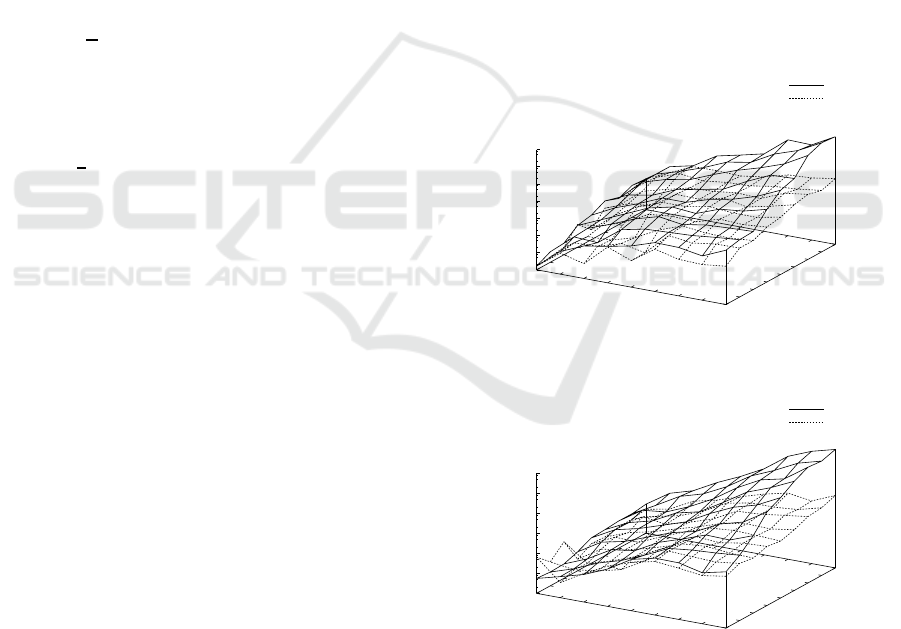
Fig. 2 shows results on the average execution time
in seconds on a log scale by ILPMed, ILPMedDiag
with w = 2, ILPCen, and ILPCenDiag with w = 2
for probability distributions p
1
(s) for N = 2, .. .,10
and n
k
= 2,. .. ,10. Table 1 shows the detailed av-
erage and standard deviation of execution time by
ILPMed, ILPMedDiag, ILPCen, and ILPCenDiag for
n = 10. We can see from these that the average exe-
cution times by ILPMed and ILPCen rapidly, almost
exponentially, increased with both of the number N
of strings and the length n
k
because the problems are
NP-hard. On the other hand, the average execution
times by ILPMedDiag and ILPCenDiag were smaller
than those by ILPMed and ILPCen, respectively, be-
cause candidate solutions for the problems were re-
stricted to the region near the diagonal.
Fig. 3 shows results on the average execution time
in seconds on a log scale by ILPMed, ILPMedDiag
with w = 2, ILPCen, and ILPCenDiag with w = 2
for probability distributions p
2
(s) for N = 2, .. .,10
and n = 5, .. ., 10. Table 2 shows the detailed av-
erage and standard deviation of execution time by
ILPMed, ILPMedDiag, ILPCen, and ILPCenDiag for
n = 10. Also for p
2
(s), the average execution times
by ILPMedDiag and ILPCenDiag were smaller than
those by ILPMed and ILPCen, respectively. The
slopes of ILPMed and ILPCen along the length for
p
2
(s) were smaller than those for p
1
(s), respectively.
In addition, the average execution times for p
2
(s)
were smaller than those for p
1
(s). It, however, is con-
sidered that ILPMed and ILPCen might be not suffi-
cient to be applied to actual data for finding their op-
timal median and center strings. Fig. 4 shows results
on the average objective value by ILPMed, ILPMed-
Diag with w = 2, ILPCen, and ILPCen with w = 2
for probability distributions p
2
(s) for N = 2, .. .,10
and n = 5, .. .,10. It is noted that the objective val-
ues by ILPMed and ILPCen for p
1
(s) were almost
the same as those by ILPMedDiag and ILPCenDiag,
respectively. In p
2
(s), three edit operations were ap-
5
6
7
8
9
10
2
3
4
5
6
7
8
9
10
0.1
1
10
100
1000
10000
Elapsed time (sec)
ILPMed
ILPMedDiag
Length
# strings
Elapsed time (sec)
(a) median string
5
6
7
8
9
10
2
3
4
5
6
7
8
9
10
0.1
1
10
100
1000
10000
Elapsed time (sec)
ILPCen
ILPCenDiag
Length
# strings
Elapsed time (sec)
(b) center string
Figure 3: Results on the average execution time in seconds
on a log scale by ILPMed, ILPMedDiag with w = 2, ILP-
Cen, and ILPCenDiag with w = 2 for probability distribu-
tions p
2
(s) for N = 2,.. .,10 and n = 5, ... ,10.
plied to strings, and differences of objective values
between ILPMed and ILPMedDiag with w = 2, and
between ILPCen and ILPCenDiag with w = 2, oc-
curred. We can obtain optimal strings using ILPMed-
Diag and ILPCenDiag by increasing the width w of
diagonal.
Integer Linear Programming Approach to Median and Center Strings for a Probability Distribution on a Set of Strings
39
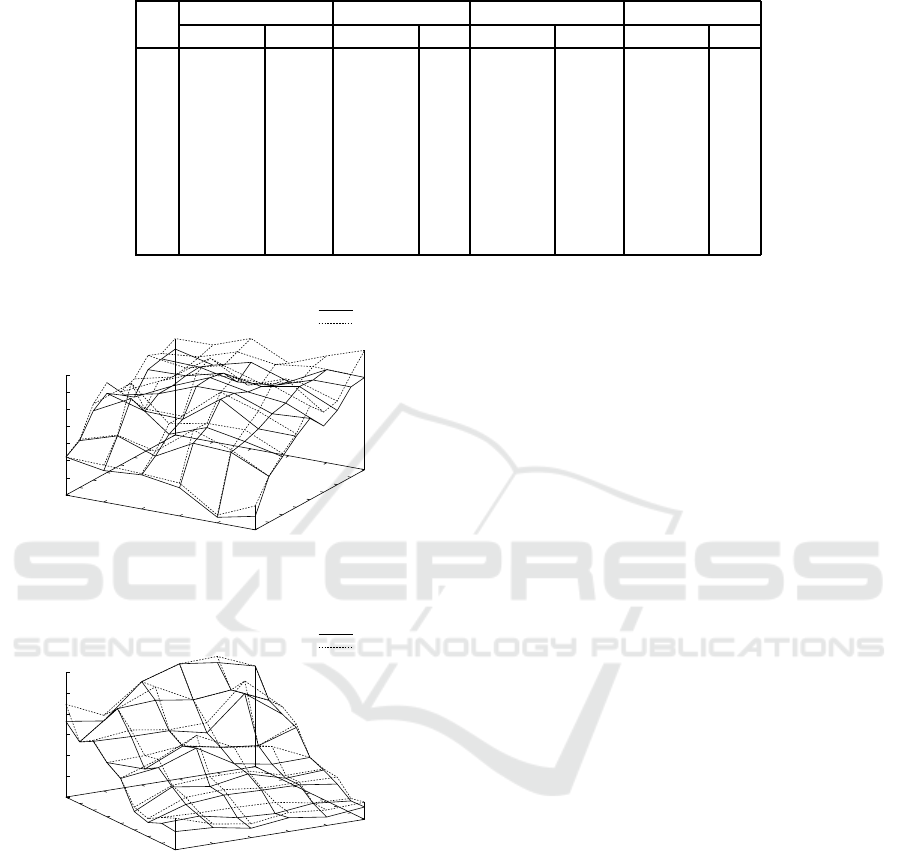
Table 2: Results on the average and standard deviation of execution time in seconds by ILPMed, ILPMedDiag with w = 2,
ILPCen, and ILPCenDiag with w = 2 for probability distributions p
2
(s) for n = 10 and N = 2,. ..,10.
N ILPMed ILPMedDiag ILPCen ILPCenDiag
average s.d. average s.d. average s.d. average s.d.
2 4.7 3.2 1.6 2.4 2.7 2.8 2.4 2.8
3 12.4 7.8 2.1 2.5 7.5 4.5 2.3 2.6
4 18.9 11.5 4.8 5.3 19.5 13.9 4.9 3.1
5 23.3 23.2 3.2 2.5 26.6 20.0 2.1 2.4
6 98.6 76.1 6.4 3.9 157.0 110.7 3.8 2.6
7 154.3 120.0 7.5 4.0 320.4 257.5 4.9 4.1
8 293.7 170.0 7.1 6.5 641.3 425.0 4.8 4.4
9 943.4 747.9 14.1 8.4 1259.2 676.6 3.1 3.3
10 1160.4 276.1 9.4 5.5 1266.7 488.1 3.9 3.6
5
6
7
8
9
10
2
3
4
5
6
7
8
9
10
0.8
1
1.2
1.4
1.6
1.8
2
2.2
Objective
ILPMed
ILPMedDiag
Length
# strings
Objective
(a) median string
5
6
7
8
9
10
2
3
4
5
6
7
8
9
10
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Objective
ILPCen
ILPCenDiag
Length
# strings
Objective
(b) center string
Figure 4: Results on the average objective value by
ILPMed, ILPMedDiag with w = 2, ILPCen, and ILPCen
with w = 2 for probability distributions p
2
(s) for N =
2,.. ., 10 and n = 5,... ,10.
4 CONCLUSION
We extended the definitions of median and center
strings, which problems are known to be NP-hard,
to those over a probability distribution p(s) on a
set of strings A
∗
, and proposed novel integer linear
programming-based methods, ILPMed, and ILPCen,
for finding median and center strings for p(s) on A
∗
,
and ILPMedDiag, ILPCenDiag for finding approxi-
mate median and center strings for p(s) on A
∗
by re-
stricting several variables of ILPMed and ILPCen to
a region near the diagonal. We performed computa-
tional experiments, and confirmed that the execution
times by ILPMedDiag and ILPCenDiag were smaller
than those by ILPMed and ILPCen, respectively, and
ILPMedDiag and ILPCenDiag reduced the execution
times. ILPMed and ILPCen, however, might be not
sufficient to be applied to actual data for finding their
optimal median and center strings. It is considered
because the number of candidate paths from the up-
per left to the lower right in ILPMed and ILPCen is
enormous and should be selected by solvers although
the Levenshtein distance between two strings can be
calculated in polynomial time. On the other hand,
ILPMedDiag and ILPCenDiag are considered to be
useful if given strings are similar to each other be-
cause the number of such candidate paths in ILPMed-
Diag and ILPCenDiag is small. As future work, we
need to analyze computational time and space com-
plexities for our proposed methods. Furthermore, we
would like to improve our methods by introducing
other types of restriction to the variables than those
in ILPMedDiag and ILPCenDiag. In addition, we
will consider decomposition of strings, linear pro-
gramming relaxation, and utilize approximate solu-
tions obtained by ILPMedDiag and ILPCenDiag in
order to find optimal solutions by ILPMed and ILP-
Cen.
ACKNOWLEDGEMENTS
This work was partially supported by Grants-in-Aid
#24500361, and #26610037 from MEXT, Japan.
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
40

REFERENCES
Abreu, J. and Rico-Juan, J. (2014). A new iterative algo-
rithm for computing a quality approximate median of
strings based on edit operations. Pattern Recognition
Letters, 36:74–80.
Bunke, H., Jiang, X., Abegglen, K., and Kandel, A. (2002).
On the weighted mean of a pair of strings. Pattern
Analysis and Applications, 5:23–30.
Casacuberta, F. and de Antoni, M. (1997). A greedy al-
gorithm for computing approximate median strings.
pages 193–198.
Chen, S., Tung, S., Fang, C., Cherng, S., and Jain, A.
(1998). Extended attributed string matching for shape
recognition. Computer Vision and Image Understand-
ing, 70:36–50.
de la Higuera, C. and Casacuberta, F. (2000). Topology of
strings: Median string is NP-complete. Theoretical
Computer Science, 230:39–48.
Dinu, L. and Ionescu, R. (2012). An efficient rank based
based approach for closest string and closest sub-
string. PLoS ONE, 7(6):e37576.
Gramm, J. (2003). Fixed-parameter algorithms for the con-
sensus analysis of genomic data. PhD thesis, Univer-
sit¨at T¨ubingen.
Gramm, J., Niedermeier, R., and Rossmanith, P. (2003).
Fixed-parameter algorithms for closest string and re-
lated problems. Algorithmica, 37:25–42.
Gusfield, D. (1997). Algorithms on strings, trees and se-
quences. Cambridge University Press.
Hamming, R. (1950). Error detecting and error correcting
codes. The Bell System Technical Journal, 29(2):147–
160.
Hufsky, F., Kuchenbecker, L., Jahn, K., Stoye, J., and
B¨ocker, S. (2011). Swiftly computing center strings.
BMC Bioinformatics, 12:106.
Jiang, X., Abegglen, K., Bunke, H., and Csirik, J. (2003).
Dynamic computation of generalised median strings.
Pattern Analysis and Applications, 6:185–193.
Kohonen, T. (1985). Median strings. Pattern Recognition
Letters, 3:309–313.
Koyano, H. and Kishino, H. (2010). Quantifying biodiver-
sity and asymptotics for a sequence of random strings.
Physical Review E, 81(6):061912.
Kruskal, J. (1983). An overview of sequence comparison:
Time warps, string edits, and macromolecules. SIAM
Reviews, 25(2):201–237.
Levenshtein, V. (1965). Binary codes capable of correcting
deletions, insertions and reversals. Doklady Adademii
Nauk SSSR, 163(4):845–848.
Lopresti, D. and Zhou, J. (1997). Using consensus sequence
voting to correct OCR errors. Computer Vision and
Image Understanding, 67(1):39–47.
Mart´ınez-Hinarejos, C., Juan, A., and Casacuberta, F.
(2003). Median strings for k-nearest neighbour clas-
sification. Pattern Recognition Letters, 24:173–181.
Nicolas, F. and Rivals, E. (2003). Complexities of the centre
and median string problems. Lecture Notes in Com-
puter Science, 2676:315–327.
Nicolas, F. and Rivals, E. (2005). Hardness results for the
center and median string problems under the weighted
and unweighted edit distances. Journal of Discrete
Algorithms, 3:390–415.
Olivares-Rodr´ıguez, C. and Oncina, J. (2008). A Stochastic
Approach to Median String Computation, pages 431–
440. Springer, Berlin.
Sim, J. S. and Park, K. (2003). The consensus string prob-
lem for a metric is NP-complete. Journal of Discrete
Algorithms, 1:111–117.
Wagner, R. and Fischer, M. (1974). The string-to-string
correction problem. Journal of the ACM, 21(1):168–
173.
Winkler, W. (1990). String comparator metrics and en-
hanced decision rules in the Fellegi-Sunter model of
record linkage. pages 354–359.
Integer Linear Programming Approach to Median and Center Strings for a Probability Distribution on a Set of Strings
41
