
Techniques to Control Robot Action Consisting of Multiple Segmented
Motions using Recurrent Neural Network with Butterfly Structure
Wataru Torii, Shinpei Fujimoto, Masahiro Furukawa, Hideyuki Ando and Taro Maeda
Information Science, Graduate School of Osaka University, Yamadaoka 2-1, 560-0871, Suita-shi, Osaka, Japan
Keywords:
Robot Manipulation, RNN, FFT Butterfly, Associative Memory, ”Tsumori”.
Abstract:
In the field of robot control, there have been several studies on humanoid robots operating in remote areas. We
propose a methodology to control a robot using input from an operator with fewer degrees of freedom than
the robot. This method is based on the concept that time-continuous actions can be segmented because human
intentions are discrete in the time domain. Additionally, machine learning is used to determine components
with a high correlation to input data that are often complex or large in quantity. In this study, we implemented
a new structure on a conventional neural network to manipulate a robot using a fast Fourier transform. The
neural network was expected to acquire robustness for amplitude and phase variations. Thus, our model can
reflect a fluctuating operator input to control a robot. We applied the proposed neural network to manipulate a
robot and verified the validity and performance compared with traditional models.
1 INTRODUCTION
1.1 Robot Manipulation
Since humanoid robots with numerous degrees of
freedom (DOFs) were first developed (Hirai et al.,
1998), a variety of studies on robot control methods
have been conducted. To manipulate such robots, we
developed the Tsumori system (Niwa et al., 2010).
It is known that the voluntary actions of human
beings have discrete time-segmented structures (Ya-
mamoto and Fujinami, 2004). According to our re-
search, the reason for this phenomenon is that human
memory has a discretesegmented structure in the time
domain, and discrete memory segments have a one-
to-one correspondence with motion segments. The
Tsumori system is based on this hypothesis. In this
system, the time series of data describing a robot’s
motion and the operator’s intentions are segmented.
These segmented robot motions and operator inten-
tions are related to each other one-to-one and con-
trol sticks are used to generate the input signals. This
method was used to control a robot, while maintain-
ing optionality on the layer of intention (Ando et al.,
2012).
However, this method has limitations in terms of
robot control. One problem is its inability to asso-
ciate a robot’s pose with a particular input because an
operator may have multiple simultaneous imitations
and because fixed poses have a one-to-one correspon-
dence with the imitations of the operator. Dancing
and operating a smart phone while walking both in-
volve multiple simultaneous motions, as the coordi-
nated movement of the entire body requires a differ-
ent velocity and displacement at each joint. Another
problem is the number of segmented motions. The
Tsumori system uses pre-recorded templates to deter-
mine a robot’s motions; therefore, it cannot deal with
motions that have not been templated.
In this paper, we propose a new manipulation
method that solves the problems with the Tsumori
framework. We chose to perform robot control by
using a neural network as a learning machine. This
choice was motivated by the fact that machine learn-
ing can almost solve the classification problem; how-
ever, it was also necessary to address the tempo-
ral continuity of the information used for robot con-
trol. Our method employs a recurrent neural net-
work (RNN); these networks produce signals that are
largely unaffected by variations in time-series data,
such as that used to control robot motions based upon
operator intentions. The RNN in the proposed sys-
tem also includes a butterfly structure that uses a fast
Fourier transform (FFT) in its hidden layer to detect
and discriminate between multiple imitations. By im-
plementing this method, robot control will be possible
in more diverse situations.
174
Torii, W., Fujimoto, S., Furukawa, M., Ando, H. and Maeda, T.
Techniques to Control Robot Action Consisting of Multiple Segmented Motions using Recurrent Neural Network with Butterfly Structure.
DOI: 10.5220/0005664801740181
In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 3: BIOINFORMATICS, pages 174-181
ISBN: 978-989-758-170-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

1.2 Tsumori Control
The Tsumori system can be implemented as Figure
1. First, the robot motion intended by the operator is
translated into motion segments x. This transforma-
tion makes it possible to cause the robot to automati-
cally perform continuous motion z by linking motion
segments x’. The operator observes the robot and in-
puts y, intending the robot to perform motion x. This
control flow involves changing the operator’s input y
into motion segment x and dividing continuous mo-
tion z of the robot into motion segments (x’ z x y)
(Figure 1). A learning controller is employed to re-
member the correspondence Gc. The operator then
controls the robot using the learning controller. The
operator inputs y by using the control sticks, intending
the robot to perform motion x. The learning controller
changes the operator’s input into motion segments x’
and transmits the appropriate motion data to the robot.
The robot receives the data and performs motion z as
desired. This flow makes it possible to control the
robot as intended. In this research, we used an RNN
with a butterfly structure as the learning controller.
In general, the motion trajectory of a robot can
be described by the sum of a number of trigonomet-
ric functions with different frequencies. If complex
movements or movements with multiple intentions
are required, it is necessary use a neural network for
robot control, as such networks can describe not only
spatial-domain information, but also the frequency
distribution of the signals.
Figure 1: Control flow of Tsumori system.
1.3 Neural Network
Neural networks have been studied to obtain new
models and structures to solve complex problems.
One famous example is deep learning, which is mod-
eled on the structure of the human brain (G. E. Hinton
and Teh, 2006). These networks have been reported
to be capable of recognizing objects (Le et al., 2012).
However, their recognition ability poor at finding the
features in the time domain as its structure has no abil-
ity to represent the time-varying information.
Against it, recurrent neural networks (RNN) con-
tain layers separate from the general layers that can
retain previous network states (Mikolov et al., 2011).
This structure allow them to determine the structures
in temporal order. However, RNNs still have limi-
tations with respect to periodicity, because the back-
propagation error is erased by cyclical integration and
the number of layers are finite.
The Tsumori system must determine the tempo-
ral ordering of structures with multiple DOFs to en-
able robots to be manipulatedto perform multiple seg-
mented actions simultaneously. Furthermore, the sys-
tem must determine the frequency distribution of the
inputs. However, a simple RNN is not able to de-
scribe the frequency distribution of the operator in-
puts. Therefore, this function was realized by using
an RNN to enable the Tsumori system to determine
the frequency features of the operator’s multiple ac-
tion inputs in detail in each time segment.
Thus, it is necessary for a network to be able to
identify structures in the input data and reflect them in
the output while retaining the frequency information.
The multiple operator input segments would thus be
associated with multiple robot actions.
The FFT method is an established technique for
expressing information in the frequency domain, as
FFTs can express all of the information in both the
time and frequency domains. Therefore, we expected
that an RNN utilizing an FFT strategy would be able
to describe both the temporal orders and the frequency
distributions of the input signals. In this study, we
applied an FFT structure in an RNN and verified the
reproducibility of the input frequency distribution by
comparingthe results with those of other types of neu-
ral networks.
2 PROPOSED METHODOLOGY
2.1 FFT
We employed an FFT butterfly structure in an RNN
to describe the frequency domain information. It was
believed that if the frequency information was given
to the neural network, the system could achieve ro-
bustness in spite of phase or amplitude variations.
Figure 2 shows a diagram of the FFT butterfly
structure. In this type of structure, a wide window
is first applied to the signal. As the flow advances,
low-frequency information is integrated, and high-
frequency information appears. In this discussion, the
operator that transmits the signal from the i-th butter-
fly flow to the j-th butterfly flow is denoted as w
i, j
,
and the result of each butterfly is represented by f
j,n
,
where n is the number of butterfly operations. Then,
each f is given by
f
j,n
= w
i, j
x
i
, (1)
Techniques to Control Robot Action Consisting of Multiple Segmented Motions using Recurrent Neural Network with Butterfly Structure
175

Figure 2: FFT butterfly structure.
where f
j,0
has been set equal to x
i
. To extract the
features at each frequency, we believed that it would
be necessary to use not only the obtained complex
Fourier coefficients, but also all of the f
i,n
values be-
cause it is obvious from Figure 2 that holding f
j,n
in the middle layer enables the extraction of features
from both low and high frequencies.
In our model, we implemented the FFT butterfly
structure in the middle layer, which also had the RNN
structure as shown in Figure 3.
Figure 3: Structure of third layer.
When implementing the FFT in this layer, three
points required attention. First, if all of the neurons
had FFT structures, it is conceivable that the learning
would not converge(the dashed line in Figure 3). Sec-
ond, even though the RNN had a mechanism to update
the weights of the connections between the cells (the
solid lines in Figure 3), the weights of the FFT butter-
fly connections weights were constant. Finally, if the
FFT butterfly structure had a feedback path to itself
from the RNN, the FFT would not work correctly, as
the inputs were time integrals. This composition is
expected to enable expression of both time and fre-
quency information without losing the RNN’s nature.
2.2 Proposed Model
Our proposed model consists of five layers, with the
third layer incorporating both the FFT butterfly and
RNN structures. Our proposed neural network was
developed based on the deep belief network (DBN)
model (G. E. Hinton and Teh, 2006).
In a DBN, the weights of the network are initial-
ized from the input layer to the output layer by learn-
ing without a teacher as pre-processing for learning.
After that, the weights are updated by using back-
propagation (Hinton and Salakhutdinov, 2006). In
this paper, we set the probability p equal to 0.5 for
drop-out. The first and last layers are for the input
and output layers, respectively. Thus, this model has
three middle layers. The second and fourth layers are
normal DBN layers and bind the previous and subse-
quent layers. The only difference between this struc-
ture and that of a normal DBN is in the third layer with
the hidden layer for RNN and FFT butterfly struc-
ture. The hidden layer separate from the normal lay-
ers. At time t, the RNN stores the current informa-
tion on the hidden layer after outputting the results.
Next, at time t+1, the hidden layer feeds the informa-
tion corresponding to the previous time back to the
normal layers. Thus, the RNN can learn patterns that
vary with time. We used the equation 2 to perform
forward propagation:
u
t
j
=
∑
i
w
(in)
ji
x
t
i
+
∑
j
′
w
j j
′
z
t−1
j
′
. (2)
The indices i and j correspond to the previous
and subsequent layers, respectively, in the RNN; u
t
is the middle layer input at time t; w
(in)
is the weight
between the input and middle layer; and w
j j
′
is the
weight of the RNN feedback path . The initial value
of w
j j
′
was calculated using autocorrelation, and back
propagation through time was used. The error δ prop-
agated to the previous layer was calculated using the
equation 3. Subsequently, the weight of each connec-
tion was updated using Equation 4.
δ
t
j
=
∑
k
w
out
kj
δ
out,t
k
+
∑
j
′
w
j j
′
δ
t+1
j
′
!
(3)
∂E
∂w
j j
′
=
T
∑
t=1
∂E
∂u
t
j
∂u
t
j
∂w
j j
′
=
T
∑
t=1
δ
t
u
t−1
j
(4)
3 EXPERIMENT
Before controlling a robot with the Tsumori system, it
was necessary to verify the performance of our model.
We expected it to perform well when supplied with
input signals with deviations in their frequency distri-
butions because of the FFT butterfly structure. There-
fore, we evaluated the performance of our model
when supplied with signals both with and without de-
viations in their frequency distributions.
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
176
3.1 Preparation
To verify the feasibility of using our neural network
model to control a robot, we compared the perfor-
mances of four kinds of neural networks: deep learn-
ing (A), deep learning with FFT butterfly (B), RNN
(C), and RNN with FFT butterfly (D). The third layer
of model (B) consisted of FFT parts and ordinal neu-
rons for deep learning. All of them have five layers to
construct the neural network model. The output and
input layers each contained 32 neurons. The second
and fourth layers each had 150 neurons, and the third
layer had 402 neurons. The remaining 352 neurons in
models (B) and (D) also had FFT butterfly structures.
We used 32 points for the FFT, with five butterfly op-
erations. We used two neurons to store f
j,n
, which
consisted of real and imaginary parts. The weights
were updated 20 times during the pre-processing of
the Boltzmann machine. In addition, equation 5 was
used as the activation function, where u is the input to
each neuron:
f(u) =
1
1+ e
−u
(5)
3.2 Performance Verification
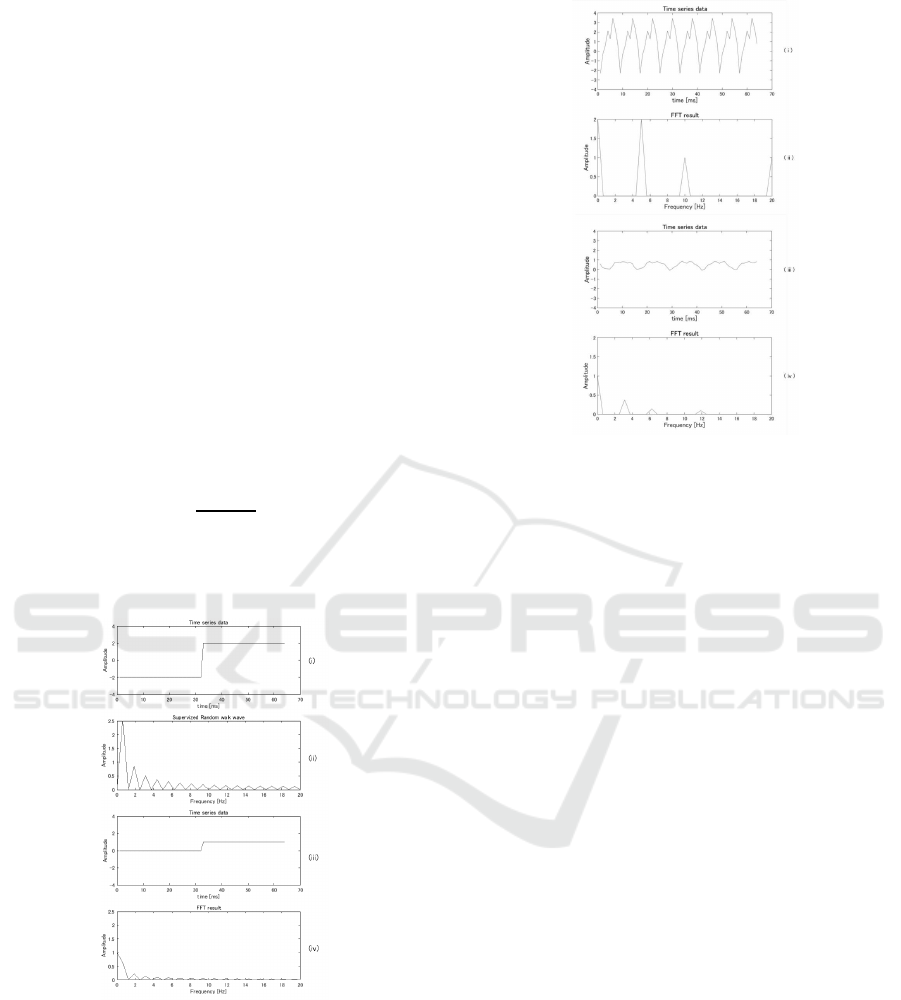
Figure 4: Step function signals.
We verified the above models from the viewpoint of
frequency distribution. First, we prepared signals that
were uniform in the frequency domain for verifica-
tion. The signals were step functions whose spec-
tra incorporated all of the frequency bands. Figure
6 shows the waveforms and FFT results for the input
and output layers when step function signals with the
form of Equation 6 were applied:
x(t) = au(t − τ) − b (6)
Figure 5: Random walk signals.
In this equation, u(t-) is a step function. The pa-
rameters were set as follows: a = 4, b = 2, andτ = 32
for the input signal, and a = 1, b = 0, andτ = 32 for
the output signal. The signals were fed to the input
layer by shifting them by 1 neuron as time progressed
from t to t + 1. The output data obtained from each
model after 16 steps were used for verification.
As step signals are uniform in the frequency do-
main, the implemented FFT structure would not find
the structure in the frequency domain. Therefore,
model (A) was expected to perform well when sup-
plied with a step function signal.
The results are shown in Figure 6. In each graph,
the gray lines show the waveforms and frequency dis-
tributions of the supervised data (Figure 4, 5). The
black lines show the results from each model. Model
(A) best reproduced the input data. However, model
(B) could not do so since the almost all of the neurons
in the third layer were employed for the FFT.
The same can be said about model (C). Though the
increases in the signal were identified by both models,
in model (C), the temporal information about the sig-
nal increases was lost. Model (D) successfully repro-
duced the supplied signal, although it fluctuated. The
frequency distribution generated by model (A) is al-
most identical to that of the original signal, whereas in
the other models, energy leakage is evident. However,
the distribution produced by model (D) is better than
that of model (C) in the low-frequency band. There-
fore, deep learning is the best means of reproducing a
pattern that has a spatial structure, and RNNs cannot
accurately reproduce rising or falling signals. How-
ever, performing an FFT in an RNN could improve
its ability to reproduce such waveforms.
Techniques to Control Robot Action Consisting of Multiple Segmented Motions using Recurrent Neural Network with Butterfly Structure
177
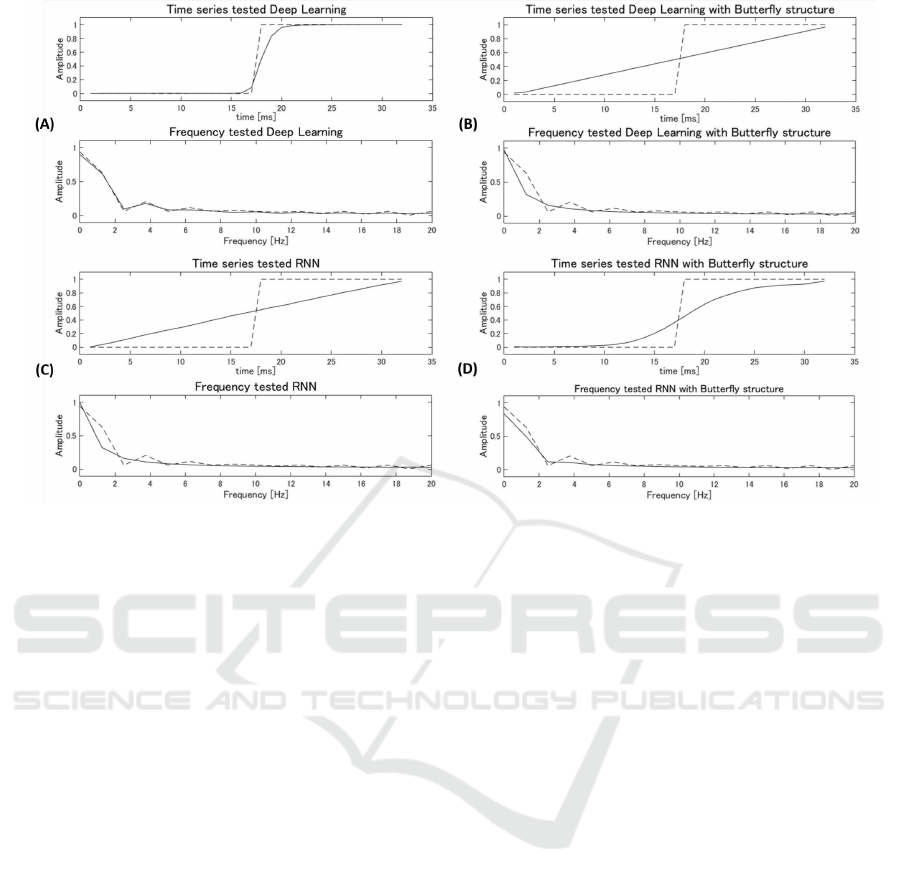
Figure 6: Output from each neural network (step function).
Next, instead of step signals, we used random
walk signals; such signals have variations in their
frequency distributions. In the real world, signals
with uniform frequency distributions, such as step sig-
nals, are few. Instead, most signals have biased fre-
quency distributions, like those of random walk sig-
nals. Therefore, it was reasonable to use these to
verify the abilities to reproduce the signals by using
FFTs. The signals had the following form (Tachi,
1993):
x(t) =
n
∑
k=1
(a
0
p
−k
sin2π f
min
p
k
t + φ
k
). (7)
The parameters were set as follows: a
0
= 2, p =
2, n = 3, and f
min
= 5 for the input signal, and a
0
=
20, p = 2, n = 3, and f
min
= 3 for the output supervised
signal. The amplitudes of both the input and output
signals were inversely proportional to the frequency
from Equation 5. Hence, the energies of the signals
at each frequency and the velocity amplitudes were
constant, and the sine wave at each frequency was in-
dependent of φ
k
and the sampling frequency was 40
Hz. The waveforms and FFT results for the input and
output layers when supplied with random walk sig-
nals are shown in Figure 7. Graphs (i) and (ii) cor-
respond to the input signal, and graphs (iii) and (iv)
correspond to the supervised.
Figure 7 shows the results. Ideally, the waveforms
obtained by the neural network would have peaks in
the frequency domain at 3 Hz, 6 Hz, or 12 Hz. Models
(A) and (B) show no marked differences, regardlessof
the presence of the FFT butterfly. In the FFT results
for these two models, the energies of the signals at
each frequency were largely lost.
Model (B) failed to reproduce the waveform and
frequency distribution of the signal. The reason for
this failure is believed to be that, as this model had
no recurrent structure, it could not identify the time-
varying components of the signal. Although model
(C) lost less energy than model (A), the energy leak-
age occurred across a wide frequency range, and it
was very difficult to estimate the original waveform
from the measured one. On the other hand, the out-
put from model (D) has peaks at 3 Hz and 6 Hz in the
FFT results. Although there is no peak at 12 Hz, the
energy is not zero. Therefore, it is said that model (D)
best reproduced the original waveform.
3.3 Tsumori by RNN with FFT
Next, we used our model to control a robot through
the Tsumori framework, as the inputs of the Tsumori
system have temporal continuity and contain multi-
frequency information. The sampling frequency was
40 Hz, and each segmented robot action was de-
scribed with 64 units in the Tsumori system. We
asked one subject to generate inputs using the con-
trol stick based on the robot’s action, such as raise its
hands” with the intention, ”I move this robot”. This is
a basic operation required to enable a robot to lift an
object and is applicable to many situations. The sub-
ject repeated this operation 10 times; the ninth data
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
178
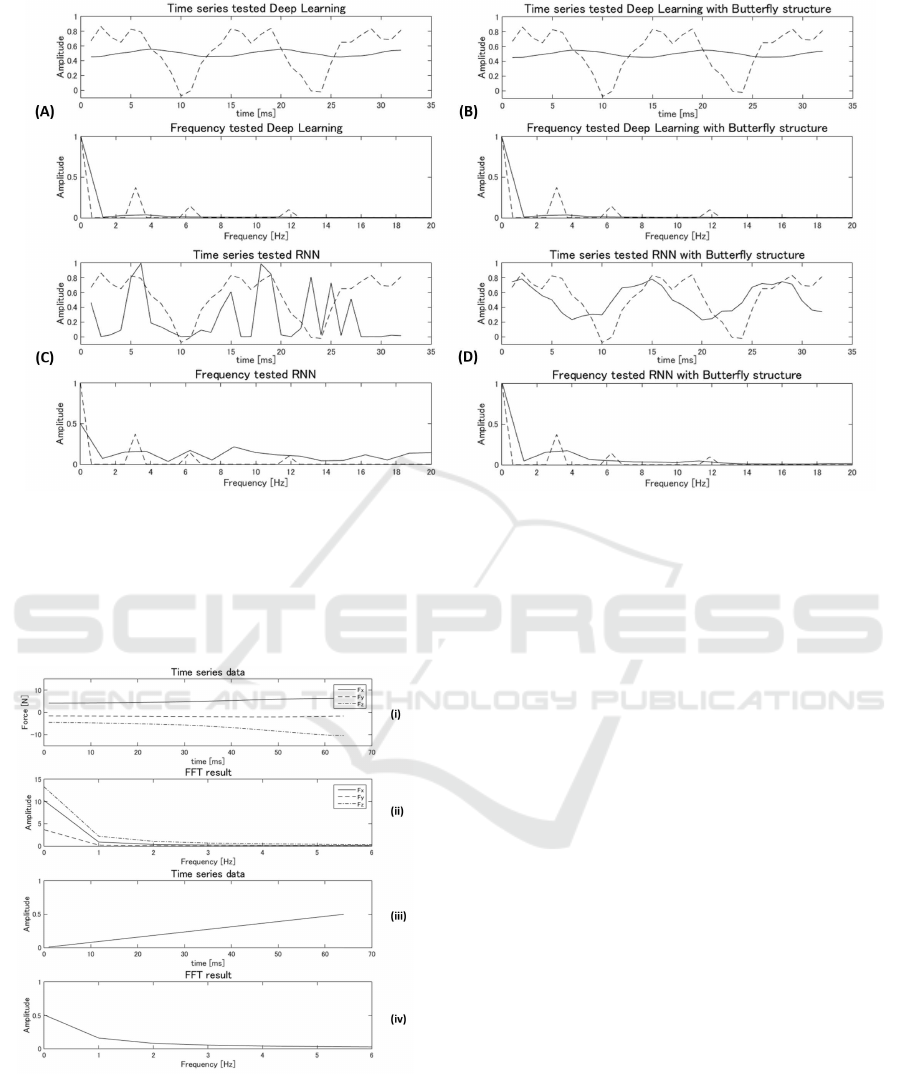
Figure 7: Output from each neural network (random walk).
set was used for learning, and the 10th was used to
test the neural network. Figure 8 shows the wave-
forms and FFT results corresponding to the input by
the subject and the actual movement of the robot servo
motor.
Figure 8: Operator input.
In Figure 8, (i) and (ii) show only three DOFs, the
forces along the three axes, and (iii) and (iv) corre-
spond to just the pitch of the right shoulder. In fact,
the operator inputs had 12 DOFs, which consisted of
forces along and moments about the three Euclidian
axes for both hands. In this study, six DOFs were
used in total because the inputs from the operator’s
two hands were considered to be symmetrical. Fur-
thermore, the number of DOFs of the robot’s upper
limbs was reduced from six to three: the roll and pitch
of the right shoulder and the pitch of the right elbow.
In this experiment, a KHR3HV robot was controlled
by the Tsumori system.
Some changes were made to the neural network to
apply it to the Tsumori system. We prepared 192 neu-
rons for the input layer and 96 for the output layer, be-
cause the operator input consisted of six DOFs, while
the robot had only three DOFs. A total of 1000 neu-
rons for the second layer, 600 for the fourth layer, and
2262 neurons for third layer were prepared. In the
third layer, 2112 neurons had FFT butterfly connec-
tions and the remaining 150 neurons were used for
the RNN. In this experiment, the neural networks re-
ceived operator inputs corresponding to two motion
segments for the robot. Therefore, 32 pieces of data
were input simultaneously, corresponding to a total of
64 with one DOF each, and each piece of data was
recorded in a separate time interval. Therefore, the
time varied from 0 and 63. As Figure 9 shown, the re-
sulting frequency distribution and waveform are both
quite similar to those of the original signal.
4 DISCUSSION
For the step function signals, model (A) best repro-
duced the original signals, because the deep learning
Techniques to Control Robot Action Consisting of Multiple Segmented Motions using Recurrent Neural Network with Butterfly Structure
179
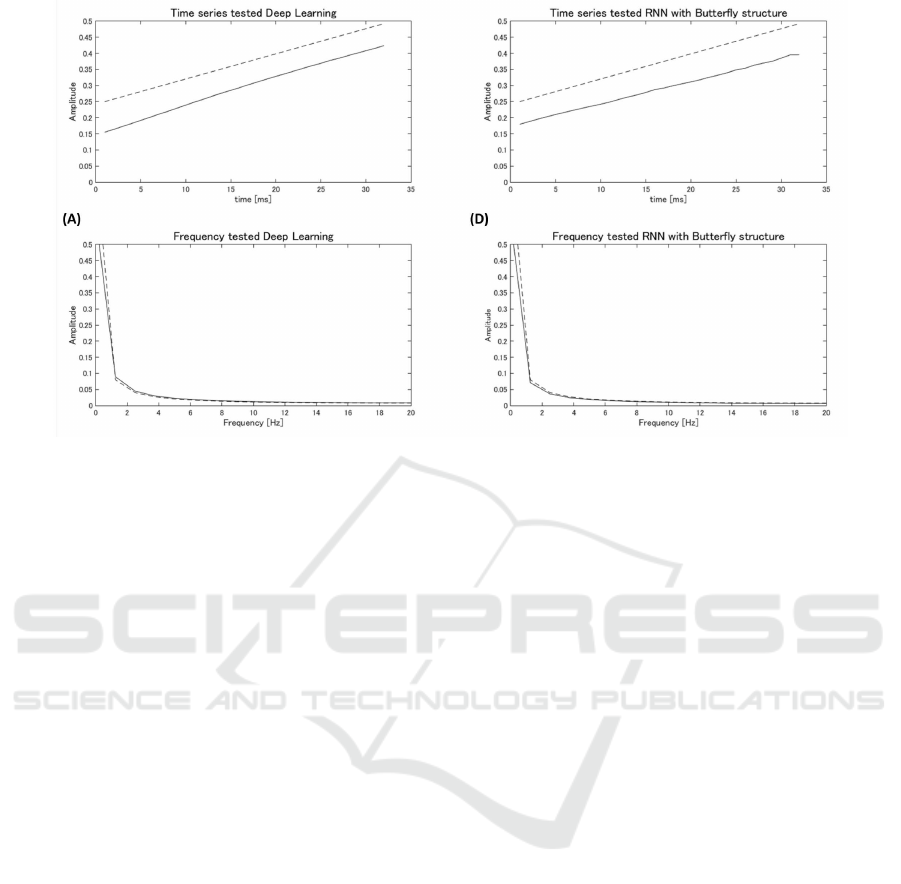
Figure 9: Output Tsumori system output.
method can accurately determine spatial structures.
For this reason and because the rising of the signal
appeared locally, it was considered that model (A) re-
membered only that information. On the other hand,
although some of the structure of model (B) was the
same as that of model (A), the waveform was lost be-
cause the FFT result for the step signal contained less
information (from Figure 4) and the number of neu-
rons for deep learning was lower than that of model
(A). Model (C) also could not reconstruct the wave-
form. Although an RNN can accurately reproduce
time-varying data, the learning process was ineffec-
tive, as the change was local. On the other hand, the
waveform and frequency distribution were both well
reproduced by model (D) by performing an FFT. The
FFT did not provide information about the energy, but
it did yield information about the phase of each fre-
quency. From this information, the RNN could find
the change in the time domain.
Next, we compare the performances of the models
when random walk signals were applied. Models (A)
and (B) could not reproduce the random walk wave-
forms, as deep learning cannot identify the features
of time-varying data. In model (B), though the FFT
provided frequency information, it lacked the infor-
mation about the temporal variations. The results of
model (C) were the worst of all the models, however,
upon implementing the FFT structure, model (C) be-
came the best model. Except for the energy leakage
at lower frequencies, model (C) maintained the en-
ergy of the entire system. Accordingly, RNNs might
enable complete reproduction of frequency informa-
tion if the energy leakage problem can be solved.
Two problems related to energy leakage were con-
sidered. First, the recursion times of the RNN were
few to converge to the optimal network. In this study,
the recursive method of the RNN was employed only
once. It is conceivable that the energy leakage would
decrease by performing the RNN method repeatedly.
Another problem was that the temporally continuous
data we used were long for the RNN. Therefore, the
RNN might not have been able to remember old in-
formation about the weights of the connections. To
solve this problem, it might be beneficial to imple-
ment a long short-term memory (LSTM) (Hochreiter
and Schmidhuber,1997) structure or more hidden lay-
ers than were used in this model.
Finally, we compare the robot control signals of
the Tsumori framework. Both models (A) and (D)
produced waveforms and frequency distributions sim-
ilar to those of the original data. It is believed that
model (A) could learn the spatial features of the sig-
nal since it was monotonous. However, as shown in
the results corresponding to the random walk signals,
model (A) failed to reproduce the signals if they con-
sisted of multiple frequencies. Our objective in this
research was to enable robot control based on input
consisting of multiple operator intentions; therefore,
it is necessary to verify the performances of robots
when given such inputs.
5 CONCLUSION
This paper introduced a new deep-learning model for
learning signals consisting of multiple frequencies,
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
180

and its ability to reproduce the original signals was
discussed by comparing its performance with those
of the existing models. We also experimentally veri-
fied its practicality for robot control by using operator
inputs applied through the Tsumori framework. Our
approach yielded the optimum results for determining
information in the frequency domain when an RNN
with an FFT structure was used. The results indicate
that a neural network with RNN and FFT butterfly
structures could learn data consisting of multiple fre-
quencies. This corresponds to a robot learning an ac-
tion consisting of multiple segments. Therefore, this
neural network can be used to construct learning ma-
chines that associate multiple operator intentions with
robot actions in the Tsumori framework. In the future,
we plan to verify the ability of this model to produce
robot movements when presented with multiple seg-
mented operator intentions through the Tsumori ar-
chitecture. These inputs will resemble the random
walk signals used in this study.
ACKNOWLEDGEMENTS
This work was funded by the ImPACT Program of
the Council for Science, Technology and Innovation
(Cabinet Office, Government of Japan). It was also
supported by Osaka University, Institute for Aca-
demic Initiatives, Division 4, Humanware Innovation
Program and a JSPS KAKENHI Grant-in-Aid for Sci-
entific Research (A), Grant Number 15H01699.
REFERENCES
Ando, H., Niwa, M., IIzuka, H., and Maeda, T., editors
(2012). Effects of observed motion speed on segment-
ing behavioural intention.
G. E. Hinton, S. O. and Teh, Y. (2006). A fast learn-ing
algorithm for deep belief nets. Neural Computation,
18(2):1527–1544.
Hinton, G. E. and Salakhutdinov, R. (2006). Reducing the
dimensionality of data with neural networks. Science,
313:504–507.
Hirai, K., Hirose, M., Haikawa, Y., and Takenaka, T., ed-
itors (1998). The Development of Honda Humanoid
Robot, volume 2. IEEE.
Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. Neural Computation, 9(8):1735–1780.
Le, Q., Ranzato, M. A., Monga, R., Devin, M., Chen, K.,
Corrado, G., Dean, J., and Ng, A., editors (2012).
Building high-level features using large scale unsu-
pervised learning.
Mikolov, T., Kombrink, S., Burget, L., Cernocky, J., and
S.Khudanpur, editors (2011). Recurrent Neural Net-
work Based Language Model.
Niwa, M., S.Okada, Sakaguchi, S., Azuma, K., Iizuka, H.,
H, A., and Maeda, T., editors (2010). Detection and
Transmission of Tsumori : an Archetype of Behav-
ioral Intention in Controlling a Humanoid Robot.
Yamamoto, T. and Fujinami, T. (2004). Synchronisation
and differentiation: Two stage of coordinative struc-
ture. In Third International Work-shop on Epigenetic
Robotics, pages 97–104.
Techniques to Control Robot Action Consisting of Multiple Segmented Motions using Recurrent Neural Network with Butterfly Structure
181
