
A Comparative Analysis of Pickup Forecasting Methods for Customer
Arrivals in Airport Carparks
Andreas Papayiannis, Paul Johnson and Peter Duck
School of Mathematics, University of Manchester, Manchester, U.K.
Keywords:
Lead Time, Booking Curve, Pick Up.
Abstract:
Accurate forecasts of customer demand lie at the core of any successful revenue management system. Most
research has focused upon studying such methods for the airline and hotel industry. In this paper, we present a
comparative analysis of various forecasting methods which we apply to the rapidly evolving airport carparking
(ACP) industry. We use real ACP booking data from four distinct carparks of a major airport in UK to forecast
customer arrivals for one to eight weeks out in the future. Conclusions are reached with regards to which
forecasting methods perform best in this operating environment, and whether there is any benefit in employing
complex methods over simpler ones.
1 INTRODUCTION
Accurate forecasts of customer demand lie at the core
of any successful revenue management (RM) system,
as several reports point out a significant further in-
crease on generated revenues. In particular, for the
airline industry (Lee, 1990) shows that a 10% im-
provement in forecasting accuracy can result in up to
3% increase on revenues, while in hotels a 20% fore-
casting improvement leads to 1% revenue increase
(P
¨
olt, 1998). As a result, several studies on forecast-
ing methods have been presented; a good review on
these methods may be found in (Sa, 1987) and (Lee,
1990) for the airlines and (Weatherford et al., 2001),
(Weatherford and P
¨
olt, 2002) and (Weatherford and
Kimes, 2003) for hotels.
In carparks, the forecasting requirements and
models are closely related to those in the hotel indus-
try. One such study refers to the masters thesis of
(Rojas, 2006) who developed a neural network model
to forecast demand on an hourly basis and compared
it against some traditional historical time-series mod-
els. His results indicate that the ability of the neural
network method to capture the demand changes from
high to low periods improves performance accuracy.
In airport carparks, the setting is similar; multi-
ple carparks are located around the airport and people
choose among them based on their intended duration-
of-stay, proximity to the airport and price. Over the
last decade, the implementation of online reserva-
tion systems for airport carparks has gained interest,
with all major airports in UK and Europe offering
online pre-booking through their official websites as
well as through third parties. This enabled managers
to use traditional RM techniques to forecast demand
per length-of-stay (LoS) and per rate category offered
(product) in a each carpark.
According to (Weatherford and Kimes, 2003) RM
forecasting methods fall into three main types:
• Historical booking models
they only consider the final number of arrivals on
a given day in history
• Booking curve (pickup) models
they take into account the booking build-up pat-
tern of arrivals during the lead time
• Combined models
they combine historical and booking curve models
using either a weighted average or regression, to
develop better forecasts.
In this paper, we use real ACP booking data from
four distinct carparks of a major airport in UK to
forecast customers arrivals. Normally, such forecasts
are fed into the optimization routines to drive capac-
ity or pricing decisions. Consequently, this piece of
work comes as a pre-requisite for the revenue opti-
mization algorithms developed in (Papayiannis et al.,
2012; Papayiannis et al., 2013) for ACP. Our aim is
to provide a comparative analysis of various forecast-
ing models and make valid conclusions on balancing
between a method’s simplicity and accuracy. Moti-
vated by the results presented in (Wickham, 1995) for
Papayiannis, A., Johnson, P. and Duck, P.
A Comparative Analysis of Pickup Forecasting Methods for Customer Arrivals in Airport Carparks.
DOI: 10.5220/0005631900150024
In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 15-24
ISBN: 978-989-758-171-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
15

the airline industry, where the booking curve methods
were found in general to be the most accurate, we re-
strict our focus to these type of methods. Three main
attributes shape up the exact type of the pickup vari-
ation to be used; the first two control the structure of
the pickup method while the third refers to the under-
lying time-series model. In a similar study, (Zakhary
et al., 2008) tested the resulting pickup variations, us-
ing simulated hotel data, for two models; the mov-
ing average and the exponential smoothing model.
Our work implements the same structural methodol-
ogy, but it also extends further to cover more complex
time-series models that account for seasonality and/or
autocorrelation in the data. Consequentially, in order
to describe the pickup methodology and its variations
we find it convenient to use similar notation.
In section 2, we introduce and describe the pickup
methodology, its structural variations and the time-
series models under study. Further, we design a cross-
validation procedure to recursively obtain forecasts as
time unfolds and define the three performance mea-
sures that are used to assess the accuracy of the meth-
ods. The best models are selected based on all three
measures. Finally, results of our analysis are found in
section 3 while conclusions on the best practices as
well as further work are summarised in section 4.
2 BACKGROUND
Booking curve models are quite popular in practice
because they are intuitive and easy to set up. Their
special feature is that they use the build-up pattern
of reservations of past days, as opposed to only their
complete arrival histories. In general, booking build-
up models forecast total arrivals on a future day T by
estimating the bookings-to-come between now and T .
They are often called pickup models as they estimate
reservations to be picked up from a given point in time
to a different point in time during the booking process
(Zakhary et al., 2008).
Table 1 shows the evolution of customer demand
in a matrix form. Each row represents the booking
build-up of arrivals for each arrival date in August.
More precisely, each column on the right hand side is
a snapshot of on-hand bookings for the given arrival
day on the left, as of some lead time. Seven review
points are shown, on the day, one day in advance, two
days in advance up to six days in advance. Let us
assume that today’s date is the 9
th
of August. Then,
the number of total arrivals on, say, the 6
th
of August
was 234, where 190 of them had booked four days and
more in advance (they had already booked by the 2
nd
of August). For arrival dates that have not occurred
Table 1: Cumulative booking (build-up) table.
August Lead time (days prior arrival)
2014 0 1 2 3 4 5 6
1 261 258 254 245 232 221 212
2 209 206 195 195 185 176 167
3 236 232 218 205 205 194 184
4 216 213 200 189 181 181 173
5 253 251 237 224 213 201 201
6 234 230 214 200 190 180 173
7 216 211 197 188 178 167 156
8 209 203 192 183 173 163 154
9 217 203 194 181 171 161
10 210 199 189 182 175
11 263 253 242 233
12 241 229 221
yet the build-up row is incomplete; i.e for these future
dates only partial bookings data is available.
The different variations of the booking curve mod-
els can be grouped into three types, whether it is
• additive or multiplicative,
• classical or advanced,
• or with regards to the time-series model used to
estimate pickup increment/ratio.
Below we go through these in more detail.
2.1 Additive vs Multiplicative Pickup
Additive pickup models assume that the number of
on-hand reservations is independent of the number
of parking spaces that will be sold later on. In other
words, a pickup forecast of say 25 is calculated inde-
pendently of whether the on-hand bookings are 5 or
105. As as result, the pickup forecast is added to the
on-hand bookings to obtain the total arrivals forecast.
Alternatively, multiplicative pickup assumes that fu-
ture bookings-to-come are positively correlated to the
the current on-hand booking level. As such, the to-
tal arrivals forecast is computed by multiplying the
on-hand bookings to the forecast pickup ratio. Both
techniques are explained below.
2.1.1 Additive Technique
The additive technique requires that the cumulative
booking matrix in table 1 is expressed into pickup in-
crements on each lead day. In particular, if C
i, j
is the
on-hand bookings as of j days in advance for arrival
date i, then the pickup increment in reservations from
day j to j − 1 in advance is given by
A
i, j
= C
i, j
−C
i, j−1
. (1)
Applying this on the matrix in table 1 we get the ad-
ditive matrix as shown in table 2.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
16

Table 2: An additive booking matrix showing the bookings
to be picked up on each day prior.
August Lead time (days prior arrival)
2014 0 1 2 3 4 5 6
1 3 4 9 13 11 9 212
2 3 11 0 10 9 9 167
3 4 14 13 0 11 10 184
4
3 13 11 8 0 8 173
5 2 14 13 11 12 0 201
6 4 16 14 10 10 7 173
7 5 14 9 10 11 11 156
8 6 11 9 10 10 9 154
9 14 9 13 10 10 161
10 11 10 7 7 175
11 10 11 9 233
12 12 8 221
Table 3: A multiplicative booking matrix showing the book-
ings to be picked up on each day prior.
August Lead time (days prior arrival)
2014 0 1 2 3 4 5 6
1 1.012 1.015 1.036 1.056 1.050 1.042 212
2 1.015 1.056 1.000 1.054 1.051 1.054 167
3 1.017 1.064 1.063 1.000 1.057 1.054 184
4 1.014 1.065 1.058 1.044 1.000 1.046 173
5 1.008 1.059 1.058 1.052 1.060 1.000 201
6
1.017 1.075 1.070 1.053 1.056 1.040 173
7 1.024 1.071 1.048 1.056 1.066 1.071 156
8 1.030 1.057 1.049 1.058 1.061 1.058 154
9 1.069 1.046 1.072 1.058 1.062 161
10 1.055 1.053 1.038 1.040 175
11 1.040 1.045 1.039 233
12 1.052 1.036 221
2.1.2 Multiplicative Technique
The multiplicative technique requires that the cumula-
tive booking matrix in table 1 is expressed into pickup
ratios on each lead day. In this case, the pickup ratio
in reservations from day j to j −1 in advance is given
by
M
i, j
=
C
i, j
C
i, j−1
. (2)
Applying this on the matrix in table 1 we get the mul-
tiplicative matrix as shown in table 3.
2.2 Classical vs Advanced Pickup
Classical pickup uses only historical data of booking
curves for arrival days that have already passed. In
this way, all the arrival days that are used in the fitting
stage would consist of completed booking curves. For
example, if we are to forecast arrivals on date 11
th
of
August, a classical pickup method would use data up
to the 8
th
of August (see table 2). Alternatively, an
advanced pickup method would use all data available
up to today, i.e. taking into account the partially com-
pleted booking curves in rows (arrival dates) 9, 10 and
11. In this way, sudden changes in demand patterns
are better handled, however at the cost of robustness.
Moreover, under the classical method one does not
need to forecast the individual pickup increments but
rather the combined pickup that results from today un-
til the arrival day. For example, the forecast for the
11
th
of August is equal to the on-hand bookings as
of today plus
1
the forecast of combined bookings-to-
come between now and the arrival day. Alternatively,
under the advanced pickup the same forecast would
have been calculated as the sum of three individual
pickups, namely the pickup on two days before, that
on one day before and on the arrival day. Therefore,
the classical methodology is simpler as only one fore-
cast is required.
2.3 Underlying Time-series Models
Each column in tables 2 and 3 can be considered as
an individual 1D time-series (vertically) and thus any
method can be used to forecast its unknown entries.
By proceeding column-by-column we can fill out the
matrices and ultimately an arrival forecast for a given
date can be found by adding or multiplying the en-
tries in that row, for additive or multiplicative pickup
respectively.
Common methods in the literature are a simple
historical averaging (HA) or a weighted averaging ex-
ponential smoothing ES-(α) by day of week; that is
to compute arrival forecasts for say next Monday by
only using previous Mondays (Zakhary et al., 2008;
Weatherford and Kimes, 2003). This simplification
is reasonable in the presence of a strong weekly cy-
cle in the historical data and, as this is often the case,
forecasting by day-of-week has been widely used in
practice. Such techniques, however, have two clear
limitations:
1. they assume that the series is a stationary process
with no trends and,
2. they ignore any short-term interactions between
the neighbouring days.
Thus in this study, we aim to extend these by fur-
ther implementing several forecasting methods that
can model trends and seasonal patterns explicitly and
thus they can operate directly on the entire data set,
these are described below.
1
Assuming additive pickup.
A Comparative Analysis of Pickup Forecasting Methods for Customer Arrivals in Airport Carparks
17

2.3.1 Time-series Models to Account for Linear
Trends
Two methods are employed that fall into a category of
models that also consider for the presence of a linear
trend in the data.
1. Holt’s method (Holt)
Intuitively, this method is similar to the exponen-
tial smoothing method with the enhanced ability
to account for a linear trend in the data. To achieve
this, two update equations (and thus two corre-
sponding parameters) are required, the first to ac-
count for the level (α) and the second for the linear
trend (β).
2. ARMA/ARIMA time series methods
ARMA models are frequently used in financial
econometrics and their unique feature is that
they account for autocorrelation among the data.
ARIMA models can adjust for non-stationarity in
the data applying ARMA models into the differ-
enced series. Further details may be found in
(Shumway et al., 2000). This family of models
are more complex and statistically sophisticated
than exponential smoothing methods, and as so
they have been used in earlier studies for histori-
cal forecasting (first type of forecasting methods).
However, several studies shown that they not in
general perform better than simpler ones (Weath-
erford and Kimes, 2003; Sa, 1987). Nonetheless,
we believe that the unsatisfactory performance of
ARMA models was mostly due to the nature of
the historical booking models, as the reservation
build-up data is not considered when developing
the forecast. Thus our study aims to examine them
under a pickup setting.
Since these methods do not model seasonality explic-
itly, we use them in a day-of-week framework. There-
fore, and similarly to HA and SE, any interaction
among neighbouring days is not captured by these
models.
2.3.2 Time-series Models to Model Trend and
Seasonality Explicitly
Three methods are employed which consider both the
presence of a linear trend as well as seasonality in the
data. In this way, interactions among neighbouring
days are considered in the forecast.
1. Holt-Winter’s method (HW)
Intuitively, this method is similar to the exponen-
tial smoothing method with the enhanced ability
to account for any linear trends and/or season-
ality that appears in the data. To achieve this,
three update equations are required, one for each
of level (α), linear trend (β) and seasonal compo-
nent (γ). As such, this technique is often referred
to as triple exponential smoothing, further details
of it may be found in (Hyndman et al., 2008).
2. Seasonal-Trend decomposition by Loess (STL)
STL is an iterative filtering procedure for decom-
posing a time series into trend, seasonal and re-
mainder components, developed by (Cleveland
et al., 1990). The Loess method is also known as
a locally weighted polynomial regression; points
are estimated one at a time by fitting a low degree
polynomial to subset of data around each point.
Further, the STL decomposition may also be used
for forecasting, as proposed by (Makridakis et al.,
2008); this is done in two stages. First the sea-
sonal component is filtered out and a forecast on
the seasonally adjusted series is performed using
an exponential smoothing model, possibly allow-
ing for a linear trend. Then, the forecast for the
seasonal component is estimated by simply pro-
jecting the last season (last week) and gets added
to the seasonally adjusted forecast.
3. Seasonal ARIMA (SARIMA)
SARIMA models extend ARIMA models to fur-
ther adjust for seasonal variation. SARIMA mod-
els are described by a non-seasonal part (similar
to ARIMA) and a seasonal part. In identifying
a SARIMA model, one first checks for autocor-
relation at the seasonal lags, adjusts the data by
seasonally differencing and then apply an ARIMA
model on the resulting series, further details may
be found in (Shumway et al., 2000).
Since these methods do model seasonality explic-
itly, we use them directly into the merged data series,
the series that comes from considering all days of the
week together.
2.3.3 Automatic Model Identification and
Parameter Estimation
For each arrival day in the data, we collect
snapshots of booking activity from 18 re-
view time-points in the lead time, namely on
0, 1, . . . , 7, 14, 21, 28, 35, 42, 49, 56, 70, 84, 100
days before. This implies a pickup method would
require individual forecasts for the first 13 (vertical)
time series, one for each review point, in order to
obtain the total arrivals forecast for up to 56-days
out. Moreover, if the forecasts are to be computed by
day-of-week, then the number of time series to model
grows to 13 × 7 = 91! Each of these times series
could be assumed to be generated out of the same
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
18

model family, however their parameter estimates will
in general be different.
To deal with this large number of forecasts,
we adopt an automated identification procedure, de-
veloped by (Hyndman et al., 2002), whereby the
exponential-smoothing related models are defined in
terms of a state-space framework. Under this new
framework, an iterative approach is employed in
which the parameters (α, β, γ) are estimated based on
minimising the mean-square-error (MSE) and the best
model is selected based on minimising an informa-
tion criterion, in our case the AICc. Similarly, for
ARIMA/SARIMA models, an automatic identifica-
tion based on (Hyndman and Khandakar, 2007) is em-
ployed; a stepwise procedure whereby several mod-
els are estimated using maximum likelihood and the
best overall model is selected based on minimising the
AICc.
2.4 Framework
Setting. We use 15 months of daily (constrained)
bookings data from four distinct carparks of a major
airport in UK. Depending on their size, proximity to
the airport terminals, flight schedule and pricing these
four carparks attract different types of customers and
in different volumes and, consequently, the average
length-of-stay and build-up patterns will vary in gen-
eral. Therefore, the developed models will be tested
under four fundamentally different types of data sets.
Our aim is to forecast arrivals at the carpark level,
keeping the data aggregated as a whole. We compute
short-term arrival forecasts for various forecast hori-
zons, that is for h = 7, 14, 28 and 56 days out.
In this study we examine 28 distinct pickup vari-
ations summarised in table 4. Note that the com-
putational times for Holt, ARIMA, HW, STL and
SARIMA models are expected to be higher than MA
and ES, as not only they are more complex in nature
but also due to the automatic estimation and identifi-
cation procedure that runs underneath.
Cross-validation. Every method employed is ex-
amined to check how well it performs in forecasting
arrivals for different future horizons (different h-steps
head). To achieve this a cross-validation methodol-
ogy is implemented, as described below. We choose n
days as the length of the training data and form the ini-
tial training set using observations t
1
, t
2
, ..., t
n
. Then,
we compute h-step ahead forecasts, namely for days
t
n+7
, t
n+14
, t
n+28
and t
n+56
. Then the training set rolls
forward by one day (t
2
, t
3
, ..., t
n+1
) and new forecasts
are computed for days t
n+8
, t
n+15
, t
n+29
and t
n+57
and
the procedure continues until the end of the dataset.
Finally, k forecasts for each h-step ahead are collected
and gathered together and then performance measures
are employed to assess the accuracy of the imple-
mented model. For this study we have used n = 84,
that amounts to twelve weeks of data.
Forecast Accuracy. If Y(t + h) is the actual obser-
vation for day t + h and F
t
(t + h) the forecast for that
day as of day t (an h-step ahead forecast), the
h-step ahead forecast error is defined as
e
t
(t + h) = Y (t + h) − F
t
(t + h). (3)
Our study implements the following metrics:
Mean Absolute Error (MAE):
1
k
k
∑
t=1
|e
t
(t + h)| (4)
Root Mean Squared Error (RMSE):
v
u
u
t
1
k
k
∑
t=1
|e
t
(t + h)|
2
(5)
Symmetric Mean Abs Percent Error (sMAPE):
1
k
k
∑
t=1
|e
t
(t + h)|
Y (t + h) + F
t
(t + h)
× 200 (6)
Performance metrics MAE and RMSE measure
the forecast accuracy whose size depends on the scale
of the data. Alternatively, sMAPE are relative mea-
sures designed to enable comparisons among differ-
ent series. Note the use of the symmetric rather than
the ordinary MAPE, so that positive and negative bias
are equally weighted. Also this adjustment minimises
the cases when the divisor is exactly zero, as for this
to happen both forecast and actual have to be zero.
Also note that, in the case of a zero forecast, the per-
cent error will be 200 and as a result the mean percent
error could end up over 100.
Best Models Selection. To rank the models accord-
ing to performance, all three metrics are used; the
rank of model i, R
m
i
, among all models under study,
is measured for each metric m separately and these
are averaged to obtain the mean rank of model i, R
i
,
namely
R
i
=
1
3
R
MAE
i
+ R
sMAPE
i
+ R
RMSE
i
,
for each model i under study. Then the five models
with the lowest mean ranks are the selected best mod-
els for the specified carpark and forecast horizon h.
A Comparative Analysis of Pickup Forecasting Methods for Customer Arrivals in Airport Carparks
19
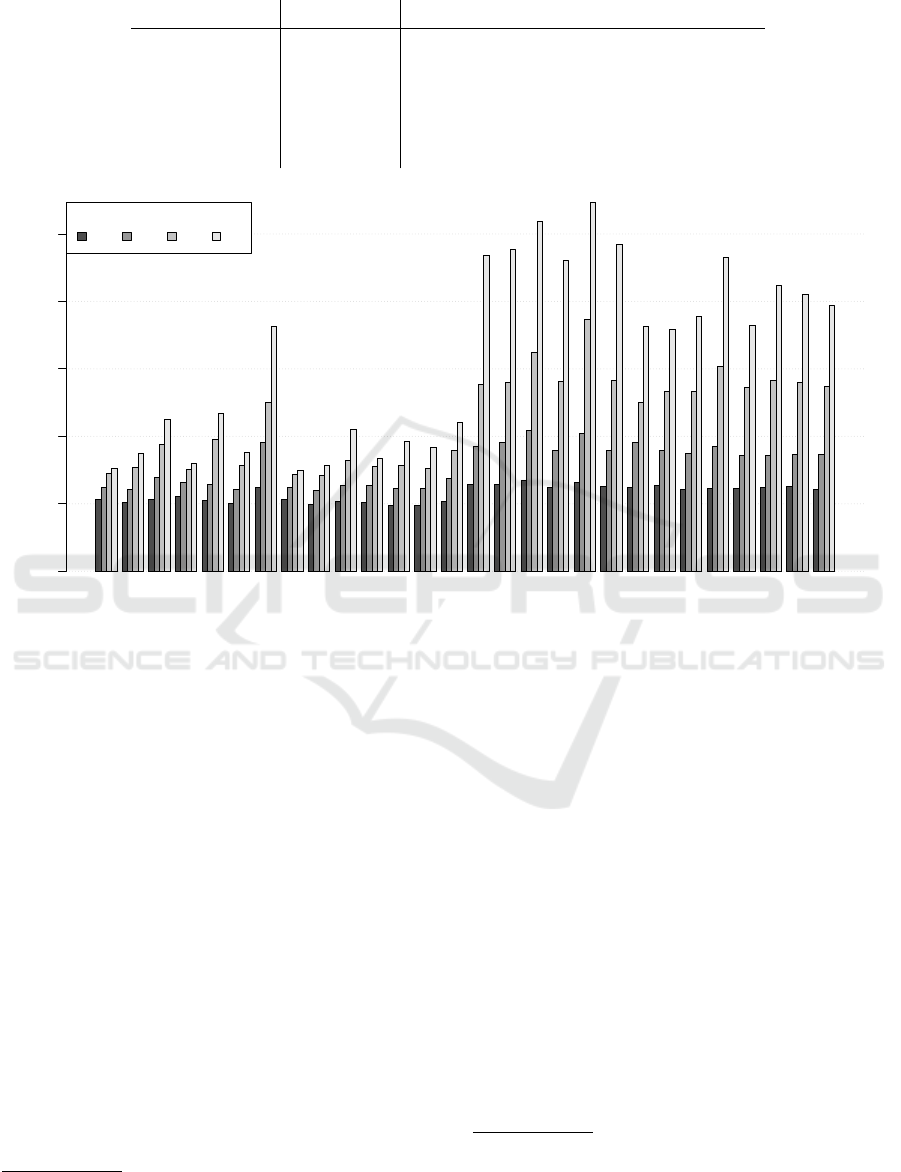
Table 4: Pickup model combinations examined.
Pickup type
Forecast type Time-series model
1. Additive 1. Classical
1. Historical average by day-of-week (HA)
2. Exponential smoothing by day-of-week (ES)
3. Holt’s method by day-of-week (Holt)
2. Multiplicative 2. Advanced
4. ARIMA by day-of-week (ARIMA)
5. Holt-Winters (HW)
6. Season-Trend-Loess decomposition (STL)
7. Seasonal ARIMA models (SARIMA)
Add−Class−HA
Add−Class−ES
Add−Class−Holt
Add−Class−ARIMA
Add−Class−HW
Add−Class−STL
Add−Class−SARIMA
Add−Advan−HA
Add−Advan−ES
Add−Advan−Holt
Add−Advan−ARIMA
Add−Advan−HW
Add−Advan−STL
Add−Advan−SARIMA
Mult−Class−HA
Mult−Class−ES
Mult−Class−Holt
Mult−Class−ARIMA
Mult−Class−HW
Mult−Class−STL
Mult−Class−SARIMA
Mult−Advan−HA
Mult−Advan−ES
Mult−Advan−Holt
Mult−Advan−ARIMA
Mult−Advan−HW
Mult−Advan−STL
Mult−Advan−SARIMA
sMAPE
0
20
40
60
80
100
Add−Class−HA
Add−Class−ES
Add−Class−Holt
Add−Class−ARIMA
Add−Class−HW
Add−Class−STL
Add−Class−SARIMA
Add−Advan−HA
Add−Advan−ES
Add−Advan−Holt
Add−Advan−ARIMA
Add−Advan−HW
Add−Advan−STL
Add−Advan−SARIMA
Mult−Class−HA
Mult−Class−ES
Mult−Class−Holt
Mult−Class−ARIMA
Mult−Class−HW
Mult−Class−STL
Mult−Class−SARIMA
Mult−Advan−HA
Mult−Advan−ES
Mult−Advan−Holt
Mult−Advan−ARIMA
Mult−Advan−HW
Mult−Advan−STL
Mult−Advan−SARIMA
0
20
40
60
80
100
Forecast Horizon (days)
7 14 28 56
Figure 1: Symmetric mean absolute percent error (sMAPE) for CP1 under all forecast horizons, 7, 14, 28 and 56 days out.
3 RESULTS
In table 5 we present the performance measures from
all 28 pickup variations and all forecast horizons with
regards to carpark CP1
2
. As described before, the
methods have been used to forecast 7, 14, 28 and
56 days out and three metrics are employed to as-
sess their performance. Figure 1 presents the sMAPE
for each pickup variation. This chart reveals four fac-
tors which influence forecast accuracy, these are the
forecast horizon and the three pickup components,
namely the choice between classical or multiplicative
variations, the choice between advanced and classical
variations and the underlying time series model used.
2
Similar tables are obtained for all other carparks but are
omitted for brevity.
3.1 Forecast Performance of Models
To better understand how each of the three com-
ponents, which make up a pickup variation, affect
forecast performance, we examine them in isolation.
More precisely, to test component X, we group the
pickup variations by their X type and take the aver-
age over their sMAPE values. Doing this by forecast
horizon and carpark we can generate graphs for visual
comparison
3
.
• Additive or Multiplicative?
In figure 2 we test all variations based on their
3
The absolute numbers on the y-axis should not be used
as a measure of forecast performance in the analysis, but
one should rather use the relative performance of the differ-
ent types of the particular component X.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
20
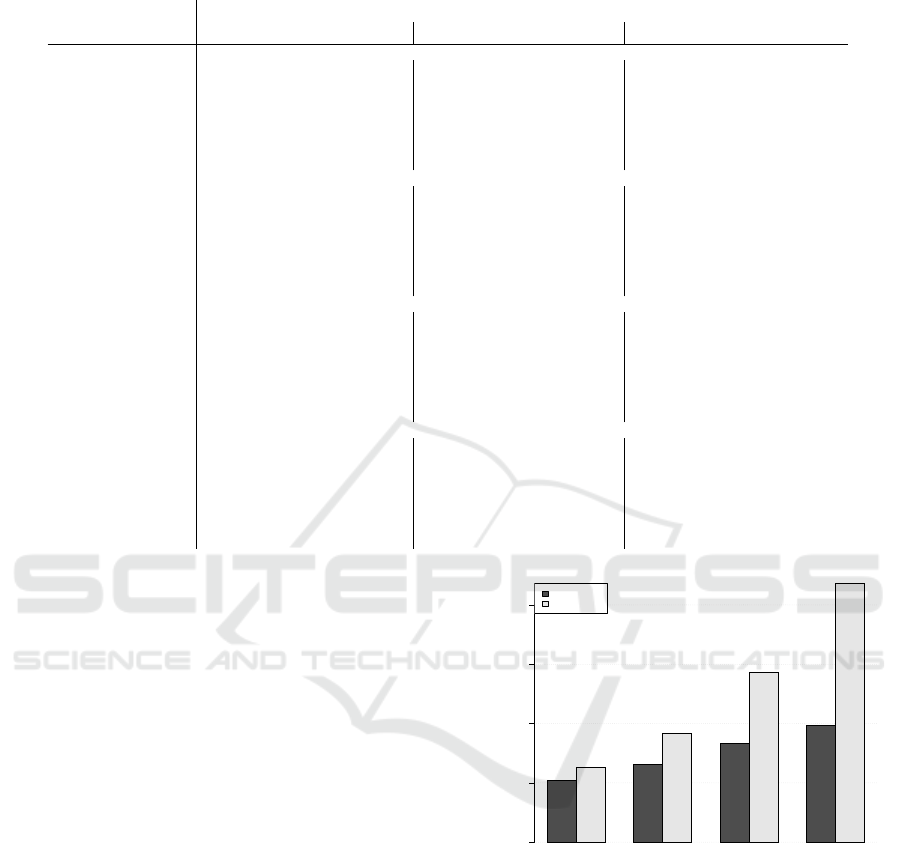
Table 5: Performance measures of pickup models under forecasting horizons, 7, 14, 28 and 56 days out. Carpark: CP1.
Pickup model
MAE sMAPE RMSE
7 14 28 56 7 14 28 56 7 14 28 56
Add-Class-HA 27.93 33.07 39.07 40.06 21.28 24.87 29.10 30.42 36.04 42.99 48.99 50.38
Add-Class-ES 26.42 32.04 41.19 47.09 20.28 24.40 30.73 34.89 34.61 43.15 53.61 59.43
Add-Class-Holt 27.69 36.05 48.63 60.38 21.15 27.89 37.59 45.13 35.57 49.83 67.45 80.54
Add-Class-ARIMA 28.69 34.42 40.06 41.28 22.18 26.26 30.29 31.99 37.11 45.15 51.77 52.07
Add-Class-HW 26.42 32.51 48.78 60.20 20.97 25.83 38.97 46.74 34.81 45.12 64.41 74.97
Add-Class-STL 25.33 31.11 41.04 46.39 19.99 24.18 31.29 35.16 33.73 42.18 53.38 58.38
Add-Class-SARIMA 30.90 45.57 64.61 103.50 24.96 38.11 49.94 72.44 41.96 60.35 84.99 138.37
Add-Advan-HA 27.93 32.95 38.76 39.48 21.28 24.77 28.76 29.94 36.04 42.82 48.79 49.44
Add-Advan-ES 25.68 31.06 38.08 41.65 19.95 23.93 28.52 31.24 33.57 41.14 49.61 52.87
Add-Advan-Holt 27.11 33.71 45.28 59.14 20.56 25.33 32.93 41.95 35.03 45.04 61.50 77.12
Add-Advan-ARIMA 26.49 33.06 41.76 45.01 20.44 25.44 30.96 33.56 34.25 43.31 53.11 60.88
Add-Advan-HW 24.42 30.76 40.63 49.83 19.61 24.64 31.52 38.39 31.97 40.82 53.78 61.15
Add-Advan-STL 24.69 31.32 39.87 49.07 19.58 24.56 30.39 36.77 32.70 40.96 52.23 60.26
Add-Advan-SARIMA 26.05 34.61 47.32 60.92 20.82 27.47 35.80 44.12 33.95 45.26 60.09 76.52
Mult-Class-HA 35.60 56.27 90.72 165.63 25.69 37.13 55.44 93.60 45.78 75.05 126.19 277.68
Mult-Class-ES 35.62 62.58 93.10 175.66 25.68 38.08 56.09 95.51 47.34 100.95 132.91 305.30
Mult-Class-Holt 38.37 74.30 109.87 257.00 26.86 41.64 64.75 103.76 51.24 129.89 158.61 556.16
Mult-Class-ARIMA 34.18 53.01 90.51 147.93 24.97 35.74 56.35 92.28 44.78 71.01 127.40 236.11
Mult-Class-HW 36.60 67.54 147.18 241.73 26.27 40.77 74.69 109.34 48.32 121.63 324.77 404.13
Mult-Class-STL 35.04 58.54 97.35 181.89 25.18 35.77 56.52 97.03 47.04 101.42 152.07 312.20
Mult-Class-SARIMA 30.90 45.57 64.61 103.50 24.96 38.11 49.94 72.44 41.96 60.35 84.99 138.37
Mult-Advan-HA 34.83 52.08 86.58 210.99 25.49 35.74 53.27 71.80 44.47 67.14 121.39 448.30
Mult-Advan-ES 32.56 51.55 91.97 195.98 24.20 34.85 53.32 75.44 41.57 70.53 143.08 333.87
Mult-Advan-Holt 34.39 57.55 119.38 341.33 24.68 36.95 60.72 92.99 46.77 85.66 207.52 649.49
Mult-Advan-ARIMA 32.75 49.01 86.63 173.32 24.63 34.42 54.38 72.92 42.45 65.08 122.94 305.91
Mult-Advan-HW 34.32 52.66 140.92 318.52 24.99 34.42 56.48 84.80 45.00 79.73 442.80 805.13
Mult-Advan-STL 34.71 53.47 130.82 279.73 25.20 34.74 55.84 82.00 46.90 82.27 449.37 825.88
Mult-Advan-SARIMA 33.36 51.64 96.25 217.97 24.22 34.71 54.81 78.87 43.65 70.43 139.45 409.44
additive or multiplicative type. Additive pickup
models seem to have outperformed the multiplica-
tive ones. In general, additive methods are more
robust as they still perform reasonably well for
longer horizons. In contrast, multiplicative meth-
ods seem to perform reasonably well for shorter
horizons, but quickly deteriorate as we move fur-
ther out in the future. Given that multiplicative
variations apply a percentage ratio to the onhand
bookings in order to obtain the final arrivals, it
implies that on-hand bookings are crucial to this
calculation; as we attempt to forecast further out
in the future, the underlying onhand bookings are
very low and highly volatile, which results in in-
flated projections.
• Advanced or Classical?
In figure 3 we compare all variations based on
their classical or advanced type. Both approaches
seem to perform similarly; advanced pickup mod-
els perform marginally better than classical ones,
with the improvement in performance to become
more apparent at longer horizons. There are two
reasons that cause this; first, advanced models
use all completed and partially completed book-
ing curves in forecasting, a strategy that more ef-
fectively utilises the short term dynamics of the
h7 h14 h28 h56
Forecast horizon (days)
sMAPE
0
20
40
60
80
h7 h14 h28 h56
0
20
40
60
80
additive
multiplicative
Figure 2: Comparison of additive versus multiplicative vari-
ations. sMAPE for CP1 under all forecast horizons, 7, 14,
28 and 56 days out.
data as these are unfolding. Second, advanced
pickup models split the forecast horizon down by
reading day and perform a forecast for each read-
ing day separately. Having the data disaggregated
down by reading day prevents the loss of data
that would have been caused from aggregating.
The further out we forecast, the larger is the ag-
gregated bookings-to-come forecast required and
given that in classical pickup this is all estimated
as a whole, leads to lower forecast accuracy.
A Comparative Analysis of Pickup Forecasting Methods for Customer Arrivals in Airport Carparks
21
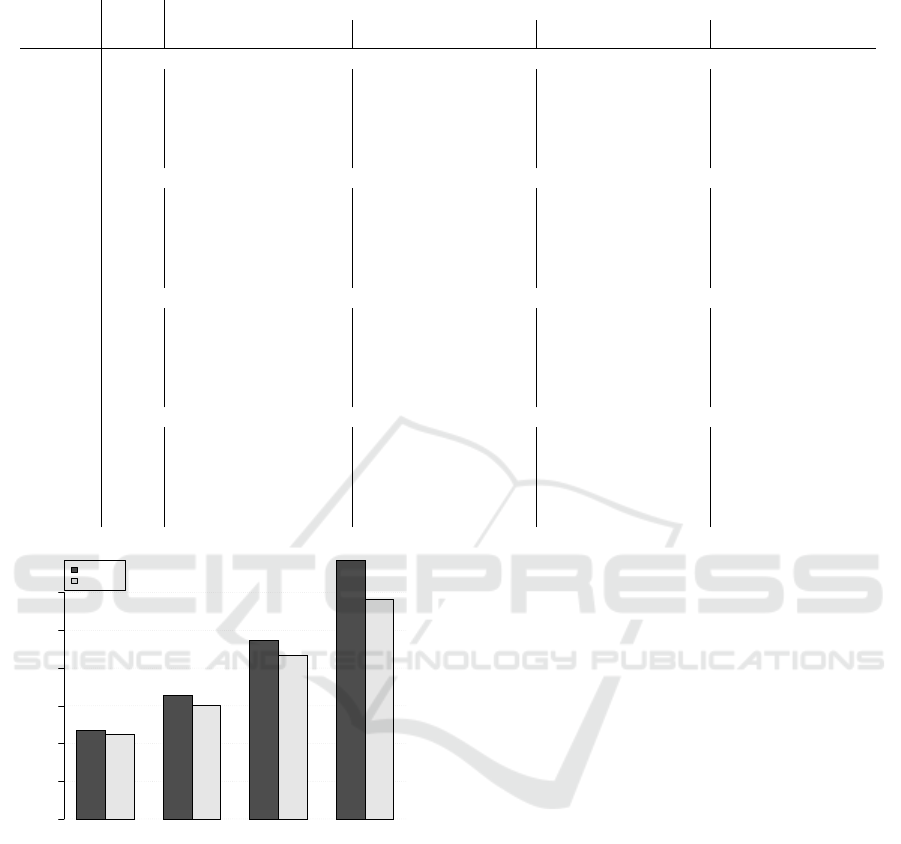
Table 6: Best five pickup models for each carpark.
Carpark Rank
Days out (h)
7 14 28 56
CP1
1 Add-Advan-HW Add-Advan-ES Add-Advan-HA Add-Advan-HA
2 Add-Advan-STL Add-Advan-HW Add-Advan-ES Add-Class-HA
3 Add-Advan-ES Add-Class-STL Add-Class-HA Add-Class-ARIMA
4 Add-Class-STL Add-Advan-STL Add-Class-ARIMA Add-Advan-ES
5 Add-Class-ES Add-Class-ES Add-Advan-STL Add-Class-STL
CP2
1 Add-Advan-ES Add-Class-ARIMA Add-Advan-ES Add-Class-ARIMA
2 Add-Class-ES Add-Advan-ES Add-Advan-HA Add-Class-HA
3 Add-Class-ARIMA Add-Advan-HA Add-Class-ARIMA Add-Advan-ES
4 Add-Advan-ARIMA Add-Class-HA Add-Class-HA Add-Advan-HA
5 Add-Advan-STL Add-Advan-HW Add-Class-ES Add-Class-ES
CP3
1 Add-Class-SARIMA Add-Advan-ES Add-Advan-ES Add-Class-ARIMA
2 Add-Advan-ES Add-Class-ARIMA Add-Advan-STL Add-Class-HA
3 Mult-Class-SARIMA Add-Advan-ARIMA Add-Advan-HW Add-Advan-ES
4 Add-Class-ES Add-Advan-HA Add-Advan-HA Add-Advan-HA
5 Add-Advan-HW Add-Advan-HW Add-Class-ARIMA Add-Advan-STL
CP4
1 Mult-Advan-SARIMA Add-Advan-ES Add-Advan-ES Add-Advan-ES
2 Add-Advan-STL Add-Advan-STL Add-Advan-STL Add-Advan-STL
3 Add-Advan-ES Add-Advan-ARIMA Add-Advan-HW Add-Advan-HW
4 Add-Advan-HW Add-Advan-HW Add-Advan-ARIMA Add-Class-ES
5 Mult-Class-STL Add-Advan-SARIMA Add-Advan-HA Add-Advan-HA
h7 h14 h28 h56
Forecast horizon (days)
sMAPE
0
10
20
30
40
50
60
h7 h14 h28 h56
0
10
20
30
40
50
60
classical
advanced
Figure 3: Comparison of classical versus advanced varia-
tions. sMAPE for CP1 under all forecast horizons, 7, 14, 28
and 56 days out.
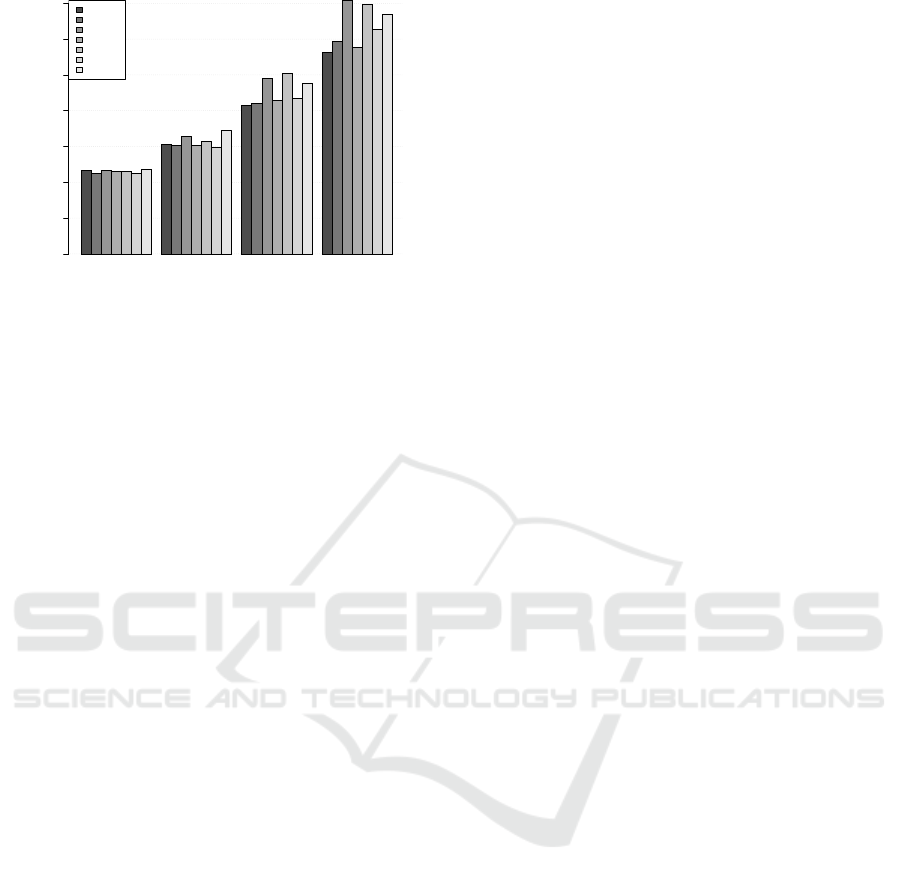
• Which Time-series model?
In figure 4 we test all variations based on their un-
derlying time series model used. For short fore-
casts horizons (h=7, 14) the most sophisticated
models seem to have been the favourites while for
longer horizons (h=28, 56) simpler models have
at least performed as well. More precisely, time
series models like HW, STL and SARIMA per-
formed very well for h = 7, indicating dealing
explicitly with seasonality, as opposed to remov-
ing, is the best approach with regards to short-
term forecasting. As we gradually step into longer
horizons, especially for h = 28, 56, simple his-
torical or weighted averages by day-of-week be-
gin to gain attention. This is because, the further
out we forecast the less the intra-day effects are
and the stronger the weekly seasonality becomes,
which implies that focusing on same days of the
week and applying a simpler forecast on the re-
sulting series gives reasonable forecasts. Note that
ARIMA and SARIMA models variations do ap-
pear among the top five in most instances but the
computations times, being much higher than the
other models, render them less attractive in prac-
tice.
3.2 Best Overall Pickup Models
Table 6 summarises the best five winning variations
based on forecast performance, by carpark and by
forecast horizon (as described in section 2.4). Our
study identified that additive advanced combinations
dominate for both carparks and all forecast horizons;
out of the eighty total instances that make up the top
five list for all horizons and carparks, only one third
are classical models, while only three instances refer
to multiplicative model variations. STL and HW seem
to be the dominant methods as they most of the times
ranked among the top five in both carparks and all
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
22
h7 h14 h28 h56
Forecast horizon (days)
sMAPE
0
10
20
30
40
50
60
70
h7 h14 h28 h56
0
10
20
30
40
50
60
70
HA
ES
Holt
ARIMA
HW
STL
SARIMA
Figure 4: Comparison of variations based on the underly-
ing time series models. sMAPE for CP1 under all forecast
horizons, 7, 14, 28 and 56 days out.
forecasting horizons. Simpler models such as HA and
ES have also shown to be consistent and performed
well, and for longer horizons they claimed top spots.
4 CONCLUSION
In this paper, we have presented 28 variations of
the pickup method. Experiments were conducted on
reservations data from four airport carparks of a major
airport in UK. The performance of each model vari-
ation was evaluated under three different error mea-
sures and for different forecast horizons, spanning
from 1 week to 8 weeks out. Our study has shown
that the best practice is to use a combination of mod-
els; perhaps a highly sophisticated model for short-
term forecasting and a simple weighted moving aver-
age for longer forecasting.
Our research aims to examine further the role of
the training set in forecast performance. More pre-
cisely, the training set can be of two types; “fixed”
for a pre-determined training size that rolls for-
ward as time progresses and updates accordingly, or
“growing” that increases with time and thus always
uses all the available data. Moreover, already under
progress is the examination of regression forecasting
models which we aim to compare against the best
pickup methods. Regression model variations relate
the total arrivals to the on-hand ones with the possibil-
ity to include other factors such as weekly seasonality,
linear trends or even flight information. Finally, we
are intrigued in exploiting the potential of combining
two or more forecasts to ultimately obtain a more ac-
curate combined forecast.
REFERENCES
Cleveland, R., Cleveland, W., McRae, J., and Terpenning,
I. (1990). Seasonal-trend decomposition procedure
based on loess. Journal of official satistics, 6(1):3–73.
Hyndman, R. and Khandakar, Y. (2007). Automatic time
series forecasting: the forecast package for r. URL
http://www. jstatsoft. org/v27/i03.
Hyndman, R., Koehler, A. B., Ord, J. K., and Snyder, R. D.
(2008). Forecasting with exponential smoothing: the
state space approach. Springer.
Hyndman, R. J., Koehler, A. B., Snyder, R. D., and Grose,
S. (2002). A state space framework for automatic fore-
casting using exponential smoothing methods. inter-
national Journal of Forecasting, 18(3):439–454.
Lee, A. O. (1990). Airline reservations forecasting; prob-
abilistic and statistical models of the booking pro-
cess. PhD thesis, Massachusetts Institute of Technol-
ogy, MIT.
Makridakis, S., Wheelwright, S. C., and Hyndman, R. J.
(2008). Forecasting methods and applications. John
Wiley & Sons.
Papayiannis, A., Johnson, P., Yumashev, D., and Duck,
P. (2013). Continuous-time revenue management in
carparks - part two: Refining the pde. In Proceed-
ings of the 2nd International Conference on Opera-
tions Research and Enterprise Systems, pages 76–81.
ICORES, SciTePress Digital Library.
Papayiannis, A., Johnson, P., Yumashev, D., Howell, S.,
Proudlove, N., and Duck, P. (2012). Continuous-
time revenue management in carparks. In Proceed-
ings of the 1st International Conference on Opera-
tions Research and Enterprise Systems, pages 73–82.
ICORES, SciTePress Digital Library.
P
¨
olt, S. (1998). Forecasting is difficult–especially if it
refers to the future. In Reservation and Yield Man-
agement Study Group Annual Meeting Proceedings,
Melbourne, Australia. AGIFORS.
Rojas, D. (2006). Revenue management techniques ap-
plied to the parking industry. Master’s thesis, School
of Industrial and Systems Engineering, University of
Florida.
Sa, J. (1987). Reservations forecasting in airline yield man-
agement. Technical report, Flight Transportation Lab-
oratory, Massachusetts Institute of Technology.
Shumway, R. H., Stoffer, D. S., and Stoffer, D. S. (2000).
Time series analysis and its applications: with R ex-
amples. Springer.
Weatherford, L. and P
¨
olt, S. (2002). Better unconstraining
of airline demand data in revenue management sys-
tems for improved forecast accuracy and greater rev-
enues. Journal of Revenue and Pricing Management,
1:234–254.
Weatherford, L. R. and Kimes, S. E. (2003). A comparison
of forecasting methods for hotel revenue management.
International Journal of Forecasting, 19(3):401–415.
Weatherford, L. R., Kimes, S. E., and Scott, D. A. (2001).
Forecasting for hotel revenue management: Testing
aggregation against disaggregation. The Cornell Ho-
A Comparative Analysis of Pickup Forecasting Methods for Customer Arrivals in Airport Carparks
23

tel and Restaurant Administration Quarterly, 4(4):53–
64.
Wickham, R. R. (1995). Evaluation of forecasting tech-
niques for short-term demand of air transportation.
Master’s thesis, Massachusetts Institute of Technol-
ogy, Dept. of Aeronautics & Astronautics, Flight
Transportation Laboratory, Cambridge, MA.
Zakhary, A., Neamat, E. G., and Amir, F. A. (2008). A com-
parative study of the pickup method and its variations
using a simulated hotel reservation data. ICGST In-
ternational Journal on Artificial Intelligence and Ma-
chine Learning, pages 15–21.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
24
