
Search for Latent Periodicity in Amino Acid Sequences with
Insertions and Deletions
Valentina Pugacheva
1
, Alexander Korotkov
2
and Eugene Korotkov
1,2
1
Institute of Bioengineering, Research Center of Biotechnology of the Russian Academy of Sciences, Leninsky
Ave. 33 bld. 2, 119071, Moscow, Russia
2
National Research Nuclear University “MEPhI”, Kashurskoe shosse, 31. Moscow 115409, Russia
Keywords: Genetic Algorithm, Latent Periodicity, Dynamic Programming, Amino Acid Sequences.
Abstract: The aim of this study was to show that amino acid sequences have a latent periodicity with insertions and
deletions of amino acids in unknown positions of the analyzed sequence. Genetic algorithm, dynamic
programming, and random weight matrices were used to develop the new mathematical algorithm for latent
periodicity search. The method makes the direct optimization of the position-weight matrix for multiple
sequence alignment without using pairwise alignments. The developed algorithm was applied to analyze the
amino acid sequences of a small number of proteins. This study showed the presence of latent periodicity
with insertions and deletions in the amino acid sequences of such proteins, for which the presence of latent
periodicity was not previously known. The origin of latent periodicity with insertions and deletions is
discussed.
1 INТRODUCTION
The development and application of mathematical
methods in the study of symbolic sequences is of
particular importance to achieve great success in the
sequencing of various genomes. It also increases the
accumulation of information about the complete
genomes of many species (Ekblom and Wolf, 2014).
If mathematical methods are not applied, a big part
of the known nucleic and amino acid sequences will
be stored away in computer data banks, without
significant usage. This is especially true for
eukaryotic genomes. The task of developing new
mathematical methods entails finding new
mathematical laws to explain sequence organization
and the relationship of these laws with the biological
functions of various parts of the genome (Almirantis
et al., 2014). These studies show the relationship
between certain mathematical regularities observed
in sequences with their biological properties.
Latent periodicity is one of the structural
regularities of sequences and is widely represented
in amino and DNA sequences (Korotkov et al.,
2003a, 2003b). A periodicity is considered as latent
if the similarity between any two periods is not
statistically significant or if it belongs to the twilight
zone (Durbin et al., 1998). Perfect periodicity can
become latent periodicity if it accumulates over 1.0
mutations per amino acid in the studied sequence
(Suvorova et al., 2014). The distinctive property of
latent periodicity is that it cannot be detected by
pairwise comparisons of amino acid sequences
(Turutina et al., 2006). However, latent periodicity
can be found if we apply a mathematical method to
directly detect the multiple alignment of amino acid
sequences without constructing pairwise alignments.
The periods of a sequence with latent periodicity are
sequences for multiple alignment and the multiple
alignment can be statistically significant. The goal of
this study was to find multiple alignments of amino
acid sequences (periods) in the absence of
statistically important pairwise alignments.
There is a significant gap in the mathematical
approaches presently used to search for latent
periodicities in symbolic and numeric sequences.
Spectral approaches enable the discovery of enough
"fuzzy" periodicity in protein sequences without
insertion(s) or deletion(s) of amino acids. Fourier
transform, wavelet transform, information
decomposition and some other methods can be
attributed to a number of spectral methods (Tiwari et
al., 1997; Lobzin and Chechetkin, 2000;
Kravatskaya et al., 2011; Korotkov et al., 2003a; de
Pugacheva, V., Korotkov, A. and Korotkov, E.
Search for Latent Periodicity in Amino Acid Sequences with Insertions and Deletions.
DOI: 10.5220/0005630401170127
In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 3: BIOINFORMATICS, pages 117-127
ISBN: 978-989-758-170-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
117

Sousa Vieira, 1999; Meng et al., 2013; Suvorova et
al., 2014; Sosa et al., 2013; Kumar et al., 2006).
However, these approaches have a significant
limitation, such as the fact that they do not allow the
detection of periodicity with insertions and
deletions.
On the other hand, methods based on dynamic
programming can accurately find insertions and
deletions (Pellegrini, 2015). However, methods
based on dynamic programming cannot detect latent
periodicity, in a situation where the statistical
significance of similarity between any two periodic
sequences is small (Korotkov et al., 2003; Turutina
et al., 2006). This is due to the fact that the
periodicity of amino acid sequences (with the
number of periods greater than or equal to 4) was
detected by pairwise alignment between periods. In
the absence of statistically significant pairwise
alignments, these approaches are incapable of
finding latent periodicity. First of all, it concerns
algorithms and programs such as REP (Andrade et
al., 2000), Internal Repeat Finder (Marcotte et al.,
1999), Prospero (Mott, 1999), RADAR (Heger &
Holm, 2000), REPRO (Heringa & Argos, 1993)
TRUST (Szklarczyk & Heringa, 2004) and
PTRStalker (Pellegrini et al., 2012). It is also
difficult to detect latent periodicity by the programs
XSTREAM (Newman & Cooper, 2007) and T-
REKS (Jorda & Kajava, 2009) because the similarity
between different periods is very low in the case of
latent periodicity. This leads to lack of seeds and
identical short strings. The Markov models and
neural networks are inefficient for finding latent
periodicity, since there are no training samples. The
following programs were used in previous studies
HHrep (Söding et al., 2006), HHRepID (Biegert &
Söding, 2008) and the approaches developed in the
works of Palidwor et al. (2009) and Rubinson &
Eichman (2012).
Therefore, in this study a mathematical method
was proposed that considers this gap and finds the
latent periodicity of any symbolic sequence in the
presence of insertions and deletions (in unknown
positions of the analyzed sequence) and in the
absence of a known position-weight matrix.
Any periodicity of the sequence S with length N
can be characterized by either the frequency matrix
(Korotkov et al., 2003b) or the position-weight
matrix M (Shelenkov et al., 2006) calculated from
frequency matrix. Amino acids are the signs of the
rows of this matrix while period positions serve as
the signs of the columns. The element of this matrix
m(i,j) indicates the weight which has the amino acid
i in position j of the period. The positions of the
period changed from 1 to n. The sequence S
1
of
length N, which is an artificial periodic sequence
1,2,...,n, was introduced. Here, the numbers were
treated as symbols and columns in the matrix M
were consistent with them. For a period equal to n,
the sequence S corresponds to a certain frequency
matrix and weight matrix M(20,n). The problem was
formulated as follows. We have a sequence S with
length N. It is necessary to find such optimal
weighting matrix M
0
, where the local alignment of
sequences S
1
and S have the greatest statistical
significance. Under the statistical significance, the
probability P is that F
r
> F
max
, where F
max
is the
maximum weight of a local alignment of sequences
S
r
and S
1
, using the some optimal matrix M
0
. Here,
F
r
is the maximum weight of a local alignment of
randomly mixed sequences S
r
and S
1
using the some
optimal matrix M
r
. We search a matrix M
0
, which
have the lowest probability P. It is always possible
to set the threshold level of the probability P
0
and if
the probability P(F
r
>F
max
) is less than P
0,
then a
local alignment of sequences S and S
1
is found
,
using
the some optimum matrix M
0
and this alignment can
be considered as statistically significant.
It is possible to use the local alignment
algorithm, for alignment of the amino acid sequence
S and an artificial periodic sequence S
1
, relative to
the known weight matrix (Smith and Waterman,
1981). It is necessary to find the optimal weight
matrix M
0
. The objective of this study was to
develop a mathematical approach for finding the
matrix M
0
, as well as a method for assessing the
probability P. To find the optimal weight matrix, a
genetic algorithm was used, as well as a local
alignment algorithm. The Monte Carlo method was
used to estimate the probability P.
A mathematical method was developed in this
paper to find more than 3 tandem repeats in amino
acid sequences. The method was used for direct
optimization of the position-weight matrix for
multiple sequence alignment without using pairwise
alignments. This means that for each n, a matrix M
0
is found, the probability P is estimated and we build
the alignment of the sequences S and S
1
using M
0
matrix. It is not the goal of this study to analyze all
the known amino acid sequences, since the
developed method requires very large computer
resources. The developed algorithm was applied to
search for latent periodicity with insertions and
deletions in the amino acid sequences of a small
number of proteins This study showed the presence
of latent periodicity with insertions and deletions in
the amino acid sequences of proteins, for which the
presence of latent periodicity was not previously
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
118
known.
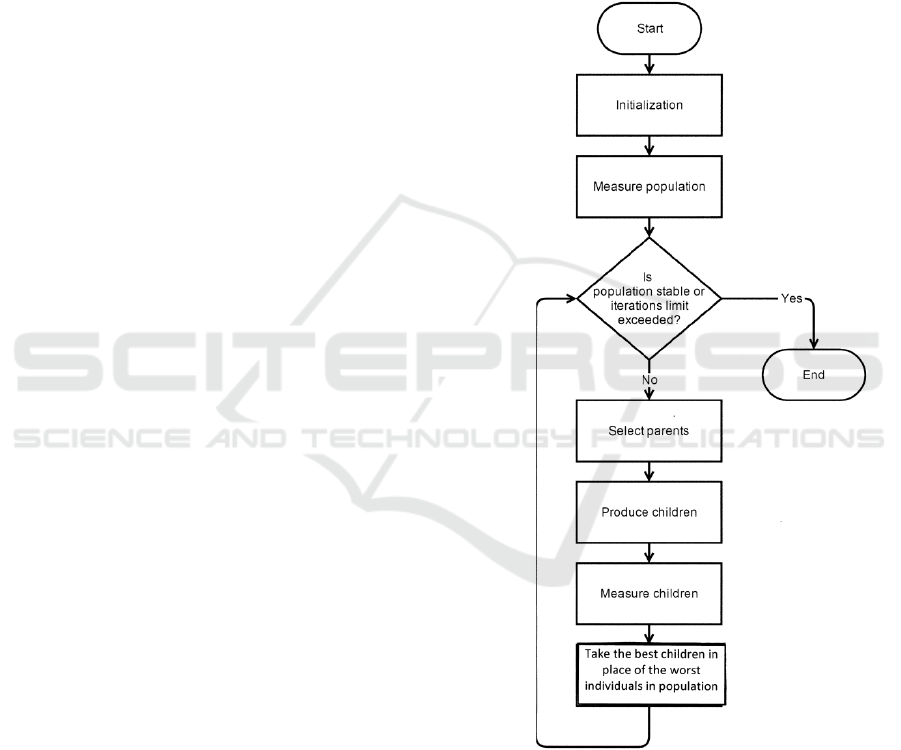
2 MATHEMATICAL METHODS
AND ALGORITHMA
A genetic algorithm was used to search for the
optimal weight matrix M
0
for period n. A genetic
algorithm is a heuristic search algorithm for solving
optimization problems and is a form of direct
random search (Mitchell, 1998). It is often used to
optimize the functions of several variables. The
general view of the algorithm is as shown in Figure
1. Usually, the problem is formalized, so that a
solution could be found as a vector, where each
element can be a bit, a number, or some other object.
This vector is considered as an "organism." Usually,
a set of initial organisms are randomly created
(Gondro and Kinghorn, 2007). Each of these
organisms was measured using an objective
function, which is regarded as a "fitness function."
As a result, every organism is associated a certain
fitness value, which determines how well the
organism solves the problem. Organisms are
selected from this set of organisms (it can be called
“generation”) for application of the "genetic
operators" (“crossing” and “mutation”, taking into
account the value of “fitness”). The new organisms
were gotten as a result of the application of these
operators. The value of fitness was also calculated
for new organisms, and then selection of the best
organisms to the next generation was done. This set
of actions was repeated iteratively, and thereby
simulating the "evolutionary process". This process
was allowed to continue for several life cycles
(generations), before executing the stop criterion of
the algorithm. Such a criterion can be either finding
the global or suboptimal solutions or exhaustion of
the number of generations released for evolution. In
this study, the organisms are the weighting matrix of
the periodicity. This set was called Q
n
or population.
Each matrix has 20 rows and n columns. Matrix
elements m(i,j) are some numbers that show the
weight amino acids i to column number j. A larger
weight of the element m(i,j) corresponds to a high
probability of the presence of the amino acid i at
position j of the period. As the assessment of fitness
(objective function) for the organism (weight matrix
M), the maximum value of the similarity function
F
max
was considered for the local alignment
(Altschul et al., 1990). A local alignment was built
between the sequences S
1
and S, using a weight
matrix M to calculate the objective function. The
calculation of F
max
was conducted for each organism
(weight matrix M). The process was repeated after
applying genetic operators to the organisms. The
process was stopped after a stable population was
achieved, that is, increase in the values of F
max
was
stopped. As a result, the matrix M
0
was defined for
the period length n with the greatest F
max
. The
alignment of sequences S
1
and S was well built using
the matrix M
0
. The algorithm discussed is as shown
in Figure 1. The algorithm was repeated for n from 2
to 100.
Figure 1: The main stages of the genetic algorithm used in
the study.
2.1 Initialization
The first step of the algorithm is to provide a zero
generation of organisms (weight matrix in our case)
for the local alignment. A random population of
organisms was selected as zero generation. The zero
generation of organisms must be maximally diverse
Search for Latent Periodicity in Amino Acid Sequences with Insertions and Deletions
119
in order to more quickly achieve a stable population
and find matrix M
0
, maximum of F
max
. Organisms
(matrix of the size 20×n) can be viewed as points in
space with a size of 20×n. It is possible to achieve
the maximum diversity of organisms, if the points
are selected in space 20×n spaced at a distance
D>D
0
. The coordinates of these points are the initial
matrices (organisms). The distance between both
matrices (organisms), the Euclidean distance
between the two points in space 20xn, was taken.
20
2,0
1 2
1 1
( ( , ) ( , ))
n
i j
D m i j m i j
(1)
where m
1
(i,j) and m
2
(i,j) are elements of the two
matrices (M
1
and M
2
) compared. The population size
should be large enough. Organisms having a high
fitness function are distributed too quickly in
populations with a small size. The population
becomes homogeneous and the probability of
continuation of the evolution becomes very small.
This means that the algorithm can find the local
rather than the global maximum of F
max,
in the case
of a small population size. At the same time,
descendants produced in large populations are likely
to be more varied, although an increase in F
max
is
much slower. A population size equal to 10
4
was
used for all the results presented here. These 10
4
weight matrices were chosen so as to cover the space
20×n, as fully as possible. Each matrix M (organism)
was created by comparing the sequence S
1
with a
random sequence of length N. The random sequence
Sr
i
was obtained by mixing the original sequence S,
with i varied from 1 to 10
4
. The frequency matrix
V(20,n) was completed as follows. To elements of
the matrix v(sr(k),s
1
(k)), a value of 1 was added for
all k from 1 to N, where sr(k) is an element of the
sequence Sr
i
. Then, based on the matrix V, the
weighting matrix M(20,n) was calculated as:
( , ) ( , )
( , )
( , ) 1 ( , )
v i j Np i j
m i j
Np i j p i j
(2)
where the partial sums for lines are
( ) ( , )
j
x i v i j
and for columns are
( ) ( , )
i
y j v i j
,
,
( , )
i j
N v i j
and probabilities
2
( , ) ( ) ( )
p i j x i y j N
. If this
matrix is the first in the population, then it is
automatically included in the initial population. If
this matrix is not the first matrix, it is compared with
all the matrices (organisms) already included in the
population and the distance from each matrix was
calculated using Formula 1. If the distances are
greater than the D
0,
then the matrix is included in the
initial population. Otherwise, this matrix is rejected
and a new matrix is created. The level of D
0
was
chosen so that the initial population will have from
10
4
to 1.05×10
4
from 5×10
5
random matrices. Let us
call the population of organisms (matrices) as Q
n
.
2.2 Calculation of Fitness and
Statistical Significance of the
Organism
After the birth of a new organism (creating a new
matrix M), the first step is to assess the fitness of the
organism. This is the determination of F
max
of the
local alignment (Smith and Waterman, 1981) for
sequences S
1
and S, using a weighting matrix M. The
higher the value, F
max
corresponds to a better
alignment and to a lower probability P(F
r
>F
max
).
The fitness of the organism (chapter 2) is higher for
larger values of F
max
. In more detail, the construction
of a local alignment is discussed subsequently in
paragraph 2.6. After completion of the genetic
algorithm, an argument of the normal distribution
for the organism M
max
(which have the highest F
max
)
was calculated using the formula:
max
max
mk
F M F
Z
D F
(3)
where
1 2
max
max max max
, ,...,
N
F F F F
are the maximum
weights of the local alignments between random
sequence Sr
i
and the sequence S
1
, is determined
using the best weight matrix M
max
.
Calculation of the vector
max
F
was performed
using random sequences Sr
i
derived from the amino
acid sequence S by random mixing. In total, 200
random sequences were created (N
R
= 200). The
necessity of using values Z
mk
instead of F
max
at the
end of the calculation, is due to the fact that the
direct calculation of the probability P(F
r
>F
max
) is
difficult, because of the very large amount of
computations. Furthermore, while reducing the
probability P(F
r
>F
max
), the amount of computations
grew very quickly and for a good periodicity in the
sequence S, the calculations could not be performed
within a reasonable time. Therefore, it is convenient
to use Z
mk
as a measure of statistical significance of
F
max
for the matrix M
max
. A similar calculation was
performed for all the investigated period of length n
and the dependence Z
mk
(n), was obtained.
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
120
2.3 Completion of the Genetic
Algorithm
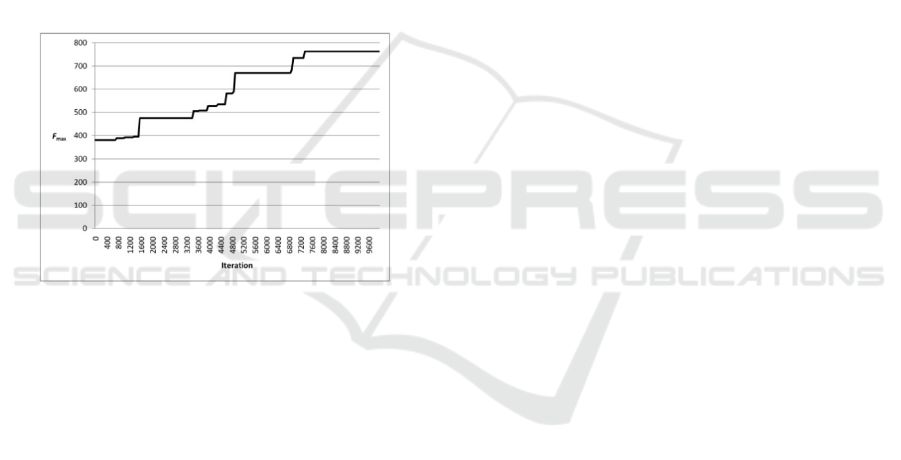
Proofs that the genetic algorithm necessarily reach
the global optimum, even for an infinite number of
iterations, are currently non-existent (Mitchell,
1998). This necessitated the decision to stop the
algorithm adopted by the heuristic criteria.
Therefore, a decision was reached to use a
combination of the two most common genetic
algorithm stopping criteria (Banzhaf et al., 1998).
The evolutionary process was continued as long as
the best organism (matrix with the highest F
max
) will
not be repeated for several generations, or will limit
the number of iterations reached (10
4
). In this paper,
the resulting solution is considered as the found
global optimum. Figure 2 shows an example of the
growth of F
max
for the best organism in the
population.
Figure 2: The graph of growth of the fitness F
max
for the
best individual in the population in the process of
evolution.
2.4 Choice of Parents in the Genetic
Algorithm
The choice of parents was made using a combination
of approaches: the elite and fitness proportionate
selection, also known as roulette-wheel selection
(Bäck, 1996). To do this, firstly, all organisms were
sorted on the degree of F
max
increase and then, 20%
of organisms with the highest F
max
, were selected.
Thereafter, two parents were selected among them
with a probability that depends on the F
max
. If
i
max
F
is the fitness of the organism i in the population,
then the probability of the organism selection is as
follows:
1
/
K
i i
i max max
k
P F F
where K is the size of the
population. It is more likely that more adapted
organisms will be selected as parents, if this
approach is used. However, for the less fit
individuals, there is still a chance of being selected
for reproduction and survival during evolution. This
is an advantage over the purely elite strategy, despite
the impracticality, an organism (weighting matrix)
can contain successful portions (successful matrix
elements). Then, these properties of the organism
can be taken up by evolution and can contribute to
the global maximum.
2.5 Reproduction of Organisms
The recombination operator was used immediately
after the selection of parents for the creation of
descendants. The essence of recombination is that
created descendants should inherit genetic
information from both parents. Then, the mutation
operator was applied for each descendant.
2.5.1 Recombination of Organisms and the
Creation of Descendants
A combination of the two-point crossover and
differential crossing was used to create descendants.
In this case, the organisms (matrix) were considered
as a linear vector. This means that the matrix rows
were built one behind the other in a line. These
vectors were then closed in a ring formed by a
compound at the ends of these vectors. Then, the
random selection of two points on the ring was
performed and the segment from one ring was used
to replace the segment of the other ring (Fogel,
1998; Fogel, 2010). Two-point crossover showed an
improvement over the single point crossover.
Further addition of crossover points impairs the
activity of the genetic algorithm as the increased
destruction of organisms and evolutionary process
slows down (Spears and De Jong, 1991; Sywerda,
1989).
Afterwards, the intermediate recombination was
used. The values of "genes" of the organism (weight
matrix elements) other than the value of the parental
"genes", occur at an intermediate recombination.
This leads to the emergence of new organisms with
fitness that could be better than that of the parents.
Such recombination operator in the literature is
sometimes called differential crossing. If
x
and
y
are two organisms in a population (two weight
matrix with elements x(i,j)
и y(i,j)), then the
descendant is calculated by the formula (Radcliffe,
1991):
ij ij ij ij
z x x y
where i=1,2,...,20,
j=1,2,...,n and
0,1
are random values with a
uniform distribution. Here, the matrix of weights
(organism) was considered as a vector. To create
Search for Latent Periodicity in Amino Acid Sequences with Insertions and Deletions
121

descendants after the two-point crossover, two
parents were involved. Then, two descendants (w
and v) were formed using Formulae 4 and 5:
( , ) ( , ) 1 ( , )
w i j x i j y i j
(4)
( , ) 1 ( , ) ( , )
v i j x i j y i j
(5)
2.5.2 Creation of Mutations
By one of two methods, mutations were introduced
in the descendants W and V. The initial method of
introducing mutations (probability for each method
was 0.5) was randomly chosen. The first method
replaced the randomly selected element of the
weight matrix on a random number that is uniformly
distributed in the range from -1 to 1. The probability
for a replacement p
1
is equal to 0.01. All elements of
all descendants exposed a random change of values.
Changes were made to the whole matrix (all its
values) on some small value, in the second method
of making mutations. The intensity of the whole
matrix mutation was determined by the probability
p
2
, which was randomly selected from the range of
0.001 to 0.03. Each descendant element
( , )
w i j
of
the matrix
W
was replaced with a new element,
calculated according to the formula:
2
( , ) ( , ) ( , )
v i j w i j p w i j
where i=1,2,...,20 and j =
1,2, ..., n. After making mutational changes, the
fitness of descendants (W and V) was evaluated, that
is, F
max
was calculated for them. The descendant
with a maximum value of F
max
was added to the
population Q
n
. Concurrently, the worst organism
with the smallest value of F
max
was removed from
the population Q
n
. This method of replacing
organisms in the population maintains the
population size.
2.6 Construction of the Alignment and
Choice of Weight for Deletion
2.6.1 Alignment of Amino Acid Sequence
using the Random Matrices
A local alignment of sequences S
1
and S was
conducted using the weight matrices (organisms)
and affine function penalty for insertions and
deletions, to search F
max
and the matrix M
0
(Durbin
et al., 1998). To construct the alignment, the
matrices for similarity functions F, F
1
and F
2
were
filled for each matrix M from the population (set
Q
n
). Matrix M changed and turned into a matrix M'.
1
1
2
1
1
2
2
0
( 1, 1) '( ( ), ( ))
( , ) max
( 1, 1)
( 1, 1)
( 1, )
( , ) max
( 1, )
( , 1)
( , ) max
( , 1)
F i j m s i s j
F i j
F i j d
F i j d
F i j d
F i j
F i j e
F i j d
F i j
F i j e
(6)
where s
1
(i) and s(i) are letters from the sequences S
1
and S, d is the price for opening insertion or deletion
in the sequences S
1
and S, e is the price for the
continued insertion or deletion in the sequences S
1
and S. Here, i and j changed from 1 to N. The
matrices F, F
1
and F
2
have a dimension equal to
N×N, where N is the length of sequences S
1
and S.
F
max
was selected as the maximum element of the
matrix F. The coordinates of this element are i
m
and
j
m
.
Simultaneously, by calculating the matrixes F, F
1
and F
2
inverse transition matrix F' (same dimensions
as the matrix F) were also filled. Each element of the
matrix F’(i,j) contains the number of the matrix (1
for F, 2 for F
1
and 3 for F
2
) and the number of
element of the matrix F or F
1
or F
2
, which has a
maximum value in Formula 6. Using the inverse
transition matrix F’, the alignment of the sequences
S
1
and S was built. The path in the matrix F’ from
the point (i
m
, j
m
) to the point (i
0
, j
0
), corresponds to
the created alignment. At the first instance, the point
(i
0
, j
0
) F’ is equal to zero and serves as the beginning
of the alignment. The matrix M (organisms) from the
set Q
n
(population) was used to create the alignment
of sequences S
1
and S. For every matrix M from the
set Q
n
, the values R and K
d
were calculated before
carrying out the alignment as:
20
2 2
1 1
( , )
n
i j
R m i j
(7)
20
1 1
( , ) ( ) ( )
n
d
i j
K m i j f i t j
(8)
where f(i)=b(i)/N, b(i) is the number of amino acids
of type i in the sequence S, t(j)=1/n, N is the total
number of amino acids in the sequence S. For
calculation of the alignment, a changed matrix
'
M
has to satisfy two conditions. The first condition is
that R for the matrix
'
M
with the same period length
n would be identical and equal to 5(20n)
1/2
. The
dependence R~n
1/2
allows a similar distribution for
F
max
to be obtained, for a study of the different
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
122

random sequences Sr
i
. These random sequences
were obtained by mixing the original sequence S.
The second condition is that the distribution
functions for F
max
for each matrix from the set Q
n
should be close to each other. Such a distribution
function can be determined for each matrix from the
set Q
n,
if this matrix is used to calculate the
alignments of the sequence S with each random
sequence from the set Sr
i
. K
d
was selected for each
matrix from the set Q
n
which would provide
maximum identity
l
(see below this paragraph).
The above two conditions enabled the
replacement of the matrix M by the matrix that
satisfies Equations 7 and 8. Equation 7 is the
equation of the sphere in space 20×n and Equation 8
is an equation of the plane. If the matrix satisfies
these conditions, then it lies on the circle C formed
by the intersection of the sphere (Equation 7) by the
plane (Equation 8). Matrix M was considered as a
point in space 20×n and from this point, the nearest
point was taken which lies on the circle C. The
coordinates of this point are the desired matrix
'
M
.
It is possible to use Equations 7 and 8 and to
calculate the matrix
'
M
. Actually, it means that if
we have the constant R, K
d
, matrix M and calculate
f(i) for the sequence S, then the matrix
'
M
(if there
is the circle C) can be clearly defined. Matrix M’ is
used in Equation 6.
The next task was to choose the constant K
d
for
each matrix from the set Q
n
, which would provide
the maximum identity of the distribution function of
the F
max
. The average length of a random alignment
l
for each matrix from the Qn set, as the average
for difference (j
m
-j
0
) along with the calculation of the
distribution function of the F
max
. Here, j
m
is the
coordinate of F
max
in sequence S, j
0
is the coordinate
where F=0.0 in the calculation of the alignment
(coordinate of the beginning of the alignment in the
sequence S). The average length of the random
alignment chosen is equal to N/5. This value
provides the best determination of the alignment
boundaries with respect to the actual boundaries for
the model sequences of length N. As model
sequences, random sequences were selected for the
insertion of a local alignment with periodicity for
which Z> 10.0 (Korotkov et al,. 2003a) and length is
from N/10 to N/2.
The constant K
d
was selected iteratively. K
d
provides
l
to be approximately N/5 and obviously
lies in the range from K
1
=0 to K
2
=-20. Then, the
middle of this interval was taken. If
l
was more
than N/5, then K
1
=(K
1
+K
2
)/2 is calculated and if
l
is
less than N/5, K
2
=(K
1
+K
2
)/2 is calculated and the
process was repeated. Upon reaching the value
l
=N/5±20, selection of the constant K
d
stopped.
Random sequences were created by the
following algorithms. A number sequence was
generated using a random number generator of the
same length as the amino acid sequence. Thereafter,
the sequence of random numbers was arranged in
ascending order and the permutations made were
memorized. These changes were applied to the
amino acid sequence. Random amino acid sequences
of good quality were created by this algorithm.
2.6.2 Weights of the Deletions and Other
Constants
The constant d for each period n was determined
separately. The constant e was selected as 0.25d. A
total of 100 test sequences were analyzed which
were created for the period n as follows. Artificial
sequences were created with length equal to 1000
amino acids and contained a period n. The statistical
significance of this periodicity Z(n) defined by the
information decomposition method is equal to 7.0
(Korotkov et al., 2003a). Insertions or deletions were
introduced into the sequence randomly for every 50
amino acids. A constant d was chosen which
provides the greatest value Z
mk
by using Formula 3.
This value was applied for alignments using
weighting matrices from the set Q
n
.
2.7 Selection of the Threshold Z
0
Initially, Z
0
was estimated as the threshold for Z
mk
(n)
to cut the influence of statistical noise. The method
of this study was used to analyze 300 amino acid
sequences. Therefore, the estimation of Z
0
for 300
random amino acid sequences was done. The
sequence had a length equal to 600 amino acids and
a period equal to 19 amino acids with 1.5 random
changes per amino acid. To create the mutation,
random positions were chosen in the sequence.
Then, we changed the amino acid in a selected
position that was randomly chosen (with probability
which is equal for all amino acids). This was done
900 times for each sequence. From 4 to 15 inserts
having the length, one amino acid was added in each
sequence at random locations. This set was called
Q
19
. The ability of the developed approach to detect
periodicity in a multitude Q
19
was tested. The results
showed that periodicity can be detected in 93% of
cases. We believe it is possible to achieve 100%
result, but the number of iterations should be
increased to approximately 10
5
(see paragraph 2.3).
Then, these 300 sequences were analyzed and
Search for Latent Periodicity in Amino Acid Sequences with Insertions and Deletions
123
Z
mk
(19) was calculated for each of them. Next, these
300 sequences were shuffled and a random sequence
was obtained. Then, the random sequences were
analyzed and a set of values Z
mk
(19) were obtained.
Then, Z
0
equal to 10.0 was chosen since
N
random
(10.0)/N
real
(10.0) < 5%. It means that the
number of errors of the first kind is less than 0.05.
Therefore, N
random
(10.0) shows a number of
R
mk
Z
(19)
with values equal to or more than 10.0; N
real
(10.0)
indicates the number of Z
mk
(19) equal to or greater
than 10.0. The level of 10.0 was chosen for all n.
The computational complexity of the algorithm is
the reason why only 300 amino acid sequences were
analyzed. An analysis of 300 sequences required
about 6 months of calculations on a computer cluster
with 10 AMD FX-8350 processors. Therefore, the
task of analyzing the entire Swiss-prot database was
not done, because it would require a lot of computer
resources. The intention of the authors was to show
that periodicity exists in amino acid sequences with
many substitutions as well as where there are amino
acid insertions and deletions. This periodicity can be
detected by the approach developed in this study,
despite being combined with other methods. The
300 amino acid sequences are enough to solve this
problem.
3 EXAMPLES OF AMINO ACID
SEQUENCES
In total, 300 amino acid sequences randomly
selected from the Swiss-prot data bank (Boeckmann
et al., 2003) were studied. In the process of
selection, any sequence having already known
amino acid repeats or repetitive domains (Kajava,
2012) were excluded from the set. As a result, 71
sequences were detected by our algorithm (any
Z(n)>10.0) of having regions with the periodicity of
various lengths. Lengths of regions with periodicity
are more than 40 amino acids and number of periods
is more than 3. Three typical examples of sequences
having insertions and deletions were considered and
were found to have latent periodicity.
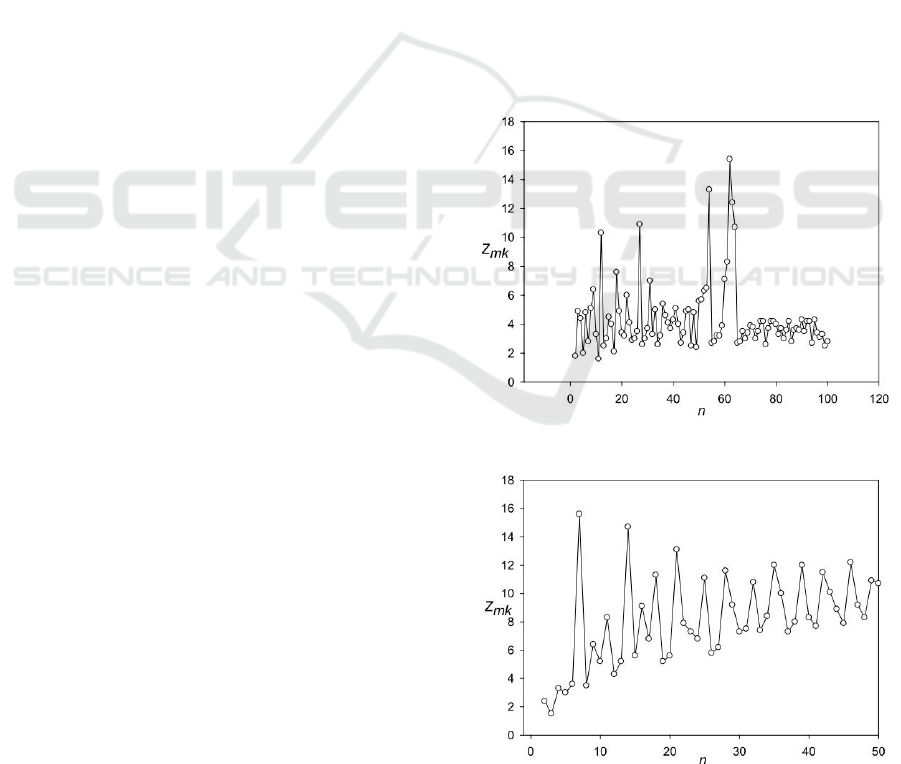
Figure 4 shows a second example of the
spectrum Z(n) for the sequence Q1D823 (Yang et
al., 2004), which contains the adventurous-gliding
motility protein. The region from 35 to 1373 amino
acids contains periodicity with length equal to 7
amino acids, which can be revealed with deletions
and insertions only. The Z(7) of this region has a
maximum value for all period lengths and is equal to
15.6. This region contains 4 extended coiled coil
regions. Alignment containing 20 deletions and
insertions of different lengths, that is, the average
length between the insertions and deletions is about
67 amino acids. Periodicity equal to 7 amino acids is
typical for the coiled coil regions. This periodicity
has the form HPPHCPC, where the positions of the
period is referred to as abcdefg. Here, H represents
hydrophobic residues, C represents typically charged
residues, and P represents polar (and therefore,
hydrophilic) residues. The positions of the heptad
repeat are commonly denoted by the lowercase
letters a through g. These motifs are the basis for
most coiled coils, particularly leucine zippers, which
have predominantly leucine in the d position of the
heptad repeat. The periodicity observed in sequence
Q1D823, is different from the periodicity specific
for the coiled coil. It can be assumed that there are
different heptad repeats, capable of forming a coiled
coil. It is also likely that such a difference is due to
insertions or deletions of amino acids. The findings
of the present work indicate that the resulting matrix
probably can be used to locate regions with long
coiled coils.
Figure 3: Spectrum Z(n) for the sequence O42918.
Figure 4: Spectrum Z(n) for the sequence Q1D823.
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
124
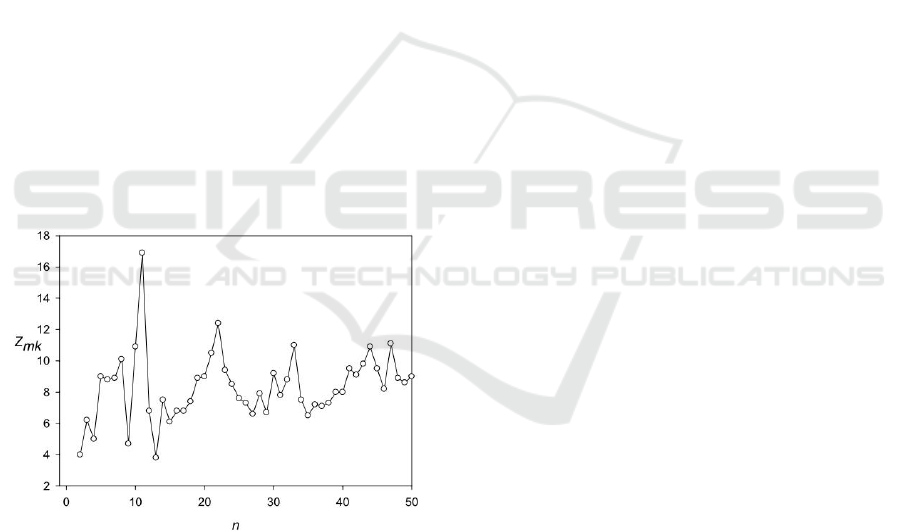
Figure 5 shows the Z(n) for the amino acid sequence
P48681 (Dahlstrand et al., 1992) in a region from
182 to 1248 amino acids. The period which is equal
to 11 amino acids is clearly visible. The periods of
22 and 33 amino acids are induced by the main
period which equals 11 amino acids. The sequence
with periodicity includes some coil regions and tail.
The periodicity was discovered only in the presence
of 24 amino acid insertions or deletions of various
lengths. In the absence of insertions and deletions,
this periodicity is not detectable.
We analyzed 71 amino sequences by the
programs REP (Andrade et al., 2000), Internal
Repeat Finder (Marcotte et al., 1999), Prospero
(Mott, 1999), RADAR (Heger & Holm, 2000),
REPRO (Heringa & Argos 1993), TRUST
(Szklarczyk & Heringa 2004) and PTRStalker
(Pellegrini et al., 2012). These programs found
periodicity in these sequences, if Z is more than
18.2. If Z lies in the interval from 18.2 to 15.5, these
programs found only ~34% of our results. Also, if
10.0<Z<15.5, then these methods found nothing.
Totally, these methods found 6 regions with latent
periodicity from 71 which was found in this work.
As is written above (see paragraph 1), it is the
consequence of using pairwise alignments between
periods for the detection of latent periodicity
(number of periods is more than 3).
Figure 5: Spectrum Z(n) for the sequence P48681.
The question arises about the role of the observed
periodicity in the structure and functions of proteins.
Two assumptions were put forward about the
functional role of the detected periodicity. Firstly,
the periodicity found could be some property which
provides a certain secondary structure (Jernigan and
Bordenstein, 2015). This assumption has been
expressed for the amino acid repeats, which were
found earlier (Jorda et al., 2010; Kajava, 2012). In
this study, there are periods of length 6 and 7 amino
acids which may participate in the formation of α-
helixes. Secondly, the periodicity found may reflect
a certain spatial repeatability of protein parts
belonging to 3D structures. For known repeats, this
can be observed for the Zn-finger domains (Lee et
al., 1989), Ig-domains (Sawaya et al., 2008) and the
human matrix metalloproteinase (Elkins et al.,
2002). In the work of Kajava (2012), "the structural
classification of the repetitive proteins based on the
length of their repeats" provides additional
information.
The origin of multiple tandem repeats in proteins
can be associated with the processes of multiple
tandem duplications in DNA (De Grassi and
Ciccarelli, 2009). It may come to the formation of
new proteins (Björklund et al., 2006). Further
evolution and accumulation of mutations (amino
acid substitutions, deletions and insertions) could
lead to the creation of latent periodicity with many
amino acid substitutions, insertions and deletions.
Periodicity was detected in the present work.
In the future, the computation time for this
algorithm can be reduced and all known amino acid
sequences accumulated in the Swiss-prot database
will be analyzed again. Increase in performance is
possible due to the use of other methods instead of a
genetic algorithm for optimization of the weight
matrix M or application for calculations using large
computing clusters.
ACKNOWLEDGEMENTS
This work was supported by the grant 2014-04-
00164 of the Russian Fund of Fundamental
Research.
REFERENCES
Almirantis, Y. et al., 2014. Editorial: Complexity in
genomes. Computational biology and chemistry, 53 Pt
A, pp.1–4.
Altschul, S.F. et al., 1990. Basic local alignment search
tool. Journal of molecular biology, 215(3), pp.403–
410.
Andrade, M. a et al., 2000. Homology-based method for
identification of protein repeats using statistical
significance estimates. Journal of molecular biology,
298(3), pp.521–537.
Bäck, T., 1996. Evolutionary Algorithms in Theory and
Practice: Evolution Strategies, Evolutionary
Programming, Genetic Algorithms, Oxford University
Press.
Search for Latent Periodicity in Amino Acid Sequences with Insertions and Deletions
125

Banzhaf, W. et al., 1998. Genetic programming: an
introduction: on the automatic evolution of computer
programs and its applications.
Biegert, a & Söding, J., 2008. De novo identification of
highly diverged protein repeats by probabilistic
consistency. Bioinformatics (Oxford, England), 24(6),
pp.807–14.
Björklund, A.K., Ekman, D. & Elofsson, A., 2006.
Expansion of protein domain repeats. PLoS
computational biology, 2(8), p.e114.
Boeckmann, B. et al., 2003. The SWISS-PROT protein
knowledgebase and its supplement TrEMBL in 2003.
Nucleic acids research, 31(1), pp.365–370.
Custer, M. et al., 1997. Identification of a new gene
product (diphor-1) regulated by dietary phosphate. The
American journal of physiology, 273(5 Pt 2), pp.F801–
F806.
Dahlstrand, J. et al., 1992. Characterization of the human
nestin gene reveals a close evolutionary relationship to
neurofilaments. Journal of cell science, 103 ( Pt 2,
pp.589–97.
Durbin, R. et al., 1998. Biological Sequence Analysis:
Probabilistic Models of Proteins and Nucleic Acids,
Cambridge University Press.
Ekblom, R. & Wolf, J.B.W., 2014. A field guide to whole-
genome sequencing, assembly and annotation.
Evolutionary Applications, 7(9), pp.1026–1042.
Elkins, P.A. et al., 2002. Structure of the C-terminally
truncated human ProMMP9, a gelatin-binding matrix
metalloproteinase. Acta crystallographica. Section D,
Biological crystallography, 58(Pt 7), pp.1182–92.
Fogel, D.B., 2010. EVOLUTIONARY COMPUTATION
Toward a New Philosophy of Machine Intelligence,
Fogel, D.B., 1998. Evolutionary Computation: The Fossil
Record.
Gondro, C. & Kinghorn, B.P., 2007. A simple genetic
algorithm for multiple sequence alignment. Genetics
and molecular research : GMR, 6(4), pp.964–82.
De Grassi, A. & Ciccarelli, F.D., 2009. Tandem repeats
modify the structure of human genes hosted in
segmental duplications. Genome biology, 10(12),
p.R137.
Heger, A. & Holm, L., 2000. Rapid automatic detection
and alignment of repeats in protein sequences.
Proteins: Structure, Function and Genetics, 41(2),
pp.224–237.
Heringa, J. & Argos, P., 1993. A method to recognize
distant repeats in protein sequences. Proteins, 17(4),
pp.391–41.
Jernigan, K.K. & Bordenstein, S.R., 2015. Tandem-repeat
protein domains across the tree of life. PeerJ, 3,
p.e732.
Jorda, J. et al., 2010. Protein tandem repeats - the more
perfect, the less structured. The FEBS journal,
277(12), pp.2673–82.
Jorda, J. & Kajava, A. V, 2009. T-REKS: identification of
Tandem REpeats in sequences with a K-meanS based
algorithm. Bioinformatics (Oxford, England), 25(20),
pp.2632–8.
Kajava, A. V, 2012. Tandem repeats in proteins: from
sequence to structure. Journal of structural biology,
179(3), pp.279–88.
Korotkov, E.V., Korotkova, M.A. & Kudryashov, N.A.,
2003. The informational concept of searching for
periodicity in symbol sequences. Molekuliarnaia
Biologiia, 37(3), pp.436–451.
Korotkov, Korotkova & Kudryashov, 2003. Information
decomposition method to analyze symbolical
sequences. Physics Letters, Section A: General,
Atomic and Solid State Physics, 312(3-4), pp.198–210.
Kravatskaya, G.I. et al., 2011. Coexistence of different
base periodicities in prokaryotic genomes as related to
DNA curvature, supercoiling, and transcription.
Genomics, 98(3), pp.223–231.
Kumar, L., Futschik, M. & Herzel, H., 2006. DNA motifs
and sequence periodicities. In silico biology, 6(1-2),
pp.71–8.
Lee, M.S. et al., 1989. Three-dimensional solution
structure of a single zinc finger DNA-binding domain.
Science (New York, N.Y.), 245(4918), pp.635–7.
Lobzin, V. V. & Chechetkin, V.R., 2000. Order and
correlations in genomic DNA sequences. The spectral
approach. Uspekhi Fizicheskih Nauk, 170(1), p.57.
Marcotte, E.M. et al., 1999. A census of protein repeats.
Journal of molecular biology, 293(1), pp.151–160.
Meng, T. et al., 2013. Wavelet analysis in current cancer
genome research: a survey. IEEE/ACM transactions
on computational biology and bioinformatics / IEEE,
ACM, 10(6), pp.1442–59.
Mitchell, M., 1998. An Introduction to Genetic
Algorithms.
Mott, R., 1999. Local sequence alignments with
monotonic gap penalties. Bioinformatics (Oxford,
England), 15(6), pp.455–62.
Newman, A.M. & Cooper, J.B., 2007. XSTREAM: a
practical algorithm for identification and architecture
modeling of tandem repeats in protein sequences.
BMC bioinformatics, 8, p.382.
Palidwor, G.A. et al., 2009. Detection of alpha-rod protein
repeats using a neural network and application to
huntingtin. PLoS computational biology, 5(3),
p.e1000304.
Pellegrini, M., 2015. Tandem Repeats in Proteins:
Prediction Algorithms and Biological Role. Frontiers
in bioengineering and biotechnology, 3, p.143.
Pellegrini, M., Renda, M.E. & Vecchio, A., 2012. Ab
initio detection of fuzzy amino acid tandem repeats in
protein sequences. BMC Bioinformatics, 13, p.S8.
Radcliffe, N.J., 1991. Equivalence Class Analysis of
Genetic Algorithms. Complex Systems, 5(2), pp.183–
205.
Rubinson, E.H. & Eichman, B.F., 2012. Nucleic acid
recognition by tandem helical repeats. Current opinion
in structural biology, 22(1), pp.101–9.
Sawaya, M.R. et al., 2008. A double S shape provides the
structural basis for the extraordinary binding
specificity of Dscam isoforms. Cell, 134(6), pp.1007–
18.
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
126

Shelenkov, A., Skryabin, K. & Korotkov, E., 2006. Search
and classification of potential minisatellite sequences
from bacterial genomes. DNA research : an
international journal for rapid publication of reports
on genes and genomes, 13(3), pp.89–102.
Smith, T.F. & Waterman, M.S., 1981. Identification of
common molecular subsequences. Journal of
Molecular Biology, 147, pp.195–197.
Söding, J., Remmert, M. & Biegert, A., 2006. HHrep: de
novo protein repeat detection and the origin of TIM
barrels. Nucleic acids research, 34(Web Server issue),
pp.W137–42.
Sosa, D. et al., 2013. Periodic distribution of a putative
nucleosome positioning motif in human, nonhuman
primates, and archaea: mutual information analysis.
International journal of genomics, 2013, p.963956.
de Sousa Vieira, M., 1999. Statistics of DNA sequences: a
low-frequency analysis. Physical review. E, Statistical
physics, plasmas, fluids, and related interdisciplinary
topics, 60(5 Pt B), pp.5932–5937.
Spears, W.M. & De Jong, K.D., 1991. On the Virtues of
Parameterized Uniform Crossover,. Proceedings of the
Fourth International Conference on Genetic
Algorithms, Morgan Kaufmann Publishers Inc. San
Francisco, CA, USA, pp.230–236.
Suvorova, Y.M., Korotkova, M.A. & Korotkov, E. V,
2014. Comparative analysis of periodicity search
methods in DNA sequences. Computational biology
and chemistry, 53 Pt A, pp.43–48.
Sywerda, G., 1989. Uniform crossover in genetic
algorithms. Proceedings of the third international
conference on Genetic algorithms, Morgan Kaufmann
Publishers Inc. San Francisco, CA, USA ©1989, pp.2–
9.
Szklarczyk, R. & Heringa, J., 2004. Tracking repeats using
significance and transitivity. Bioinformatics (Oxford,
England), 20 Suppl 1, pp.i311–7.
Tiwari, S. et al., 1997. Prediction of probable genes by
Fourier analysis of genomic sequences. Computer
applications in the biosciences CABIOS, 13(3),
pp.263–270.
Turutina, V.P. et al., 2006. Identification of Amino Acid
Latent Periodicity within 94 Protein Families. Journal
of Computational Biology, 13(4), pp.946–964.
Yang, R. et al., 2004. AglZ is a filament-forming coiled-
coil protein required for adventurous gliding motility
of Myxococcus xanthus. Journal of bacteriology,
186(18), pp.6168–78.
Search for Latent Periodicity in Amino Acid Sequences with Insertions and Deletions
127
