Microcontroller Implementation of Simultaneous Protections Against
Observation and Perturbation Attacks for ECC
Audrey Lucas
1
and Arnaud Tisserand
2
1
CNRS, IRISA UMR 6074, INRIA Centre Rennes - Bretagne Atlantique and Univ Rennes, Lannion, France
2
CNRS, Lab-STICC UMR 6285 and University South Britany, Lorient, France
Keywords:
Elliptic Curve Cryptography, Side Channel Attack, Fault Injection Attack, Protection, Countermeasure.
Abstract:
Scalar multiplication is the main operation in elliptic curve cryptography. In embedded systems, it is vulner-
able to both observation and perturbation attacks. Most of protections only target one of these two types of
attacks. Unfortunately, many protections against one type of attack may reduce the protection against the other
one. In this paper, we simultaneously deal with protections against both types of attacks. Two countermea-
sures are presented for scalar multiplication and implemented on a Cortex-M0 microcontroller. The first one
protects finite field operations over point coordinates. The second one protects the scalar (or key) bits.
1 INTRODUCTION
Elliptic curve cryptography (ECC) is promoted for
providing public-key cryptography (PKC) support in
embedded systems due to its smaller cost, e.g. sil-
icon area and energy, and better performances than
RSA (Cohen and Frey, 2005; Hankerson et al., 2004).
Embedded systems are widespread in our society,
thus their protection against various types of attacks
is essential. Due to their proximity with other users,
potentially malicious ones, embedded circuits are vul-
nerable to physical attacks. In this paper, we focus on
side channel attacks (SCAs) and fault attacks (FAs).
The first ones, use observations of physical parame-
ters, such as computation timings or power consump-
tion, which are analyzed using statistical tools to de-
duce links between physical measurements and inter-
nal secret values. The second ones, use perturbations
of the circuit such as variations of the power supply
or electromagnetic radiations to inject fault(s) during
algorithms execution. These faults are exploited to
deduce internal secret values.
Numerous countermeasures exist against SCAs
and FAs at various levels: mathematics, algorithm,
architecture, circuit. Most of these protections only
target one type of attack. For example, uniformiza-
tion schemes are efficient against SCAs but not for
FAs. Some error correcting codes can be used against
FAs but not for SCAs. Unfortunately, many protec-
tions, against one type of attack, leave or may make
the implementation vulnerable to the other type of at-
tacks.
In this work, we simultaneously deal with protec-
tions against both types of attacks. We propose two
countermeasures, developed onto specific curves, for
scalar multiplication (SM) in ECC. They are probably
adaptable onto other curves. The first one protects fi-
nite field operations over point coordinates. The sec-
ond one protects the scalar itself during SM.
Our paper is organized as follows. Sections 2, 3
and 4 respectively recall background elements on
ECC, SCAs/FAs attacks and ECC attacks and pro-
tections. Our two propositions are presented in Sec-
tion 5. Section 6 reports implementation results
on Cortex-M0 microcontrollers and the µNaCl li-
brary (D
¨
ull et al., ).
2 BACKGROUND ON ECC
ECC (Hankerson et al., 2004; Cohen and Frey, 2005)
is a PKC based on elliptic curves (ECs).
In the case of prime fields F
p
, short Weierstrass
curves form E
W S
and Montgomery (Montgomery,
1987) curves E
M
are defined, with a, b ∈ F
p
and spe-
cific conditions on a,b (see books (Hankerson et al.,
2004; Cohen and Frey, 2005)), respectively by:
E
W S
: y
2
= x
3
+ ax + b,
E
M
: by
2
= x
3
+ ax
2
+ x.
(1)
In this paper, we only consider these curves onto
prime fields F
p
.
404
Lucas, A. and Tisserand, A.
Microcontroller Implementation of Simultaneous Protections Against Observation and Perturbation Attacks for ECC.
DOI: 10.5220/0006884604040411
In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 404-411
ISBN: 978-989-758-319-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

The most critical operation in ECC is the scalar
multiplication (SM) [k]P between a curve point P and
a scalar k (either the public or private key). When k is
private, it must be protected. SM can be performed by
various algorithms based on point addition (ADD) and
point doubling (DBL) operations at curve level. When
ADD and DBL have different behaviors, their differ-
ences can be a leakage source in observation attacks.
The easiest way to perform SM is the double and
add (DA) algorithm 1. In case of E
M
, the Montgomery
ladder (ML) algorithm 2. is commonly used.
Algorithm 1: SM - double and add.
Input: P and k = (k
m−1
,. . . , k
0
)
2
Result: [k] · P
1 T ← O
2 for i = m − 1 to 0 do
3 T ← 2 · T DBL
4 if k
i
= 1 then
5 T ← T + P ADD
6 return T
Algorithm 2: SM - Montgomery ladder.
Input: P and k = (k
m−1
,. . . , k
0
)
2
Result: [k] · P
1 T
1
← O, T
2
← P
2 for i = m − 1 to 0 do
3 if k
i
= 1 then
4 T
1
← T
1
+ T
2
ADD
5 T
2
← 2 · T
2
DBL
6 else
7 T
2
← T
1
+ T
2
ADD
8 T
1
← 2 · T
1
DBL
9 return T
1
In order to perform T
1
+ T
2
, the x coordinate of
T
1
− T
2
can be known. During ML [k]P internal itera-
tions, T
1
− T
2
is always equal to the base point P.
Several ADD and DBL formulas for different curves
are available on the EFD website (Bernstein and
Lange, ).
3 BACKGROUND ON PHYSICAL
ATTACKS
Embedded systems have to face attacks at both logi-
cal and physical levels. Logical attacks target mathe-
matical properties of cryptosystems, networking pro-
tocols, weak software implementations, etc. For in-
stance, very efficient factorization algorithms and par-
allel implementations have been used against RSA
768 bits a few years ago. In this work, we do not con-
sider these attacks. Physical attacks are totally dif-
ferent from logical ones and require specific protec-
tions. Embedded systems have to be protected against
them since circuits in charge of security tasks can be
very close to the attackers. Typical physical attacks
include: reverse engineering, observation (or SCAs)
and perturbation (or FAs). In this paper, we only con-
sider SCAs and FAs. It is possible to combine them
such as (Roche et al., 2011).
3.1 SCAs and Countermeasures
SCAs observe physical parameters such as tim-
ings (Kocher, 1996), power consummation (Man-
gard et al., 2007) or electromagnetic radia-
tions (EM) (Agrawal et al., 2002) at run time.
They exploit potential correlations between measure-
ments of physical parameter(s) and some secret data
manipulated during execution.
SCAs are often decomposed into two types. On
one hand, simple power analysis (SPA) uses a sin-
gle trace of power measurements. For instance,
algorithm 1 is vulnerable to SPA. On the other
hand, various attacks use multiple traces and statis-
tical tools. For instance, differential power analy-
sis (DPA) (Kocher et al., 2011) uses difference of av-
erages and correlation power analysis (CPA) (Brier
et al., 2004) uses Pearson correlation. Both simple
and differential-like attacks exist for other physical
parameters (e.g. EM).
For SCA protection, one must avoid, or strongly
reduce, dependencies between secret values and ob-
servable variations of the physical parameter(s). A
first type of protection is denoted uniformization: op-
erations sequences must be indistinguishable what-
ever the actual secret bits manipulated in the circuit.
Useless operations can be added to uniformize some
algorithms. A second type of SCA protection is de-
noted randomization: a random activity generates a
scramble in the measurements. Statistic tools con-
sider this random activity as data and their results
are disturbed. For instance, random useless opera-
tions or random masks can be added. Many variations
and combinations of uniformization and randomiza-
tion protections have been proposed.
3.2 FAs and Countermeasures
Lasers, electromagnetic radiations, variations in sup-
ply voltage or circuit temperature, glitches in clock
signals are used to disturb the circuit by injecting
fault(s) during algorithm execution (Bar-El et al.,
2006; Verbauwhede et al., 2011). These faults can
Microcontroller Implementation of Simultaneous Protections Against Observation and Perturbation Attacks for ECC
405

be temporary or permanent and equivalent at logical
level to a bit flip, bit set, bit reset or bit stuck-at (on
single or multiple bits).
FAs exploit some unspecified circuit behavior, di-
rectly or not, in order to deduce the secret. For
instance, they can use differences between faulty
and correct outputs thanks to differential fault anal-
ysis (DFA) (Biham and Shamir, 1997).
Safe-error analysis (SEA) (Yen and Joye, 2000)
checks if the injected fault has an impact on the final
result. By determining whether a corrupted data was
effectively used or not, SEA is very efficient against
SCA protections based on useless/dummy operations.
Attackers can produce fault(s) on data, control or
external memory. In this paper, we only consider
faults on data since we target software implementa-
tions with on-chip memory.
Two types of protections exist against FAs: detec-
tion and correction schemes. Detection schemes al-
low various policy solutions when an attack occurs:
execution stop and re-run, algorithm change, eras-
ing/destroying secret values, etc. Detection can be
achieved at various levels: in hardware using intru-
sion sensors, at algorithm using redundant computa-
tions (spatial and/or temporal) or data integrity checks
for instance. Correction schemes use methods per-
forming the expected operations even in presence of
faults (e.g. use of majority voters). In this paper, we
only consider detection schemes.
4 ATTACKS AND PROTECTIONS
ON ECC
In this section, several SCAs, FAs and related protec-
tions for ECC are recalled. Attacks objective is to re-
cover the secret scalar/key k from execution(s) of the
scalar multiplication Q = [k]P.
4.1 SCAs on ECC and Protections
During SM, each sequence of curve-level operations
depends on the actual scalar bits. If ADD and DBL op-
erations can be distinguished (through physical mea-
surements) and DA algorithm is used, then SM is vul-
nerable to SPA. Indeed, a 1 key bit generates a DBL
followed by an ADD, while a 0 key bit only generates
a DBL. If partial traces for ADD and DBL are different
(even with a few differences), an attacker is able to
distinguish what operation is made and then recover
the key bits from the trace as illustrated in Figure 1.
Several other SCAs on ECC exist including tim-
ings, DPA, zero-value point attacks (Akishita and
Takagi, 2003) or doubling attacks (Fouque and
DBL ADD
1
DBL
0
DBL
0
DBL
0
DBL ADD
1
Figure 1: Basic DA algorithm.
Valette, 2003). In practice, some randomization
schemes can be applied against DPA-like attacks in
many protocols. Then SPA-like ones are considered
as a major threat in ECC. In this paper, we only deal
with SPA-like attacks.
Among SCA protections uniformization and ran-
domization have been widely used in ECC.
Among uniformization countermeasures, double
and add always (DAA) (Coron, 1999) and ML are
typical SPA protections. The DAA algorithm is simi-
lar to DA where a useless ADD is added when the key
bit is zero. This is good for SPA protection but very
bad for SEA ones (injecting a fault during the useless
ADD has not impact on the output, then the attacker
knows that the operation was a dummy one and the
corresponding key bit was 0).
ML is widely used in practice since it is SPA and
SEA resistant. The same operations sequence is made
regardless of the key bits. Attackers cannot distin-
guish ADD and DBL patterns. Furthermore, all inter-
mediate computations impact the final result.
Among randomization countermeasures, scalar
randomization and point blinding protections have
been proposed against DPA (Coron, 1999). Scalar
randomization consists in performing [k]P = [k + r ·
λ]P where r is the order of E and λ is a random num-
ber. Point blinding performs [k]P = [k](P + R) − [k]R
instead of [k]P, where R is a random point. Other
randomization countermeasures use projective coor-
dinates. Before each SM execution, P coordinates are
randomized thanks to the multiplication by a random
number λ, so P = (λx
P
,λy
P
,λz
P
). This new P is em-
ployed during SM.
4.2 FAs on ECC and Protections
Attackers can inject faults on several types of data
during SM: curves parameters, scalar, field represen-
tation (Ciet and Joye, 2005), base point (Biehl et al.,
2000) and current point (Bl
¨
omer et al., 2006). The
attacker aims DFA or transferring the ECDLP (dis-
crete logarithm problem) onto a weaker curve. Com-
monly, the transfer is possible since b parameter in
curve equation 1 is unused during SM. Below, two
attack examples with different targets are recalled.
In (Biehl et al., 2000), the base point
e
P belongs to
e
E
SW
instead of E
SW
. Curve
e
E
SW
has a smaller order
than E
SW
and it is defined by:
e
b = y
2
− x
3
− ax. (2)
SECRYPT 2018 - International Conference on Security and Cryptography
406

As [k]P = [k]
e
P, the DLP is transferred onto sub-
group of smaller order and an attacker recovers k mod
ord(
e
P). By reiterating with several other
e
P, the at-
tacker recovers the key value thanks to the Chinese
remainder theorem (CRT).
In (Bao et al., 1997), the attack proposed on RSA
can also apply to ECC. The fault is supposed one bit
flip located on the random key bit at index j. Let
e
Q
the faulty SM result, then Q and
e
Q can be written as:
e
Q = [
e
k]P =
j−1
∑
i=0
k
i
2
i
P +
e
k
j
2
j
P +
m−1
∑
i= j+1
k
i
2
i
P
Q = [k]P =
m−1
∑
i=0
k
i
2
i
P
(3)
Knowing both Q and
e
Q, one can compute Q −
e
Q
which helps to deduce the key bit k
j
. Indeed, if
Q −
e
Q = −2
j
P then k
j
= 0 and if Q −
e
Q = 2
j
P then
k
j
= 1. Finally, the attacker recovers the full key iter-
atively for the other j ranks.
Most FAs on ECC are defeated using point verifi-
cation (PV) (Biehl et al., 2000) at various steps of SM.
For instance, PV ensures that final or current point be-
longs to the curve by injecting their coordinates into
the curve equation. Thus, PV protects against FA
which targets the curve parameters and the point P
of SM [k]P.
In case of Montgomery curve, the y coordinate is
unused during SM, and PV is equivalent to verify if
C =
x
3
+ax
2
+x
b
is a square with Legendre symbol (LS).
As a reminder LS is computed by C
p−1
2
, and if C ≡
0 mod p (p is prime) then, LS equals to 0. In other
case, LS equals to 1 if C is square modulo p and −1
else. However, PV is ineffective against FA targeting
scalar bits k
j
s.
5 PROPOSED PROTECTIONS
As protections against one type of attack may weaken
the implementation against the other one, simultane-
ously dealing with both SCAs and FAs is important
but it can be tricky. For instance, basic uniformization
schemes using dummy operations for SCA protection
may be weak against SEA. Or in case of FA protec-
tion, adding redundancy checks must not reduce the
robustness against SCAs (for instance by breaking the
uniform behavior). In most of the literature, FAs and
SCAs are considered independently.
We propose two combined countermeasures for
protecting SM simultaneously against both SPA-like
attacks and major FAs. Standard protections against
DPA-like attacks can be used on top of our counter-
measures. Our first countermeasure is an extension
DBL
V
ADD
1
DBL
V
0
DBL
V
0
DBL
V
ADD
1
Figure 2: Point verification in DA.
of PV proposed for protection against FAs but we
added uniformization for SPA protection. Our sec-
ond countermeasure, called iteration counter, protects
the scalar bits against FAs with a uniform behavior
for SPA protection. In this section, we describe these
countermeasures for Weierstrass curves (with both ja-
cobian and projective coordinates) and Montgomery
curves (with XZ coordinates).
Their cost will be first evaluated in terms of the
number of F
p
operations: multiplication M, square S
and addition/subtraction A. In Section 6, detailed
comparisons will be reported for microcontroller im-
plementation.
5.1 Point Verification (PV)
PV injects point coordinates into the curve equation
to verify that the checked point effectively belongs to
the curve. PV can be integrated in SM at different
periods leading to various trade-offs between security
and performance. For low cost protection, PV can be
performed at beginning and end of SM. Then, a FA
on an intermediate point is detected very late. For
earlier detection, but with a higher run time, PV can
be performed every d iterations or randomly during
SM. The strongest protection is obtained for d = 1
where PV is performed at each SM iteration. In this
paper, we denote ` the number of executed PVs during
one SM (1 ≤ ` ≤ m + 1).
Care must be taken when applying PV to not
weakening the implementation against SCAs. For in-
stance, using PV after DBL operations is safer (they do
not depend on k bits).
For our first countermeasure, we explore and mod-
ify PV to ensure a uniform behavior against SPA-like
attacks. The sequence of F
p
operations added for PV,
denoted V, can be used to ”fill” the differences be-
tween ADD and DBL as illustrated in Figure 2. We
modified the complete computations to ensure the ex-
act same behavior, i.e. same sequence of F
p
opera-
tions, for both ADD and DBL+V to make our SM uni-
form (against SPA).
5.1.1 Uniform PV on Weierstrass Curves
We first present uniformization of SM with PV for
projective and jacobian coordinates where ADD is
more complex than DBL. We include PV in DBL, de-
noted DBL+V, to ensure a uniform behavior of SM.
Microcontroller Implementation of Simultaneous Protections Against Observation and Perturbation Attacks for ECC
407

Weierstrass curves onto F
p
in projective coordi-
nates are defined below with a = −3:
E
W P
: y
2
z = x
3
+ axz
2
+ bz
3
. (4)
Multiplication by b, denoted M
b
, can be imple-
mented with a generic multiplication or additions de-
pending on b value (e.g. sparse decomposition).
Table 1 reports the cost of curve operations and
verification V. Obviously, V cost is too small to di-
rectly uniformize SM. We add operations in V by mul-
tiplying by y such that:
V : y
3
z = x
3
y + axyz
2
+ byz
3
. (5)
After factorization of some operations and add of
operation M
b
to ADD (this is not a dummy operation,
see the source code), the new cost for DBL+V is equal
to the ADD cost (11M +6S +18A +1M
b
). The final over-
head for our uniform SM is 6`M + 4`A + 2`M
b
.
Table 1: Operations costs for Weierstrass curves.
Projective Jacobian
ADD 11M+6S+18A 11M+ 5S+13A
DBL 5M+6S+14A 3M+ 6S+ 15A
Basic V 4M+3S+5A+1M
b
1M+6A+1M
b
V 6M+4A+2M
b
7M+ 7A+2M
b
For jacobian coordinates, we first transform DBL
(remove 1 S and add 1 M):
xx = x
2
1
yy = y
2
1
t
0
= x
1
· yy
t
1
= t
0
+t
0
s = t
1
+t
1
t
2
= xx +xx
t
3
= t
2
+t
2
⇒
yy = y
2
1
t
0
= x
1
+ x
1
t
1
= t
0
+ x
1
t
2
= t
0
+t
0
s = t
2
· yy
t
3
= t
1
· x
1
(6)
Then, the verification equation is transformed
thanks to a multiplication by the z coordinate:
V : y
2
z = x
3
z + axz
5
+ bz
7
(7)
After integration into DBL and some factorizations,
our uniform SM overhead is 7`M + 7`A + 2M
b
.
Table 2: Overheads.
Projective Jacobian
PV 6`M + 4`A + 2`M
b
7`M + 7`A + 2`M
b
DAA ' 6.5`M + 3`S + 9`A ' 6.5`M + 2.5`S +7.5`A
Despite ADD and DBL have the same cost, their be-
haviors are distinguishable. Then, we reschedule the
operations sequences of ADD and DBL+V to ensure the
exact same behavior.
We compare our uniform PV with DAA in Ta-
ble 2. Our uniform SM with PV protects against both
SPA and FA (only SPA for DAA) and has a smaller
cost than DAA.
Obviously, one can use a smaller security level
with less frequent PVs (with d > 1) leading to smaller
overheads (while d = 1 for DAA).
5.1.2 Uniform PV on Montgomery Curves
Direct PV is too expensive for Montgomery curves
using XZ coordinates. The unused y coordinate forces
to check current point using LS. Furthermore, Mont-
gomery curves with XZ coordinates and ML are more
efficient than Weierstrass curves.
Our proposition takes advantage of a constant in-
side ML Algorithm 2. Indeed, T
2
− T
1
is always equal
to P at each iteration. If point T
1
is faulted, it becomes
e
T
1
and T
2
−
e
T
1
6= P. The computation T
2
− T
1
with
addition formulas is possible at each iteration since
T
1
+ T
2
is also computed.
T
1
+ T
2
= (x
3
,z
3
) is performed using the x coordi-
nate of P denoted x
P
. After, T
2
− T
1
is made with x
3
.
A first verification consist in comparing between re-
sult of T
2
− T
1
and P. This verification does not detect
attacks since the x
3
must be normalized by z
3
. Then,
a final test is equivalent to x
3
(1 − z
P
) = 0 which is
always true since z
P
= 1.
To solve this problem, SM is modified. Instead
to deal with one bit, the new ladderStep, denote
ML V, deals with simultaneously two bits (the itera-
tions number is halved). Indeed, the curve operations
are performed as in the algorithm 3. The variable T
6
is
the new T
2
after ML V. If k
i
6= k
i+1
then, T
5
replaces T
1
.
Else T
1
is replaced by T
7
. In order to perform PV, we
note that T
6
− P = T
7
and T
6
+ P = T
5
. As T
5
and T
7
are calculated earlier, T
8
= T
6
± P can be performed
with the x coordinate of the new T
1
(T
5
or T
7
).
Algorithm 3: ML V.
Input: T
1
, T
2
, xor ← k
i
⊕ k
i+1
1 T
3
← 2T
1
2 T
4
← T
1
+ T
2
3 T
5
← 2T
4
new T
1
, if xor = 1
4 T
6
← T
3
+ T
4
new T
2
5 T
7
← 2T
3
new T
1
, if xor = 0
6 T
8
← T 6 + P use x of new T
1
7 if xor = 1 then
8 T
8
= T
7
9 else
10 T
8
= T
5
If a fault is performed during SM then, the equal-
ity between T
8
and T
7
(xor = 1) and between T
8
and
T
5
(xor = 0) is wrong.
The cost of the original LadderStep is 5M + 4S +
8A + 1M
a
. As ML V deals with two key bits instead of
SECRYPT 2018 - International Conference on Security and Cryptography
408

one, its overhead equals to 8M + 4S + 7A + M
a
. Thus,
for one SM the overhead is 4`M + 2`S + 4.5`A +
`
2
M
a
.
The verification in ML V is faster than verifying if
x
3
+ ax
2
+ x is a square using LS. Nevertheless, this
PV does not ensure that P belongs to curve. Thus, the
first attack from Section 4 is possible. To avoid this,
the y coordinate is kept and a basic PV is performed at
the beginning of SM. In latter steps of SM, the y co-
ordinate can be removed without security reduction.
The cost of the beginning curve equation computa-
tion is 1M + 2S + 3A + M
a
. Finally, our uniform PV
simultaneously protects intermediate point and curve
parameters against major FAs and SPA.
As ML is uniform, if late detection is acceptable,
one can only use PV at beginning and end of SM for
a very low cost.
5.2 Iteration Counter (IC)
During SM, key bits manipulations are very short and
have a different behavior compared to field opera-
tions. But injecting faults during them is also pos-
sible (see Sec. 4). PV only protects curve parameters
and verified points against FAs but not key bits (PV is
verified with faulted key bits).
In order to protect all scalar bits against FAs, we
propose the iteration counter countermeasure. It en-
sures that the executed SM iterations effectively cor-
respond to the actual key k even in presence of FAs
with a uniform behavior.
A naive solution is a check sum which counts the
Hamming weight of k. Nevertheless, this idea is not
sufficient when attackers can flip two key bits at dif-
ferent indexes (i 6= i
0
).
Another solution is to count ADDs using a weight
depending on the iteration index i. When k
i
= 1, in-
dex i is added to a register reg (remember that i is
small). Attackers have to forge multiple bit flips ac-
cording to interesting values of i, which is very un-
likely. Then the overwhelming majority of faults in k
are detected. Unfortunately, when k
i
= 0, reg is not
modified leading to a small but measurable activity
drop. This second solution is good against FAs but
not sufficient against SPA.
Our final solution consists in splitting reg into 4
registers r
1
,. . . , r
4
as illustrated in Figure 3. Thanks to
these registers, the cswap function (used during ML)
can switch both the IC registers and current point co-
ordinates according to key bits at each ML iteration.
When k
i
6= k
i−1
, cswap switches (r
1
, r
2
) with (r
3
,
r
4
). Regardless of key bits, random values are added
to r
3
and r
4
. If i%2 = 0, i is added to first part of r
1
.
Else, i is added to first part of r
2
.
At the end of the SM, r
1
and r
2
are shifted and
added. This result is compared to a reference value.
This new version, denoted ICC, costs 1 swap, 5 small
integer additions, 2 shifts and 2m small random num-
ber generations.
r
1
0
C
1
+ i if i%2 = 0
Θ
1
+ i if i%2 = 1
r
2
0
C
2
+ i if i%2 = 1
Θ
2
+ i if i%2 = 0
r
3
Θ
3
+ λ
3
r
4
Θ
4
+ λ
4
Figure 3: ICC split on registers during SM iterations.
ICC detects bit flip attacks and is resistant to SPA.
But it does not detect bit set or bit reset faults (the bits
are forced to 1 and 0 respectively) used in some SEAs.
Indeed, if the i-th bit is set to 1 and actually k
i
= 1,
this ”non-modification” is not detected. But SEAs can
be avoided using masking schemes such as (Coron,
1999).
5.3 Fault Detection Policy
Protection against SCAs is based on good properties
of the algorithms and implementations without detec-
tion at run time. But fault detection can be an ac-
tive process. Several detection policies can be applied
at run time: stopping the execution, erasing the se-
cret data, re-computing with the same or another al-
gorithm, continuing computations with a random key.
The policy choice depends on the application and re-
lated threats.
In this work, we implemented the continuation us-
ing a random scalar. A random scalar k
r
is generated
before SM. If an attack is detected, k
r
is used instead
of k as soon as possible. The cost of this additional
protection is the random generation of m bits (i.e. k
length) and k ↔ k
r
swap when a detection occurs.
6 IMPLEMENTATION RESULTS
We implemented our countermeasures on a 32-
bit Cortex-M0 microcontroller (STM32F0 Discovery
board) and the µNaCl library (D
¨
ull et al., ) at 128-bit
security level. This is a variant of the NaCl (Daniel
J. Bernstein and Schwabe, ) library where the Bern-
stein curve (Bernstein, 2006) (E
M
with a = 48662,
b = 1 and p = 2
255
− 19) is implemented thanks to
ML and XZ coordinates.
The main SM variable is state composed of: co-
ordinates of points T
1
and T
2
, x
P
coordinate, scalar,
previous bit and downwards counter.
Microcontroller Implementation of Simultaneous Protections Against Observation and Perturbation Attacks for ECC
409

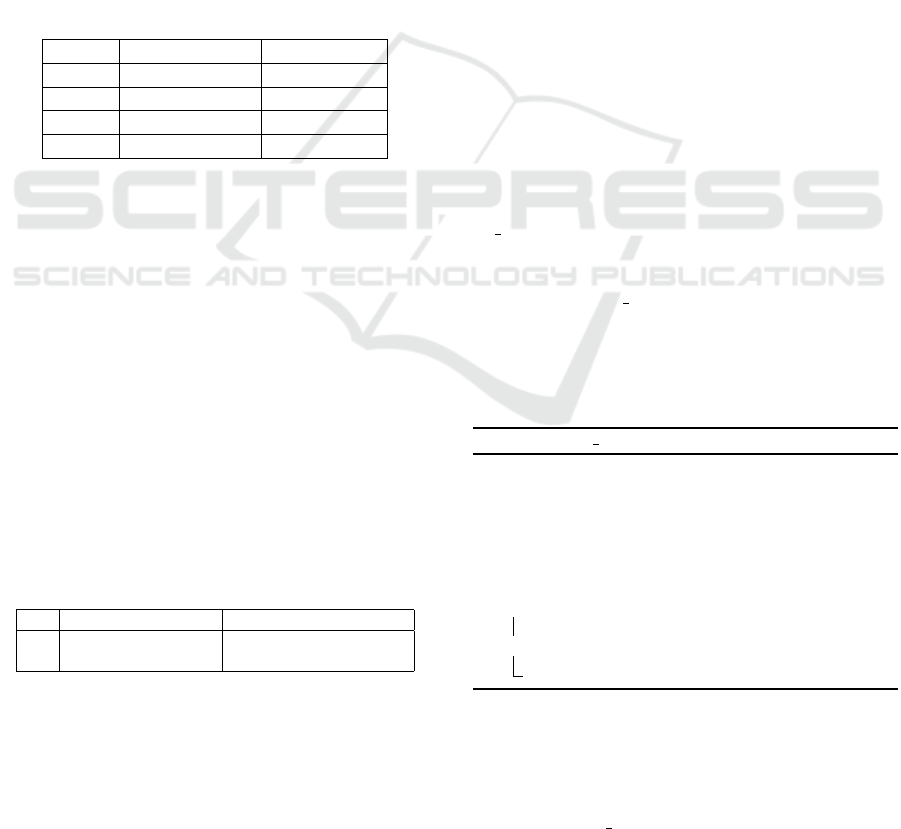
3e+06
4e+06
5e+06
6e+06
7e+06
8e+06
9e+06
1e+07
0 50 100 150 200 250
Computation time (clock cycles)
PV number during SM
Weier. − Jac.
Weier. − Proj.
Montg. − XZ
DAA − Jac.
DAA − Proj.
Figure 4: Clock cycles depending on PV numbers.
The SM loop on key bits is handled by the cswap
which swaps T
1
and T
2
when the current key bit is dif-
ferent from the last one. After cswap, a LadderStep
is performed on state.
We use the structure and parameters defined in
µNaCl for SM with ML onto Montgomery curves. In
case of Weierstrass curves, we use the same base field
with the NIST parameters and y-coordinate is added
to state.
In order to implement ICC, the variable Reg is cre-
ated to hold r
1
, r
2
, r
3
and r
4
. Moreover, the small
random numbers are generated with random number
generator of µNaCl. Before performing ICC compu-
tations, the swap function is used on Reg at each iter-
ation.
Figure 5 illustrates the overhead of PV during the
SM with a 256-bit scalar. The practical overhead
is larger than theoretical overhead. The original li-
brary was optimized to fill the processors registers ef-
ficiently. When PV is added more memory pressure
leads to slower execution.
Cost increases linearly with the number of PVs,
this leads to trade-offs between the detection level
and the performance. The PV overhead for Montgo-
mery curves is 62% in worst case against only 2.3%
when PV is only used the beginning and the end of
SM. Similar observations can be made for Weierstrass
curves. Nevertheless, overheads of uniform algorithm
(the worst case) are smaller than DAA. In addition to
the number of clock cycles, the overhead of size code
and intermediate RAM are reported in Table 3.
7 CONCLUSION
We proposed two ECC countermeasures combined si-
multaneous protection against SCAs and FAs. They
protect field operations on point coordinates and the
scalar bits against both major fault and SPA-like at-
tacks with various security vs. performance trade-
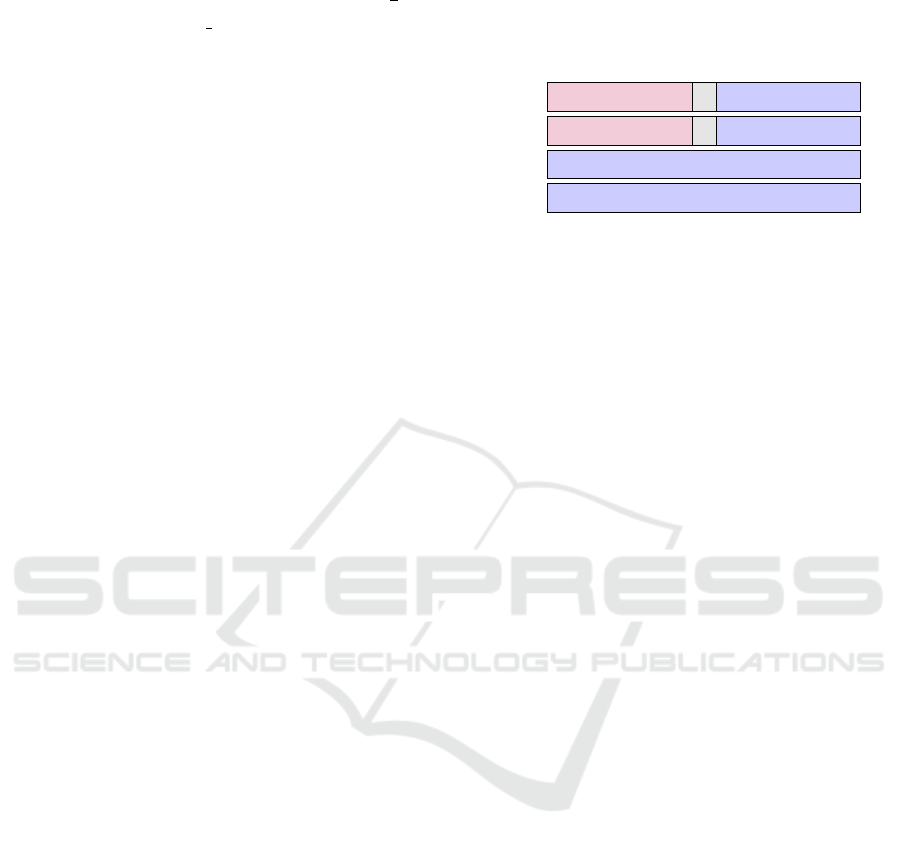
0
20
40
60
80
100
Montg. Weier. J. Weier. P.
Computation time overhead (%)
ICC
PV begin & end
PV
ICC & PV
ICC & PV & sparse key
DAA
Figure 5: Overhead depending on type of protection.
Table 3: Experimental results overhaed.
protection type code size RAM size
Montg.
XZ
ICC 2.7% 2.8%
PV end 10.6% 11%
PV 12.6% 13.2%
PV+ICC+answer 17.3% 16.9%
Weier.
Jac.
ICC 2.5% 2.6%
PV 2.9% 2.6%
PV begin+end 3.9% 4%
PV+ICC+answer 5.6% 5.8%
DAA 0.4% 0.4%
Weier.
Proj.
ICC 2.3% 2.4%
PV 2.1% 2.2%
PV begin+end 2.1% 2.2%
PV+ICC+answer 4.8% 5%
DAA 0.4% 0.2%
offs. They have been implemented for short Weier-
strass and Montgomery curves on a 32-bit microcon-
troller.
A uniform PV in Weierstrass curves was pro-
posed. It leads to faster SM than DAA with early
detection of FAs (at each SM iteration if needed) and
protection against SPA-like attacks. For Montgomery
curves, a PV was proposed against FAs (with a uni-
form behavior). For protecting scalar bits against FAs,
a specific countermeasure called iteration counter was
proposed. It is low cost and robust to SPA-like at-
tacks.
Our code will be distributed as open source soft-
ware. Future works will focus on new randomiza-
tion schemes and other types of ECs and point co-
ordinates.
REFERENCES
Agrawal, D., Archambeault, B., Rao, J. R., and Rohatgi,
P. (2002). The EM Side-Channel(s). In Proc. Cryp-
tographic Hardware and Embedded Systems - CHES,
pages 29–45.
Akishita, T. and Takagi, T. (2003). Zero-Value Point At-
SECRYPT 2018 - International Conference on Security and Cryptography
410

tacks on Elliptic Curve Cryptosystem. In Proc. Infor-
mation Security - ISC, pages 218–233.
Bao, F., Deng, R. H., Han, Y., and more authors (1997).
Breaking Public Key Cryptosystems on Tamper Re-
sistant Devices in the Presence of Transient Faults. In
Proc. Security Protocols, pages 115–124.
Bar-El, H., Choukri, H., Naccache, D., Tunstall, M., and
Whelan, C. (2006). The sorcerer’s apprentice guide
to fault attacks. Proceedings of the IEEE, 94(2):370–
382.
Bernstein, D. J. (2006). Curve25519: New Diffie-Hellman
Speed Records. In Proc. Public Key Cryptography -
PKC, pages 207–228.
Bernstein, D. J. and Lange, T. Explicit-formulas database.
http://hyperelliptic.org/EFD/.
Biehl, I., Meyer, B., and M
¨
uller, V. (2000). Differential
Fault Attacks on Elliptic Curve Cryptosystems. In
Proc. Advances in Cryptology - CRYPTO, pages 131–
146.
Biham, E. and Shamir, A. (1997). Differential Fault Anal-
ysis of Secret Key Cryptosystems. In Proc. Advances
in Cryptology, pages 513–525.
Bl
¨
omer, J., Otto, M., and Seifert, J. (2006). Sign Change
Fault Attacks on Elliptic Curve Cryptosystems. In
Proc. Fault Diagnosis and Tolerance in Cryptography
- FDTC, pages 36–52.
Brier, E., Clavier, C., and Olivier, F. (2004). Correlation
Power Analysis with a Leakage Model. In Proc. Cryp-
tographic Hardware and Embedded Systems - CHES,
pages 16–29.
Ciet, M. and Joye, M. (2005). Elliptic Curve Cryptosystems
in the Presence of Permanent and Transient Faults.
Des. Codes Cryptography, 36(1):33–43.
Cohen, H. and Frey, G., editors (2005). Handbook of Ellip-
tic and Hyperelliptic Curve Cryptography. Discrete
Maths and Applications. Chapman & Hall/CRC.
Coron, J. (1999). Resistance Against Differential Power
Analysis For Elliptic Curve Cryptosystems. In Proc.
Cryptographic Hardware and Embedded Systems -
CHES, pages 292–302.
Daniel J. Bernstein, T. L. and Schwabe, P. µNaCl library.
https://nacl.cr.yp.to/.
D
¨
ull, M., Haase, B., and S
´
anchez, A. H. µNaCl library.
http://munacl.cryptojedi.org/index.shtml.
Fouque, P. and Valette, F. (2003). The Doubling Attack -
Why Upwards Is Better than Downwards. In Proc.
Cryptographic Hardware and Embedded Systems -
CHES, pages 269–280.
Hankerson, D., Menezes, A., and Vanstone, S. (2004).
Guide to Elliptic Curve Cryptography. Springer.
Kocher, P. (1996). Timing Attacks on Implementations of
Diffie-Hellman, RSA, DSS, and Other Systems. In
Proc. Advances in Cryptology - CRYPTO, pages 104–
113.
Kocher, P., Jaffe, J., Jun, B., and Rohatgi, P. (2011). In-
troduction to differential power analysis. J. Crypto-
graphic Engineering, 1(1):5–27.
Mangard, S., Oswald, E., and Popp, T. (2007). Power Anal-
ysis Attacks: Revealing the Secrets of Smart Cards.
Springer.
Montgomery, P. L. (1987). Speeding the pollar and ellip-
tic curves methods of factorisation. Mathematics of
Computation, 48(177):243–264.
Roche, T., Lomn
´
e, V., and Khalfallah, K. (2011). Com-
bined Fault and Side-Channel Attack on Protected Im-
plementations of AES. In Proc. Smart Card Research
and Advanced Applications -CARDIS, pages 65–83.
Verbauwhede, I., Karaklajic, D., and Schmidt, J. (2011).
The Fault Attack Jungle - A Classification Model to
Guide You. In Proc. Workshop on Fault Diagnosis
and Tolerance in Cryptography, pages 3–8.
Yen, S. and Joye, M. (2000). Checking Before Output May
Not Be Enough Against Fault-Based Cryptanalysis.
IEEE Trans. Computers, 49(9):967–970.
Microcontroller Implementation of Simultaneous Protections Against Observation and Perturbation Attacks for ECC
411