Hash-Based Signature with Constant-Sum Fingerprinting and

Partial Construction of Hash Chains

Yuichi Kaji

, Jason Paul Cruz

and Yoshio Yatani

Nagoya University, Furo-cho, Chikusa-ku, Nagoya, 464-8601, Japan

Osaka University, 1-5 Yamadaoka, Suita, Osaka 565-0871, Japan

Nara Institute of Science and Technology, 8916-5 Takayama, Ikoma, Nara 630-0101, Japan

Keywords:

One-time Signature, Winternitz Scheme, Fingerprinting Function, Hash Chain, Security Proof, IoT Security,

Post-quantum Security.

Abstract:

A hash-based one-time signature (OTS) is a light-weight and quantum-immune alternative to conventional

digital signature schemes. This study focuses on the possible use of hash-based OTS in a wireless sensor net-

work and investigates techniques that improve the eﬃciency of Winternitz OTS. The improvement is made by

two means; introduction of a novel ﬁngerprinting function and partial construction of hash chains. The tech-

niques contribute to a better trade-oﬀ between signature size and computational complexity, and they can be

used together with other improvement techniques on Winternitz OTS. This study also shows that the proposed

OTS is strongly existentially unforgeable if ﬁngerprinting and hash functions are chosen appropriately.

1 INTRODUCTION

1.1 Background and Related Studies

Conventional digital signature schemes that are based

on number theoretic problems pose two possible

problems; large computational complexity and the

threat of quantum computers. It is not favorable

for small battery-operated devices to perform energy-

consuming computation over large numbers, and the

security of the scheme is fatally threaten by quantum

computers because they are able to solve number the-

oretical problems eﬃciently(Shor, 1997).

A hash-based digital signature is a light-weight

and quantum-immune alternative to conventional dig-

ital signature schemes(Buchmann et al., 2011b; Dods

et al., 2005). As the name suggests, the scheme makes

use of cryptographic hash functions instead of num-

ber theoretic problems. The scheme is light-weight

because the computation of a hash function can be

performed with much less time and energy than the

computation over large numbers. The scheme is

quantum-immune because a hash function involves

tricky mechanisms that make the function mathemat-

ically disordered and thus diﬃcult to tackle even by

quantum computers(Bernstein et al., 2009).

In a typical hash-based digital signature, a secret

signing key is a set of elements randomly selected

from the domain of a hash function. These elements

are provided to an acyclic hash-network, and the out-

put of the network is used as a public veriﬁcation key.

The message to be signed selects certain points in the

hash-network, and the hash values of those selected

points are used as the signature. A veriﬁer conﬁrms

the integrity of a signature by checking if the veri-

ﬁcation key that is reconstructed from the signature

coincides with the veriﬁcation key that has been dis-

tributed in advance. In this framework, an issuance

of a signature discloses some secret, and a once used

key pair should not be reused. For this reason, a hash-

based digital signature is sometimes called a one-time

signature (OTS) in literature, although the practical-

ity issue of handling multiple keys can be mitigated

by using a Merkle tree(Merkle, 1990) which consoli-

dates several veriﬁcation keys to a single key.

The ﬁrst hash-based OTS was proposed in

(Lamport, 1979), which is improved in (Merkle,

1990). As described in (Merkle, 1990), Merkle OTS

can be generalized to Winternitz OTS. The hash-

network of Merkle OTS consists of hash chains of

length one, while Winternitz OTS allows the use

of longer hash chains than Merkle OTS. Bleichen-

bacher and Maurer extended the hash-network from

chains to complicated graphs(Bleichenbacher and

Maurer, 1996b)(Bleichenbacher and Maurer, 1996a)

Kaji, Y., Cruz, J. and Yatani, Y.

Hash-Based Signature with Constant-Sum Fingerprinting and Partial Construction of Hash Chains.

DOI: 10.5220/0006828202970304

In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 297-304

ISBN: 978-989-758-319-3

297

(see also (Dods et al., 2005)). Other investiga-

tions include BiBa(Perrig, 2001) and HORS(Reyzin

and Reyzin, 2002). Among these OTS, Winter-

nitz OTS seems promising because it is simple, ex-

tensible(Buchmann et al., 2011b)(Hulsing, 2013),

and has become a basement of practical frame-

works such as XMSS(Buchmann et al., 2011a) and

SPHINCS(Bernstein et al., 2015).

We note that there are investigations that try to

realize data authentication by using hash functions

but in a diﬀerent manner. For example, SPINS (Per-

rig et al., 2002) makes use of a hash chain, where

each hash value in the chain is used as a signing key.

The authorization issue of the data authentication is

controlled by gradually disclosing hash values in the

hash chain. A single key pair can be used several

times, but the veriﬁer is not able to complete the in-

tegrity check of a signature until the signer discloses a

hash value that was used to make a signature. SPINS

has diﬀerent characteristics and functionality from the

above described OTS, and this paper does not discuss

schemes of this type due to the page restriction.

1.2 Contribution of this Study

This study investigates another improvement of Win-

ternitz OTS. The improvement focuses possible use of

the scheme in a wireless sensor network, and the pro-

posed techniques can be combined with other investi-

gations, including (Buchmann et al., 2011b; Hulsing,

2013; Buchmann et al., 2011a; Bernstein et al., 2015).

A wireless sensor network (WSN) typically con-

sists of a power-provided server and battery-operated

sensor nodes. Sensor nodes are deployed in a target

ﬁeld and constitute a wireless ad-hoc network. The

battery lifetime of nodes is a concern in WSN be-

cause the shutoﬀ of a single node can disconnect a

major part of the network. A node is commonly a

tiny device that monitors its environment and sends

collected information to the server. If data authenti-

cation is needed in the communication from a node

to the server, then a simple message authentication

code (MAC) is available because the communication

is one-to-one. On the other hand, the server some-

times sends important messages, such as control com-

mands, to multiple nodes. MAC is not available

for the data authentication in the one-to-many com-

munication because MAC does not have the non-

repudiation property, and a digital signature is needed

in this case. In this framework, signed messages are

always constructed by the sever, and nodes just verify

signatures. To extend the battery lifetime of nodes,

the complexity of veriﬁcation is more substantial than

the complexities of key generation and signing.

To reduce the complexity of veriﬁcation, we con-

sider two modiﬁcations of Winternitz OTS. The ﬁrst

modiﬁcation includes a ﬁngerprinting function called

constant-sum ﬁngerprinting function, which has been

discussed in (Cruz et al., 2016). This function con-

tributes to reducing the complexity of veriﬁcation to a

small constant amount, but it can increase the com-

plexities of key generation and signing(Cruz et al.,

2016). To avoid this problem, we introduce in this pa-

per the second modiﬁcation of partially constructing

the hash chains and using a nonce in the signing pro-

cedure. Instead of fully constructing long hash chains,

we construct hash chains partially and use auxiliary

information of a nonce to avoid inconvenient access to

the unconstructed part of the hash chains. This tech-

nique is compatible with the mathematical property

of the constant-sum ﬁngerprinting and suppresses the

complexities of key generation and signing.

Winternitz OTS is brieﬂy reviewed in Sect. 2, and

the proposed OTS scheme is introduced in Sect. 3.

The complexity of the scheme is discussed in this sec-

tion also. It is proved in Sect. 4 that the proposed

OTS is strongly existentially unforgeable under some

assumptions of the ﬁngerprinting and hash functions.

2 WINTERNITZ OTS

For the sake of clarity, we use slightly diﬀerent deﬁ-

nition of Winternitz OTS from (Merkle, 1990) at the

following two points: (i) The ﬁngerprinting function

is explicit in this paper, while it is implicit in litera-

ture. (ii) Integers in a ﬁngerprint indicate positions

from the head, not from the tail of hash chains.

A hash-based OTS has three algorithms KeyGen

for generating keys, Sign for the computation of sig-

natures, and Verify for the veriﬁcation of signatures,

which are implemented as follows in Winternitz OTS.

• KeyGen(1

): Select a hash function h : {0, 1}

→

{0, 1}

, where L is the length of a hash image, and

a ﬁngerprinting function f : {0, 1}

∗

→ {0, 1}

The hash function h and the ﬁngerprinting func-

tion f are public information, and veriﬁers are as-

sumed to know h and f . Choose a positive inte-

ger parameter l and deﬁne w = w

+ w

, where



n log



and w



log

(l − 1))



+ 1. Se-

lect s

, . . . , s

uniformly from {0, 1}

at random

and compute v

= h

l−1

) for 1 ≤ i ≤ w. The

signing key and the veriﬁcation key are deﬁned

as SK = (s

, . . . , s

) and VK = (v

, . . . , v

), re-

spectively. We call the sequence of hash values s

h(s

), h

), . . . , h

l−1

) a hash chain (of length

l − 1), where s

and h

l−1

) are called the head

and the tail of the chain, respectively.

SECRYPT 2018 - International Conference on Security and Cryptography

298

• Sign(SK, m): Compute the ﬁngerprint f (m) of

m, and convert f (m) to a base-l representation

, . . . , a

) by regarding f (m) as a binary in-

teger (note that w

digits in l-ary suﬃce to ac-

commodate an integer of n-bits binary). Then,

compute the check-sum C = w

(l − 1) −

i=1

and let (c

, . . . , c

) be the base-l representation

of C (note again that w

digits in l-ary suf-

ﬁce to accommodate the value of C). Write

( f

, . . . , f

) = (a

, . . . , a

, c

, . . . , c

), and the

signature for the message m is deﬁned as σ =

l−1− f

), . . . , f

l−1− f

)).

• Verify(VK, m, σ): Determine ( f

, . . . , f

) as in

Sign(SK, m). Accept m and σ = (σ

, . . . , σ

) if

and only if VK = (h

(σ

), . . . , h

(σ

)).

The signing key, veriﬁcation key, and signatures

of Winternitz OTS are all wL-bits in size. The cost

of an algorithm is deﬁned as the number of compu-

tations of the hash function h performed in the al-

gorithm. The cost of KeyGen algorithm is always

w(l − 1), and the costs of Sign and Verify algorithms

are both w(l − 1) at the maximum. For several values

of l, the left part of Tab. 1 shows the values of w

, w

w, the cost of each algorithm, and the signature length

|σ| for the security parameter n = 160. Remind that

L is the length of a hash image. If we use SHA-1

as h for example, then L = 160 and the signature is

|σ| = 22L = 3520 bits in length for l = 256. From the

table, we can observe a trade-oﬀ relation between the

signature length |σ| and the costs of operations.

3 PROPOSED SCHEME

3.1 Fingerprinting Function

For positive integers l and w, deﬁne

l,w

= {(t

, . . . , t

) : t

∈ {0, . . . , l}, t

+ · · · + t

= l},

which is the set of tuples of w non-negative integers

that sum to l. We note that



l,w



= (l + w − 1)!/l!(w −

1)!. An (l, w)-constant-sum ﬁngerprinting function is

a function that maps a message of an arbitrary length

to a tuple in T

l,w

. In this paper, an (l, w)-constant-

sum ﬁngerprinting function is denoted by f

l,w

. Our

basic idea is to use f

l,w

to specify positions in the hash

chains in Winternitz OTS. Before proceeding to the

discussion of OTS, we ﬁrst see that f

l,w

can be con-

structed from a usual ﬁngerprinting function.

For a security parameter n, choose l and w so that



l,w



≥ 2

. Prepare a ﬁngerprinting function f that

has exactly



l,w



ﬁngerprints in its range. We as-

sume without loss of generality that the range of f

is I

l,w

= {0, . . . ,



l,w



− 1}. A constant-sum ﬁnger-

printing function f

l,w

is obtained by bijectively map-

ping integers in I

l,w

to tuples in T

l,w

. For this sake,

assign each tuple in T

l,w

with a unique integer in I

l,w

according to a descending dictionary order. For ex-

ample, if l = 4 and w = 3, then tuples in T

4,3

are or-

dered as (4, 0, 0), (3, 1, 0), (3, 0, 1), (2, 2, 0), . . . , and

they are assigned with integers 0, 1, 2, 3, . . . , respec-

tively. Note that if (l − k, t

, . . . , t

) ∈ T

l,w

, where

0 ≤ k ≤ l, then t

+ · · · + t

= k and hence T

l,w

con-

tains



k,w−1



= (k + w − 2)!/(k!(w − 2)!) tuples of the

form (l − k, t

, . . . , t

). This implies that any tuple of

the form (l − k, t

, . . . , t

) must be assigned with an

integer that is b

or more and b

k+1

− 1 or less where

k−1

i=0



i,w−1



for 0 ≤ k ≤ l + 1. Notice that b

can

be easily computed by using the recursion



i,w−1



(i + w − 2)!

i!(w − 2)!

i + w − 2



i−1,w−1



with



0,w−1



= 1 as a basis. To map an integer j ∈ I

l,w

to a tuple (t

, . . . , t

) ∈ T

l,w

, we ﬁrst determine k that

satisﬁes b

≤ j < b

k+1

(i.e. j ∈ [b

, b

k+1

)) and set

= l − k. The other w − 1 components t

, . . . , t

are

determined by mapping j− b

(which is 0 or more and



k,w−1



− 1 or less) to a tuple in T

k,w−1

in a recursive

manner. This computation is summarized as follows.

Procedure 1. This procedure M

l,w

( j) maps j ∈ I

l,w

to (t

, . . . , t

) ∈ T

l,w

1. If w = 1, then terminate with (t

) = (l) as an out-

put. If w > 1, then continue to the next step;

2. i ← 0, a ← 1, b

= 0, b

← a;

/* a is used to record the value of



i,w−1



3. while j < [b

, b

) {

4. i ← i + 1;

5. a ← a(i + w − 2)/i;

6. b

← b

, b

← b

+ a;

7. }

8. t

← l − i; /* because j ∈ [b

, b

) = [b

, b

i+1

) */

9. (t

, . . . , t

) ← M

i,w−1

( j − b

);

10. Output (t

, . . . , t

);

We remark that the constant-sum ﬁngerprinting

function f

l,w

(m) = M

l,w

( f (m)) has the same statisti-

cal property as f because M

l,w

is a bijective mapping.

If f is collision-resistant, then so is f

l,w

, for example.

3.2 Tentatively Improved OTS

The following OTS is obtained by using a constant-

sum ﬁngerprinting function in Winternitz OTS in a

straightforward manner. This OTS is still tentative

because we will subsequently employ a second mod-

iﬁcation. Nevertheless, this construction is important

Hash-Based Signature with Constant-Sum Fingerprinting and Partial Construction of Hash Chains

299

Table 1: Parameters of Winternitz OTS and tentatively improved OTS (Sect. 3.)

Winternitz tentatively improved

l w

w KeyGen Sign Verify |σ| l w KeyGen Sign Verify

16 40 3 43 645 ≤ 645 ≤ 645 43L 211 43 9, 073 8, 862 211

32 32 2 34 1, 054 ≤ 1, 054 ≤ 1, 054 34L 363 34 12, 342 11, 979 363

64 27 2 29 1, 827 ≤ 1, 827 ≤ 1, 827 29L 579 29 16, 791 16, 212 579

128 23 2 25 3, 175 ≤ 3, 175 ≤ 3, 175 25L 984 25 24, 600 23, 616 984

256 20 2 22 5, 610 ≤ 5, 610 ≤ 5, 610 22L 1, 695 22 37, 290 35, 595 1, 695

because it will help explain the idea of the improve-

ment that will be discussed in the next section.

• KeyGen(1

): Select parameters l and w, a hash

function h : {0, 1}

→ {0, 1}

, and a constant-

sum ﬁngerprinting function f

l,w

. Select s

, . . . , s

uniformly from {0, 1}

at random, and compute

= h

) for 1 ≤ i ≤ w. The signing key and the

veriﬁcation key are deﬁned as SK = (s

, . . . , s

)

and VK = (v

, . . . , v

), respectively.

• Sign(SK, m): The signature for the message m is

σ = (h

l− f

), . . . , f

l− f

)) where ( f

, . . . , f

) =

l,w

(m).

• Verify(VK, m, σ): The pair of the message m and

the signature σ = (σ

, . . . , σ

) is accepted if

and only if VK = (h

(σ

), . . . , h

(σ

)) where

( f

, . . . , f

) = f

l,w

(m).

The size of keys and the size of signatures are wL-

bits. The costs of KeyGen, Sign, and Verify are lw,

lw − l, and l, respectively, where the cost is measured

by the number of computations of the hash function

h. Remark however that we should not compare these

formulas naively with those of Winternitz OTS. Given

a security parameter n, the values of l and w in the

above scheme are determined according to a diﬀer-

ent constraint from Winternitz OTS. For example, the

choice of l = 256 and w = 22 is allowed in Win-

ternitz OTS (See Tab. 1) for the security parameter

of n = 160, but we need to take l = 1695 in the

above scheme to make w = 22 for n = 160 because



1694,22



< 2

160



1695,22



. Long chains are needed

because T

l,w

is a small subset in the entire set of w-

tuples of integers. The right part of Tab. 1 shows the

parameters and costs of the above tentative scheme

for n = 160. Comparing the values in Tab. 1, we can

see that the cost of veriﬁcation is reduced in this tenta-

tive OTS scheme, but the costs of key generation and

sign are much greater than those of Winternitz OTS

because of the long hash chains that are needed in the

scheme. This problem is tackled by introducing an-

other idea; partial construction of hash chains.

3.3 Partial Construction of Hash Chains

In the tentatively improved OTS, the i-th hash chain

consists of l + 1 hash values; s

, h(s

), . . . , h

Each hash value in the i-th hash chain has the chance

to be used as an i-th component of a signature, but

that probability is not equally likely. For example,

= h

l−l

) is used as a signature if and only if

l,w

(m) = (0, . . . , 0, l, 0 . . . , 0), which is taken with

very small probability. In general, hash values that

are close to the head of the chain (i.e., hash values

) with small j) have small probabilities to be used

as a signature component. Based on this observation,

we consider constructing a hash chain from an inter-

mediate point, omitting the construction of the “head

portion” of the hash chain. In the Sign algorithm, we

can start tracing the hash chain from that intermedi-

ate point. The unconstructed hash values are hardly

needed by the Sign algorithm, and thus, a valid sig-

nature is likely to be computed in most of the cases.

Obviously, the trick does not work all of the time. The

computation fails if Sign accesses an unconstructed

hash value. To avoid this unfortunate case from hap-

pening, we use a nonce in the signing process and al-

low a message to not have an undesired ﬁngerprint.

Let θ be an integer with θ ≤ l and deﬁne

[θ]

l,w

= {(t

, . . . , t

) : t

∈ {0, . . . , θ}, t

+ · · · + t

= l},

which is a subset of T

l,w

such that integer components

are upper-bounded by θ. Remark that T

[θ]

l,w

= ∅ if θ <

l/w, and we take θ so that T

[θ]

l,w

contains suﬃciently

many tuples. We deﬁne a nonce of a message m as the

smallest positive integer r that makes f

l,w

(m||r) ∈ T

[θ]

l,w

where m||r denotes the concatenation of m and r. The

proposed OTS is described as follows.

• KeyGen(1

): The algorithm is the same as

KeyGen(1

) of the tentatively improved scheme

except that v

is computed as v

= h

) for

1 ≤ i ≤ w. In other words, s

is used as an in-

termediate value in the i-th hash chain.

• Sign(SK, m): Determine the nonce r of the mes-

sage m. The signature for the message m is

deﬁned as σ = (h

θ− f

), . . . , f

θ− f

)) where

( f

, . . . , f

) = f

l,w

(m||r).

SECRYPT 2018 - International Conference on Security and Cryptography

300

• Verify(VK, m, σ): The pair of the message m and

the signature σ = (σ

, . . . , σ

) is accepted if

and only if VK = (h

(σ

), . . . , h

(σ

)) where

( f

, . . . , f

) = f

l,w

(m||r) with r as the nonce of the

message m.

Notice the following diﬀerences from the tentative

OTS in the previous section.

• KeyGen generates hash chains of length θ, which

is the “tail portion” of the original hash chains.

• Sign uses the nonce r to generate a ﬁngerprint in

[θ]

l,w

. The signature is computed from SK because

all components of the ﬁngerprint are θ or less.

The size of keys and the size of signatures are wL-

bits, and the costs of KeyGen, Sign, and Verify are

θw, θw − l, and l, respectively. Because θ < l, we

reduced the costs of KeyGen and Sign, while the cost

of Verify is the same as in the tentative scheme.

For the fairness of comparison, however, we need

to consider the computational burden of ﬁnding the

nonce r besides the number of computations of the

hash function h. Basically, there is no means of

determining the nonce r except through exhaustive

search; examine r = 1, 2, . . . in a sequential manner

until we get f

l,w

(m||r) ∈ T

[θ]

l,w

. Under the assumption

that f

l,w

(m||r) distributes uniformly over T

l,w

, the ex-

pected number of such examinations is 1/p

l,w,θ

, where

l,w,θ



[θ]

l,w



l,w



is the probability that f

l,w

(m||r)

belongs to T

[θ]

l,w

for an examined value of r. It is known

that



[θ]

l,w



is characterized by generalized Pascal tri-

angles(Bollinger and Burchard, 1990), and



[θ]

l,w



θ+1

(w, l), where

(n, r) =

min(n,br/mc)

j=0

(

−1

)

n + r − 1 − jm

n − 1

Using this formula, we can compute p

l,w,θ

and then es-

timate the expected number of examinations that are

needed to ﬁnd the nonce r.

To illustrate the relationship between p

l,w,θ

and θ,

take l = 1695 and w = 22 for example (which are

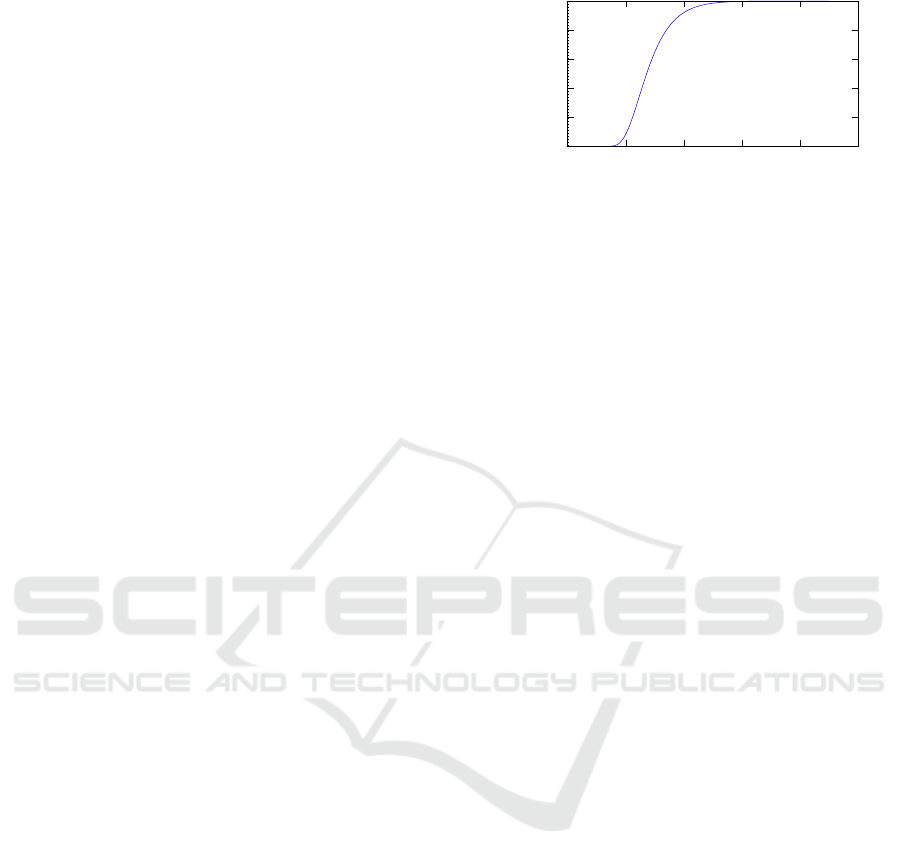
from the bottom line of Tab. 1). Fig. 1 sketches the

value of p

1695,22,θ

where the horizontal axis is θ and

the vertical axis is p

1695,22,θ

. We can conﬁrm from

the graph that p

1695,22,θ

converges to 1 with rather

small values of θ. Numerical computation shows that

1695,22,θ

approximately equals to 0.50, 0.25 and 0.125

at θ = 272, 232 and 209, respectively. If we take

θ = 209 for example, then KeyGen generates w = 22

hash chains of length θ = 209 each, and thus its cost

is θw = 4598. The cost of Sign is θw − l = 2903, and

the Sign algorithm needs to examine 1/p

1695,22,209

≈ 8

candidates of the nonce on average. The cost of Verify

l,w,θ

0.2

0.4

0.6

0.8

0 200 400 600 800 1000

Figure 1: The probability p

1695,22,θ

is l = 1695 which remains the same as the tentatively

improved OTS as in Tab. 1. Parameters for θ = 272

and 232, and also parameters for w = 29 and 25 with

1/p

w,l,θ

≈ 2, 4 and 8, are shown in Tab. 2. The costs

of KeyGen and Sign are reduced from the tentatively

scheme while preserving the eﬃciency of Verify.

4 SECURITY OF THE PROPOSED

SCHEME

The security proof of the proposed scheme is provided

in this section. The basic idea of the proof is almost

the same as that for Winternitz OTS (Buchmann et al.,

2011b), but the proof must be generalized to cope

with the ﬁngerprinting function which was implicit in

literature, and advantage (the success probability) of

the adversary must be revised. After reviewing re-

lated notions, the proposed OTS scheme is shown to

be strongly existentially unforgeable.

4.1 Formal Notions of Security

A function h is one-way if the probability



y = h(x

) : x ← {0, 1}

∗

; y ← h(x); x

← A(y)



(1)

is negligible(Goldwasser and M. Bellare, 2018) for

an arbitrary polynomial-time algorithm A. This deﬁ-

nition is based on Deﬁnition 2.2 of (Goldwasser and

M. Bellare, 2018) but we allow x to have an arbitrary

length. A function h is collision-resistant if



h(z) = h(z

) : (z, z

) ← A



(2)

is negligible for an arbitrary polynomial-time algo-

rithm A. This deﬁnition coincides with the CR2-KK

property in (Goldwasser and M. Bellare, 2018) with

the small diﬀerence that a key (the deﬁnition of h) is

explicitly given to A in (Goldwasser and M. Bellare,

2018) while the key is implicit in (2).

The strong existential unforgeability is deﬁned in

terms of a game between a challenger and an adver-

sary(Boneh et al., 2006).

Hash-Based Signature with Constant-Sum Fingerprinting and Partial Construction of Hash Chains

301

Table 2: Comparison of Winternitz OTS and the proposed OTS.

Winternitz proposed

l w KeyGen Sign Verify |σ| l θ 1/p

w,l,θ

KeyGen Sign Verify

64 29 1, 827 ≤ 1, 827 ≤ 1, 827 29L 579 76 2 2, 204 1, 625 579

579 66 4 1, 914 1, 335 579

579 59 8 1, 711 1, 132 579

128 25 3, 175 ≤ 3, 175 ≤ 3, 175 25L 984 144 2 3, 600 2, 616 984

984 123 4 3, 075 2, 091 984

984 111 8 2, 775 1, 791 984

256 22 5, 610 ≤ 5, 610 ≤ 5, 610 22L 1, 695 272 2 5, 984 4, 289 1, 695

1, 695 232 4 5, 104 3, 409 1, 695

1, 695 209 8 4, 598 2, 903 1, 695

Setup. The challenger runs KeyGen and provides the

public veriﬁcation key VK to the adversary. The

private key SK is kept secret by the challenger.

Query. The adversary requests the challenger to

compute the signatures σ

, . . . , σ

for query mes-

sages m

, . . . , m

of its choice. The query can be

made adaptively, that is, m

can be determined af-

ter the adversary has obtained σ

, . . . , σ

i−1

Output. The adversary outputs (m

, σ

) expecting

that σ

is a valid signature of m

. It is required

that (m

, σ

) is diﬀerent from any of (m

, σ

) with

1 ≤ i ≤ q (it is allowed that m

= m

but in that

case σ

must be diﬀerent from σ

The adversary wins the game if (m

, σ

) is accepted

by Verify(VK, m

, σ

). A signature scheme is said

to be strongly existentially unforgeable if there is

no polynomial-time algorithm that plays the role of

the adversary and wins the game with non-negligible

probability. In the discussion of OTS schemes, a key

pair is used only once. Therefore, we restrict our-

selves to q = 1 in the Query phase in the game above:

the adversary chooses a message m, obtains a signa-

ture σ for m, and tries to forge (m

, σ

) , (m, σ).

4.2 Formal Security Proof

Assume that |T

[θ]

w,l

| > 1. The following lemma is

needed in the subsequent discussion.

Lemma 2. For ( f

, . . . , f

) and ( f

, . . . , f

) that are

chosen from T

[θ]

w,l

uniformly and independently, and

for any i with 1 ≤ i ≤ w;

1. Pr[ f

= f

] is not overwhelming (i.e., (1 − Pr[ f

]) is not negligible), and

2. Pr[ f

> f

] is bounded as

1 − Pr[ f

= f

]

≤ Pr[ f

> f

] <

Proof: Assume that Pr[ f

= f

] has overwhelming

probability. Write p

= Pr[ f

= j] for 0 ≤ j ≤ θ.

Notice that all of f

, . . . , f

, f

, . . . , f

obey the same

probability distribution as f

, and Pr[ f

= f

] is equal

j=0

. Because Pr[ f

= f

] is overwhelming

as assumed, there is j with 0 ≤ j ≤ θ such that

is overwhelming. This implies that ( f

, . . . , f

) =

( f

, . . . , f

) = ( j, . . . , j) with overwhelming probabil-

ity, which contradicts the assumption that ( f

, . . . , f

)

and ( f

, . . . , f

) are chosen uniformly from T

[θ]

w,l

with

[θ]

w,l

| > 1. This proves the (1) part of the lemma. The

(2) part is obvious because Pr[ f

> f

] = Pr[ f

< f

]

and Pr[ f

> f

] + Pr[ f

< f

] + Pr[ f

= f

] = 1. 

We write p

w,l,θ

for Pr[ f

= f

]. It is diﬃcult to

write down p

w,l,θ

in a simple formula, but Lemma 2(1)

guarantees that 1 − p

w,l,θ

is not negligible.

Theorem 3. If f

l,w

is collision-resistant and h is one-

way and collision-resistant, then the proposed OTS

scheme is strongly existentially unforgeable.

Proof: We show that if there is a polynomial-time al-

gorithm A

that wins the game of the strong existential

unforgeability, then we can construct A

that succeeds

in an attack on f

l,w

or h. The algorithm A

is given a

hash value y of the hash function h and attempts to

achieve either one of the following three goals.

• A

ﬁnds a collision of f

l,w

(i.e., A

makes (2) non-

negligible for f

l,w

• A

ﬁnds a pre-image of the given hash value y of

h (i.e., A

makes (1) non-negligible for h).

• A

ﬁnds a collision of h (i.e., A

makes (2) non-

negligible for h).

To make this possible, the algorithm A

plays the role

of the challenger of the game of the strong existential

unforgeability and let A

(which acts as the adversary

of the game) output a pair of a message and a sig-

nature. If A

succeeds in forging a valid signature,

then the signature contains essential information that

makes the attempts of A

succeed.

The algorithm A

performs the followings steps

for a given hash value y.

SECRYPT 2018 - International Conference on Security and Cryptography

302

e e e e e

6 6 6 6 6

e e u e e

6 6 6 6

e e e e e

· · · · · ·

α−1

α+1

Figure 2: Modiﬁcation of the veriﬁcation key.

1. Run KeyGen and obtain a signing key SK =

, . . . , s

) and a veriﬁcation key VK =

, . . . , v

), where v

= h

) for 1 ≤ i ≤ w.

2. Choose m

randomly, determine the nonce r

of m

, and also choose α uniformly at random

from {1, . . . , w}. Let β be the α-th component of

the constant-sum ﬁngerprint f

l,w

||r

). Deﬁne

= (v

, . . . , v

), where











(i , α),

(y) (i = α),

and provide the altered veriﬁcation key VK

to the

algorithm (adversary) A

as the outcome of the

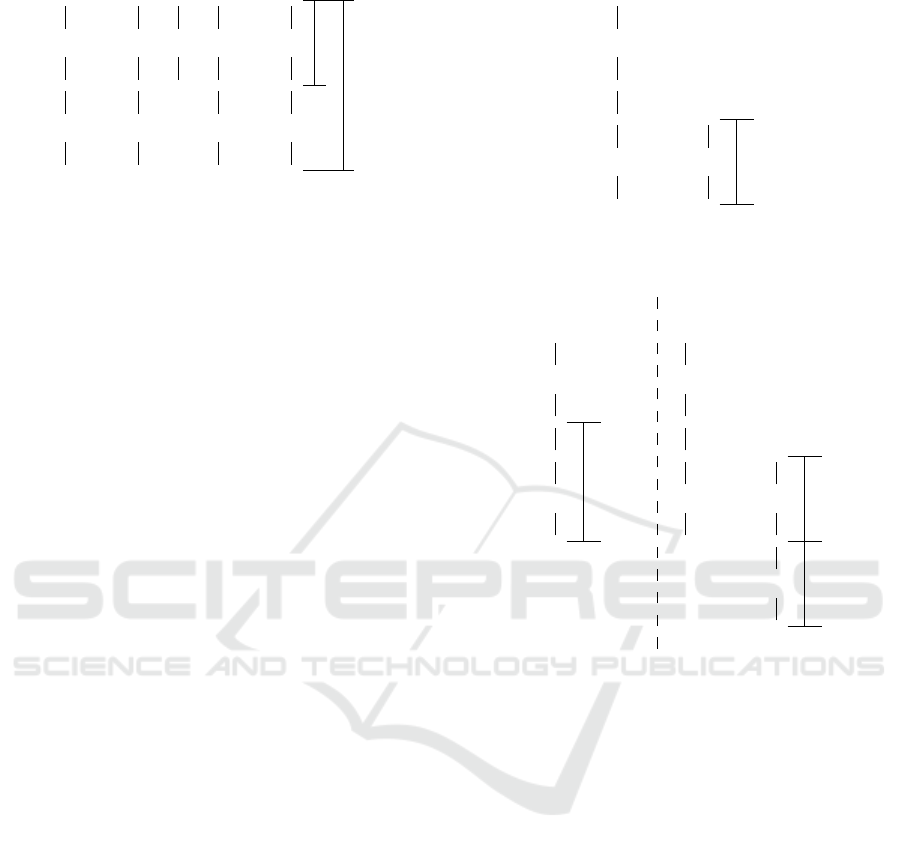
Setup phase of the game. Fig. 2 illustrates the

construction of VK

where vertices represent hash

values and directed edges represent the applica-

tion of the hash function h.

3. Receive m from A

in the Query phase.

4. Find the nonce r of m and let f

l,w

(m||r) =

( f

, . . . , f

) ∈ T

[θ]

l,w

. If f

> β, then abort this

attack with failure. If f

≤ β, then compute

σ = (σ

, . . . , σ

), where











θ− f

) (i , α),

β− f

) (i = α),

and return σ to A

as the signature of the query m.

5. Receive (m

, σ

) from the adversary A

in the Out-

put phase, and determine the nonce r

of m

. Con-

tinue one of the following options depending on

related values. We write σ

= (σ

, . . . , σ

) and

l,w

||r

) = ( f

, . . . , f

(a) If m = m

, then we have r = r

and f

l,w

(m||r) =

l,w

||r

). In this case, we must have σ , σ

due to the rule of the game, and there is i ∈

{1, . . . , w} with σ

, σ

. Note that diﬀerent

hash chains starting from σ

and σ

eventually

converge to v

if (m

, σ

) is accepted by Verify

algorithm (see Fig. 3). Determine j such that

(σ

) , h

(σ

) and h

j+1

(σ

) = h

j+1

(σ

), and

output (z, z

) = (h

(σ

), h

(σ

)) as a pair that

causes a collision of h.

e e

6 6

e e

z z

Figure 3: Convergence of two hash chains.

− β

(c)-i (c)-ii

e e

6 6

u e

z z

− β

Figure 4: Relation among hash values.

(b) If m , m

and f

l,w

(m||r) = f

l,w

||r

), then out-

put (z, z

) = (m||r, m

||r

) as a pair that causes a

collision of f

l,w

, f

l,w

(m||r) , f

l,w

||r

) and f

> β,

then compute y

= h

−β

(σ

i. If y = y

, then output x

= h

−β−1

(σ

) as the

pre-image of y. The relation among hash val-

ues is illustrated in the left-part of Fig. 4.

ii. If y , y

, then determine j such that h

(y) ,

) and h

j+1

(y) = h

j+1

(y), and output

(z, z

) = (h

(y), h

)) as a pair that causes a

collision of h. This case is illustrated in the

right-part of Fig. 4.

(d) If none of the above conditions holds, then

abort this attack with failure.

Write the winning probability of A

as p

+ p

where p

is the probability that m = m

and A

wins

the game (we call this scenario A), p

is the probabil-

ity that m , m

, f

l,w

(m||r) = f

l,w

||r

) and A

wins

the game (scenario B), and p

is the probability that

m , m

, f

l,w

(m||r) , f

l,w

||r

) and A

wins the game

(scenario C). If A

wins the game with non-negligible

Hash-Based Signature with Constant-Sum Fingerprinting and Partial Construction of Hash Chains

303

probability, then at least one of p

, p

, and p

is non-

negligible. The algorithm A

may abort at Step 4,

but that probability is less than 1/2 by Lemma 2(2).

With probability more than 1/2, A

proceeds to Step

5. The algorithm A

performs Step 5(a) only if A

wins the game with the scenario A, and in this case,

the pair (z, z

) produced by A

is a collision pair of

h. The algorithm A

performs Step 5(b) only if A

wins the game with the scenario B, and in this case,

the pair (z, z

) produced by A

is a collision pair of

l,w

. The algorithm A

performs Step 5(c) only if A

wins the game with the scenario C, and furthermore,

> β is fulﬁlled simultaneously. This is an event

that occurs with probability p



1 − p

w,l,θ



/2 or more

by Lemma 2(2), and in this case, A

discovers a pre-

image x

of y or a collision pair (z, z

) of the hash func-

tion h. Summarizing the discussion, the algorithm A

succeeds in one of three attacks over f

l,w

and h with

probability is equal to or more than



+ p



1 − p

w,l,θ





If the winning probability of A

is non-negligible,

then so is the success probability of A

. 

5 CONCLUSION

Constant-sum ﬁngerprinting functions and partial

construction of hash chains are investigated to im-

prove Winternitz OTS. The constant-sum ﬁngerprint-

ing function contributes to reduce the complexity of

the signature veriﬁcation, which is advantageous in

certain services including wireless sensor networks.

The integer components of constant-sum ﬁngerprints

distribute non-uniformly, which makes the partial

construction of hash chains an eﬀective means to re-

duce the complexities of key generation and signing.

It is conﬁrmed that the proposed scheme is more eﬃ-

cient than Winternitz OTS in terms of the number of

computations of the hash function, while the scheme

is shown to be strongly existentially unforgeable. It

is noted that the technique that is investigated in this

study is compatible with other improvements that are

studied in (Buchmann et al., 2011b; Hulsing, 2013;

Buchmann et al., 2011a; Bernstein et al., 2015). We

can further improve the eﬃciency by combining the

investigated techniques with those in literature.

REFERENCES

Bernstein, D., Buchmann, J., and Dahmen, E. (2009). Post-

Quantum Cryptography. Springer.

Bernstein, D., Hopwood, D., Hulsing, A., et al. (2015).

Sphincs: Practical stateless hash-based signatures. In

EUROCRYPT 15, pages 368–397.

Bleichenbacher, D. and Maurer, U. (1996a). On the eﬃ-

ciency of one-time digital signature schemes. In ASI-

ACRYPT 96, pages 145–158.

Bleichenbacher, D. and Maurer, U. (1996b). Optimal tree-

based one-time digital signature schemes. In Symp. on

Theoretical Aspects of Comp. Sci., pages 363–374.

Bollinger, R. and Burchard, C. (1990). Lucas’s theorem and

some related results for extended pascal triangles. The

American Math. Monthly, 97(3):198–204.

Boneh, D., Shen, E., and Waters, B. (2006). Strongly un-

forgeable signatures based on computational diﬃe-

hellman. In Intl. Conf. on Theory and Practice of

Public-Key Cryptography, pages 229–240.

Buchmann, J., Dahmen, E., , and Hulsing, A. (2011a).

Xmss—a practical forward secure signature scheme

based on minimal security assumptions. In Intl. Conf.

on Post-Quantum Cryptography, pages 117–129.

Buchmann, J., Dahmen, E., Ereth, S., et al. (2011b). On the

security of the winternitz one-time signature scheme.

In AFRICACRYPT 11, pages 363–378.

Cruz, J., Yatani, Y., and Kaji, Y. (2016). Constant-sum ﬁn-

gerprinting for winternitz one-time signature. In Intl.

Symp. on Inf. Theory and Its App., pages 703–707.

Dods, C., Smart, N., and Stam, M. (2005). Hash based dig-

ital signature schemes. In Intl. Conf. on Cryptography

and Coding, pages 96–115.

Goldwasser, S. and M. Bellare, M. (2018). Lecture

notes on cryptography. https://cseweb.ucsd.edu/ ˜mi-

hir/papers/gb.pdf, accessed February 14.

Hulsing, A. (2013). W-ots

— shorter signatures for

hash-based signature schemes. In AFRICACRYPT 13,

pages 173–188.

Lamport, L. (1979). Constructing digital signatures from

a one-way function. Technical Report SRI-CSL-98,

SRI Intl. Computer Sci. Lab.

Merkle, R. (1990). A certiﬁed digital signature. In CRYPTO

89, pages 218–238.

Perrig, A. (2001). The biba one-time signature and broad-

cast authentication protocol. In ACM Conf. on Com-

puter and Communications Security, pages 28–37.

Perrig, A., Szewczyk, R., Wen, V., et al. (2002). Spins:

Security protocols for sensor networks. Wireless Net-

works J., 8(5):521–534.

Reyzin, L. and Reyzin, N. (2002). Better than biba: Short

one-time signatures with fast signing and verifying. In

Intl. Inf. Security and Privacy Conf., pages 1–47.

Shor, P. (1997). Polynomial-time algorithms for prime fac-

torization and discrete logarithms on a quantum com-

puter. SIAM J. of Computing, 26(5):1484–1509.

SECRYPT 2018 - International Conference on Security and Cryptography

304