
A Stream Clustering Algorithm using Information Theoretic
Clustering Evaluation Function
Erhan Gokcay
Software Engineering Department, Atilim University, Incek, Ankara, Turkey
Keywords: Stream Clustering, Data Stream, Cluster Analysis, Information Theory, Distance Function, Clustering
Evaluation Function.
Abstract: There are many stream clustering algorithms that can be divided roughly into density based algorithms and
hyper spherical distance based algorithms. Only density based algorithms can detect nonlinear clusters and
all algorithms assume that the data stream is an ordered sequence of points. Many algorithms need to receive
data in buckets to start processing with online and offline iterations with several passes over the data. In this
paper we propose a streaming clustering algorithm using a distance function which can separate highly
nonlinear clusters in one pass. The distance function used is based on information theoretic measures and it
is called Clustering Evaluation Function. The algorithm can handle data one point at a time and find the correct
number of clusters even with highly nonlinear clusters. The data points can arrive in any random order and
the number of clusters does not need to be specified. Each point is compared against already discovered
clusters and each time clusters are joined or divided using an iteratively updated threshold.
1 INTRODUCTION
Rapid increase of Cloud Systems and Internet of
Things concept have started to generate a huge
amount of data as streams. The processing of stream
data requires different approaches as data mining
algorithms that require the whole data set for
processing are having problems in terms of memory
and speed. The data that is already collected and
called Big Data can also be considered as a stream
since reading and processing Big Data in one step is
not possible because of memory constraints. One of
the important data mining algorithms is clustering the
data into several similar groups. There are several
challenges that needs to be addressed here. One of the
problems is the unknown number of clusters in the
data set where many clustering algorithms require this
information before processing. Another problem is
the arriving order of the data. Each data point from
any cluster can arrive in any order. The evolving
nature of some real-time generated data features also
increases the difficulty of clustering such streams.
During the analysis no special processing is done
for categorical data. One of the basic assumptions in
this paper is that the total data set contains groups that
can be clustered offline; even theoretically; by a
clustering algorithm. The motivation of this
assumption is that although the data arrives as a
stream one at a time, the total set should contain
clusters otherwise no algorithm; streaming or not; can
cluster the data.
In this paper we propose an algorithm that
requires one pass over the previous data to cluster a
stream of data where total number of clusters are not
known and not needed. To separate clusters properly,
we need a distance metric between clusters. The
Cluster Evaluation Function (CEF) developed by the
author (Gokcay, 2002) is chosen as a metric since
CEF can cluster nonlinear data sets. Many distance
measures are using hyper spherical distances and
cannot cluster nonconvex data sets. The algorithm is
called CEFStream and it can analyze data streams
containing nonlinearly separated clusters.
The order of data points are considered as random.
The order of arrival should not change the results.
Each arriving data point is tested against the clusters
created so far. If the distance is closer than a threshold
then the point is joined to that cluster. If not, a
different cluster is created. After each addition, the
cluster distances are measured again to find out
cluster groups that need to be merged together.
The paper is organized as follows. Section 2 gives
information about previous work. Section 3
582
Gokcay, E.
A Stream Clustering Algorithm using Information Theoretic Clustering Evaluation Function.
DOI: 10.5220/0006786205820588
In Proceedings of the 8th International Conference on Cloud Computing and Services Science (CLOSER 2018), pages 582-588
ISBN: 978-989-758-295-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

introduces the CEFStream Clustering algorithm.
Section 4 presents simulation of the algorithm using
synthetic data. Finally Section 5 presents future work
and Section 6 presents conclusion.
2 RELATED WORK
In this section we briefly review different approaches
in clustering data streams.
In the past decades, many stream clustering
algorithms have been proposed based on adaption of
off-line algorithms, such as BIRCH (Tian, 1997),
CluStream (Charu, 2003), DenStream (Feng, 2006),
StreamKM++ (Marcel, 2012), etc. These algorithms
can be generally summarized into two steps: an online
learning step that derives a data abstraction from
input data stream, and an offline clustering step that
generates the final result. During the online learning
step, input data stream is reduced to smaller size
representations so that storing the whole data is not
needed. Obviously these representations should
represent the original distributions properly to be
effective. Different algorithms gave different names
to these abstract representations like “micro-clusters”
in DenStream, or “coreset” in StreamKm++. After
receiving new data, there is an online step which
determines micro-clusters and an offline step that
uses abstract data to finalize clustering. In this step,
K-Means (James, 1967) is used by BIRCH,
CluStream and StreamKM++, while DBSCAN
(Martin, 1996) is used by DenStream.
Although many stream clustering algorithms
adopt K-Means or DBSCAN in their offline
clustering step. However, both methods have their
disadvantages. K-Means needs to know the number
of clusters k, and tends to generate similar sized
spherical clusters. DBSCAN and similar methods
(Xu 2016; Lin 2009; Alazeez 2017) can detect a
suitable number of arbitrary shaped clusters, but it has
parameters to be decided, which is critical for the
result but difficult to decide.
A good review of stream clustering methods is
given in (Reddy, 2017).
3 STREAM CLUSTERING USING
CEF
Many clustering algorithms are using hyper
ellipsoidal distance functions resulting in clusters of
similar shape. One exception is density based
algorithms (Xu 2017; Chen 2016; Khan 2016;
Hassani 2016) where there is no assumption about the
shape of the clusters. The problem with density is
how to decide the density value so that points are
considered to be part of a cluster. In this paper the
Clustering Evaluation Function (CEF) developed by
the author using Information Theory is chosen. The
derivation is described in (Gokcay, 2002) and will not
be repeated here. The distance measured by CEF can
differentiate nonlinearly separated clusters and
therefore it is suitable to cluster data with highly
nonconvex regions. The CEF function defined for
two clusters is given in (1).
,
,=
1
−
,2
(1)
In (1),
and
are clusters of size
and
respectively where
∈
and
∈
. The
Gaussian kernel (G) needs a parameter σ for the
kernel size which should be determined using the
scale of the data.
3.1 Data Stream
The algorithm assumes that each data point
arrives
in a random order where ∈ () and
is the total number of points in the stream. Obviously
N is not restricted in a real data stream but this will
not change the assumption about random arrival.
Another assumption is that the data has d dimensions
and it is scaled between [-1 .. 1]. Although this seems
as a strong assumption, it would be easy to scale the
data online using a pre calculated scaling factor if the
data has known maximum and minimum limits. The
time stamp is not important in the analysis.
3.2 Data Structures
During processing we need to create several data
structures besides the data itself. For each generated
cluster
in the dataset, we have to store number of
points in the cluster, an array holding the CEF
distance to other clusters and data points that belong
to the cluster. The need to store the data stream will
increase the processing time since although there is
no requirement to copy all data to memory, disk
access time will increase total access and processing
time. As a future study to reduce the storage and
processing requirements, we can replace these points
with data skeleton centers (Gokcay, 2016).
A Stream Clustering Algorithm using Information Theoretic Clustering Evaluation Function
583

:
[1..
] (data points of
)
(the number of clusters in the dataset
discovered so far)
(number of data points in
)
[1..−1] (CEF distances from current cluster
to
where ∈
[
1..
]
andp ≠ m)
The combined storage complexity of the data
stream is () which is proportional to the number
of points in the stream. The extra information that
needs to be stored has a complexity of () and the
distance calculated has a storage complexity of
(
) where is the number of clusters discovered
so far. We also assume ≪ .
3.3 CEFStream Algorithm
The CEFStream algorithm will use one pass over the
currently stored dataset. There is no online and offline
parts of the algorithm.
For each newly arrived sample point , the
distance to already formed clusters is measured once
as in (2).
(
)
=,
, ∈
[
1..
]
(2)
The next step is to find the closest cluster as in (3).
CEF function is inversely proportional to the distance
between clusters. Therefore we have to maximize the
function.
= {
(
)
,∈
[
1..
]
}
(3)
The next step is to check if the closest cluster is
larger than a threshold T. If
(
)
> then the new
sample point is added to
. Otherwise a new cluster
is created.
After processing the sample point, the data
structure of each cluster needs to be updated. If a new
cluster is generated, M will be increased by one for
each cluster data structure. The size of CEF distance
array is also increased by one to include the new
cluster. The distance from the new cluster to other
clusters are added to the array. Since these distances
are already obtained in the previous step, there is no
need recalculate CEF distances again.
When a new sample point is added to an existing
cluster, M is not changed but the distances between
clusters still should be updated. Since the distance
from the new point to other clusters are already
obtained, we only need one step operation to update
each distance.
Once the new sample is processed, it is time to
check if there are clusters that need to be merged
together using the threshold T. Using the updated
distance array in each cluster, we will check if there
are clusters closer to each other than the threshold T
as in (4). The cluster joining operation will continue
until there are no clusters left to be joined.
,
,
> (4)
3.4 Threshold Estimation
The threshold T used in the calculation to differentiate
clusters from each other can be estimated using an
iterative calculation by averaging all distances
obtained. Since most of the points are close to each
other to form a cluster, the average will give a nice
estimation to decide if a point can be considered part
of a cluster or not.
3.5 Processing Complexity
The distance calculation using the new point is done
only once using the available dataset. Therefore the
algorithm can be considered as a one-pass algorithm
and the complexity is () where the total number
of points stored so far is . When there is a new
cluster, updating the existing array and adding the
distance of the new cluster to other clusters has a
complexity of (). When an existing cluster needs
to be updated by adding the sample point, we have to
recalculate all distances. This calculation needs one
iteration over all clusters and it should be repeated for
every cluster, hence it requires a complexity of
(
). Although the CEF distance calculation
between clusters
and
requires a complexity of
∗
, the complexity can be reduced to (1)
by using the already calculated distances and the
distance calculation of new point x.
Assume that we have a new point and we
already calculated the distances
(
)
,∈
[
1..
]
from the point to all clusters during cluster
assignment. Assume that the new point belongs to
cluster
and we have to update all distances from
to all other clusters. For example assume that we
want to update the distance
,
from cluster
q to cluster k. When we update cluster q by adding x,
the new distance is given as (
,
).
Cluster C
has N
+1 points and cluster C
has
N
points. The computational complexity of CEF is
O(N
∗N
). The calculation can be simplified using
CLOSER 2018 - 8th International Conference on Cloud Computing and Services Science
584
the previously calculated distance iteratively. The
iteration is shown in (5).
,
=((
∗
∗
,
)
+
(
)
)/((
+1)∗
)
(5)
In the calculation
,
is already
calculated in the previous iteration and
(
)
=
(
,
)
is calculated during one pass cluster
assignment operation. So the complexity of the
calculation is(1).
The final complexity is
(
)
∗(
) where N is
the # of points in the stream and M is the number of
clusters in the stream. Although N is not limited,
(
)
means that the algorithm is a one-pass
algorithm. Also we assume ≪ and not chancing
drastically (will not increase during the flow of the
stream), so that practically (
) can be considered
as constant.
3.6 Algorithm
The CEFStream algorithm is given below. As long as
there is a new sample, the calculation continues as
indicated by the while loop.
____________________________________
Algorithm 1: CEFStream algorithm.
____________________________________
Input : Data stream X
Output : Cluster Data Structure
while
∈
do
for each Cluster
,∈[1..]
D[k] = CEF(x,
)
update T
end
q =
, ∈ [1..]
if (
(
)
> )
Join
and x
else
create a new cluster using x
end
for each Cluster
,∈[1..]
for each Cluster
, ∈
[
1..
]
update
.(
)
end
end
for each Cluster
,∈[1..]
for each Cluster
, ∈ [1..]
if
.(
)> T
join
and
end
end
end
end
___________________________________
3.7 Outliers
There is no special processing for outliers like in
(Thakran, 2012). Outliers can be detected by testing
the number of points in each cluster. When the
number is below a certain threshold we can mark that
cluster as an outlier.
3.8 Evolving Data Streams
No special processing is used to track changing
clusters as the algorithm can track the clusters as long
as the change is not drastic and sudden. But if the
change of a cluster starts overlapping with other
clusters, the algorithm may combine these
overlapping clusters. To overcome this problem a
window can be applied to the data stream to slowly
discard old data.
4 EXPERIMENTS
The algorithm is tested using several synthetic
datasets. Each time the data arrival is randomly
modified to test whether the clusters depend on the
arrival order or not. Using a simple dataset given in
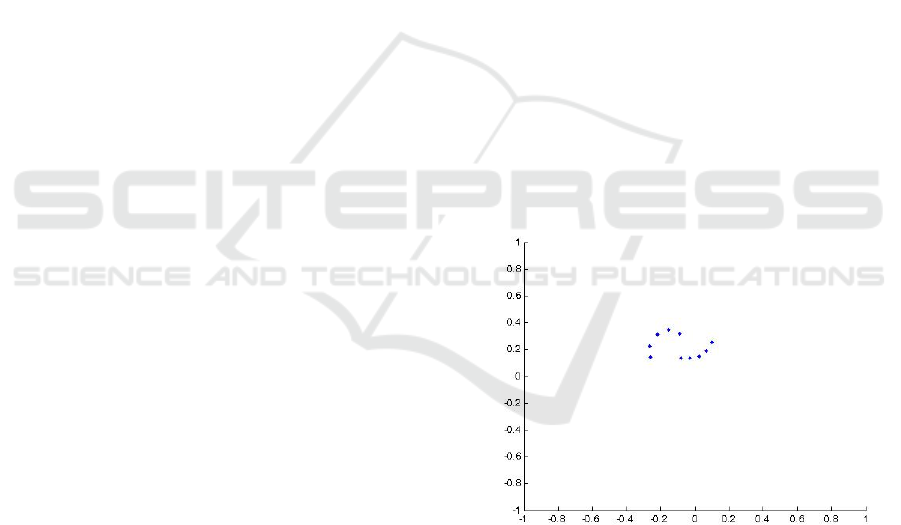
Fig. 1 the dependency to the order is tested.
Figure 1: Sample data set.
There are 10 points in the data set and each point
is taken from the set using a random permutation
simulating a stream. The result after each random
generation is the same with correct clustering as in
Fig. 2.
A Stream Clustering Algorithm using Information Theoretic Clustering Evaluation Function
585
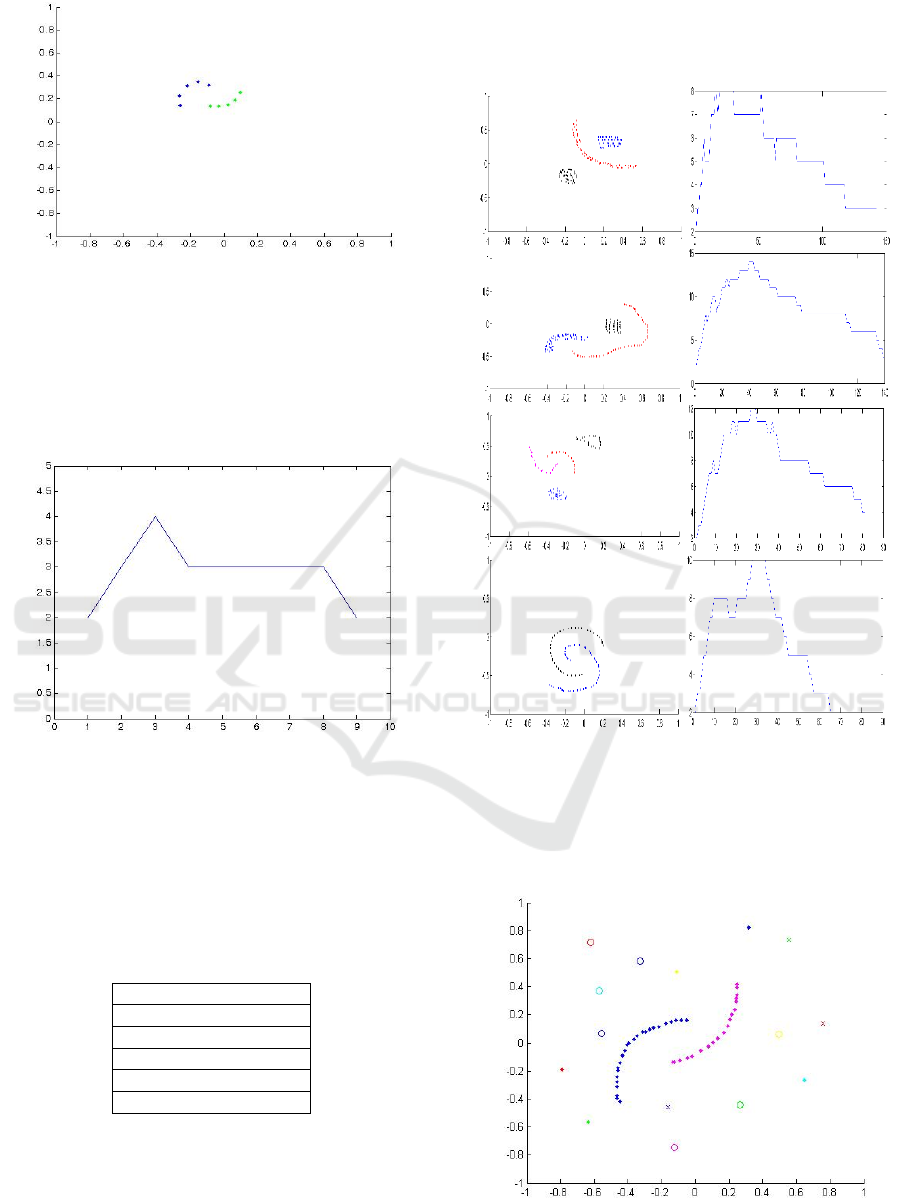
Figure 2: Result of CEFStream showing 2 clusters.
The number of clusters generated during
iterations can be seen in Fig. 3. During the start of the
computation number of clusters increase, which is
expected as the sample order is random. After
processing several samples the clusters start to merge
and stays the same.
Figure 3: Number of Groups vs. Iterations.
The algorithm is tested using several times where
each time the arrival order is changed using a random
permutation as given in Table 1. The precision is
%100 each time which means that the result matches
with the original labels of the data.
Table 1: Different arrival orders of 10 sample points using
random permutations.
1 5 9 6 7 8 10 4 2 3
4 9 8 5 3 2 6 7 1 10
4 1 9 2 10 7 8 6 3 5
6 5 2 7 8 9 10 1 3 4
8 4 9 1 10 3 7 5 2 6
8 6 1 7 9 4 2 10 3 5
4.1 Test Results
The CEFStream algorithm is tested using several
different datasets and each resulting cluster is
displayed using a different color. The change of
number of groups is also given in Fig. 4. Each set is
tested several times using random permutations to
change the arriving order of points.
Figure 4: Test results with clusters and number of groups.
The algorithm is also tested with outliers where
each outlier is assigned to a different cluster which
will be very easy to eliminate by checking the cluster
size. The result is given in Fig. 5.
Figure 5: Outliers detected as different clusters.
CLOSER 2018 - 8th International Conference on Cloud Computing and Services Science
586

4.2 Difficult Datasets
There are cases where points from two different
clusters starts forming a single cluster during the early
phase of the iterations. For example occasionally the
dataset given in Fig. 6 generates clusters incorrectly
depending to the order of arrival.
Figure 6: Occasional incorrect clusters.
The original algorithm can merge similar clusters
but what we need is to separate a cluster into 2
clusters if the addition of a new point start forming a
different sub-cluster. The extra step will come with
additional computational complexity.
After adding the new point to a cluster, that cluster
will be tested if there is a need to separate the clusters
into two different clusters. For this operation we will
use the OptimalNumberofClusters algorithm
developed (Gokcay, 2017) to find the number of
clusters in any dataset. The derivation of the
algorithm will not be repeated here. The motivation is
not to determine the number of clusters but to test the
minimum point of the distance plot created by the
algorithm against the threshold T and separate the
clusters if necessary. Assuming that the points are
arriving one at a time, the running complexity of this
algorithm is (
) where q is the current cluster.
5 FUTURE WORK
As a position paper there is work that needs to be
completed. The threshold calculation needs to be
improved because in some cases the average
calculation may not be enough to detect the boundary
between clusters. The other improvement will be in
the incremental version of the data skeleton algorithm
to reduce the storage requirements. Also the
algorithm needs to be tested using real data sets as
well. Although the algorithm performs well against
random arrivals with nonlinearly separated synthetic
clusters, the case will be different with more
complicated cluster shapes.
6 CONCLUSIONS
In this paper we have developed a one-pass stream
clustering algorithm where the clusters are
independent of the arrival order and highly
nonconvex cluster distributions pose no problem. The
distance measure used in the algorithm can cluster
nonlinearly separable clusters efficiently. This is not
the case with K-means and all its derivatives since the
distance measure is hyper-ellipsoidal. No assumption
is needed about the possible number of clusters where
many algorithms require this number. Each new
sample point is processed once and a snapshot can be
taken from the algorithm at any time since there are
no on-line and off-line iterations.
REFERENCES
Alazeez, A., A., Jassim, S., and Du, H., 2017, EDDS: An
Enhanced Density-Based Method for Clustering Data
Streams, in 46th International Conference on Parallel
Processing Workshops (ICPPW), Bristol, 2017, pp.
103-112.
Charu A. C., et al. 2003, A framework for clustering
evolving data streams, in Proceedings of the 29th
international conference on Very large data bases-
Volume 29. VLDB Endowment, 2003.
Chen, J., He, H., 2016, A fast density-based data stream
clustering algorithm with cluster centers self-
determined for mixed data, In Information Sciences,
Volume 345, 2016, Pages 271-293
Feng, A. et al., 2006, Density-Based Clustering over an
Evolving Data Stream with Noise, in SDM. Vol. 6.
2006.
Gokcay E., Principe J. C., 2002, Information theoretic
clustering, in IEEE Transactions on Pattern Analysis
and Machine Intelligence, vol. 24, no. 2, pp. 158-171,
Feb 2002.
Gokcay, E., Karakaya M., Bostan A., 2016, A new
Skeletonization Algorithm for Data Processing in
Cloud Computing, in UBMK-2016, First International
Conference on Computer Science and Engineering,
Çorlu, Turkey, 20-23 Oct, 2016.
Gokcay, E., Karakaya M., Sengul, G., 2017, Optimal
Number of Clusters, in ISEAIA 2017, Fifth
International Symposium on Engineering, Artificial
Intelligence & Applications, Girne, North Cyprus, 1-3
Nov, 2017.
Hassani, M., Spaus, P., Cuzzocrea A., and Seidl,T., 2016,
"I-HASTREAM: Density-Based Hierarchical
Clustering of Big Data Streams and Its Application to
Big Graph Analytics Tools," 2016 16th IEEE/ACM
A Stream Clustering Algorithm using Information Theoretic Clustering Evaluation Function
587

International Symposium on Cluster, Cloud and Grid
Computing (CCGrid), Cartagena, 2016, pp. 656-665.
James, M., 1967, Some methods for classification and
analysis of multivariate observations, Proceedings of
the fifth Berkeley symposium on mathematical statistics
and probability. Vol. 1. No. 14. 1967.
Khan, I., Huang, J., Ivanov K., 2016, Incremental density-
based ensemble clustering over evolving data streams,
In Neurocomputing, Volume 191, 2016, Pages 34-43
Lin J., and Lin, H., 2009, A density-based clustering over
evolving heterogeneous data stream, in ISECS Inter-
national Colloquium on Computing, Communication,
Control, and Management, Sanya, 2009, pp. 275-277.
Marcel A.R., et al. 2012, StreamKM++: A clustering
algorithm for data streams, in Journal of Experimental
Algorithmics (JEA) 17 (2012): 2-4.
Martin, E., et al, 1996, A density-based algorithm for
discovering clusters in large spatial databases with
noise, Kdd. Vol. 96. No. 34. 1996.
Reddy, K., and Bindu, C., S., 2017, A review on density-
based clustering algorithms for big data analysis, in
International Conference on I-SMAC (IoT in Social,
Mobile, Analytics and Cloud) (I-SMAC), Palladam,
2017, pp. 123-130.
Thakran Y., and Toshniwal, D., 2012, Unsupervised outlier
detection in streaming data using weighted clustering,
in 12th International Conference on Intelligent Systems
Design and Applications (ISDA), Kochi, 2012, pp. 947-
952.
Tian Z., Ramakrishnan R., and Livny, M., 1997, BIRCH: A
new data clustering algorithm and its applications. In
Data Mining and Knowledge Discovery 1.2 (1997):
141-182.
Xu, B., Shen F., and Zhao, J., 2016, Density Based Self
Organizing Incremental Neural Network for data
stream clustering, in 2016 International Joint
Conference on Neural Networks (IJCNN), Vancouver,
BC, 2016, pp. 2654-2661.
Xu, J., Wang, G., Li, T., Deng, W., Gou, G., 2017, Fat node
leading tree for data stream clustering with density
peaks, In Knowledge-Based Systems, Volume 120,
2017, Pages 99-117
CLOSER 2018 - 8th International Conference on Cloud Computing and Services Science
588
