Genetic Programming Hyper-heuristic for the Automated Synthesis

of Selection Operators in Genetic Algorithms

Evgenii Sopov

Department of Systems Analysis and Operations Research,

Reshetnev Siberian State University of Science and Technology, Krasnoyarsk, Russia

Keywords: Genetic Algorithms, Genetic Programming, Constructive Hyper-heuristic, Selection Operator.

Abstract: Genetic algorithms have proved their efficiency with many hard optimization problems, but in order to achive

the best results they must be fine-tuned. One such method of fine-tuning is a synthesis of new genetic

operators. Hyper-heuristics represent search techniques that can be used for automating the process of

selecting or generating simpler heuristics with the aim of designing new metaheuristic algorithms. In this

study, we have proposed a new hyper-heuristic based on genetic programming for the automated synthesis of

a selection operator in genetic algorithms. Black-Box Optimization Benchmarking is used as a training set for

the genetic programming algorithm and as a test set for estimating the generalization ability of a synthesized

selection operator. The results of numerical experiments are presented and discussed. The experiments have

shown that the proposed approach can be used for designing new selection operators that outperform standard

selection operators on average with new, previously unseen instances of hard black-box optimization

problems.

1 INTRODUCTION

Metaheuristics, such as genetic algorithms (GAs),

have proved their efficiency over a wide range of real-

world search optimization problems. GAs realize the

"blind" search strategy and do not require any specific

information about the features of the search space and

objectives. Nevertheless, the performance of a GA

strongly depends on the algorithm’s structure, the

chosen types of genetic operators and their

parameters. Such fine-tuning of the GA can be

performed using some a priori information on a given

problem, through a series of numerical experiments

with different algorithm settings or in an automated

way during the algorithm’ run. The last option has

become more popular in recent times and often

outperforms traditional schemes of applying GAs.

There exist many self-adaptive and self-configuring

approaches in GAs (Eiben et al., 2007).

The most recent studies in the field propose more

complex approaches for the automated design of

search metaheuristics, which are called hyper-

heuristics (HHs). Genetic programming (GP) has

been proposed as a method for automatically

generating computer programs. Today GP is used in

the field of machine-learning for a wide range of

applications. GP can be also applied as a hyper-

heuristic for generating search heuristics and

metaheuristics (so-called GPHH) (Burke et al., 2013).

In the field of GAs, the problem of configuring

and fine-tuning an algorithm is usually solved only

once for a given instance of an optimization problem.

At the same time, machine-learning approaches are

aimed to find or to build an algorithm (a classifier, a

regression model, etc.) based on a set of training

instances, which can deal efficiently with new

instances of a problem. This concept can be

transferred to the GPHH approach. An objective of

the GPHH is to design a metaheuristic that

demonstrates high performance on average over a set

of complex optimization problems. Such feature is

necessary for “black-box” optimization, because the

synthesized metaheuristic should not adapt to a

specific problem, but cover a range of problems.

This study is devoted to improving the GA

performance by generating and tuning new selection

operators using the GPHH. We will focus on the

standard binary GA for solving single-objective

unconstrained “black-box” optimization problems.

The well-known benchmark problems from the

GECCO and IEEE CEC conferences (Black-Box

Optimization Benchmarking (BBOB)) are used as a

Sopov E.

Genetic Programming Hyper-heuristic for the Automated Synthesis of Selection Operators in Genetic Algorithms.

DOI: 10.5220/0006497002310238

In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 231-238

ISBN: 978-989-758-274-5

training set. The benchmark contains GA-hard

problems and combines many features of

optimization problems.

The rest of the paper is organized as follows.

Section 2 describes related work. Section 3 describes

the proposed approach. In Section 4, the results of

numerical experiments are discussed. In the

Conclusion the results and further research are

discussed.

2 RELATED WORK

2.1 Hyper-heuristics for Automated

Algorithm Synthesis

Hyper-heuristic approaches perform a search over the

space of heuristics or metaheuristics when solving

optimization problems. In a HH approach, different

heuristics or heuristic components can be selected,

generated or combined to solve a given problem in an

efficient way. In (Burke et al., 2010), a general

classification of HHs is given according to two

dimensions: the nature of the heuristic search space

and the source of feedback during learning. The first

characteristic defines the following two classes:

 Heuristic selection: Methodologies for choosing

or selecting existing heuristics.

 Heuristic generation: Methodologies for

generating new heuristics from components of

existing heuristics.

The first class is similar to the idea of the self-

configuration in evolutionary algorithms. The

selection can be performed with a set of predefined

evolutionary and genetic operators (for example,

Population-level Dynamic Probabilities in GP

(Niehaus and Banzhaf, 2001), Linear Genetic

Programming for the Synthesis of Evolutionary

Algorithms (Oltean, 2005)) or from a set of

predefined algorithms (for example, the Population-

based Algorithm Portfolio (Tang et al., 2010), the

Multiple Evolutionary Algorithm (MultiEA) (Yuen et

al., 2013) or the Self-configuring Multi-strategy

Genetic Algorithm (Sopov, 2016)).

In this study, we will focus on the second class of

HHs. As we can see from many papers (a good survey

of HHs is proposed in (Burke et al., 2013)), the

majority of HHs have been proposed for solving

combinatorial optimization problems. Nevertheless,

there exist some examples of HHs for general

optimization problems, and the best results are

achieved with HHs based on GP (Burke et al., 2009).

With respect to the source of feedback during

learning there exist:

 Online learning HHs: Learn while solving a given

instance of a problem.

 Offline learning HHs: Learn from a set of training

instances a method that would generalize to

unseen instances.

 No-learning HHs: Do not use feedback from the

search process.

In many real-world applications, a chosen heuristic

optimization method is applied to find the best

solution with respect to a single instance of a certain

optimization problem. In such applications, the

generalization ability of the method applied does not

matter, as the problem should be solved only once. In

this case, we can use a no-learning HH if there is

presented a priori information on the problem, or we

can use an online learning HH to solve the problem in

an automated, adaptive way.

In this study, we will use an offline learning

approach to provide the generalization feature and to

synthesize a GA with a new selection operator, which

outperforms the standard GA on average.

The application of GP as a HH is a rather new

direction in the field of automated algorithm design.

GP builds candidate solutions to the problem from a

set of primitives, which are represented by single

operators, functions or whole heuristics and

metaheuristics. One of the main advantages of GP is

that it simultaneously provides the structural

synthesis of a solution and the tuning of its

parameters. The solution can be a human-readable

symbolic expression (a formula) or a computational

algorithm (an executable computer program).

In the majority of studies, GPHH is applied for the

automated design of data mining tools and

combinatorial optimization algorithms. There are

only a small number of works on applying GPHH for

the design of new operations in evolutionary and

genetic algorithms. In (Hong et al., 2013), GPHH is

used for the automated design of mutation operators

for evolutionary programming and in (Woodward and

Swan, 2012) the same problem is solved for GAs. In

(Woodward and Swan, 2011), selection operators are

synthesised using a register machine as a tool for

automated programming.

2.2 Selection Operator in GA

A selection operator is an important component of

any evolutionary or genetic algorithm. The selection

operator is intended to improve the average fitness of

a population by giving individuals with better fitness

a higher probability to be copied into the next

generation. From the point of view of search

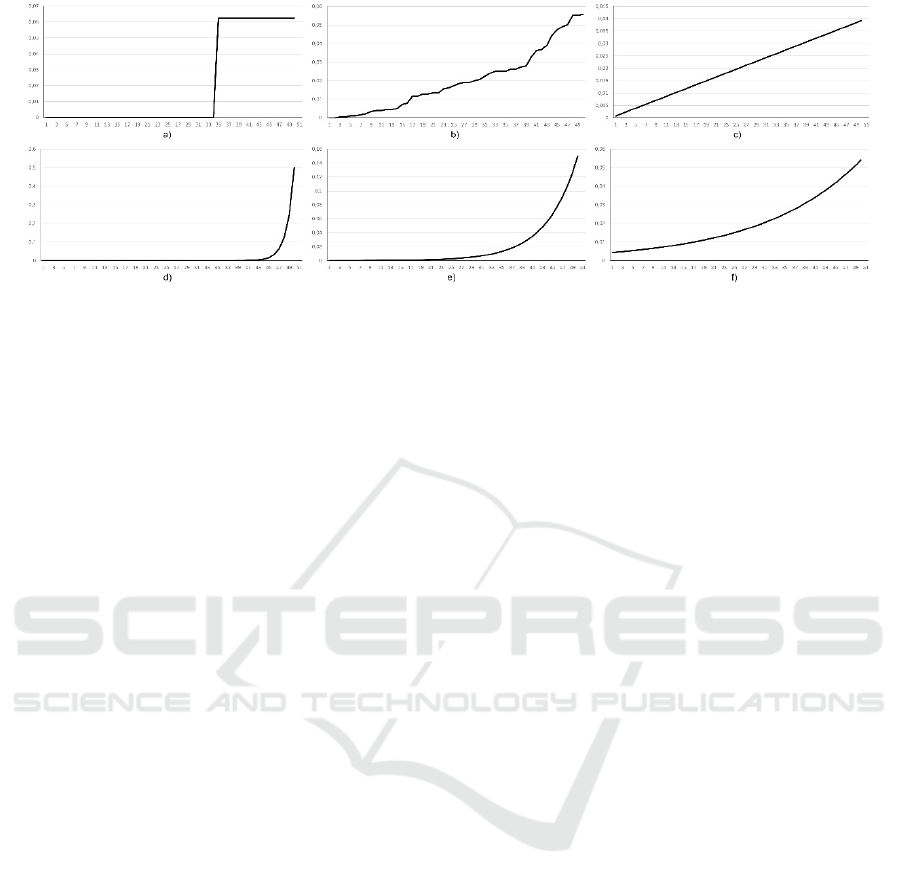
Figure 1: The probability distributions of commonly used selection operators: a) truncation, b) proportional, c) linear ranking,

d) exponential ranking (base of the exponent is c=0.5), e) exponential ranking (c=0.8), f) exponential ranking (c=0.95). The

horizontal axis contains ranks of an individual; the vertical axis is the probability of being selected.

optimization, selection focuses the search process on

promising regions in the search space, while

recombination performs a random search within

previously explored regions, and mutation discovers

new points in the search space.

Any selection operator can be viewed as a

probability distribution that assigns the chance of

being chosen for further operations to every

individual in a population. Thus, selection can be

defined as a mapping (of a function) s to the [0, 1]

interval. The domain of the s function comprises

ranks for the ranking, tournament and truncation

selection schemes, and comprises fitness values for

the proportional selection (1). The s function should

satisfy the normalization requirement (2).









:



→



0,1



,



∈











:







→



0,1









∈



(1)



∈

1

(2)

where Pop is a population and i is an individual in the

population.

A comprehensive analysis of selection schemes in

GAs is presented in (Blickle and Thiele, 1996), where

selection operators are described and compared using

estimations of average fitness, fitness variance,

reproduction rate, loss of diversity, selection intensity

and selection variance. Unfortunately, the proposed

models are too complicated and can be applied only

for simple optimization problems such as the

ONEMAX function. Nevertheless, it can be seen that

the characteristics of probability distributions

presented by selection schemes are different and there

is no guarantee that the best-chosen scheme from a set

of traditional selection schemes will be optimal or

even efficient enough for solving an arbitrary

optimization problem.

We have visualized the probability distributions

of commonly used selection operators (Figure 1). We

have ranked solutions for all types of selection in such

a way that the first rank is assigned to the worst

solution. The tournament selection is not presented,

because it is asymptotically equal to the linear

ranking. As we can see, the probability distributions

are always monotonically increasing functions. The

functions for the ranking and tournament are smooth.

The function graph of the proportional selection

strongly depends on a distribution of the fitness

values. If the fitness distribution is uniform, the graph

is close to the graph of the linear ranking, otherwise

it is closer to the exponential ranking.

The traditional selection operators are inspired by

nature and use straightforward and simple ways for

calculating the probability of being selected. In this

study will use GPHH to synthesize new selection

operations, which maximize the average performance

of a GA.

3 PROPOSED APPROACH

In this study, we propose the following conception of

applying GP as a HH for the automated design of

selection operators. We will use a GP algorithm as a

problem, in which tree solutions represent probability

distributions. A raw solution is normalized, and after

that is executed as a selection algorithm in a certain

GA. For evaluating fitness of the GP solution, we

estimate the average performance of the GA with the

meta-procedure for solving a symbolic regression

designed selection operator over a series of runs. The

BBOB functions are used and they are divided into

training and test sets to estimate the generalization

ability of the solution. The proposed scheme of GHPP

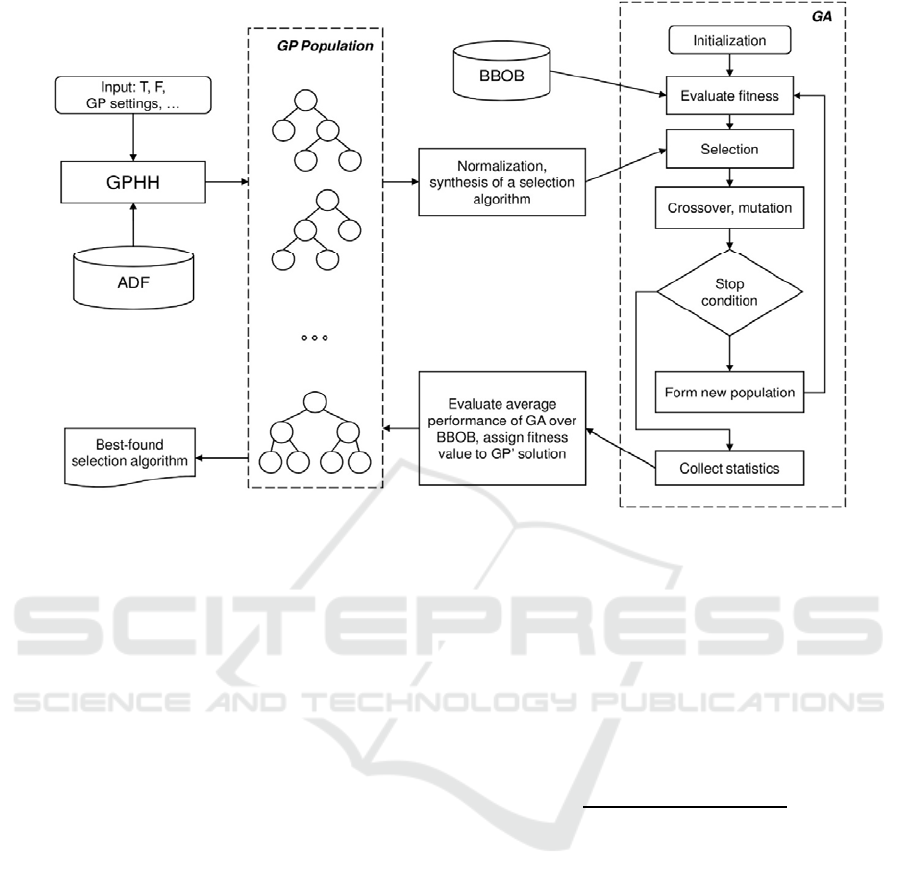
Figure 2: The general scheme of the proposed GPHH for automated synthesis of selection operators in GAs.

is presented in Figure 2.

We will discuss the components and stages of the

approach in detail.

It is obvious that the proposed GPHH is a

computationally costly procedure. Thus, we will

introduce some modifications to the standard GP

algorithm. As was shown in the previous section, the

probability distributions of selection are rather

simple, smooth and increasing functions. We will

strongly control the bloat of the tree solutions by

limiting their maximum depth (Luke and Panait,

2006). In standard GP, a grow method on the

initialization step uses equal probabilities for all

elements of the functional set. We will use a higher

probability for the addition to get more simple and

smooth expressions. The same probabilities for

elements of the functional set will be used for a point-

mutation operation.

A terminal set in GP includes variables and

constants for a given problem. The selection

probability of a solution in the GA may depend on

many factors. Usually all requirements of an

optimization problem are presented in the fitness

function. Thus, we can include in the terminal set only

one input variable based on the fitness value. To

avoid fitness scaling, we will rank individuals in the

GA, and will use the ranks as the variable in the

terminal set (in this work, the first rank corresponds

to the worst individual). We will also include two

automatically defined functions (ADFs) in the

terminal set, which are the linear ranking and the

exponential ranking with с=0.8.

Each tree solution in the GP is a function with

arbitrary codomain (denoted as f(i), where i is the

rank of an individual after the ranking). We need to

provide some transformation of the function for

applying it as a selection operator s(i). We will bound

the domain with rank values and will apply

normalization (3).

























∆

∑















∆











min

∈



,







(3)

where PopSize – is the size of a population, i is an

individual in the population, 



shifts the function

into the positive range, ∆ is a parameter that

guarantees a non-zero probability for the worst

individual.

The GA used in this study is a standard GA with

standard binary representation. The crossover

operator is two-parent uniform recombination. The

mutation operator is a bit inversion and has average

intensity, which is calculated as

(1/chromosome_length) (one mutation per string on

average). The stop criterion is a limitation of fitness

evaluations in terms of the number of generations

with a fixed-sized population. Each new population is

formed by copying offspring into it. The worst

individual is replaced by the best-found solution

(elitism). The fitness function for a single run of the

GA is the same as the chosen objective from the

BBOB set, and it is to be maximized.

We have chosen the BBOB, because this

benchmark is widely used by other researchers. It is

well-developed and contains a wide range of complex

optimization problems with many different features.

This benchmark has also been used at the Black-box

Optimization Competition within the IEEE CEC and

GECCO conferences since 2009. More detailed

information and source codes can be found in

(http://coco.gforge.inria.fr/, 2017).

In this study, only noiseless functions have been

used. The set contains 24 benchmark problems, which

are grouped in 5 subsets: separable functions (the

subset contains 5 problems), functions with low or

moderate conditioning (4 items), functions with high

conditioning and unimodal (5 items), multi-modal

functions with adequate global structure (5 items) and

multi-modal functions with weak global structure (5

items).

To balance benchmark problems in the training

and test sets, we have divided the problems in the

following way: one random problem from each subset

has been chosen into the test set, and all the other

problems from the subsets have been added to the

training set. As result, the training set contains 19

problems, and the test set contains 5 problems. The

training set is used for evaluating the fitness function

in the GP algorithm. Finally, we will examine the

generalization ability of the best-found selection

operator with the test set.

All benchmark functions are scalable with the

dimension. In this work, we have set the dimension

for all problems equal to D=2. The accuracy for the

binary coding is ε=10E-3. The chromosome length is

equal to 28 (14 bits per one real-valued variable).

In order to estimate the average performance of

the GA over the training set, we have to evaluate a

quality metric for every problem in equal scale. In the

BBOB, the position of the global optimum for a

problem is initialized at random in [-5, 5]

. We can

estimate the GA performance by calculating the

distance between the best-found solution and the

global optimum position. The Euclidian metric is

used (4). As the search domain is given and we can

calculate the maximum and minimum values for the

metric, we will transform the metric in the following

way: it is equal to 1 if the global optimum has been

found and is equal to 0 if the distance is maximum.

Thus, we can represent the performance measure for

the GA as a percentage (5). Finally, we can assign the

fitness of a solution in the GP as in (6).















(4)











































max



max

1,



,1,



(5)





































(6)

where Dist is the distance between the best-found

solution 



and the global optimum position 







is the GA performance estimated

with the k-th training problem on the l-th algorithm

run, F is the number of the training functions, R is the

number of runs, 



 is the fitness

assigned in the GP to a solution 



We will also estimate the performance of the

standard GA with proportional selection, linear

ranking and exponential ranking with с=0.8 and their

average. The average value can be viewed as the

average performance of the GA with a randomly

chosen selection operator. Such an estimate is very

useful for black-box optimization problems, because

we have no information about problem features and,

consequently, about what type of selection to use. The

Mann-Whitney-Wilcoxon Test at the significance

level α=0.05 is used for defining the statistical

significance of difference in the results.

4 EXPERIMENTAL RESULTS

All algorithms and benchmark problems have been

implemented in the R language. The BBOB source

codes in R are available in (http://coco.gforge.

inria.fr/, 2017). The GP algorithm is based on the R

genetic programming framework (RGP) from the

CRAN repository (RGP: R genetic programming

framework, 2017). The GA was realized in R by

authors.

The experimental settings are presented in Table

1. Settings for the GP and the GA algorithms are

presented in Tables 2 and 3.

Table 1: The experiment settings.

Paramete

Value

The BBOB problems in the

training set

{f1-2, f4-8, f10-11, f13-14,

f16-19,

f21-24}

The BBOB problems in the test set {f3, f9, f12, f15, f20}

The search domain for all problems [-5, 5]x[-5, 5]

Encoding accuracy ε=10E-3

Table 2: The GP settings.

Paramete

Value

Population size

=50

The grow method Full

Max depth of trees 6

The functional set / probability

for initialization

{+/0.5, -/0.2,

*/0.1, %/0.1,

sin/0.05,exp/0.05}

The terminal set / probability for

initializa

ion

{i/0.5, Constants/0.3,

ADF1/0.1, ADF2/0.1}

Constants

Random uniform

in [0,1]

ADF1 (the linear ranking)

2∙







1



∙



ADF2 (the exponential ranking

with c=0.8)

1∙









1







Crossover / probability One-point / 0.95

Mutation / probability One-point / 0.01

Fitness function See (s6)

Max number of generations 1000

Table 3: The GA settings.

Paramete

Value

Population size

=50

Chromosome length n=28

Initialization

Random in the binary search

space

Selection Based on GP solutions

Crossover / probability

Two-parent random uniform

/ 1.0

Mutation / probability

Bits inversion /





Fitness function

Objectives from

the training se

Max number of generations 50

Number of runs 15

The fitness convergence diagram for the GP run

on the training set is presented in Figure 3. The bold

line corresponds to the best-found solution and the

thin line corresponds to the average of population.

Figure 3: The fitness convergence in the GPHH.

The expression of the best-found solution

(0.83) is presented in (7). The

expression after normalization is presented in (8) and

its graph is shown in Figure 4.

Figure 4: The graph of the best-found selection operator.









10sin



0.15





(7)











10sin



0.15



9.82453

7.4

(8)

The performance of the GA with the standard

selection operators and the GPHH best-found

selection operator (7) on the test set is shown in Table

Table 4: The experimental results for the test problems.

The test set Proportional selection Linear ranking Exponential ranking (c=0.8) Average GPHH best-found selection

f3 50.14/4.56 66.97/8.86 73.47/6.02 63.53/6.48 78.86/6.56

f9 76.71/7.64 81.64/6.84 82.93/6.24 80.24/6.91 90.55/5.11

f12 78.48/11.43 88.13/6.53 89.02/7.2 85.21/8.39 91.43/3.64

f15 64.43/11.10 85.17/5.37 79.48/8.20 76.36/8.22 82.26/7.86

f20 61.86/13.74 83.01/8.26 76.51/14.50 73.79/12.17 81.44/11.81

Table 5: The results of the Mann-Whitney-Wilcoxon tests.

The test set Selection Proportional selection Linear ranking Exponential ranking (c=0.8)

GPHH best-found

selection

>> >

f9 > > >

f12 > = >

f15 > < =

f20 > = =

The table contains results over 15 independent

runs of the GA in the form of “mean/STD”. We have

also estimated the statistical significance of

differences in the results (Table 5). We use the

following notations: the sign “=” is used when the

difference is not significant, the sign “>” is used when

the GPHH best-found selection provides significantly

better results, and the sign “<” when the GPHH best-

found selection provides significantly worse results.

As we can see, the synthesized selection operator

performs better with 3 of the 5 problems. The linear

ranking performs better on f15 and f20, but the

difference is significant only with the f15 problem.

The proposed selection operator always outperforms

the proportional selection and it is better or equal to

the exponential ranking.

The synthesized selection operator outperforms

the average of three standard selection operators on

the whole range of test problems. Thus, we can

recommend it for black-box optimization problems.

5 CONCLUSIONS

In this study, we have proposed a hyper-heuristic

approach based on genetic programming which is

used for the automated synthesis of selection

operators in genetic algorithms. The approach

implements the generalization conception taken from

the machine-learning field. A selection operator is

designed in order to maximize the average

performance of a GA with a given set of training

instances of black-box optimization problems.

As numerical experiments have shown, the

approach can deal with the problem of automated

synthesis. Moreover, the synthesized selection

operator provides statistically significant better

performance or at least performance not worse than

standard operators do. It also performs well on a test

set with new, previously unseen instances of

optimization problems, and thus, the generalization

feature of the proposed GPHH is proved.

In our further works, we will extend training and

test sets and will perform more numerical

experiments. We will also try to apply the approach

to the problem of the automated synthesis of other

genetic operators such as crossover and mutation. The

standard GP algorithm can be substituted with

Grammatical Evolution in order to better control the

syntax of synthesized operators.

ACKNOWLEDGEMENTS

This research is supported by the Ministry of

Education and Science of Russian Federation within

State Assignment № 2.1676.2017/ПЧ.

REFERENCES

Blickle, T., Thiele, L., 1996. A comparison of selection

schemes used in evolutionary algorithms. In: Evol.

Comput. 4(4). pp. 361-394.

Burke, E., Gendreau, M., Hyde, M., Kendall, G., Ochoa, G.,

Ozcan, E., Qu, R., 2013. Hyper-heuristics: A survey of

the state of the art, Journal of the Operational Research

Society, 64 (12), pp. 1695-1724.

Burke, E., Hyde, M., Kendall, G., Ochoa, G., Ozcan, E.,

Woodward, J., 2009. Exploring hyper-heuristic

methodologies with genetic programming, In:

Computational Intelligence: Collaboration Fusion and

Emergence, New York, Springer. pp. 177-201.

Burke, E., Hyde, M., Kendall, G., Ochoa, G., Özcan, E.,

Woodward, J.R., 2010. A classification of hyper-

heuristic approaches. In Handbook of metaheuristics.

International Series in Operations Research &

Management Science, Vol. 146. pp. 449-468.

Eiben, A.E., Michalewicz, Z, Schoenauer, M., Smith, J.E.,

2007. Parameter Control in Evolutionary Algorithms,

In: Parameter Setting in Evolutionary Algorithms,

Volume 54 of the series Studies in Computational

Intelligence. pp. 19-46.

Hong, L., Woodward, J., Li, J., Ozcan, E., 2013. Automated

design of probability distributions as mutation

operators for evolutionary programming using genetic

programming, In: Genetic Programming: 16th

European Conference, EuroGP 2013. pp. 85-96.

Luke, S., Panait, L., 2006. A comparison of bloat control

methods for genetic programming, Evolutionary

Computation, 14(3). pp. 309-344.

Niehaus, J., Banzhaf, W., 2001. Adaption of Operator

Probabilities in Genetic Programming, EuroGP 2001,

LNCS 2038. pр. 329.

Oltean, M., 2005. Evolving evolutionary algorithms using

linear genetic programming, Evol. Comput., 13. pp.

387–410.

RGP: R genetic programming framework, 2017 [online]

Available at: https://cran.r-project.org/web/packages/

rgp/index.html.

Sopov, E., 2016. A Self-configuring Multi-strategy

Multimodal Genetic Algorithm, Advances in Nature

and Biologically Inspired Computing, Volume 419 of

the series Advances in Intelligent Systems and

Computing. pp. 15-26.

Tang, K., Chen G., Yao, X., 2010. Population-Based

Algorithm Portfolios for Numerical Optimization, In

IEEE Transactions on Evolutionary Computation,

14(5). pp. 782-800.

The Black-Box-Optimization-Benchmarking (BBOB)

documentation and source codes, 2017. [online]

Available at: http://coco.gforge.inria.fr/

Woodward, J.R., Swan, J., 2011. Automatically designing

selection heuristics, In: Proceedings of the 13th annual

conference companion on Genetic and evolutionary

computation (GECCO '11). pp. 583-590.

Woodward, J.R., Swan, J., 2012. The automatic generation

of mutation operators for genetic algorithms, In:

Proceedings of the 14th annual conference companion

on Genetic and evolutionary computation (GECCO

'12). pp. 67-74.

Yuen, S.Y., Chow, Ch.K., Zhang, X., 2013. Which

Algorithm Should I Choose at any Point of the Search:

An Evolutionary Portfolio Approach, In: the

Proceedings of the 15th annual conference on Genetic

and evolutionary computation, GECCO '13. pp. 567-

574.