Differential Security Evaluation of Simeck with Dynamic Key-guessing
Techniques
Kexin Qiao
1,2
, Lei Hu
1,2,∗
and Siwei Sun
1,2
1
State Key Laboratory of Information Security, Institute of Information Engineering,
Chinese Academy of Sciences, Beijing, 100093, China
2
Data Assurance and Communication Security Research Center, Chinese Academy of Sciences, Beijing, 100093, China
Keywords:
Simeck, Dynamic Key-guessing, Differential Cryptanalysis.
Abstract:
The Simeck family of lightweight block ciphers was proposed in CHES 2015 which combines the good
design components from NSA designed ciphers SIMON and SPECK. Dynamic key-guessing techniques were
proposed by Wang et al. to greatly reduce the key space guessed in differential cryptanalysis and work well
on SIMON. In this paper, we implement the dynamic key-guessing techniques in a program to automatically
give out the data in dynamic key-guessing procedure and thus simplify the security evaluation of SIMON and
Simeck like block ciphers regarding differential attacks. We use the differentials from K¨olbl et al.’s work and
also a differential with lower Hamming weight we find using Mixed Integer Linear Programming method to
attack Simeck. We improve the previous best results on all versions of Simeck by 2 rounds.
1 INTRODUCTION
SIMON and SPECK (Beaulieu et al., 2013) are two
lightweight block cipher families designed by NSA
that have attracted numerous cryptanalysis since their
publication in 2013 (Biryukov et al., 2014; Shi et al.,
2014; Abed et al., 2013; Alkhzaimi and Lauridsen,
2013; Alizadeh et al., 2013; Wang et al., 2014a;
Wang et al., 2014b; Sun et al., 2014c). SIMON is
optimized for hardware implementation and SPECK
is optimized for software. In CHES 2015, Yang et al.
combine their good components and get a new design
of block cipher family, called Simeck (Yang et al.,
2015). The Simeck family applies a slightly modified
version of SIMON’s round function and reuses it in
the key schedule like SPECK does. The hardware
implementations of Simeck block cipher family are
even smaller than that of SIMON in terms of area and
power consumption (Yang et al., 2015).
In 2014, a new differential attack applying dy-
namic key-guessing techniques was proposed to work
on the reduced SIMON family (Wang et al., 2014a).
The basic idea of the attack is to merge the classic
differential attack (Biham and Shamir, 1991) and
the modular differential attack which is widely used
to attack hash functions (Canni`ere and Rechberger,
∗
corresponding author: Lei Hu
2006; Mendel et al., 2011; Leurent, 2013; Theobald,
1995; Wang et al., 2005). This technique is aimed at
block ciphers with bitwise AND operator. Based on
observations of differential propagation of the AND
operator, attackers can deduce values of some subkey
bits and thus greatly reduce the key space that need to
be guessed. With differentials with high probability
in previous papers (Biryukov et al., 2014; Abed
et al., 2013; Sun et al., 2014b), dynamic key-guessing
techniques were used to improve the best previous
cryptanalysis results by 2 to 4 rounds on family of
SIMON block ciphers (Wang et al., 2014a).
As dynamic key-guessing techniques were newly
proposed, the designers of Simeck did not consider
its security regarding this technique. The designers
of Simeck give some other security analysis results
including differential attacks (Biham and Shamir,
1991), linear attacks (Matsui, 1994), impossible dif-
ferential attacks (Biham et al., 1999), etc., mainly
following the attack procedure of SIMON due to
their similarity. Recently, cryptanalysis covering
more rounds are given (Bagheri, 2015; K¨olbl and
Roy, 2015). K¨olbl and Roy give differentials with
high probability of all three versions and launch
differential attacks covering 19, 26 and 33 rounds
of Simeck32/64, Simeck48/96 and Simeck64/128 re-
spectively (K¨olbl and Roy, 2015). Though they
noticed the dynamic key-guessing method, they did
74
Qiao, K., Hu, L. and Sun, S.
Differential Security Evaluation of Simeck with Dynamic Key-guessing Techniques.
DOI: 10.5220/0005684400740084
In Proceedings of the 2nd International Conference on Information Systems Security and Privacy (ICISSP 2016), pages 74-84
ISBN: 978-989-758-167-0
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

not implement it.
In this paper, we reveal some details in imple-
menting the dynamic key-guessing techniques and
thus make it easy to launch a differential attack with
these techniques on SIMON and Simeck like block
ciphers. Specifically, we write a program to calculate
the complexity in dynamic key-guessing procedure
and then estimate the complexities in differential
cryptanalysis on family of Simeck block ciphers.
We find a 13-round differential of Simeck32/64 with
lower hamming weight with probability 2
−29.64
. Ap-
plying this differential and differentials from K¨olbl et
al.’s work (K¨olbl and Roy, 2015) to attack Simeck
with dynamic key-guessing techniques, we improve
the best previous results on all versions of Simeck
block ciphers by 2 rounds. The comparison of the
cryptanalysis results for Simeck is in Table 1.
The organization of the paper is as follows. In
Section 2 we give a brief introduction of the Simeck
family block ciphers. In Section 3 we describe Wang
et al.’s dynamic key-guessing techniques in a general
way and provide some details in implementing the
techniques. In Section 4 we give a 13-round differ-
ential of Simeck32/64 found by Mixed Integer Linear
Programming (MILP) method and use it as well as
differentials in references to launch differential attack
with dynamic key-guessing techniques on Simeck.
We conclude the paper in Section 5.
2 THE SIMECK LIGHTWEIGHT
BLOCK CIPHER
2.1 Notations
In this paper, we use notations as follows.
X
r−1
input of the r-th round
L
r−1
left half of X
r−1
R
r−1
right half of X
r−1
K
r−1
subkey used in r-th round
X
i
i-th bit of X, indexed from left to right
X ≫ r right rotation of X by r bits
⊕ bitwise exclusive OR (XOR)
∧ bitwise AND
∆X X ⊕ X
′
, difference of X and X
′
+ addition operation
% modular operation
∪ union of sets
∩ intersection of sets
2.2 Description of Simeck
The family of Simeck lightweight block ciphers
was introduced in CHES 2015 (Yang et al.,
2015). It is a Feistel structure and is denoted
by Simeck2n/mn, where 2n is the block size and
mn the master key size. It includes three versions:
Simeck32/64, Simeck48/96 and Simeck64/128 with
number of rounds n
r
=32, 36 and 44 respectively.
The left half of input texts to the i-th round is
L
i−1
= {X
i−1
n
,X
i−1
n+1
,··· ,X
i−1
2n−1
} and the right half
is R
i−1
= {X
i−1
0
,X
i−1
1
,··· ,X
i−1
n−1
} and the subkey is
K
i−1
= {K
i−1
0
,K
i−1
1
,··· ,K
i−1
n−1
}. The round function
of Simeck is
(L
i
,R
i
) = (R
i−1
⊕ F(L
i−1
) ⊕ K
i−1
,L
i−1
)
where
F(x) = (x∧ (x ≪ 5)) ⊕ (x ≪ 1)
for i = 1,··· n
r
. It can be seen that the round function
of Simeck is similar to that of SIMON. For coherence,
we denote the rotation offsets by a,b and c. In
Simeck, a = 0,b = 5,c = 1 and in SIMON a = 1,b =
8,c = 2.
The structure of the key schedule of Simeck is
similar to that of SPECK while the update function
reuses the round function of Simeck with constants
acting as round key. We refer the readers to Yang et
al.’s work (Yang et al., 2015) for details of Simeck.
3 DIFFERENTIAL ATTACK WITH
DYNAMIC KEY-GUESSING
TECHNIQUES
Differential attack (Biham and Shamir, 1991) is one
of the most powerful attacks on iterative block ci-
phers. If there is an input difference that results in
an output difference with high probability against a
reduced-round block cipher (called a differential), by
adding extra rounds before and after the differential,
an attacker can choose and encrypt an amount of
plaintext pairs that may satisfy the input difference,
and then guess the subkey bits in the added rounds
that influence the differential. Right guess will lead
conspicuous number of plaintext and ciphertext pairs
to the differential.
In 2014, Wang et al. proposed dynamic key-
guessing techniques to greatly reduce the number of
secret key bits that need to be guessed in differential
cryptanalysis (Wang et al., 2014a). These techniques
were based on observations that some subkey bits
can be deduced from equations invoked by certain
Differential Security Evaluation of Simeck with Dynamic Key-guessing Techniques
75

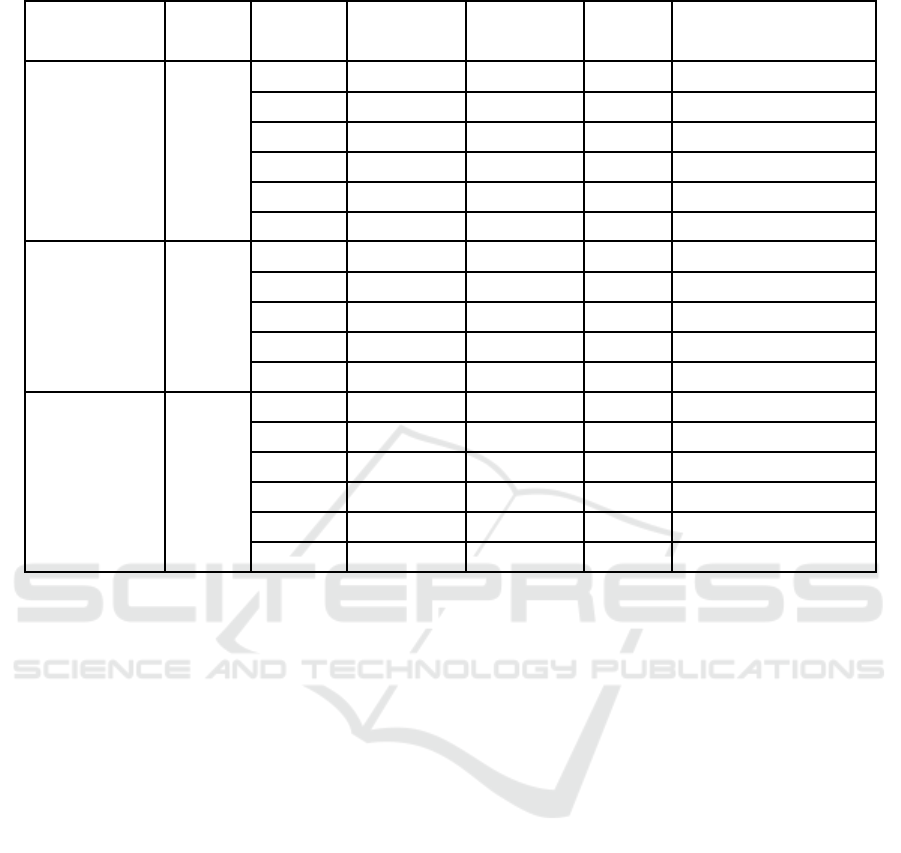
Table 1: Comparison of Cryptanalysis Results of Simeck.
Versions
Total Attacked Time Data Success
Reference
Rounds Rounds Complexity Complexity Prob.
Simeck32/64
32
18 2
63.5
2
31
47.7% (Bagheri, 2015)
19 2
36
2
31
- (K¨olbl and Roy, 2015)
20 2
62.6
2
32
- (Yang et al., 2015)
20 2
56.65
2
32
- (Zhang et al., 2015)
21 2
48.5
2
30
41.7% This paper
22 2
57.9
2
32
47.1% This paper
Simeck48/96
36
24 2
94
2
45
47.7% (Bagheri, 2015)
24 2
94.7
2
48
- (Yang et al., 2015)
24 2
91.6
2
48
- (Zhang et al., 2015)
26 2
62
2
47
- (K¨olbl and Roy, 2015)
28 2
68.3
2
46
46.8% This paper
Simeck64/128
44
25 2
126.6
2
64
- (Yang et al., 2015)
27 2
120.5
2
61
47.7% (Bagheri, 2015)
27 2
112.79
2
64
- (Zhang et al., 2015)
33 2
96
2
63
- (K¨olbl and Roy, 2015)
34 2
116.3
2
63
55.5% This paper
35 2
116.3
2
63
55.5% This paper
input differences of AND operator. Different in-
put differences of AND operator result in different
conditions of subkey bits involved in the equations.
Before using these observations, attackers should find
out the sufficient bit conditions that act as equa-
tions in the extended rounds to make the differential
hold. Thus the preprocessing phase of differential
cryptanalysis with dynamic key-guessing techniques
is divided into two stages when a differential with
high probability of the cipher has been found: firstly,
generate the extended path and identify the sufficient
bit conditions to be processed and secondly generate
the related subkey bits corresponding to each bit
condition in the first stage. In the following we
illustrate the differential attacks with dynamic key-
guessing techniques in a general way and reveal some
details of the implementation of the technique. We
refer the readers to Wang et al.’s work (Wang et al.,
2014a) for some principles of the technique.
3.1 Generate the Extended Path with
Sufficient Bit Conditions
Suppose a differential with probability p covering R
rounds has been found, we prefix r
0
rounds on the
top and append r
1
rounds at the bottom. To get the
differential path of the prefixed r
0
rounds, “decrypt”
the input difference of the differential according to
the rules that the output differences of AND operator
is 0 if and only if its input differences are (0, 0).
Otherwise set the output difference of AND operator
to ∗. For the appended r
1
rounds,“encrypt” the output
difference of the differential according to the same
rules.
The bit conditions to be processed in the extended
path are sufficient bit-difference conditions to make
the differential path hold. Specifically, when the input
differences of AND operator are not (0, 0) and its
output difference is definite (0 or 1, not ∗), then this
output difference is a sufficient bit condition. Note
that the prefixed r
0
rounds should be processed in
encryption direction to lable sufficient bit conditions
and the appended r
1
rounds should be processed in
decryption direction. In this step, we get an extended
path table with sufficient conditions labeled (see Table
4 for example).
3.2 Data Collection
Suppose there are l
0
definite conditions in the plain-
text differences and l
1
sufficient bit conditions in ∆X
1
according to the the extended path table. Divide
the plaintexts into 2
l
0
+l
1
structures with 2
2n−l
0
−l
1
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
76

plaintexts in each structure. In each structure, the
(l
0
+ l
1
) bits are constants.
For two structures with different bits in positions
where the differences are 1 in the above (l
0
+ l
1
) bits
in the extended path table, save the corresponding
ciphertexts into a table indexed by ciphertext bits in
positions where the differences are 0 in the last row
of the path table. Suppose there are l
2
ciphertext
bits with difference 0, then for each such structure
pair, there are about 2
2(2n−l
0
−l
1
)−l
2
plaintext pairs
remaining.
We build 2
t
plaintext structures, and filter out the
remaining pairs by decrypting one round. Suppose
there are another k bit conditions to be satisfied
in ∆X
r
0
+R+r
1
−1
after one round decryption of the
ciphertexts, then there are 2
t−1+2(2n−l
0
−l
1
)−l
2
−k
pairs
left. Store them in a table T. At the same time, we
expect to get λ
r
= 2
t−1+2n−l
0
−l
1
· p right pairs.
The plaintext pairs in the table T can still be
filtered by bit conditions in ∆X
2
and ∆X
r
0
+R+r
1
−2
as
some plaintext pairs may result in no subkey bit solu-
tion to equations regarding sufficient bit conditions in
∆X
2
and ∆X
r
0
+R+r
1
−2
. The procedure of generating
subkey bits related to each sufficient bit condition is
described in next subsection.
3.3 Generate Related Subkey Bits for
Each Sufficient Bit Condition
For each sufficient bit condition, we get two kinds
of subkey bits related to this bit - the subkey bits as
variables of the equation and subkey bits that need to
be guessed to get the specific equation. In encryption
direction, we have an equation for sufficient bit con-
dition ∆X
i
j+n
= 0 or 1 where j ∈ [0,n− 1] and
∆X
i
j+n
=∆X
i−1
( j+a)%n+n
∧ X
i−1
( j+b)%n+n
⊕ ∆X
i−1
( j+b)%n+n
∧ X
i−1
( j+a)%n+n
⊕ ∆X
i−1
( j+a)%n+n
∧ ∆X
i−1
( j+b)%n+n
⊕ ∆X
i−1
( j+c)%n+n
⊕ ∆X
i−2
j+n
,
(1)
where
X
i−1
( j+b)%n+n
=X
i−2
( j+b+a)%n+n
∧ X
i−2
( j+b+b)%n+n
⊕ X
i−2
( j+b+c)%n+n
⊕ X
i−2
( j+b)%n
⊕ K
i−2
( j+b)%n
,
X
i−1
( j+a)%n+n
=X
i−2
( j+a+a)%n+n
∧ X
i−2
( j+a+b)%n+n
⊕ X
i−2
( j+a+c)%n+n
⊕ X
i−2
( j+a)%n
⊕ K
i−2
( j+a)%n
.
(2)
When (∆X
i−1
( j+a)%n+n
,∆X
i−1
( j+b)%n+n
) = (0,0) and
∆X
i−1
( j+c)%n+n
⊕ ∆X
i−2
j+n
6= ∆X
i
j+n
, it is an invalid equa-
tion and we get no subkey bit solution. Therefore, for
sufficient bit conditions in ∆X
2
and ∆X
r
0
+R+r
1
−2
, this
property can be used to filter out the wrong plaintext
pairs as ∆X
1
,∆X
0
and ∆X
r
0
+R+r
1
−1
,∆X
r
0
+R+r
1
are
independent of keys. For remaining plaintext pairs in
the table T, filter out the wrong ones with sufficient
bit conditions in ∆X
2
and ∆X
r
0
+R+r
1
−2
. Put the
remaining plaintext pairs in a table T
1
.
We refer to ∆X
i−1
( j+a)%n+n
,∆X
i−1
( j+b)%n+n
,∆X
i−1
( j+c)%n+n
⊕ ∆X
i−2
j+n
as parameter differences for equation
∆X
i
j+n
= 0 or 1. For valid equations, the subkey bits
related to the equation ∆X
i
j+n
= 0 or 1 are divided
into the following 3 conditions:
1. When
(∆X
i−1
( j+a)%n+n
,∆X
i−1
( j+b)%n+n
) = (1,0),
the variables of the equation are the subkey bits that
are linear to X
i−1
( j+b)%n+n
and the subkey bits to be
guessed are those that influence
X
i−2
( j+b+a)%n+n
,X
i−2
( j+b+b)%n+n
,X
i−2
( j+b+c)%n+n
,X
i−2
( j+b)%n
and have not been deduced or guessed before;
2. When
(∆X
i−1
( j+a)%n+n
,∆X
i−1
( j+b)%n+n
) = (0,1),
the variables of the equation are the subkey bits that
are linear to X
i−1
( j+a)%n+n
and the subkey bits to be
guessed are those that influence
X
i−2
( j+a+a)%n+n
,X
i−2
( j+a+b)%n+n
,X
i−2
( j+a+c)%n+n
,X
i−2
( j+a)%n
and have not been deduced or guessed before;
3. When
(∆X
i−1
( j+a)%n+n
,∆X
i−1
( j+b)%n+n
) = (1,1),
the variables of the equation are the linear combina-
tion of subkey bits linear to X
i−1
( j+b)%n+n
and subkey
bits linear to X
i−1
( j+a)%n+n
and the subkey bits to be
guessed are those that influence
X
i−2
( j+b+a)%n+n
,X
i−2
( j+b+b)%n+n
,X
i−2
( j+b+c)%n+n
,X
i−2
( j+b)%n
,
X
i−2
( j+a+a)%n+n
,X
i−2
( j+a+c)%n+n
,X
i−2
( j+a)%n
and have not been deduced or guessed before.
For each text bit, we use a recursive algorithm
to determine the subkey bits that influence it and
subkey bits that are linear to it. The pseudo code is
in Algorithm 1.
For sufficient key bits in the appended r
1
rounds,
we process each bit in the decryption direction and
give the formulas and pseudo code in Appendix
5. After processing all sufficient bit conditions in
the prefixed and appended rounds, we get a table
of subkey bits variables corresponding to different
Differential Security Evaluation of Simeck with Dynamic Key-guessing Techniques
77

Algorithm 1: Generate related key bits for X
i
j
in encryption
direction.
1: Input Round i and bit position j
2: Output: [Influen
keys,Linear keys]
3: function RELATEDKEYS(i, j)
4: Inf luent
keys= [ ], Linear keys=[ ]
5: if i = 0 then
6: return [Influent
keys,Linear keys]
7: else
8: if j < n then
9: return RELATEDKEYS(i− 1, j + n)
10: else
11: [I
0
,L
0
]=RELATEDKEYS(i − 1,( j +
a)%n+ n)
12: [I
1
,L
1
]=RELATEDKEYS(i − 1,( j +
b)%n+ n)
13: [I
2
,L
2
]=RELATEDKEYS(i − 1,( j +
c)%n+ n)
14: [I
3
,L
3
]=RELATEDKEYS(i− 1, j%n)
15: Linear
keys=L
2
∪ L
3
∪ K
i−1
j%n
16: In fluent
keys= I
0
∪I
1
∪I
2
∪I
3
∪K
i−1
j%n
17: return [Inf luent
keys,Linear keys]
18: end if
19: end if
20: end function
parameter conditions for each sufficient bit condition
(see Table 5 for example).
It can be seen that whether a specific subkey bit
can be deduced in an equation corresponding to a
sufficient bit condition depends on the other three
parameter bit differences. Some bit differences may
act as parameters in more than one sufficient bit
conditions and therefore we should process such suf-
ficient bit conditions together. Specifically, we gather
sufficient bit conditions with related parameters into
one groupand calculate the average number of subkey
bits values for the group. In each round, suppose we
put the original order of sufficient bit conditions in
Index
order and the corresponding parameter sets in
Para
sets, we use Algorithm 2 to group sufficient bit
conditions.
In an actualattack, for each round, firstly guess the
subkey bits to get the specific equations in this round.
Then deduce the values of subkey bit variables in the
equations according to parameter difference values
group by group. In the j-th group, if we guess g
j
sub-
key bits to get specific equations that totally involve
k
j
subkey bit variables and there are t
j,i
parameter
conditions in each of which we correspondingly get
v
j,i
values of the subkey bit variables, the average
number of values for the (g
j
+ k
j
) subkey bits in
this group is 2
g
j
·
∑
i
t
j,i
v
j,i
∑
i
t
j,i
. For all groups, we get
Algorithm 2: Group sufficient bit conditions in one round.
1: procedure GROUP(Index order,Para sets)
2: Assert length(Index
order)=length(Para sets)
3: k=0
4: while k <length(Index
order) do
5: flag=0
6: j=k+1
7: while j <length(Index
order) do
8: if Para sets[ j] ∩ Para sets[k] is not
empty then
9: Index
order[k]=Index order[k]∪
Index
order[ j]
10: Remove Index order[ j] from
Index
order
11: Para sets[k] = Para sets[k]∪
Para
sets[ j]
12: Remove Para sets[ j] from
Para
sets
13: flag=1
14: else
15: j++
16: end if
17: end while
18: if flag=0 then
19: k++
20: end if
21: end while
22: end procedure
∏
j
(2
g
j
·
∑
i
t
j,i
v
j,i
∑
i
t
j,i
) values of
∑
j
(g
j
+ k
j
) subkey bits.
For all extended rounds (or say groups), if the number
of involved subkey bits (include the guessed ones and
deduced ones) is less thanthe length of the master key,
we are able to launch an attack with time complexity
less than exhaustive search.
Note that there are two types of repeats in subkey
bit variables and guessed subkeybits when combining
the numbers of values of subkey bits in all groups.
The first type is due to that some subkey bits are
variables of more than one group. The second type
is that a linear combination of some subkey bits is
a variable of an equation that may be deduced and
then each of the subkey bits is again need to be
guessed and thus one bit is repeated. When launching
an actual attack, all these bits should be preserved
as there are conditions that no specific value of the
subkey bit variable is get from an equation. However,
when calculating the complexity of the attack, we
should eliminate the repeated bits as we take expected
number of values of variables in each group.
3.4 Calculate Complexity of the Attacks
Given the differential with high probability and num-
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
78

Table 3: The distribution of the characteristics of Simeck32 in the differential with input and output difference (0000,0002) →
(0002,0000). The invalid characteristics is due to the special property of the dependent inputs of the AND operations in
Simeck (Biryukov et al., 2014; Sun et al., 2014b; Sun et al., 2014c).
Prob. 2
−38
2
−40
2
−41
2
−42
2
−43
2
−44
2
−45
2
−46
2
−47
2
−48
2
−49
2
−50
Invalid
#Char. 4 62 52 427 637 2427 4384 12477 22742 48324 62039 50411 169458
Table 4: Sufficient Conditions of Extended Differential Path of 21-round Simeck32/64.
Rounds Input Differences of Each Round
0 1,∗,0, 0,0, ∗, ∗,∗,0, ∗, ∗,∗, ∗, 1,∗,∗, ∗, ∗,∗, 0,∗,∗, ∗,∗, ∗,∗, ∗,∗, ∗ , ∗,∗,∗
1
0,∗ , 0,0,0,0,∗, 0,0, 0,∗,∗, ∗,0,1,∗, 1, ∗,0,0, 0, ∗,∗, ∗ , 0,∗,∗,∗, ∗,1, ∗, ∗
2 0,1,0,0, 0, 0,0, 0, 0, 0,0,1,0,0, 0,1,0,∗,0, 0,0,0, ∗,0, 0, 0,∗,∗, ∗, 0,1, ∗
3
1,0,0,0,0, 0,0,0,0, 0, 0,0,0, 0, 0,0,0,1, 0, 0,0,0,0, 0,0, 0, 0,1,0, 0, 0,1
3→16 13-round differential
16 0,1,0, 0,0,0, 0,0,0, 0,0, 0, 0,0,0,0, 0,0, 0,0,0,0, 0,0, 0, 0,0,0, 0,0, 0,0
17
1,∗,0, 0,0,0, 0,0,0, 0,0, 0, ∗,0,0,0, 0,1,0, 0, 0,0,0, 0,0,0,0, 0,0, 0,0,0
18 ∗,∗,0, 0,0,0, 0,∗,0, 0,0, ∗, ∗,0,0,1, 1,∗,0, 0, 0,0,0,0, 0,0,0,0,∗, 0,0,0
19
∗,∗,∗, 0,0,0, ∗,∗,0, 0,∗, ∗, ∗,0,1,∗, ∗,∗, 0,0, 0,0,0, ∗, 0,0,0,∗,∗, 0,0,1
20 ∗,∗,∗, 0,0,∗, ∗,∗,0, ∗,∗, ∗, ∗,∗,∗,∗, ∗,∗, ∗, 0,0,0,∗, ∗, 0,0, ∗,∗, ∗, 0,1,∗
21
∗,∗,∗, 0,∗,∗, ∗,∗,∗, ∗,∗, ∗, ∗,∗,∗,∗, ∗,∗, ∗, 0,0,∗, ∗, ∗,0,∗,∗, ∗, ∗,∗,∗,∗
Table 2: A differential characteristic of 13-round
Simeck32/64 with probability 2
−38
.
Rnds The input differences
0 0000000000000000 0000000000000010
1 0000000000000010 0000000000000000
2 0000000000000100 0000000000000010
3 0000000000001010 0000000000000100
4 0000000000010000 0000000000001010
5 0000000000111010 0000000000010000
6 0000000000001100 0000000000111010
7 0000000000101010 0000000000001100
8 0000000000010000 0000000000101010
9 0000000000001010 0000000000010000
10 0000000000000100 0000000000001010
11 0000000000000010 0000000000000100
12 0000000000000000 0000000000000010
13 0000000000000010 0000000000000000
ber of rounds that we add before and after the dif-
ferential, the program can give out the number of
all subkey bits involved in the extended rounds |sk|
and the number of solutions to these subkey bits for
each pair in T
1
, say C
s
. A wrong subkey occurs
with probability p
e
=
C
s
2
|sk|
and the expected count of
a wrong subkey for all pairs in T
1
is λ
e
= N
r
× p
e
.
Combining the complexity of searching subkey bits
involved in the extended paths that get more than
s = ⌊λ
r
⌋ hits and the complexity of traversing the
remaining subkey bits, the time complexity of the
attack is dominated by
T
es
= 2
mn
× (1− Poisscd f(s,λ
e
)), (3)
where Poisscd f(·,y) is the cumulative distribution
function of Poisson distribution with expectation y.
The success probability is
1− Poisscd f (s,λ
r
), (4)
where Poisscd f(s,λ
r
) denotes the probability that
there is no subkey bits with more than s hits.
4 DIFFERENTIAL ATTACKS ON
SIMECK WITH DYNAMIC
KEY-GUESSING TECHNIQUES
4.1 A Differential of Simeck32/64
Though several differentials with high probability of
Simeck family were given (K¨olbl and Roy, 2015),
we want to get new differentials with lower hamming
weight. Using automatic search method with MILP
techniques (Qiao et al., 2015; Sun et al., 2014a;
Sun et al., 2014b; Sun et al., 2014c), we find a 13-
round differential characteristic of Simeck32/64 with
probability 2
−38
(see Table 2). Then we search for
all differential characteristics with the same input and
output differences and with probability q such that
2
−50
≤ q ≤ 2
−38
. The distribution of the differential
characteristics is given in Table 3. Combing all the
differential characteristics we get that the probability
of the differential (0x0, 0x2) → (0x2,0x0) is about
2
−29.64
.
Differential Security Evaluation of Simeck with Dynamic Key-guessing Techniques
79

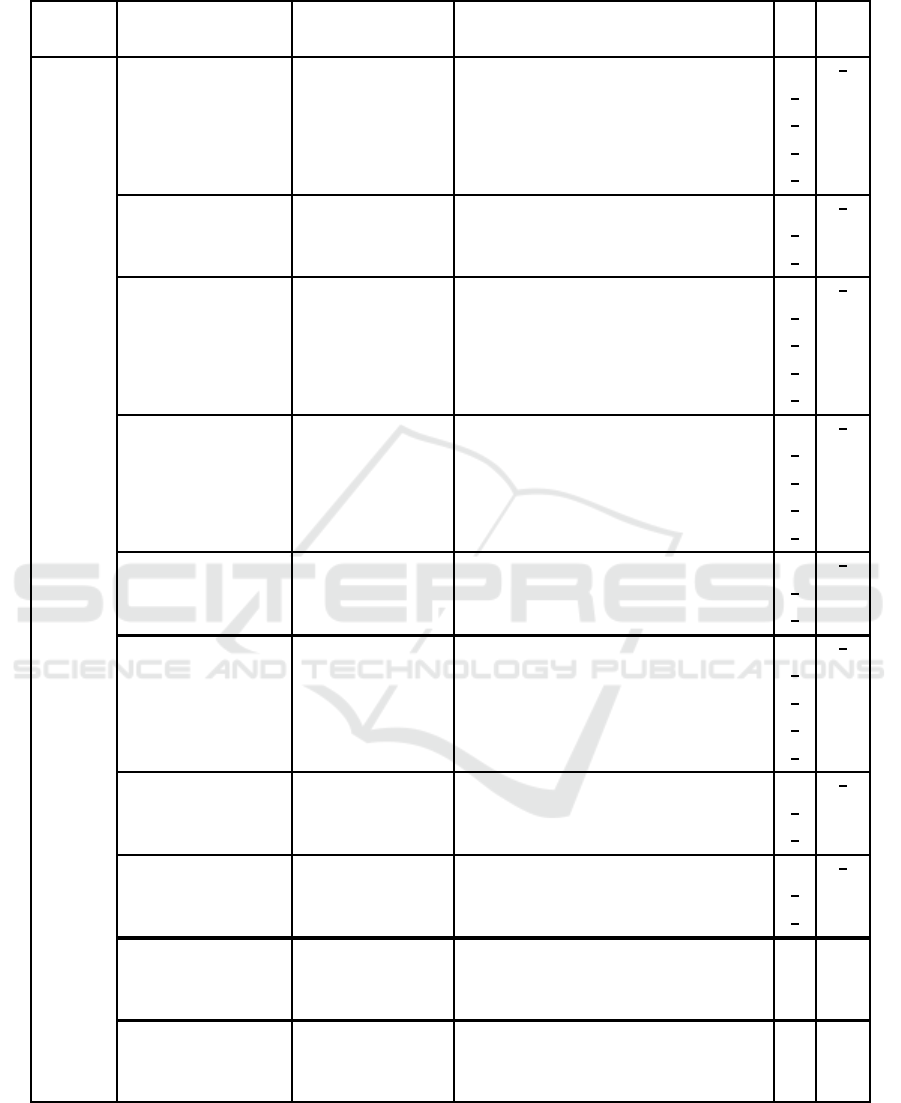
Table 5: Solutions of Subkey Bits in Round 2 of 21-round Simeck32/64.
Rounds Bit Conditions
Solutions of Key Conditions Leading
Pr Pr
F
Bits to Equations to Solutions
2(10)
Discard the pair (∆X
1
17
,∆X
1
22
,∆X
0
17
) = (0,0,0)
1
8
∆X
2
17
= 1 ⇔ * (∆X
1
17
,∆X
1
22
,∆X
0
17
) = (0,0,1)
1
8
∆(X
1
17
∧ X
1
22
) K
0
1
(∆X
1
17
,∆X
1
22
) = (0,1)
1
4
⊕∆X
0
17
= 1 K
0
6
(∆X
1
17
,∆X
1
22
) = (1,0)
1
4
k
0
1
⊕ K
0
6
(∆X
1
17
,∆X
1
22
) = (1,1)
1
4
∆X
2
27
= 1 ⇔ Discard the pair (∆X
1
27
,∆X
1
28
⊕ ∆X
0
27
) = (0,0)
1
4
∆X
1
27
∧ X
1
16
∗ (∆X
1
27
,∆X
1
28
⊕ ∆X
0
27
) = (0,1)
1
4
⊕∆X
1
28
⊕ ∆X
0
27
= 1 K
0
0
∆X
1
27
= 1
1
2
Discard the pair (∆X
1
28
,∆X
1
17
,∆X
0
28
) = (0,0,1)
1
8
∆X
2
28
= 0 ⇔ ∗ (∆X
1
28
,∆X
1
17
,∆X
0
28
) = (0,0,0)
1
8
∆(X
1
28
∧ X
1
17
) K
0
12
(∆X
1
28
,∆X
1
17
) = (0,1)
1
4
⊕∆X
0
28
= 0 K
0
1
(∆X
1
28
,∆X
1
17
) = (1,0)
1
4
K
0
1
⊕ K
0
12
(∆X
1
28
,∆X
1
17
) = (1,1)
1
4
Discard the pair (∆X
1
22
,∆X
1
27
,∆X
0
22
) = (0,0,1)
1
8
∆X
2
22
= 0 ⇔ ∗ (∆X
1
22
,∆X
1
27
,∆X
0
22
) = (0,0,0)
1
8
∆(X
1
22
∧ X
1
27
) K
0
6
(∆X
1
22
,∆X
1
27
) = (0,1)
1
4
⊕∆X
0
22
= 0 K
0
11
(∆X
1
22
,∆X
1
27
) = (1,0)
1
4
K
0
6
⊕ K
0
11
(∆X
1
22
,∆X
1
27
) = (1,1)
1
4
∆X
2
23
= 0 ⇔ Discard the pair (∆X
1
28
,∆X
0
23
) = (0,1)
1
4
∆X
1
28
∧ X
1
23
∗ (∆X
1
28
,∆X
0
23
) = (0,0)
1
4
⊕∆X
0
23
= 0 K
0
7
∆X
1
28
= 1
1
2
Discard the pair (∆X
1
26
,∆X
1
31
,∆X
1
27
⊕ ∆X
0
26
) = (0,0,1)
1
8
∆X
2
26
= 0 ⇔ ∗ (∆X
1
26
,∆X
1
31
,∆X
1
27
⊕ ∆X
0
26
) = (0,0,0)
1
8
∆(X
1
26
∧ X
1
31
) K
0
10
(∆X
1
26
,∆X
1
31
) = (0,1)
1
4
⊕∆X
1
27
⊕ ∆X
0
26
= 0 K
0
15
(∆X
1
26
,∆X
1
31
) = (1,0)
1
4
K
0
10
⊕ K
0
15
(∆X
1
26
,∆X
1
31
) = (1,1)
1
4
∆X
2
21
= 0 ⇔ Discard th pair (∆X
1
26
,∆X
1
22
⊕ ∆X
0
21
) = (0,1)
1
4
∆X
1
26
∧ X
1
21
∗ (∆X
1
26
,∆X
1
22
⊕ ∆X
0
21
) = (0,0)
1
4
⊕∆X
1
22
⊕ ∆X
0
21
= 0 K
0
5
∆X
1
26
= 1
1
2
∆X
2
31
= 1 ⇔ Discard th pair (∆X
1
31
,∆X
0
31
) = (0,0)
1
4
∆X
1
31
∧ X
1
20
∗ (∆X
1
31
,∆X
0
31
) = (0,1)
1
4
⊕∆X
0
31
= 1 K
0
4
∆X
1
31
= 1
1
2
∆X
2
25
= 0 ⇔
K
0
9
1X
1
25
⊕∆X
1
26
⊕ ∆X
0
25
= 0
∆X
2
30
= 0 ⇔
K
0
3
1X
1
19
⊕∆X
1
31
⊕ ∆X
0
30
= 0
In the first column, 2(10) means there are 10 bit conditions in Round 2. In the third column, ∗ means the variables in this
equation can take both values (0 and 1) and a specific subkey bit means this bit takes a definite value. The bold lines are
group split lines.
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
80

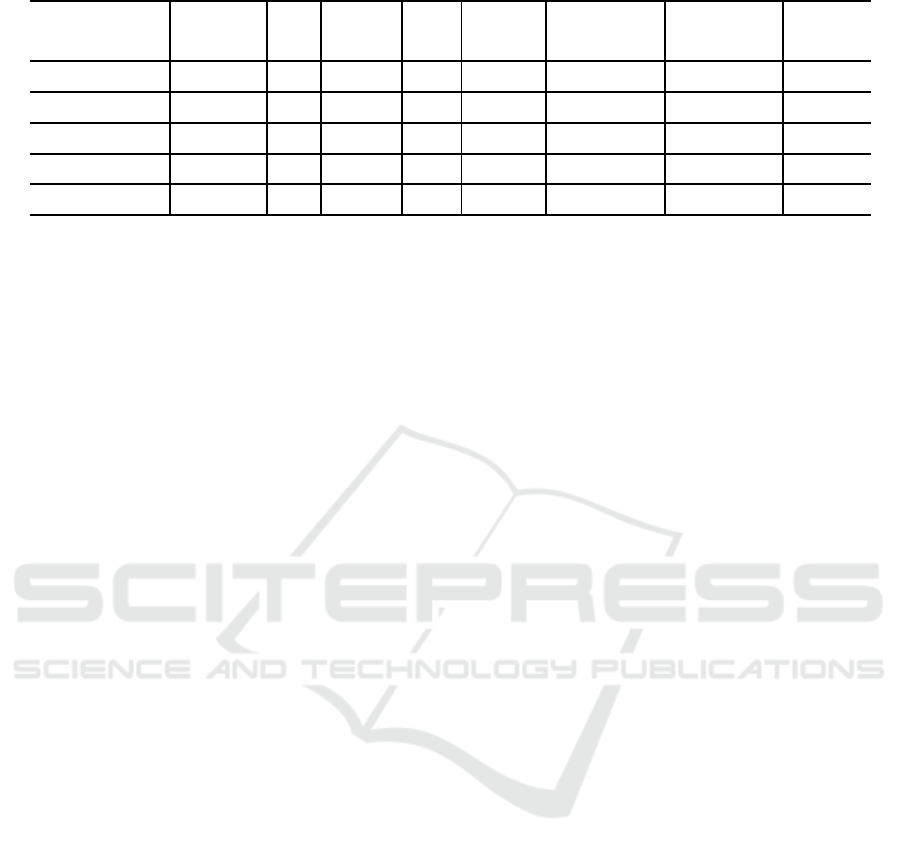
Table 6: Differential Attacks on Reduced Simeck.
Versions
Attacked
|sk| λ
e
λ
r
Chosen Data Time Success
Rounds Count Complexity Complexity Prob.
Simeck32/64 21 53 2
−2.678
3.29 4 2
30
2
48.52
41.7%
Simeck32/64 22 54 2
−1
2.56 3 2
32
2
57.88
47.1%
Simeck48/96 28 75 2
−8.365
2.54 3 2
46
2
68.31
46.8%
Simeck64/128 34 82 2
−1.678
3.94 4 2
63
2
116.34
55.5%
Simeck64/128 35 118 2
−1.678
3.94 4 2
63
2
116.34
55.5%
4.2 Results on Simeck
We use differentials with high probability to eval-
uate the security of Simeck family regarding dif-
ferential attacks with dynamic key-guessing tech-
niques. The outputs of our program provide all
information about the subkey bits corresponding to
all sufficient bit conditions. Due to page limits,
we give the details of dynamic key-guessing data
in http://pan.baidu.com/s/1jGyBwj0 and give basic
information of the attacks in the following.
For Simeck32/64, we adapt two differentials. The
first one is (0x8000,0x4011) → (0x4000,0x0) that
covers 13 rounds with probability 2
−27.28
(K¨olbl and
Roy, 2015). We prefix 3 rounds and append 5
rounds to the differential. Building 2
14
structures
with 2
16
plaintexts in each structure we are expect to
get 2
31.2
pairs in T
1
and finally 3.29 right pairs. In
the dynamic key-guessing procedure we are expect
to get 2
19.11
values of 53 subkey bits. According
to the calculation method in Section 3.4, the time
complexity and success probability of the attack are
2
48.52
and 41.7%. The extended differential path
of the 21-round Simeck32/64 is in Table 4. We
demonstrate the solutions of subkey bits in Round 2
in Table 5.
The second differential we use is the one from
Section 4.1. We add 4 rounds on the top and 5 rounds
at the bottom. With 2
18
structures containing 2
14
plaintexts each, we are expected to get 2
31.9
pairs
in T
1
and finally 2.56 right pairs. We are expect to
get 2
21.09
values of 54 subkey bits in dynamic key-
guessing procedure. The time complexity and success
probability are 2
57.88
and 47.1%. The extended
differential path of 22-round Simeck32/64 is in Table
7 in Appendix.
For Simeck48/96, we use the differential
(0x400000,0xe00000) → (0x400000,0x200000) that
covers 20 rounds with probability 2
−43.65
(K¨olbl and
Roy, 2015). We append 4 rounds on top and 4 rounds
at bottom. With 2
18
structures with 2
28
plaintexts in
each, we are expected to get 2
50.46
plaintext pairs in
T
1
and finally 2.54 right pairs. There are 2
32.89
values
of 75 subkey bits in dynamic key-guessing procedure
and the time complexity and success probability are
2
68.31
and 46.8%. The extended differential path of
the 28-round Simeck48/96 is in Table 8 in Appendix.
For Simeck64/128, we use the differential
(0x0,0x4400000) → (0x8800000, 0x400000) that
covers 26 rounds with probability 2
−60.02
(K¨olbl and
Roy, 2015) . We append 4 rounds on top and 4 rounds
at bottom. With 2
42
structures with 2
21
plaintexts in
each, we are expected to get 2
38.59
plaintext pairs in
T
1
and finally 3.94 right pairs. There are 2
41.72
values
of 82 subkey bits in dynamic key-guessing procedure
and the time complexity and success probability are
2
116.27
and 55.5%. If we add one more round on
top, we are able to attack 35-round Simeck64/128
with the same data and time complexity and success
probability. The difference is that we choose 2
31
structures of 2
32
plaintexts in each to encrypt, and
expect to get 2
49.05
pairs in T
1
and 2
67.26
values
of 118 subkey bits in the dynamic key guessing
procedure. The extended differential path of the
35-round Simeck64/128 is in Table 9 in Appendix.
The data of the attacks on all reduced versions of
Simeck are summarized in Table 6.
5 CONCLUSION
In this paper, we apply Wang et al.’s dynamic key-
guessing techniques to a new lightweight block cipher
family Simeck and give cryptanalysis results on it.
The differentials we use include ones in references
and also the one we get using MILP based method.
We implement the dynamic key-guessing techniques
in a program and in some way it can help to au-
tomatically give the security estimation of SIMON
and Simeck like block ciphers regarding differential
attacks. As far as we are concerned, the results
on Simeck in this paper are the best ones in terms
of rounds attacked. Future work includes finding
differentials with lower hamming weight that is more
Differential Security Evaluation of Simeck with Dynamic Key-guessing Techniques
81

adaptable to dynamic key-guessing techniques and
expand the dynamic key-guessing techniques to block
ciphers of other structures.
ACKNOWLEDGEMENT
The work of this paper was supported by the
National Key Basic Research Program of China
(2013CB834203), the National Natural Science
Foundation of China (Grants 61472417, 61472415
and 61402469), the Strategic Priority Research
Program of Chinese Academy of Sciences under
Grant XDA06010702, and the State Key Laboratory
of Information Security, Chinese Academy of
Sciences.
REFERENCES
Abed, F., List, E., Lucks, S., and Wenzel, J. (2013).
Differential and linear cryptanalysis of reduced-round
SIMON. IACR Cryptology ePrint Archive, Report
2013/526. http://eprint.iacr.org/2013/526.
Alizadeh, J., Bagheri, N., Gauravaram, P., Kumar, A., and
Sanadhya, S. K. (2013). Linear cryptanalysis of round
reduced SIMON. IACR Cryptology ePrint Archive,
Report 2013/663. http://eprint.iacr.org/2013/663.
Alkhzaimi, H. A. and Lauridsen, M. M. (2013). Crypt-
analysis of the SIMON family of block ciphers.
IACR Cryptology ePrint Archive, Report 2013/543.
http://eprint. iacr. org/2013/543.
Bagheri, N. (2015). Linear Cryptanalysis of Reduced-
Round SIMECK Variants. Cryptology ePrint Archive,
Report 2015/716. http://eprint.iacr.org/2015/716.
Beaulieu, R., Shors, D., Smith, J., Treatman-Clark, S.,
Weeks, B., and Wingers, L. (2013). The SIMON
and SPECK families of lightweight block ciphers.
IACR Cryptology ePrint Archive, Report 2013/404.
http://eprint.iacr.org/2013/404.
Biham, E., Biryukov, A., and Shamir, A. (1999).
Cryptanalysis of Skipjack Reduced to 31 Rounds
Using Impossible Differentials.
Biham, E. and Shamir, A. (1991). Differential cryptanalysis
of DES-like cryptosystems. Journal of Cryptology,
4(1):3–72.
Biryukov, A., Roy, A., and Velichkov, V. (2014).
Differential analysis of block ciphers SIMON and
SPECK. In Fast Software Encryption. Springer.
Canni`ere, C. D. and Rechberger, C. (2006). Finding SHA-
1 Characteristics: General Results and Applications.
In Advances in Cryptology–ASIACRYPT 2006, pages
1–20. Springer.
K¨olbl, S. and Roy, A. (2015). A Brief Comparison of Simon
and Simeck. Cryptology ePrint Archive, Report
2015/706. http://eprint.iacr.org/2015/706.
Leurent, G. (2013). Construction of Differential Charac-
teristics in ARX Designs Application to Skein. In
Advances in Cryptology–CRYPTO 2013, pages 241–
258. Springer.
Matsui, M. (1994). Linear cryptanalysis method for DES
cipher. In Advances in Cryptology–EUROCRYPT
1993, pages 386–397. Springer.
Mendel, F., Nad, T., and Schl¨affer, M. (2011). Finding
SHA-2 Characteristics: Searching Through a Mine-
field of Contradictions. In Advances in Cryptology–
ASIACRYPT 2011, pages 288–307. Springer.
Qiao, K., Hu, L., Sun, S., Ma, X., and Kan, H.
(2015). Improved MILP Modeling for Automatic
Security Evaluation and Application to FOX. IEICE
Transactions on Fundamentals of Electronics, Com-
munications and Computer Sciences, E98-A(1):72–
80.
Shi, D., Hu, L., Sun, S., Song, L., Qiao, K.,
and Ma, X. (2014). Improved Linear (hull)
Cryptanalysis of Round-reduced Versions of SI-
MON. Cryptology ePrint Archive, Report 2014/973.
http://eprint.iacr.org/2014/973.
Sun, S., Hu, L., Song, L., Xie, Y., and Wang, P. (2014a).
Automatic security evaluation of block ciphers with S-
bP structures against related-key differential attacks.
In Inscrypt 2013.
Sun, S., Hu, L., Wang, M., Wang, P., Qiao, K., Ma, X., Shi,
D., Song, L., and Fu, K. (2014b). Towards Finding
the Best Characteristics of Some Bit-oriented Block
Ciphers and Automatic Enumeration of (Related-
key) Differential and Linear Characteristics with
Predefined Properties. Cryptology ePrint Archive,
Report 2014/747. http://eprint.iacr.org/2014/747.
Sun, S., Hu, L., Wang, P., Qiao, K., Ma, X., and Song, L.
(2014c). Automatic Security Evaluation and (Related-
key) Differential CharacteristicSearch: Application to
SIMON, PRESENT, LBlock, DES(L) and Other Bit-
oriented Block Ciphers. In Advances in Cryptology–
ASIACRYPT 2014.
Theobald, T. (1995). How to break Shamir’s asymmetic
basis. In Advances in Cryptology–CRYPTO 1995,
pages 136–147. Springer.
Wang, N., Wang, X., Jia, K., and Zhao, J. (2014a).
Differential Attacks on Reduced SIMON
Versions with Dynamic Key-guessing Techniques.
Cryptology ePrint Archive, Report 2014/448.
http://eprint.iacr.org/2014/448.
Wang, N., Wang, X., Jia, K., and Zhao, J. (2014b).
Improved differential attacks on reduced SIMON
versions. IACR Cryptology ePrint Archive, Report
2014/448. http://eprint. iacr. org/2014/448.
Wang, X., Yin, Y. L., and Yu, H. (2005). Finding Collisions
in the Full SHA-1. In Advances in Cryptology–
CRYPTO 2005, pages 17–36. Springer.
Yang, G., Zhu, B., Suder, V., Aagaard, M. D., and Gong,
G. (2015). The Simeck Family of Lightweight Block
Ciphers. Cryptology ePrint Archive, Report 2015/612.
http://eprint.iacr.org/2015/612.
Zhang, K., Guan, J., Hu, B., and Lin, D. (2015). Security
Evaluation on Simeck against Zero Correlation Linear
Cryptanalysis. Cryptology ePrint Archive, Report
2015/911. http://eprint.iacr.org/2015/911.
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
82

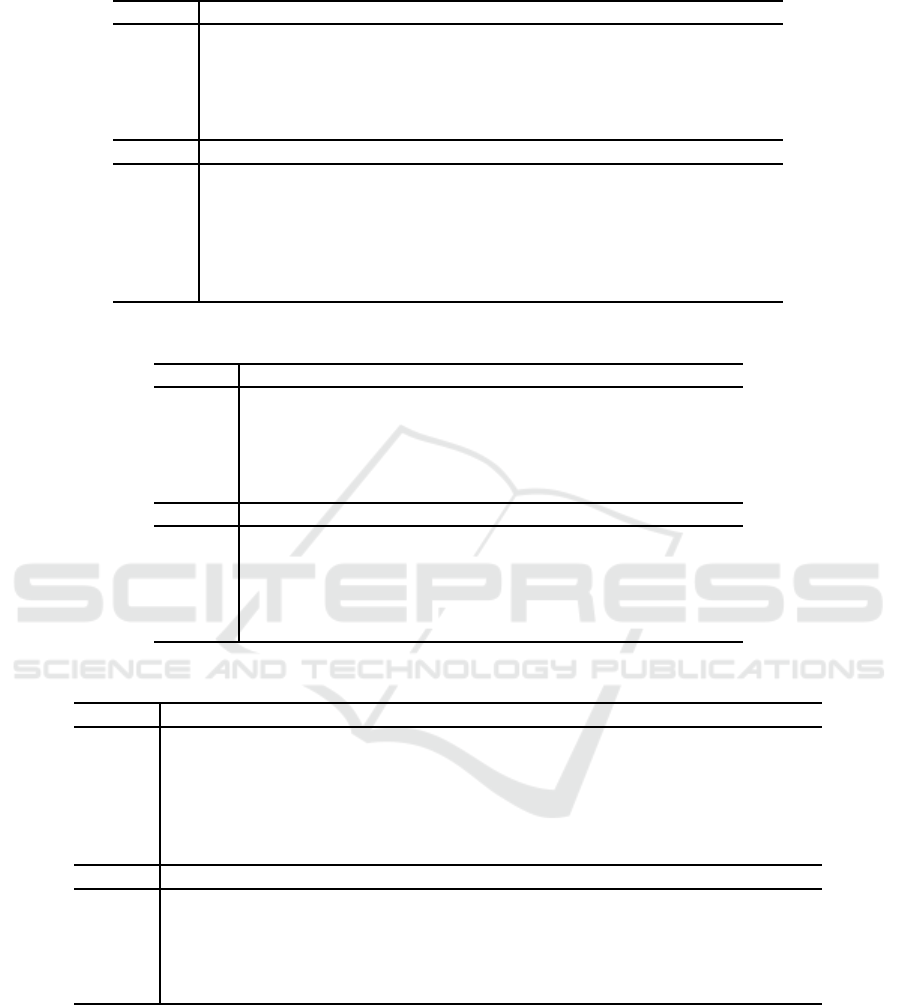
Table 7: Sufficient Conditions of Extended Differential Path of 22-round Simeck32/64.
Rounds Input Differences of Each Round
0 0,0,0, ∗,∗, 0, 0,∗,∗, ∗, 0,1, ∗, ∗,∗,∗, 0, 0,∗, ∗ , ∗,0,∗,∗,∗, ∗, ∗,∗, ∗,∗, ∗,∗
1
0,0,0,0,∗, 0,0,0,∗,∗, 0,0,1,∗,∗, 0, 0, 0,0, ∗, ∗,0,0, ∗, ∗,∗, 0,1,∗, ∗,∗,∗
2 0,0,0, 0, 0,0, 0,0,0,∗,0, 0,0,1,∗, 0,0, 0,0,0, ∗,0, 0, 0,∗, ∗ , 0,0,1,∗, ∗,0
3
0,0,0, 0,0,0, 0,0, 0,0, 0,0,0, 0,1, 0,0,0, 0,0, 0, 0,0,0, 0, ∗,0, 0,0,1, ∗,0
4 0,0,0, 0,0, 0, 0,0,0, 0,0, 0,0,0, 0,0, 0,0, 0, 0,0,0,0, 0,0, 0, 0,0,0, 0, 1,0
4→17 13-round differential
17 0,0,0, 0,0,0, 0,0,0, 0,0, 0, 0,0,1,0, 0,0, 0, 0,0,0, 0,0, 0,0,0,0, 0,0,0,0
18 0,0,0, 0,0,0, 0,0,0, ∗,0, 0, 0,1,∗,0, 0,0, 0, 0,0,0,0, 0, 0,0, 0,0, 0, 0,1,0
19
0,0,0, 0,∗,0, 0,0,∗, ∗,0, 0, 1,∗,∗,0, 0,0, 0, 0,0,0, 0, 0,0, ∗,0, 0, 0,1, ∗,0
20 0,0,0, ∗,∗,0, 0,∗,∗, ∗,0, 1, ∗,∗,∗,∗, 0,0, 0,0,∗, 0,0,0,∗,∗, 0, 0, 1,∗,∗,0
21
0,0,∗, ∗,∗,0, ∗,∗,∗, ∗,∗, ∗, ∗,∗,∗,∗, 0,0, 0,∗,∗,0,0,∗,∗, ∗,0,1,∗,∗, ∗,∗
22 0,∗,∗, ∗,∗,∗, ∗,∗,∗, ∗,∗, ∗, ∗,∗,∗,∗, 0,0,∗, ∗, ∗,0,∗,∗, ∗, ∗,∗,∗,∗, ∗,∗, ∗
Table 8: Sufficient Conditions of Extended Differential Path of 28-round Simeck48/96.
Rounds Input Differences of Each Round
0 ***000000***0**************0***0****************
1
***00000000000***0****1****000000***0***********
2 ***0000000000000000***01***00000000000***0****1*
3
111000000000000000000000***0000000000000000***01
4 010000000000000000000000111000000000000000000000
4→24 20-round differential
24 010000000000000000000000001000000000000000000000
25 1*100000000000000000*000010000000000000000000000
26
***000000000000*000***011*100000000000000000*000
27 ***0000000*000***0****1****000000000000*000***01
28
***00*000***0**************0000000*000***0****1*
Table 9: Sufficient Conditions of Extended Differential Path of 34-round Simeck64/128.
Rounds Input Differences of Each Round
0 **********0000000*000**00***0*************00*000**00***0********
1
*0****1***000000000000*000**00************0000000*000**00***0***
2 *00***01**00000000000000000*000**0****1***000000000000*000**00**
3
*000**001*0000000000000000000000*00***01**00000000000000000*000*
4 00000100010000000000000000000000*000**001*0000000000000000000000
5
0000000000000000000000000000000000000100010000000000000000000000
5→31 26-round differential
31 0000100010000000000000000000000000000000010000000000000000000000
32
000**001*1000000000000000000000*00001000100000000000000000000000
33 00***01***0000000000000000*000**000**001*1000000000000000000000*
34
0****1****00000000000*000**00***00***01***0000000000000000*000**
35 **********000000*000**00***0****0****1****00000000000*000**00***
APPENDIX
Related Keys in Decryption Direction
For sufficient bit condition ∆X
i
j
= 0 or 1 and
j ∈ [0,n − 1], in decrypt direction we have
∆X
i
j
=∆X
i+1
( j+b)%n
∧ X
i+1
( j+a)%n
⊕ ∆X
i+1
( j+a)%n
∧ X
i+1
( j+b)%n
⊕ ∆X
i+1
j+b
∧ ∆X
i+1
( j+a)%n
⊕ ∆X
i+1
( j+c)%n
⊕ ∆X
i+2
j
,
(5)
Differential Security Evaluation of Simeck with Dynamic Key-guessing Techniques
83

where
X
i+1
( j+a)%n
=X
i+2
( j+a+b)%n
∧ X
i+2
( j+a+a)%n
⊕ X
i+2
( j+a+c)%n
⊕
X
i+3
( j+a)%n
⊕ K
i+1
( j+a)%n
,
X
i+1
( j+b)%n
=X
i+2
( j+b+b)%n
∧ X
i+2
( j+b+a)%n
⊕ X
i+2
( j+b+c)%n
⊕
X
i+3
( j+b)%n
⊕ K
i+1
( j+b)%n
.
(6)
Algorithm 3 demonstrates how to get subkey bits
that influence X
i
j
and that are linear to X
i
j
.
Algorithm 3: Generate related key bits for X
i
j
in decryption
direction.
1: Input: Round i and bit position j
2: Output: [Influen
keys,Linear keys]
3: function RELATEDKEYS(i, j)
4: Influent
keys= [ ], Linear keys=[ ]
5: if i = r
0
+ R+ r
1
then
6: return [Influent
keys,Linear keys]
7: else
8: if j ≥ n then
9: return RELATEDKEYS(i+ 1, j%n)
10: else
11: [I
0
,L
0
]=RELATEDKEYS(i,( j+ a)%n+ n)
12: [I
1
,L
1
]=RELATEDKEYS(i,( j+ b)%n+ n)
13: [I
2
,L
2
]=RELATEDKEYS(i,( j+ c)%n+ n)
14: [I
3
,L
3
]=RELATEDKEYS(i+ 1, j+ n)
15: Linear
k
eys=L
2
∪ L
3
∪ K
i
j
16: Influent
keys = I
0
∪ I
1
∪ I
2
∪ I
3
∪ K
i
j
17: return [Influent keys,Linear keys]
18: end if
19: end if
20: end function
Sufficient Conditions of Extended
Differential Path
In the following, we provide the sufficient
conditions of extended differential paths of 22-
round Simeck32/64, 28-round Simeck48/96 and
35-round Simeck64/128.
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
84