
Simulation of Stochastic Activity Networks
Bajis M. Dodin
1
and Abdelghani A. Elimam
2
1
College of Business, Alfaisal University, P.O. Box 50926, Riyadh, 11533, Saudi Arabia
2
School of Science and Engineering, Mechanical Engineering Department, American University in Cairo, Cairo, Egypt
Keywords: Probabilistic Durations, Network Structure, Simulation, Sample Size, Project Variance.
Abstract: Stochastic Activity Networks (SANs) are used in modeling and managing projects that are characterized by
uncertainty. SANs are primarily managed using Monte Carlo Sampling (MCS). The accuracy of the results
obtained from MCS depends on the sample size. So far the required sample size has been determined
arbitrarily and independent of the characteristics of the SAN such as the number of activities and their
underlying distributions, number of paths, and the structure of the SAN. In this paper we show that the
accuracy of the SANs simulation results would depend on the sample size. Contrary to existing practices,
we show that such sample size must reflect the project size and structure, as well as the number of activities.
We propose an optimization-based approach to determine the project variance, which in turn is used to
determine the number of replications in SAN simulations.
1 INTRODUCTION
Activity networks (AN) are known to be useful
models for managing many real world projects. In
routine projects such as construction projects, the
time and resources required by each activity are
known with certainty. In none-routine projects, the
time or resources requirements of an activity may
be, at best, characterized by a random variable with
a given probability distribution function. Such
networks are known as stochastic activity networks
(SANs).
Many of the measures required for managing the
SAN projects are hard to calculate using analytical
methods. To illustrate the difficulty in calculating
activity or project completion times consider the
problem of calculating the probability distribution
function (pdf) of the completion time of a project
represented by the AN of Figure 1. The duration of
activity i is represented by an independent random
variable Y
i
for i = 1, 2, 3, 4, 5, each with a specified
pdf. The completion time of the project, represented
by the random variable T, is the maximum of the
duration of the three paths in SAN. Therefore,
T = max {T
1
,T
2
,T
3
} where T
j
is the duration of path j
= 1, 2, 3; or explicitly
T
1
=Y
1
+ Y
4
, T2
=Y
1
+ Y
3
+ Y
5
, and T
3
=Y
2
+ Y
5.
In general T = max
{T(k) over all k ε P} where P is
the set of all paths in SAN. Consequently, T is the
maximum over many dependent random variables.
While it is possible to calculate the exact pdf of T
for small size SANs, such as the one in Figure 1, and
for some underlying activity pdfs, it is not possible
to calculate the exact pdf of T for larger size SANs
and for various underlying activity distributions.
This difficulty led to most of the research in SANs
starting with the development of the well-known
PERT procedure, Clark (1961). The research is
focused on approximating or bounding the pdf of T
or its statistics, Adlakha and Kulkarni (1989); and
Herroelen and Leus (2005).
The difficulty in calculating pdf of T or any of
the other measures stated above has led to the use of
Monte Carlo sampling (MCS). It is assumed that as
the number of simulation runs, known as sample size
n, increases the resulting pdf of T and all of its
statistics improve in their accuracy, and eventually
converge to the exact values as n → ∞. How large n
should be to guarantee a certain level of accuracy in
the estimated measures? The Central Limit
Theorem (CLT) has been used to answer this
question. For instance, in case of the mean value for
the T, denoted by μ
T
, if μ
s
denotes the corresponding
simulated value, then the level of accuracy is
measured by the absolute difference ε = | μ
s
- μ
T
|,
where it is desired to have the difference to be ≤ ε
with a very high probability. Let α =1 - Pr(| μ
s
- μ
T
| ≤
ε), then from the CLT it is concluded that
205
M. Dodin B. and A. Elimam A..
Simulation of Stochastic Activity Networks.
DOI: 10.5220/0005561502050211
In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),
pages 205-211
ISBN: 978-989-758-120-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Example of a stochastic activity network.
2
2
2
2
standard deviate for
2
confidence level
where
and tandard deviation of T.
n
Z
Z
s
In case of SANs, the above determination of the
sample size n is problematic as it assumes that:
Standard deviation of T, σ, is known
The pdf of T converges to a normal
distribution
Sample size n is independent of SAN size
or number of paths in the AN
n is also independent of the underlying pdf
of the activity durations
n is also independent of the structure or
complexity of the AN.
To illustrate some of the above problems, is it
possible that for a given confidence level α that the
required n to simulate the SAN of Figure 1 (with
five activities, four nodes, and three paths) is equal
to the n required to simulate a much larger SAN
(such as a SAN with 60 nodes, 500 activities, and
thousands of paths)? Second, it has been proven that
in most SANs the pdf of T is not normally
distributed, Dodin and Sirvanci (1990). This paper
focuses on exploring the relationships that may exist
between the sample size and the above factors.
2 SAN CHARACTERIZATION
The following notation is used throughout the paper:
A: Set of activities/arcs in the project
M = |A|; Number of activities in the project/SAN
N: Number of nodes in the SAN.
Y
ij
: A random variable denoting the duration of arc
(i,j) ε A which starts in node i and ends in node j.
P: The set of all paths in the network.
K = |P|; number of paths in the SAN.
T(k): The duration of path k ε P; T(k) =
(, ) ( )
ij
ij Pk
Y
.
T: The duration of the longest path in SAN
designating node N realization time as well as the
project completion time. Hence T =
P k
max
{T(k)}.
The shape of the AN also may reflect the degree of
dependency among the paths. A rectangular shaped
AN tends to have many paths in parallel; hence, less
dependencies among paths than a triangular one. It is
well known that the higher the precedence relations
between activities the greater the dependency among
paths and the harder the task of managing. One of
the ways to measure some of the above attributes is
to use the the following AN complexity index, as
suggested by Kolisch, Sprecher, and Drexl (1995).
ANCI = [sum of all precedence relations]/N. In
some studies N in the ANCI expression is replaced
by M. ANCI is often used in designing ANs to test
the efficiency of algorithms/heuristics that are used
to manage the corresponding projects.
In case of SANs, ANCI can be used to characterize
such networks in addition to other characterizations.
The above expression of T indicates that the
following factors can play a role in characterizing
SANs:
1. Underlying pdf of the activities
2. Number of paths in the set P
3. Dependency among the paths
4. The gap between the duration (expressed in
terms of the mean and variance) of the longest
path in SAN and the next longest.
From the definition of T we notice that the longest
path is not unique. In fact each path k ε P can be the
longest path but with certain probability. This
probability is known in the literature as the
criticality index of the path, and it is used in SANs
to rank the paths and the activities, Dodin and
Elmaghraby (1985). The pdf of T, denoted by F(t), is
given by F(t) = PR (T ≤ t) = Pr (T(k) ≤ t for all k ε
P). Hence, F(t) ≤ Pr(T(k)) for any one path k ε P.
This shows that approximating F(t) by the pdf of the
duration of only one path forms an upper bound on
F(t). In general, SANs examples can be given to
show that such an approximation is grossly
optimistic. It can be shown that the joint pdf of any
paths combination continues to form an upper bound
2
1
5
4
1
3
4
2
3
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
206
on F(t). Therefore, the mean value of the duration of
any individual path, or a surrogate SAN consisting
of any combination of the P paths of the original
SAN continue to form a lower bound on E(T), Feller
(1968), and Dodin (1985).
The above shows that, in general, T cannot be
approximated by one T(k) for k ε P, or a
combination of paths in the set P and simulation may
become necessary to determine the realizations of T
and its pdf. We show below how the above factors
characterize SAN with respect to the ease of
calculating the pdf of T. To pursue this consider first
the following two cases:
Case 1: A SAN consisting of only one path where
the M activities are in series. In this case the CLT is
applicable, and as M increases, the pdf of T
converges to a normal distribution regardless of the
pdf of the activity distribution. The project
completion time T, mean, and variance of T are
given by:
T = Σ
ij
Y
ij
, µ(T) = Σ
ij
μ(i,j), and σ
2
(T) = Σ
ij
σ
2
(i,j),
and F(t) can be easily calculated for any value of t
≥0. In this case there is no need for simulation. This
is also the case if a path j ε P in SAN dominates all
other paths k ε P, where a path j dominates a path k
if
Pr(T(j) ≤ t) ≤ Pr(T(k) ≤ t) for all t ≥ 0.
The dominance test is easy to implement if the
number of paths in SAN is small as, based on CLT,
each path is normally distributed. Its mean, variance,
and pdf are calculated as above. However if the
number of paths is large, then the dominance test
can be cumbersome. In this case the dominance test
can be replaced by calculating the gap between the
longest path, j, and the second longest path, k, in
mean; then perform the above dominance test
between these two paths, j and k, or the weaker form
of dominance given by:
Pr(T(j)≥ T(k)) ≥ Pr(T(k) ≥ Pr(T(j))=1-Pr(T(j) ≥ T(k))
If j dominates k then in all of these instances T can
be approximated by T(j) and no need for simulation.
In this case PERT Estimates are excellent regardless
of the activities underlying distributions. For this
type of network structure simulation is not needed as
illustrated by Table 1 below.
What if there is no one path in SAN that dominates
all other paths? The next case responds to this
question:
Case 2: SAN consists of K independent paths in
parallel. In this case F(t) is given by: F(t) = PR
(T(k) ≤ t for all k ε P) =
P k
F
k
(t), and F(t) is not
normal even if any or all of the underlying K
distributions are normal, David (1981), Galambos
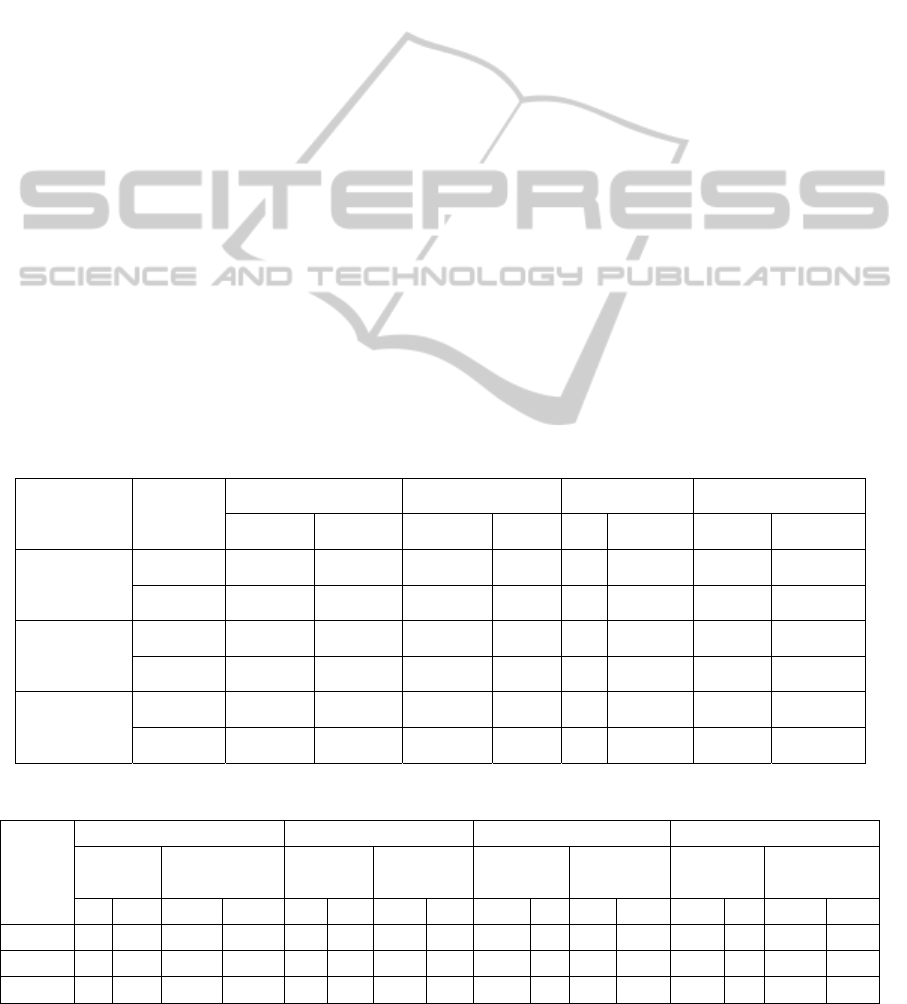
Table 1: Mean, µ, and Standard Deviation, σ, for One Path Network.
Number of
Activities
Parameter
Normal Uniform Exponential Mixed
PERT Sim PERT Sim. PERT Sim PERT Sim
10
µ 104.4 104.4 80.9 80.9 7.6 7.6 52.9 53.1
σ 6.82 6.82 5.48 5.61 2.5 2.46 11.76 11.88
20
µ 208.3 208.2 170.3 170.4 42.5 42.5 124.3 124.3
σ 9.701 10.15 7.74 7.67 13.86 13.77 8.30 8.44
40
µ 414.2 414.2 281.1 280.7 56.8 56.8 292.9 293.1
σ 13.49 13.34 10.95 11.00 11.00 11.23 11.92 11.82
Table 2: Contrast of μ & σ for T of a SAN with K parallel paths.
Number
of Paths
Normal Uniform Exponential Mixed
Longest
Path
Simulated
for T
Longest
Path
Simulated
for T
Longest
Path
Simulated
for T
Longest
Path
Simulated
for T
μ σ μ σ μ σ μ σ μ σ μ σ μ σ μ σ
10
10 2 13.09 1.20 8 1.73 10.46 .50 .67 .67 1.97 .88 10 2 20.32 11.05
20
10 2 13.76 1.05 8 1.73 10.69 .28 .67 .67 2.41 .86 10 2 22.09 11.21
40
10 2 14.36 0.99 8 1.73 10.86 .14 .67 .67 2.87 .82 10 2 33.83 13.64
SimulationofStochasticActivityNetworks
207
(1978). If the K paths are also identically
distributed, then F(t) = [Pr(T(k) ≤ t)]
K
. In this case
F(t) converges to an Extrême Value (EV)
distribution with long right hand tail. Table 2 shows
that as K increases μ(T) increases where the longest
path mean and variance stay constant. Table 2 also
shows that the underlying distributions and SAN’s
size affect T and its statistics. The increase in μ(T) is
large especially if some of the underlying
distributions have long right tails such as the
exponential distribution. In spite of the fact that all
paths are iid, except for the mixed case, μ(T)
continues to increase as the number of paths
increases. Consequently, if SAN consists of K iid
paths, then T has an EV distribution. Its pdf, mean
and variance can be easily computed without the
need for simulation, Dodin and Sirvanci (1990).
Consider a large SAN with several paths. In Case 1
above, the CLT continues to apply for any network
as long as it contains a single path that dominates all
other paths. Similarly in Case 2, the EV theory can
be applied to many SANs with certain
characteristics, while there are not many SANs that
consist of many iid paths. As explained by Case 1,
the duration of each path is normally distributed and
the paths may not be independent. However, many
of the paths may become normally distributed with
close means, and variances, and the degree of
dependencies is very low. Consequently, the
conditions of the EV theory also exists in these
networks, and T can be approximated by an EV
distribution. This is the case for large SANs with
rectangular or diamond shapes. For these networks
the distribution of T is affected by two
convergences: convergence to a normal distribution
for the individual paths as the number of activities
on each path increases, and convergence to an EV as
the number of paths increases and more of them
become more iid. It was shown in Dodin and
Sirvanci (1990) that if SAN has m ≥ 4 dominating
paths ; i.e. m close to being iid, then pdf of T can be
accurately approximated by:
F(t) = Pr(T ≤ t) = exp[- e
-(b
m
- a
m
)
]
μ(T) = a
m
+ 0.57722 / b
m
, and σ(T) = π /(2.45 b
m
)
where.
a
m
= µ + σ[(2 ln m)
1/2
- (l/2)(ln ln m + ln 4π) / (2 ln
m)
1/2
], b
m
=
m)ln (2
,
and μ & σ are the mean and standard deviation of
the first dominating paths.
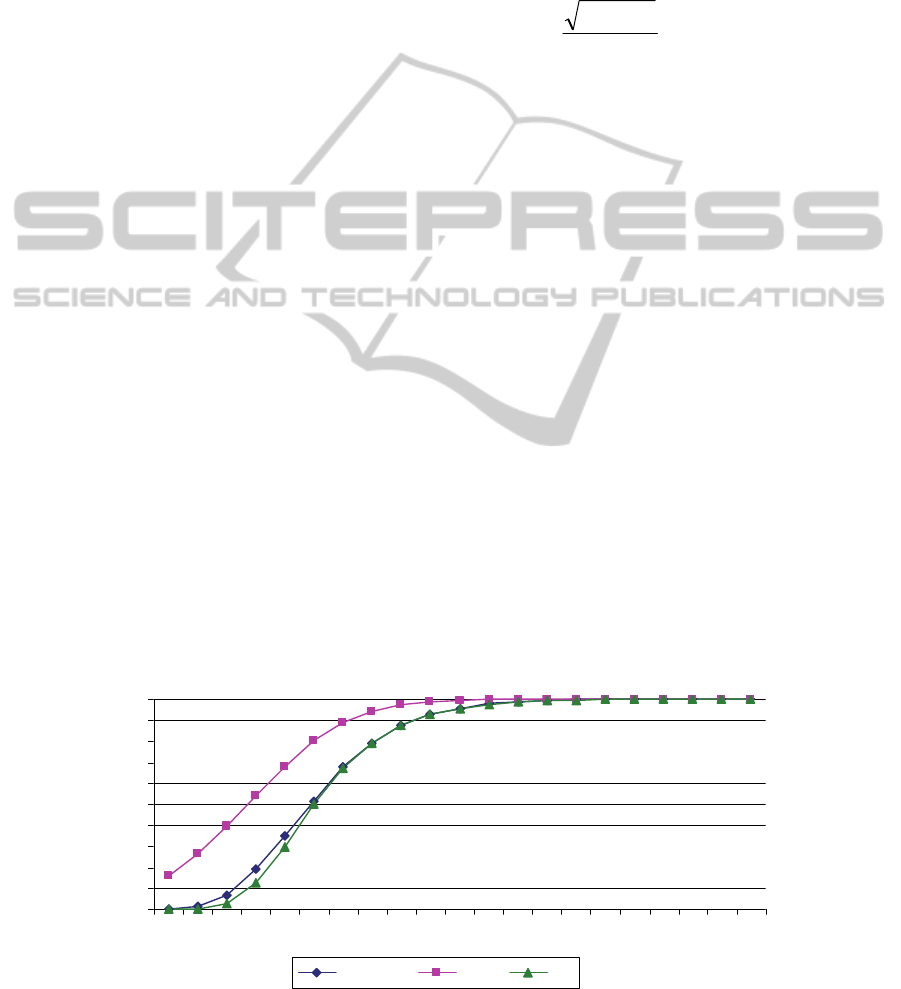
Figure 2 and Table 3 show three estimates for the
pdf of T for a large SAN (with N=40 nodes and
M=100 activities) where the activities have varying
exponential distributions. SAN does not have one
dominating path, but it has many dominating paths.
It is clear that the pdf based on one of the longest
paths (normal distribution known also as PERT
distribution) provides a weak upper bound on pdf of
T; where that EV estimates are very close to the
simulated F(t).
The above two cases prove that if SAN has one
dominating path, then T is normally distributed; and
if it has several dominating paths then T has an
Extreme value distribution. In both cases simulation
can be avoided. Determining if SAN has one or
several dominating paths is relatively easy. This
follows from repeating the dominance test stated in
Case 1.
If one path is not the dominating path, then the
test is repeated by contrasting one of the first two
longest in mean to the third longest in mean, then
the fourth, and so on. This leaves us with the third
case where SAN does not have either of these two
characterizations.
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
123456789101112131415161718192021
Simulat ion PERT EV
Figure 2: Cumulative distributions for the estimates of Normal, Simulation, and Extreme value.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
208

Case 3: This includes SANs where the longest
path/s in mean may not be the longest path/s in
variance or vice-versa. The SAN is in between the
above two extremes. Hence the pdf of T is not
normally distributed and cannot be approximated by
longest average (PERT), and cannot have the EV
distribution. In this case simulation becomes
necessary for obtaining an accurate approximation
for T where determining the required sample size n
is the main issue. The next section deals with the
issue of determining the n required for achieving the
desired level of accuracy.
3 SIMULATION SAMPLE SIZE
This section shows that project variance depends on
the network structure expressed by the number of
activities and activity precedencies. In order to
prove such result, we first represent the project
network into a longest path formulation. We assume
that all projects have one dummy starting activity
and a final ending dummy activity, whose variances
and durations are equal to zero. So, all paths in the
network must start and end with these two starting
and ending dummy activities. The formulation
assumes activity on arc (AOA) representation. Let
1
,) 1, ,
set of nodes connecting to i by activity (i,j) 1, ,
where =
set of nodes connecting to i by activity (j,i) 1, ,
where =
( ) maximum varia
variance of activity (
i
N
i
ij
ji N
v
iN
A
A
iN
B
B
VP
i
nce in the project network P
1 if activity (i,j) is on the longest variance path
=0 otherwise
ij
x
Then program (P) represents the project network.
1
1
1
1
1
0 j 2, , -1
Pr (P):
V(P) =
:
i
N
jj
i
j
j
A
iN
i
B
ij jk
ik
BA
N
ij ij
ij
A
N
ogram
Max
Subject to
x
x
xx
vx
The above model contains N nodes (constraints) and
D=
1
N
i
i
A
precedence or arcs (variables). Program
(p) solution would provide the maximum variance
path in the project network, V(P), regardless of its
completion time. The size of program (P) in terms
of number of variables and constraints reflects the
network structure and accordingly its complexity.
Projects with larger number of nodes would have
more constraints and an increased number of
precedence among these activities would be
reflected into higher number of variables.
Proposition: consider two project networks:
i. The first is a project P
0
consisting of N
0
activities and D
0
precedencies among these
activities.
ii. The second project, P
1,
is a sub-network of
project P
0
and, consists of N
1
activities and D
1
precedencies among these activities, where N
1
≤N
0
and D
1
≤ D
0,
showing that the network complexity
index of project P
0
, is greater than or equal to that of
project P
1
, NCI (P
1
) ≤ NCI (P
0
)
Then the variance of V(P
1
) ≤ V(P
0
)
Proof: The number of paths in project P
0
is ≥ than
that of project P
1
since it contains N
1
≤N
0
and D
1
≤
D
0
. Therefore the feasible region for program V (P
1
)
is a subset of program V(P
0
). Clearly maximizing
over a larger feasible region (larger number of paths)
for project P
0
would yield a higher objective
function than that of P
1
. Therefore the optimum
objective function value of program (P
1
), V(P
1
) ≤ the
optimum objective function value of program (P
0
),
V(P
0
).
The above Proposition ensures that the network
structure is represented in calculating the project
variance, V (P
0
).
The following example illustrates that the project
variance is dependent upon the network structure
including the number of activities and the number of
precedencies.
In order to maintain the same project structure,
we will formulate program (P) using both AOA and
AON. The AOA model would be used to illustrate
the impact of the number of activities on the
variance, while the AON would be applied to show
the impact of the number of precedencies on the
variance. Table 4 presents a sample eight-activity
project.
Solving the longest variance route AOA model
for the Eight-Activity project yields a variance = 44.
Suppose we drop two activities (3,4) and (4,6) while
maintaining the same project precedence among the
remaining activities. The longest variance route for
the resulting six-activity project provides a variance
= 42, which illustrates that a project with a larger
number of activities would have a project variance
that is greater than or equal to a project with a subset
of those activities. Table 5 summarizes the results of
variances for the three models solved for the same
project. The table also shows that as the NCI
SimulationofStochasticActivityNetworks
209
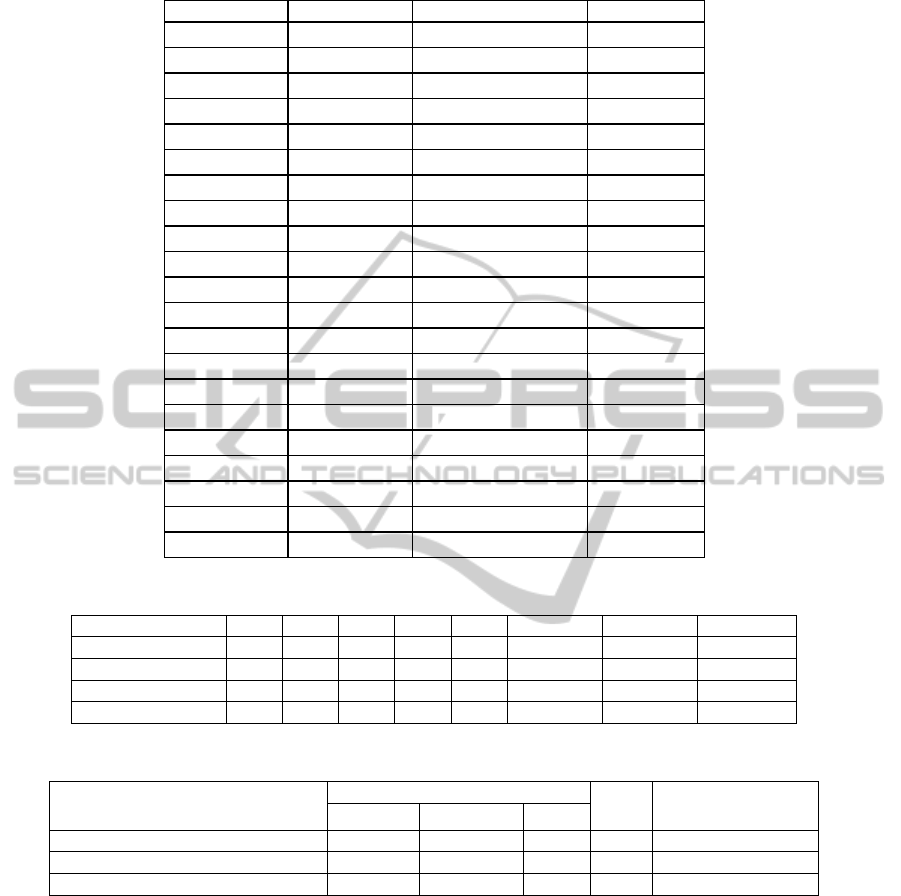
Table 3: Three estimates of F(t): Normal, Simulation, and Extreme value.
t Simulation Normal (PERT) EV
26.35 0.00 0.16 0.00
31.79 0.02 0.26 0.00
37.23 0.07 0.39 0.03
42.67 0.19 0.54 0.12
48.11 0.35 0.68 0.30
53.55 0.52 0.80 0.50
58.99 0.68 0.89 0.67
64.43 0.79 0.94 0.79
69.87 0.88 0.97 0.87
75.31 0.93 0.99 0.93
80.75 0.96 1.00 0.96
86.19 0.98 1.00 0.97
91.63 0.99 1.00 0.99
97.07 0.99 1.00 0.99
102.51 1.00 1.00 0.99
107.95 1.00 1.00 1.00
113.39 1.00 1.00 1.00
118.83 1.00 1.00 1.00
124.27 1.00 1.00 1.00
129.71 1.00 1.00 1.00
135.15 1.00 1.00 1.00
Table 4: Sample Eight-Activity Project.
Activity (AoA) (1,2) (1,3) (2,4) (3,4) (3,5) (4,5) (4,6) (5,6)
Activity (AoN) A B C D E F G H
Precedence (AoA) - - (1,2) (1,3) (1,3) (2,4),(3,4) (2,4),(3,4) (3,5) ,(4,5)
Precedence (AoN) - - A B B C, D C,D E, F
Variance 9 6 10 15 12 10 8 13
Table 5: Maximum Variances for eight-activity project and its subset projects.
ProjectDescription
Number of
NCI Maximum Variance
Activities Precedence Nodes
Original 8 9 6 1.5 44
Subset(activities D & G deleted) 6 5 6 0.83 42
Subset(No C-F & F-H precedence ) 8 7 8 0.875 31
increases the project variance increases. Please note
that in all cases, the variance provided by optimizing
the longest variance route model would always be
greater than or equal the variance of the longest path
T.
Therefore, the variance given by the longest
variance model would serve as the basis for
computing the simulation sample size. Our
proposed approach would ensure that the project
network structure, expressed by the number of
activities and precedence relationships, have a direct
impact on the project variance and accordingly on
the project simulation sample size. Let
2
v
= the maximum variance V(P)
= the critical path expected length
E
T
Then the proposed approach would be as follows:
4 PROPOSED SIMULATION
APPROACH
a. Formulate a longest variance model using
program (P) with the variances as the cost
coefficients of the (0, 1) variable corresponding to
each activity.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
210

b. Optimize the model to get the maximum
variance,
2
v
. This provides the value for the project
variance. Please recall that the CLT would ensure
that project duration distribution is a normal
distribution with an expected project duration T
E
and
a standard deviation σ
v
.
c. For a specified upper bound on the error in
T
E
, given by ϵ, we can then compute a lower limit on
the value of n, as follows:
2
2
2
v
n
Z
d. Replicate the simulation according to this n.
5 CONCLUDING REMARKS
In this position paper, we classify SANs based on
the probability distributions of the activity durations
as well as the network structure. We identify the
situations where stochastic simulation is required.
For those simulation experiments, we have also
shown that the existing approaches for determining
the number of replications based on the central limit
theorem is inaccurate. The paper illustrates the need
for determining the simulation sample size based on
the project network structure and size. We proposed
an optimization based approach to determine the
number of replications based on the SAN structure
and size. Future work would involve conducting
extensive computational experiments on SANs with
a variety of structures and size.
REFERENCES
Adlakha, V. G. and Kulkarni, V. G., 1989, A Classified
Bibliography of Research on Stochastic PERT
Networks: 1966-1987, INFOR. 27(3): 272 296.
Clark, C. E., 1961, The Greatest of a Finite Set of Random
Variables. Opns Res. 9:146 162.
David, H. A., 1981, Order Statistics, 2nd ed. Wiley, New
York.
Demeulemeester, E, Herroelen, W., 2002, Project
Scheduling: A Research Handbook, Kluwer Academic
Publishing.
Dodin, B. M.,2006, “Practical & Accurate Alternative to
PERT” Perspectives in Modern Project Scheduling, J.
Weglarz, Springer International series; pp 3-23.
Dodin, B. M. and Elmaghraby, S. E., 1985,
Approximating the Criticality Indices of the Activities
in PERT Networks, Magt. Sci. 31: 207 223.
Dodin, B., and Sirvanci, M., 1990, Stochastic Networks
and the Extreme Value Distribution, Computers and
Opns. Res. 17(4): 397 409.
Feller, W., 1968, An Introduction to Probability Theory
and its Applications, Vol. I, 3rd ed., John Wiley &
Sons, New York.
Galambos, J., 1978, The Asymptotic Theory of Extreme
Order Statistics. Wiley, New York.
Glover, F., Klingman, D., and Phillips, N. V., 1992,
Network Models in Optimization and their
Applications in Practice, John Wiley & Sons, New
York.
Herroelen, W., and Leus, R., 2005, Project scheduling
under uncertainty: Survey and research potentials,
European J. of Opnl. Res., 165(2): 289 306.
SimulationofStochasticActivityNetworks
211
