Conics Detection Method based on Pascal’s Theorem

Musfequs Salehin, Lihong Zheng and Junbin Gao

School of Computing & Mathematics, Charles Sturt University, Wagga Wagga, Australia

Keywords: Conics Detection, Pascal’s Theorem, Ellipse Detection, Parabola Detection.

Abstract: This paper presents a novel conics detection method that can be applied for real images. The existing

methods usually detect either circular or elliptical, or parabolic shape at one operation. Most of them need

the information about center, radius, major axis, minor axis, vertex, and more. In our proposed method, the

tangents on curve segments, conic parts, and conics are constructed using Pascal’s theorem. The conic parts

can be used to detect different types of conic sections from an image. The performance of the proposed

method has been tested on the sample images selected from Caltech-256 database and various types of conic

sections can be identified from the real images compared to other method.

1 INTRODUCTION

Conics are the curves formed by the intersection of a

plane with a right circular cone. They include

circles, ellipses, parabolas, and hyperbolas. Among

conics, the most common geometric shapes are

circles, ellipses, and parabolas to present various

conic shaped objects for detection in computer

vision. Many traditional methods can detect only

circles or ellipses, or parabolas individually. Though

such methods are robust to noise and show good

performance, it is hard to find an existing method

that can detect all types of conic shaped objects in a

single operation. Again, conics detection from an

image is still a very challenging problem due to

various reasons. Not every edges of an image are

smooth and clear. Some edges might be blurry and

disconnected due to reflections or varied

illumination. In addition to this, object contours may

be distracted in the presence of clatters, occlusion,

and perspective errors. Consequently, in most of

these cases, the conic shape of a desired object is

distorted, disconnected, or even overlapped by other

objects.

In this paper, we aim at detecting conic shaped

edges in an image based on Pascal’s theorem.

Firstly, we apply Triangular Area Ratio (TAR)

(Alajlan et al. 2007) to break each edge contour into

two or more segments based on sharp turns or

inflection points. Secondly, we calculate two

tangents at two ending points of a curve segment

using Pascal’s theorem (Coxeter & Greitzer 1967).

From the two tangents, conic part is constructed and

fitted with edge segments using least squares fitting

method. Lastly, the validated edge segments are

grouped together to match the conic shaped object in

an image. We apply Pascal’s theorem to detect

conics in the image. Our contribution is that the

proposed method does not need to calculate the

center, major axis, or minor axis to detect conic

shaped object. Simply, it identifies conic shaped

object by verifying the best matching between conic

shaped object and grouped edge segments.

The organization of this paper is as follows. The

background of conics detection is presented in

Section 2. The proposed approach is discussed in

Section 3; the visual results are displayed in Section

4. Lastly, we conclude the paper in Section 5.

2 BACKGROUND

Conics detection from an image is an important and

recurring research problem. Various methods for the

detection or fitting of different types of conics have

been developed in the last few decades. These

algorithms can be categorized into three main

approaches. They are (1) Hough Transform (HT)

based approaches, (2) optimization based

approaches and (3) edge following based

approaches.

In general, Hough Transform based method is a

standard technique for detecting any parameterized

curve. One of the key advantages of HT based

491

Salehin M., Zheng L. and Gao J..

Conics Detection Method based on Pascal’s Theorem.

DOI: 10.5220/0005299804910497

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 491-497

ISBN: 978-989-758-089-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

method is that it can detect fragmented ellipses. The

reason of this is that, it does not require the edge

pixels to be connected consecutively on the ellipse.

This method maps two dimensional image space into

the higher dimensional parameter space. For

example, an ellipse can be defined by five

parameters, such as its center (c

, c

), the major axis

a, the minor axis b, and the orientation θ. Therefore,

O(N

) space is required for an ellipse to accumulate

the parameter space, where N is the size of each

dimension of the parameter space. As a result, this is

a combinatory complexity. Moreover, in the basic

HT based method, the accumulator’s bin sizes are

determined by “windowing and sampling the

parameter space in a heuristic way” (Xu et al. 1990).

However, a large window size is necessary to detect

curves from the image with different sizes and a

high dimensional parameter space to increase

accuracy. Again, these obviously lead to large

storage and more processing time. Additionally, in

case of poorly defined accumulator, (Xu et al. 1990)

identified four difficulties may occur, such as (a)

problems in finding an optimal local maxima, (b)

low precision, (c) large storage, and (d) low speed.

For example, coarse quantization may have poor

influence on accurate ellipse detection while fine

quantization may lead to missing the true ellipses.

Besides this, the accuracy of HT decreases at the

increased number of ellipses in an image

(McLaughlin 2000).

Optimization based approaches include Genetic

Algorithms (GA), Least Squares Fitting (LSF)

method, or Robust Regression (RR) based approach

for ellipse detection. GA based methods represent

each potential solution as a chromosome and the

population of chromosomes are generated

iteratively. This process terminates when some

predefined conditions are satisfied. However,

finding the best possible evaluation criteria and

thresholds for fitness function are often very hard

(Qiao & Ong 2007). Both LSF and RR methods

extract ellipse by optimizing an objective function to

fit edge pixels to a standard ellipse. However, in

presence of outliers, these methods may produce

false or missing detection (Qiao & Ong 2007).

Edge following based approaches extract some

arc fragments and group them together based on

geometric properties of ellipse. Recently, a method

for ellipse detection based on edge following is

proposed by (Chia & Rahardja 2011). In their

method, line segments are formed from the edge

map and elliptical-arcs are constructed from these

line segments. These arcs are then grouped to form

ellipses and false ellipses are neglected by the

developed feedback loop method. This method

performs very well both in synthetic as well as in

real-world images. However, it is computationally

very expensive (Wong & Lin 2012).

Another edge following method for ellipse

detection is proposed by (Prasad et al. 2012). This

method uses edge curvature and convexity instead of

continuity as a constraint for the ellipse detection.

Hough Transform is then applied to assign a

relationship score to the edge contours for grouping.

Three robust non-heuristic saliency criteria are used

for generating the good elliptic hypotheses. This

method does not require any threshold or control

parameter. Although this method achieves a high

accuracy, it is also very time consuming in the

presence of outliers and it often provides false or

missing detection (Akinlar & Topal 2013).

Akinlar and Topal proposed a real-time and

parameter free method (Akinlar & Topal 2013) to

detect both circles and near-circular ellipses. This

algorithm first extracts edge segments from a given

image by implementing Edge Drawing Parameter

Free (EDPF) edge detector. The detected edge

segments are converted into line segments. Circular

arcs are then detected from these line segments

based on line direction and angle between two lines.

Candidate circles and near-circular ellipses are

detected based on the constraint of center distance

and radius difference with the root mean square

error. Finally, the candidates are validated using

Helmholtz principle (Akinlar & Topal 2013).

However, its success depends on the accurate edges

detected by EDPF and the presence of noise in the

image (Akinlar & Topal 2013).

In this paper, we propose a novel method based

on the edge following method. We extract edge or

part of edge that can be a part of a conic section. To

construct the conic part by Pascal’s theorem, two

tangents, and a point on the curve are required. We

construct tangent using the theorem proposed by

Pascal (Coxeter & Greitzer 1967). Instead of

applying LSF method or HT-based method for

detecting circle or ellipse or parabola, we apply

Pascal’s theorem for detecting different types of

conic sections. Method based on LSF is designed for

detecting only one specific type of conic section at a

time. For example, LSF method proposed for

detecting for circle cannot detect parabola and vice-

versa. In contrast, our method based on Pascal’s

theorem can detect any sorts of conics. Again, for

grouping edge fragments to construct conics, we

apply conic part construction method by Pascal

theorem.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

492

Thus, the contributions of the proposed method

are listed below:

1. A novel technique for detecting conic part

using Pascal’s theorem

2. A novel method for constructing tangent on a

curve using the theorem proposed by Pascal

3. A novel approach for grouping edge fragments.

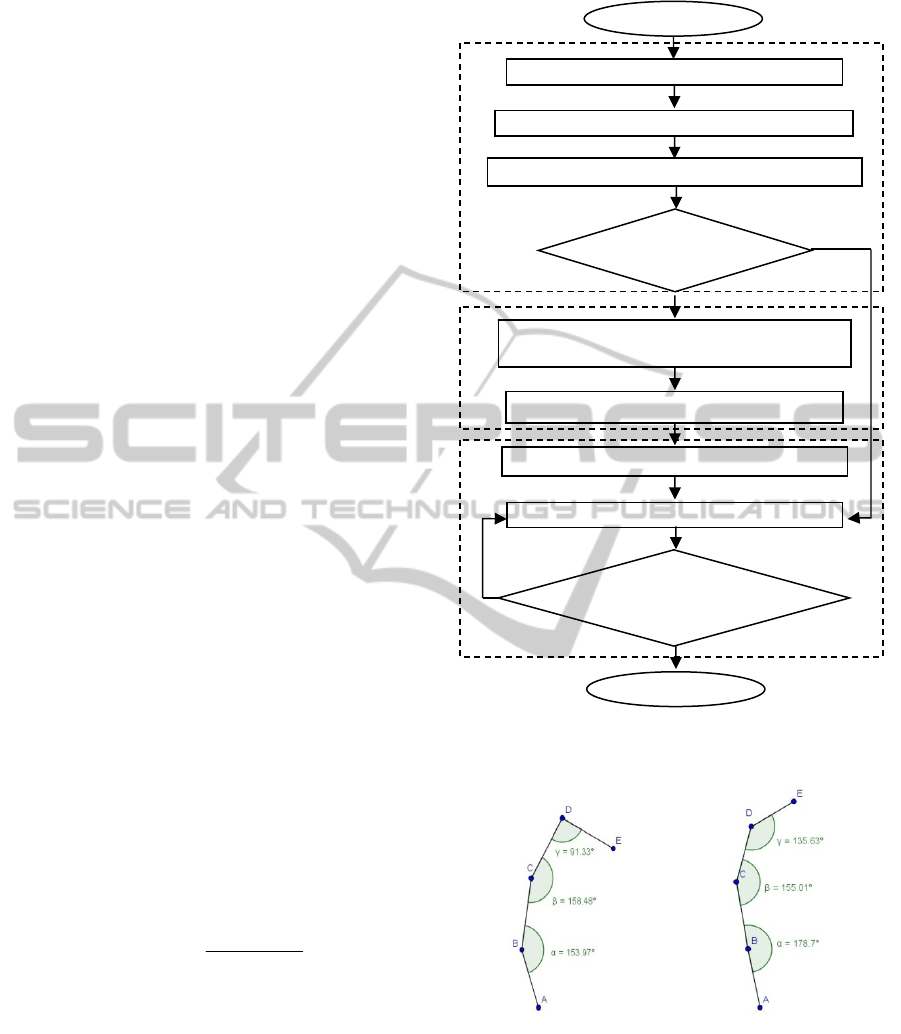
3 THE PROPOSED METHOD

The proposed method follows three main steps to

detect conic shaped objects in an image. The flow

chart of the proposed method is presented in Figure

1. The first step is to extract smooth conic edge

curves from the edge map obtained by Canny edge

detector; the second step is to generate the conic

hypothesis; and the last step is to detect conics from

the conic hypothesis. Each step of the proposed

method is discussed in details in the following

subsections.

3.1 Extraction of the Conic Edge

Segment

Firstly, an edge map is generated from a given

image using Canny edge detection method. Then,

connected edge contours and line segments are

obtained from the edge map using Kovesi’s codes

(Kovesi 2000).

3.1.1 Sharp Turn and Zero Curvature

Detection

Using two consecutive line segments with points

pre

, y

pre

), (x

curr

, y

curr

) and (x

, y

) in counter

clockwise direction, a triangle is formed. The angle

between two consecutive line segments is obtained

by the following equation



















acb

CoscurrAngle

)(

222

(1)

where

cba ,,

are triangle sides between (x

pre

, y

pre

) &

curr

, y

curr

), (x

curr

, y

curr

) & (x

, y

) and (x

, y

)

& (x

pre

, y

pre

) respectively. If the Angle(Curr) is less

than 100° or greater than 175°, line segments are

divided into two parts at (x

curr

, y

curr

) point. The

reason is that angle less than 100° suppose to be a

corner point and angle greater than 175° is almost

similar to a straight line (see Figure 2). Again, if the

value of a or b exceeds 100 pixels, the line segment

is divided at (x

curr

, y

curr

Figure 1: The flow chart of the proposed method.

(a) (b)

Figure 2: The sharp turn and zero curvature elimination.

(a) sharp turn point is D, (b) zero curvature point is B.

3.1.2 Inflection Point Detection

If (x

curr

, y

curr

) is not considered as a sharp turn point,

the TAR is calculated by the following equation

Star

Edge detection by Canny edge

Line segments formation by Kovesi

Split edges at sharp turn and inflection

Construct tangents to ends of each edge

segments

Conic parts grouping

Is edge segment

closed?

Verification of object of interes

Conic parts construction & fittings

Is there any edge

contours remaining?

ConicsDetectionMethodbasedonPascal'sTheorem

493















)(

nextnext

currcurr

prepre

DetcurrTAR

(2)

where, Det presents the matrix determinant. The

negative, positive, and zero values of TAR(curr)

represent concave, convex and straight-line

respectively (Alajlan et al. 2007). Here, we split

edge segment at a point containing zero TAR(curr)

value. As a result, the extracted line-segments only

contain negative (n) or positive (p) values. Let, {T

, T

… T

} be the sequence of line segments

where M represents the total number of positive and

negative values within an edge segment. T

{i=1, 2,

3, … M} contains either n or p values. To identify

the inflection points, the following criteria are

applied.

if T

= n and T

i-1

1i

= p, the splitting point

1i

= n and

2i

1i

= p, the

splitting point is

and

1i

= n and

3i

2i

1i

= p, the splitting

point is

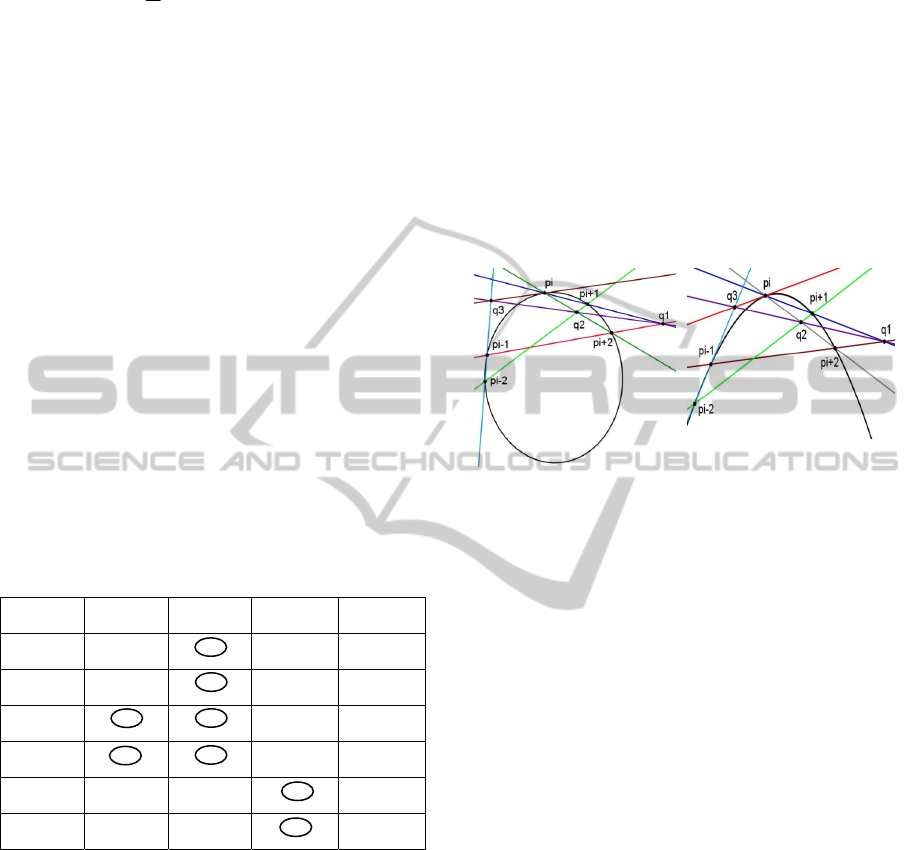
Table 1: Representation of the inflection points.

i-2

i-1

i+1

i+2

p p n p p

n n p n n

p n n p p

n p p n n

p p p n n

n n n p p

Table 1 summaries the possible cases to reflect the

selective criteria that find out the inflection points.

After splitting edge segments at the inflection points,

edge segments containing at least three n or p values

are selected. Later, the closed edge contours and the

selected edge segments are considered for the next

step to generate conic hypothesis.

3.2 Generation of the Conic Hypothesis

To validate an edge segment as a conic part,

tangents are drawn at each endpoint of an edge

segment using Pascal’s theorem (Coxeter & Greitzer

1967). This is one of the main contributions of the

paper. Consider p

i-2

, p

i-1

, p

i+1

, and p

i+2

are five

points of an ellipse (see Figure 3(a)) and a parabola

(see Figure 3(b)). To avoid exceptional case of this

theorem, these five points are selected in such a way

that no three collinear and no parallel lines can be

formed using these points. Point q

is the

intersection of line p

i+1

and line p

i-1

i+2

, and q

the intersection of p

i+2

and p

i-2

i+1

respectively.

Again, p

i-1

i-2

and q

must meet at point q

. The

expected tangent line of the conic at point p

obtained by connecting p

and

. Similarly, we can

get tangent line at point p

i+1

or other points. The

pseudo-code for tangent detection is described in

Figure 4.

(a) (b)

Figure 3: The construction of tangent on a point of the

conic sections using Pascal’s theorem. Tangents (p

) are

drawn on the point p

of (a) an ellipse and (b) a parabola.

Tangent (p

i-2

, p

i-1

, p

i+1

, p

i+2

)

// p

i-2

, p

i-1

, p

i+1

, p

i+2

are five

//points. Tangent will be constructed

//on point p

Begin

1. Find the intersecting point (q

)

between p

i+1

and p

i-1

i+2

2. Find the intersecting point (q

)

between p

i+2

and p

i-2

i+1

3. Find the intersecting point (q

)

between p

i-1

i-2

and q

4. Draw the tangent on p

connecting p

and q

End

Figure 4: Pseudocode of the proposed tangent detection

algorithm.

These tangents are then used to construct conic

part using the Pascal’s Theorem. In our method,

these five points are obtained from an edge segment

so that these points can divide it into four equal

parts. We follow this approach as it represents the

conic more accurately than the random sampling.

Now, another main contribution of this work to

construct conic parts is discussed here. To construct

a conic part, two tangent lines (t

and t

on x

i-1

and

i+1

respectively) and a point (x

) on the conic part

are required (see Figure 5). First, t

and t

intersect at

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

494

point y

. The Point z

is taken from line x

i+1

. The

intersection of y

and x

i-1

is y

. Connecting x

i-1

and x

i+1

, y

is crossing the conic at point y

. If z

moves from x

i+1

to y

(intersection of t

and x

i+1

the conic part x

i-1

i+1

will be constructed. Here, we

obtained points, x

i-1

, x

and x

i+1

from the two ends

and the midpoint of the edge segment. In this way,

we get rid of the influence of traditional construction

of tangent line on the unsmoothed digital curves.

The edge segments fitted with the corresponding

conic parts using LSF method with residual two

pixels are kept for further processing. Otherwise, the

edge segments are neglected.

(a) (b)

Figure 5: Conic part construction using two tangents and a

point on the conic (a) ellipse part construction and (b)

parabola part construction.

3.3 Detection of the Conics

Following the previous step, the obtained edge

segments are sorted according to their length in a

descending order. After selecting an edge segment

from the list, other edge neighboring fragments

satisfying the convexity constraints are grouped with

edge segment to form a conic. Here, we follow the

method applied by (Prasad et al. 2012). Consider e

and e

are two edge segments and P

and P

are the

midpoints obtained from two ends of e

and e

respectively (Figure 6). Suppose line P

intersects

(a) (b)

Figure 6: The condition of associated convexity (a) e1 an

e2 cannot be grouped together, (b) e1 and e2 can be

grouped together.

and e

at P'

and P'

respectively. The edge

segments e

and e

can be grouped if they satisfy the

following condition

2221

PPPPPPPP 

(3)

Here, the procedure to group segments to form a

conic section is presented. This is one of the key

contributions of this paper. Suppose, an edge

segment A

has two other edge segments

and C

) that satisfy the convexity

constraints (see Figure 7). These edge contours are

sorted based on the distance from the ends of the

edge segments A

. After that, tangents are

drawn on the midpoints of each segment as

discussed in subsection 3.2 (see Figure 7(a1) &

7(b1)). It is seen that C

is closer to A

than

. As a result, a conic part is constructed

according to subsection 3.2 shown in Figure 7(a2) &

7(b2). If the constructed conic part fits with the

and C

by LSF method with residual

two pixels, they are merged together. Next, another

segments B

is selected and the same procedure

is followed to connect two edge segments (see

Figure 7(a3) & 7(b3)).

(a1) (b1)

(a2) (b2)

(a3) (b3)

Figure 7: The procedure to merge the conic edge

segments as a part of an ellipse (a1-a3) and a parabola

(b1-b3).

After merging the groups of edge segments in to a

single curve C

, now, we need to verify whether this

curve is a conic matching the interested object.

ConicsDetectionMethodbasedonPascal'sTheorem

495

Hence, on this curve, five equally spaced points are

picked up in such a way that no three collinear and

no parallel lines can be formed using these points.

The points are selected from the curve at equally

distance as this approach presents the curve more

accurately. Based on Pascal Theorem, a conic C

can be constructed crossing these five points. The

difference D between the grouped curve C

and the

conic C

is calculated by least square distance. If D

is less than a predefined threshold, this curve C

identified as a valid conic shaped boundary of the

interested object.

Next, another edge segment is selected from the

list sorted in a descending order and the same

process is followed. The process mentioned in this

section will be iterated until there is no edge

segment to process.

4 RESULTS & DISCUSSION

We selected some images containing round shaped

objects from Caltech-256 database (Griffin et al.

2007) to evaluate the performance of the proposed

method and compared with the recently proposed

method for detecting the circle and ellipse known as

EDCircles method (Akinlar & Topal 2013). The

EDCircles uses two different LSF based methods for

detecting both circle and ellipse. In this method, the

least square fitting algorithm is applied for detecting

circle and direct least square fitting of ellipse is

implemented for ellipse detection from an image.

Four sample images and their comparison results

are shown in Figure 8. The first column (Figure

8(a1-a4)) shows four sample images. The results of

canny edge detector and the proposed method are

shown in the second and third column respectively.

The edge detection result obtained by EDPF is

Sample Image Canny Proposed Method EDPF EDCircles

(a1) (a2) (a3) (a4) (a5)

(b1) (b2) (b3) (b4) (b5)

(c1) (c2) (c3) (c4) (c5)

(d1) (d2) (d3) (d4) (d5)

Figure 8: Comparison results by the proposed method and EDCicles. First column (a1-d1) the sample image, secon

column (a2-d2) Canny edge detection, third column (a3-d3) the results obtained by the proposed method, forth column (a4-

d4) edge detection by EDPF and last column (a5-d5) the results obtained by EDCircles.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

496

presented in the forth column. The last column

represents the outputs of EDCircles method.

It can be seen from Figure 8(a3-d3) that our method

can detect both elliptical and parabolic shape.

Conversely, EDCircles detects only circular shape

and misses parabolic shape although their EDPF

method (Akinlar & Topal 2013) can detect the edge

representing the parabolic shape (see Figure 8(c4)

and 8(d4)). The reason is that circle and ellipse

detection methods are applied in EDCircles. As this

method does not apply any parabola detection

method, it cannot detect any parabolic shaped object

shown in Figure 8(c5) and 8(d5). Instead of using

several different methods for detecting different

conic shape, we use only a single procedure based

on Pascal’s theorem to detect any conic shaped

object (see Figure 8(a3-d3)).

It has been noted that the result of the proposed

method depends on the Canny edge detection

method. If edges of a conic shaped (such as, circle,

ellipse or parabola) object are not detected by Canny

edge detector, this method will fail to detect that

conic shaped object. Another drawback is that our

method completely depends on the conic edge

segments detected by subsection 3.1. If two different

conic segments merged such a way that there is no

sharp turn or inflection point exist, this method will

consider it as a non-conic edge segment. This

problem is also unsolved by other methods such as

(Prasad et al. 2012).

5 CONCLUSIONS

The proposed method can detect any type of conic

shaped object from the real image in a single

operation by constructing tangent, conic parts and

conic using Pascal’s theorem. The existing method

such as EDCircles (Akinlar & Topal 2013) uses

separate methods (least squares circle fit and direct

least square fitting of ellipses) for detecting different

type of conic sections. Another traditional method

for detecting conic sections is based on Hough

Transform. This method detects parameter for

detecting conic shape. For example, Hough

Transform constructs three-dimensional, five-

dimensional, four-dimensional parameter space for

detecting circle, ellipse and parabola respectively.

As a result, a single Hough Transform method

cannot be used to detect any type of conics. In future

work, we will compare other geometric shape based

methods and Pascal’s theorem based method to

detect the conic shaped objects.

REFERENCES

Akinlar, C. & Topal, C., 2013. EDCircles: A real-time

circle detector with a false detection control. Pattern

Recognition, 46(3), pp.725–740.

Alajlan, N. et al., 2007. Shape retrieval using triangle-area

representation and dynamic space warping. Pattern

Recognition, 40(7), pp.1911–1920.

Chia, A. & Rahardja, S., 2011. A split and merge based

ellipse detector with self-correcting capability. Image

Processing, IEEE Transaction on, 20(7), pp.1991–

2006.

Coxeter, H. & Greitzer, S., 1967. Geometry revisited,

Mathematical Association of America Washington,

DC.

Griffin, G., Holub, A. & Perona, P., 2007. Caltech-256

object category dataset.

Kovesi, P.D., 2000. MATLAB and Octave functions for

computer vision and image processing. Online:

http://www. csse. uwa. edu. au/~

pk/Research/MatlabFns/# match.

McLaughlin, R.A., 2000. Intelligent algorithms for finding

curves and surfaces in real world data, PhD Thesis,

Department of Electrical and Electronic Engineering,

University of Western Australia, 2000.

Prasad, D.K., Leung, M.K.H. & Cho, S.-Y., 2012. Edge

curvature and convexity based ellipse detection

method. Pattern Recognition, 45(9), pp.3204–3221.

Qiao, Y. & Ong, S.H., 2007. Arc-based evaluation and

detection of ellipses. Pattern recognition, 40(7),

pp.1990–2003.

Wong, C. & Lin, S., 2012. A survey on ellipse detection

methods. Industrial Electronics (ISIE), 2012 IEEE

International Symposium on, pp.1105–1110.

Xu, L., Oja, E. & Kultanen, P., 1990. A new curve

detection method: randomized Hough transform

(RHT). Pattern recognition letters, 11(5), pp.331–338.

ConicsDetectionMethodbasedonPascal'sTheorem

497