
Monte Carlo Tree Search in The Octagon Theory
Hugo Fernandes, Pedro Nogueira and Eug
´
enio Oliveira
LIACC, Faculty of Engineering of the University of Porto, Porto, Portugal
Keywords:
Monte Carlo Tree Search (MCTS), Upper Confidence Bounds for Trees (UCT), Monte Carlo Search, Artificial
Intelligence (AI), The Octagon Theory.
Abstract:
Monte Carlo Tree Search (MCTS) is a family of algorithms known by its performance in difficult problems
that cannot be targeted with the current technology using classical AI approaches. This paper discusses the
application of MCTS techniques in the fixed-length game The Octagon Theory, comparing various policies
and enhancements with the best known greedy approach and standard Monte Carlo Search. The experiments
reveal that the usage of Move Groups, Decisive Moves, Upper Confidence Bounds for Trees (UCT) and Limited
Simulation Lengths turn a losing MCTS agent into the best performing one in a domain with estimated game-
tree complexity of 10
293
, even when the provided computational budget is kept low.
1 INTRODUCTION
Board games present a simple and entertaining mean
of competition between opponents, focused solely on
the intelligence and decision making capability of
their intervenients when confronted with players of
different characteristics and playing levels. In light
of this, most work done regarding game-theory was
accomplished on deterministic board games (Allis,
1994). The main advantage in using these games as
a test-bed for decision making research is that board
games provide a wide complexity range, facilitating
the comparison of approaches across different do-
mains of varying complexity classes (Papadimitriou,
1994). Although many games, such as Chess, can be
targeted with the current technology using classical
AI approaches (Allis, 1994), higher complexity ones,
such as Go (M
¨
uller, 2002), cannot.
With the breakthrough of Monte Carlo Tree
Search (MCTS) (Cazenave and Helmstetter, 2005),
the main focus of research in the field of game the-
ory moved from the already approachable games to
higher complexity ones, as new solution perspectives
emerged (Kroeker, 2011).
Over the last few years, research in this field has
greatly expanded and MCTS has been successfully
applied to various non-traditional games featuring dif-
ferent characteristics, such as modern single player
games (Schadd, 2009), multi-player games (Nijssen
and Winands, 2011), real-time games (Den Teuling,
2011) and non-deterministic games (Ponsen et al.,
2010). Moreover, MCTS has also been applied in
various non-game related domains such as planning
(Silver and Veness, 2010), scheduling (Silver and Ve-
ness, 2010) and optimization (Rimmel et al., 2011)
problems. However, most of MCTS research is still
focused on deterministic board games with unknown
game lengths, such as Go. While improvements are
still being constantly proposed in this domain, the
fact that many of them are domain-dependent allied
to the large difference in length of the problems be-
ing solved has been inciting research in other domains
where specific domain knowledge is not so relevant
and the length of the problem is kept consistent, as the
effectiveness and comparison of different approaches
becomes simpler and clearer.
The Octagon Theory (TOT) is a deterministic two-
player board game that falls in the previously men-
tioned conditions. The consistent length of the prob-
lem, simple rules, and complex board configuration,
turn TOT into an interesting challenge for AI and
a promising test-bed for comparison between algo-
rithms. This paper presents the results of a com-
parison of MCTS methods with the current approach
used by the best known solvers, using standard Monte
Carlo search as a baseline. For the MCTS solver, vari-
ous policies and enhancements found in the literature
were considered, and the effectiveness of such poli-
cies in each sub-step of the algorithm is discussed.
The remainder of this paper begins with an in-
troduction to the game of TOT and its complexity
in Section 2, followed by an overview of the MCTS
328
Fernandes H., Nogueira P. and Oliveira E..
Monte Carlo Tree Search in The Octagon Theory.
DOI: 10.5220/0004757603280335
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 328-335
ISBN: 978-989-758-015-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Large version of the board in The Octagon The-
ory.
algorithm and its considered variations in Section 3.
Section 4 presents the obtained experimental results,
while Section 5 summarizes the conclusions of this
research.
2 THE OCTAGON THEORY
In this Section, the game The Octagon Theory is first
presented, followed by an analysis and comparison of
its state-space and game-tree complexities. Finally,
previous work done in this game context is discussed
and domain-specific knowledge found in this research
is demonstrated.
2.1 Game Description
The Octagon Theory (TOT) is a deterministic two-
player board game available for iOS and Web. TOT is
a turn-based pushing game in which two players fight
for the control of an octagonal board by pushing their
opponents’ pieces off the edges of the board, by us-
ing a limited selection of pieces over a predetermined
number of turns. The winner of the game is the player
who has more pieces on the board after all turns have
been played. If both players have the same amount of
pieces, the game ends in a tie.
Although TOT can be played in boards of three
different sizes, the only changes in the rules related to
the size of the board are the starting amount of pieces
per player and the number of turns to be disputed until
the game ends. The larger version of the board, used
as focus of this research, is presented in Fig. 1.
Each player has four different kinds of pieces with
increasing pushing capabilities. The four pieces and
their respective starting amounts for the large version
of the board are presented in Fig. 2. Each piece is
represented as an octagon and contains one or more
straight lines from the center to the edges, representa-
tive of the piece’s pushing capabilities. When a piece
is placed on the board in any of the eight possible ori-
entations (achieved by rotating the piece), any oppo-
nent pieces in neighbour positions pointed at by the
Figure 2: Starting amounts of pieces per player in The Oc-
tagon Theory.
Figure 3: Example of the pushing and cannoning processes
after placement of an 8-piece in The Octagon Theory.
placed piece are pushed back one position, provided
the positions behind them are free or off the board. If
a pushed piece does not have a free position behind it,
the push occurs on the last piece of the stack of pieces,
as long as all pieces belong to the player whose piece
is being pushed. This kind of push is referred to as
cannoning. An example of the pushing and cannon-
ing processes that occur after placement of an 8-piece
(i.e. a piece with 8 pushing directions) on a board is
shown in Fig. 3.
2.2 Complexity
In order to gain some insight on which approaches
should be explored in a TOT game-playing scenario, a
study on both the state-space and game-tree complex-
ity of the three versions of the board was conducted.
2.2.1 State-space Complexity
The state-space complexity of a game represents the
number of legal game states reachable from the initial
one. In TOT, the initial game state is an empty board.
As the game is played between two players P1 and
P2, each position of the board can be in one of three
different states: occupied by a P1 piece, occupied by
a P2 piece, or empty. Thus, for a given board with N
positions, the state-space (SS) is given by:
SS = 3
N
(1)
As shown in Table 1, the state-space complexity
of the large board version of TOT is similar to the
one of Chess. As such, finding equivalent board-states
throughout the game is very uncommon, turning state
detection and classification into an impractical prob-
lem with the current technology (Allis, 1994).
MonteCarloTreeSearchinTheOctagonTheory
329
0
20
40
60
80
100
120
140
160
180
200
1
5
9
13
17
21
25
29
33
37
41
45
49
53
57
61
65
69
Unique moves
Turn number
Large
Medium
Small
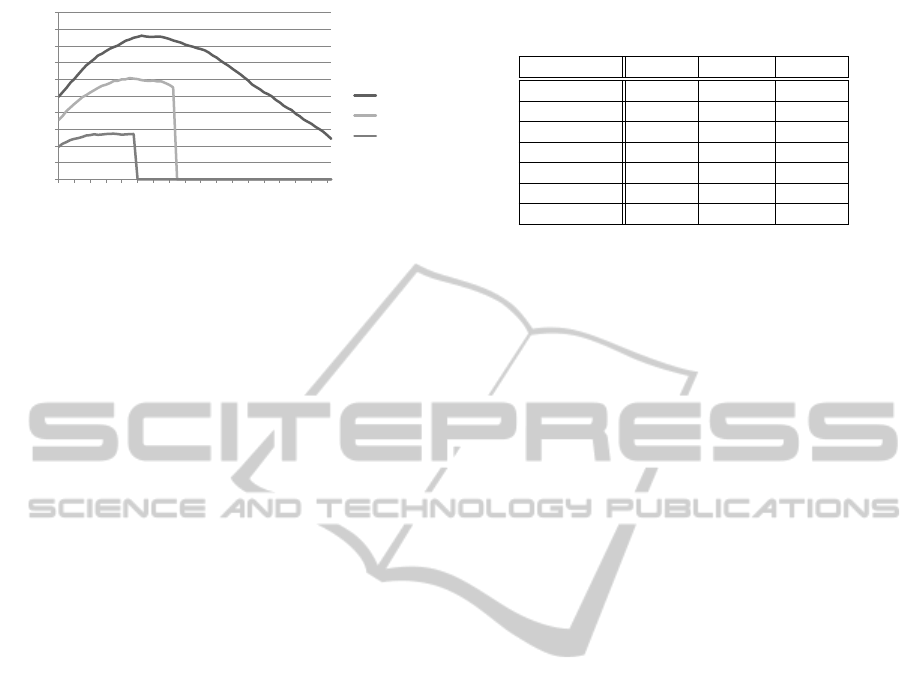
Figure 4: Average number of unique moves per turn after
100,000 simulations in the various boards of The Octagon
Theory.
2.2.2 Game-tree Complexity
The game-tree complexity of a game represents the
number of nodes that need to be visited to determine
the value of the initial game position through a full-
width tree search (Allis, 1994). A full-width game
tree considers all the reachable nodes in any depth
level.
Since TOT is a fixed-length game, the average
game length is easily defined according to the used
version of the board. However, the rules of the game,
namely pushing, cause the branching factor to vary
throughout the game, as the strategy of both players
influences the number of possible moves in each turn.
With this in mind, the game-tree complexity of TOT
was estimated through a set of 100,000 simulated
games between pseudo-random players (i.e. players
that randomly bias their move selections) on each ver-
sion of the board. In each simulation, the number of
unique moves (i.e. moves that leave the board in a
unique state) per turn were recorded. The remaining
(non-unique) moves were not considered in order to
prevent an artificial increase of the problem complex-
ity. The results of these simulations are displayed in
Fig. 4.
As shown in Fig. 4, the branching factor initially
grows in every version of the board, as more pieces
emerge, leading to a higher amount of unique moves
(e.g. by pushing a single piece in eight possible di-
rections). However, while the branching factor stabi-
lizes on the smaller versions of the board, as the board
fills up and pieces start being pushed off more often,
the larger version of the board suffers a decrease in
unique moves as the game approaches the end. This
decrease derives from the fact that the number of turns
disputed on the large version of the board is much
higher than on the lower versions (70 versus 20 in the
smaller version and 30 on the medium one), causing
a large amount of pieces to be blocked from further
pushes as more pieces start being stacked together.
Table 1: State-space and game-tree complexity comparison
of The Octagon Theory with other popular games.
Game name Board size State-space Game-tree
Go (19x19) 361 10
171
10
360
TOT (large) 96 10
46
10
293
Chess 64 10
47
10
123
TOT (medium) 68 10
33
10
121
Hex (11x11) 121 10
57
10
98
TOT (small) 36 10
17
10
69
Checkers 32 10
20
10
31
2.2.3 Comparison with other Popular Games
With the state-space and game-tree complexity re-
sults, the positioning of TOT in relation to other well-
known games found in the literature can be estimated.
This comparison, ordered by game-tree complexity,
is presented in Table 1. As shown in this table, the
game-tree complexity of the large board version of
TOT is located in the upper range limit of complex-
ities found in the literature, suggesting it belongs in
the complexity class EXPTIME-Complete (Papadim-
itriou, 1994).
2.3 Previous Work
At this point in time, all known agents capable of
playing TOT follow the same greedy approach, based
on the official AI included in the TOT AI modders kit
described in (richardk, 2012). This approach essen-
tially consists in evaluating game states by crossing
a weight matrix with each players pieces, selecting
moves that lead to the maximum positional gain (or
minimum loss) over the opponent in each turn. As
such, for a given board-state (B), the chosen move is
the move that satisfies the following condition:
Π
B
= argmax
x∈[1,n],y∈[1,n], p∈[1,4],o∈[1,8]
[ f
W
(B + a
x,y, p,o
) − f
W
(B)],
(2)
where n is the width/height of the board, a is the
resulting action of placing a piece (p) with orientation
(o) in a position of the board (x, y) and f is the evalu-
ation function (i.e. the function that crosses a weight
matrix (W) with a specific board-state). Despite its
simplicity, the highest level AI (i.e. the AI with the
best tuned W matrix found) is capable of defeating
most human players.
3 MONTE CARLO TREE
SEARCH
In this Section, the basic Monte Carlo Tree Search al-
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
330

gorithm is first described and its main steps are intro-
duced. Afterward, the enhancements applied in each
policy are identified and their usage on the context of
TOT is discussed.
3.1 Overview
Monte Carlo Tree Search (MCTS) (Cazenave and
Helmstetter, 2005) is a product of the integration of
Monte Carlo search methods with tree search meth-
ods. Therefore, MCTS is a best-first search algorithm
that creates and asymmetrically expands a game tree
based on the outcome of random simulations. Once
enough samples have been drawn, a decision is made
based on the estimated values of the tree nodes. As
such, the effectiveness of MCTS algorithms is greatly
dependent on the overall accuracy of these nodes, be-
ing higher as coverage of the tree increases (e.g. by
increasing the number of performed iterations until a
decision is made).
The basic MCTS algorithm is divided in four dif-
ferent sequential steps (Chaslot et al., 2008):
1. Selection: Select an expandable node of the tree
to explore.
2. Expansion: Expand the selected node by adding
one or more child nodes to it and select a child
node.
3. Simulation: Randomly simulate a game starting
at the selected node until an ending condition is
found.
4. Back-propagation: Back-propagate the result
across the path followed on the tree.
These steps run continuously, for as long as they
are allowed to, building and updating the nodes and
edges of the tree that is ultimately used for the final
selection of the action to perform.
3.2 Selection
The child selection policy controls the balance be-
tween exploration and exploitation (Rejeb et al.,
2005). Exploration consists in selecting nodes with
previously found bad scores to explore, possibly turn-
ing the bad scores into more favorable ones. Exploita-
tion consists in selecting nodes with promising scores,
in order to approximate their score to the actual value
and increase the confidence of performing such ac-
tions. Balancing exploration and exploitation is a cru-
cial task, as the score of a node is only as good as the
process that led to it.
In this study, the considered selection policy en-
hancements were move groups, decisive moves and
1 2 3 2 1
4 5 6 7 6 5 4
8 9 10 11
12 13 14
15 16
10 9 84 4
1 2 3 2 1
4 5 6 7 6 5 4
8 9 10 11 10 9 84
13 12
15
15
15
16
16
16
12 13 14 13 12
1
1
1
1
2
2
3
2
2
3
55
5 5
6
6
7
6
6
7
10
10
11
10
10
11
13
13
14
13
13
14
9 9
9 9
4
Figure 5: Symmetric positions on the large version of the
board of The Octagon Theory.
upper confidence bounds for trees. As a baseline pol-
icy, a random selection policy (i.e. a policy that ran-
domly selects child nodes for exploration) was also
considered.
3.2.1 Move Groups
Childs et al. (Childs et al., 2008) proposed the defi-
nition of move groups when selecting nodes in a tree.
The idea behind move groups is that if not all nodes
correspond to different moves (i.e. moves leading to
different outcomes), they should be grouped together.
In TOT, every version of the board resembles an
octagon (i.e. a regular polygon with eight sides).
While the small version of the board is a regular oc-
tagon (i.e. an octagon with eight lines of reflective
symmetry and rotational symmetry of eighth order),
the remaining board versions are irregular octagons of
equivalent opposite side lengths and rotational sym-
metry of fourth order. Thus, on the larger version of
the board, the 96 positions can be defined from a pool
of only 16 different ones, as shown on Fig. 5.
3.2.2 Decisive Moves
As the selection policy is the process in charge of
selecting what nodes should be explored, it is also
the process in charge of finding decisive moves (i.e.
moves that end the game) and anti-decisive moves
(i.e. moves that prevent the opponent from ending the
game) (Teytaud and Teytaud, 2010). Although these
moves can be found using pure sampling techniques
(Browne et al., 2012), doing so might contradict the
default selection policy. As such, decisive move anal-
ysis can be performed before the default selection pol-
icy is applied, at the cost of computational time.
In the case of fixed-length games, such as TOT,
nodes of the tree representing decisive moves are all
at the same level. As such, once the game reaches a
certain point in time, fully determining winning se-
quences (i.e. sequences of moves that lead to decisive
moves regardless of the opponent’s moves) and losing
MonteCarloTreeSearchinTheOctagonTheory
331

sequences might be possible within the given compu-
tational budget, effectively replacing the standard se-
lection policy until the end of the game.
3.2.3 Upper Confidence Bounds for Trees
Upper Confidence Bounds for Trees (UCT) is cur-
rently the most popular selection policy among
MCTS implementations found in the literature. UCT
was proposed by Kocsis et al. (Kocsis et al., 2006),
as a MCTS method that uses an Upper Confidence
Bound function (UCB1) as its default selection pol-
icy. As such, UCT essentially turns the node selection
problem into a Multi-armed bandit problem, in which
each starting move is a slot machine with a limited
amount of money (i.e. wins) and an unknown distri-
bution for returning it (i.e. win ratio).
In a typical UCT strategy, the value of the nodes
begins by being calculated according to the default
selection policy (Coulom, 2007). Once the number
of visits of a node crosses a predefined threshold, the
calculation of its value swaps to a UCB1 based func-
tion. For a given set of child nodes reachable from a
parent node j, the selected child node is the node i that
maximizes the following equation:
UCT = X
i
+C
s
lnn
j
n
i
, (3)
where X
i
is the normalized average reward of node
i, n
j
is the visit count for node j, n
i
the visit count
for node i and C is a positive constant. If more than
one child node have the same UCT value, the win-
ner is usually selected randomly. The constant C is
the exploration constant, and can be adjusted to in-
crease - or decrease - the ratio between exploration
and exploitation. Although a starting value of C = 2
is suggested in the literature, this parameter is typi-
cally experimentally tuned (Browne et al., 2012), as
the optimal value is largely dependent on the domain,
computational budget and the MCTS implementation.
3.3 Expansion
The only varying factor between implementations
found in the literature regarding expansion policies is
the number of child nodes to be added per expansion.
However, this number typically varies according to
the domain and computational budget, ranging from
a single expansion (i.e. adding one single node) to a
full expansion (i.e. adding every possible node).
Out of all the games recorded between the best
performing agents, over 95% of the moves (exclud-
ing the initial one) were pushes and kills (i.e. pushes
that throw a piece off the board), while the amount
of pieces placed in positions with no neighbouring
pieces (here referred to as free moves) represent less
than 1% of the total recorded moves. In light of this,
an expansion policy here referred to as move abstrac-
tion was also experimented with. When using this
policy, only one free move per symmetric board po-
sition (Fig. 5) is considered during expansion.
3.4 Simulation
The default simulation policy in MCTS is the same
as in regular Monte Carlo approaches: random sam-
pling. The main advantage of this approach, besides
is that since it is simple and domain independent,
its time complexity is inherently lower than domain
knowledge based policies.
When dealing with domains with large branching
factors such as TOT, the length of the simulations (i.e.
the number of nodes traversed until an end-game con-
dition is met) may be too high to ensure sufficient cov-
erage of the game tree in limited thinking times. Since
low game tree coverage leads to less-informed deci-
sions, the length of the simulations can be artificially
reduced to boost the number of performed iterations.
In TOT, for a given turn (n) of a game played on a
board size with a number of turns (T
f
) as its game-
ending condition, the artificial ending turn (T
a
) for a
limited simulation length (L) is given by:
T
a
= min(T
f
, T
n
+ L). (4)
3.5 Back-propagation
TOT is a zero-sum game with no added bonus on
heavier wins (i.e. wins by a larger margin). As such,
the chosen back-propagation policy was a simple dis-
crete function with V = {-1, 0, 1} for {losses, ties,
wins}, as suggested in the literature (Browne et al.,
2012).
3.6 Final Selection
Final selection is the process responsible for deter-
mining which move should be chosen once a decision
has to be made. Four different criteria were found for
this selection (Schadd, 2009):
• Max child: Select the root child node that pro-
duces the highest reward value.
• Robust child: Select the node with the highest
visit count.
• Max-Robust child: Select the node with both the
highest value and visit count. If no such node
exists, resume the search process until a suitable
node is found (Coulom, 2007).
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
332

• Secure child: Select the node representing the
lowest risk for the player.
As this research is focused on a domain with lim-
ited thinking time (as most games are), the Max-
Robust child criteria cannot be successfully applied
without budgeting additional thinking time for addi-
tional search rounds. In light of this, only the remain-
ing three criteria were considered.
4 EXPERIMENTS
This Section presents and discusses the experimental
results obtained during this study.
4.1 Experimental Setup
The following results were obtained on a single 3.4
GHz processor, with a limited maximum heap size of
8192 MB.
For every experiment, 100 test games were con-
ducted between each pair of agents under comparison.
Out of these games, each agent played 50 of them as
player 1 and 50 as player 2. In order to keep the re-
sults consistent with the literature, the computational
budget was defined as the time required by a standard
MCTS agent to perform 20,000 iterations per move
on average throughout the course of a game. As such,
the standard thinking time was set to 3 seconds on the
machine used for the experiments. This thinking time
led to 7 minute games, ensuring enough experiments
could be performed in a realistic time-span.
4.2 Parameter Tuning and Policy
Selection
This Subsection presents and discusses the performed
experiments for electing and tuning the researched
policies.
4.2.1 UCT
As mentioned in Subsection 3.2, the exploration con-
stant C is typically experimentally tuned for the do-
main, and a starting value of C = 2 is suggested in
the literature. Furthermore, it has been observed that
decreasing this value (i.e. favoring exploitation) typ-
ically leads to better performance in domains with
larger branching factors, while increasing it (i.e. fa-
voring exploration) enhances performance in lower
complexity ones (Browne et al., 2012).
Table 2 shows the win, loss and tie rates for dif-
ferent values of C against a baseline UCT agent with
Table 2: UCT parameter tuning.
C 0.2 0.4 0.6 0.8 1.0 1.5 2.5 3.0 4.0
Win 25% 40% 40% 38% 46% 26% 35% 26% 22%
Loss 30% 30% 27% 29% 27% 44% 40% 41% 53%
Tie 45% 30% 33% 33% 27% 30% 25% 33% 25%
equal exploration-exploitation ratio (C = 2). As seen
from the results, the importance of exploitation was
found to be higher than that of exploration. The
best found value for C was 1.0, winning 46% of the
matches against the baseline agent, which was only
able to win 27% of the matches. However, it is worth
noting that values in the [0.4, 0.8] range also obtained
promising results and could prove to be more efficient
when facing different opponents (versus the baseline
agent).
4.2.2 Limited Simulation Length
The simulation length parameter (L), described in
Subsection 3.4 was tuned by following a similar pro-
cess to the one used for tuning the UCT agent, albeit
with the regular thinking time of 3 seconds per move
(versus a number of fixed iterations).
When using the larger version of the board, TOT
is played over 70 turns (i.e. 140 moves). As such, a
regular MCTS agent has to traverse a maximum num-
ber of 140 tree nodes to reach the end of the game.
However, this number linearly decreases as the game
progresses. In light of this, different agents for every
L∈[100, 10] in increments of 10 were paired against
their limit-free counterpart.
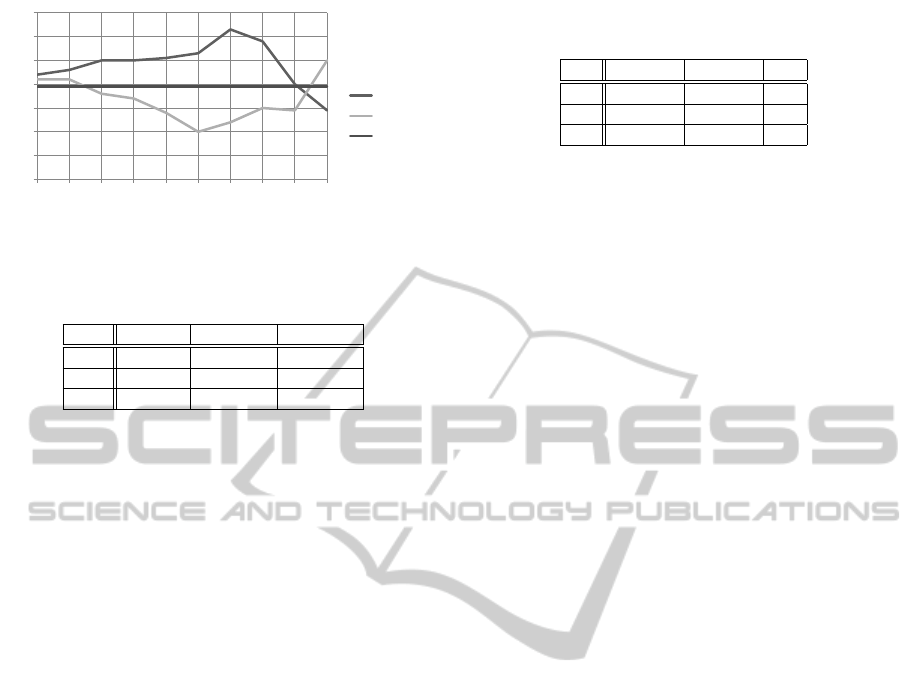
As shown in Fig. 6, the best found value for L
was 40, winning 63% of the matches against its un-
limited version. An interesting observation is the fact
that while the win rate of the limited length agent
rises steadily over the [100, 50] interval, it suffers a
large performance loss right after peaking, reaching
lower win rates and higher loss rates than the regu-
lar agent. This sudden decrease suggests that limiting
the length of the simulations too much leads to an es-
sentially greedy behavior, causing the limited agent to
lose considerably more often despite making more in-
formed decisions regarding what it considers the end
of the game.
4.2.3 Final Selection
The final selection policy, described in Subsection
3.6, was tested by performing a round-robin between
the three mentioned criteria. As shown in Table 3,
Max Child was found to be the best of the three tested
criteria, winning 43% of the matches. Although Se-
cure Child presented the worst results, it was capable
of forcing over 50% of the matches to end in a tie.
MonteCarloTreeSearchinTheOctagonTheory
333
0%
10%
20%
30%
40%
50%
60%
70%
100
90
80
70
60
50
40
30
20
10
Simulation Length Limit
Win Rate
Loss Rate
Baseline
Figure 6: Limited Simulation Length parameter tuning.
Table 3: Results of a round-robin of 100 rounds played be-
tween three differenet final selection criteria.
Policy Max Child Robust Child Secure Child
Win 43.0% 26.0% 10.5%
Loss 16.5% 28.5% 34.5%
Tie 40.5% 45.5% 55.0%
This outcome suggests that using a hybrid final selec-
tion policy could prove to be an interesting strategy
(e.g. by using one criteria to gain an advantage and a
different one to hold it).
4.2.4 Decisive Moves
For the established thinking time of 3 seconds per
move, the implemented MCTS agent is capable of
fully exploring the game tree once its length is equal
or less than 3, as long as the branching factor stays
below 88 on the last 3 moves (on the tested ma-
chine). With this in mind, a standard MCTS agent
was matched against an agent that uses the same se-
lection policy as its opponent until the last 3 moves
of the game, switching to a pure decisive move policy
afterward, as long as the number of unique moves at
that point is lower than 88.
Unlike every other experiment, the test games for
this experiment were started at turn 50 on board-states
obtained from standard MCTS mirror matches (i.e.
matches between the same agent) that led to a tie.
This process was chosen as restricting the number
of turns allows the results to be focused on the lat-
est portion of the game, removing unnecessary noise
that could otherwise exist (e.g. bad openings that con-
demned the entire match).
As shown in Table 4, the addition of decisive
moves was found to improve the performance of the
agent when playing as player 2. Although the sec-
ond player does have an advantage over the first one
when playing a full game, as the first move of the
game is the only move in the entire game that is not a
counter-move, this advantage is diminished by start-
ing the games at later stages when the board is no
longer empty. The fact that the player does not bene-
fit from the addition of decisive moves when playing
Table 4: Results of 100 games of a hybrid MCTS agent with
decisive moves against a standard MCTS agent.
As Player 1 As Player 2 Total
Win 32% 78% 55%
Loss 38% 10% 24%
Tie 30% 12% 21%
as player 1 suggests that one single move (versus two
moves as player 2) is not enough to make a difference
at the end of the game. However, the positive results
as player 2 suggest that both players should benefit
from the addition of decisive moves as the computa-
tional budget increases.
4.3 Results
Once the parameters were tuned and the policies cho-
sen, a round-robin with 100 rounds was conducted be-
tween the best found agents in each approach. For this
experiment, the best known Greedy approach, stan-
dard Monte Carlo search (MC) and standard MCTS
were included as baseline agents. For both Monte
Carlo versions, agents with an added L adhere to the
Limited Simulation Length policy, while agents with
added MG make use of the Move Groups algorithm in
both the selection and expansion phases, as described
in Section 3. Furthermore, every agent uses a Max
Child Policy and Decisive Moves. The agent UCT-
L-MG considers every enhancement discussed in this
paper. The results of the round-robin are presented in
Table 5.
As shown in this experiment, both UCT versions
were able to surpass the best known greedy approach,
even with the limited thinking time of 3 seconds. The
addition of move groups also proved to be worthy, as
it was able to improve every agent even further, espe-
cially in the case of UCT. From the results, it is also
clear that standard MCTS and Monte Carlo search
(i.e. with no limits on the length of the simulations)
perform poorly for the given thinking time. However,
the simple addition of an artificial limit and a UCB1
selection policy (i.e. UCT) greatly increase the per-
formance of MCTS.
5 CONCLUSIONS AND FUTURE
RESEARCH
This paper presented a research on various MCTS
policies and enhancements applied to the game
The Octagon Theory: a game of fixed-length and
high game-tree complexity (10
293
), suitable for clear
comparisons between different problem solving ap-
proaches. For the MCTS solver, the considered poli-
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
334

Table 5: Win rate of the various agents after a round-robin of 100 rounds.
Agent UCT-L-MG UCT-L Greedy MCTS-L-MG MC-L-MG MC-L MCTS-L MCTS MC Average win rate
UCT-L-MG - 51% 75% 55% 55% 61% 57% 87% 92% 66.625%
UCT-L 26% - 69% 53% 58% 60% 52% 82% 85% 60.625%
Greedy 10% 14% - 55% 45% 61% 53% 78% 75% 48.875%
MCTS-L-MG 20% 32% 30% - 38% 41% 48% 55% 61% 40.625%
MC-L-MG 7% 29% 30% 36% - 42% 38% 50% 54% 35.750%
MC-L 11% 24% 22% 38% 38% - 36% 50% 57% 34.500%
MCTS-L 17% 26% 24% 40% 25% 25% - 48% 63% 33.500%
MCTS 0% 0% 0% 14% 12% 10% 18% - 42% 12.000%
MC 0% 0% 0% 16% 9% 12% 17% 38% - 11.500%
cies and enhancements included Move Groups, De-
cisive Moves, Upper Confidence Bounds for Trees
(UCT), Limited Simulation Lengths, Max Child Se-
lection, Robust Child Selection and Secure Child Se-
lection.
Although the described approach was able to turn
a losing MCTS agent into the best performing one,
there is still a clear dependency on enhancements that
aid the agent in the starting moments of the game, as
the number of performed iterations per turn is lower
and the branching factor keeps increasing. This sug-
gests that the attribution of a game-based computa-
tional budget could lead to an interesting challenge.
Under these rules, the player would not only face a
game theory problem, but also a resource allocation
task when determining which moves should be priori-
tized (i.e. given more thinking time) during the course
of the game.
REFERENCES
Allis, V. L. (1994). Searching for Solutions in Games and
Artificial Intelligence. PhD thesis, University of Lim-
burg.
Browne, C., Powley, E., Whitehouse, D., Lucas, S., Cowl-
ing, P., Rohlfshagen, P., Tavener, S., Perez, D.,
Samothrakis, S., and Colton, S. (2012). A survey of
monte carlo tree search methods. Computational In-
telligence and AI in Games, IEEE Transactions on,
4(1):1–43.
Cazenave, T. and Helmstetter, B. (2005). Combining tacti-
cal search and monte-carlo in the game of go. In IN:
CIG05, pages 171–175.
Chaslot, G., Bakkes, S., Szita, I., and Spronck, P. (2008).
Monte-carlo tree search: A new framework for game
ai. In Darken, C. and Mateas, M., editors, AIIDE. The
AAAI Press.
Childs, B., Brodeur, J., and Kocsis, L. (2008). Transpo-
sitions and move groups in monte carlo tree search.
In Computational Intelligence and Games, 2008. CIG
’08. IEEE Symposium On, pages 389 –395.
Coulom, R. (2007). Efficient selectivity and backup op-
erators in monte-carlo tree search. In Proceedings
of the 5th international conference on Computers
and games, CG’06, pages 72–83, Berlin, Heidelberg.
Springer-Verlag.
Den Teuling, N. (2011). Monte-carlo tree search for the
simultaneous move game tron. Univ. Maastricht,
Netherlands, Tech. Rep.
Kocsis, L., Szepesv
´
ari, C., and Willemson, J. (2006). Im-
proved monte-carlo search. Univ. Tartu, Estonia, Tech.
Rep, 1.
Kroeker, K. L. (2011). A new benchmark for artificial in-
telligence. Commun. ACM, 54(8):13–15.
M
¨
uller, M. (2002). Computer go. Artificial Intelligence,
134(1):145–179.
Nijssen, J. and Winands, M. (2011). Enhancements for
multi-player monte-carlo tree search. Computers and
Games, pages 238–249.
Papadimitriou, C. M. (1994). Computational complexity.
Addison-Wesley, Reading, Massachusetts.
Ponsen, M., Gerritsen, G., and Chaslot, G. (2010). Inte-
grating opponent models with monte-carlo tree search
in poker. In Proc. Conf. Assoc. Adv. Artif. Intell.: In-
ter. Decis. Theory Game Theory Workshop, Atlanta,
Georgia, pages 37–42.
Rejeb, L., Guessoum, Z., and MHallah, R. (2005).
The exploration-exploitation dilemma for adaptive
agents. In Proceedings of the 5th European Work-
shop on Adaptive Agents and Multi-Agent Systems
(AAMAS05). Citeseer.
richardk (2012). The ai in the octagon theory. url:
http://aigamedev.com/open/interview/the-octagon-
theory/ (last visited on 2013-05-16).
Rimmel, A., Teytaud, F., and Cazenave, T. (2011). Opti-
mization of the nested monte-carlo algorithm on the
traveling salesman problem with time windows. Ap-
plications of Evolutionary Computation, pages 501–
510.
Schadd, F. C. (2009). Monte-carlo search techniques in the
modern board game thurn and taxis. Master’s thesis,
Department of Computer Science, Maastricht Univer-
sity.
Silver, D. and Veness, J. (2010). Monte-carlo planning in
large pomdps. Advances in Neural Information Pro-
cessing Systems (NIPS), 46.
Teytaud, F. and Teytaud, O. (2010). On the huge bene-
fit of decisive moves in monte-carlo tree search al-
gorithms. In Computational Intelligence and Games
(CIG), 2010 IEEE Symposium on, pages 359 –364.
MonteCarloTreeSearchinTheOctagonTheory
335
