Qualitative Analysis of Gene Regulatory Networks using Network Motifs
Sohei Ito
1
, Takuma Ichinose
2
, Masaya Shimakawa
2
, Naoko Izumi
3
, Shigeki Hagihara
2
and Naoki Yonzezaki
2
1
Department of Computer Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo, Japan
2
Department of Computer Science, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo, Japan
3
The Department of Social and Information Sciences, Jumonji University, 2-1-28 Sugasawa, Niiza, Saitama, Japan
Keywords:
Gene Regulatory Network, Temporal Logic, Formal Methods, Network Motif.
Abstract:
We developed a method for analysing gene regulatory networks in a purely qualitative fashion. Behaviours
of networks are captured as transition systems using propositions for gene states (ON or OFF), and those
related to threshold values for gene activation/inhibition. Possible behaviours of networks are specified by
logical formulae in Linear Temporal Logic (LTL). With this specification, it is possible to check whether
some/all behaviours satisfy a biological property, which is difficult for quantitative analyses like an ordinary
differential equation approach. Our method uses satisfiability checking of LTL. Due to the complexity of LTL
satisfiability checking, analyses of large networks are generally intractable in this method. To tackle this issue,
in this paper, we propose approximate analysis method in which we specify behaviours in simpler formulae
which compress/expand the possible behaviours of networks. We present approximate specifications for some
network patterns called network motifs.
1 INTRODUCTION
In the analysis of gene regulatory networks, we have
to consider various possible behaviours that are de-
pendent on initial conditions, scenarios of external in-
puts, and settings of parameters. Quantitative meth-
ods, such as numerical simulations based on ordinary
differential equations, are not suitable for analysing
all possible behaviours. To overcome this problem,
we developed a qualitative method for analysing all
possible behaviours of gene regulatory networks, by
focusing on essential qualitative features (Ito et al.,
2010). Qualitative approaches are useful when we do
not have precise kinetic parameters but are interested
in checking some qualitative property, e.g. is a certain
gene oscillates? If such property is computationally
possible, biologists are motivated to check whether
the property is really observed.
In our method, behaviours are captured as transi-
tion systems using propositions for gene states (ON or
OFF), and for threshold on gene activation and inhibi-
tion. We characterise possible behaviours of networks
by specifying changes in concentration levels of gene
products and changes in gene states using linear tem-
poral logic (LTL). The constraints are intended to co-
ver all possible behaviours of networks. Expected bi-
ological properties such as reachability, stability and
oscillation are also described in LTL. We check satis-
fiability of these formulae to investigate whether some
or all behaviours satisfy the corresponding biological
property.
Our method depends on satisfiability checking of
LTL. The complexity of this problem is PSPACE-
complete (Sistla and Clarke, 1985), and known algo-
rithms have exponential time complexity with respect
to the length of an input formula. The length of a for-
mula specifying possible behaviours of a network is
proportional to the size of the network in our method,
and thus analyses of large networks are generally in-
tractable.
In this paper, we developed approximate analy-
sis method to enable analysis of large networks in
our framework. We approximate the set of possible
behaviours by simple specifications. It is not trivial
to find approximate specifications for any network.
Thus we consider some common network patterns
which can be used for many gene networks and give
approximate specifications for them. Network motifs
are such common patterns in gene networks (Alon,
2007). The motifs we study in this paper are neg-
15
Ito S., Ichinose T., Shimakawa M., Izumi N., Hagihara S. and Yonezaki N..
Qualitative Analysis of Gene Regulatory Networks using Network Motifs.
DOI: 10.5220/0004188400150024
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2013), pages 15-24
ISBN: 978-989-8565-35-8
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

ative auto-regulation, coherent type 1 feed-forward
loops, incoherent type 1 feed-forward loops, single-
input modules and multi-output feed-forward loops.
This paper is organised as follows. Section 2 in-
troduces the logical structure which describes abstract
behaviours of gene regulatory networks. In Section
3, we show how networks are qualitatively analysed
by satisfiability checking of LTL and demonstrate our
method by analysing a gene regulatory network for
mucus production in Pseudomonas aeruginosa. Most
part of section 2 and 3 is based on our previous work
(Ito et al., 2010), but we modify some behaviour de-
scriptions and introduce two manners in behaviour
descriptions. In Section 4, we present the approxi-
mate analysis method and show some experimental
results. In Section 5, we compare our method to
other qualitative analysis methods of biological sys-
tems. The final section offers some conclusions and
discusses future directions.
2 LOGICAL
CONCEPTUALISATION OF
BEHAVIOURS
In gene regulation, a regulator is often inefficient be-
low a threshold concentration, and its effect rapidly
increases above this threshold (Thomas and Kauff-
man, 2001). The sigmoid nature of gene regulation is
shown in Fig. 1, where gene u activates v and inhibits
w. Each axis represents the concentration of products
for each gene.
u
w
u
v
u
v
u
w
Figure 1: Regulation effect.
Important landmark concentration values for u
are, 1) the level u
v
at which u begins to affect v, and 2)
the level u
w
at which u begins to affect w. In this case,
whether genes are active or not can be specified by the
expression levels of their regulator genes. If the con-
centration of u exceeds u
v
then v is active (ON), and
if the concentration of u exceeds u
w
then w is not ac-
tive (OFF). We exploit this switching view of genes
to capture behaviours of gene networks in transition
systems.
We now illustrate how we capture behaviours of
gene regulatory networks as transition systems using
a simple example network (Fig. 2) in which gene x
activates gene y and gene y activates gene z, and its
behaviour depicted in Fig. 3 where x
y
is the threshold
of x for y and y
z
that of y for z.
Figure 2: Simple example.
x
y
z
t
t
t
base
base
base
x
y
y
z
t
0
t
1
t
2
t
3
t
4
t
5
t
6
t
7
t
8
t
9
Figure 3: Change of concentrations with time.
To obtain a symbolic representation of behaviours
of this network, we introduce logical propositions that
represent whether genes are active or not (ON or OFF)
and whether concentrations of products of genes ex-
ceed threshold values. In this network, we introduce
the propositions on
x
, on
y
, on
z
, x
y
and y
z
. Propositions
on
x
, on
y
, on
z
mean whether or not gene x, y or z is ac-
tive, x
y
whether gene x is expressed beyond the thresh-
old x
y
1
, and y
z
whether gene y is expressed beyond the
threshold y
z
.
Using these propositions, we discretise the above
behaviour to the sequence of states (called transition
system) shown in Fig. 4, where 0, . . . , 10 are states, ar-
rows represent state transitions that abstract the tem-
poral evolution of the system, and the propositions be-
low each state are true in that state.
0 1 2 3 4 5 6 7 8 9 10
Figure 4: State transition system corresponding to Fig. 3.
State 0 represents the interval [0, t
0
), state 1 rep-
resents the interval [t
0
,t
1
), ... and state 10 represents
[t
9
, ∞).
A single state transition can represent any length
of time, since the actual duration of the transition (in
real time) is immaterial. Therefore, the difference be-
tween t
2
−t
0
and t
7
−t
4
, the duration of the input sig-
1
Note that the symbol x
y
is used for both the threshold
and proposition but we can clearly distinguish from the con-
text.
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
16

nal to x, in Fig. 3 is not captured directly. Fig. 4 cap-
tures whether the concentration of y exceeds y
z
; that
is, we can infer that the latter duration is sufficiently
long for x to activate y by comparing the propositions
in state 1 to 3 and in state 5 to 9. Moreover, the real
values of thresholds are irrelevant. Propositions such
as x
y
merely represent the fact that the concentration
of x is above the level at which x affects y.
In our abstraction, behaviours are identified with
each other if they have the same transition system.
Such logical abstraction preserves essential qualita-
tive features of the dynamics (Snoussi and Thomas,
1993; Thomas and Kauffman, 2001).
3 QUALITATIVE ANALYSIS OF
GENE REGULATORY
NETWORKS IN LTL
In this section, we show how to analyse behaviours of
gene regulatory networks using LTL.
3.1 Linear Temporal Logic
First we introduce the time structure of LTL. If A is a
finite set, A
ω
denotes the set of all infinite sequences
on A. The i-th element of σ ∈ A
ω
is denoted by σ[i].
Definition 1. Let AP be a set of propositions. A time
structure is a sequence σ ∈ P(AP)
ω
where P(AP) is
the powerset of AP.
We next define formulae in LTL.
Definition 2. Let AP be a set of propositions. Then
p ∈ AP is a formula. If ϕ and ψ are formulae, then
¬ϕ, ϕ ∧ ψ, ϕ ∨ ψ, and ϕUψ are also formulae.
We introduce the following abbreviations: ⊥ ≡
p ∧ ¬p for some p ∈ AP, ⊤ ≡ ¬⊥, ϕ → ψ ≡ ¬ϕ ∨ ψ,
ϕ ↔ ψ ≡ (ϕ → ψ) ∧ (ψ → ϕ), Fϕ ≡ ⊤U ϕ, Gϕ ≡
¬F¬ϕ, and ϕW ψ ≡ (ϕUψ) ∨ Gϕ.
Intuitively, ¬ϕ means ‘ϕ is not true’, ϕ ∧ ψ ’both
ϕ and ψ are true’, ϕU ψ ‘ϕ continues to hold until ψ
holds’, ⊥ a false proposition, ⊤ a true proposition,
ϕ∨ψ ’ϕ or ψ is true’, Fϕ ‘ϕ holds at some future time’,
Gϕ ‘ϕ holds globally’, and ϕW ψ is the ‘weak until’
operator in that ψ is not obliged to hold, in which case
ϕ must always hold. The formal semantics are given
below.
Definition 3. Let σ be a time structure and ϕ be a
formula. We write σ |= ϕ for ‘ϕ is true in σ’. The sat-
isfaction relation |= is defined inductively as follows:
σ |= p iff p ∈ σ[0] for p ∈ AP
σ |= ¬ϕ iff σ ̸|= ϕ
σ |= ϕ ∧ ψ iff σ |= ϕ and σ |= ψ
σ |= ϕ ∨ ψ iff σ |= ϕ or σ |= ψ
σ |= ϕU ψ iff (∃i ≥ 0)(σ
i
|= ψ and
∀ j(0 ≤ j < i)σ
j
|= ϕ)
where σ
i
= σ[i]σ[i + 1] . . . , the i-th suffix of σ.
Finally we introduce the notion of satisfiability.
Definition 4. An LTL formula ϕ is satisfiable if there
exists some time structure σ such that σ |= ϕ. A time
structure σ such that σ |= ϕ is called a model of ϕ.
3.2 Analysis of Gene Regulatory
Networks by Satisfiability checking
in LTL
As we can see in Section 2, a behaviour of a gene
regulatory network can be seen as a time structure
on atomic propositions for the network. Let AP be
the set of propositions for a network. Formally, a be-
haviour of a network is an element of P(AP)
ω
. How-
ever, not all of the sequences in P(AP)
ω
are possible
behaviours. For example, in the network in Fig. 2,
y cannot be ON before x becomes ON when y com-
pletely depends on x. We characterise the possible
behaviours of a network in LTL
2
.
Assume that we obtain a formula ϕ which char-
acterises possible behaviours of a network. We also
specify a biological property of interest in LTL and
call it ψ. Then we can check whether some possi-
ble behaviour satisfies a given biological property by
checking whether ϕ ∧ ψ is satisfiable which means
there exists a sequence such that this is a possible be-
haviour of the network (satisfying ϕ) and that satis-
fies a biological property (satisfying ψ). Also, we can
check whether all possible behaviours satisfy a given
biological property by checking whether ϕ∧¬ψ is not
satisfiable which means if a sequence σ is possible in
the network (satisfying ϕ), then it is impossible that σ
violates a biological property ψ.
3.3 Specification of behaviours in LTL
We now show how we specify ϕ for a given network.
As in Section 2, we assume that we have the following
propositions:
• on
u
for each node u in a given network.
• u
v
for each regulation from u to v in a given net-
work.
2
This contrasts with the framework in which behaviours
are described in ordinary differential equations.
QualitativeAnalysisofGeneRegulatoryNetworksusingNetworkMotifs
17

Additionally, we may introduce other propositions
representing landmark concentration values that are
not thresholds for other nodes (say, representing ‘low
level’, ‘maximum’ and so on).
The basic idea of specifying possible behaviours
of a network is the following qualitative principle:
• Genes are ON when their activators express over
some threshold.
• Genes are OFF when their inhibitors express over
some threshold.
• If genes are ON, the concentrations of their prod-
ucts increase.
• If genes are OFF, the concentrations of their prod-
ucts decrease.
Thus we specify the above rules in LTL using the
propositions introduced earlier. The switching condi-
tions for gene u can be specified by regulators x, y, . . .
using their threshold values x
u
, y
u
, . . . . The concen-
tration increase or decrease for some gene u relates to
the propositions u
v
, u
w
, . . . , that is, the threshold val-
ues that u has. For this, the total order of threshold
values must be fixed.
We show how we specify the above rules in LTL.
The specification is written so that the behaviours that
satisfy it are as large as possible.
Conditions for Gene Activation and Inhibition.
First we consider the simple case in which a gene is
regulated by a single gene. For example, let gene v
be regulated only by u. If the effect of u on v is pos-
itive, then v is turned on when the concentration of
u exceeds the threshold u
v
. We have two choices for
description in LTL. One is
G(u
v
→ on
v
)
and the other is
G(u
v
↔ on
v
).
The former allows on
v
to be true when u
v
is not, but
the latter does not. The former specification takes
hidden activators or external regulation for v into ac-
count. The choice of which of the two specifications
to use depends on the system or the situation.
On the other hand, if the effect of u on v is nega-
tive, this case is described by:
G(u
v
→ ¬on
v
)
Similarly we may write G(u
v
↔ ¬on
v
) depending on
the system or situation.
Now we consider a gene that is regulated by mul-
tiple genes. In general, the multivariate regulation
functions of organisms are unknown (Alon, 2007).
Thus we only describe the trivial facts. For example,
we assume that genes u, v activate x and that w in-
hibits x. In this example, the following two facts hold
trivially.
• If u and v exceed u
x
and v
x
respectively, and w
does not exceed w
x
, then x is ON. This is de-
scribed as follows:
G((u
x
∧ v
x
∧ ¬w
x
) → on
x
).
• If u and v do not exceed u
x
and v
x
respectively, and
w exceeds w
x
, then x is OFF. This is described as
follows:
G((¬u
x
∧ ¬v
x
∧ w
x
) → ¬on
x
).
If we know more information, such as the positive
effect of u and v on x is conjunctive; that is, both u and
v need to exceed their thresholds, or the negative reg-
ulation effect of w is dominant and overpowers other
positive effects, then we can append these conditions.
In gene regulation, some genes regulate not genes
but the regulation effect itself, for example when
some gene’s product intercepts another gene’s prod-
uct. Let us consider a case where x inhibits y and z
inhibits the regulation effect of x on y. In this case y is
turned OFF when x affects y but z does not affect the
regulation. To describe this, we introduce a threshold
z
x
above that z inhibits the effect of x. We can describe
this as follows:
G((x
y
∧ ¬z
x
) → ¬on
y
).
In this case, z
x
may not be a fixed value but a func-
tion that takes the concentration of x and returns the
threshold of z. The proposition z
x
simply says that z
influences the regulation effect of x and the real value
of the concentration of z does not matter.
To capture alternative splicing we can use multi-
ple (virtual) genes to represent one gene with multiple
states. If a gene has two states (namely one produces
A and the other B), we use propositions on
A
and on
B
and individually have the switching conditions and
concentration changes for them.
Total Order of Threshold Values. We now spec-
ify the fixed total order of threshold values. Assume
that u regulates x
1
, x
2
, . . . , x
m
and the threshold values
for them are in this order. This order relation can be
described in LTL as follows:
∧
1≤i<m
G(u
x
i+1
→ u
x
i
).
Concentration Changes when Genes are ON. If
gene u is ON the concentration of its product in-
creases with time. There are two kinds of specifica-
tion: a strong one and a weak one.
In what follows, we assume that gene u has thresh-
old values u
1
, u
2
, . . . , u
m
in this order.
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
18

First we introduce the strong specification:
G((on
u
→ F(¬on
u
∨ u
1
)) ∧ (1)
((on
u
∧ u
1
) → (u
1
U(¬on
u
∨ u
2
))) ∧ (2)
((on
u
∧ u
2
) → (u
2
U(¬on
u
∨ u
3
))) ∧ (3)
.
.
.
((on
u
∧ u
m−1
) → (u
m−1
U(¬on
u
∨ u
m
))) ∧ (4)
((on
u
∧ u
m
) → (u
m
W ¬on
u
))). (5)
To explain the above formula, suppose that u is ON
and its concentration is between u
2
and u
3
. Recall that
u
i
means the concentration of u exceeds u
i
. Thus the
left-hand sides of (1)-(3) in the above formula hold.
From the total order of threshold values, u
3
im-
plies u
1
and u
2
, and u
2
implies u
1
. Accordingly, (1)-
(3) may be summed up as the concentration of u being
not less than u
2
until v is turned OFF or the concen-
tration of u exceeds u
3
. Behaviours that satisfy this
constraint have a starting concentration of u between
u
2
and u
3
, and in some future state the concentration
of u exceeds u
3
but until that time it remains above u
2
.
The exception is that u is turned OFF before reaching
u
3
, so u may not exceed u
3
. Behaviours in which u
falls below u
2
while being ON are excluded. More-
over, u is not allowed to remain between u
2
and u
3
indefinitely although it is ON. We consider such be-
haviours to be incorrect in the strong specification. If
the concentration of u is basal, only (1) applies. If u
is above u
m
, which is the greatest threshold, then all
clauses apply but are absorbed into (5). As a conse-
quence, the above formula says that the concentration
of u does not decrease as long as u is ON and must
increase (unless u is greater than u
m
) if u is always
ON.
Next we introduce the weak specification:
G((on
u
→ F(¬on
u
∨ u
1
)) ∧
((on
u
∧ u
1
) → (u
1
W ¬on
u
)) ∧
.
.
.
((on
u
∧ u
m
) → (u
m
W ¬on
u
))).
The difference compared with the strong specification
is that behaviours in which u keeps its concentration
although it is always ON are allowed; that is, the con-
centration does not have to increase strictly. This rep-
resents a situation where generation and degradation
are equilibrated.
Concentration Changes when Genes are OFF.
This is symmetric to the case when genes are ON.
We again assume that gene u has threshold values
u
1
, u
2
, . . . , u
m
in this order. We also have both a strong
specification and a weak one.
The strong specification is as follows:
G((¬on
u
→ F(on
u
∨ ¬u
m
)) ∧
((¬on
u
∧ ¬u
m
) → (¬u
m
U(on
u
∨ ¬u
m−1
))) ∧
.
.
.
((¬on
u
∧ ¬u
2
) → (¬u
2
U(on
u
∨ ¬u
1
))) ∧
((¬on
u
∧ ¬u
1
) → (¬u
1
W on
u
))).
The weak specification is as follows:
G((¬on
u
→ F(on
u
∨ ¬u
m
)) ∧
((¬on
u
∧ ¬u
m
) → (¬u
m
W on
u
)) ∧
.
.
.
((¬on
u
∧ ¬u
1
) → (¬u
1
W on
u
))).
In the strong specification, it is not possible that u
keeps its concentration when it is always OFF but this
is possible in the weak specification.
Remark. The choice between a strong and weak
specification is made for both the ON and OFF be-
haviour of each gene. Thus, there are two options
(i.e., strong or weak) for the ON behaviour and two
for the OFF behaviour. For example, if there are
two genes, there are 2
4
= 16 possible combinations
of specifications.
3.4 Biological Properties in LTL
Many biologically interesting properties can be de-
scribed in temporal logic. For example, the property
‘the system eventually reaches a state in which gene
x is active but gene y is not active’ is a type of reach-
ability described as F(on
x
∧ ¬on
y
). The property ‘the
concentration of x is always above x
y
’ is a type of
stability described as Gx
y
. Oscillation, where ‘some
property ϕ is alternately true and false indefinitely’,
is described as G((ϕ → F¬ϕ) ∧ (¬ϕ → Fϕ)). Condi-
tional properties can also be specified. For example,
‘if gene x is always OFF then the property ϕ holds’ is
described as (G¬on
x
) → ϕ. Furthermore, we can use
any combination of the above.
Nor should we confine ourselves to the above tem-
plates. We can use full LTL to specify properties of
interest.
3.5 Example Analysis
We apply our method to analysing the mucus produc-
tion system in the bacteria Pseudomonas aeruginosa.
P. aeruginosa produces a heavy mucus (alginate) in
the lungs of cystic fibrosis patients, causing respira-
tion deficiency and being the major cause of mortal-
ity (Govan and Harris, 1986). Bacteria isolated from
QualitativeAnalysisofGeneRegulatoryNetworksusingNetworkMotifs
19

the lungs of such patients can form stable mucous
colonies, with a majority of these bacteria present-
ing a mutation. Hence it is natural to think that the
mutation is the cause of the transition to the mucoid
state. However, we show that wild-type bacteria can
have multi-stationarity where one stable state regu-
larly produces mucus while the other does not; that is
to say, the change from the non-mucoid state to the
mucoid state is epigenetic. This example is borrowed
from (Bernot et al., 2004).
The gene regulatory network that controls mucus
production has been elucidated (Schurr et al., 1994;
Guespin and Kauffman, 2001) and is depicted in Fig.
5. In this figure, z represents alginate synthesis (i.e.
mucus production), x activates mucus production, and
y
is an inhibitor of
x
.
Figure 5: The network of mucus production in P. aerugi-
nosa, where x positively regulates mucus production, repre-
sented as z, and y inhibits x, which x positively regulates.
We introduce the set of propositions {on
x
, on
y
,
on
z
, x
x
, x
y
, x
z
, y
x
}, where z is not a gene, but on
z
means that mucus is produced.
Among the thresholds for concentrations of x, it
has been shown that x
z
is the highest (Guespin and
Kauffman, 2001). Thus there are two possibilities for
the order, x
x
< x
y
< x
z
or x
y
< x
x
< x
z
. Thus we have
two specifications for each order.
The properties that should be checked are as fol-
lows:
• The bacteria regularly produces mucus : Gon
z
.
• The bacteria never produces mucus: G¬on
z
.
We check whether each property, in conjunction
with the behavioural specification, is satisfiable. We
used our implementation (in OCaml) of the LTL sat-
isfiability checker based on the algorithm of Aoshima
(Aoshima et al., 2001). Our implementation takes
a formatted text file like shown in Fig.6 and returns
whether an input formula is satisfiable in command
line. We found that both properties are satisfiable in
both threshold orderings. Therefore, it is computa-
tionally possible that the wild-type bacteria have both
mucoid and non-mucoid behaviour. This result moti-
vates us to verify this hypothesis experimentally.
In the above analysis we do not constrain the mul-
tivariate regulation function for x which merges the
inputs from x and y. That is, when both x and y are
effective, x may be active or inactive since x activates
x and y inhibits x. Now we assume that the negative
G( (x_z -> x_y) &&
(x_y -> x_x) &&
( (x_x && !y_x) -> onx) &&
( (!x_x && y_x) -> !onx) &&
...
Figure 6: Specification for possible behaviours of the net-
work for mucus production in P.aeruginosa.
effect from y is superior to the positive effect from x.
In this case the bacteria may not become mucoid state
since x
y
< x
z
. We check this hypothesis. We modify
the behavioural specification by replacing the clause
((¬x
x
∧ y
x
) → ¬on
x
) with (y
x
→ ¬on
x
). We check
whether the modified behavioural specification with
the property Gon
z
is not satisfiable. This is actually
the case for both orderings of x
x
and x
y
. These results
mean the hypothesis that wild-type P. aeruginosa has
a stable mucoid state is rebutted by the assumption
that the negative effect of y overpowers the positive
effect of x.
3.6 About Complexity
Analysis in our method is based on LTL satisfiabil-
ity checking, which is a PSPACE-complete problem
(Sistla and Clarke, 1985). Therefore, the known algo-
rithms require exponential time related to the size of
an input formula. As we can see from Section 3.3, the
length of a formula specifying possible behaviours of
a network is proportional to the size of the network,
and accordingly, analyses of large networks are gener-
ally intractable in our method. To tackle this issue, we
develop an approximate analysis which is discussed
in Section 4.
4 APPROXIMATE ANALYSIS
In this section, we describe approximate analysis
method and introduce approximate specifications for
network motifs. The key of approximation is to re-
duce the number of propositions. By omitting some
propositions, we approximately specify the possible
behaviours of networks.
To guarantee the correctness of analysis, if ap-
proximate specifications are satisfiable or unsatisfi-
able, so be the original ones. These conditions can
be assured by the fact that the set of behaviours of
approximate specifications are smaller or larger than
that of original ones. Thus there are two ways in ap-
proximation. One is lower approximation in which
the set of behaviours are smaller than the original
specification, and the other is upper approximation in
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
20

which the set of behaviours are larger than the original
specification.
Theorem 1. If lower approximated specification is
satisfiable, so be the original one. If upper approxi-
mated specification is unsatisfiable, so be the original
one.
We omit the formal presentation and proof of this
theorem due to the page limitations.
To find approximate specifications for any net-
work is not a trivial task. However, there is a small set
of recurring regulation patterns, called network motifs
(Alon, 2007), in gene regulatory networks. Therefore,
we present approximate specifications for network
motifs. In this paper we consider five motifs: neg-
ative auto-regulation, coherent type 1 feed-forward
loops, incoherent type 1 feed-forward loops, single-
input modules and multi-output feed-forward loops.
The reason why we focus on these five motifs is that
they have certain functions. So the approximate spec-
ifications are given by considering their functions.
Remark. It is worth noting that the weak specifica-
tion is an upper approximation of the strong specifi-
cation (recall these definitions from Section 3.3).
In the following, lower approximations are given
for strong specifications and upper approximations
are given for weak specifications. From the above
remark, lower approximations for strong specifica-
tions are also lower approximations for weak speci-
fications, and upper approximations for weak specifi-
cations are also upper approximations for strong spec-
ifications.
Negative Auto-regulation. Negative auto-
regulation is depicted in Fig. 7. This motif has
x
-
Figure 7: Negative auto-regulation.
the function of response acceleration. In our ab-
straction, this function cannot be described since
we cannot refer to an actual response time in LTL;
that is, accelerated behaviours and non-accelerated
behaviours cannot be distinguished. Therefore, we
may ignore negative auto-regulation in our analysis.
For simplicity we assume that there is one input and
one output for x but this is easily generalised. We
now present the following lower approximation in
which negative auto-regulation of x is ignored:
G( (in
x
↔ on
x
) ∧
(on
x
→ F(x
out
∨ ¬on
x
)) ∧
((on
x
∧ x
out
) → (x
out
W ¬on
x
)) ∧
(¬on
x
→ F(¬x
out
∨ on
x
)) ∧
((¬on
x
∧ ¬x
out
) → (¬x
out
W on
x
)) ).
The abstracted proposition is x
x
.
It is difficult to present a meaningful upper ap-
proximation for the weak specification since the be-
haviour principles prescribed in Section 3.3 will be
violated by weakening the specification.
Coherent Type 1 Feed-forward Loop. A feed-
forward loop (FFL) is a pattern consisting of three
nodes as depicted in Fig. 8. There are 8 patterns in
FFL depending on regulation effects of three edges.
The coherent type 1 FFL (C1-FFL) is the pattern in
z
x
y
Figure 8: Feed-forward loop.
which all edges represent activation. There are two
types of input function (AND/OR) for z that merge
the influence of x and y. For the AND function, C1-
FFL shows a delay after stimulation, but no delay
when stimulation stops. For the OR function, the FFL
has the opposite effect to the AND case; that is, it
shows no delay after stimulation but shows a delay
when stimulation stops. These functions are real-time
properties and do not make a difference in our ab-
straction. For lower approximation, we ignore y and
consider them simple regulations. Thus the difference
between AND and OR does not occur in the approxi-
mate formula. Although the original specifications for
this motif depend on the orderings of the thresholds x
y
and x
z
, we can present a single lower approximation
as follows:
G( (on
x
→ F(on
z
∨ ¬on
x
)) ∧
((on
x
∧ on
z
) → (on
z
W ¬on
x
)) ∧
(¬on
x
→ F(¬on
z
∨ on
x
)) ∧
((¬on
x
∧ ¬on
z
) → (¬on
z
W on
x
)) ).
The abstracted propositions are x
y
, x
z
, y
z
and on
y
.
It is also difficult to present a consistent upper ap-
proximation since that would allow behaviours vio-
lating the behaviour principles. For example, we may
weaken the constraint concerning activation of z and
inactivation of z by allowing z to not be turned ON
when x is ON or not be turned OFF when x is OFF.
However, this amounts to regarding z to be indepen-
dent of x.
QualitativeAnalysisofGeneRegulatoryNetworksusingNetworkMotifs
21

Incoherent Type 1 Feed-forward Loop. In inco-
herent type 1 FFL (I1-FFL), x activates y and z but y
inhibits z in Fig. 8. Assume that the threshold of x
for z is higher than that of x for y. When x becomes
ON, z will be turned ON. After some time y becomes
ON. At that time y inhibits z, so z becomes OFF. As a
result, this motif generates pulse-like dynamics on z.
We specify this pulse-like dynamics as the following
lower approximation.
G( (on
x
∧ ¬on
y
) → F(on
z
∨ ¬on
x
)) ∧
((on
x
∧ on
z
) → (on
z
Uon
y
)) ∧
((on
x
∧ on
y
) → ((on
y
∧ ¬on
z
)W ¬on
x
)) ∧
(¬on
x
→ (¬on
z
∧ ¬on
y
)) ).
The abstracted propositions are x
y
, x
z
and y
z
.
It is difficult to give an upper approximation repre-
senting this pulse-like dynamics since this dynamics
is a part of behaviours of I1-FFL.
Single-input Module. A single-input module is a
pattern in which one regulator (called the master
gene) regulates a group of target genes (Fig. 9). All
regulations from the master gene are of the same type
(positive or negative). We only consider the positive
case but the negative case is similar.
x
z z z
…
…
Figure 9: Single-input module.
The function of this motif is a last-in first-out
(LIFO) temporal order on expressions of target genes.
Assume that the thresholds for z
1
, z
2
, . . . , z
n
occur in
this ascending order. When the master regulator x is
ON, the regulated genes z
1
, z
2
, . . . , z
n
are turned ON
in this order. When x is turned OFF, z
n
, z
n−1
, . . . z
1
are
turned OFF in this order.
We first present a lower approximation. For sim-
plicity we set n = 2 but this is easily generalised:
G( (on
z
2
→ on
z
1
) ∧
(on
x
→ (on
x
Uon
z
2
)) ∧
((on
x
∧ on
z
1
) → (on
z
1
W ¬on
x
)) ∧
((on
x
∧ on
z
2
) → (on
z
2
W ¬on
x
)) ∧
(¬on
x
→ (¬on
x
U¬on
z
1
)) ∧
((¬on
x
∧ ¬on
z
2
) → (¬on
z
2
W on
x
)) ∧
((¬on
x
∧ ¬on
z
1
) → (¬on
z
1
W on
x
)) ).
The abstracted propositions are x
z
1
and x
z
2
. Be-
haviours that satisfy this formula are such that once
x is turned ON it remains ON until all target genes
become active, and once x is turned OFF it remains
OFF until all target genes become inactive. Therefore,
behaviours such that x is turned OFF before all tar-
get genes become active or x is turned ON before all
target genes become inactive are eliminated from the
possible behaviours obtained using the original spec-
ification.
We now present an upper approximation:
G( (on
z
2
→ on
z
1
) ∧
((on
x
∧ on
z
1
) → (on
z
1
W ¬on
x
)) ∧
((on
x
∧ on
z
2
) → (on
z
2
W ¬on
x
)) ∧
((¬on
x
∧ ¬on
z
2
) → (¬on
z
2
W on
x
)) ∧
((¬on
x
∧ ¬on
z
1
) → (¬on
z
1
W on
x
)) ).
Propositions x
z
1
and x
z
2
are ignored. This upper ap-
proximation says that the temporal order of activa-
tion and inactivation of target genes is preserved but
some genes may not be activated when x is turned
ON or inactivated when x is turned OFF. Such be-
haviours are also allowed in the weak specification
but we can specify the same constraint without some
propositions.
Multi-output Feed-forward Loop. A multi-output
feed-forward loop is a generalisation of a feed-
forward loop with n target genes (Fig. 10). The
y
z z z
…
…
x
Figure 10: Multi-output feed-forward loop.
function of this motif is interesting when each input
function for z
i
is OR and the threshold orders for x
and y are inverted, that is, x
z
1
< x
z
2
< ··· < x
z
n
and
y
z
1
> y
z
2
> ··· > y
z
n
. In this case this motif can
generate a first-in first-out (FIFO) temporal order on
expression of target genes. The activation order is
z
1
z
2
. . . z
n
and the inactivation order is the opposite.
The position of threshold x
y
does not matter. Focusing
on this property we have the following lower approx-
imation (we set n = 2 but this is easily generalised):
G( (on
x
→ (on
z
2
→ on
z
1
)) ∧
(¬on
x
→ (¬on
z
2
→ ¬on
z
1
)) ∧
((on
x
→ (on
x
Uon
z
1
))) ∧
((on
x
∧ on
z
1
) → ((on
x
∧ on
z
1
)U(on
x
∧ on
z
2
))) ∧
((on
x
∧ on
z
2
) → (on
z
2
W ¬on
x
)) ∧
(¬on
x
→ (¬on
x
U¬on
z
1
)) ∧
((¬on
x
∧ ¬on
z
1
) →
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
22

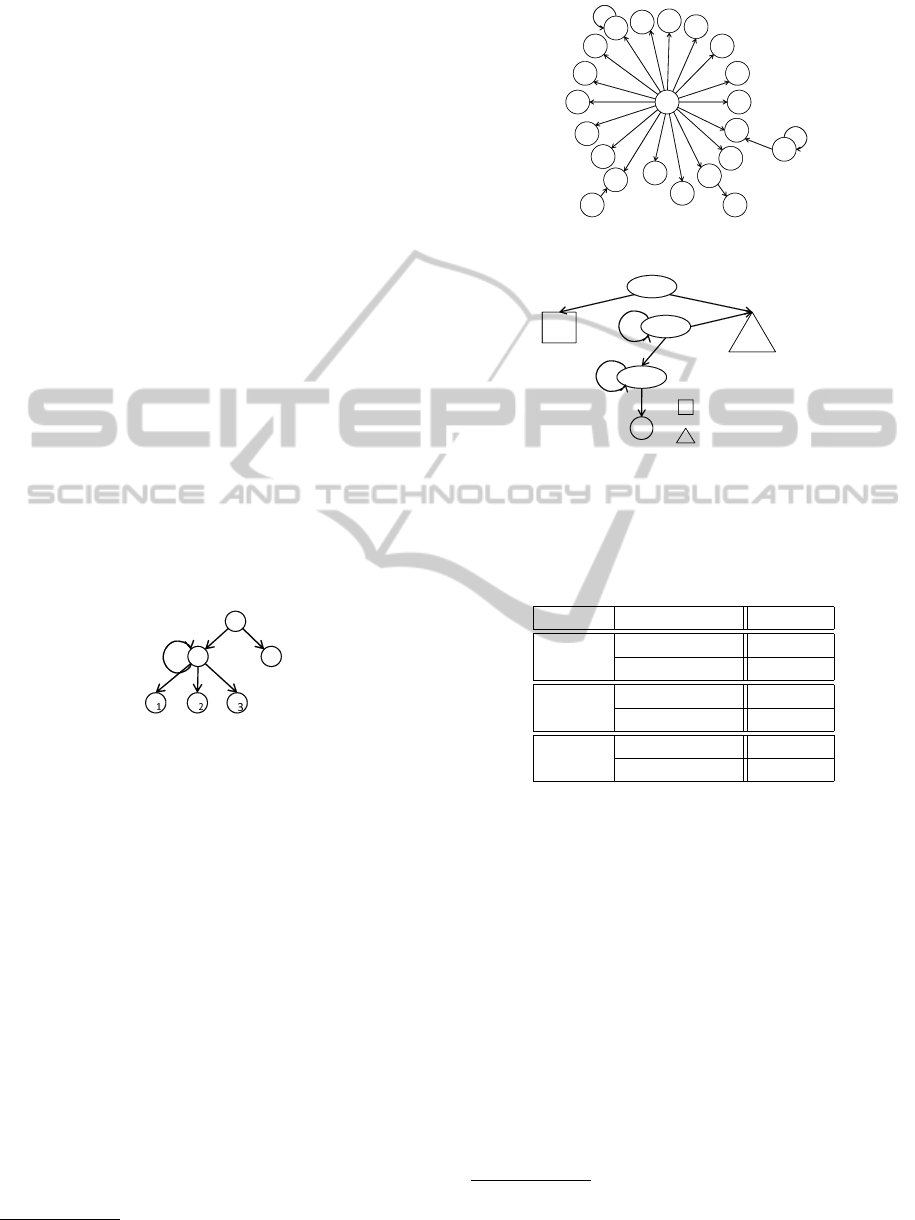
((¬on
x
∧ ¬on
z
1
)U(¬on
x
∧ ¬on
z
2
))) ∧
((¬on
x
∧ ¬on
z
2
) → (¬on
z
2
W on
x
)) ).
The abstracted propositions are x
y
, x
z
1
, x
z
2
, on
y
,
y
z
1
, and y
z
2
. This formula says that when x is turned
ON, z
1
and z
2
are activated in this order, and that when
x is turned OFF, z
1
and z
2
are inactivated in the oppo-
site order.
Note that this motif can generate other tempo-
ral orders on expressions of target genes even if the
threshold ordering is as assumed. Thus there are
many possible behaviours, and we cannot give an
upper approximation without violating the behaviour
principles.
4.1 Experiments
We demonstrate the approximate analysis using three
example networks and compare the approximate
specifications for the original specification. Lower
approximation is used in this experiments.
The first example is the network depicted in Fig.
11. There are two motifs in Fig. 11, one a negative
auto-regulation and the other a single-input module.
x
a
-
z
b
z z
+
+
+ + +
Figure 11: Example.
The second example is a network in Arabidopsis
thaliana depicted in Fig. 12. This network is obtained
from ReIN
3
. In this network, we can find a single-
input module which has 18 target genes in the mo-
tif. In this network, there are some genes which have
regulators other than master gene. Thus we cannot
use the approximate specification introduced above
directly. But the modification is not difficult. We do
not omit propositions x
y
if y has a regulator other than
the master gene x, and specify the conditions for ac-
tivation and inhibition of y the same as the original
ones.
The third example is a network in Escherichia coli
involving the malT gene. The numbers in the box
and the triangle are the numbers of target genes in
each motif. In this network we approximate two neg-
ative auto-regulations, one single-input module and
one multi-output feed-forward loop. We show the re-
sult of satisfiability checking of these specifications
3
http://arabidopsis.med.ohio-state.edu/REIN/
ARP7
FDH
At3g50790
RBR1
SIM
ATMYBL2
ETC1
GL2
At5g28350
MYC
At3g50800
TRY
CAPRICE
AtGRAS30
At4g20960
KIS
TTG2
CPL3
GL1/
GL3
AP2
-
-
AtPLDf1
-
HY5
Figure 12: A network in Arabidopsis.
malT
2
3
crp
malI
-
-
-
-
+
+
+
Multi-output FFL
Single-input module
Figure 13: A network in E. coli.
with our satisfiability checker. The results are shown
in Table 1
4
.
Table 1: Results of satisfiability checking.
Specification Time
Fig. 11 Original 0.020s
Approximate 0.016s
Fig. 12 Original 17.357s
Approximate 1.636s
Fig. 13 Original 94.454s
Approximate 0.340s
In all cases, the cost of analysis is improved. Es-
pecially, in the last case, the improvement is drastic.
5 RELATED WORKS
BIOCHAM (Fages et al., 2004) is a language and
programming environment for modelling and simu-
lating biochemical systems, and checking their tem-
poral properties. Reactions are written as rewriting
rules, and simulations are performed by replacing ob-
jects on the left-hand side with those on the right-
hand side. The result of simulation are represented
as a transition graph whose nodes are possible states
of objects. A biological property is given in compu-
4
The following computational environment was used:
openSUSE 11.0, Intel(R) Pentium(R) D CPU 3.00GHz and
2GB of RAM.
QualitativeAnalysisofGeneRegulatoryNetworksusingNetworkMotifs
23

tational tree logic and checked in the resulting tran-
sition graph. In BIOCHAM, presence or absence of
objects is the only matter considered in contrast to our
method.
SMBioNet (Bernot et al., 2004) is a tool for for-
mally analysing temporal properties of gene regula-
tory networks. In SMBioNet, genes have concentra-
tion thresholds to activate or inhibit each of their reg-
ulating genes. A temporal evolution of a system is
specified by a transition function on the vectors of
expression levels of genes. The specification of be-
haviours is more flexible in our method than that of
SMBioNet in the sense that we can express temporal
ordering of event occurrences by LTL.
GNA (de Jong et al., 2003) is a computational tool
for the modelling and simulation of gene regulatory
networks. GNA archives simulation using piecewise
linear differential equation models and generates state
transition systems that represent possible behaviours.
This method assumes that the functions of multivari-
ate regulation are known but such functions are un-
known in most of networks. Therefore our method
is more applicable for the current databases of gene
regulation.
Although the above tools are useful for checking
whether a biological property can be true in network
behaviours, it is unknown how to utilise network mo-
tifs in analysing networks with them.
6 CONCLUSIONS
In this paper, we have presented a method for
analysing the dynamics of gene regulatory networks
using LTL satisfiability checking. To ease analysis of
large networks, we developed the approximate analy-
sis method and showed how it works well.
For the purpose of analysing large networks, we
presented approximate specifications for five network
motifs. For further development, it is important to
find approximate specifications for more network pat-
terns. However, there is another approach to handle
large networks. It is a modular analysis method, in
which we decompose a network into a few subnet-
works, check them individually, and then integrate
them. The modular analysis method is applicable to
arbitrary network and is not approximate but precise.
REFERENCES
Alon, U. (2007). Network motifs: theory and experimental
approaches. Nature reviews. Genetics, 8(6):450–461.
Aoshima, T., Sakuma, K., and Yonezaki, N. (2001). An ef-
ficient verification procedure supporting evolution of
reactive system specifications. In Proceedings of the
4th International Workshop on Principles of Software
Evolution, IWPSE ’01, pages 182–185, New York,
NY, USA. ACM.
Bernot, G., Comet, J., Richard, A., and Guespin, J. (2004).
Application of formal methods to biological regula-
tory networks: extending Thomas’ asynchronous log-
ical approach with temporal logic. J. Theor. Biol.,
229(3):339–347.
de Jong, H., Geiselmann, J., Hernandez, G., and Page, M.
(2003). Genetic network analyzer: Qualitative simu-
lation of genetic regulatory networks. Bioinformatics,
19(3):336–344.
Fages, F., Soliman, S., and Chabrier-Rivier, N. (2004).
Modelling and querying interaction networks in the
biochemical abstract machine BIOCHAM. Journal of
Biological Physics and Chemistry, 4:64–73.
Govan, J. R. W. and Harris, G. S. (1986). Pseudomonas
aeruginosa and cystic fibrosis: unusual bacterial adap-
tation and pathogenesis. Microbiological Sciences,
3(10):302–308.
Guespin, J. and Kauffman, M. (2001). Positive feedback
circuits and adaptive regulations in bacteria. Acta bio-
theoretica, 49(4):207–218.
Ito, S., Izumi, N., Hagihara, S., and Yonezaki, N. (2010).
Qualitative analysis of gene regulatory networks by
satisfiability checking of linear temporal logic. In Pro-
ceedings of the 10th IEEE International Conference
on Bioinformatics & Bioengineering, pages 232–237.
Schurr, M. J., Martin, D. W., Mudd, M. H., and Deretic,
V. (1994). Gene cluster controlling conversion to
alginate-overproducing phenotype in Pseudomonas
aeruginosa: functional analysis in a heterologous host
and role in the instability of mucoidy. Journal of Bac-
teriology, 176:3375–3382.
Sistla, A. P. and Clarke, E. M. (1985). The complexity of
propositional linear temporal logics. J. ACM, 32:733–
749.
Snoussi, E. and Thomas, R. (1993). Logical identification
of all steady states: the concept of feedback loop char-
acteristic states. Bulletin of Mathematical Biology,
55(5):973–991.
Thomas, R. and Kauffman, M. (2001). Multistationarity,
the basis of cell differentiation and memory. II. logi-
cal analysis of regulatory networks in terms of feed-
back circuits. Chaos: An Interdisciplinary Journal of
Nonlinear Science, 11(1):180–195.
BIOINFORMATICS2013-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
24