
A Game-Theoretic Framework to Identify Top-K Teams in Social
Networks
Maryam Sorkhi, Hamidreza Alvari, Sattar Hashemi and Ali Hamzeh
Department of Computer Science and Engineering, Shiraz University, Shiraz, Iran
Keywords: Game-Theoretic Framework, Nash Equilibrium, Team of Experts, Social Networks.
Abstract: Discovering teams of experts in social networks has been receiving the increasing attentions recently. These
teams are often formed when a given specific task should be accomplished by the collaboration and the
communication of the small number of connected experts and with the minimum communication cost. In
this study we propose a game theoretic framework to find top-k teams satisfying such conditions. The
importance of finding top-k teams is revealed when the experts of the best discovered team do not have an
incentive to work together for any reason and hence we must refer to the next found teams. Finally, the local
Nash equilibrium corresponding to the game is reached when all of the teams are formed. The experimental
results on DBLP co-authorship graph show the effectiveness and efficiency of the proposed method.
1 INTRODUCTION
Finding teams of experts has become one of the
most important and interesting subjects in the realm
of social network analysis. It is necessary for many
companies or departments to detect persons who
have enough relevant experiences and expertise to
accomplish a given specific task. However the
success of the project is not merely defined as the
completeness of the task and the project manager
must also takes care about the amount of the
communication and the collaboration exchanged
between the members of team. In addition, it is
important to satisfy the minimum possible costs
when accomplishing the project.
Game theory is a good tool to capture both the
behavior of individuals and strategic interactions
among them (Adjeroh and Kandaswamy 2007),
because it can model strategic interactions between
rational, autonomous and intelligent agents
mathematically. In this paper, we modify the game-
theoretic framework proposed in (Alvari et al., 2011)
to address the problem of forming teams in social
networks. Specifically, we assume each node of the
underlying social network graph as a rational agent
who joins the adjacent groups based on her utilities.
The utility of each agent with regards to each of the
groups she belongs to is defined as a difference of
her gain and loss functions in that team. Finally, the
Nash equilibrium of the game results in discovering
all of the existing teams.
The most important contribution of our method
is that it can find top-k teams simultaneously. The
importance of finding teams is intensified in two
cases. First, when the members of the best found
team do not have incentives to form the team and
second, when they form the team but suddenly
decide to leave the project because of any reason. As
a result, in these cases, we must be able to assign the
project to other next teams if it is applicable.
The remainder of this paper is organized as
follows. Section 2 gives brief reviews on the related
works. In Section 3, our proposed framework is
introduced in detail. The experimental results are
presented in Section 4, and finally we conclude the
paper in Section 5.
2 RELATED WORK
A considerable number of works in the literature
have been devoted to studying team formation
problem. In these works, the authors study the team
formation problem by transforming it into an integer
programming. Simulated annealing (Baykasoglu et
al., 2007), branch-and-cut (Zakarian and Kusiak,
2004), and genetic algorithm (Wi et al., 2009) are
used to find an optimal match between individuals
and requirements. Chen et al. use a psychological
test to form a team by estimating the individuals’
252
Sorkhi M., Alvari H., Hashemi S. and Hamzeh A..
A Game-Theoretic Framework to Identify Top-K Teams in Social Networks.
DOI: 10.5220/0004142302520257
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2012), pages 252-257
ISBN: 978-989-8565-29-7
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

interpersonal relationship attributes and their
personalities (Chen and Lin, 2004). However Gaston
et al., show the correlation between different graph
structures and performance of a team but they don’t
consider a computational problem of finding team
formation (Gaston et al., 2004). Cheatham et al.,
consider the structure of social network by collecting
the neighbours surrounding each skill in a social-
concept graph (Cheatham and Cleereman, 2006).
But they don’t pay attention to the communication
cost among individuals.
The team formation problem in the presence of a
social network of individuals by considering the
communication cost is first addressed by Lappas et
al. (Lappas et al., 2009). They also proved that the
problem of finding such teams is NP-hard. In their
work, they propose two algorithms RarestFirst
algorithm and the EnhancedSteiner algorithm to
solve the team formation problem based on diameter
and minimum spanning tree (MST) respectively.
In RarestFirst approach, the algorithm, first
estimates each required skills supporter and the skill
with rarest sponsors is determined. Then for each of
its candidates, a sub-graph is defined by
investigating the closest connected individuals in
other support sets. In the last step it selects the sub-
graph with minimum communication cost with
diameter metric. The EnhancedSteiner algorithm
consists of two steps. First, it enhances the given
graph as follow: it creates the virtual nodes for each
of the required skills in the given task and connects
them to their supporters by the heavy weighted edge.
Second, it can find the solution by searching the
Steiner Tree of this enhanced graph. To find a
Steiner tree, they use a greedy heuristic algorithm.
3 PROPOSED FRAMEWORK
3.1 Problem Statement
Given the social network graph ,, the skill set
of individuals and a task which is composed of the
required skills
, the team formation problem is
formally defined as finding a set of experts V
'
⊆
V
who best support the required skills. To be specific,
a sub-graph ′ is formed such that: (1) all of the
required skills in the given task should be
accomplished by team and (2) the total
communication cost denoted by ’ among
selected individuals must be minimized as much as
possible.
Additionally, the problem of discovering top-k
teams is simply a generalized version of the well-
known team formation problem. It is formally
defined as finding a set of teams whose experts
V
'
,
V
'
,..
,
V
'
⊆
V best support the given task
independently. In this case, a set of sub-graphs
V
'
,
V
'
,…,
V
'
is formed and the above
two conditions for team formation problem must be
satisfied for each of these teams.
3.2 Our Approach
The social network is modelled as an undirected and
weighted graph ,, where the vertices
,
,…,
are experts, and the edges represent
collaborations in co-activities. The edge weight ,
describes the cost (distance) between any of two
experts. The small-weight edges show that the
experts have more frequent collaborations than high-
weight edges. Here, we suppose that is connected,
but in the case of graphs with disconnected
components (i.e., dissimilar components), we can
also add very high-weight edges between every pair
of nodes that belong to different disconnected
components. This weight is much higher than the
sum of all pair-wise shortest paths in each connected
component and is used when there are some
disconnected teams in the network in addition to
connected teams.
The definitions of the necessary symbols for the
remaining of the paper are shown in Table 1.
Table 1: Definition of symbols.
SYM. DEFINITION
, Undirected and weighted graph
, Number of individuals and skills
Set of skills of agent i
Set of neighbours of agent i
Given task consisting of required skills
Set of skills
Φ Strategies profile
Strategy of agent i
Potential group k to become one of top teams
U
Utility value for agent i corresponding to group k
G
Gain value for agent i corresponding to group k
L
Loss value for agent i corresponding to group k
Furthermore, assume that we have a set of m skills,
,
,..
where each expert has a skill set
X
i
⊆
S. We denote by s
j
∈
X
i
that the individual has
skill s
. Also, a subset of individuals
V
'
⊆
V has skill
s
, if there is at least one individual in
V
'
associated
with s
. A task is simply a subset of skills
required to accomplish the project. The graph
distance function for every two nodes i,j
∈
V is the
AGame-TheoreticFrameworktoIdentifyTop-KTeamsinSocialNetworks
253

weight of the shortest path between them in G,
denoted by ,. The distance between node ∈
and a set of nodes
⊆ is then defined by
di,
′
min
j
∈
V'
d(i,j).
The set of all feasible teams of the network is
denoted by 1,2,…,Δ where is
polynomial in , however the number of our final
teams, Δ, may be much smaller than . As
mentioned earlier, we put each vertex down to a
rational agent who has a utility function and
preserves a vector of group labels that she belongs to
as her strategies. Formally, the strategy of each
agent is denoted by
⊆ and strategy profile
denotes the set of strategies of all agents, i.e.
,
,…
. The group is considered as a
team only if it can accomplish the task.
Naturally, when joining to a new group, each of
the agents will be beneficiary, but on the other hand,
it must pay some costs (e.g. fees). The utility for
agent who belongs to group is calculated by:
(1)
Where,
and
are respectively, gain
and loss functions for agent :
|
|
∩
∈
∪
(2)
∪
(3)
In equation 2,
∈
∪
is the number of skills
which are covered by both the members of
and
agent . However, we consider just the skills which
are in the subset of required skills
⊆ in the task
. Here, is a coefficient to weight the gain
function over the loss function. The main reason for
contributing this coefficient is to encourage the
agents to form teams. The significance of using is
revealed when the supporters of the required skills
are so far from each other or there is not any
connected team in our social graph. In equation 3,
′ is the communication cost function defined
as a diameter of ′.
In our framework, the best response strategy of
an agent with respect to strategies
of other
agents is calculated by:
⊆
,
′
,
′
(4)
The strategy profile forms a pure Nash
equilibrium of the team formation game if all agents
play their best strategies. In other words, in Nash
equilibrium no agent can improve its own utility by
changing its strategy; that is each agent is satisfied
with its current utility:
∀,
,
,
,
(5)
We are satisfied with local Nash equilibrium in
this game, because reaching global one is not
feasible (Lorrain and White, 1971). In other words,
the strategy profile forms a local equilibrium if all
agents play their local optimal strategies. Here
refers to local strategy space of agent :
∀,
∈
,
,
,
(6)
The GameTeamFormation algorithm, shown in
the algorithm 1, takes as input, the graph and the
set of required skills
⊆ to specify the task .
Each agent is selected randomly from a pool of
agents. The selected agent searches for its
neighbours and what they belong to. After
discovering the neighbour groups the agent
constructs the virtual relationship with them. So in
this step we have a set
consisting of
|
|
∑|
|
∈
virtual groups, except those which were
computed previously. In the next step, the gain
function is computed by equation 2. This function is
defined as the fraction of covered skills to the
required skills in the task . For the loss function,
we calculate the minimum diameter corresponding
to these virtual groups. Recall that the diameter of
the graph is the largest shortest path between any
two nodes in the graph. As it is mentioned before,
the utilities of the current agent corresponding to
each of these virtual groups are calculated according
to equation 1. Then, the maximum utility value for
this agent is calculated according to equation 7 and
the winner group
is determined.
∈
(7)
Finally, the label
is added to the labels of the
current agent according to equation 8 and receives
utility
only if it is greater than the maximum of
the previous utilities.
←
∪
(8)
On the other hand, if this utility equals the
previous utilities or is smaller than them, the agent
performs no specific action and remains indifferent.
Since all of the members of the selected group
collaborate to do the task, we consider here that they
share a common utility and loss values. Therefore,
all of the remaining members of this group also
update their corresponding utility value to
.
We now consider this group as one of the final
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
254

top-k teams if its members are able to accomplish
the task. Furthermore, in each stage of detecting
teams, if it is revealed that merging some of the
existing teams to one team can increase their
individual utilities, these teams will be immediately
merged. Finally, all of the teams will be discovered
when the game reaches the Nash equilibrium. As
mentioned before, since reaching global Nash
equilibrium is not feasible, we stop the game after
reaching the local Nash equilibrium.
In this algorithm, k is the group which is
constructed previously,
is one of the virtual
groups and
"
is a new group which will be added to
the list of current teams.
Algorithm 1: The GameTeamFormation algorithm
Input: ,,
,
,…
and .
Output: Teams V
'
,V
'
,…,V
'
.
1. Teams={}
2. Repeat
3. = Random_Select(Agents)
4. for every ∈
5. for every ∈
6.
←
|
|
⋃
∩
∈
∪
7. ={ Diameter(a) | a
∈
}
8.
min
9.
10.
′
max
11. if (
′
max
∈
)
12. if (
′
∈)
13.
"
←
′
∪,
i
←φ
i
∪
{
"
},
"
←
′
14. else
15.
′
←
′
∪, {
′
←
′
,∀j
∈
′
}
16. if (
′
==1)
17. ←
18. Until local equilibrium is reached
19. Sort(Teams)
4 EXPERIMENTS
4.1 Dataset
For our experiments, we use the DBLP dataset as a
benchmark dataset which is publicly available from
the DBLP portal. The snapshot of this dataset was
taken on April 12, 2006, while the data is related to
papers which are published in areas of Database
(DB), Data mining (DM), Artificial intelligence (AI),
and Theory (T) conferences. They are used in order
to balance the necessity of covering the diverse
fields of study (including 19 venues as follows:
{SIGMODE, VLDB, ICDE, ICDT, EDBT, PODS,
WWW, KDD, SDM, PKDD, ICDM, ICML, ECML,
COLT, UAI, SODA, FOCS, STOC and STACS}).
We construct the expert social network using co-
authorship graph in the following way. First, to
collect the experts, the authors who have less than
three papers in DBLP are discarded. Then, the skill
set
of each author is filled with the terms that
appear in at least two titles of their papers in the co-
authorship graph. For the skill extraction, we use the
terms extracted from Bibsonomy tag tools to avoid
noisy tags. Two authors are called connected if they
co-authored in at least two papers. The weights on
edges are computed by equation 9:
,
1
|
∩
|
|
∪
|
(9)
Where
is a set of papers published by author .
The graph distance between two nodes in graph
is computed by using the shortest path
distance. In this graph, the total number of authors is
5508 where there are 1792 distinct skills and 5588
edges.
The preliminaries for performing our method are
as follow. Each task T=
p,q
is characterized by two
parameters: (1) , the number of required skills in
task T; (2) , the minimum required number of
experts to accomplish each skills of T. Specifically,
a task is generated as follows: first, skills are
picked randomly from the terms appearing in
published papers. In all experiments reported in this
section, we use p
∈
{2,4,…,20} and 1. Then, for
every , configuration, we generate 100 random
tasks for all of the algorithms and take the average
performance achieved by different methods.
4.2 Quantitative Results
In this section, our results compared with two well-
known algorithms, RarestFirst and EnhancedSteiner
(Lappas et al., 2009) are presented. The comparisons
are done with respect to the communication cost,
team cardinality, the number of disconnected teams,
stability and scalability.
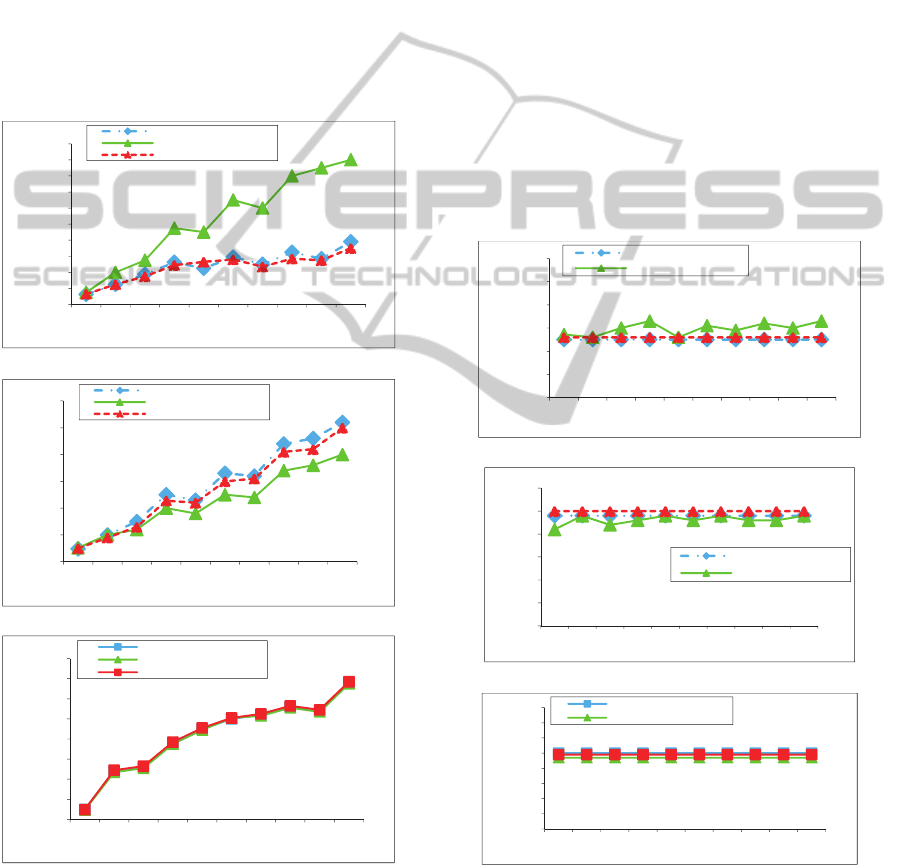
Figure 1, compares the average communication
cost, team cardinality and the number of
disconnected teams on the DBLP dataset. The
following observations are achieved from the
analysis of Figure 1. As we can see in Figure 1(a),
by increasing the number of required skills, the
communication costs of the algorithms grow
considerably, since in this case, the search space
which is needed to be explored, will be expanded. In
AGame-TheoreticFrameworktoIdentifyTop-KTeamsinSocialNetworks
255
other words, because of the sparsity of the
underlying graph, the probability of the existence of
experts who are capable to do the required skills
decreases. Our final evaluation is in term of the
number of disconnected teams. In the real world
projects, the employees who are in the same
department can communicate and collaborate more
easily than other employees who are in the outside.
Therefore, it is of great importance to detect
connected teams to minimize the communication
cost. As it is depicted in Figure 1(c), the
GameTeamFormation algorithm as well as
EnhancedSteiner and RarestFirst algorithms first try
to find the connected teams, and if these teams are
not available, they determine the disconnected ones.
(a)
(b)
(c)
Figure 1: Average effective measures for k=1 is reported
by GameTeamFormation, RarestFirst, EnhancedSteiner
algorithms: (a) Average communication cost. (b) Average
cardinality. (c) Average number of disconnected teams.
The stability status of the algorithm for each
specified task is depicted in Figure 2. The results
show that although each of the agents is selected
randomly from the pool of the agents, this does not
affect our final results and this shows that our
method is stable. As it is mentioned before, this is
due to the fact that in each run of our method, it
finally reaches its equilibrium, meaning that the
agents will not change their strategies. However, the
fact of getting the average of 100 runs for each in
Figure 1 does not imply the instability of our method
and it is for thwarting the effect of randomness of
the selected required skills in each run. On the
other side, although RarestFirst algorithm
demonstrates stability in its runs, EnhacedSteiner
algorithm is somehow sensitive to the random
selection which is done in the greedy heuristic
algorithm used in its Steiner Tree algorithm.
Therefore, EnhacedSteiner algorithm outputs its
results with fluctuation in each run for the specific
skills.
(a)
(b)
(c)
Figure 2: The stability of GameTeamFormation algorithm
for p=2, k=1, the two specified required skills. (a)
Communication cost. (b) Team cardinality. (c) Average
number of disconnected teams.
Finally, Figure 3 shows the scalability of our
0
2
4
6
8
10
12
14
16
18
20
2 4 6 8 10 12 14 16 18 20
Average Communication
Cost of the Team
# of Required Skills (p)
RarestFirst
Enhanced Steiner
GameTeamFormation
0
5
10
15
20
25
30
2468101214161820
Average Team cardinality
# of Required Skills (p)
RarestFirst
Enhanced Steiner
GameTeamFormation
0
10
20
30
40
50
60
70
80
2 4 6 8 10 12 14 16 18 20
Number of disconnected
teams
# of Required Skills (p)
RarestFirst
EnahnecdSteiner
GameTeamFormation
0
0,5
1
1,5
2
2,5
3
10 20 30 40 50 60 70 80 90 100
Average
Communication Cost of
the Team
# of Runs
RarestFirst
Enhanced Steiner
0
0,5
1
1,5
2
2,5
3
10 20 30 40 50 60 70 80 90 100
Average Team
cardinality
# of Runs
RarestFirst
Enhanced Steiner
0
1
2
3
4
5
6
7
8
10 20 30 40 50 60 70 80 90 100
Number of
disconnected teams
# of Runs
RarestFirst
EnahnecdSteiner
KDIR2012-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
256
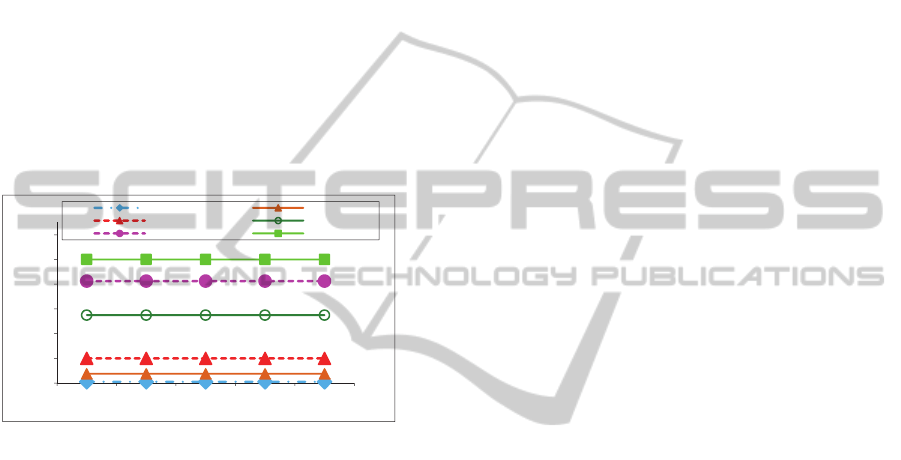
method. First, as we can see in this figure, by
increasing the number of , the running time of our
method remains constant. This is because after
reaching the Nash equilibrium, all of the applicable
teams are always detected regardless of the value of
. Furthermore, since we use local Nash equilibrium
in our method, the time complexity of our method to
discover all of the applicable teams is comparable
with other methods considering that they are
extended to support finding all of the teams instead
of just finding the best team. Second, the average
running time increases when the number of required
skills grows. The main reason is that, here, the
underlying social network’s graph is very sparse
w.r.t the given task. Therefore, to satisfy the task
with low communication cost, when the number of
the required skills increases, the agents have to
explore their neighbourhoods more.
Figure 3: The scalability of GameTeamFormation
algorithm.
Totally, it can be seen that our proposed
framework is capable of forming finer top-k teams
of experts. The analysis of the experiments shows
that our method performs well in the terms of
communication cost, team cardinality of the selected
teams and the number of disconnected teams,
stability and scalability.
5 CONCLUSIONS
In this paper, the problem of finding top-k teams
which can independently accomplish a specific
given task with minimum communication cost is
studied and the game-theoretic framework is
presented for finding these teams.
The experimental results on DBLP show that the
effective teams can be found with minimum
communication cost and cardinality. Also the
stability and scalability of the proposed method is
studied.
For the future works, more constraint teams can
be considered. Furthermore, the generalized tasks
can be studied and defined with the required skills
which should be supported with the minimum
number of experts.
ACKNOWLEDGEMENTS
This work is supported by Iranian Tele-
communication Research Center (ITRC) under
Grant No. T/500/13266.
REFERENCES
Adjeroh, D., Kandaswamy, U, 2007. Game-Theoretic
Analysis of Network Community Structure. Vol.3,
No.4, pp. 313-325, doi:10.5019/j.ijcir.2007.112.
Alvari, H., Hashemi, S., Hamzeh, A, 2011. Detecting
Overlapping Communities in Social Networks by
Game Theory and Equivalence Concept. AICI 2011,
Part II, LNAI 7003, pp.620 - 630, Springer-Verlag.
Baykasoglu, A., Dereli, T., Das, S., 2007. Project Team
Selection Using Fuzzy Optimization Approach.
Presented at Cybernetics and Systems, pp.155-185.
Cheatham, M., Cleereman, K., 2006. Application of Social
Network Analysis to Collaborative Team Formation.
In Proc. of Intl. Symposium on Collaborative
Technologies and Systems, pp.306–311.
Chen, S.-J., Lin, L., 2004. Modeling team member
characteristics for the formation of a multifunctional
team in concurrent engineering. IEEE Transactions on
Engineering Management, pp.111-124.
Gaston, M., Simmons, J., Desjardins, M., 2004. Adapting
Network Structures for Efficient Team Formation. In
Proceedings of the AAAI Fall Symposium on Artificial
Multi-agent Learning.
Lappas, T., Liu, K., Terzi, E., 2009. Finding a Team of
Experts in Social Networks. In Proc. of ACM Intl.
Conference on Knowledge Discovery and Data
Mining (KDD’09), pp.467-476.
Lorrain, F., White, H. C., 1971. Structural equivalence of
individuals in social networks. The Journal of
Mathematical Sociology 1(1): 49–80.
Wi, H., Oh, S., Mun, J., Jung, M., 2009. A Team
Formation Model Based on Knowledge and
Collaboration. Expert Syst. Appl., vol. 36, pp.9121-
9134.
Zakarian, A., Kusiak, A., 2004. Forming Teams: An
Analytical Approach. IIE Transactions, 31:85-97.
0
2
4
6
8
10
12
1..20 20..40 40..60 60..80 80..100
Run Time (hours)
Top-k answers
2 skills 4 skills
6 skills 8 skills
10 skills 12 skills
AGame-TheoreticFrameworktoIdentifyTop-KTeamsinSocialNetworks
257
